1
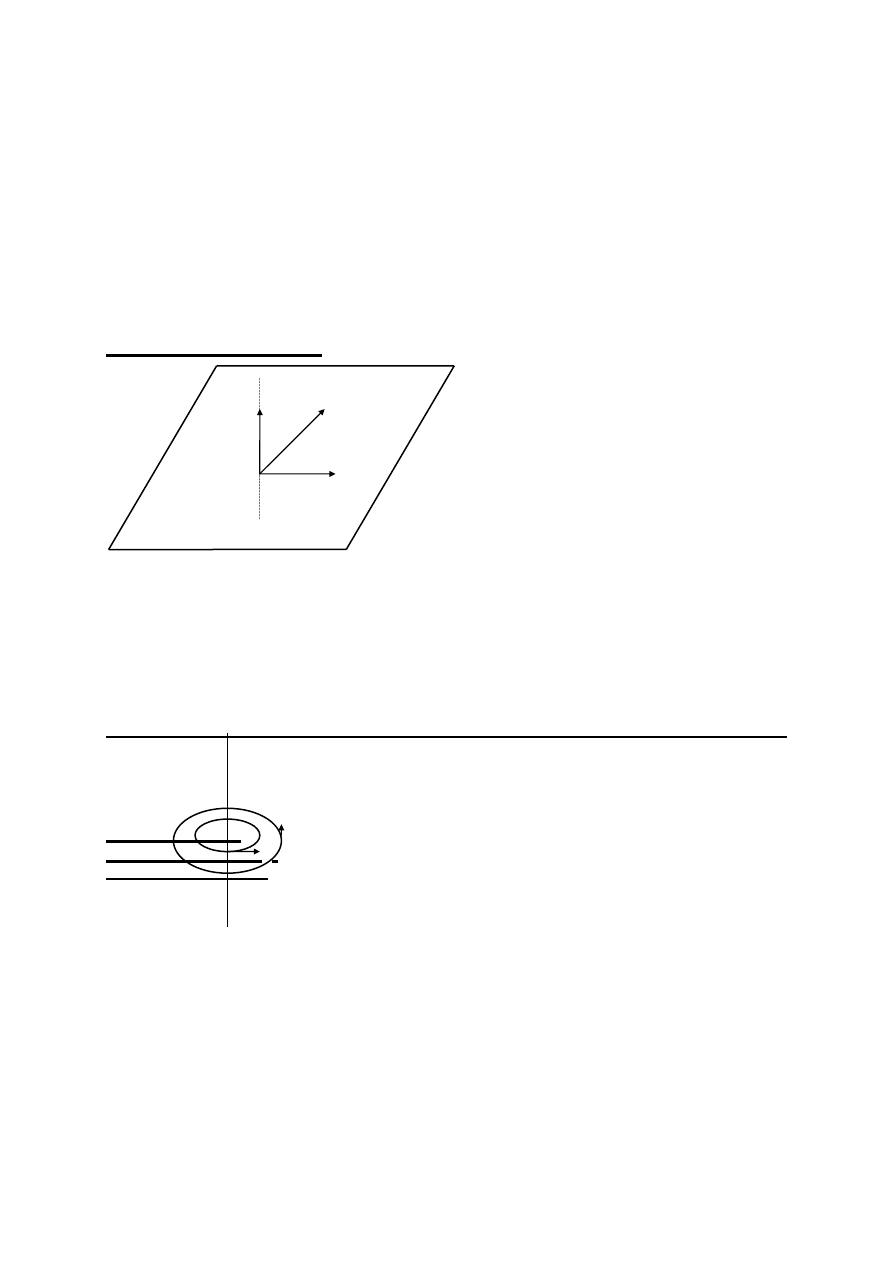
POLE MAGNETYCZNE
to pole w którym na poruszający ładunek magnetyczny działa siła.
jedna z postaci , w jakiej przejawia się pole elektromagnetyczne . Działające
tylko na poruszające się ciała obdarzone ładunkiem elektrycznym oraz na
ciała mające moment magnetyczny ,niezależnie od ich stanu ruchu.
→
→
→
F=q(V
×β
)
F=qVBsin
α
→
→
F
β
V
⊥
B
α
F
max
=qVB
V
B=F
max
/qV [T]=[Ns/Cm]
PRAWO AMPERA - prawo przedstawiające zależność wartości całki okrężnej
wektora natężenia pola magnetycznego od wartości natężeń stałych prądów
elektrycznych płynących przez powierzchnię objętą całką.
I LINIE SIŁ POLA -możemy wyznaczyć
metodą korkociągu lub regułą prawej dłoni.
B
dl
∫∫∫∫Bdl=
µµµµ
o
I
dl - wektor elementarny długości
B - wektor indukcji styczny do lini pola
B∫U=
B
B2
Π
R=
µ
o
I
2
B=
µµµµ
o
I/2
Π
Π
Π
Π
R
µ
o - przenikalność magnetyczna próżni = 4
Π•
10
-7
[Tm/A]
Wykład nr 2 - 27 lutego początek godzina 8
15
wykładowca dr Janicki
PRAWO BIOTA - SAWARTA - prawo określające wielkość i kierunek
wektora indukcji magnetycznej w dowolnym punkcie pola magnetycznego
wytwarzanego przez prąd elektryczny , pozwalające znaleźć rozkład pola
magnetycznego wytworzonego przez dowolny układ przewodników z prądem.
dB=UoI(dl
×
r)/4
Π
r
3
dB
dB=
µ
o
I/4
Π
r
2
2
Π
r 2
Π
r 2
Π
r 2
Π
r
B= ∫dB=∫
µ
o
I/4
Π
r
2
dl =
µ
o
I/4
Π
r
2
∫dl=
µ
o
I/4
Π
r
2
[ l ] =
µ
o
I
•
2
Π
r/4
Π
r
2
=
µ
o
I/2r
0 0 0 0
H=I/2r [A/m.] natężenie pola magnetycznego
→
→
B=
µµµµ
o
••••
H
→
→
B=
µ
r
µ
o
H
µ
r
<
1 ;
µ
r
>
1 ;
µ
r
>>
1
Wartość
µ
r
uzależniona jest od zewnętrznego pola magnetycznego albo od pola
indukcji.
DIAMAGNETYKI-gazy szlachetne , a także cynk,błoto,rtęć,krzem
PARAMAGNETYKI-metale w wysokich temperaturach ,tlenki kobaltu , sole
żelaza .
FERROMAGNETYKI-rudy żelaza.
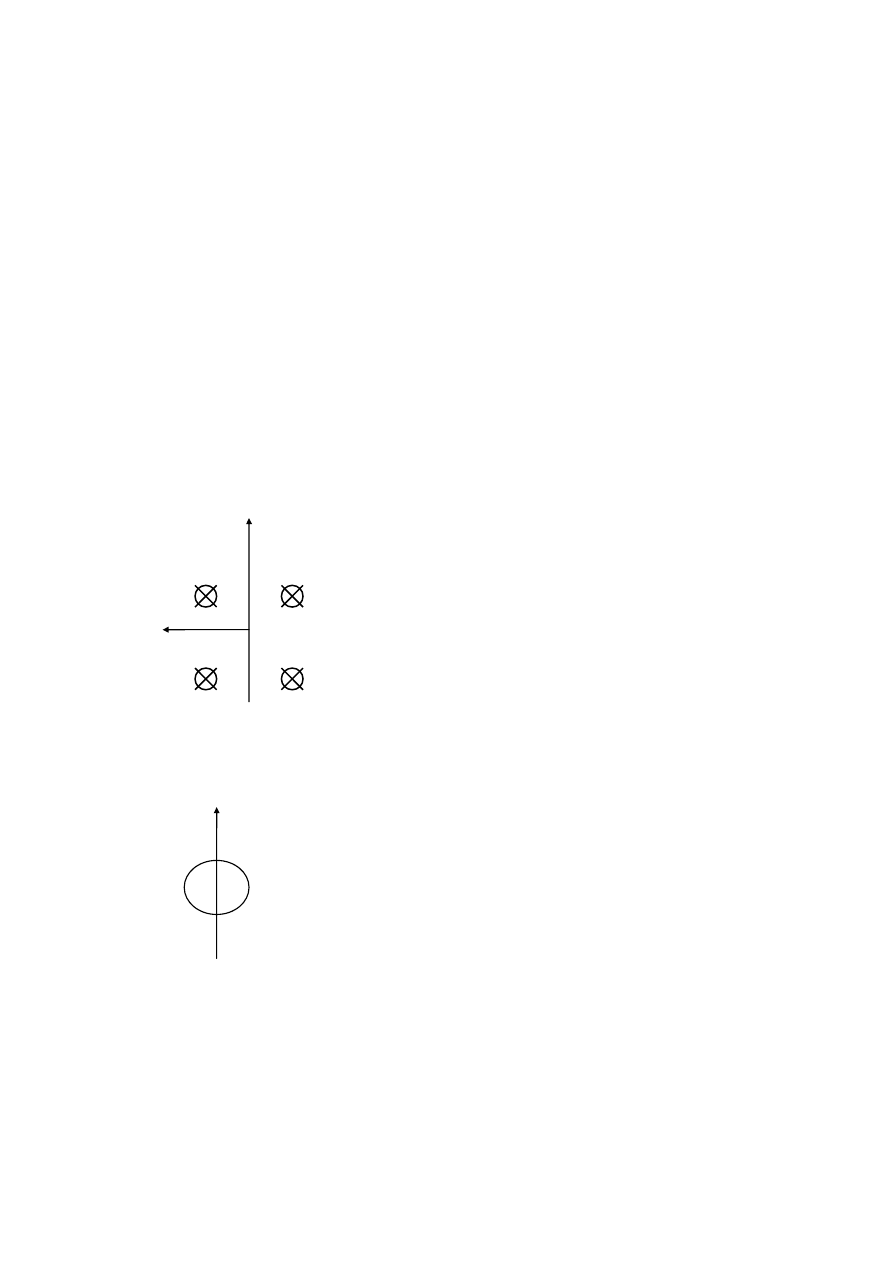
POLE MAGNETYCZNE A PRZEWODNIK PRZEZ , KTÓRY
→
→
→
→
→
→
→
→
→
→
→
→
BIEGNIE PRĄD.
F=q(V
×
B)
PRĄD-to uporządkowany przepływ ładunków elektrycznych w jednostce czasu.
3
NATĘŻENIE PRĄDU ELEKTRYCZNEGO-wielkość skalarna równa
ładunkowi elektrycznemu przepływającemu przez poprzeczny przekrój
przewodnika.
I=dQ/dt
Na przewodnik z prądem znajdujący się w polu magnetycznym działa siła
elektrodynamiczna wyrażona wzorem :
→
→
→
→
→
→
F=I(l
×
B) ; dF=I(dl
×
B)
F jest równoległa do natężenia pola magnetycznego.
REGUŁA LEWEJ DŁONI-linie sił wchodzą do wewnętrznej strony dłoni ,
palce pokazują kierunek prądu.
I
F=IlB sin ( l , B )
F=BIlsin
α
F
F=B I l
l - długość przewodnika
B-indukcja natężenia prądu
I -natężenie
POLE MAGNETYCZNE - to przestrzeń w której na ładunki działa siła
magnetyczna.
I
I
→
B
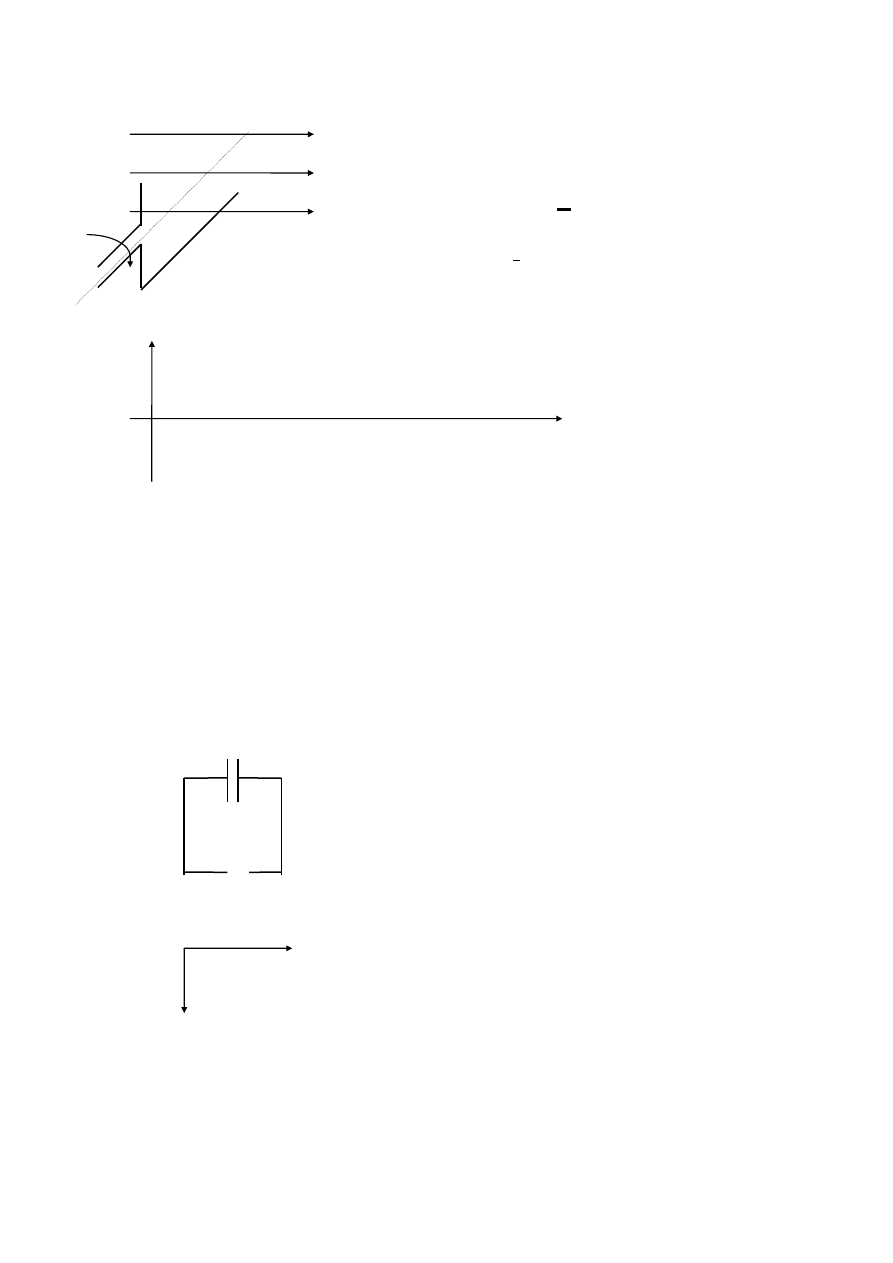
Tworzymy układ złożony z miernika i solenoidu.Do solenoidu będziemy
wsuwali magnez.Gdy będziemy poruszali magnez , miernik będzie się
wychylał.Prąd płynie wtedy gdy będzie się zmieniała ilość linii sił , które
przenikają przez ten zwój.
STRUMIEŃ MAGNETYCZNY-to iloczyn skalarny indukcji magnetycznej i
wektora powierzchni.
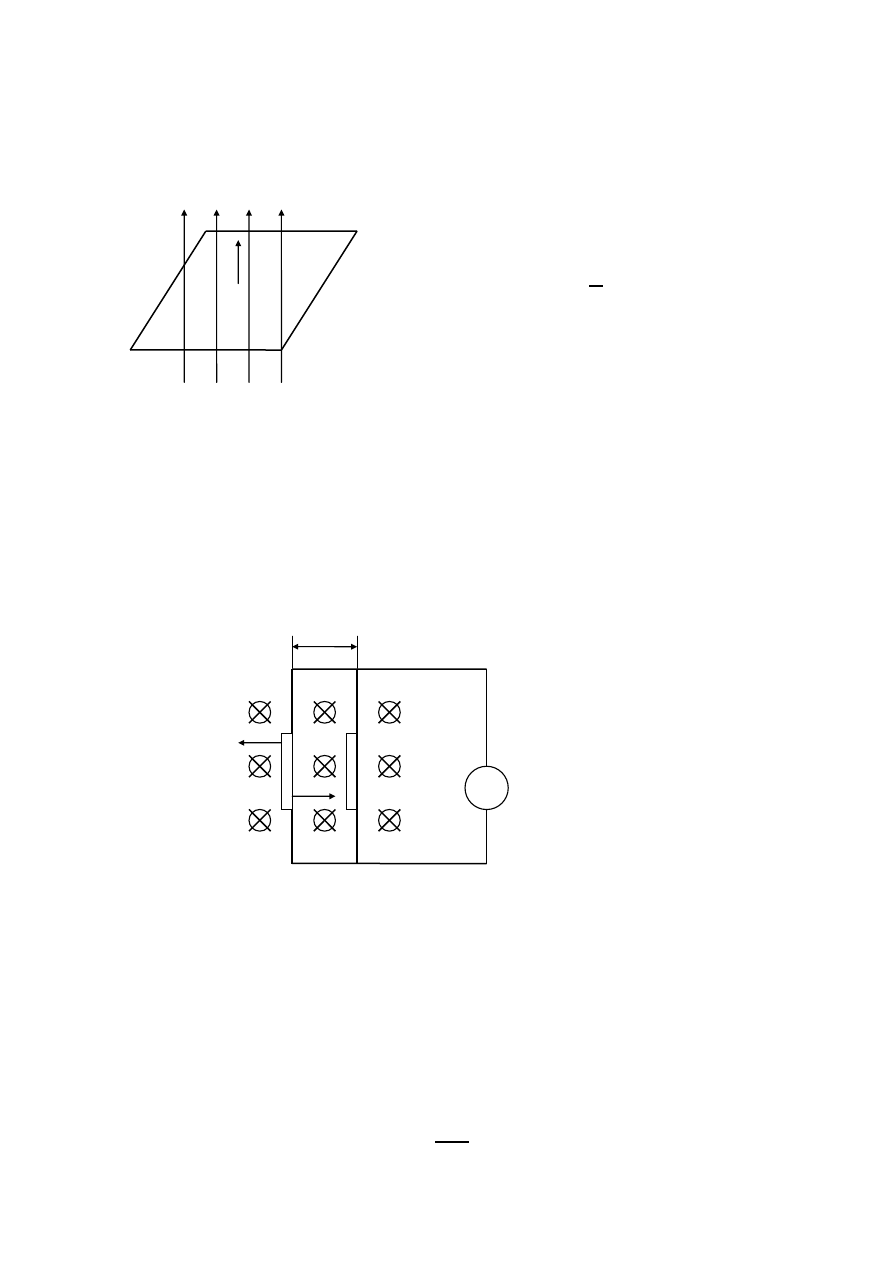
4
Jeśli pole jest jednorodne tzn. Że przez powierzchnię S przepływa taka sama
ilość linii sił ,wartość jest stała.
Φ
=BS
n
Φ
Φ
Φ
Φ
=BScos (B,n) [Wb]=[Tm
2
]
S
Wektory indukcji są prostopadłe do powierzchni.
Jeśli pole nie jest jednorodne:
→
→
d
Φ
=B dS
→
→
Φ
Φ
Φ
Φ
=∫∫∫∫B dS
W polu magnetycznym jednorodnym linie sił są równoległe do siebie a indukcja
ma stałą wartość.
dx
F
F
z
A
Przeciwko sile elektrodynamicznej F przeciwstawia się siłę zewnętrzną Fz .
→
→
→
→
F
z
= -F = -I( l
×
B )
Siła zewnętrzna wykonuje pracę przy przesunięciu tego przewodnika o dx .
dW=F
z
dx = -Fdx
dW= -I B l dx
ds= l dx
dW= -I B ds
dW= -I d
Φ
Φ
Φ
Φ
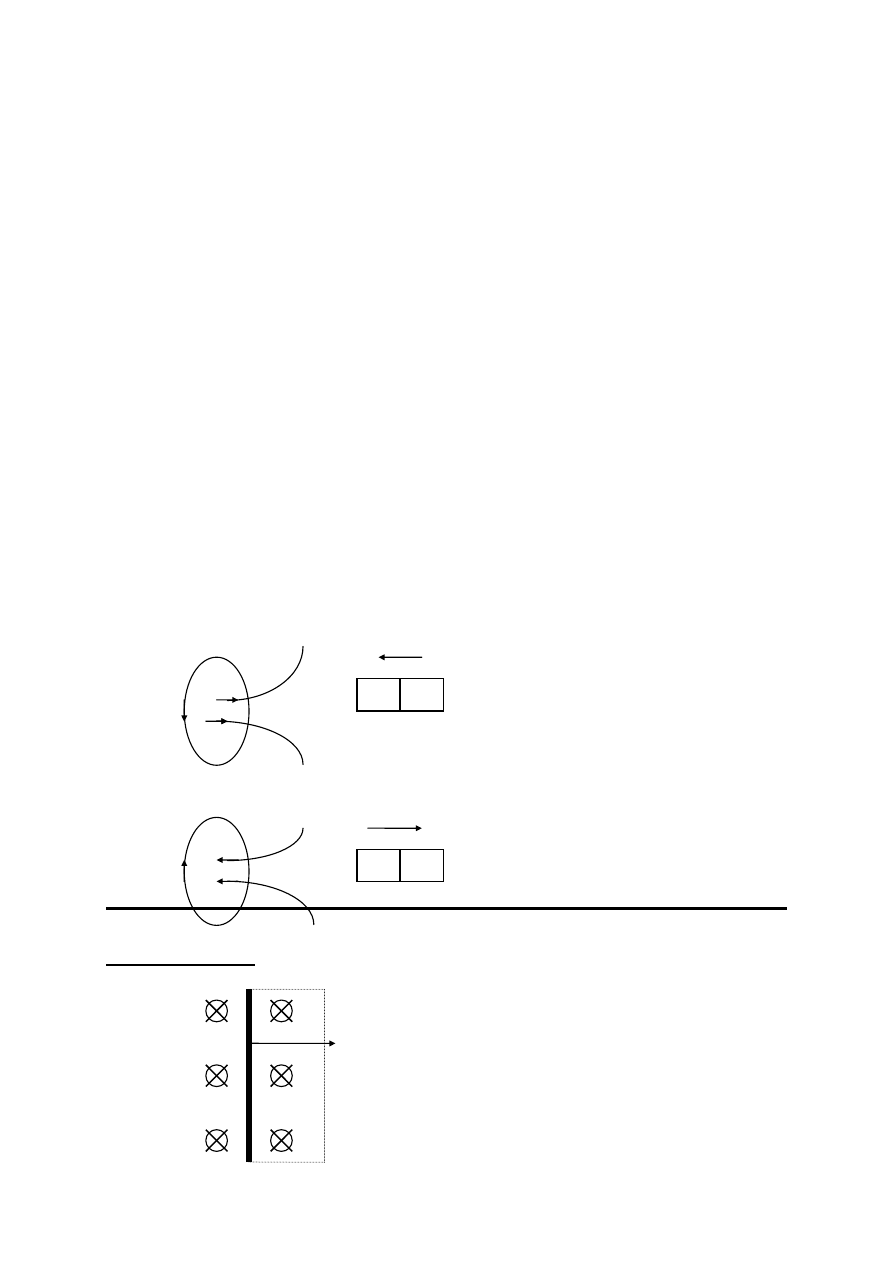
5
Elementarny strumień magnetyczny.
dW= -E
I dt
E I dt = -I d
Φ
E= -d
Φ
Φ
Φ
Φ
/dt
Siła elektromotoryczna indukcji .
d
Φ
/dt - szybkość zmian strumienia magnetycznego
PRAWO INDUKCJI FARADAYA (elektromotorycznej) - indukowana siła
elektromotoryczna jest proporcjonalna do szybkości zmian strumienia
magnetycznego.
REGUŁA PRZEKORY LENCA - kierunek prądu indukowanego jest zawsze
taki że pole magnetyczne przezeń wytworzone przeciwstawia się zmianie
strumienia magnetycznego zewnętrznego.
B
L
↑
→
Φ
→
E
in
→
I
→
B
in
Wykład 3 - 5 marca wykładowca dr Janicki
Wyindukowane pole magnetyczne przeciwdziała zmianom , które go wywołują.
N
N S
I
S
I N S
s E
ind
= d
Φ
/dt = d(Bs)/dt
S = ls
V E
ind
= Bl ds/dt = B l V
l
E
ind
= B l V sin
αααα
6
STRUMIEŃ SKOJARZONY - jest wprost proporcjonalny do przepływającego
w czasie prądu.
N
Φ
= LI
L=N
Φ
Φ
Φ
Φ
/I
[ H ] [henr] Indukcyjność
N dQ/dt = - L dI/dt
E
sin
= - L dI/dt
Siła elektromotoryczna samoindukcji
zależy od szybkości zmian natężenia prądu w cewki
L =
µµµµ
o
N
2
S/l
Indukcyjność cewki (solenoidu)
L =
µµµµ
r
µµµµ
o
N
2
S / l
Indukcyjność cewki z ferromagnetykiem
l - długość solenoidu
U
dW = U dq
+ W = CU
2
/2
-
U = L dI / dt
L dW = (L dI / dt) dq
dW = L dI dq/dt
dW = (L I) dI
dW = ∫ (L I) dI = L ∫ I dI = L I
o
2
/2
dW = L I
o
2
/2
W = L I
o
2
/2
Praca
E
m
= W
E
m
= L I
2
/2
Energia pola magnetycznego
Eind =d
Φ
/dt
7
Φ
= B S
Φ
= B S cos (B,S)
Φ
= B S cos
ω
t
Eind = -B S (-sin
ω
t)
ω
Eind = B S
ω
(sin
ω
t)
Eind = Em sin
ω
t
ω
Prąd zmienia się w sposób sinusoidalny.
I = Im sin
ω
ω
ω
ω
t
U = Um sin
ω
ω
ω
ω
t
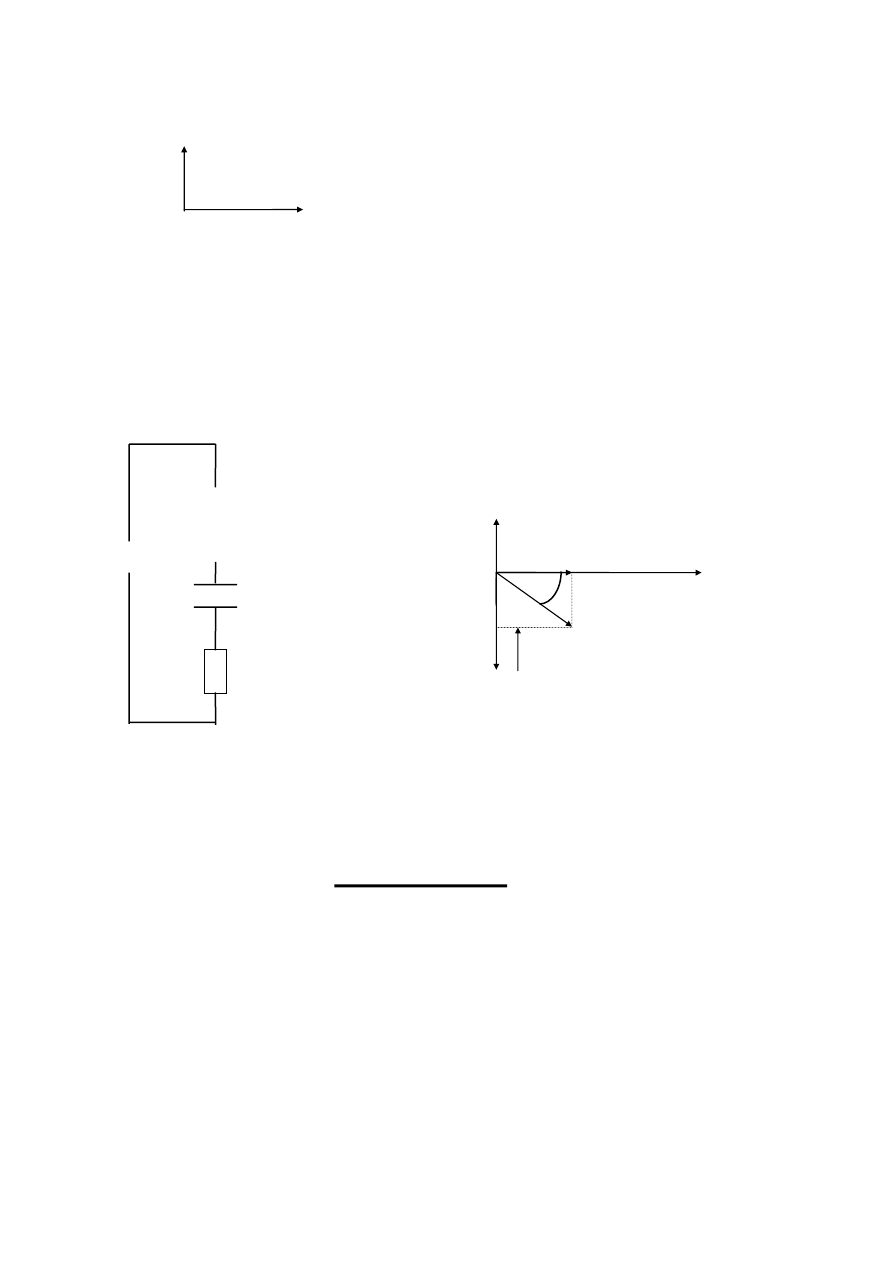
Dla kondensatora
C U = Um sin
ω
t
U = q/C
dU/dt = (1/C) dq/dt I = dq/dt
Um(cos
ω
t) = I/C
I =
ω
CUm (cos
ω
t) Xc = 1/
ω
t
∼
Um/Xc = Im
I = Im(sin
ω
ω
ω
ω
t + 90
o
)
I
Uc
Dla cewki
8
UL.
U = - Eind = L dI/dt
Um sin
ω
t = L dI/dt
1/2 Um sin
ω
t = dI
I I = ∫ 1/L Um sin
ω
t dt
I = (1/L
ω
) (-cos
ω
t)Um
I = (-Um/
ω
L)cos
ω
t
I = (Um/
ω
L)sin(
ω
t-90
0
)
X
L
=
ω
L
I = Im sin (
ω
ω
ω
ω
t-90
o
)
L U
L
+
∼
U
R
_
γ
C
U
U
C
U
L
R
U
2
=(U
C
- U
L
.)
2
+U
R
2
U = I Z
U
R
= I R
U
C
= I X
C
U
L
= I X
L
Z =
√√√√
(X
C
- X
L
)2 + R
2
RÓWNANIA MAXWELLA
→
→
1.
s
∫ E ds = 1/
ε
∑Q Prawo Gaussa dla elektryczności
→
→
2.
L
∫ E dl = 0 Prawo indukcji Faradaya
→
→
3.
s
∫ B ds = 0 Prawo Gaussa dla magnetyzmu
→
→
9
4.
L
∫ B dl =
µ
o
I Prawo Ampere’a
W równaniu (1) zamiast ∑Q można zapisać ∫
ρ
dV
→
→
1’.
s
∫ E ds = 1/
ε
o ∫
ρ
dV
2’.
I
E
ind
= -d
Φ
/dt
→
→
∫ E dl = -dQ/dt
L
→
→
Φ
=
s
∫ B dS
→
→
→
→
∫ E dl = -d/dt
s
∫ B dS
→
→
→
→
→
→
→
→
→
→
→
→
→
→
→
→
L
∫∫∫∫ E dl = -∫∫∫∫ (
δδδδ
B/
δδδδ
t) ds
L
∫ - kontur zamknięty
Zmienne pole magnetyczne wywołuje pole elektryczne.
→
→
3’.
s
∫ B dS = 0
→
→
→
→
4’.
L
∫ B dl =
µ
o
I +
µ
o
ε
o ∫ (
δ
E/
δ
t) dS
Zmienne pole elektryczne wywołuje pole magnetyczne.
Zmiana w czasie wektora pola elektrycznego E spowoduje powstanie wiru
pola magnetycznego lecz powstanie wiru pola magnetycznego stanowi
zmianę w czasie tego wektora więc zmiana wektora B spowoduje
powstanie wiru wektora E.
E Zmienny w czasie strumień elektryczny
•
B E = dE/dt
E
B
10
Wykład 5 -19 marca wykładowca dr Janicki
FALA ELEKTROMAGNETYCZNA
C =
λλλλνννν
prędkość rozchodzenia się wszystkich fal elektromagnetycznych
λ
- długość fali
ν
- częstość
E
x
B
E
x
B
WEKTOR POYNTINGA - sens fizyczny : moduł jest liczbowo równy energii
przenoszonej przez falę elektromagnetyczną w jednostce czasu przez jednostkę
powierzchni prostopadłej do kierunku rozchodzenia się fali.
→
→
→
→
→
→
→
→
→
→
→
→
S = E
××××
H
→
→
B =
µ
o
µ
r
H
MODUŁ WEKTORA POYNTINGA- jest równy liczbowo energii
przenoszonej przez fale energii w jednostce czasu do jednostki powierzchni
prostopadle do kierunku rozchodzenia się fali.
Średnie natężenie fali S
sr
= E
o
H
o
/2
FALE ELEKTROMAGNETYCZNE :
- promieniowanie kosmiczne
- promieniowanie
γ
- promieniowanie rendgenowskie
11
- ultrafiolet
- energia fotonów
- światło widzialne
- podczerwień
- mikrofale
- fale radiowe
Wykład 6 26 marzec 1996 wykładowca dr Janicki.
Siatka dyfrakcyjna:
d
λ
∆
d -stała siatki dyfrakcyjnej (odległość między szczelinami)
∆
- różnica dróg optycznych
ŚWIATŁO MONOCHROMATYCZNE -światło o wyznaczonej długości fali.
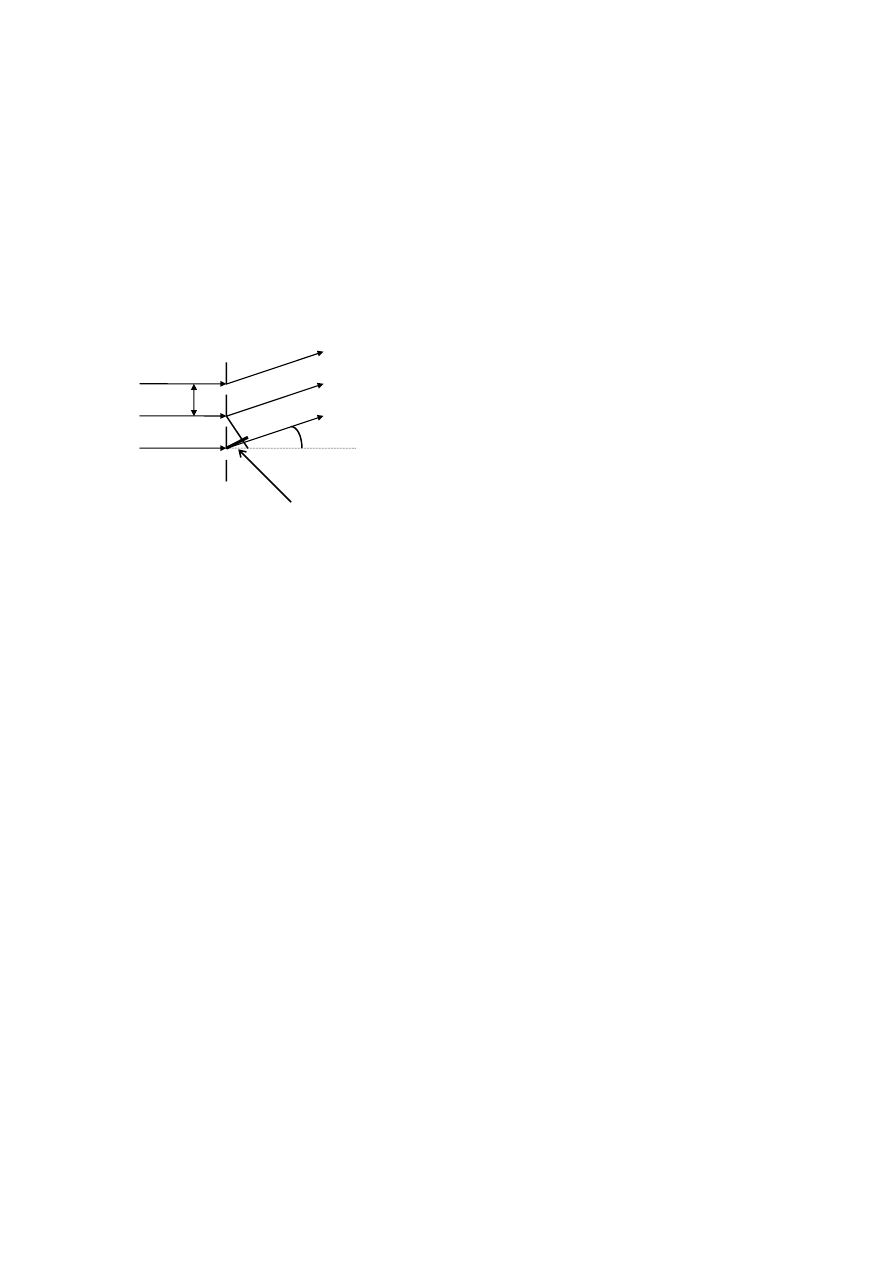
DYFRAKCJA - ugięcie światła , najogólniej mówiąc jeśli na drodze wiązki
świetlnej znajduje się przeszkoda , to dyfrakcja przejawia się uginaniem się
światła przy przejściu obok krawędzi przeszkody.
W wyniku dyfrakcji :
∆
/d = sin
α
∆
= n
λ
n
λλλλ
= d sin
αααα
równanie siatki dyfrakcyjnej
λ
f
= d sin
α
f
λ
c
= d sin
α
c
λ
c
>
λ
f
d sin
α
c
>
d sin
α
Kąty ugięcia promieni czerwonych są
bardziej ugięte niż promieni fioletowych.
Znając kąt
α
można określić długość fali.
Światło jest falą elektromagnetyczną.
Przykładem interferencji światła monochromatycznego są Pierścienie Newtona.
Przyrządem
do
badania
interferencji
fali
jest
INTERFEROMETR
MAICKELSONA.
Hologram to przykład interferencji fal , poprzez padanie dwóch promieni
świetlnych powstaje obraz trójwymiarowy.
12
PROMIENIOWANIE TERMICZNE CIAŁ- to emitowanie energii przez
ciała w postaci fal elektromagnetycznych , ma długości większe niż światło
widzialne , leży w zakresie podczerwieni.
ZDOLNOŚĆ EMISYJNA - to energia promieniowania wysyłanego w
jednostce czasu z jednostki powierzchni pozostającej w temperaturze T , w
postaci fal elektromagnetycznych o częstościach zawartych w przedziale (
ν
,
ν
+d
ν
).
e(
νννν
, T ) d
νννν
ν
- częstotliwość
e - zdolność emisyjna
ZDOLNOŚĆ
ABSORPCYJNA-
określa
jaka
część
energii
fali
elektromagnetycznej o częstościach zawartych w przedziale (
ν
,
ν
+d
ν
)
padających na jednostkę powierzchni ciała zostaje przez nie pochłonięta.
a(
νννν
, T )
a - zdolność absorpcyjna
CIAŁO DOSKONALE CZARNE- ciało pochłaniające całkowicie padające
nań promieniowanie świetlne , niezależnie od długości fali , stanowi doskonałe
źródło promieniowania , tzn. w danej temperaturze promieniuje największą
możliwą ilością energii , widmo promieniowania ciała doskonale czarnego jest
ciągłe , przy czym w miarą wzrostu temperatury ciała maksimum natężenia jego
promieniowania przesuwa się w kierunku fal krótkich.
e(
νννν
,T )/a(
νννν
,T ) =
εεεε
(
νννν
,T )
zdolność emisyjna ciała doskonale czarnego
Wykład 7 wykładowca dr Janicki
PRAWO PROMIENIOWANIA KIRCHOFFA- prawo zrównoważonego
promieniowania temperaturowego głoszące , że stosunek zdolności emisyjnej
ciała do jego zdolności absorpcyjnej nie zależy od rodzaju ciała i jest równy
zdolności emisyjnej ciała doskonale czarnego.
εεεε
(
νννν
,T ) = (2
Π
Π
Π
Πνννν
2
/C
2
) U(
νννν
,T )
U-uśredniona w czasie energia
U = kT
εεεε
(
νννν
,T ) = (2
Π
Π
Π
Πνννν
2
/C
2
) kT
13
zdolność emisyjna jest funkcją kwadratową częstotliwości
PRAWO WIENA- iloczyn częstotliwości maksymalnej razy pewna stała da
nam temperaturę.
νννν
max
const. = T
PRAWO BOLTZMANA STEFANA - prawo wyrażające zależność całkowitej
zdolności emisyjnej E ciała doskonale czarnego od jego temperatury
bezwzględnej.
E =
σσσσ
T
4
STAŁA BOLTZMANA
σσσσ
= 5,6 10
-8
W/m
2
K
4
Max Planck powiedział że energia może się zmieniać porcjami.
PRAWO PLANCKA - prawo rozkładu energii w widmie promieniowania ciała
doskonale czarnego
E
n
= nh
νννν
E = n
εεεε
o
energia najmniejszego kwantu
U(
ν
,T ) =
ε
o
/ (e
ε
o/kT
-1)
E (
νννν
,T ) = (2
Π
Π
Π
Πνννν
2
/C
2
)(h
νννν
/e
h
νννν
/kT
-1)
∞
E = ∫∫∫∫
εεεε
(
νννν
,T ) d
νννν
o
STAŁA PLANCKA
h = 6,62 10
-34
J/s
Dla każdego metalu istnieje graniczna częstotliwość gdzie zaczyna się zjawisko
fotoelektryczne.
Energia elektronu zależy od częstotliwości światła.
Ilość wybijanych elektronów ( prąd anodowy ) zależy od natężenia padającego
światła.
Każdy foton posiada energię którą możemy określić wzorem:
Ef = h
νννν
h
ν
= W + E
k
W - praca wyjścia
h
ν
o
= W
Ek = eU
n
14
PRACA WYJŚCIA
- to energia którą musimy dostarczyć aby elektron opuścił metal.
- to energia jaką musimy dostarczyć do elektronu aby przenieść go z
poziomu
Ferniego do nieskończoności.
POZIOM FERNIEGO -najwyżej położony poziom.
Każdy foton posiada pęd
p = mV
Fotony nie posiadają masy spoczynkowej więc energię fotonu wiążemy z masą:
E
f
= h
ν
E = mC
2
w ten sposób fotonowi przypisujemy masę
p
f
= mC
m. = E
f
/C
2
p = mC = ( E
f
/C
2
) C = h
ν
/C
p = h
ν
/C
ν
= C/
λ
p
f
= h/
λλλλ
pêd fotonu
Światło padające na powierzchnię wywiera odpowiednie ciśnienie , które jest
mierzalne.
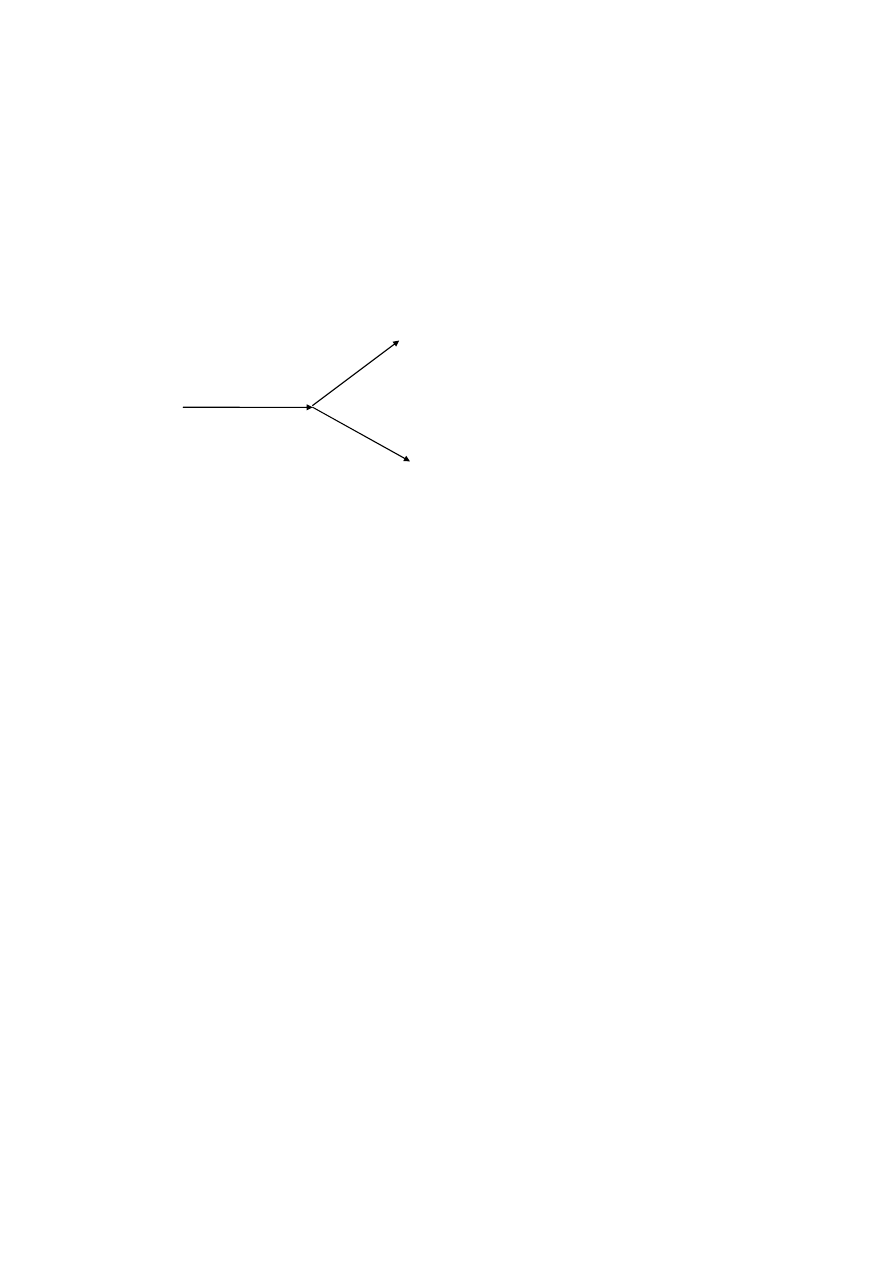
ZJAWISKO COMPTONA - rozpraszanie promienia elektromagnetycznego
(głównie rendgenowskiego ) na swobodnych elektronach , polega na tym że w
wyniku zderzenia pojedynczego fotonu z elektronem , część energii fotonu
zostaje przekazana elektronowi , co powoduje zwiększenie się długości fali
rozproszonego promieniowania i odrzucenie elektronu. Zjawisko Comptona jest
jednym ze zjawisk świadczących o nieciągłej strukturze promieniowania.
Ek
λ
elektron
λ
h
ν
o
Wpadający foton ma energię h
ν
,a elektron posiada E
k
ZASADA ZACHOWANIA ENERGII
15
h
νννν
o
= h
νννν
’ + ( m - m
o
)C
2
( m - m
o
)C
2
- energia kinetyczna elektronu ( gdy prędkości są porównywalne z
prędkością światła
ZASADA ZACHOWANIA PĘDU
p
p
= p
f
+ p
e
p
p
- pęd początkowy
p
e
p
p
= h/
λ
o
p
f
= h/
λ
’
p
p
p
f
∆∆∆∆λλλλ
=
λλλλ
’ -
λλλλ
o
= h/m
o
C ( 1 - cos
θθθθ
)
DUALIZM FALOWO KORPUSKULARNY - właściwość materii polegająca
na tym , że w pewnych zjawiskach ujawnia się natura falowa (interferencja ,
dyfrakcja) , w innych korpuskularna (efekt Comptona).
ATOM WODORU -
STAŁA RYTBERGA R = 1,097 10
7
1/m
1/
λλλλ
= R( (1/K
2
)-(1/n
2
))
k,n - kolejne liczby naturalne
n
>
k
jeśli k = 1 Seria Lymana
jeśli k = 2 Seria
jeśli k = 3 Seria Paschena
MODEL BOHRA - elektrony mogą zmieniać się na określonych orbitach
stacjonarnych dla których model pędu elektronu jest wartością stałej Plancka
podzielonej przez 2
Π
.
PIERWSZY POSTULAT BOHRA - atom nie promieniuje energii , jeżeli atom
porusza się po orbicie , na której jego kręt jest całkowitą wielokrotnością h/2
Π
(są to tzw. orbity dozwolone , stacjonarne)
mVr = nh/2
Π
Π
Π
Π
ћ = h/2
Π
ћ - h kreślne
16
Wykład 8 23 kwietnia wykładowca dr Janicki.
DRUGI POSTULAT BOHRA - jeśli elektron przechodzi z niższej powłoki na
wyższą to foton otrzymuje energię.
E
n
- E
m
= h
νννν
E
n
>
E
m
emisja fotonu
E
n
<
E
m
pochłanianie fotonu
K L M
+
k(e
2
/r
n
2
) = mV
2
/r
n
r
n
k(e
2
/2r
n
) = mV
2
/2
E
k
= mV
2
/2
E = E
k
+ E
p
E
p
= -ke
2
/r
n
Ek = ke
2
/2r
n
E = ke
2
/2r
n
- ke
2
/r
n
E = -ke
2
/2r
n
Wykład 23 kwiecień , wykładowca dr Janicki.
Uzależnienie energii od numeru orbity.
mVr = nђ
V = nђ / mr
m/2 = n
2
ђ
2
/m
2
r
2
= ke
2
/2r
r = n
2
ђ
2
/mke
2
r
n
= ђ
2
/mke
2
· n
2
PROMIEŃ KOLEJNEJ ORBITY
n - numer kolejnej orbity
k = 1/ 4
Πε
o
r
o
= ђ
2
/mke
2
PROMIEŃ BOHRA ATOMU WODORU
dla n = 1 wynosi r = 5,28 · 10
-11
m
En = -k
2
e
4
m/2ђ
2
· 1/n
2
ENERGIA W ZALEŻNOŚCI OD NUMERU ORBITY n .
E
o
= 13,6 eV
energia stanu podstawowego w atomie wodoru.
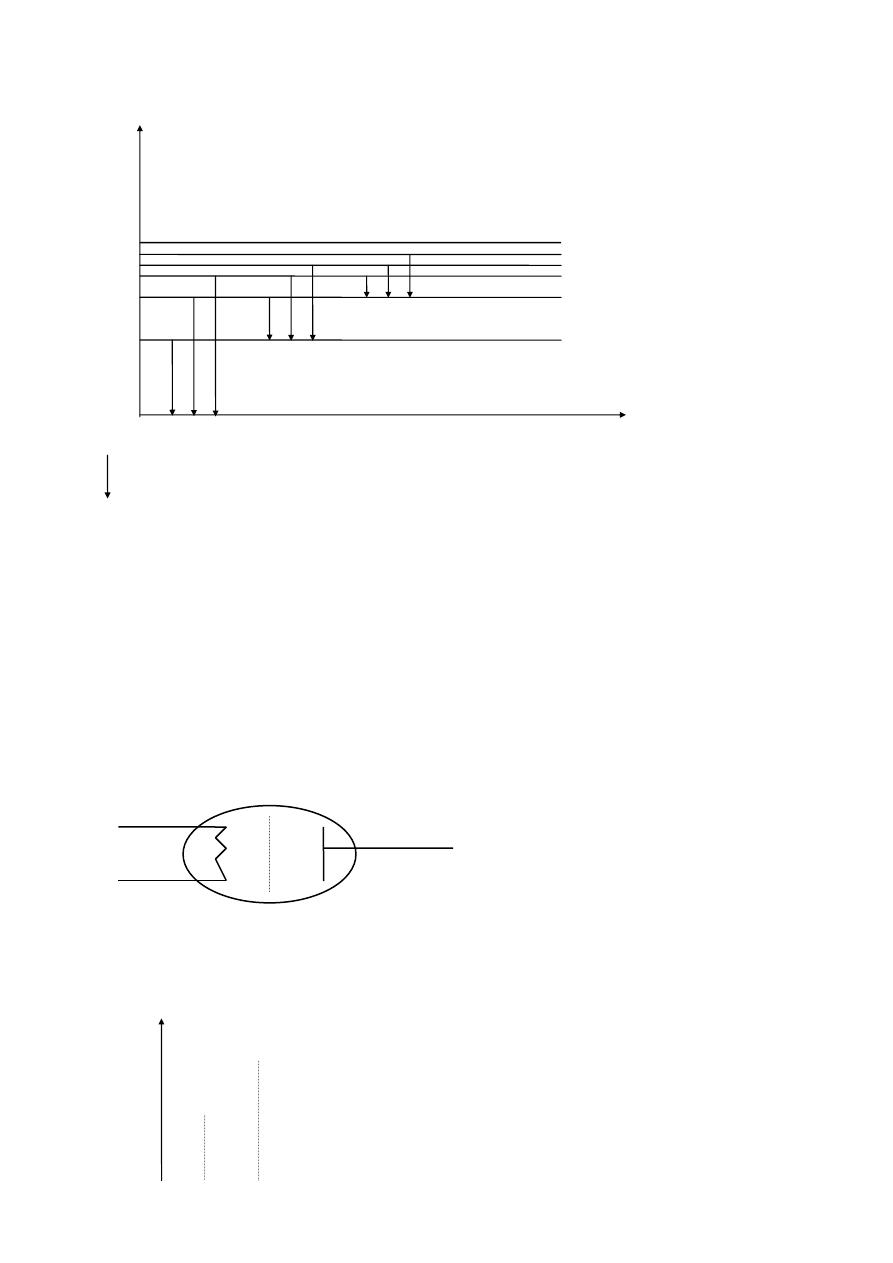
17
E [eV]
0
n=
∞
-1,5
seria Paschena n=3
seria Balmera
-3,4
n=2
seria Lymana
-13,6
n=1
- Drugi Postulat Bohra graficznie
h
ν
= E
2
- E
1
= 10,2 eV przejście z drugiej orbity na pierwszą daje nam foton
o energii równej 10,2 eV
- natomiast przejście z nieskończoności na pierwszą orbitę daje foton o
energii 13,6 eV
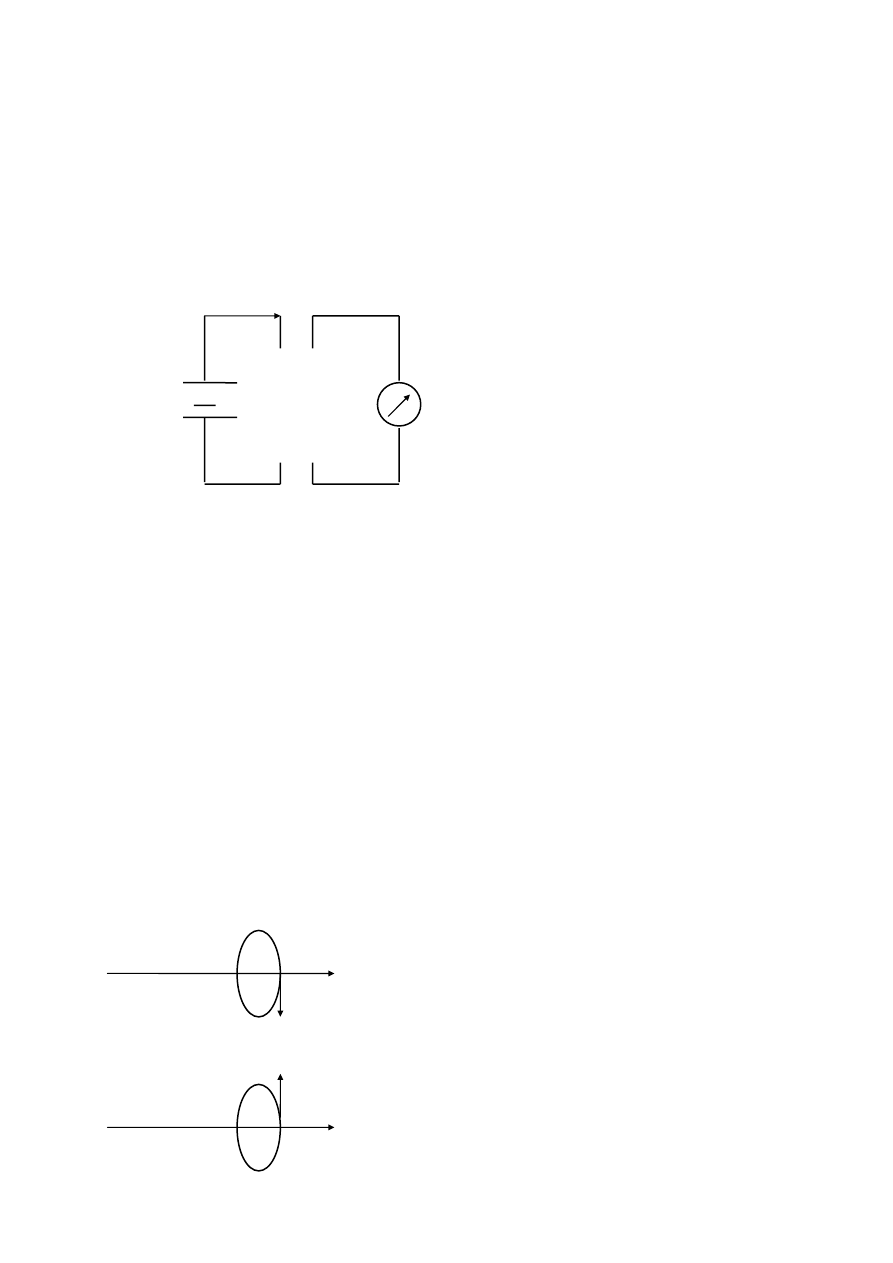
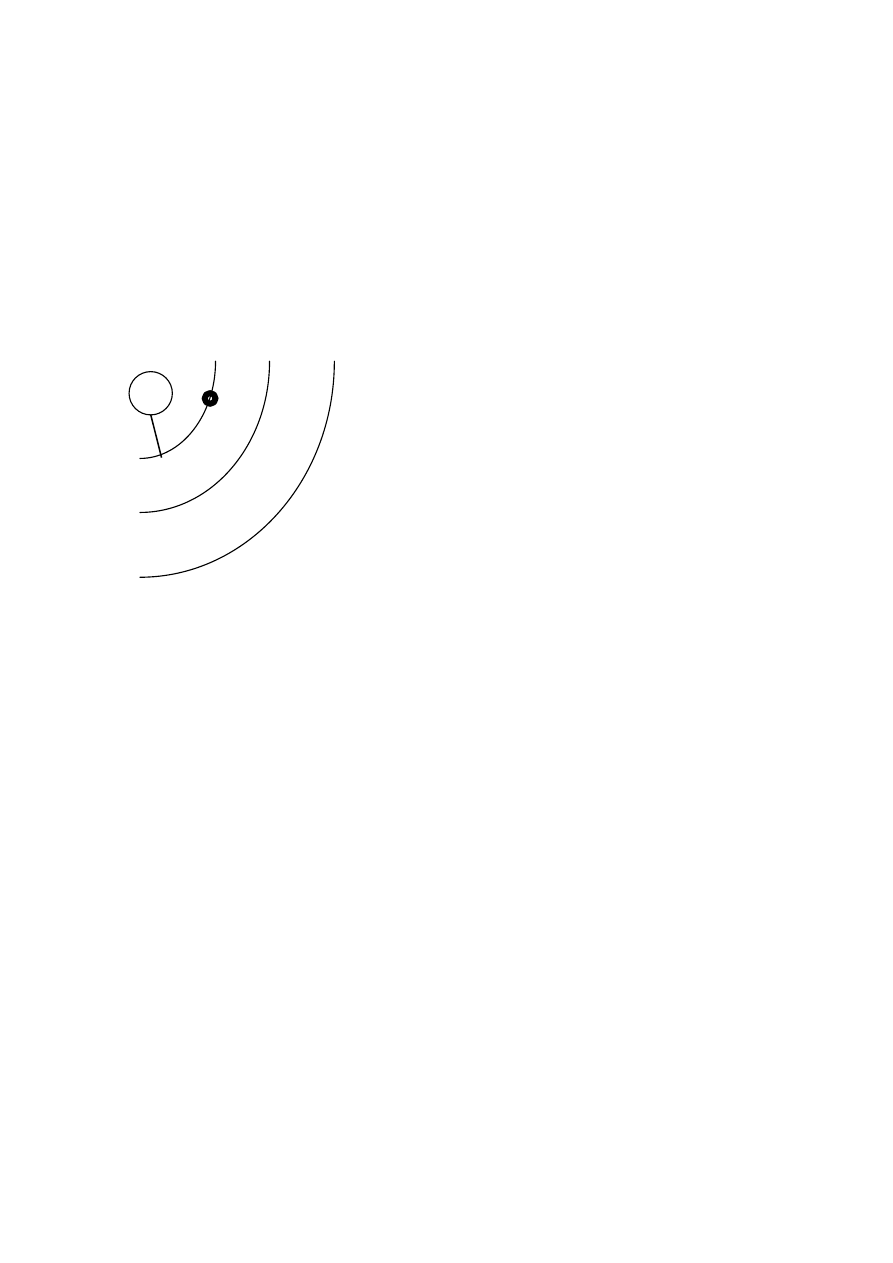
Doświadczenie FRANCKA HERTZ’A
katoda siatka anoda Lampa wypełniona oparami
rtęci przy bardzo małym
ciśnieniu.
- do katody przyłożony był potencjał ujemny
I
o
18
Us
4,81 9,62
Spadek prądu anodowego zaobserwujemy przy 4,81 a następnie przy krotności
tej wartości.
Przyspieszone elektrony tylko przy odpowiednich energiach zderzają się
sprężyście z atomami rtęci i wtedy elektrony nie docierają do anody i wówczas
obserwujemy duży spadek napięcia.
WNIOSEK Z DOŚWIADCZENIA :
Tylko pewne wartości energii są dozwolone dla każdego atomu.
WIDMO ABSORPCYJNE - to widmo optyczne odpowiadające rozłożeniu
światła po przejściu przez daną substancję .
WSTĘP DO MECHANIKI KWANTOWEJ
HIPOTEZA de BROGLI’A - mówi ze dualizm falowo-korpuskularny wykryty
w związku z badaniem natury światła , jest właściwy także innym cząstkom
materii. Między pędem p cząstki i długością
λ
fal de Broglie zachodzi związek
λ
=h/p. Natężenie fal de Broglie w danym punkcie przestrzeni jest wprost
proporcjonalne do gęstości prawdopodobieństwa znalezienia cząstki w tym
punkcie.
Bezpośrednim potwierdzeniem hipotezy de Broglie’a byl wynik Davissona i
Germera , którzy zaobserwowali ugięcie wiązki elektronów przez monokryształ.
Od tego czasu przebadano szczegółowo własności różnych cząstek
elementarnych oraz atomów i nie znaleziono żadnych odstępstw od fal de
Broglie,a.
FUNKCJA FALOWA - nie ma żadnego sensu fizycznego.
- to opis matematyczny.
Ψ
(x,y,z,y)
KWADRAT AMPLITUDY FUNKCJI FALOWEJ
ΨΨ
* =
Ψ
(X,Y,Z,T)
2
określa prawdopodobieństwo znalezienia cząstki w chwili t w punkcie (x,y,z)
SUPERPOZYCJA FUNKCJI FALOWEJ
Ψ
=
Ψ
1
+
Ψ
2
GĘSTOŚĆ PRAWDOPODOBIEŃSTWA d
ω
d
ω
=
Ψ
2
dV - określa nam że cząstka znajduje się w elemencie objętości dV
∫∫∫
Ψ
2
dV = 1
Wykład 9 30 kwietnia 1996 wykładowca dr Janicki.
19
Funkcja falowa nie może być falą płaską.
Ψ
= Ae
i(kx-
ω
t)
Ψ
= A sin (
ω
t-kx) + i B cos(
ω
t-kx)
PACZKĘ FAL - otrzymujemy poprzez nałożenie funkcji sinusoidalnej o
niewielkiej częstotliwości.
- „reprezentuje” cząstkę
ZASADA NIEOZNACZONOŚCI HEISENBERGA - jeżeli cząstka jest
zlokalizowana w przestrzeni z odchyleniem standartowym
∆
x to nie ma
określonego pędu lecz pewien rozkład pędów.
-im dokładniej określamy położenie cząstki tym z mniejszą dokładnością
określamy pęd cząstki.
-z fizycznego punktu widzenia niemożliwe jest jednoczesne dokładne określenie
położenia i pędu cząstki.
∆
x
∆
p
x
≥
ђ
∆
y
∆
p
y
≥
ђ
∆
z
∆
p
z
≥
ђ
∆
x -nieoznaczoność położenia
∆
p
x
- nieoznaczoność pędu
∆∆∆∆
E
∆∆∆∆
t
≥≥≥≥
ђ
- nieoznaczoność energii w czasie
RÓWNANIE SCHRÖDINGERA
ђ/T
δδδδΨ
Ψ
Ψ
Ψ
/
δδδδ
T = -ђ
2
/2m.
∆∆∆∆Ψ
Ψ
Ψ
Ψ
+ U(x,y,z,t)
Ψ
Ψ
Ψ
Ψ
∆
=
δ
2
/
δ
x
2
+
δ
2
/
δ
y
2
+
δ
2
/
δ
z
2
Równanie zależy od czasu i od współrzędnych
UPROSZCZONE RÓWNANIE SCHRÖDINGERA
d
2
Ψ
Ψ
Ψ
Ψ
/dx
2
= -2m/ђ
2
[E - U(x)]
Ψ
Ψ
Ψ
Ψ
Vg = d
ω
/dk
E = h
ν
= h2
Πν
/2
Π
= ђ
ω
ω
ω
ω
k = 2
Π
/
λ
p = h/
λ
= h2
Π
/2
Πλ
= ђk
E = p
2
/2m.
ђ
ω
= (ђ k)
2
/2m.
ђ d
ω
/dk =ђ
2
2k/2m.
d
ω
/dk = ђk/m.
ђk = p
Vg = d
ω
ω
ω
ω
/dk = p/m. = V
Prędkość grupowa paczki fal jest równa prędkości poruszającej się cząstki.
CZĄSTKA STUDNI POTENCJAŁÓW .
20
U U=
∞
o L
x
Na odcinku oL może się mieścić całkowita połówka długości fali.
D2y/dx2 = -ђ
2
E
Ψ
/2m.
Ψ
= A
ikx
+B
-ikx
Ψ
(o) =
Ψ
(L) = 0 -warunki brzegowe
Ψ
(x) =C sin kx
Ψ
(L) = C sin kL = 0
k L = n
Π
k
n
= n
Π
/L
więc funkcja falowa przyjmuje postać :
Ψ
Ψ
Ψ
Ψ
(x) = C sin (n
Π
Π
Π
Π
x/L)
Ψ
o L x
Amplituda zawsze taka sama.
L = n(
λ
/2)
p
n
= ђkn = ђn
Π
/L
p
n
= ђ
Π
n/L
E = p
2
/2m.
En = ђ
2
Π
Π
Π
Π
2
n
2
/L
2
2m
21
dla n = 1 En = ђ
2
Π
2
/L
2
2m
L = 10
-10
m. E
1
= 37,2 eV
dla n = 2 E
2
= 37,3
•
2
2
= 149,2 eV
dla n = 3 E
3
= 335,7 eV
Są to pewne dopuszczalne wartości energii.
E E E
3
E
2
E
1
p. p.
„
n
” - główna liczba kwantowa , określa dozwolone wartości energii.
RÓŻNICE MIĘDZY OSCYLATOREM KWANTOWO-MECHANICZNYM A
OSCYLATOREMREM KLASYCZNYM.
Oscylator klasyczny:
U(x) = kx
2
/2 = m
ω
kl
2
x
2
/2
E
x
E
n
= (n - 1/2)ђ
ω
oscylator kwantowo-mechaniczny
d
2
Ψ
/dx
2
= -2m/ђ
2
[E - U(x)]
Ψ
d
2
Ψ
/dx
2
= -2m/ђ
2
[E -
ω
kl
2
x
2
/2m.]
Ψ
Ψ
(x) = e
-ax2
d
Ψ
/dt = (-2ax)e
-ax2
d
2
Ψ
/dt
2
= -2a e
-ax2
+ (-2ax)(-2ax)e
-ax2
d
2
Ψ
/dt
2
= -2a e
-ax2
+ 4a
2
x
2
e
-ax2
-2a e
-ax2
+ 4a
2
x
2
e
-ax2
= -2m/ђ
2
[E -
ω
2
x
2
/2m.]
-2a + 4a
2
x
2
= [-2m.E/ђ
2
+ 2m
2
ω
2
x
2
/ђ
2
]
-2a +4a
2
x
2
= 2m. E/ђ
2
+ m
2
ω
2
x
2
/ђ
2
-2a =-2m E/ђ
2
ha
2
= m
2
ω
2
/ђ
2
22
Wykład 10 14 maja 1996 wykładowca dr Janicki.
4a
2
= m
2
ω
kl
2
/ђ
2
-2a = -2m. E/ђ
2
a = m
ω
kl
/2ђ
E = aђ
2
/m.
E
= m
ω
kl
ђ
2
/2ђm =
ω
ω
ω
ω
kl
ђ/2
E
n
= (n - 1/2) ђ
ω
Ψ
1
(x) =e
-ax2
E = ђ
ω
/2
Ψ
1
(x) = exp (-m
ω
n
x
2
/2h)
Ψ
2
= xe
-ax2
E
2
= 3ђ
ω
/2
E
n
= (n - 1/2)h
ω
E
3/2 ђ
ω
1/2 ђ
ω
Ψ
1
x
23
Ψ
2
x
ATOM WODORU W UJĘCIU KWANTOWO-MECHANICZNYM.
(x,y,z) współrzędne kartezjańskie zmienione są na współrzędne kuliste (
Γ
,
θ
,
ϕ
)
z
p
r
θ
y
ϕ
x p’
r sin
θ
x = r sin
θ
cos
ϕ
y = r sin
θ
sin
ϕ
z = r cos
θ
RÓWNANIE SCHRÖDINGERA
δδδδ
2
Ψ
Ψ
Ψ
Ψ
/d
δδδδ
2
+
δδδδ
2
Ψ
Ψ
Ψ
Ψ
/
δδδδ
y
2
+
δδδδ
2
Ψ
Ψ
Ψ
Ψ
/
δδδδ
z
2
= -2m.(E-U)
Ψ
Ψ
Ψ
Ψ
/ђ
2
1/r
2
⋅
δ
/
δ
r
⋅
(
δΨ
/
δ
r) + 1/r
2
sin
θ
δ
θ
⋅
(sin
θ
⋅δΨ
/
δθ
) + 1/r
2
sin
2
ϕ
⋅δ
2
Ψ
/
δϕ
2
=
= -2m/ ђ
2
⋅
(E-U)
Ψ
24
ograniczamy się tylko do rozwiązania zależności energi od odległości jednej
cząstki od drugiej
U = -ke
2
/r
Ψ
= e
r/a
1/r
2
⋅
δ
/
δ
r
⋅
r
2
⋅δ
/
δ
r
⋅
e
-r/a
= 1/r
2
⋅
δ
/
δ
r
r
2
e
-r/a
(-1/a)
=1/r
2
(-2r/a e
-r/a
+
+(-r
2
/a)e
-r/a
(-1/a) = 2r/ar
2
e-r/a + r2/ra
2
e
-r/a
= (-2/a 1/r +1/a
2
)e
-r/a
(-2/a 1/r +1/a
2
)e
-r/a
= (-2mE/ђ
2
- 2mke
2
/ђ
2
1/r)e
-r/a
warunki jakie muszą być spełnione :
-2/a + -2mke
2
/ђ
2
1/a
2
= -2mE/ђ
2
a = ђ
2
/mke
2
= 5,29 · 10
-11
m. E = ђ
2
/2ma
2
promień dla atomu wodoru
a podstawiamy do wzoru na E
E = -ђ
2
/2m.(ђ
4
/m
2
k
2
e
4
) = -mk
2
e
4
/2ђ
E = -mk
2
e
4
/2ђ
2
= -13,6 eV energia dla atomu wodoru
Ψ
1
= e
-r/a
Jest to fala stojąca najniższego rzędu i nie ma węzłów
Ψ
2
= (1 - r/2a)e
-r/2a
E
2
= -mk
2
e
4
/8ђ
2
Ψ
3
= (1 - 2r/3a - 2r
2
/27a
2
)e
-r/3a
E
3
= -mk
2
e
4
/18ђ
2
E
n
= -mk
2
e
4
/n2ђ
2
· 1/n
2
Ψ
1
Ψ
Ψ
Ψ
Ψ
(r,
θθθθ
,
ϕϕϕϕ
)
1 2 3
10
-10
m
Ψ
2
Ψ
3
25
→
→
→
L = r
×
p
L
z
= r
⋅
p
p. = ђ
⋅
k
L
z
= r
⋅
ђ
⋅
k
k
⋅
r całkowita liczba
L
z
= m
L
⋅
ђ
L
z
= 0
L
, +/- ђ , +/- 2ђ , +/- 3ђ ......
m
L
≤
l
Lz =
√√√√
l(l+1) ђ
całkowity moment pędu
„ l ” - orbitalna liczba kwantowa (może przyjmować wartości 0,1,2,3, ... , n-1
„ m
L
” - magnetyczna liczba kwantowa
Wykład 11 , 21 maja 1996 , wykładowca dr Janicki.
m
L
- rzut momentu pędu na wybrany kierunek , wymuszony najczęściej polem
magnetycznym
Lz = m
L
⋅
ђ
Z
2ђ m.=2
ђ m.=1
m
L
=0
- ђ
- 2ђ
Jeśli chcemy określić kąt
θ
to cos
θ
= L
z
/L = mL
⋅
ђ/
√
l(l+1)
m
L
= +/- l
„ m
s
” - spinowa liczba kwantowa , związana z ruchem obrotowym wokół osi
elektronu
L
s
= ђ
⋅⋅⋅⋅√√√√
s(s+1)
s - przyjmuje zawsze wartość 1/2
L
sz
= m
⋅
s
⋅
ђ
26
Z
ђ/2 Ls
m
s
= 1/2 m
s
= -1/2
- ђ/2
ZASADA PAULINIEGO - w atomie nie mogą istnieć 2 elektrony o
identycznych wszystkich liczbach kwantowych.
n = 2 s p d e
l = 0 , 1 L = 0 , 1 , 2 , 3
m
L
= -1 , 0 , 1
m
s
= -1/2 , 1/2
jeśli n = 1 to l = 0 i jest to stan 1s
jeśli n = 2 l = 0 i jest to stan 2s
2
2p
6
Ψ
n,l,ml
(r,
θ
,
ϕ
) = R
n,l
(r)
θ
l,ml
(
θ
)
ϕ
ml
(
ϕ
)
n = 1 , l = 0
ρ
( r )
r/r
o
1 2 3
gęstość prawdopodobieństwa znalezienia elektronu
n = 2 , l = 0 (2s)
ρ
(r)
r/r
o
27
n = 2 , l = 1 (2p.)
ρ
(r)
r/r
o
l = 0 , m
L
= 0
Z
Prawdopodobieństwo znalezienia
θ
elektronu jest wszędzie takie samo.
y
l = 1 , m
L
= 0
Z
θ
Lm
2
Są różne prawdopodobieństwa
znalezienia elektronu
y
l = 1 , m
L
= 1
Z
y
28
PROMIENIOTWÓRCZOŚĆ
A
X - jądro atomowe
Z
z - liczba atomowa , określa liczbę protonów w jądrze
A
- liczba masowa , określa całkowitą liczbę nukleonów w jądrze
( A - Z ) -ilość neutronów w jądrze
MASA ATOMOWA - podaje masę jądra w jednostkach atomowych masy
( Junitach ).
1 4 7 235
H , He , Li , U
1 2 3 92
1
p - proton
1
1
n - neutron
0
masy protonu i neutronu nie są identyczne
IZOTOPY - to odmiany jąder atomowych o tym samym ładunku ale o różnych
masach.
1 2 3 12 13 14
H , H , H C , C , C
1 1 1 6 6 6
wodór deuter tryt - izotop węgla C14 (czas
połowicznego zaniku 5700 lat) , za
pomocą tego izotopu określa się
wiek wykopalisk.
238 235
U , U - wykorzystywany w reaktorach atomowych
92 92
IZOBARY - jądra o takich samych masach , a o różnych ładunkach
- mają takie same liczby masowe , a różne liczby atomowe.
Przemiany jąder atomowych zależą od liczby masowej.
Ro = 1,2
⋅
10
-15
m promień atomu wodoru
Promień nie rośnie wprost proporcjonalnie tylko według wzoru :
R = Ro
⋅⋅⋅⋅
A
1/3
gdzie A to liczba masowa
MODEL JĄDRA KROPLOWY - porównuje jądro do kropli , w podobny jak z
kroplą sposób zmieniają się jądra podczas rozszczepienia.
29
MODEL JĄDRA POWŁOKOWY -który nawiązuje do budowy atomu ,
zajmuje się energetyką strony jądra atomowego.
Jeżeli jądro jest wzbudzone to zajmuje wyższy poziom energetyczny. Jądro
wzbudzone
emituje
energię
przez
jądro
atomowe
(kwant
energii
(promieniowanie
γ
)) i przechodzi w stan spoczynkowy.
Dlaczego jądro atomowe składające się z dodatnich protonów i obojętnych
neutronów jest jądrem trwałym ?
odp. Protony (dodatnie) odpychają się co wynika z tw Kulomba , więc powinno
się rozlecieć , ale widocznie istnieją inne siły które to trzymają razem.
Przyczyną trwałości jąder są siły jądrowe.
Siły jądrowe - to siły krótkiego zasięgu , które działają na odległość 10
-15
m.
Aby można było rozłożyć jądro na nukleony trzeba wykonać określoną pracę
(jest ona równa energii nukleonów)
ENERGIA NUKLEONÓW - to energia potrzebna na usunięcie nukleonu z jądra
bez nadania mu energii kinetycznej.
CAŁKOWITA ENERGIA WIĄZANIA JĄDRA ATOMOWEGO - praca
potrzebna na rozłożenie jądra atomowego na składowe nukleony bez nadania
energii kinetycznej.
Masa wolnych protonów i neutronów jest większa od masy jądra atomowego.
DEFEKT MASY (deficyt masy) to różnica między łączną masą protonów i
neutronów a łączną masą jądra atomowego.
∆
m. = (Z
⋅
m
p
) - (A - Z)
⋅
mn - mj
Z - całkowita masa protonów
Ew =
∆∆∆∆
m.
⋅⋅⋅⋅
C
2
całkowita energia wiązania
Jeśli podzielimy energię wewnętrzną przez ilość nukleonów to otrzymamy
energię wewnętrzną na jeden nukleon , jest ona różna dla różnych jąder.