Entropię
możemy zdefiniować następująco:

jeżeli w danym procesie odwracalnym układ pobiera ciepło
w temperaturze
, to przyrost entropii układu wynosi

.

Entropia
jest funkcja stanu układu termodynamicznego. Dla każdego układu izolowanego i we wszystkich możliwych procesach wartość entropii nie zmniejsza się. Stwierdzenie to znane jest jako prawo wzrostu entropii. Entropia układu izolowanego, w którym zachodzą procesy nieodwracalne może tylko rosnąć. Jeżeli w układzie zachodzą wyłącznie procesy odwracalne, albo układ osiągnął stan równowagi termodynamicznej wtedy entropia pozostaje stała.

Ponieważ
, to dla kołowego procesu odwracalnego mamy

.

Dla przemiany przeprowadzającej w sposób odwracalny układ ze stanu A do stanu B

.

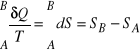
Podana tu definicja nie pozwala na wyznaczenie bezwzględnej wartości entropii, bowiem z powyższej zależności widać, że

.

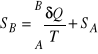
Dla wyznaczenia entropii układu w danym stanie musielibyśmy znać wartość bezwzględną entropii stanu początkowego. Możemy jednak wyznaczyć przyrost entropii w danym procesie i to (jak zobaczymy) ma zasadnicze znaczenie dotyczące określenia możliwości zachodzenia oraz kierunku przebiegu procesów w przyrodzie.

Ważną cechą entropii jest także jej addytywność, co oznacza, że entropia układu jest sumą entropii podukładów.

Warto też zwrócić uwagę, że ponieważ w przemianie adiabatycznej, odwracalnej mamy
, to wartość entropii jest dla tej przemiany stała:
. Proces adiabatyczny, odwracalny nazywa się, dlatego procesem izoentropowym. Zauważmy, że w przypadku procesów nieodwracalnych wzrasta oddane otoczeniu ciepło o znaku ujemnym w stosunku do ciepła pobranego, któremu przypisaliśmy znak dodatni. Przyczyną jest niekwazistatyczny przebieg procesu, niedoskonała izolacja układu itp.

GAZY RZECZYWISTE. Dla gazów rzeczywistych obserwuje się odstępstwa od równania gazu doskonałego przy wysokich ciśnieniach i niskich temperaturach. Uwzględnienie w równaniu stanu gazu dwu poprawek - na objętość cząsteczek i oddziaływania międzycząsteczkowe, prowadzi do równania van der Waalsa. Równanie to opisuje zachowanie się gazów rzeczywistych w szerokim zakresie gęstości. Zawiera dwie, wyznaczone doświadczalnie, stałe van der Waalsa a oraz b.

Przy opisie mikroskopowych własności gazu doskonałego zakłada się, że cząsteczki gazu zajmują znikomą objętość, a ich oddziaływania sprowadzają się do zderzeń sprężystych. W rzeczywistości, objętość dostępna dla ruchu cząsteczek jest pomniejszona, bowiem nie mogą one zbliżać się do siebie na odległość mniejszą niż wynosi średnica cząsteczki i nie mogą zbliżyć się do ścianek na odległość mniejszą od ich promienia. Ciśnienie także jest wynikiem nie tylko sprężystych i natychmiastowych zderzeń cząsteczek, ale również rezultatem ich wzajemnych oddziaływań poza momentami zderzeń. Objętość dostępna dla ruchu cząsteczek jest, zatem pomniejszona w stosunku do objętości gazu doskonałego, a ciśnienie - powiększone. Efekty te zostały uwzględnione w równaniu van der Waalsa w postaci dodatkowych członów, które dodaje się do ciśnienia i odejmuje od objętości

.

Jeśli wartości
i
są równe zeru, otrzymujemy znane nam równanie stanu gazu doskonałego dla jednego mola gazu.

Ciśnienie
zwane jest ciśnieniem kohezyjnym. Ciśnienie to proporcjonalne jest do gęstości gazu
i sił wzajemnego oddziaływania cząsteczek. Siły te także wzrastają proporcjonalnie do gęstości gazu, a gęstość jest odwrotnie proporcjonalna do objętości. Mamy, więc

.

Zmniejszenie objętości proporcjonalne jest do liczby cząsteczek, a liczba ta, przy danym ciśnieniu, jest proporcjonalna do objętości naczynia. Objętość
stanowi, tę część objętości, która jest efektywnie zajęta przez cząsteczki gazu. Wprowadzając oznaczenia:
oraz
, otrzymujemy równanie stanu gazu znane jako równanie van der Waalsa.

.

Stałe a i b charakteryzują własności jednego mola danego gazu rzeczywistego.

Zależność ciśnienia od objętości przy stałej temperaturze dla jednego mola gazu wynikająca z równania van der Waalsa ma postać

.

Przykładowe izotermy van der Waalsa dla dwutlenku węgla
pokazane są na wykresie. Temperatury: 264 K, 284 K, 304 K, 334 K, 364 K, 404 K.

Z postaci wzorów oraz kształtu izoterm widzimy, że sprężając gaz przy stałej temperaturze mamy dla temperatur wysokich systematyczny wzrost ciśnienia przy zmniejszaniu się objętości, podobnie jak dla gazu doskonałego. Najmniejsza wartość objętości równa jest parametrowi b, który opisuje efektywną objętość zajmowaną przez jeden mol cząsteczek gazu. Kiedy objętość staje się bliska b, to ciśnienie dąży do nieskończoności, bowiem różnica w mianowniku wyrażenia
dąży do zera. Z kolei, wyrażenie
obniża wartość ciśnienia, co przy stosunkowo niskich temperaturach powoduje powstanie lokalnego minimum w obszarze pomiędzy punktami C i B.

Naturalnym wnioskiem z analizy izoterm van der Waalsa jest to, że dla określonej temperatury (izoterma krytyczna) nie pojawia się minimum, ale jedynie punkt przegięcia na krzywej. Punkt ten zwany jest punktem krytycznym i na rysunku oznaczony jest literą K. Odpowiadające temu punktowi wartości ciśnienia, objętości i gęstości gazu noszą nazwę wartości krytycznych. Parametry krytyczne można wyznaczyć, zauważając, że dla izotermy krytycznej pierwiastki równania van der Waalsa są sobie równe:
. Można też analitycznie zbadać przebieg zmienności funkcji
. W punkcie krytycznym styczna do izotermy jest pozioma, co oznacza zerowanie się pierwszej pochodnej ciśnienia względem objętości. Punkt ten jest też punktem przegięcia, co oznacza zerowanie się drugiej pochodnej. Mamy, zatem dla

oraz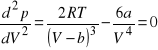
.

Z równań tych wyznaczamy

,
,
.

Współczynniki równania van der Waalsa wyrażone przez wartości krytyczne wynoszą

,
.

Tak wyznaczone współczynniki zostały użyte do naszych wykresów izoterm van der Waalsa dla dwutlenku węgla, gdzie
,
.

Na koniec warto zaznaczyć, że nasze dotychczasowe rozważania w tej lekcji odnosiły się do jednego mola gazu. Kiedy rozważamy
moli, wówczas dodatkowe człony równania van der Waalsa są:
,
, a równanie ma postać

.

Należy dodać, że równanie van der Waalsa ma charakter empiryczny i jest jednym z kilku różnych równań stanu gazu rzeczywistego, najbardziej popularnym.

Przeanalizujmy nieco dokładniej postać izoterm van der Waalsa, dla różnych wartości temperatur. Przykładowe kształty izoterm dla trzech różnych temperatur spełniających warunek
przedstawia rysunek.

Zacznijmy od przypadku temperatury niższej od temperatury krytycznej. Kiedy poprzez zmniejszanie objętości naczynia sprężamy izotermiczne gaz rozpoczynając od dużej objętości i małego ciśnienia w temperaturze poniżej temperatury krytycznej (punkt oznaczony symbolem temperatury
) - przesuwamy się po krzywej w kierunku punktów A i B. W punkcie B krzywa ma lokalne maksimum. Dalsze zwiększanie siły wywieranej na tłok powinno spowodować obniżenie ciśnienia wewnątrz naczynia. Musiałoby to doprowadzić do raptownego przejścia układu do stanu E o tym samym ciśnieniu, bowiem ciśnienie zewnętrzne byłoby większe od ciśnienia wewnętrznego. Tak się jednak nie dzieje. W punkcie A rozpoczyna się nowe zjawisko - skraplanie, czyli tworzenie się fazy ciekłej.

Para nienasycona, będąc w fazie gazowej, wskutek sprężania zwiększa swą gęstość i w punkcie A osiąga gęstość pary nasycanej w temperaturze
, czyli staje się parą nasyconą. Dalsze zmniejszanie objętości powoduje skraplanie pary nasyconej. Proces ten odbywa się wzdłuż prostej AD, przy stałym ciśnieniu. Przy zmniejszeniu się objętości na odcinku AD coraz więcej gazu ulega skropleniu. W naczyniu współistnieją wtedy dwie fazy - ciecz i para nasycona. W punkcie D cały gaz ulega skropleniu i następuje gwałtowny wzrost ciśnienia, ponieważ ściśliwość cieczy jest wielokrotnie mniejsza od ściśliwości gazów. Fakt, że w punkcie A rozpoczyna się skraplanie nie oznacza, że odcinek krzywej AB jest dla gazu nieosiągalny. Proces skraplania rozpoczyna się na istniejących zwykle w gazie niejednorodnościach, które są centrami kondensacji. Jeśli proces sprężania przeprowadzany jest ostrożnie a gaz nie zawiera zanieczyszczeń możliwe jest przemieszczenie się do punktu B. Gaz w takim stanie nazywamy parą przesyconą. Analogicznie do efektu powstawania pary przesyconej możliwe jest przejście w odwrotnym kierunku - od punktu D do punktu C. Uzyskujemy wtedy stan cieczy przegrzanej. Stany te są stanami metastabilnymi. Oznacza to, że wystarczy niewielkie zaburzenie, aby wyprowadzić ciecz lub gaz z takiego stanu. Następuje wtedy gwałtowna kondensacja (w przypadku pary przesyconej) lub wrzenie cieczy (w przypadku cieczy przegrzanej). Proces skraplania bądź wrzenia rozpoczyna się na występujących niejednorodnościach, a następnie obejmuje cała objętość.

Proces przechodzenia ze stanu stałego w stan ciekły nazywamy topnieniem. Proces ten wymaga dostarczenia ciepła, które dla jednostkowej masy substancji nosi nazwę ciepła topnienia. Proces ten dla substancji krystalicznych zachodzi w określonej temperaturze. Zakładając, że ilość dostarczanego ciepła na jednostkę czasu ma wartość stałą otrzymamy zależność temperatury od czasu dla ciała, które podlega procesowi topnienia w postaci przedstawionej na rysunku. Kolorem czerwonym pokazana jest zależność temperatury od czasu dla ciał krystalicznych. Temperatura ciała wzrasta wraz z upływem czasu, kiedy dostarczane jest ciepło. Po osiągnięciu temperatury topnienia, punkt A, ciepło zużywane jest na proces topnienia i temperatura pozostaje stała. Kiedy stopieniu ulega cała masa, punkt B, temperatura fazy ciekłej zaczyna dalej wzrastać.

W przypadku ciał amorficznych nie ma określonej temperatury topnienia. Przechodzenia ciała w stan ciekły odbywa się w określonym przedziale temperatury. Jest to rezultatem podobnej struktury ciał amorficznych i cieczy (brakiem uporządkowania atomów i cząsteczek na dużych odległościach). Trzeba tu dodać, że rysunek jest schematyczny. Nachylenia odcinków do punktu A i od punktu B będą różne, gdyż zależą one od ciepła właściwego, które dla fazy ciekłej ma inną wartość niż dla fazy stałej. Procesem odwrotnym do topnienia jest proces krzepnięcia albo inaczej - krystalizacji. W procesie tym ciało oddaje ciepło, a sam proces rozpoczyna się także na centrach krystalizacji, podobnie jak na centrach kondensacji w przypadku skraplania. Także podobnie i tu możliwy jest proces przechłodzenia cieczy i pozostawanie jej w stanie metastabilnym. Drobna niejednorodność w postaci zanieczyszczenia może wówczas spowodować proces krystalizacji (bardziej ogólnie - solidyfikacji, gdyż nie zawsze powstający stan stały ma strukturę krystaliczną). W przypadku silnych, gwałtownych przechłodzeń możliwe jest przejście cieczy w stan amorficzny ciała stałego.

---