Do wykładu № 1

Wiadomości ogólne. Przestrzeń i czas - fizyczne układy odniesienia. Opis ruchu ciał w przestrzeni - tor, droga i przemieszczenie; wektor wodzący, prędkość i przyspieszenie; ruch postępowy i obrotowy.

1. Resnik R., Holliday D. Fizyka. - Warszawa: WN PWN, 1998. W 2 t.

2. Feynman R.P., Leighton R.B., Sands M. Feynmana wykłady z fizyki. - Warszawa: PWN, 1971. - W 5 t.

3. Bobrowski C. Fizyka - krótki kurs. - Warszawa: WNT, 2007.

Wielkością fizyczną
nazywamy taką własność ciała, którą można ilościowo porównać z taką samą własnością innego ciała.

Pomiar wielkości fizycznej
oznacza określenie liczbowego stosunku danej wielkości do wielkości tego samego rodzaju, która przyjęta za jednostkę
.

Rozróżniamy podstawowe i pochodne wielkości fizyczne. Pomiędzy podstawowymi wielkościami nie występują żadne zależności fizyczne, wtedy jak w przypadku pochodnych wielkości fizycznych możemy ich zdefiniować przez inne wielkości.

Jeśli wielkość
jest określona przez zależność funkcyjną

,

gdzie
(
) są inne wielkości fizyczne, to przyjmujemy, że jednostka tej wielkości
jest taką samą funkcją jednostek
wielkości
(
)

.

UKŁAD SI

SIEDEM JEDNOSTEK PODSTAWOWYCH I DWIE UZUPEŁNIAJĄCE

№	Wielkość	Symbol wielkości	Jednostka	Symbol jednostki
1.	Długość		metr
2.	Masa		kilogram
3.	Czas		sekunda
4.	Liczność materii (ilość substancji)		mol
5.	Natężenie prądu elektrycznego		amper
6.	Temperatura termodynamiczna		kelwin
7.	Światłość	, ɟ	kandela
8.	Kąt płaski		radian
9.	Kąt bryłowy		steradian

ZASADY TWORZENIA JEDNOSTEK WTÓRNYCH

Przedrostek	Oznaczenie	Mnożnik
eksa	E
penta	P
tera	T
giga	G
mega	M
kilo	k
hekto	h
deka	da
—	—
decy	d
centy	c
mili	m
mikro
nano	n
piko	p
femto	f
atto	a

DEFINICJI JEDNOSTEK

Metr (m) jest to długość drogi przebytej w próżni przez światło w czasie 1/299792458 s (XVII Gen. Konf. Miar, 1983 r.).

Kilogram (kg) jest to masa międzynarodowego wzorca tej jednostki masy, który przechowuje się w Międzynarodowym Biurze Miar w Sevres (III Gen. Konf. Miar, 1901 r.).

Wstępnie masa tego wzorca (stopu platyny z irydem) miała być równa masie
wody destylowanej w temperaturze
, jednakże okazało się po dokładnych pomiarach, że
wody destylowanej w
wynosi
.

Sekunda (s) jest to czas równy 9 192 631 770 okresom promieniowania, które odpowiada przejściu między dwoma nadsubtelnymi poziomami stanu podstawowego atomu cezu
(XII Gen. Konf. Miar, 1964 r.).

Kelwin (K) jest to 1/273,16 część temperatury termodynamicznej punktu potrójnego wody destylowanej (XIII Gen. Konf. Miar, 1967/68 r.).

Mol (mol) jest to liczność materii występująca, gdy liczba cząsteczek jest równa liczbie atomów zawartych w masie
węgla
(XIV Gen. Konf. Miar, 1971 r.).

Definicja mola oparta jest na prawie Avogadra: jeden mol (masa w gramach liczbo równa masie atomowej) każdej substancji zawiera liczbę cząsteczek
(liczba Avogadra).

Amper (A) jest to natężenie prądu stałego, który płynąc w dwóch równoległych prostoliniowych przewodach nieskończenie długich o przekroju kołowym znikomo małym, umieszczonych w próżni w odległości
, wywołuje między tymi przewodami siłę równą
na każdy metr długości przewodu (IX Gen. Konf. Miar, 1948 r.).

Kandela (cd) jest to światłość, jaką ma w określonym kierunku źródło emitujące promieniowanie monochromatyczne o częstotliwości
i którego natężenie w tym kierunku jest
(XVI Gen. Konf. Miar, 1979 r.).

Radian (rad) jest to kąt płaski zawarty między dwoma promieniami, które wycinają łuk na dowolnym okręgu z centrum w punkcie początku promieni o długości równej odległości do centrum.

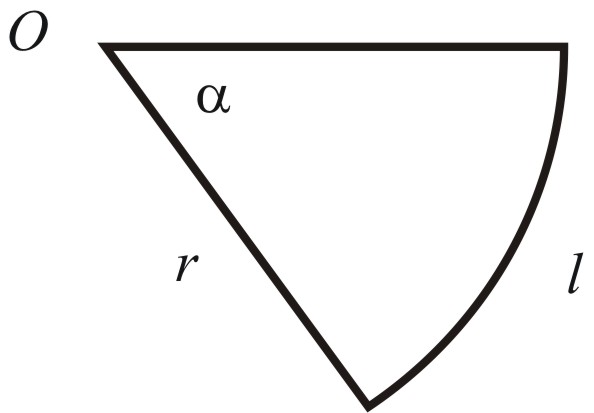
Dla obliczeń wartości kąta
w radianach obowiązuje wzór

,

gdzie
jest długością łuku wyciętego dwoma promieniami na okręgu koła o promieniu
.

Kąt płaski — część płaszczyzny ograniczonej dwoma promieniami ze wspólnym początkiem.

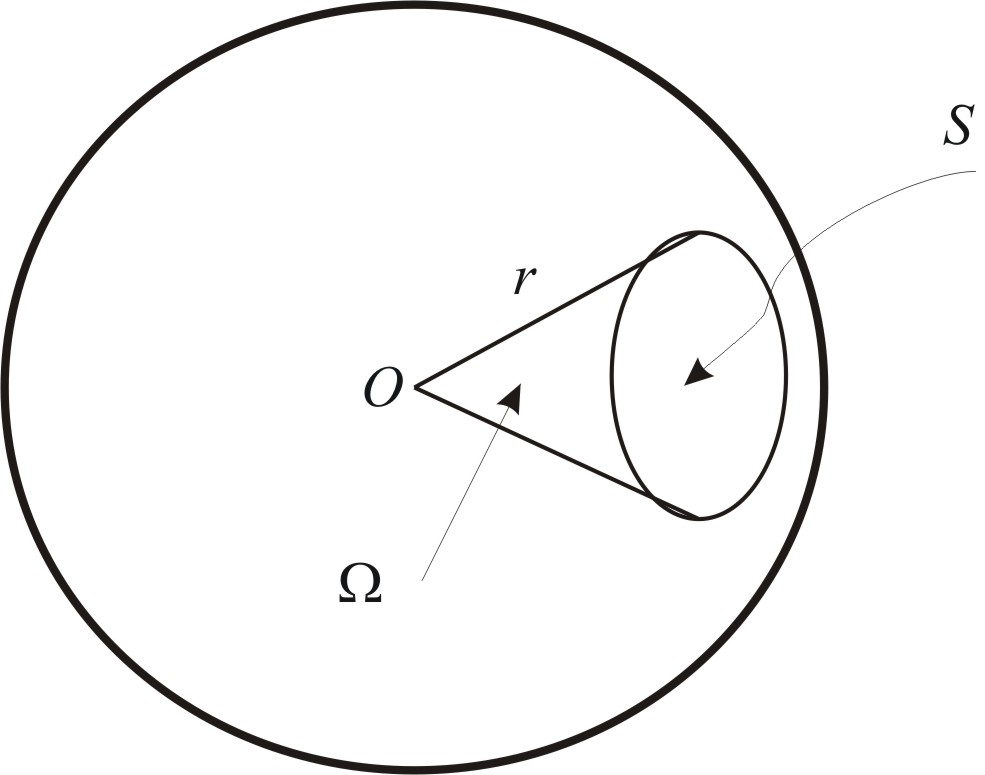
Steradian (sr) jest kątem bryłowym o wierzchołku w środku kuli, który wycina z jej powierzchni część równą powierzchni kwadratu o boku równym promieniowi tej kuli.

Dla obliczeń wartości kąta
w radianach obowiązuje wzór

,

gdzie
jest pole powierzchni wyciętej powierz­chnią stożkową na powierzchni kuli o promieniu
.

Kąt bryłowy — część przestrzeni ograniczonej powierzchnią stożkową.

POLA SKALARNE I WEKTOROWE

Pojęcia wstępne. W prawach fizycznych występują wielkości skalarne, wektorowe i tensorowe.

Jeśli wartość wielkości fizycznej może być wyczerpująco określona przez liczbę, to mówimy o fizycznej wielkości skalarnej.

Przykładamy takich wielkości są masa, objętość, gęstość, ciśnienie, temperatura i wielu innych.

Jeżeli wartość wielkości fizycznej może być wyczerpująco określona przez wektor, to mówimy o fizycznej wielkości wektorowej.

Podstawowymi przykładamy takich wielkości są prędkość i siła. Należę podkreślić, że w różnych prawach fizyki występują dwa rodzaje wektorów - polarne i aksjalne.

Jeśli wartość wielkości fizycznej może być wyczerpująco określona przez tensor, to mówimy o fizycznej wielkości tensorowej.

Typowymi przykładamy takich wielkości są odkształcenie i naprężenie ciała stałego, itp. Zaznaczmy także, że tensory są szeroko wykorzystywane dla opisu struktury kryształów. Jak i przypadku wektorów należę rozróżniać różne rodzaje tensorów.

W pewnym przybliżeniu modelowym przyjmujemy, że ciało fizyczne znajduje się w trójwymiarowej przestrzeni.

Intuitywnie oznacza to, że przestrzeń jest ciągły zbiór punktów, każdy z których może być jednoznacznie scharakteryzowany przez trzy uporządkowane liczby. W tej przestrzeni ciało fizyczne zajmuje pewien ograniczony, obszar. W punktach przestrzeni, które należą do tego obszaru, wielkości fizyczne przyjmują różne wartości. W tym przypadku mówimy o ich polu, tzn. zależności funkcyjnej od trzech uporządkowanych liczb „przypisanych” poszczególnym punktom przestrzeni.

Układ współrzędnych.

Układ współrzędnych jest to jeden ze sposobów „przypisania” każdemu punktu przestrzeni trzech uporządkowanych liczb.

Najczęściej stosowanymi w fizyce układami są prostokątny (kartezjański) układ współrzędnych, ukośny układ współrzędnych, a także walcowy (cylindryczny) i sferyczny układ współrzędnych.

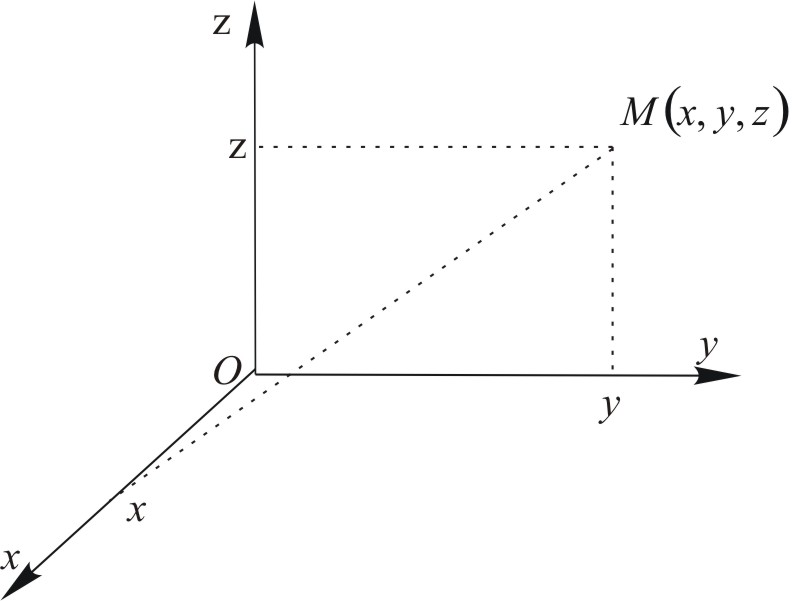
Jeżeli stosujemy kartezjański układ współ­rzędnych, to wymienioną procedurę „przypisania” dokonujemy w następujący sposób. Weźmiemy trzy wzajemnie prostopadłe osi
,
i
, które przecinają się w punkcie
(początek układu współ­rzędnych). Z wybranego punktu
przeprowa­dzamy prostopadłą do osi
. Odległość od punktu
do punktu przecięcia z prostopadłą oznaczmy jako
. W sposób podobny otrzymamy liczby
i
dla osi
i
. Tak określone liczby
,
i
postawimy w jednoznaczną odpowiedniość punktu
(„przypisujemy” punktu
)

,

co zwykle zapisuje się w postaci

lub
.

Wektor. W prawach natury występują dwa rodzaje wektorów - polarne i aksjalne, różnice, pomiędzy którymi omówimy później. Teraz scharakteryzujemy ogólne właściwości nowego pojęcia - wektora.

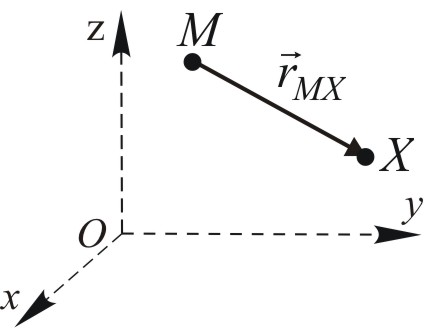
Wektorem zaczepionym w trójwymiarowej przestrzeni nazywamy uporządkowaną parę punktów
i
, gdzie punkt
nazywamy jego początkiem, a punkt
jego końcem. Często notuje się to w postaci
lub
.

Graficznie wektor zaczepiony oznacza się strzałką (skierowanym odcinkiem) w przestrzeni, która łączy dwa różne punkty tej przestrzeni
i
.

Wektor zaczepiony jest określony, jeśli podano: punkt zaczepienia
; odległość między punktami
i
(długość wektora) i kierunek prostej, na której leżą punkty
i
. Zaznaczmy, że pojęcie kierunku w niektórych przypadkach definiują za pomocą pojęcia zwrotu pół-prostej.

Oprócz wektora zaczepionego, dla sformułowania praw fizyki niezbędne jest pojęcie, wektora swobodnego. Dla określenia wektora swobodnego wykorzystujemy tylko jego długość i kierunek, nie ważnym jest, gdzie on zaczepiony. Dwa wektory swobodne znajdujące się na równoległych prostych w przestrzeni uważamy za jednakowe. Oznacza to, że wektor swobodny możemy równolegle przemieszczać w przestrzeni.

Wektor zaczepiony o jednostkowej długości nazywamy wersorem lub wektorem jednostkowym, zaś wektor, którego początek pokrywa się z końcem — wektorem zerowym
.

Dwa wektory są kolinearne (równoległe), gdy proste, na których one znajdują się są równoległe.

Można definiować podstawowe działania nad wektorami: mnożenie przez liczbę rzeczywistą, dodawanie i odejmowanie. Graficznie te działania można zilustrować następująco.

Mnożenie wektora
przez skalar
notujemy jako
.

Dodawanie wektorów zapisujemy jako

lub

Odejmowanie wektorów zapisujemy jako

Układ współrzędnych i wektory bazy

Stosują pojęcie wektora można dokonać pewnego uogólnienia opisu położenia punktów przestrzeni fizycznej.

Zaopatrzymy, każdą z osi
,
i
o jednostkowe wektory
,
i
, odpowiednio, tak żeby każdy z nich był zaczepiony w punkcie
, a jego kierunek był zgodny do wybranego wcześnie na określonych osiach.

Załóżmy liniową niezależność wektorów
,
i
. Oznacza to, że równość

,

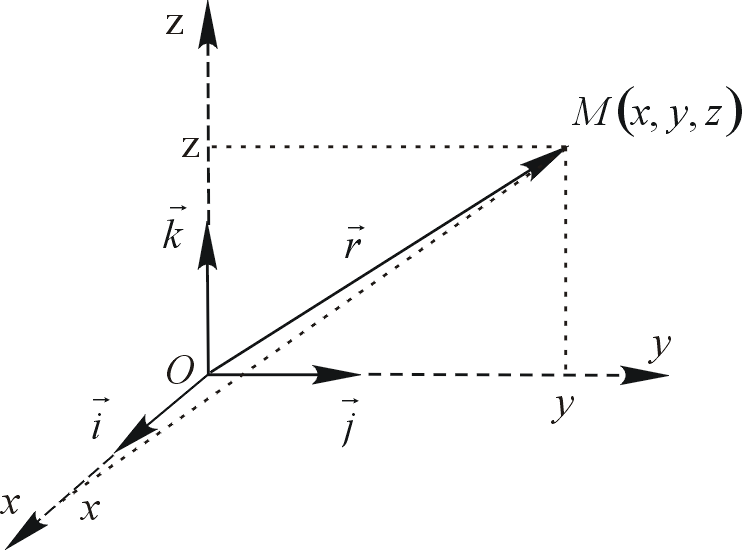
gdzie
są liczby rzeczywiste, wykonuje się wtedy i tylko wtedy kiedy
(
). Wynika stąd, że zależności rodzaju
lub
, czuli
, gdzie
i
są stałymi rzeczywistymi, nie jest możliwa.

Jeżeli dla każdego innego wektora
, który różnie się od wektorów
,
i
, spełnia się zależność (wektory
,
,
i
są liniowo zależne)

,

gdzie
są liczby rzeczywiste (
), to mówimy wtedy o trójwymiarowej przestrzeni wektorowej.

Definiujemy wtedy wektor wodzący
jako wektor łączący punkty
i
, czyli
. Dla wektora wodzącego również mamy

i jeżeli przyjąć, że
, to

.

Skąd wynika, że każdy trójwymiarowej przestrzeni fizycznej może być jednoznacznie scharakteryzowany przez odpowiedni wektor wodzący.

Przykład - płaszczyzna.

Współrzędne wektora

Rzutem wektora
na oś
nazy­wamy wektor
, łączący punkty przecięcia prostopadłych rzutów punktu
początku wektora i punktu
jego końca. Podobnie określamy rzuty
i
na osi
i
, odpowiednio.

Zgodnie z regułą dodawania wektorów mamy

.

Współrzędną wektora
względem osi
nazywamy liczbę, która równa długości wektora
, i wzięta ze znakiem plus, jeśli jego kierunek jest zgodny ze zwrotem wektora
lub znakiem minus w przeciwnym przypadku. Analogicznie określamy współrzędne względem osi
i
.

Z ich wykorzystaniem często stosuje się skrócona notacja wektora

.

Ze względy na to, że
,
i
są wersorami układu współrzędnych, mamy

,
,
.

Wówczas wektor może być zapisany też w postaci

.

Podstawowe działania na wektorach

i
,

wtedy mogą być zapisane następująco

,
;

,

.

Warunek równoległości

.

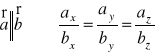
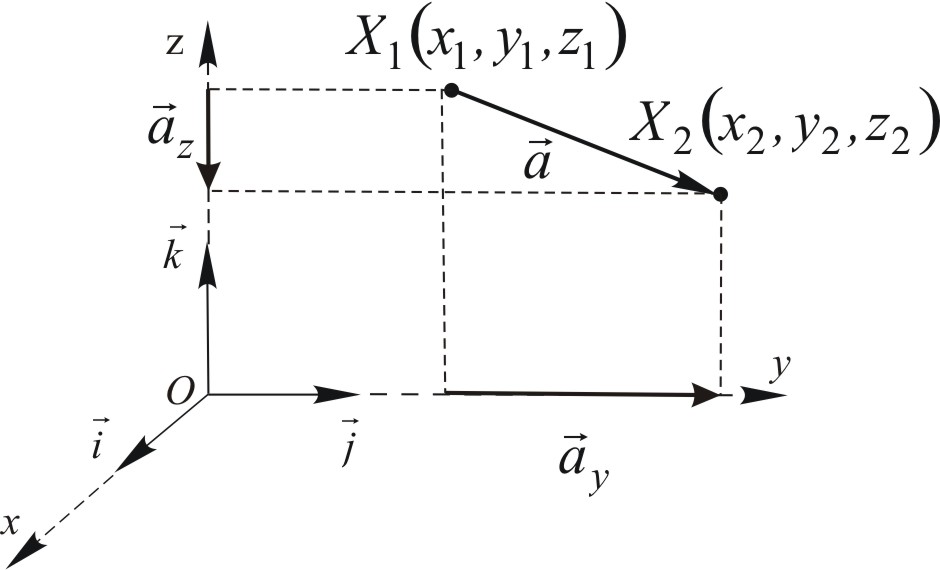
Zmiana jakościowa opisu działań z wektorami. Wektor
przedstawimy jako różnice wektorów wodzących
i
jego punktu początkowego
i punktu końcowego
, mianowicie

,

wiec

.

Długość wektora
wyraża się wzorem

lub
.

Unormować wektor
oznacza znaleźć wersor

.

Kosinusami kierunkowymi wektora
nazywamy kosinusy kątów
,
,
, jakie tworzy ten wektor odpowiednio z osiami
,
i
, tzn.

,

,

.

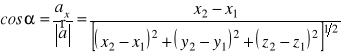
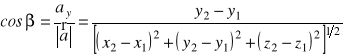
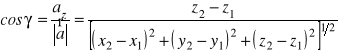
Przy warunku
.

Iloczyn skalarny (mnożenie skalarne).

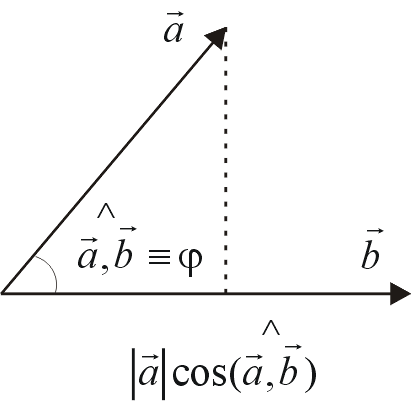
Dwóm dowolnym wektorom
i
postawimy w odpowiedniość skalar - liczbę rzeczywistą, którą oznaczymy
, tj.

,

gdzie
- kąt pomiędzy wektorami
i
(rys.3.1).

Iloczyn skalarny dwóch wektorów bazy
i
spełnia warunek (wektory jednostkowe i prostopadłe)

,

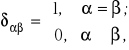
gdzie
- symbol Kronekera.

Ponieważ

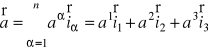
i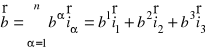
,

to

.

Łatwo sprawdzić następne podstawowe właściwości iloczynu skalarnego:

,

,

,

.

gdzie
- dowolne liczby rzeczywiste.

Zaznaczmy, że długość wektora definiuje się przez iloczyn skalarny w następujący sposób

.

Iloczyn wektorowy (mnożenie wektorowe).

Jest to działanie (operacja, odwzorowanie), które dwóm wektorom
i
stawi w odpowiedniość również wektor
. Długość tego wektora wyznacza się wzorem

.

Wektor
prostopadły do płaszczyzny, w której znajdują się wektory
i
, i skierowany tak, żeby z jego końca powrót wektora
do kierunku wektora
dokonany był przeciwko strzałki zegarka.

Interpretacja geometryczna pokazana na rys.4.1. Długość tego wektora
równia się wielkości pola, które ma romb zbudowany na wektorach
i
.

Łatwo sprawdzić, że iloczyn wektorowy dwóch wektorów bazy
i
będzie

Zaznaczmy, że

.

I wtedy dla dwóch dowolnych wektorów

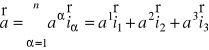
i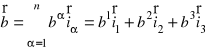

możemy otrzymać

.

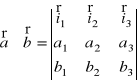
W kartezjańskim układzie współrzędnych odpowiednio będzie

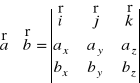
lub

,

tzn. współrzędne tego wektora będą

,
,
.

Bezpośrednio z definicji łatwo sprawdzić główne właściwości iloczynu wektorowego

,

,

,

gdzie
− dowolny liczby rzeczywiste.

Niektóre ważne właściwości operacji kompozycji iloczynu skalarnego i wektorowego

,

,

,

.

Pojęcie przestrzeni n - wymiarowej

Sformułowanie wielu praw fizyki wymaga pewnego uogólnienia określonych wyżej pojęć.

Załóżmy, że mamy zbiór X elementów (punktów) X. Jeżeli w zbiorze określona jest granica ciągu elementów, to mówimy, ze mamy przestrzeń abstrakcyjną. Wówczas, jeżeli wszystkie elementy końcowe (granicy) dowolnych zbieżnych ciągów elementów przestrzeni należą do przestrzeni, to taką przestrzeń nazywamy kompaktną przestrzenią topologiczną.

Jeśli w jakości elementów (punktów) przestrzeni wybrano uporządkowane liczby rzeczywiste
(
), co notujemy w postaci
, to mówimy o przestrzeni arytmetycznej
wymiaru n.

Kiedy, że każdemu punktu X przestrzeni X (piszemy:
) postawiono w odpowiedniość jednoznaczną punkt
przestrzeni arytmetycznej
(piszemy:
), to mówimy, że punkty przestrzeni X zostały sparametryzowane i zapisujemy to w postaci

.

Wtedy liczbę n - nazywamy wymiarem przestrzeni X, oraz liczby
- współrzędnymi punktu X (
).

Liniowa przestrzeń wektorowa E.

W tym przypadku na elementach (wektorach) zbioru podstawowego (przestrzeni) oznaczona operacja dodawania tak, że tworzą oni komutatywną grupę abelową. Oprócz tego określono działanie (operację) zewnętrzne na elementy zbioru podstawowego - mnożenie na liczby rzeczywiste, które tworzą ciało liczb rzeczywistych. Przy tym definiowano szereg właściwości tych operacji.

Załóżmy, że wśród elementów przestrzeni E mamy n liniowo niezależnych pomiędzy sobą elementów, które oznaczymy przez

(
). Oznacza to, że równość

,

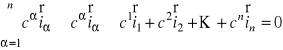
gdzie
- liczby rzeczywiste, wykonuje się wtedy i tylko wtedy, kiedy wszystkie liczby
są równe zero, tzn.
(
).

Liczbę n nazywamy wymiarem liniowej przestrzeni wektorowej E, a zbiór wektorów
(
) oznaczymy
i nazywamy bazą przestrzeni.

Dowolny element (wektor) przestrzeni
zapisuje się przez wektory bazy
w postaci

,

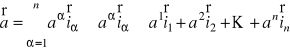
gdzie liczby
(
), które nie wszystkie równe zero, nazywamy współrzędnymi wektora
.

Liniowa przestrzeń wektorową E może być jednoznaczne związana ze wcześniej definiowaną przestrzenią X w następny sposób. Niechaj punktu
odpowiada punkt
, tzn.
, a dla innego dowolnego punktu X mamy
. Przyjmiemy za współrzędne
wektora
wielkości
. Tym samym ustaliliśmy związek - odwzorowanie

,

gdzie
- iloczyn kartezjański przestrzeni X samej na siebie.

Jeżeli
, to punkt B nazywamy początkowym punktom odniesienia i oznaczamy przez
. W tym przypadku
i wektor
oznaczymy przez
, tzn.
. Wektor
wtedy nazywamy - wektor wodzącym punktu X. Dla wektora wodzącego mamy

.

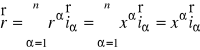
Przykład. Załóżmy, że wymiar przestrzeni liniowej równia się
. Wtedy wektor wodzący zapiszę się w postaci

.

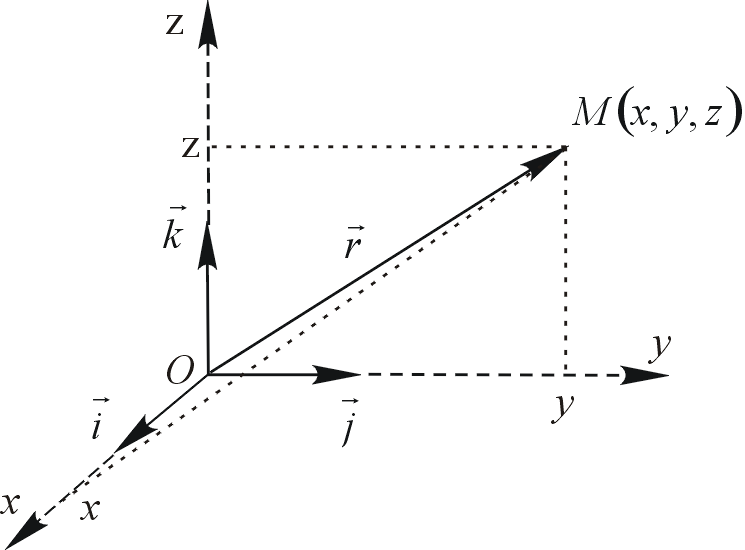
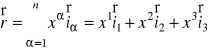
Jeżeli stosujemy kartezjański układ współrzędnych, to

oraz

i wówczas mamy

.

---