Do wykładu № 3
Zasady zachowania wielkości mechanicznych. Praca i moc. Energia (kinetyczna i potencjalna). Zasada zachowania pędu i energii.
Wykłady realizowany są w ramach projektu pt. „Mechatronika kierunkiem przyszłości - dostosowanie oferty edukacyjnej Uniwersytetu Kazimierza Wielkiego do potrzeb rynku pracy”, Działanie 4.1.1, Programu Operacyjnego Kapitał Ludzki, współfinansowanego ze środków Europejskiego Funduszu Społecznego”.
Resnik R., Holliday D. Fizyka. - Warszawa: WN PWN, 1998. W 2 t.
Feynman R.P., Leighton R.B., Sands M. Feynmana wykłady z fizyki. - Warszawa: PWN, 1971. - W 5 t.
Bobrowski C. Fizyka - krótki kurs. - Warszawa: WNT, 2007.
Praca mechaniczna.
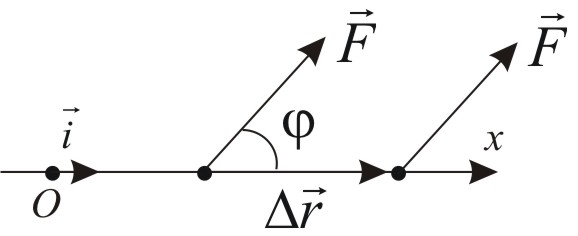
Na ciało (punkt materialny) działa siła ![]()
i ciało w ciągu czasu ![]()
dokonuje przemieszczenia ![]()
.
Podkreślimy, że przemieszczenie ciała ![]()
nie koniecznie jest wynikiem działania tylko siły ![]()
.
Określimy pojęcie pracy mechanicznej ![]()
przez wzór
![]()
,
gdzie ![]()
jest kątem między wektorami ![]()
i ![]()
.
Moc definiujemy następująco
![]()
.
Jeśli ![]()
, to
![]()
.
Energią ciała nazywamy wielkość fizyczną, która określa możliwość wykonania przez ciało pracy mechanicznej.
Energią kinetyczną nazywamy wielkość fizyczną, która określa możliwość wykonania przez ciało pracy mechanicznej po przez ruch względny ciała.
Postać wzoru dla energii kinetycznej otrzymamy dla prostoliniowego ruchu ze stałym przyspieszeniem (siła równoległa z przemieszczeniem: ![]()
).
Ponieważ
![]()
i ![]()
,
to
![]()
.
Jeśli określić energię kinetyczną wzorem
![]()
,
to prace zapisuje się w postaci
![]()
.
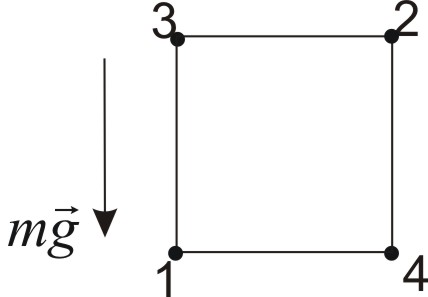
Siłę nazywamy zachowawczą, jeśli
![]()
.
Jako przykład, przeanalizujmy prace w polu sił grawitacyjnych. Zapiszemy prace z punktu 1 do punktu 2 przez punkt 3
![]()
,
oraz z punktu 2 do punktu 1 przez punkt 4
![]()
.
Wówczas
![]()
.
Ponieważ ![]()
(dokonano zmiany kierunku ruchu z punktu 1 do punktu 2), to
![]()
i ![]()
.
Otrzymany wynik oznacza, że w przypadku sił zachowawczych praca zależy wyłącznie od wyboru punktu początkowego i końcowego, i nie zależy od kształtu drogi.
Energią potencjalną ciała w punkcie 1 względem punktu 2 nazywamy pracę siły zachowawczej przy jego przesunięciu z punktu 2 do punktu 1.
Oto kilka prostych przykładów.
W wyniku działania siły ciężkości
![]()
i ![]()
.
W wyniku działania sił sprężystych mamy
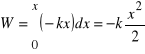
i ![]()
Środek masy.
Mamy układ fizyczny, który złożony jest z ![]()
punktów materialnych o masach ![]()
(![]()
). Wektor wodzący środka masy określamy przez wzór
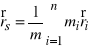
, 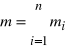
,
lub przez współrzędne
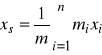
, 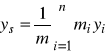
, 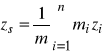
.
W przypadku ciała rozciągniętego (ośrodka ciągłego)
![]()
, ![]()
lub
![]()
, ![]()
, ![]()
,
gdzie wielkość
![]()
jest gęstością ośrodka w punkcie określonym przez wektor-wodzący ![]()
, ![]()
— masa znajdująca się w objętości ![]()
(obszar ![]()
ściąga się ku punktu z wektorem-wodzącym ![]()
.
Ruch środka masy
Dla poszczególnych punktów materialnych układu spełnia się drugie prawo Newtona
![]()
, ![]()
, ![]()
,
lub
![]()
,
gdzie ![]()
— zewnętrzna siła działająca na wybrany punkt materialny, ![]()
— wewnętrzna siła działająca na wybrany punkt materialny ze strony pozostałych ciał układu.
Dokonamy sumowania
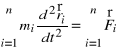
.
Masy ![]()
przyjmujemy stałymi (![]()
). Wówczas
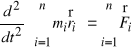
.
Ponieważ siły wewnętrzne równoważą się
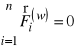
,
to ostatecznie otrzymamy
![]()
.
gdzie 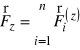
jest wypadkową siłą zewnętrzną.
Bryła sztywna
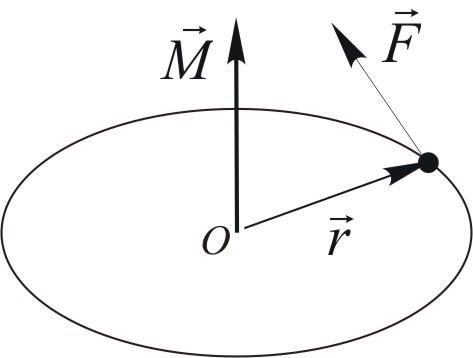
Ruchem postępowym bryły sztywnej nazywamy ruch, przy którym każdy odcinek prostej przeprowadzony między dwoma jej punktami pozostaje równoległy sam do siebie.
Ruchem obrotowym bryły sztywnej nazywamy ruch, przy którym wszystkie punkty poruszają się po okręgach, środki których znajdują się na jednej osi obrotu.
Moment siły ![]()
względem punktu ![]()
nazywamy wielkość fizyczną określoną przez iloczyn wektorowy
![]()
.
Moment bezwładności ![]()
określa się wzorem
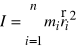
lub dla ciągłej bryły
![]()
, ![]()
czyli
![]()
, ![]()
, ![]()
.
W wielu przypadkach moment bezwładności można zapisać w postaci
![]()
,
gdzie ![]()
— nazywamy ramieniem bezwładności.
Łatwo udowodnić twierdzenie Steinera
![]()
,
gdzie ![]()
jest odległość między równoległymi osiami, względem których moment bezwładności ![]()
i ![]()
.
Dynamika ruchu obrotowego
Jeśli bryła złożona jest z oddzielnych punktów materialnych, to jej moment określimy wzorem
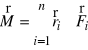
.
Tylko styczna składowa ![]()
siły ![]()
daje swój wkład do wypadkowego momentu bryły, a zatem mamy
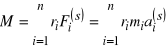
.
Ponieważ przyspieszenie styczne można zapisać przez przyspieszenie kątowe w postaci
![]()
,
to dla momentu układu otrzymamy
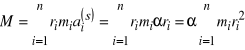
.
Skąd, uwzględniając definicję momentu bezwładności, ostatecznie mamy
![]()
lub w postaci wektorowej
![]()
, ![]()
.
Moment pędu (kręt) określamy przez wzór
![]()
lub, ponieważ tylko styczna składowa ![]()
prędkości ![]()
daje swój wkład do wartości bezwzględnej iloczynu wektorowego, to możemy zapisać
![]()
oraz w postaci wektorowej
![]()
.
Moment pędu dla bryły w całości jest sumą poszczególnych momentów pędu dla punktów materialnych
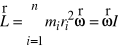
.
Drugie prawo Newtona dla ruchu obrotowego bryły otrzymamy następująco. Rozpoczynamy ze wcześniej otrzymanego wzoru
![]()
i wykorzystujemy definicję przyspieszenia kątowego
![]()
.
Ponieważ, moment bezwładności jest stały, to zapisujemy
![]()
.
Wówczas, uwzględniając, że ![]()
, drugie prawo Newtona dla ruchu obrotowego bryły znajdziemy w postaci
![]()
.
Także mogą być zmodyfikowane pierwsze i trzecie prawo Newtona dla bryły sztywnej.
Energia kinetyczna w ruchu obrotowym. Z definicji energii kinetycznej punktu materialnego dla układu punktów materialnych możemy zapisać
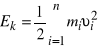
.
Zapisujemy prędkości liniowe poszczególnych cząsteczek przez prędkość kątową
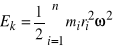
.
Prędkość kątowa jest stała, więc
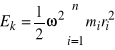
.
Wówczas, z definicji momentu bezwładności wynika, że
![]()
.
Energia kinetyczna toczenie się bryły sztywnej o postaci walca może być zapisana w postaci
![]()
lub dla cylindra
![]()
.
Zasada zachowania pędu
Rozważmy drugie prawo Newtona dla poszczególnego punktu materialnego w postaci
![]()
, ![]()
.
Wtedy dla układu w całości
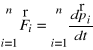
![]()
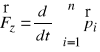
.
Wówczas
![]()
.
Jeżeli ![]()
, to ![]()
. Jest to prawo zachowania pędu.
Zaznaczmy, że często stosowana postać prawa zachowania pędu jest następująca
![]()
.
Zasada zachowania momentu pędu
Rozważmy drugie prawo Newtona dla poszczególnego punktu materialnego w postaci
![]()
, ![]()
.
Wtedy dla układu w całości
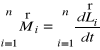
![]()
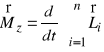
.
Wówczas
![]()
.
Jeżeli ![]()
, to ![]()
. Jest to prawo zachowania momentu pędu.
Przy tym często stosowana postać prawa zachowania momentu pędu jest następująca
![]()
.
Zasada zachowania energii
Dla odosobnionego i zachowawczego układu mamy
![]()
.
W przypadku osobnego punktu materialnego
![]()
.
Wyszukiwarka
Podobne podstrony:
Fizyka W 6 B, Fizyka wykłady i zagadnienia Czapla
Pyt Ekz Fiz, Fizyka wykłady i zagadnienia Czapla
Zagad Fiz, Fizyka wykłady i zagadnienia Czapla
Fizyka W 1, Fizyka wykłady i zagadnienia Czapla
Fizyka W 2, Fizyka wykłady i zagadnienia Czapla
Fizyka W 9, Fizyka, FIZYKA, Fizyka wykłady i zagadnienia Czapla, Elektrodynamika
Fizyka W 10b, Fizyka, FIZYKA, Fizyka wykłady i zagadnienia Czapla, Elektrodynamika
Fizyka W 6 A, Fizyka wykłady i zagadnienia Czapla
Fizyka W 10c, Fizyka, FIZYKA, Fizyka wykłady i zagadnienia Czapla, Elektrodynamika
temp krytyczna, TRANSPORT PWR, STUDIA, SEMESTR II, FIZYKA, fizyka-wyklad, zagadnienia opracowane, za
sprawozdanie 33a, fizyka 2 wykład i zagadnienia, 33
Zjawisko dopplera, TRANSPORT PWR, STUDIA, SEMESTR II, FIZYKA, fizyka-wyklad, zagadnienia opracowane,
Sprawko 89, fizyka 2 wykład i zagadnienia, 89
sprawdzanie prawa hooke a wyznaczanie modu u younga 1, fizyka 2 wykład i zagadnienia, sprawozda
Pomiar zależności rezystancji metali i półprzewodników od temperatury, fizyka 2 wykład i zagadnienia
siła i energia, TRANSPORT PWR, STUDIA, SEMESTR II, FIZYKA, fizyka-wyklad, zagadnienia opracowane, za
więcej podobnych podstron