Politechnika Cz stochowska

Wydział In ynierii Mechanicznej i Informatyki

Kierunek: Informatyka

Specjalno : In ynieria Oprogramowania i Systemy Informatyczne

PRACA MAGISTERSKA

ANALIZA POZIOMU YCIA W POSZCZEGÓLNYCH

WOJEWÓDZTWACH Z WYKORZYSTANIEM TEORII

ZBIORÓW ROZMYTYCH

ROBERT J DRUSZEK

Nr albumu: 9262
Rok akademicki: 2002/2003
Promotor:

Prof. dr hab. in . Ludmiła Dymowa

Data oddania pracy:
Ocena : ............................................ Podpis ..............................................

2

Spis tre ci.

1. Wst p i cele pracy. .............................................................................. 3
2. Wiadomo ci teoretyczne...................................................................... 6

2.1. Wybór kryteriów szczegółowych....................................................................... 6
2.2. Hierarchiczna struktura kryteriów...................................................................... 8
2.3. Sporz dzenie lingwistycznej macierzy parzystych porówna ............................10
2.4. Ustalenie współczynników wzgl dnej wa no ci dla poszczególnych kryteriów
szczegółowych.........................................................................................................11
2.5. Wybór odpowiedniej funkcji u yteczno ci i wyznaczenie jej punktów
kluczowych. ............................................................................................................12
2.6. Sformułowanie kryteriów globalnych. ..............................................................18

3. Algorytmizacja zadania. .................................................................... 21

3.1. Schemat blokowy aplikacji. ..............................................................................21
3.2. Schemat bazy danych. ......................................................................................22

4. Cykl pracy programu......................................................................... 26

4.1. Inicjalizacja programu. .....................................................................................26
4.2. Kryteria szczegółowe........................................................................................26
4.3. Kryteria globalne..............................................................................................34
4.4. Wykresy. ..........................................................................................................38

5. Wnioski............................................................................................. 49
6. Literatura........................................................................................... 50
7. Zał czniki.......................................................................................... 51
8. Spis ilustracji..................................................................................... 55
9. Spis tabel........................................................................................... 56

3

1. Wst p i cele pracy.

Teoria zbiorów rozmytych [6], rozpocz ta w 1965 roku artykułem "Fuzzy

Sets" w czasopi mie "Information and Control", autorstwa matematyka
ameryka skiego, Lotfiego A. Zadeha, dzi emerytowanego profesora
Uniwersytetu Columbia w Nowym Jorku i profesora w Berkeley w Kalifornii,
jest obecnie rozwijana bardzo intensywnie i odgrywa coraz wi ksz rol
w zastosowaniach informatycznych matematyki, w tym tak e w zastosowaniach
u ytkowo-technicznych.

W wi kszo ci dziedzin praktycznej działalno ci człowieka mamy do

czynienia z niedoskonało ci informacji. Mo na wymieni ró ne rodzaje
niedoskonało ci, np. niepewno , niekompletno informacji i inne. Informacje
w warunkach niepewno ci rozmytej, któr spotykamy cz sto w j zyku
naturalnym, mo na nazywa informacj lingwistyczn . Przykładem za
informacji lingwistycznej mog by takie okre lenia jak: mały, du y, bardzo
mały, bardzo du y itp., które s zrozumiałe dla człowieka, ale trudne do
wyra enia w postaci liczbowej. Warto zwróci uwag na fakt, e ka de z tych
okre le lingwistycznych, z uwagi na nieprecyzyjnie zdefiniowane ró nice
miedzy nimi, stanowi pojecie nieostre, niejednoznaczne, rozmyte. Trzeba
podkre li wyst powanie w wy ej wymienionych okre leniach pewnego stopnia
subiektywizmu.

Nale y równie zauwa y , e do czasu sformułowania teorii zbiorów

rozmytych, komputery mogły prawie w cało ci wykorzystywa i przetwarza
informacje numeryczne, natomiast informacje lingwistyczne w bardzo
niewielkim stopniu. Z tego powodu wynikła potrzeba stworzenia aparatu
matematycznego, który umo liwiałby przetwarzanie informacji lingwistycznej
dla celów wspomagania decyzji, które człowiek musi podejmowa w zło onych
sytuacjach. Takim narz dziem słu cym do formalizowania przybli onego
wnioskowania w otoczeniu nieostrych i niejednoznacznych terminów jest
wła nie teoria zbiorów rozmytych. Stworzyła ona mo liwo konstrukcji

4

automatycznych systemów przybli onego wnioskowania. Znalazła te
zastosowanie w systemach wspomagania decyzji w takich dziedzinach jak
technika, medycyna, ekonomia i zarz dzanie.

Teoria zbiorów rozmytych wywiera równie gł boki wpływ na nauki

podstawowe jak matematyka, fizyka i chemia, co wiadczy o du ym stopniu jej
uniwersalno ci. ródeł logiki rozmytej niektórzy upatruj w pracach wielkiego
polskiego matematyka i logika Jana Łukasiewicza.

Zaproponował on taki

rachunek zda , w którym danemu zdaniu mo na przypisa nie tylko jedn
z dwóch warto ci (0 i 1, prawda i fałsz), ale dowoln liczb , zawart pomi dzy
0 a 1. To wła nie wielowarto ciow logik Łukasiewicza zastosował w swej
pionierskiej pracy Lotfi Zadeh, dlatego te logika rozmyta powstała faktycznie
jednocze nie z teori zbiorów rozmytych. Co wi cej, zarówno ona sama, jak
w ogóle teoria zbiorów i liczb rozmytych, znalazły bardzo szybko zastosowanie
w informatyce i to tej najbardziej praktycznej, in ynierskiej; tak szybko, e
wła ciwie dzi mo na mówi o wzajemnej i bezpo redniej inspiracji. Działem
informatyki naj ci lej zwi zanym z rozmytymi poj ciami jest teoria i praktyka
systemów ekspertowych, a tak e teoria i praktyka systemów czasu
rzeczywistego, niezb dnych dzi w sterowaniu wieloma procesami
technologicznymi.

Zbiory rozmyte (ang. fuzzy sets) s wykorzystywane do formalnego

okre lania nieostrych, nieprecyzyjnych lub wieloznacznych poj . Maj one
swoje ródło w rozwoju teorii sterowania, teorii systemów i logik
wielowarto ciowych. Zauwa ono, bowiem, e chocia umysł ludzki jest zdolny
do rozumowania w kategoriach przybli onych, to mimo to jest w stanie
przetwarza dane przybli one i niejednoznaczne oraz wyznacza przybli one
rozwi zania, czego nie s w stanie zrobi komputery działaj ce w oparciu
o cisłe reguły. W teorii zbiorów rozmytych funkcja charakterystyczna została
uogólniona

i

nazywa si

funkcj

przynale no ci

(u yteczno ci).

Przyporz dkowuje ona ka demu elementowi zbioru warto ci z przedziału [0,1],

5

a nie tylko jedn z warto ci z dwuelementowego zbioru {0,1}, jak to jest
w klasycznej teorii zbiorów.

Logiczn podstaw poj cia podzbioru rozmytego jest logika

wielowarto ciowa. Podzbiór rozmyty umo liwia opisanie poj , których granica
mi dzy posiadaniem pewnej własno ci i jej brakiem jest rozmyta.

Celem pracy jest opracowanie metody i oprogramowania pomocnego przy

analizie poziomu ycia w poszczególnych województwach. W pracy zostanie

wykorzystana metodologia zbiorów rozmytych, w tym wybór kryteriów
szczegółowych, podział kryteriów na kategorie, wyznaczenie lingwistycznej
macierzy parzystych porówna , obliczenie współczynników wzgl dnej
wa no ci, wyznaczenie funkcji przynale no ci (u yteczno ci) i jej punktów
kluczowych, wyznaczenie warto ci kryteriów globalnych oraz sporz dzenie
odpowiednich wykresów ilustruj cych wizualnie uzyskane wyniki. W tym celu
opracowano oprogramowanie, w którym zostały zaimplementowane powy sze
mechanizmy, a tak e utworzono baz danych, w której umieszczono informacje
na temat kryteriów szczegółowych w poszczególnych województwach jak
równie umieszczono dane uzyskane z wylicze przeprowadzonych
z wykorzystaniem zaimplementowanych w aplikacji metodologii matematycznej.

Nale y zaznaczy , e wszystkie dane wykorzystane w programie

pochodz z 31 grudnia 2001r. i s oparte na Roczniku Statystycznym [7].

6

2. Wiadomo ci teoretyczne.

2.1. Wybór kryteriów szczegółowych.

W celu wyboru odpowiednich kryteriów szczegółowych nale y zastanowi

si , jakie parametry dotycz ce poziomu ycia nas interesuj . W tym miejscu
pojawia si pierwszy problem, jaki napotykamy, a mianowicie subiektywizm
tego wyboru. Ludzie przy ocenie jako ci ycia w okre lonym miejscu kieruj si
ró nymi czynnikami, np. liczba miejsc w teatrach, liczba lekarzy, rednia płaca
w wybranym mie cie, itp. Niestety nale y wybra te kryteria, które maj dla nas
znaczenie, w ten sposób ogranicza si do pewnego stopnia mo liwo analizy
poziomu ycia dla innych osób o innych potrzebach. Podczas doboru kryteriów
mo na napotka na nast puj ce problemy:
-

nierównowa no kryteriów: cz

kryteriów jest bardziej istotna, a cz

mniej istotna,

-

cz

kryteriów jest w stosunkach antagonistycznych, oznacza to, e

ulepszenie jakiego kryterium spowoduje automatycznie pogorszenie innego,

-

kryteria szczegółowe dziel si najcz ciej na dwie grupy:

kryteria ilo ciowe

(np. rednia płaca na danym terenie), kryteria jako ciowe - oszacowywane na
podstawie ocen ekspertów z danych dziedzin (np. ocena stopnia ryzyka danej
inwestycji). W tym drugim wypadku powstaje problem wła ciwego ustalenia
warto ci dla danego kryterium - oceny poszczególnych ekspertów mog si
od siebie ró ni , czasami nawet znacz co, dlatego kryteria z grupy
jako ciowych s obarczone du ym stopniem subiektywizmu,

-

ilo kryteriów mo e by zbyt du a przez co trudne staje si oszacowanie,
które z parametrów s wa niejsze, a które mniej wa ne.
W przypadku analizy poziomów ycia w poszczególnych województwach

wykorzystywane s tylko kryteria ilo ciowe, dzi ki czemu udało si zmniejszy
stopie subiektywizmu kryteriów szczegółowych.

Kryteria szczegółowe podzielono na sze kategorii:

7

-

zdrowie,

-

finanse,

-

infrastruktura,

-

czysto ,

-

praca,

-

przest pczo ,
W kategorii zdrowie umieszczono kryteria:

-

lekarze, kryterium to oznacza liczb lekarzy na 10 tys. ludno ci,

-

łó ka szpitalne, oznaczaj ce ilo łó ek szpitalnych na 10 tys. ludno ci,
W kategorii finanse umieszczono kryteria:

-

rodki trwałe, kryterium to oznacza warto brutto rodków trwałych

w przeliczeniu na jednego mieszka ca danego województwa,

-

produkt krajowy brutto - warto produktu krajowego brutto w zł.
w przeliczeniu na jednego mieszka ca,

-

dochody - warto nominalnych dochodów brutto w sektorze gospodarstw
domowych w zł. na jednego mieszka ca.
Kategoria infrastruktura zawiera nast puj ce kryteria:

-

kolej - linie kolejowe eksploatowane normalnotorowe w km na 100 km²
powierzchni ogólnej,

-

drogi - drogi publiczne o twardej nawierzchni w km na 100 km² powierzchni
ogólnej województwa,

-

sklepy - ilo sklepów w danym województwie w przeliczeniu na 10 tys.
ludno ci,
Nast pn kategori jest czysto i zawiera nast puj ce kryteria:

-

oczyszczalnie - ludno korzystaj ca z oczyszczalni cieków w procentach
ludno ci ogółem,

-

emisja gazów - emisja przemysłowych zanieczyszcze powietrza gazowych
i pyłowych z zakładów szczególnie uci liwych dla czysto ci powietrza
w tys. ton na 1 km² powierzchni województwa,

8

-

lesisto - powierzchnia gruntów le nych w procentach powierzchni
całkowitej województwa,
Kategoria praca zawiera nast puj ce kryteria:

-

pracuj cy - liczba osób zatrudnionych w przeliczeniu na 10 tys. ludno ci
w danym województwie,

-

bezrobotni - liczba zarejestrowanych bezrobotnych w przeliczeniu na 10 tys.
ludno ci w danym województwie,

-

rednia płaca - przeci tne miesi czne wynagrodzenie brutto w zł. w danym

województwie,
Ostatni kategori jest przest pczo , która zawiera kryteria:

-

przest pstwa - ilo przest pstw stwierdzonych w zako czonych
post powaniach przygotowawczych na 10 tys. ludno ci,

-

wska nik - wska nik wykrywalno ci sprawców przest pstw stwierdzonych
w procentach.

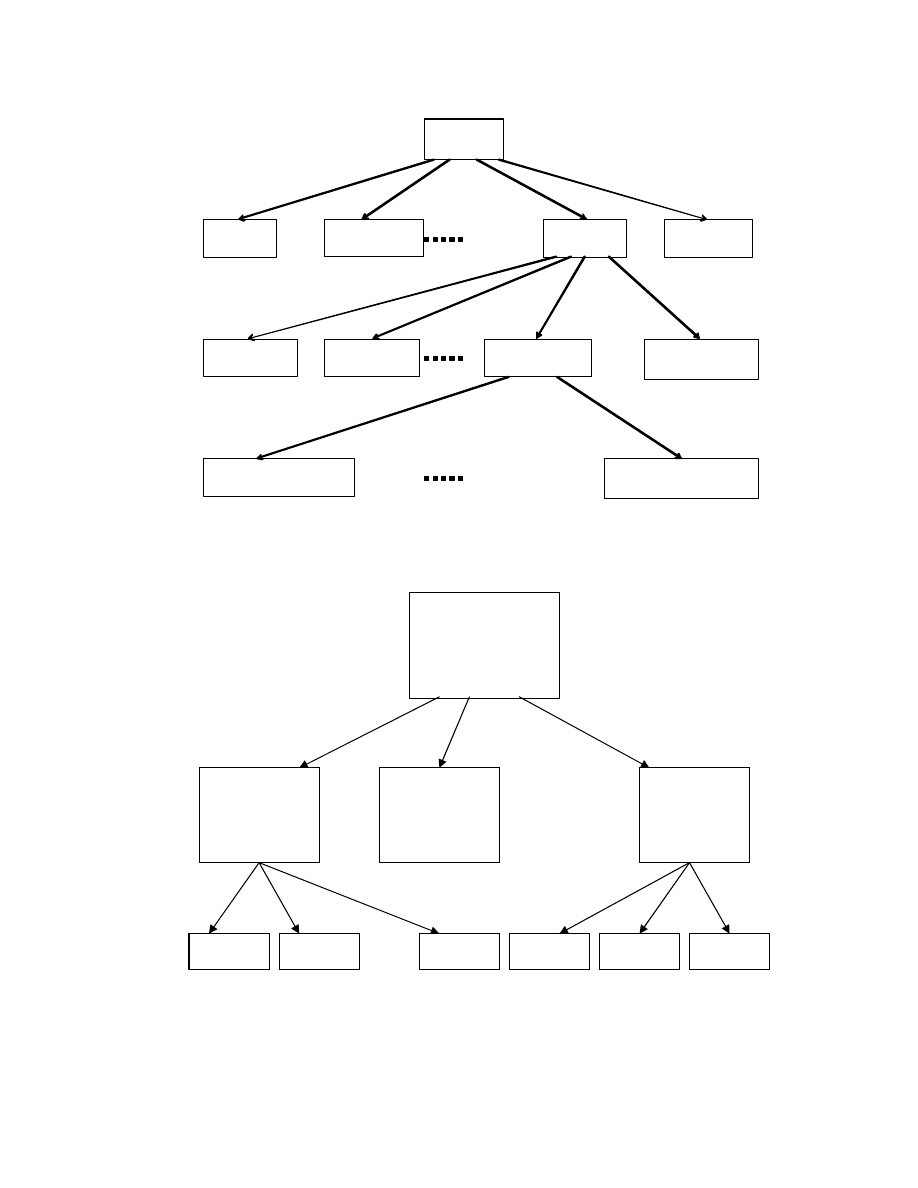
2.2. Hierarchiczna struktura kryteriów.

Dzi ki zastosowaniu hierarchii kryteriów szczegółowych udało si

uzyska czyteln struktur zale no ci mi dzy poziomami hierarchii. Rys. 2.1
przedstawia schemat budowania struktury hierarchicznej.

W naszym przypadku odpowiednia struktura b dzie wygl dała jak na rys.

2.2., b d wyst powa trzy poziomy hierarchii: kryteria szczegółowe i kategorie
tych kryteriów i ogólne kryterium jako ci. Kryteria globalne poszczególnych
kategorii oblicza si zgodnie ze wzorami 2.3 - 2.5, natomiast w przypadku
ogólnego kryterium jako ci zamiast warto ci funkcji przynale no ci
wykorzystuje si warto ci kryteriów globalnych poszczególnych kategorii,
wcze niej wyznaczaj c dla poszczególnych kategorii macierz parzystych
porówna i obliczaj c współczynniki wzgl dnej wa no ci kategorii.

9

1

,

1

−

n

D

D

n

2

1 ,

n

D

−

1

1

−

−

n

i,

n

D

1

1

−

−

n

m

,

n

D

1

2

1

,

i,

n

n

D

−

−

2

2

1

,

i,

n

n

D

−

−

2

1

2

−

−

−

n

n

i

,

i,

n

D

1

1

2

−

−

−

n

i

n

m

,

i,

n

D

1

2

1

3

,

n

n

i

,

i

,

n

D

−

−

−

2

1

2

1

3

−

−

−

−

−

n

i,

n

i

n

n

m

,

i,

i,

n

D

Rys. 2.1. Ogólny schemat budowania struktury hierarchicznej.

Rys. 2.2. Hierarchiczna struktura u yta w analizowanym problemie.

Ogólne

kryterium

jako ci

Kategoria 1

Kategoria 2

Kategoria n

...

Kryterium 1 Kryterium 2

Kryterium n

...

Kryterium 1 Kryterium 2 Kryterium n

10

2.3. Sporz dzenie lingwistycznej macierzy parzystych porówna .

W celu porównania wa no ci kryteriów budowana jest kwadratowa

macierz parzystych porówna , w której oszacowuje si które kryteria i jak
bardzo s wa niejsze od innych kryteriów.

Zgodnie z danymi bada psychofizycznych przeci tny człowiek rozró nia

nie wi cej ni od 7 do 9 poziomów na skali pewnego parametru. Wynika to ze
specyficznych cech konkretnych j zyków, w których nie ma odpowiednio
precyzyjnych cz ci mowy (przymiotników), aby mo na było w sposób
precyzyjny ustali wi ksz ilo poziomów. Je eli udost pnione byłoby wi cej
poziomów wówczas cz

poziomów uległaby zbyt du emu rozmyciu, przez co

niemo liwe byłoby rozró nienie ró nic w s siaduj cych ze sob poziomach.
Ustalono nast puj ce odpowiedniki lingwistyczne dla poszczególnych
poziomów:
-

poziom 1 - identyczno parametrów,

-

poziom 2 - po rednia warto mi dzy poziomami 1 i 3,

-

poziom 3 - umiarkowana wy szo pierwszego parametru nad drugim,

-

poziom 4 - po rednia warto mi dzy poziomami 3 i 5,

-

poziom 5 - istotna wy szo pierwszego parametru nad drugim,

-

poziom 6 - po rednia warto mi dzy poziomami 5 i 7,

-

poziom 7 - znaczna wy szo pierwszego parametru nad drugim,

-

poziom 8 - po rednia warto mi dzy poziomami 7 i 9,

-

poziom 9 - nadzwyczajnie silna wy szo pierwszego parametru nad drugim.

Tablica 2.1. przedstawia przykładow macierz parzystych porówna dla
kryteriów z grupy rynek pracy.

11

Tab. 2.1. Macierz parzystych porówna dla kryteriów z grupy rynek pracy.

Pracuj cy

Bezrobotni

rednia płaca

Pracuj cy

1

1/2

1/4

Bezrobotni

2

1

1/2

rednia płaca

4

2

1

Jak wida wystarczy wypełni macierz z jednej strony przek tnej,

warto ci z drugiej strony przek tnej s odwrotno ci warto ci le cych
symetrycznie po drugiej stronie przek tnej zgodnie ze wzorem 2.1.:

i

j

j

i

a

a

1

=

(2.1)

2.4. Ustalenie

współczynników

wzgl dnej

wa no ci

dla

poszczególnych kryteriów szczegółowych.

Macierz parzystych porówna posiada struktur pozwalaj c oceni , który

z czynników jest wa niejszy od innych, natomiast nie daje oceny wprost
wa no ci konkretnego kryterium, dlatego w celu ustalenia konkretnej warto ci
wa no ci dla danego kryterium wykorzystuje si metod współczynników
wzgl dnej wa no ci kryteriów.

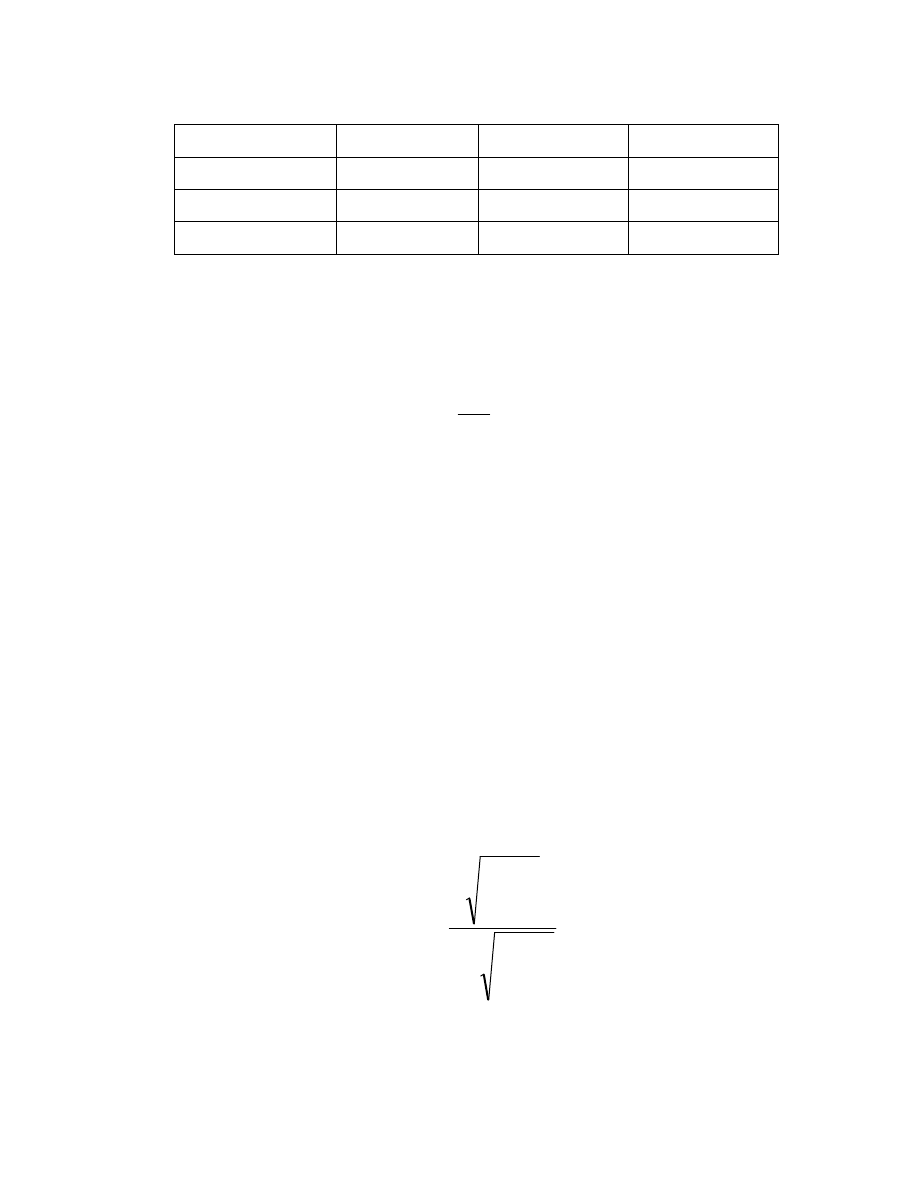
W celu obliczenia warto ci wzgl dnej wa no ci (rangi) [1] danego

kryterium nale y zastosowa wzór 2.2:

n

a

a

a

n

i

n

n

j

ij

n

n

j

ij

i

∗

=

∏

∏

=

=

=

1

1

1

(2.2)

12

Po zastosowaniu tego wzoru dla danych z tablicy 2.1. otrzymamy

nast puj ce wyniki zamieszczone w tablicy 2.2:

Tab. 2.2. Macierz parzystych porówna z wyliczonymi rangami kryteriów.

Pracuj cy

Bezrobotni

rednia płaca

Ranga

Pracuj cy

1

1/2

1/4

0,4285

Bezrobotni

2

1

1/2

0,8571

rednia płaca

4

2

1

1,7143

Jak wida z oblicze najwa niejszym kryterium w tej tabeli jest rednia

płaca, nast pnym w kolejno ci pod wzgl dem wa no ci jest kryterium
Bezrobotni, za najmniej istotnym kryterium w tej macierzy jest Pracuj cy.

Taka metodologia daje czytelny obraz wa no ci okre lonych kryteriów,

dzi ki czemu uzyskuje si mo liwo precyzyjnego zastosowania tych wyników
w dalszej cz ci zastosowanych algorytmów.

2.5. Wybór odpowiedniej funkcji u yteczno ci i wyznaczenie jej

punktów kluczowych.

Okre lenie warto ci rang pozwoli na u ycie tych wyników we wzorach na

kryteria globalne, ale wcze niej nale y okre li kształt oraz wybra punkty
kluczowe funkcji u yteczno ci.

Nie zawsze wzrost warto ci jakiego kryterium jest pozytywnym

zjawiskiem, np. w przypadku kryterium Przest pstwa stwierdzone wzrost
warto ci tego kryterium musi powodowa obni enie poziomu ycia. Z kolei
wzrost warto ci kryterium rednia płaca jest sytuacj jak najbardziej pozytywn ,
co z kolei powinno powodowa zwi kszenie warto ci funkcji tego kryterium.

Funkcje u yteczno ci (przydatno ci) pozwalaj okre li , w jakich

przypadkach wzrost warto ci jakiego kryterium powoduje zwi kszenie si

13

warto ci funkcji tego kryterium, a w jakich przypadkach spadek warto ci
kryterium powoduje wzrost warto ci jego funkcji.
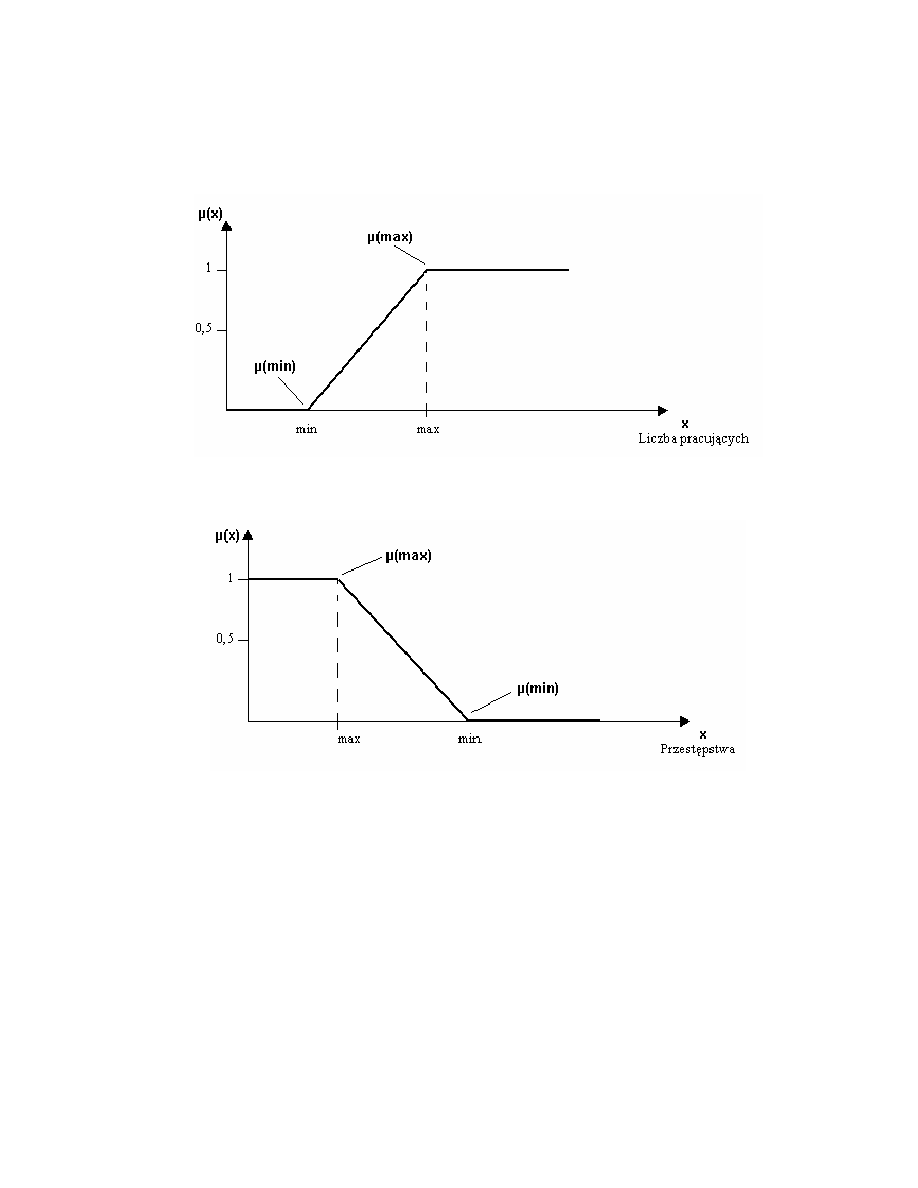
Poni sze rysunki przedstawiaj ró ne typy funkcji u yteczno ci:

Rys. 2.3. Typ funkcji dla kryterium Pracuj cy.

Rys. 2.4. Typ funkcji dla kryterium Przest pstwa.

14

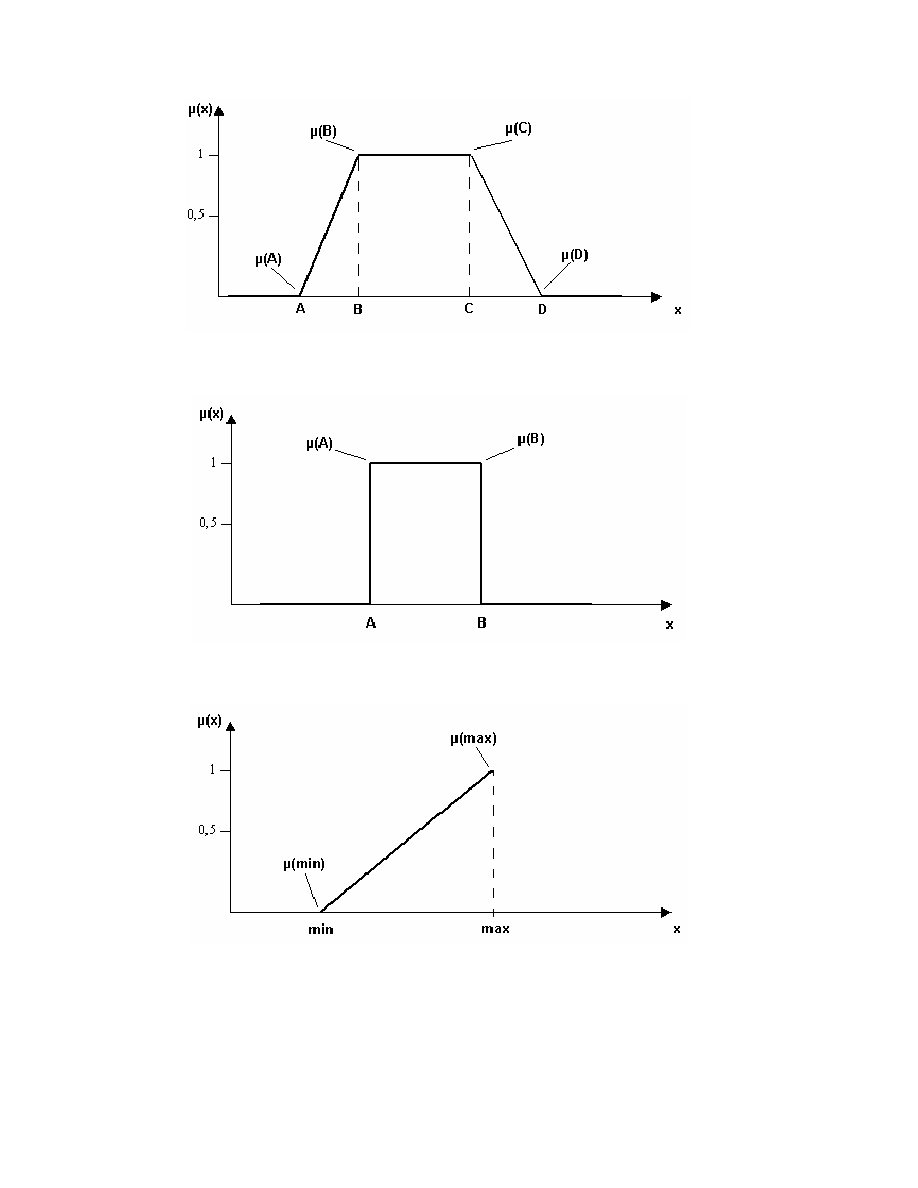
Rys. 2.5. Typ funkcji trapezoidalnej.

Rys. 2.6. Typ funkcji dwuwarto ciowej.

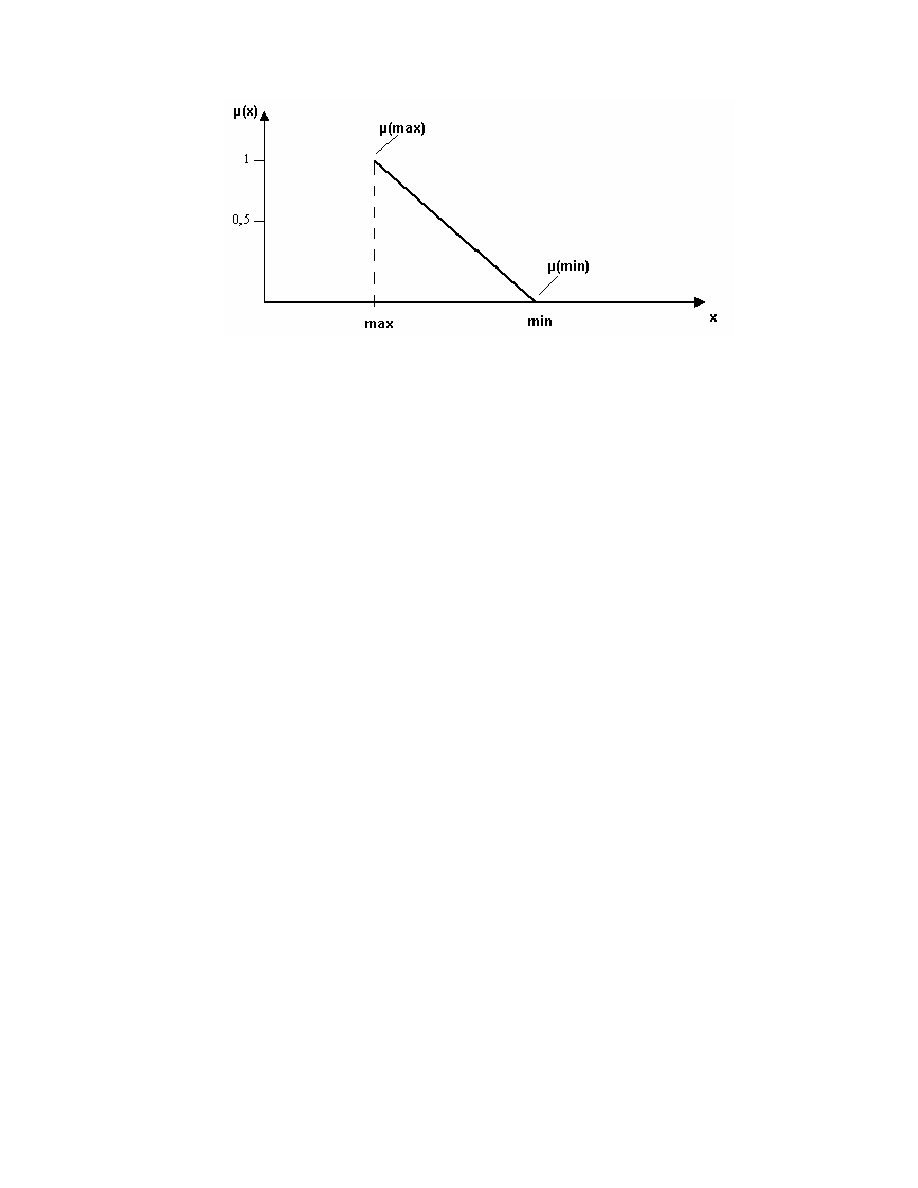
Rys. 2.7. Funkcja wzrastaj ca.

15

Rys. 2.8. Funkcja opadaj ca.

Rysunek 2.3. przedstawia najcz stsze wykorzystanie funkcji u yteczno ci.

W tym przypadku wzrost warto ci parametru powoduje wzrost warto ci funkcji
u yteczno ci. Podczas gdy warto kryterium ma nisk warto funkcja ma
warto zerow , w miar wzrastania warto ci kryterium ro nie warto funkcji a
do warto ci, po której wzrost warto ci kryterium nie powoduje ju wzrostu
warto ci funkcji. Mo na takie zachowanie funkcji zinterpretowa na przykładzie
funkcji opisuj cej liczb osób pracuj cych: niewielka ilo pracuj cej ludno ci
na danym terenie nie daje wymiernych korzy ci finansowych, w efekcie warto
funkcji, mimo zwi kszania si warto ci kryterium, nie zwi ksza si ; po
przekroczeniu warto ci kryterium b d cej pierwszym punktem kluczowym
funkcji zwi ksza si warto funkcji czyli liczba osób pracuj cych zwi kszyła si
do tego stopnia, e dalszy wzrost, poprzez zwi kszanie si ilo ci pieni dzy na
rynku, jest pozytywn tendecj dla całego województwa; zwi kszanie si ilo ci
ludzi pracuj cych zwi ksza warto funkcji do momentu, gdy liczba pracuj cych
jest na tyle du a, e dalsze jej wzrastanie jest ju niemo liwe lub gdy
zwi kszanie si liczby pracuj cych nie powoduje wzrostu poziomu ycia
w województwie - jest to drugi punkt kluczowy tej funkcji, warto funkcji
w tym punkcie wynosi 1 i dalszy wzrost warto ci kryterium nie powoduje
wzrostu warto ci funkcji.

Rysunek 2.4. przedstawia równie cz sto wykorzystywany rodzaj funkcji

u yteczno ci. Przy niskiej warto ci kryterium warto funkcji wynosi 1,

16

wzrastanie warto ci kryterium nie powoduje zmniejszania warto ci funkcji, a do
momentu gdy funkcja przekroczy swój punkt kluczowy kiedy to warto funkcji
zaczyna spada ; dalszy wzrost warto ci kryterium powoduje spadek warto ci
funkcji a do momentu gdy warto funkcji spadnie poni ej drugiego punktu
kluczowego, od tego momentu dalszy wzrost warto ci kryterium nie powoduje
zmniejszania si warto ci funkcji, która wynosi 0. Tak funkcj mo na
zinterpretowa na przykładzie ilo ci przest pstw na danym terenie: niewielka
ilo przest pstw nie powoduje uci liwo ci dla mieszka ców, st d na pocz tku
warto funkcji mimo zwi kszania si kryterium (ilo przest pstw) nie
zmniejsza si , ale po przekroczeniu pewnej warto ci, która jest dla tej funkcji
punktem kluczowym, warto funkcji zaczyna spada oznacza to, e ilo
przest pstw na danym terenie zwi kszyła si do tego stopnia, e powoduje to
zwi ksznie uci liwo ci tego procederu i dlatego warto funkcji u yteczno ci
zaczyna spada ; dalszy wzrost przest pczo ci powoduje pogarszanie si jako ci

ycia, st d warto funkcji u yteczno ci spada; spadek odbywa si a do

momentu gdy ilo przest pstw na danym terenie jest ju na tyle wysoka, e
dyskomfort zwi zany z uci liwo ci tych przest pstw powoduje niemo no
dalszego mieszkania na tym terenie; jest to kolejny punkt kluczowy danej funkcji
u yteczno ci, funkcja przyjmuje w tym punkcie warto 0.

Rysunek 2.5. przedstawia funkcj u yteczno ci, w której wzrost warto ci

kryterium nie powoduje zwi kszenia a do punktu kluczowego A, po
przekroczeniu tego punktu, w miar zwi kszania warto ci kryterium warto
funkcji zaczyna rosn . Wzrost warto ci funkcji zwi ksza si w miar
zwi kszania warto ci kryterium w przedziale od punktu kluczowego A do punktu
kluczowego B. Po przekroczeniu punktu kluczowego B warto funkcji osi ga
warto 1 i w miar dalszego zwi kszania warto ci kryterium funkcja nie
zwi ksza swojej warto ci a do punktu kluczowego C, po przekroczeniu którego
warto funkcji u yteczno ci zaczyna spada mimo zwi kszania si warto ci
kryterium. Warto funkcji spada a do punktu kluczowego D, w którym warto

17

funkcji spada do zera. Po przekroczeniu punktu kluczowego D pomimo
zwi kszania si warto ci kryterium, warto funkcji nie zmienia si .

Rysunek 2.6. przedstawia funkcj u yteczno ci przyjmuj c tylko dwie

warto ci 0 i 1. Warto funkcji wynosi 0 gdy warto kryterium ro nie od 0 do
pierwszego punktu kluczowego, po jego przekroczeniu warto funkcji
przyjmuje 1 i nie zmienia si a do nast pnego punktu kluczowego , po którego
przekroczeniu warto funkcji przyjmuje 0.

Nale y zauwa y , e ka da funkcja u yteczno ci posiada okre lone

punkty kluczowe, które nale y oszacowa . Dla przykładu przeanalizujmy
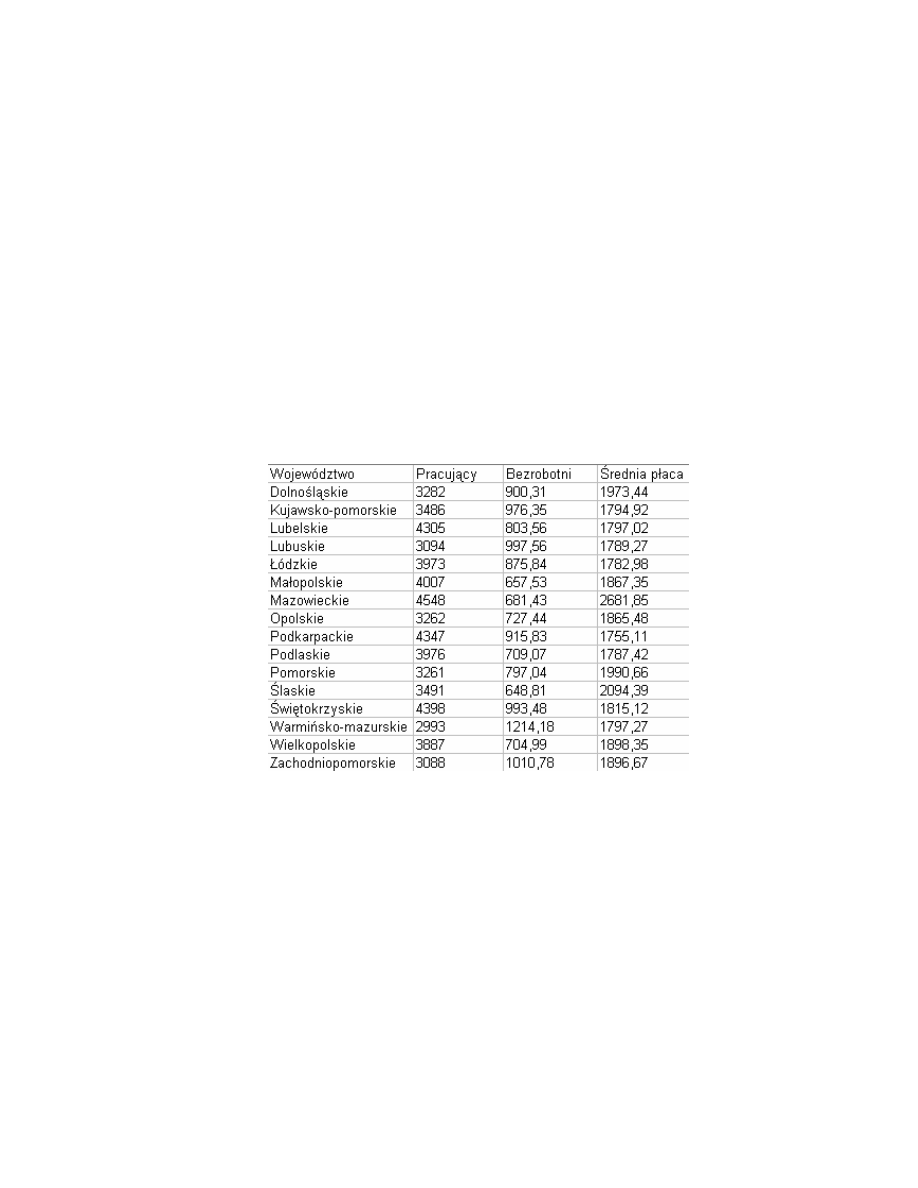
kryterium Pracuj cy w tabeli Praca:

Tab. 2.3. Tabela Praca.

Jak wida najmniejsza liczba osób pracuj cych jest w województwie
Warmi sko-mazurskim: 2993 osoby na 10 tys. ludno ci, z kolei najwi cej osób
pracuje w województwie Mazowieckim: 4548 osób na 10 tys. ludno ci. W obu
przypadkach warto ci kryterium mogłyby by punktami kluczowymi funkcji
u yteczno ci przedstawionej na rys. 2.3. jednak wtedy w przypadku
województwa Warmi sko-mazurskiego warto funkcji wynosiłaby 0. Jako, e
nie chcemy przypisywa temu województwu tak niskiej oceny (by mo e ma ono
jakie inne walory analizowane przez program) dlatego jako pierwszy punkt

18

kluczowy wybieramy warto 2900. Drugim punktem kluczowym funkcji
oznaczaj cym najlepsze województwo według tego kryterium mogłaby by
warto kryterium oznaczaj ca województwo Mazowieckie, ale przyjmiemy
warto 5000 oznaczaj ca połow ludno ci aktywn zawodowo. W ten sposób
wyznaczyli my funkcj u yteczno ci zgodnie z rys. 2.3.; pierwszy punkt
kluczowy to warto 2900, natomiast drugi punkt kluczowy to warto kryterium
równe 5000. Podobnie ustalamy punktu kluczowe dla pozostałych kryteriów.

2.6. Sformułowanie kryteriów globalnych.

W celu rozstrzygni cia problemu nale y opracowa sposoby agregowania

wszystkich dost pnych informacji w globalne ilo ciowe oceny. Wynikiem musi
by liczba - warto globalnego wska nika jako ci.

Poni sze wzory [1] przedstawiaj metodologi pozwalaj c na obliczenie

globalnych kryteriów na podstawie kryteriów szczegółowych i ich rang.

( )

( )

( )

(

)

,...

,

,

min

3

2

1

3

3

2

2

1

1

1

α

α

α

µ

µ

µ

x

x

x

DD

=

(2.3)

( )

∏

=

=

N

i

i

i

i

x

DD

1

2

α

µ

(2.4)

( )

=

=

N

i

i

i

i

N

x

DD

1

3

*

µ

α

(2.5)

gdzie:

1

(x

1

),

2

(x

2

), ...,

N

(x

N

) - funkcje u yteczno ci,

{x

i

}, i=1, 2, ..., N - jako ciowe i ilo ciowe parametry jako ci,

1

,

2

, ...,

N

- współczynniki wzgl dnej wa no ci kryteriów.

19

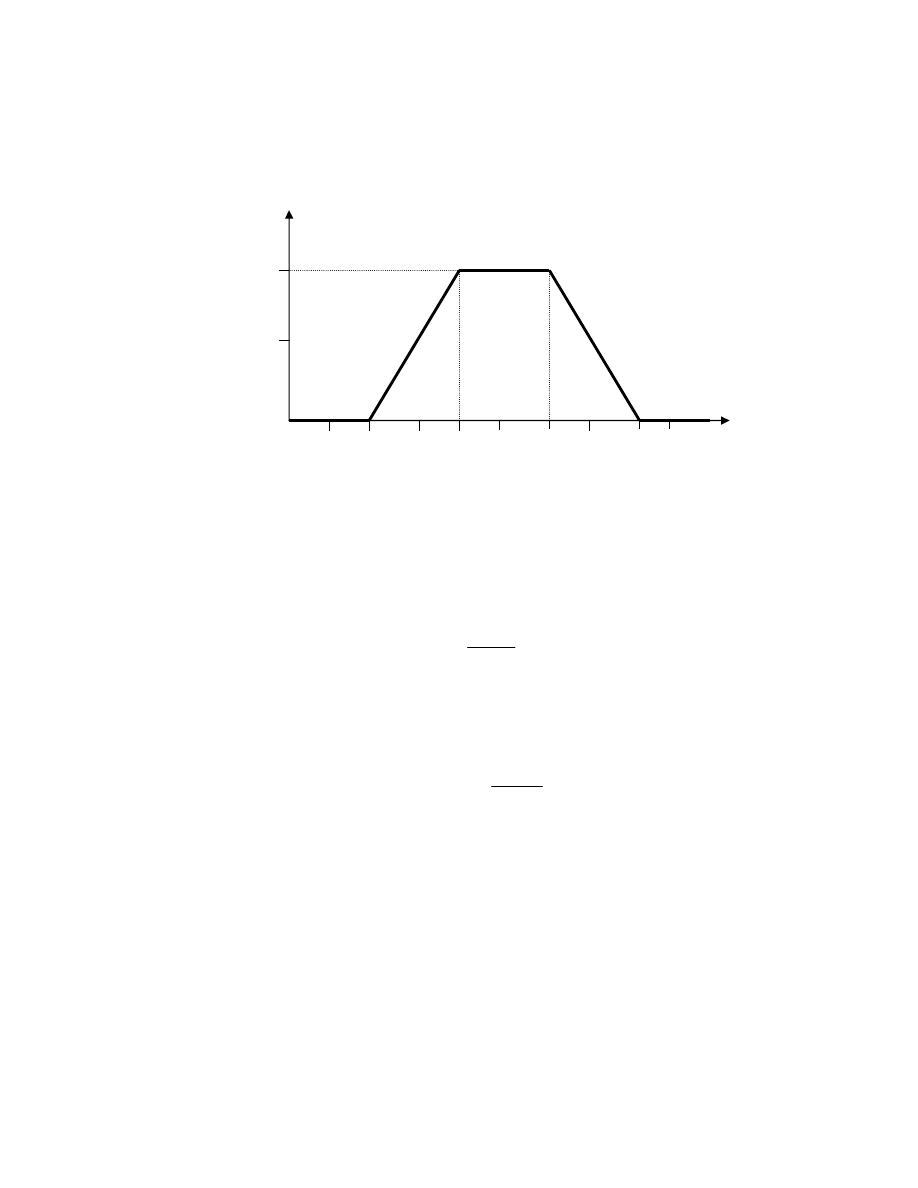
W ka dym z trzech wzorów nale y przeprowadzi operacj obliczenia

warto ci funkcji dla okre lonej warto ci kryterium szczegółowego (rys.2.9).

Rys. 2.9. Obliczenie warto ci funkcji u yteczno ci.

Poni ej przedstawiono wzory potrzebne do obliczenia warto ci funkcji

w poszczególnych punktach.

;

0

)

(

;

0

)

(

;

1

)

(

;

1

)

(

;

1

)

(

;

1

)

(

;

)

(

;

0

)

(

;

0

)

(

=

=

−

−

−

=

=

=

=

−

−

=

=

=

I

f

H

f

F

H

F

G

G

f

F

f

E

f

D

f

B

D

B

C

C

f

B

f

A

f

Wszystkie warto ci

i

(x

i

) zostały wyliczone za pomoc powy szych

wzorów.

Wzory DD

2

i DD

3

maj własno wyrównywania małych własno ci

jednego kryterium szczegółowego poprzez powi kszanie innych, co nie jest
dobrym zjawiskiem. Wzór DD

1

nie ma tej wady, dzi ki czemu prowadzi do

1

0,5

0

A

B

C

D

E

F

G

H

I

20

wnikliwej oceny, wzór ten nazywany jest kryterium maksymalnego pesymizmu,
w zwi zku z czym w wypadkach zada wielokryterialnej optymalizacji
najbardziej racjonalne jest u ycie wzoru DD

1

.

W rozwa aniu problemu oceny jako ci ycia w poszczególnych

województwach wykorzystano wszystkie trzy warianty obliczania kryterium
globalnego. We wszystkich trzech przypadkach otrzymujemy oceny od 0 do 1.
Przy czym ocena 0 oznacza najgorszy wariant, natomiast ocena 1 - najlepszy
przypadek. Zgodno rezultatów otrzymanych za pomoc podanych kryteriów
zwi ksza zaufanie, co do prawidłowo ci przeprowadzonych oblicze .

21

3. Algorytmizacja zadania.

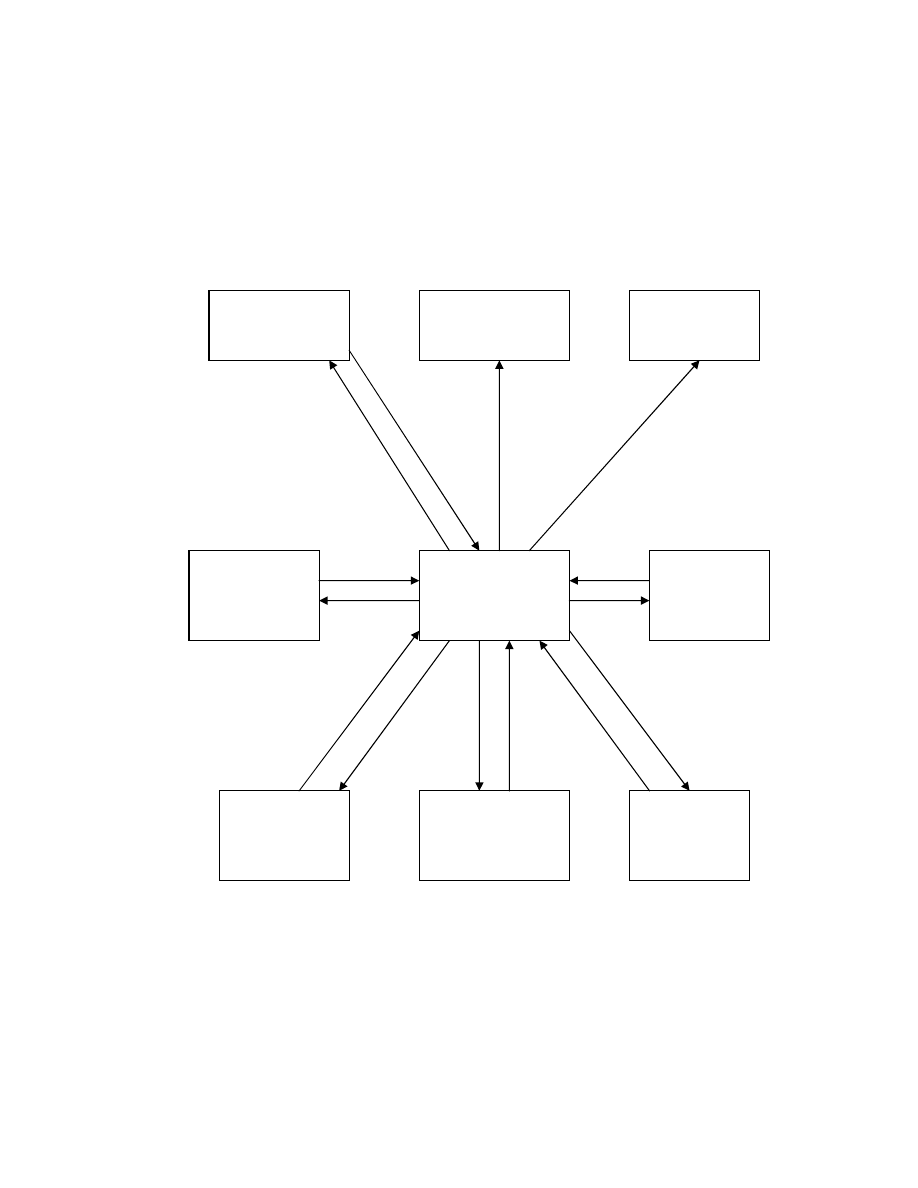
3.1. Schemat blokowy aplikacji.

Rysunek 3.1 przedstawia schemat blokowy oprogramowania.

Rys. 3.1. Schemat blokowy oprogramowania.

Centralnym punktem oprogramowania jest baza danych, do której

przekazywane s dane pobrane z formularzy i wyniki oblicze , a z której
pobierane s dane do prezentacji. Edycja danych kryteriów szczegółowych jak

Wy wietlenie

warto ci kryteriów

globalnych

Baza danych

Typy funkcji i

ich punkty

kluczowe

(interfejs)

Macierz

parzystych

porówna

(interfejs)

Obliczanie

warto ci kryteriów

globalnych

Obliczenia

współczynników

wzgl dnej

wa no ci

kryteriów

Obliczenia

warto ci

funkcji

przynale no ci

Wy wietlenie

wykresów

Kryteria

szczegółowe

(interfejs)

22

równie wyboru funkcji u yteczno ci oraz macierzy parzystych porówna
odbywa si na poziomie interfejsu u ytkownika, dane s odczytywane
i zapisywane w bazie danych. Przeprowadzanie oblicze odbywa si poprzez
pobranie danych z bazy danych, obliczone wyniki s przesyłane do bazy danych.
Wy wietlanie obliczonych danych odbywa si jednostronnie: adne informacje
w tym przypadku nie s wpisywane do bazy danych; w takim trybie
przeprowadzane jest wy wietlanie kryteriów globalnych oraz wykresów.

3.2. Schemat bazy danych.

Rysunek 3.2 przedstawia struktur bazy danych.

Rys. 3.2. Struktura bazy danych.

Oprogramowanie wykorzystuje baz danych dBase w wersji III+.

Poni sze tabele przedstawiaj struktur poszczególnych grup.

Kryteria

szczegółowe

Typy funkcji dla

kryteriów

szczegółowych i

ich punkty

kluczowe

Macierze parzystych

porówna i

współczynniki

wzgl dnej wa no ci

kryteriów

szczegółowych

Kryteria

globalne

23

Tab. 3.1. Struktura grupy Kryteria szczegółowe.

Kryteria szczegółowe

Kategoria

Nazwa pliku

Pola

Zdrowie

b_zdrowie.dbf

województwo, lekarze,

łó ka szpitalne

Finanse

b_finanse.dbf

województwo, rodki

trwałe, pkb, dochody

Infrastruktura

b_infra.dbf

województwo, kolej,

drogi, sklepy

Czysto

b_czystosc.dbf

województwo,

oczyszczalnie, emisja

gazów, lesisto

Praca

b_praca.dbf

województwo, pracuj cy,

bezrobotni, rednia płaca

Przest pczo

b_przest.dbf

województwo,

przest pstwa, wska nik

wykrywalno ci

Tab. 3.2. Struktura grupy Macierze parzystych porówna i współczynniki wzgl dnej wa no ci

kryteriów szczegółowych.

Macierze parzystych porówna i współczynniki wzgl dnej wa no ci

kryteriów szczegółowych

Kategoria

Nazwa pliku

Pola

Zdrowie

m_zdrowie.dbf

województwo, lekarze,

łó ka szpitalne, ranga

Finanse

m_finanse.dbf

województwo, rodki

trwałe, pkb, dochody,

ranga

Infrastruktura

m_infra.dbf

województwo, kolej,

drogi, sklepy, ranga

24

Czysto

m_czystosc.dbf

województwo,

oczyszczalnie, emisja

gazów, lesisto , ranga

Praca

m_praca.dbf

województwo, pracuj cy,
bezrobotni, rednia płaca,

ranga

Przest pczo

m_przest.dbf

województwo,

przest pstwa, wska nik

wykrywalno ci, ranga

Wszystko

m_wszystko.dbf

kategoria, zdrowie,

finanse, infrastruktura,

czysto , praca,

przest pczo , ranga

Tab. 3.3. Struktura grupy Typy funkcji dla kryteriów szczegółowych i ich punkty kluczowe.

Typy funkcji dla kryteriów szczegółowych i ich punkty kluczowe

Kategoria

Nazwa pliku

Pola

Zdrowie

Finanse

Infrastruktura

Czysto

Praca

Przest pczo

funkcje.dbf

kryterium szczegółowe,

typ funkcji, punkty

kluczowe: X1, X2, X3,

X4

Tab. 3.4. Struktura grupy Kryteria globalne.

Kryteria globalne

Kategoria

Nazwa pliku

Pola

Zdrowie

dd_zdrowie.dbf

województwo, DD1,

DD2, DD3

25

Finanse

dd_finanse.dbf

województwo, DD1,

DD2, DD3

Infrastruktura

dd_infra.dbf

województwo, DD1,

DD2, DD3

Czysto

dd_czystosc.dbf

województwo, DD1,

DD2, DD3

Praca

dd_praca.dbf

województwo, DD1,

DD2, DD3

Przest pczo

dd_przest.dbf

województwo, DD1,

DD2, DD3

Wszystko

dd_wszystko.dbf

województwo, DD1,

DD2, DD3

26

4. Cykl pracy programu.

4.1. Inicjalizacja programu.

Wł czenie aplikacji spowoduje wy wietlenie okna przedstawionego na

rys. 4.1.

Rys. 4.1. Ekran startowy programu.

4.2. Kryteria szczegółowe.

Menu Kryteria szczegółowe zawiera pogrupowane dane na temat

okre lonych kryteriów szczegółowych. Menu jest przedstawione na rys. 4.2.

Rys. 4.2. Podmenu Kryteria szczegółowe.

27

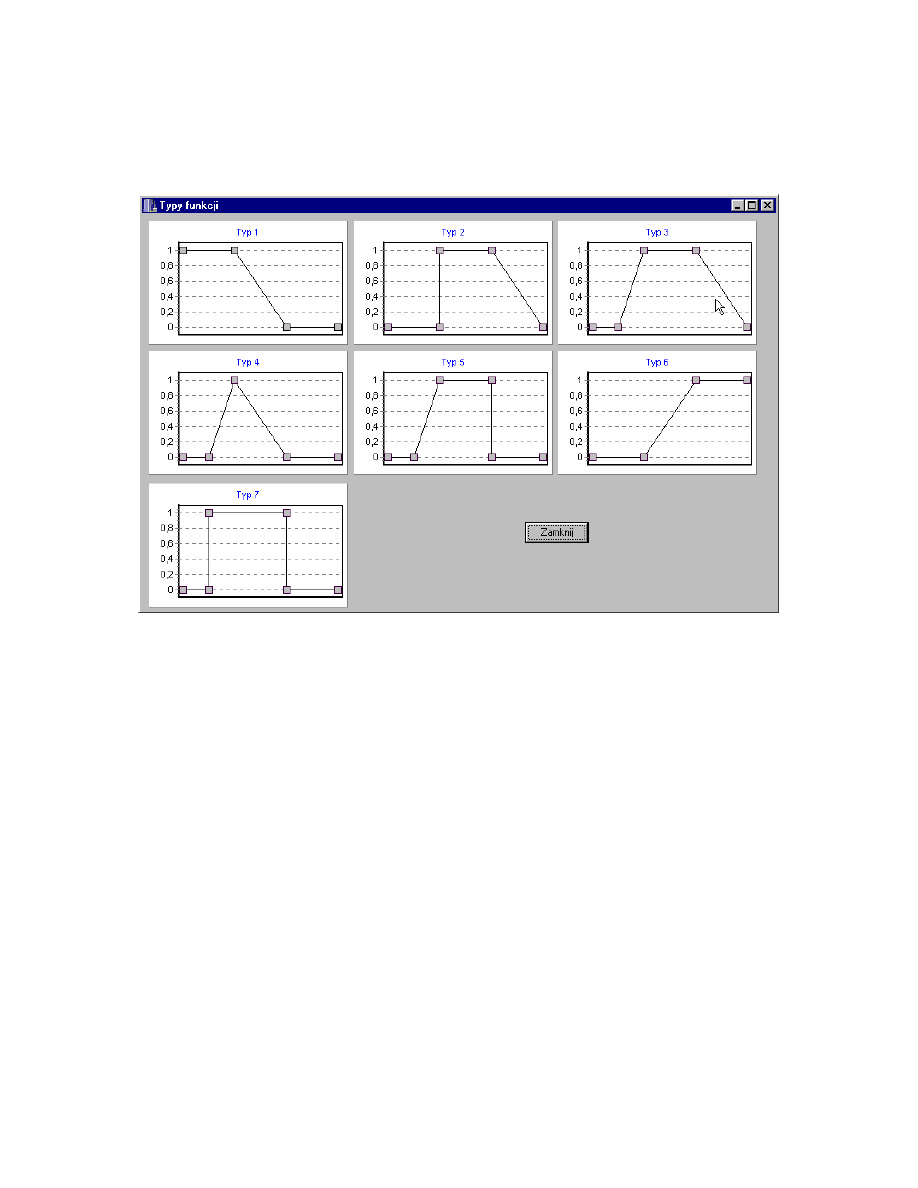
Wybór kategorii Zdrowie spowoduje wy wietlenie formularza z danymi

dotycz cymi ochrony zdrowia w danym województwie. Formularz taki
przedstawiono na rys. 4.3.

Rys. 4.3. Formularz Zdrowie.

Jak wida na zamieszczonym rysunku formularz ten zawiera dane z trzech

tabel: dane dotycz ce ochrony zdrowia: Lekarze (liczba lekarzy w danym
województwie w przeliczeniu na 10 tys. ludno ci), Łó ka szpitalne (ilo łó ek
szpitalnych w danym województwie w przeliczeniu na 10 tys. ludno ci). Poni ej
jest umieszczona macierz parzystych porówna dla tych danych, natomiast obok
tej macierzy jest przycisk powoduj cy przeliczenie współczynników wzgl dnej
wa no ci dla tej macierzy. Przycisk Zamknij powoduje zamkni cie okna. Na dole
znajduje si tabela z typami funkcji, które nale y przypisa do konkretnego
kryterium szczegółowego i punktami kluczowymi funkcji, przycisk Typy funkcji

28

spowoduje wy wietlenie formularza z typami funkcji przedstawionymi na rys.
4.4.

Rys. 4.4. Formularz z typami funkcji.

Rys. 4.4. zawiera wszystkie podstawowe typy funkcji u yteczno ci.

Wci ni cie przycisku Zamknij spowoduje zamkni cie formularza i powrót do
formularza z rys. 4.3.

W przypadku wci ni cia opcji Finanse w podmenu Kryteria szczegółowe

przedstawionym na rys. 4.2. zostanie wy wietlony formularz przedstawiony na
rys. 4.5. Jak wida formularz ten jest podobny do formularza dotycz cego
zdrowia przedstawionego na rys. 4.3. Na górze znajduje si tabela z kryteriami
szczegółowymi dotycz cymi stanu finansów w danym województwie: rodki
trwałe (warto brutto rodków trwałych w przeliczeniu na jednego mieszka ca
danego województwa), PKB (warto produktu krajowego brutto w zł.
w przeliczeniu na jednego mieszka ca województwa), Dochody (warto
nominalnych dochodów brutto w sektorze gospodarstw domowych w zł. na

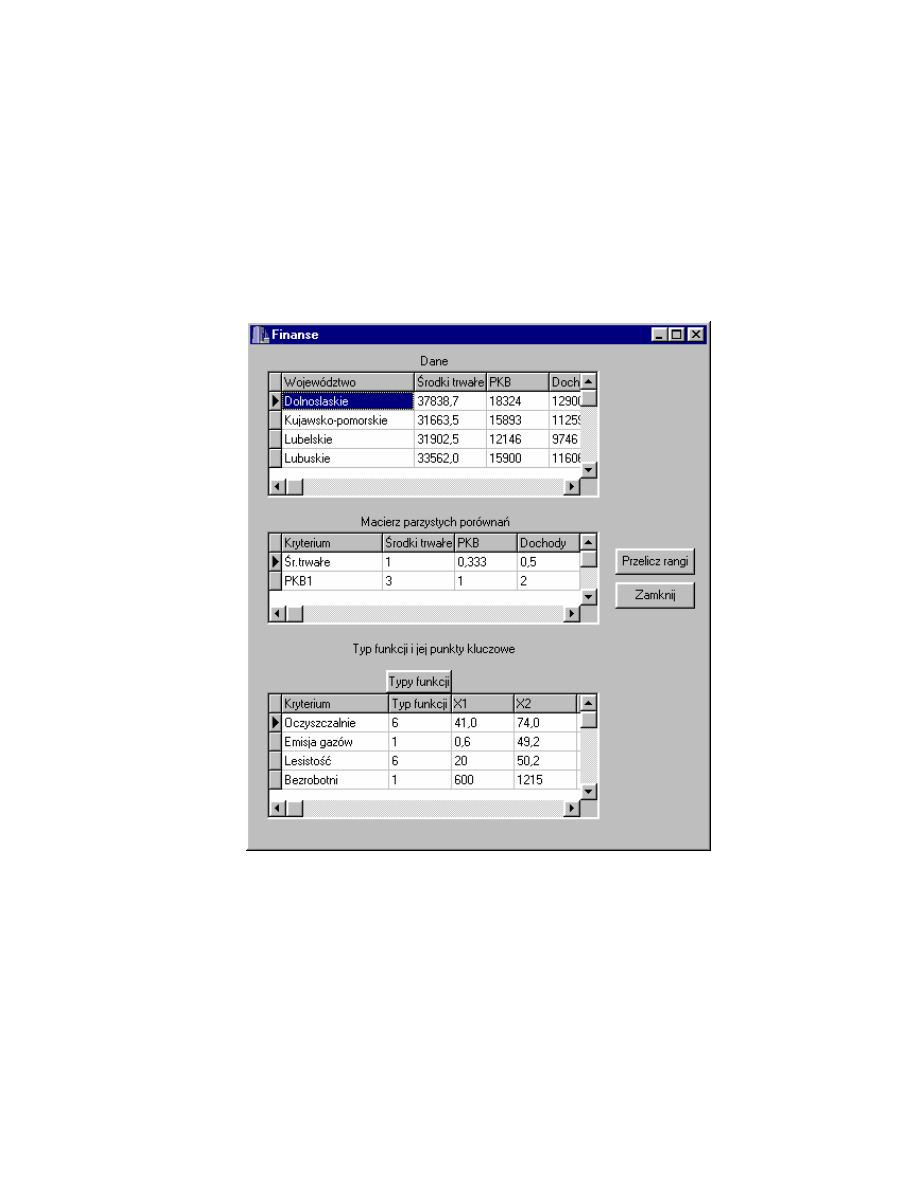
29

jednego mieszka ca). Ni ej umieszczona jest tabela z macierz parzystych
porówna dla tabeli Finanse. Wci ni cie przycisku Przelicz rangi spowoduje
obliczenie współczynników wzgl dnej wa no ci dla kryteriów z tej macierzy.
Wszystkie formularze z podmenu Kryteria szczegółowe zawieraj wspólne
elementy: przyciski Przelicz rangi, Typy funkcji, Zamknij, tabela: Funkcje
i punkty kluczowe.

Rys. 4.5. Formularz Finanse.

Rys. 4.6. przedstawia formularz Infrastruktura, który zostanie

wy wietlony po wybraniu opcji Infrastruktura z podmenu Kryteria szczegółowe.
Formularz zawiera tabel z danymi dotycz cymi stanu infrastruktury w danym
województwie: Kolej (linie kolejowe eksploatowane normalnotorowe w km na
100 km² powierzchni ogólnej województwa), Drogi (drogi publiczne o twardej

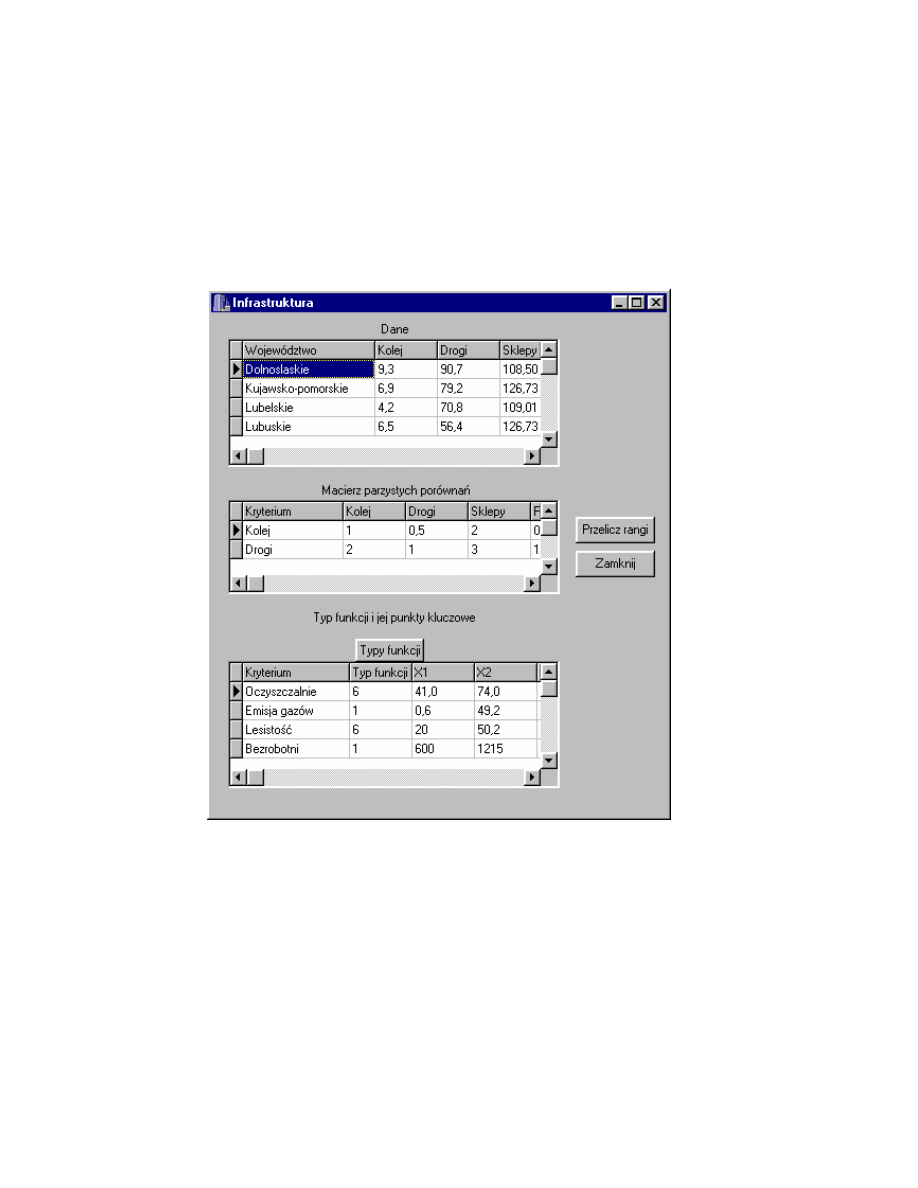
30

nawierzchni w km na 100 km² powierzchni ogólnej województwa), Sklepy (ilo
sklepów w danym województwie w przeliczeniu na 10 tys. ludno ci). Macierz
parzystych porówna dotycz ca kategorii Infrastruktura jest umieszczona pod
tabel główn , pozostałe elementy s takie same jak we wcze niejszych
formularzach.

Rys. 4.6. Formularz Infrastruktura.

Rys. 4.7 przedstawia formularz Czysto z podmenu Kryteria

szczegółowe. Zawiera on dane dotycz ce stanu ekologicznego województwa:
Oczyszczalnie (ludno korzystaj ca z oczyszczalni cieków w procentach
ludno ci ogółem), Emisja gazów (emisja przemysłowych zanieczyszcze
powietrza gazowych i pyłowych z zakładów szczególnie uci liwych dla
czysto ci powietrza w tys. ton na 1 km² powierzchni województwa), Lesisto

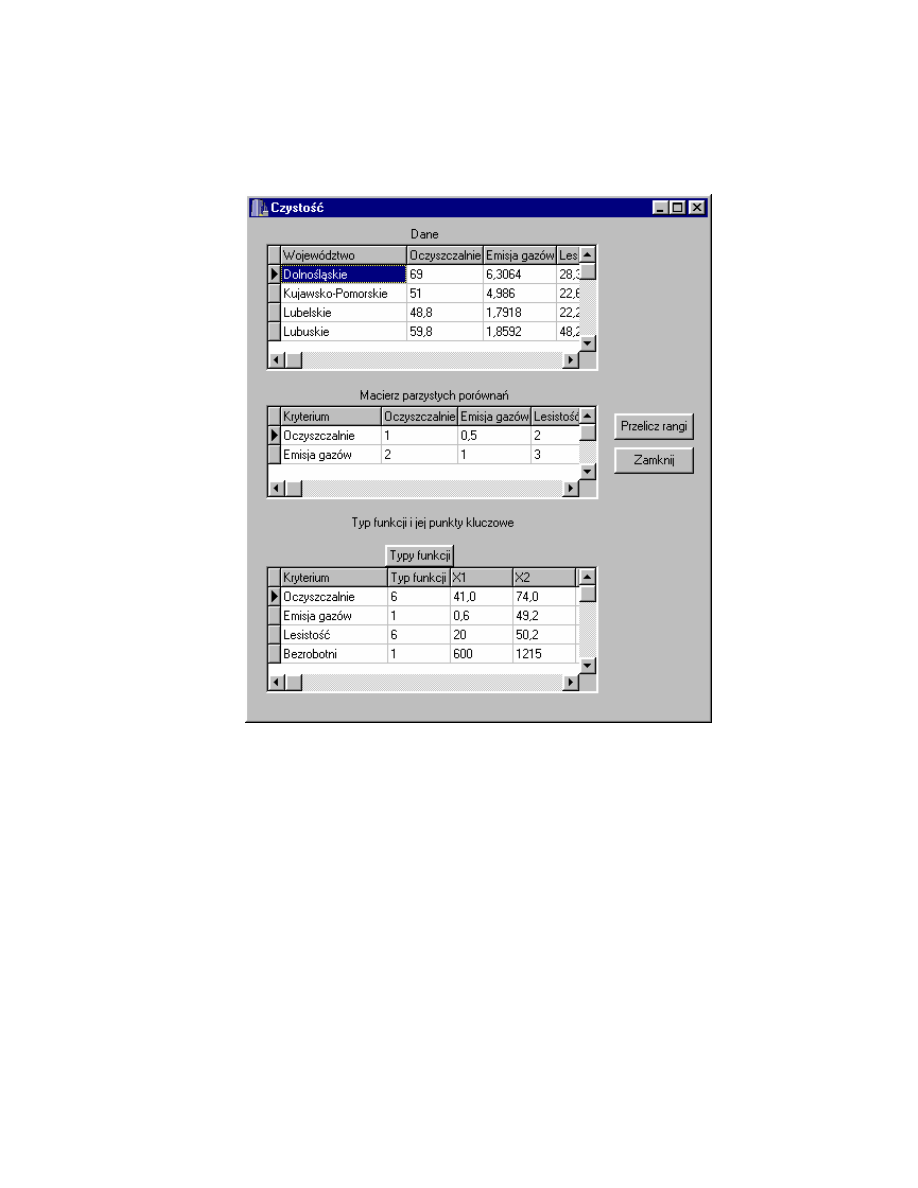
31

(powierzchnia gruntów le nych w procentach powierzchni całkowitej
województwa).

Rys. 4.7. Formularz Czysto .

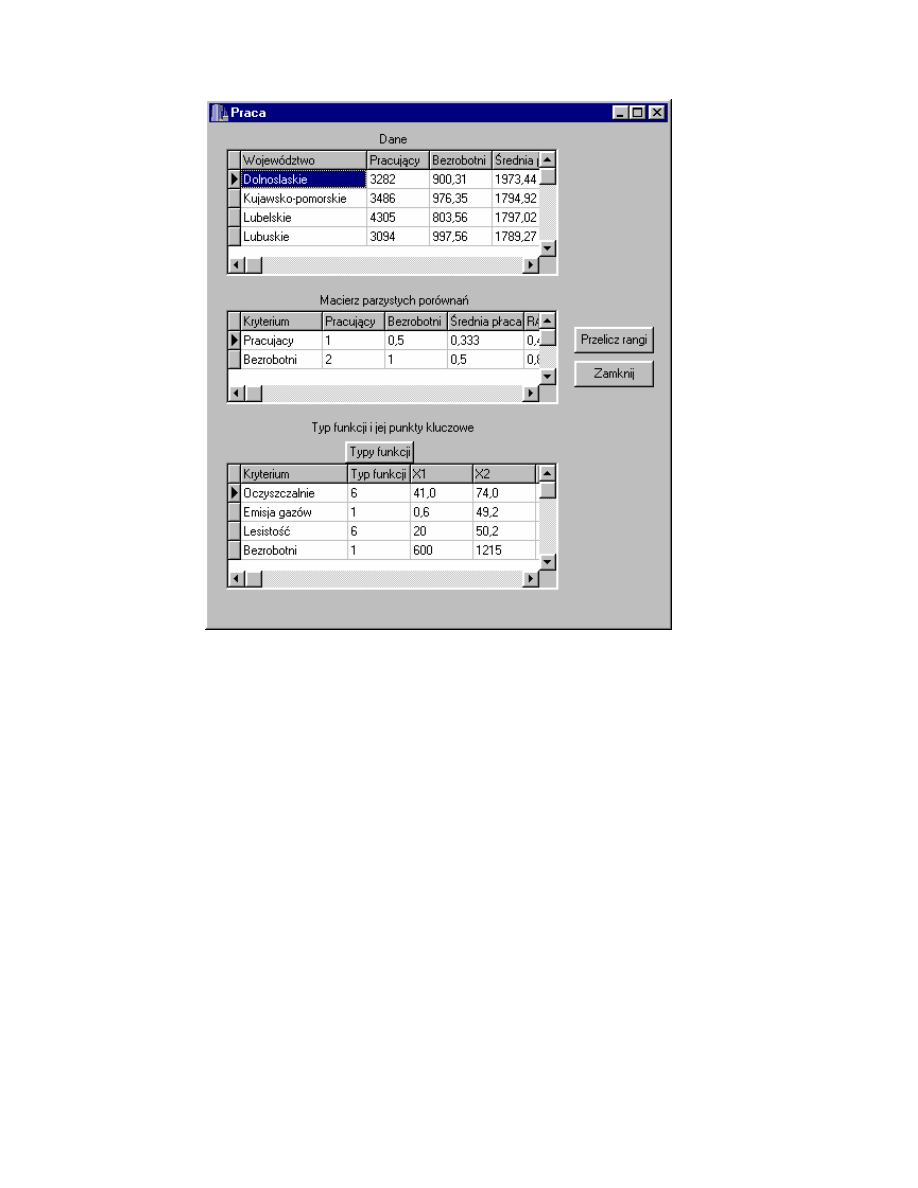
Rys. 4.8 przedstawia formularz Praca wywoływany z podmenu Kryteria

szczegółowe. Formularz ten zawiera dane dotycz ce rynku pracy w danym
województwie: Pracuj cy (liczba osób zatrudnionych w przeliczeniu na 10 tys.
ludno ci w danym województwie), Bezrobotni (liczba zarejestrowanych
bezrobotnych w przeliczeniu na 10 tys. ludno ci w danym województwie),

rednia płaca (przeci tne miesi czne wynagrodzenie brutto w zł. w danym

województwie).

32

Rys. 4.8. Formularz Praca.

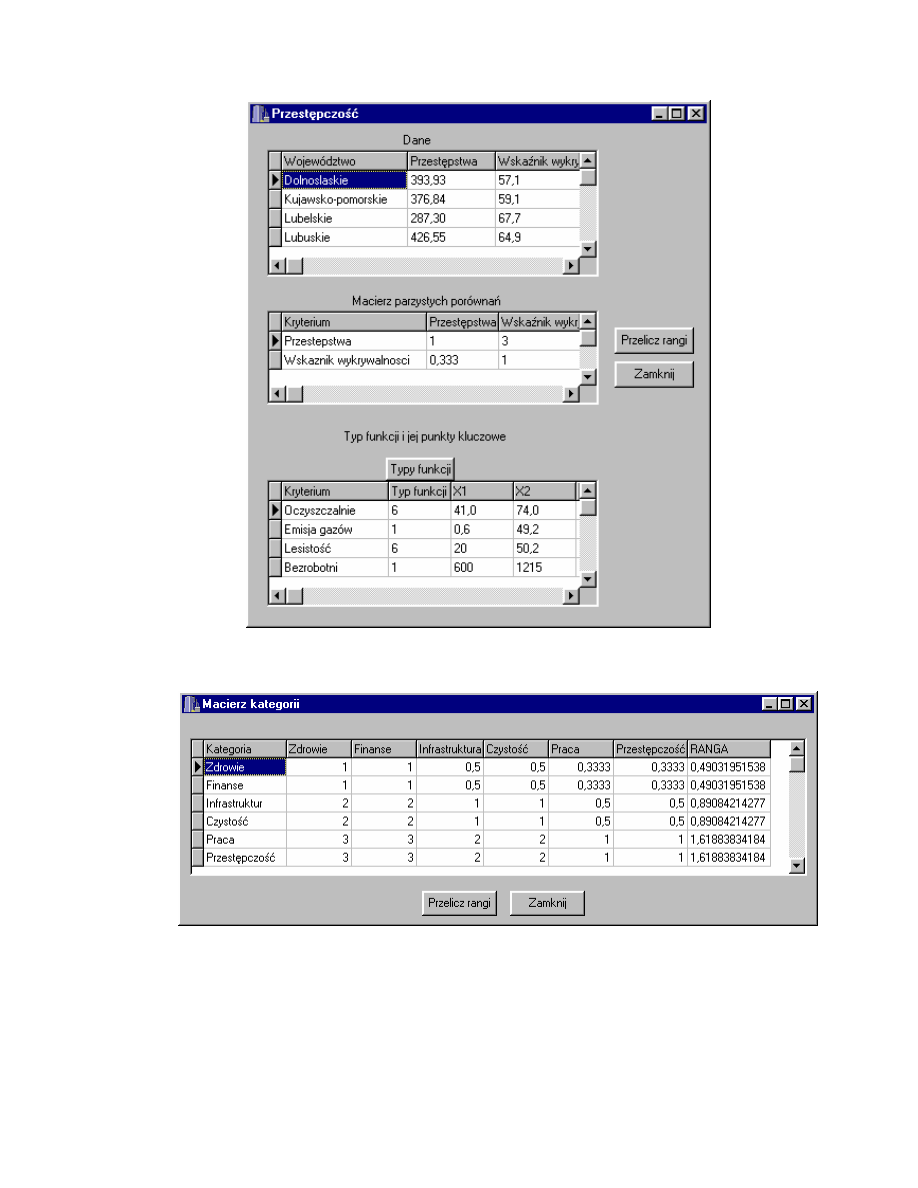
Rys. 4.9 przedstawia formularz Przest pczo zawieraj cy dane dotycz ce

stopnia bezpiecze stwa w danych województwach: Przest pstwa (ilo
przest pstw stwierdzonych w zako czonych post powaniach przygotowawczych
na 10 tys. ludno ci), Wska nik wykrywalno ci (wska nik wykrywalno ci
sprawców przest pstw stwierdzonych w procentach).

Rys. 4.10 przedstawia formularz Macierz kategorii pozwalaj cy na edycj

danych w macierzy parzystych porówna w drugim poziomie hierarchii
opracowywanego problemu.

33

Rys. 4.9. Formularz Przest pczo .

Rys. 4.10. Formularz Macierz kategorii.

34

Wybór Kryteriów globalnych z ekranu startowego przedstawionego na

rys. 4.1 spowoduje wy wietlenie podmenu Kryteria globalne przedstawione na
rys. 4.11.

4.3. Kryteria globalne.

Rys. 4.11. Podmenu Kryteria globalne.

Wybór opcji Zdrowie z podmenu Kryteria globalne powoduje

wy wietlenie okna przedstawionego na rys. 4.12. Przedstawia ono tabel
z obliczonymi warto ciami kryteriów globalnych dotycz cych zdrowia
w województwach, tabela przedstawia obliczone wyniki wszystkich trzech
kryteriów dla ka dego z województw. Naci niecie przycisku Przelicz kryteria
spowoduje ponowne przeliczenie wszystkich kryteriów globalnych dla kategorii
Zdrowie. Naci ni cie przycisku Zamknij spowoduje zamkni cie poni szego okna
i powrót do stanu z rys. 4.1.

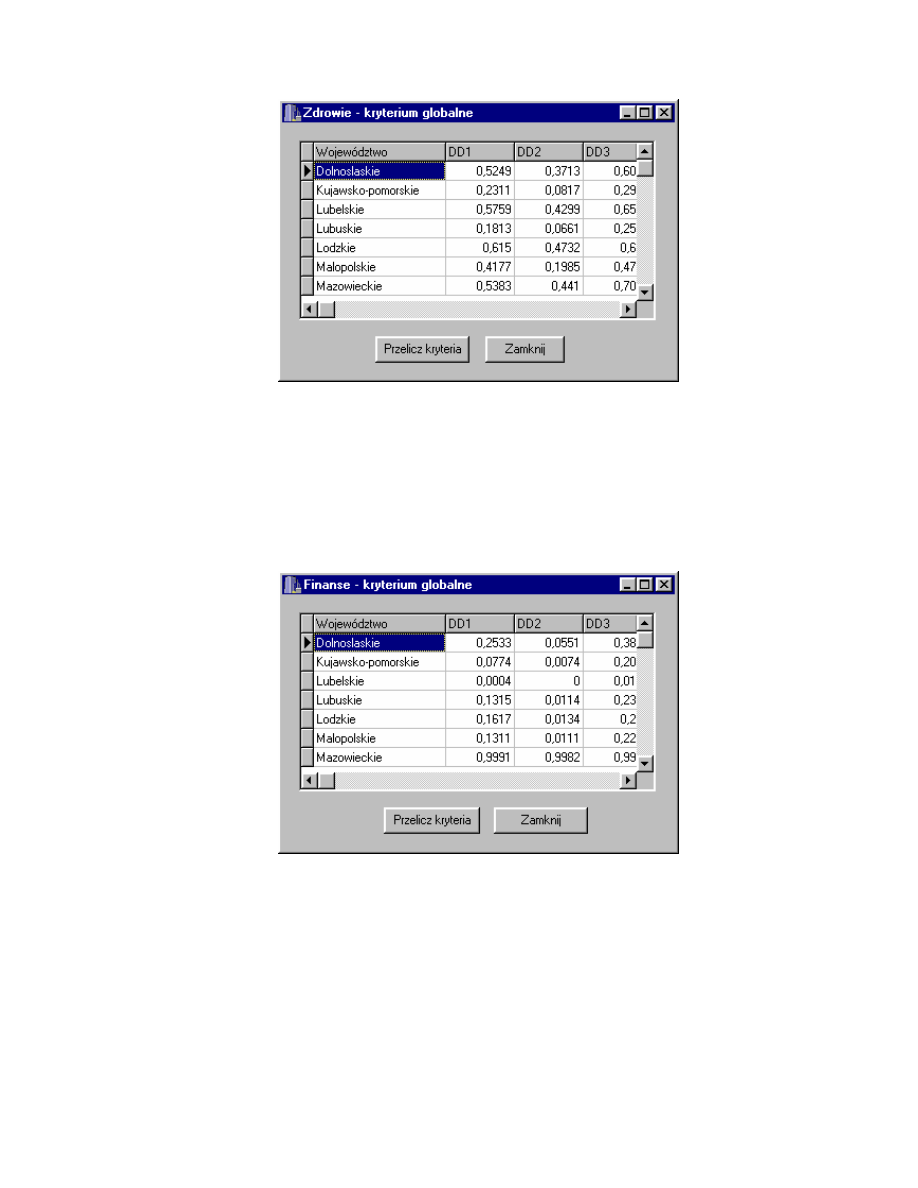
35

Rys. 4.12. Okno Zdrowie - kryterium globalne.

Dla pozostałych kategorii wy wietlanych w podmenu Kryteria globalne

przedstawionego na rys. 4.11 wy wietlane s takie same okna. S one
przedstawione kolejno na rys. 4.13, 4.14, 4.15, 4.16, 4.17.

Rys. 4.13. Okno Finanse - kryterium globalne.

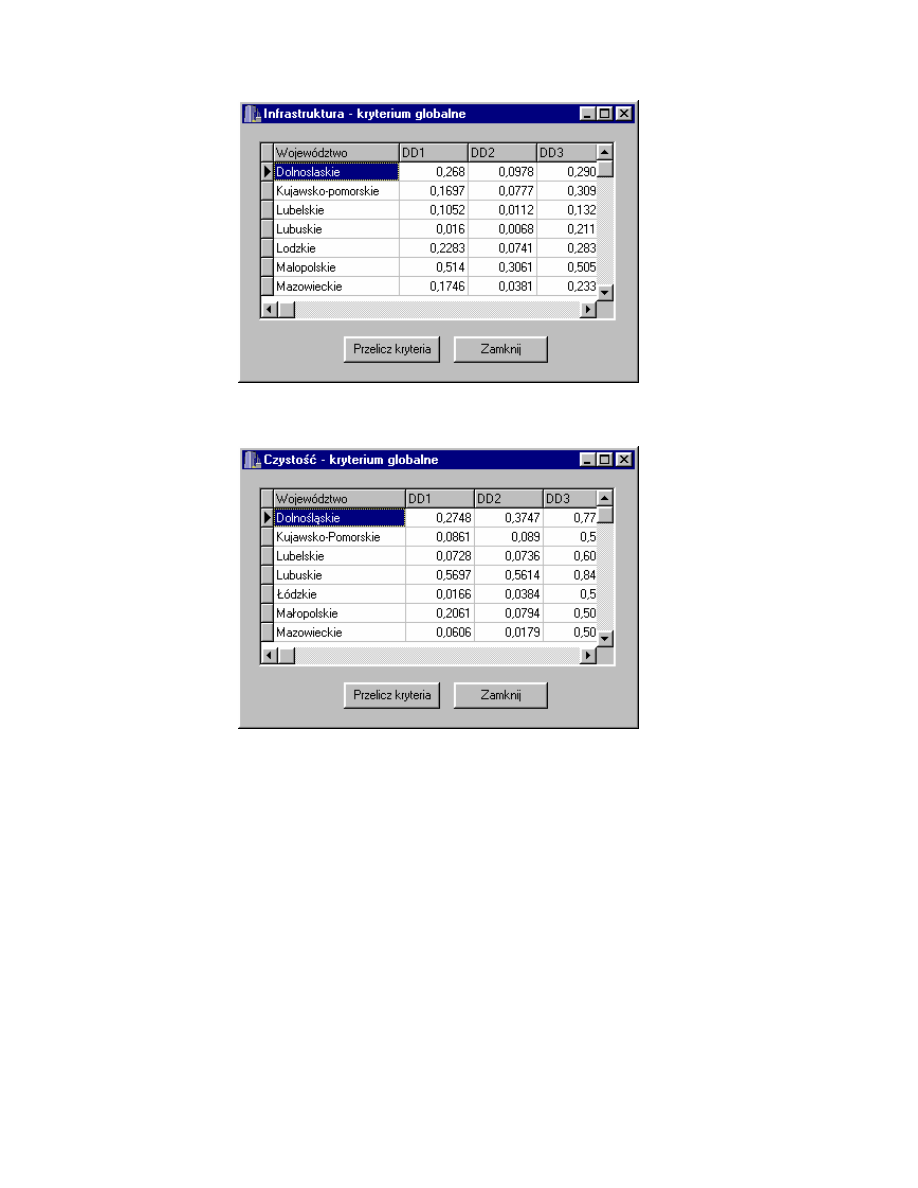
36

Rys. 4.14. Okno Infrastruktura - kryterium globalne.

Rys. 4.15. Okno Czysto - kryterium globalne.

37

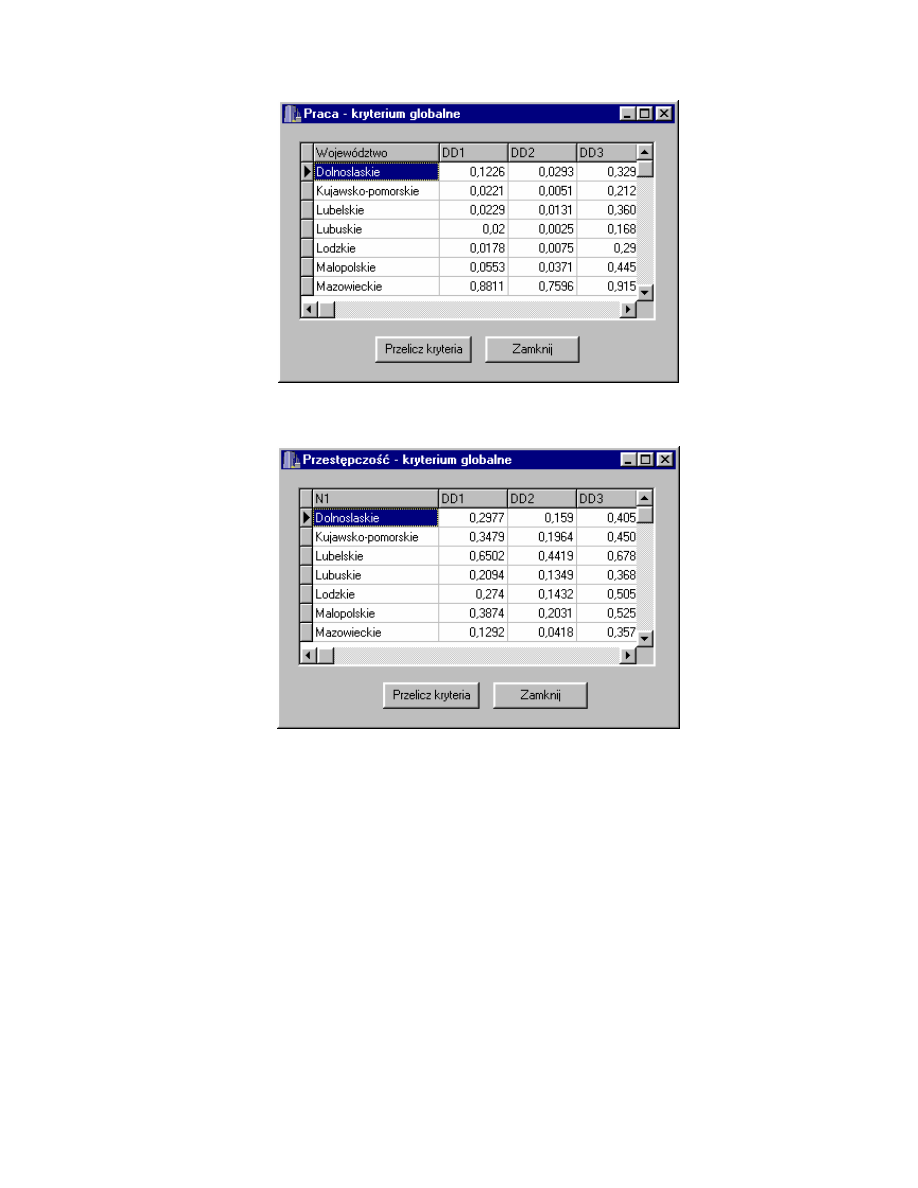
Rys. 4.16. Okno Praca - kryterium globalne.

Rys. 4.17. Okno Przest pczo - kryterium globalne.

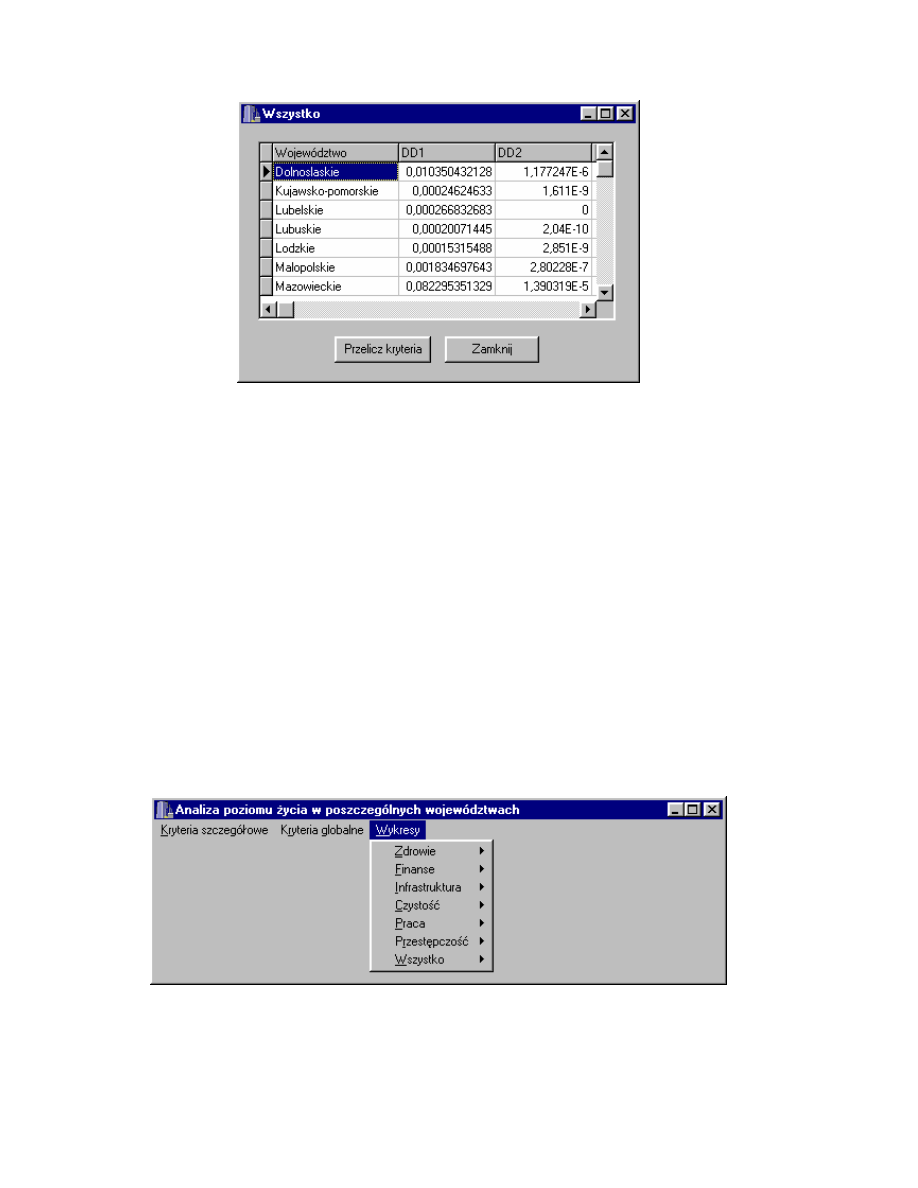
38

Rys. 4.18. Okno Wszystko - kryterium globalne.

Przedstawione na rys. 4.18 okno Wszystko - kryterium globalne zawiera

podsumowanie wszystkich kryteriów globalnych w postaci zgodnej z rozdz. 2.2

Trzecim głównym podmenu menu głównego s Wykresy (rys. 4.19).

Dost p do poszczególnych wykresów jest pogrupowany, tak jak do tej pory,
w kategorie. Ka da z kategorii wy wietla dwa rodzaje wykresów (rys. 4.20) :
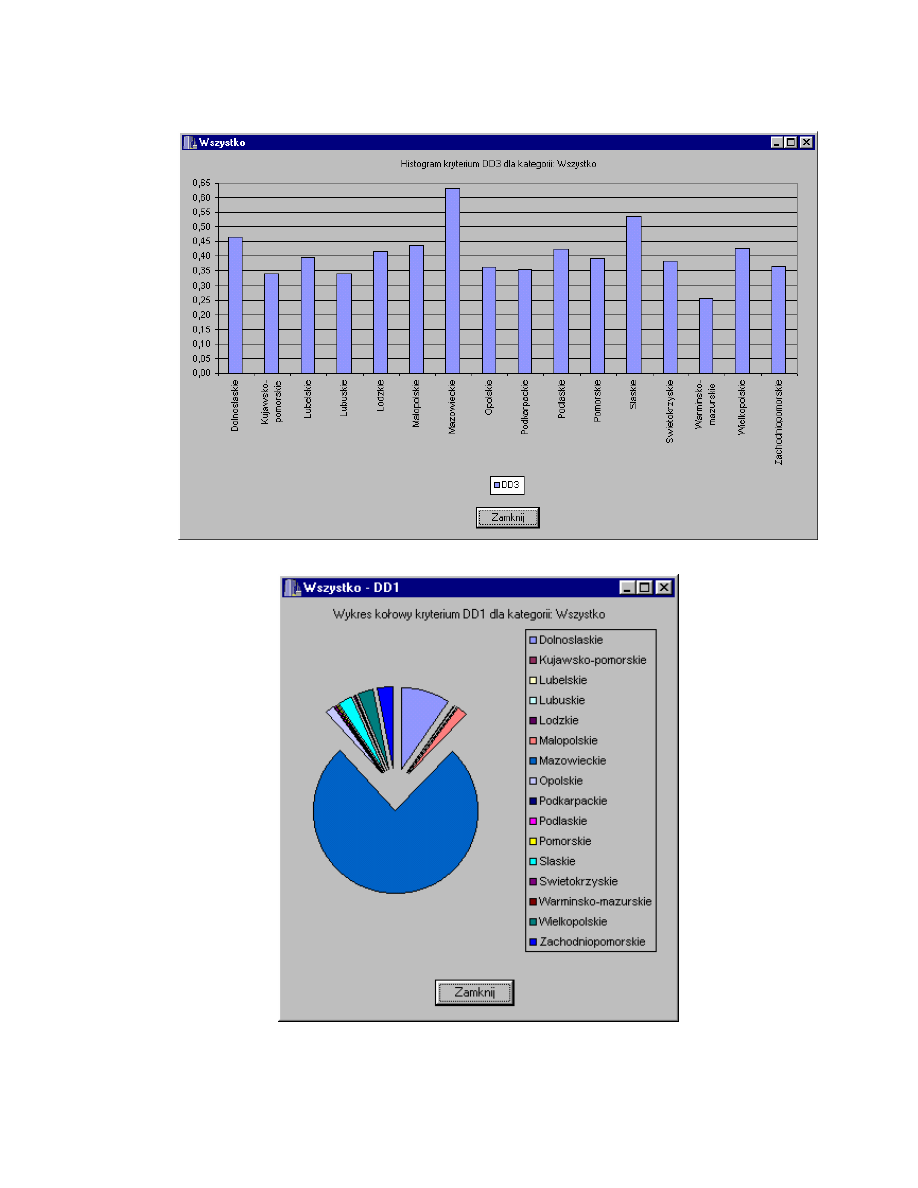
histogram kryteriów globalnych DD1, DD2 i DD3 konkretnej kategorii dla
ka dego z województw (rys. 4.21), a tak e wykres kołowy wska nika DD1
konkretnej kategorii dla wszystkich województw (rys.4.22).

4.4. Wykresy.

Rys. 4.19. Podmenu Wykresy.

39

Wybór kategorii Zdrowie spowoduje wy wietlenie dodatkowego podmenu

z typami wykresów do wy wietlenia (rys. 4.20).

Rys. 4.20. Typy wykresów do wy wietlenia.

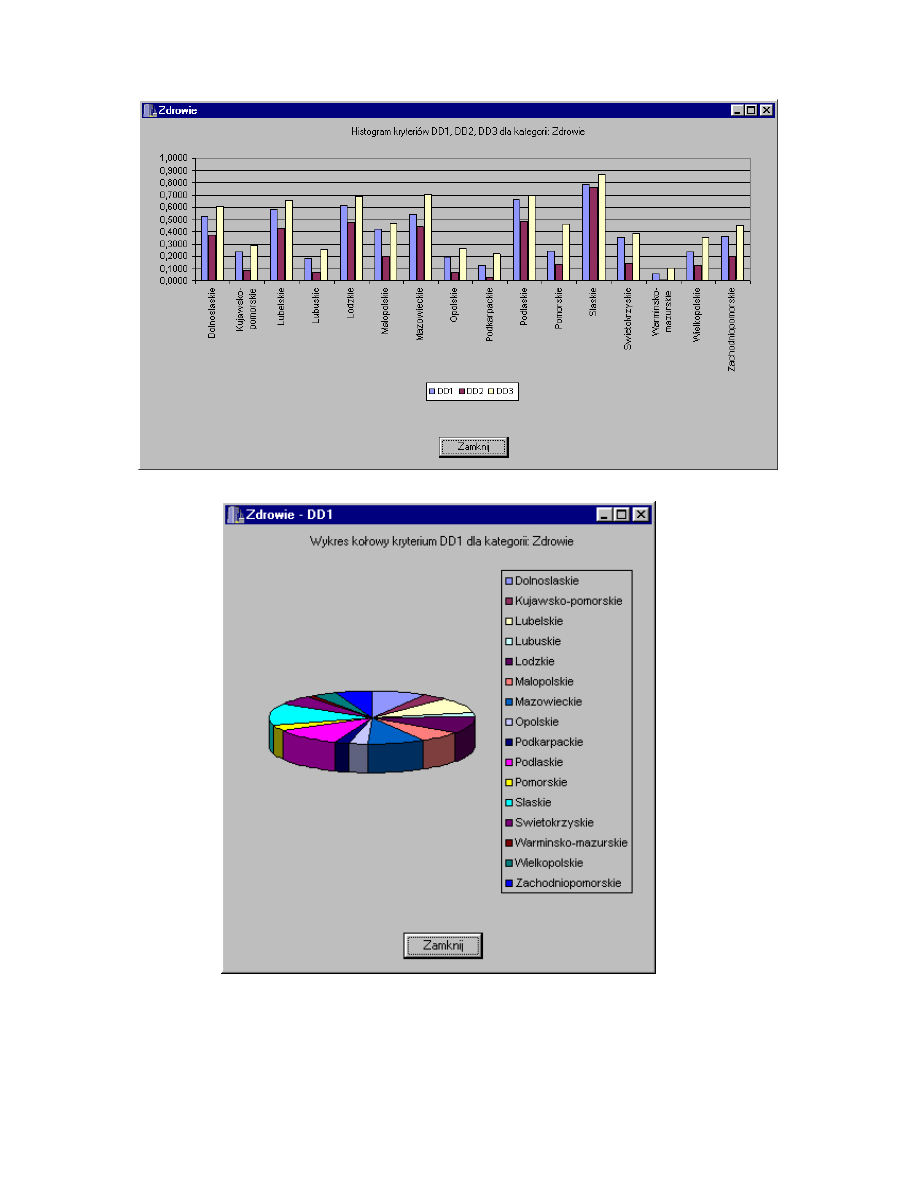
Wybór

opcji

Histogram

spowoduje

wy wietlenie

wykresu

histogramowego dotycz cego kategorii Zdrowie z podziałem na województwa
(rys. 4.21). Kolorem niebieskim oznaczono kryterium globalne DD1, kolorem
czerwonym kryterium globalne DD2, kolorem ółtym kryterium globalne DD3.
Z kolei wybór opcji Wykres kołowy dla kategorii Zdrowie spowoduje
wy wietlenie wykresu przedstawionego na rys. 4.22. Podobnie wygl daj okna
wykresów pozostałych kategorii przedstawione na rys. 4.23 - 4.34.

40

Rys. 4.21. Histogram kryteriów DD1, DD2, DD3 dla kategorii Zdrowie.

Rys. 4.22. Wykres kołowy kryterium DD1 dla kategorii Zdrowie.

41

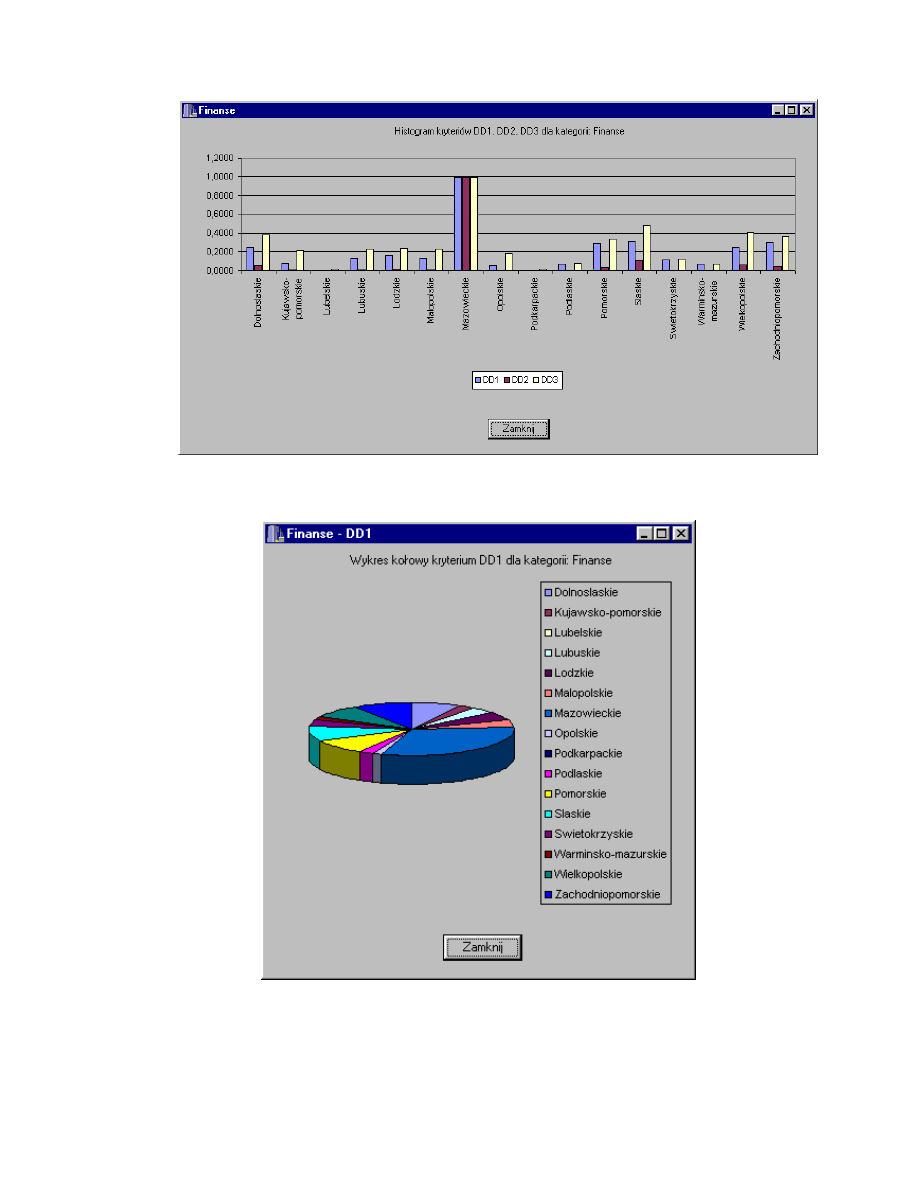
Rys. 4.23. Histogram kryteriów DD1, DD2, DD3 dla kategorii Finanse.

Rys. 4.24. Wykres kołowy kryterium DD1 dla kategorii Finanse.

42

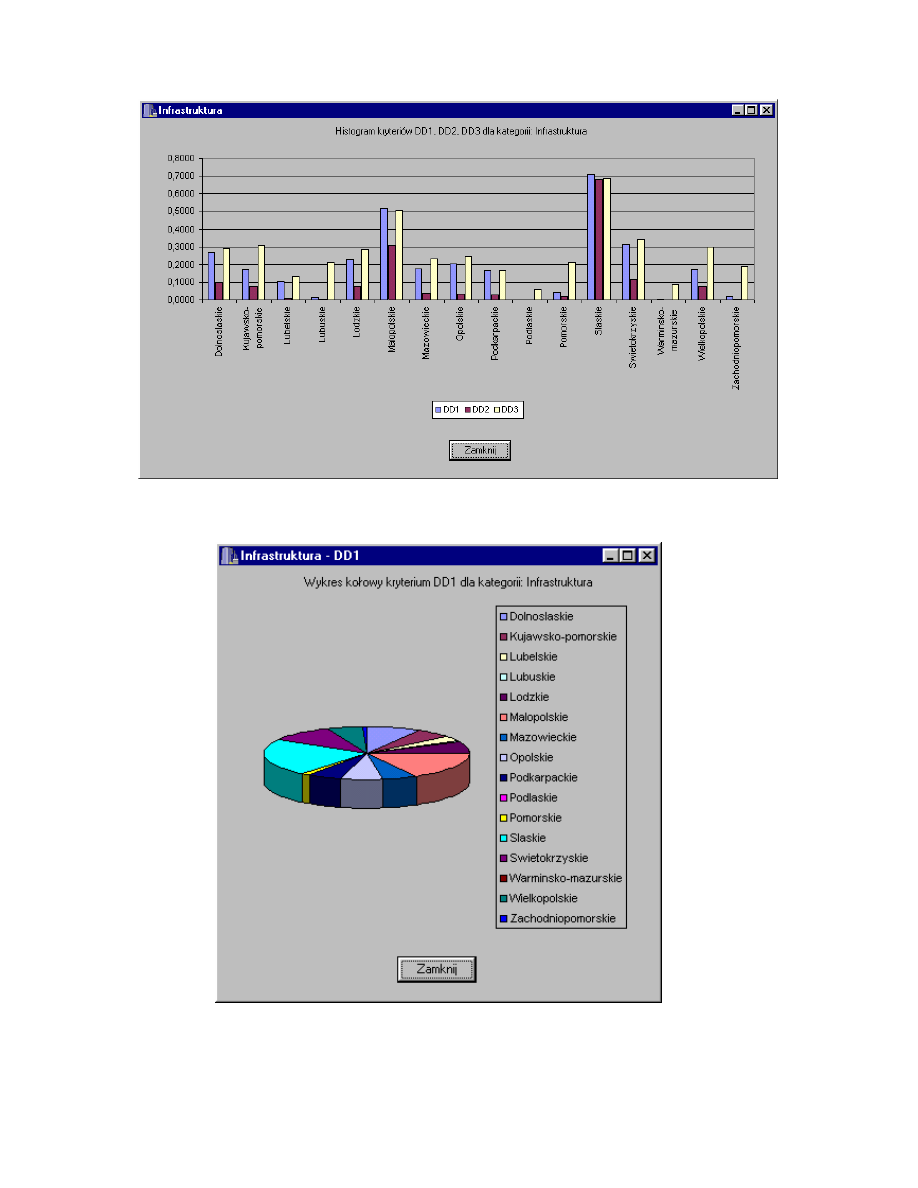
Rys. 4.25. Histogram kryteriów DD1, DD2, DD3 dla kategorii Infrastruktura.

Rys. 4.26. Wykres kołowy kryterium DD1 dla kategorii Infrastruktura.

43

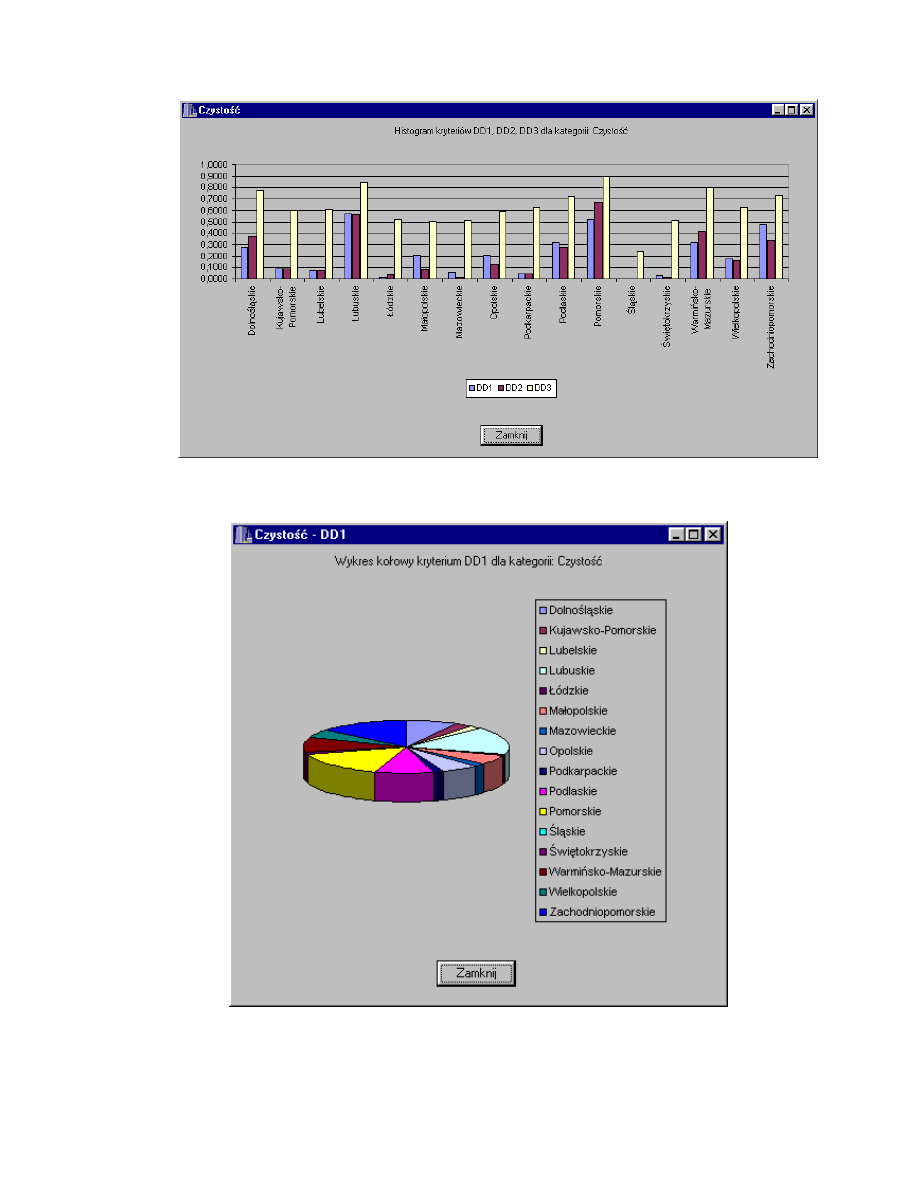
Rys. 4.27. Histogram kryteriów DD1, DD2, DD3 dla kategorii Czysto .

Rys. 4.28. Wykres kołowy kryterium DD1 dla kategorii Czysto .

44

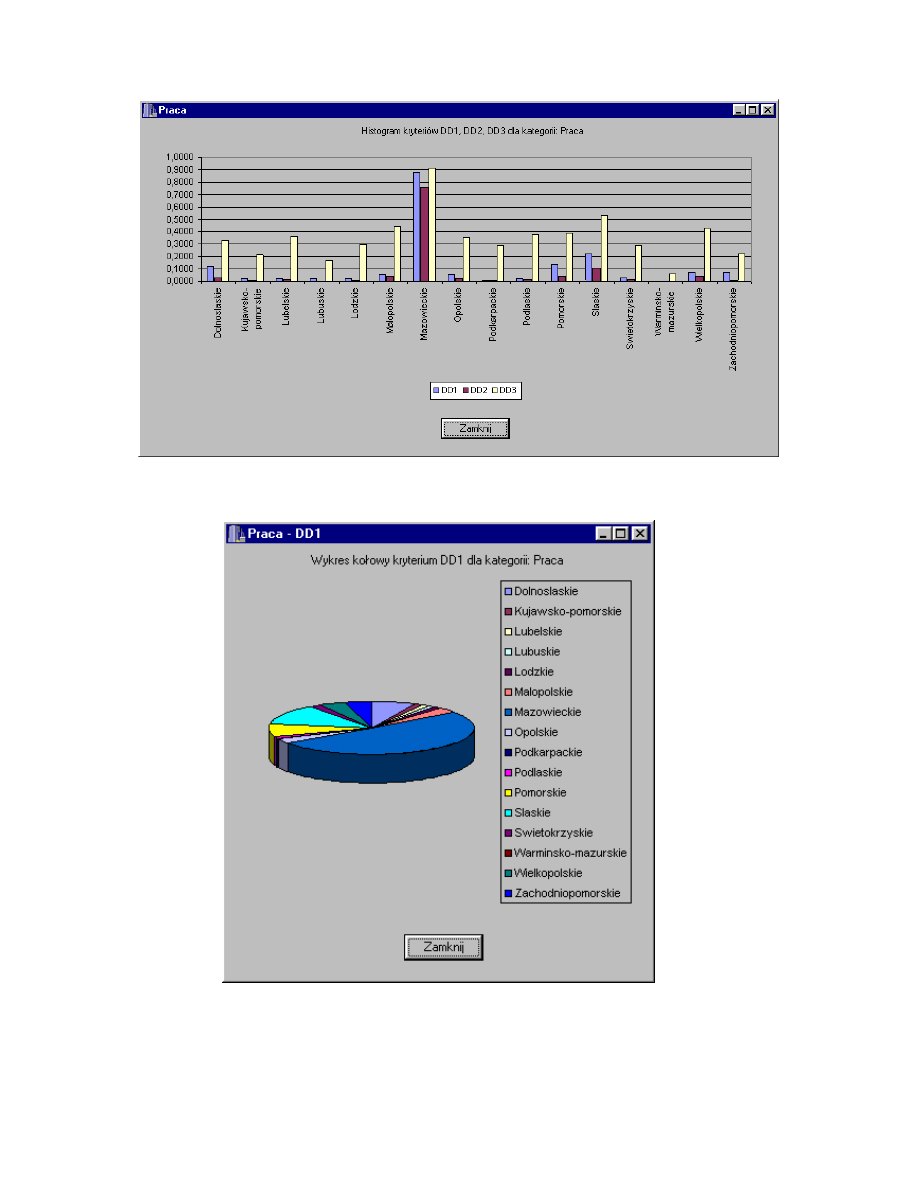
Rys. 4.29. Histogram kryteriów DD1, DD2, DD3 dla kategorii Praca.

Rys. 4.30. Wykres kołowy kryterium DD1 dla kategorii Praca.

45

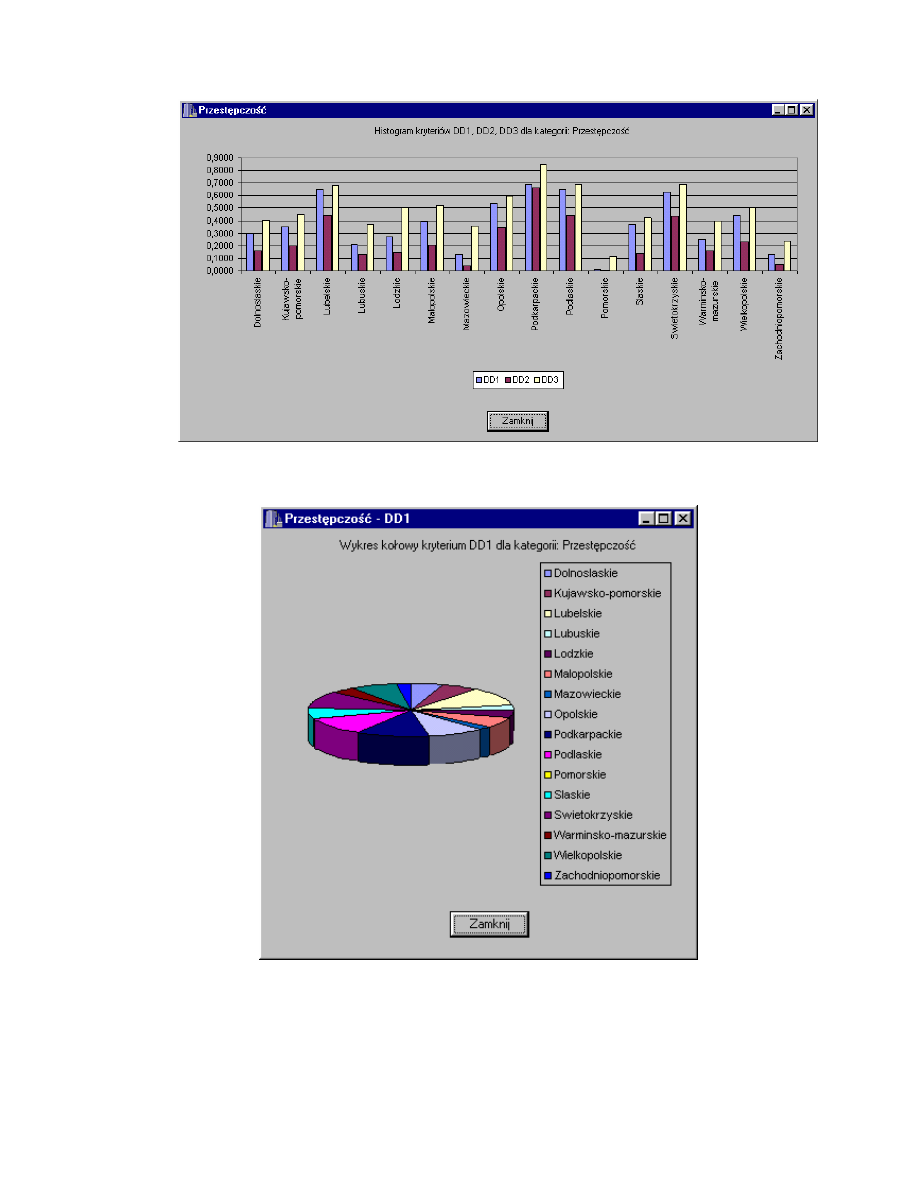
Rys. 4.31. Histogram kryteriów DD1, DD2, DD3 dla kategorii Przest pczo .

Rys. 4.32. Wykres kołowy kryterium DD1 dla kategorii Przest pczo .

46

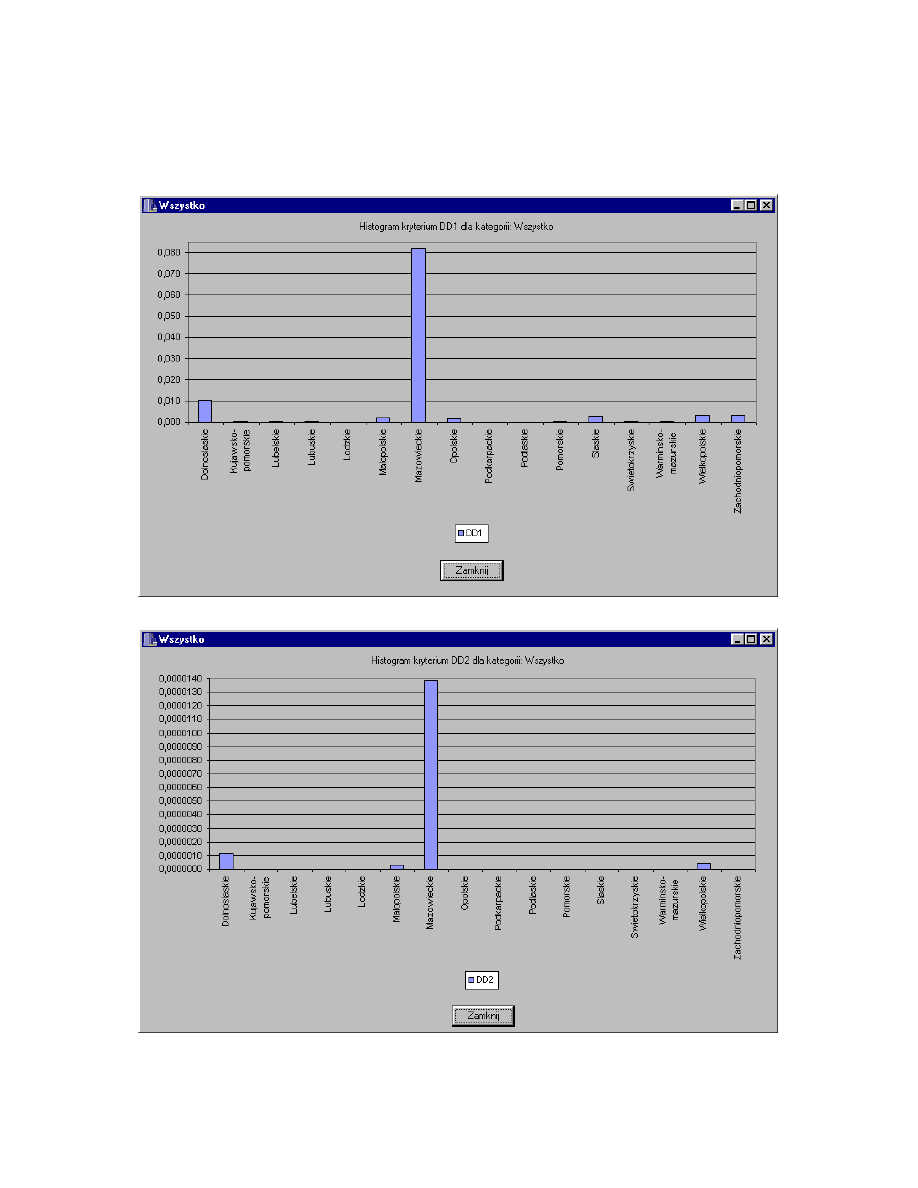
Kategoria Wszystko zawiera wykresy histogramowe i kołowe z podziałem

na wszystkie trzy kryteria DD1, DD2, DD3. Podział taki wynika z du ej ró nicy
wyników poszczególnych kryteriów.

Rys. 4.33. Histogram kryterium DD1 dla kategorii Wszystko.

Rys. 4.34. Histogram kryterium DD2 dla kategorii Wszystko.

47

Rys. 4.35. Histogram kryterium DD3 dla kategorii Wszystko.

Rys. 4.36. Wykres kołowy kryterium DD1 dla kategorii Wszystko.

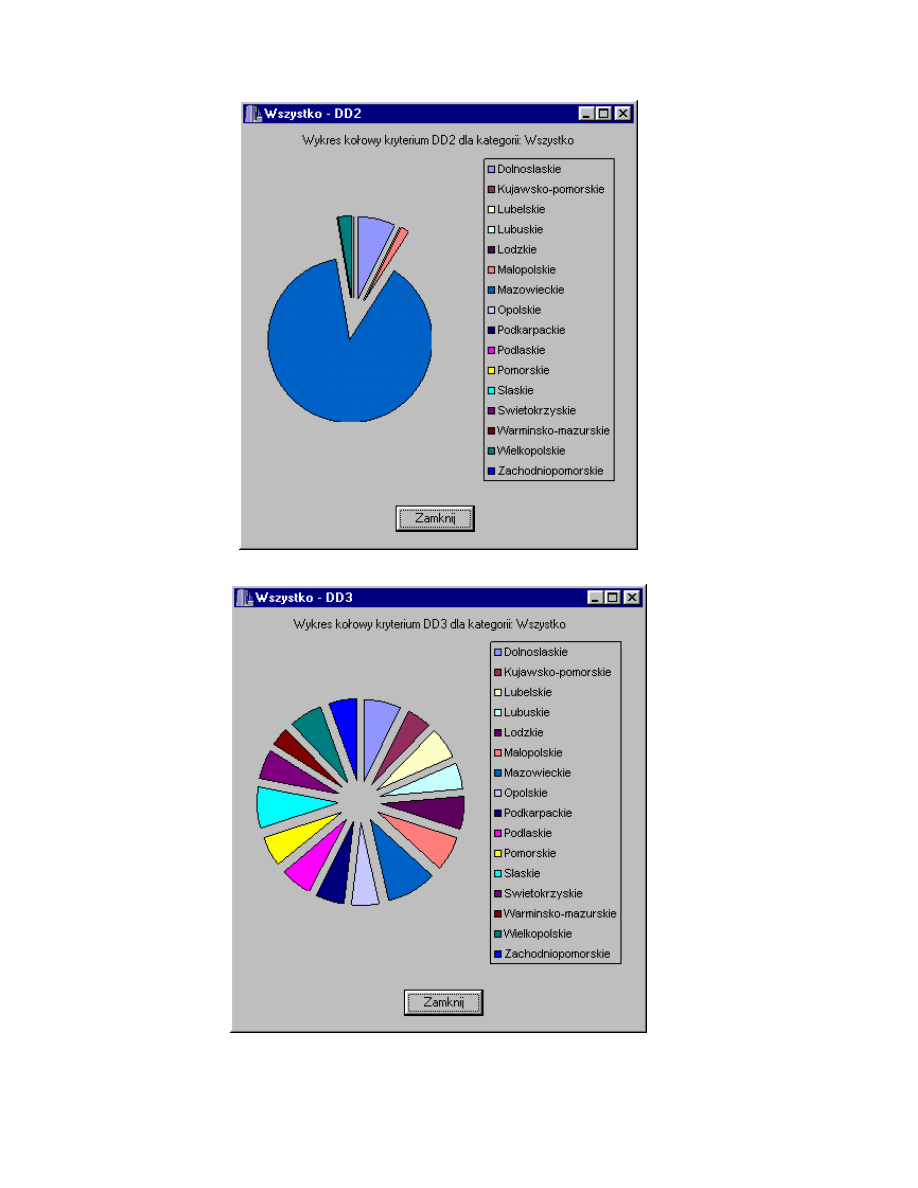
48

Rys. 4.37. Wykres kołowy kryterium DD2 dla kategorii Wszystko.

Rys. 4.38. Wykres kołowy kryterium DD3 dla kategorii Wszystko.

49

5. Wnioski.

Zastosowana metodologia zbiorów rozmytych daje mo liwo ci stabilnego

przeprowadzania analiz matematycznych dotycz cych oceny jako ci ycia
w poszczególnych województwach. Wykorzystanie technologii opisanej w pracy
pozwoliło na sprawdzenie poziomu ycia w ró nych jego aspektach uj tych
w kategorie. Z wygenerowanych wykresów mo na wywnioskowa , e
najwy szy poziom zycia notuje si w województwach: Mazowieckim, l skim,
Dolno l skim, Małopolskim, Zachodnipomorskim i Opolskim. Z kolei najni szy
poziom ycia jest w województwach: Warmi sko-Mazurskim, Podkarpackim,
Lubuskim, Kujawsko-Pomorskim.

Nale y jednak pami ta , e uzyskany wynik zale y od kilku czynników:

-

wyboru odpowiednich kryteriów szczegółowych: wybór innych kryteriów
mogłby spowodowa , e uzyskany wynik ró niłby si od otrzymanego,

-

wyboru kryteriów ilo ciowych i unikanie kryteriów jako ciowych:
w przypadku kryteriów jako ciowych du e znaczenie ma subiektywizm
oszacowania, omini cie tego problemu zwi kszyło wiarygodno uzyskanych
wyników,

-

uwa ne sporz dzenie macierzy parzystych porówna : prawidłowe
oszacowanie co do stopnia wa no ci poszczególnych spoowoduje, e
wyliczenie rang b dzie bardziej dokładne.

Warto zauwa y , e wykorzystan metod mo na zastosowa w wielu
dziedzinach np. do oszacowania warto ci nieruchomo ci ,samochodu, do analizy
rynku papierów warto ciowych, w medycynie do oszacowania stanu zdrowia
i w wielu innych dziedzinach.

50

6. Literatura.

[1] Saaty T., A Scaling Method for Priorities in Hierarhical Structures, J. of
Mathematical Psychology 1977.
[2] Zadeh L.A., Fuzzy Sets, Inf. Contr. 1965.
[3] „Komputerowy system wspomagania decyzji przy wyborze projektów
inwestycyjnych”, Informatyka Teoretyczna i Stosowana, Rocznik 1, Nr 1, 2001,
L.Dymowa, A.Zenkowa, P. Figat.
[4] Zollo G., Iandoli L., Cannavacciuolo A., The Performance Requirements
Analysis with Fuzzy Logic, Fuzzy Economic Review 1999, IV, 1, 35-69.
[5] Chu A., Kalaba R., Springarn R., A Comparsion of Two Methods for
Determining the Weight of Belonging to Fuzzy Sets, J. of Optimisation Theory
and Applications 1979, 27, 4, 531-538.
[6] http://kpkm.mt.polsl.gliwice.pl/projekty/klas/k006/zbiory_rozmyte.htm.
[7] "Rocznik Statystyczny 2001" Główny Urz d Statystyczny, Warszawa 2002.

51

7. Zał czniki.

Zał cznik A - fragmenty najwa niejszych procedur zawartych w programie

Procedura obliczaj ca współczynniki wzgl dnej wa no ci kryteriów

szczegółowych:

//---------------------------------------------------------------------------

double Pierwiastek(double a, int i)

{

int l,g;

double wart;

for(l=1;l<=(a+1);l++){

g=l;

if(pow(l,i)==a) {

wart=(double)g;

break;}

if(pow(l,i)>a){

g--;

wart=(double)g;

while(pow(wart,i)<a){

wart=wart+0.0001;

}

break;

}

}

return wart;

}

void __fastcall TForm3::Button2Click(TObject *Sender)

{

double aprim, suma_aprim, aprim2[10];

int n,l1;

aprim=1, suma_aprim=0;

n=(Table2->FieldCount)-2;

Table2->DisableControls();

Table2->First();

l1=1;

while (!Table2->Eof)

{

//Table1->Edit();

aprim=1;

for(int j=1;j<=n;++j)

{

aprim=aprim*((Table2->Fields->Fields[j]->Value));

}

aprim2[l1]=Pierwiastek(aprim,n);

suma_aprim=suma_aprim+aprim2[l1];

++l1;

Table2->Next();

}

l1=1;

Table2->Close();

Table2->Open();

Table2->First();

while (!Table2->Eof)

52

{

Table2->Edit();

Table2->Fields->Fields[Table2->FieldCount-1]->AsString = (aprim2[l1]/suma_aprim)*n;

++l1;

Table2->Post();

Table2->Next();

}

Table2->EnableControls();

}

//---------------------------------------------------------------------------

Procedura obliczaj ca warto ci kryteriów globalnych:

void TForm6::Oblicz_dd1()

{

int n;

int n1;

double wart, wart1[16], wart2;

Table6->Open();

n=(Table6->FieldCount)-1;

n1=(Table11->FieldCount)-1;

Table6->DisableControls();

Table6->First();

int l1=1;

while (!Table6->Eof)

{

Table11->First();

wart=pow((Table6->Fields->Fields[1]->Value),(Table11->Fields->Fields[n1]->Value));

for(int j=2;j<=n;++j)

{

Table11->Next();

wart2=pow((Table6->Fields->Fields[j]->Value),(Table11->Fields->Fields[n1]-

>Value));

if(pow((Table6->Fields->Fields[j]->Value),(Table11->Fields->Fields[n1]-

>Value))<wart)

{

wart=pow((Table6->Fields->Fields[j]->Value),(Table11->Fields->Fields[n1]->Value));

}

}

wart1[l1]=wart;

++l1;

Table6->Next();

}

l1=1;

Table6->Close();

Table1->Open();

Table1->First();

while (!Table1->Eof)

{

Table1->Edit();

Table1->Fields->Fields[1]->AsString = wart1[l1];

++l1;

Table1->Post();

Table1->Next();

53

}

Table1->EnableControls();

}

void TForm6::Oblicz_dd2()

{

int n;

int n1;

int l1;

double wart, wart1[16];

Table6->Open();

n=(Table6->FieldCount)-1;

n1=(Table11->FieldCount)-1;

Table6->DisableControls();

Table6->First();

l1=1;

while (!Table6->Eof)

{

Table11->First();

wart=1;

for(int j=1;j<=n;++j)

{

wart=wart*(pow((Table6->Fields->Fields[j]->Value),(Table11->Fields->Fields[n1]-

>Value)));

Table11->Next();

}

wart1[l1]=wart;

++l1;

Table6->Next();

}

l1=1;

Table6->Close();

Table1->Open();

Table1->First();

while (!Table1->Eof)

{

Table1->Edit();

Table1->Fields->Fields[2]->AsString = wart1[l1];

++l1;

Table1->Post();

Table1->Next();

}

Table1->EnableControls();

}
void TForm6::Oblicz_dd3()

{

int n;

int n1;

int l1;

double wart, wart1[16],wart3,wart4;

Table6->Open();

n=(Table6->FieldCount)-1;

n1=(Table11->FieldCount)-1;

Table6->DisableControls();

Table6->First();

l1=1;

while (!Table6->Eof)

{

Table11->First();

54

wart=0;

for(int j=1;j<=n;++j)

{

wart3=(Table6->Fields->Fields[j]->Value)*(Table11->Fields->Fields[n1]->Value);

wart4=wart3/(double)n;

wart=wart+wart4;

Table11->Next();

}

wart1[l1]=wart;

++l1;

Table6->Next();

}

l1=1;

Table6->Close();

Table1->Open();

Table1->First();

while (!Table1->Eof)

{

Table1->Edit();

Table1->Fields->Fields[3]->AsString = wart1[l1];

++l1;

Table1->Post();

Table1->Next();

}

Table1->EnableControls();

}

55

8. Spis ilustracji.

Rys. 2.1. Ogólny schemat budowania struktury hierarchicznej. .................................................................. 9

Rys. 2.2. Hierarchiczna struktura u yta w analizowanym problemie. ......................................................... 9

Rys. 2.3. Typ funkcji dla kryterium Pracuj cy...........................................................................................13

Rys. 2.4. Typ funkcji dla kryterium Przest pstwa. .....................................................................................13

Rys. 2.5. Typ funkcji trapezoidalnej. ..........................................................................................................14

Rys. 2.6. Typ funkcji dwuwarto ciowej. ....................................................................................................14

Rys. 2.7. Funkcja wzrastaj ca.....................................................................................................................14

Rys. 2.8. Funkcja opadaj ca. ......................................................................................................................15

Rys. 2.9. Obliczenie warto ci funkcji u yteczno ci....................................................................................19

Rys. 3.1. Schemat blokowy oprogramowania.............................................................................................21

Rys. 3.2. Struktura bazy danych. ................................................................................................................22

Rys. 4.1. Ekran startowy programu. ...........................................................................................................26

Rys. 4.2. Podmenu Kryteria szczegółowe. ..................................................................................................26

Rys. 4.3. Formularz Zdrowie. .....................................................................................................................27

Rys. 4.4. Formularz z typami funkcji..........................................................................................................28

Rys. 4.5. Formularz Finanse.......................................................................................................................29

Rys. 4.6. Formularz Infrastruktura. ............................................................................................................30

Rys. 4.7. Formularz Czysto ......................................................................................................................31

Rys. 4.8. Formularz Praca..........................................................................................................................32

Rys. 4.9. Formularz Przest pczo . ............................................................................................................33

Rys. 4.10. Formularz Macierz kategorii. ....................................................................................................33

Rys. 4.11. Podmenu Kryteria globalne.......................................................................................................34

Rys. 4.12. Okno Zdrowie - kryterium globalne. .........................................................................................35

Rys. 4.13. Okno Finanse - kryterium globalne...........................................................................................35

Rys. 4.14. Okno Infrastruktura - kryterium globalne. ................................................................................36

Rys. 4.15. Okno Czysto - kryterium globalne..........................................................................................36

Rys. 4.16. Okno Praca - kryterium globalne..............................................................................................37

Rys. 4.17. Okno Przest pczo - kryterium globalne. ................................................................................37

Rys. 4.18. Okno Wszystko - kryterium globalne. ........................................................................................38

Rys. 4.19. Podmenu Wykresy......................................................................................................................38

Rys. 4.20. Typy wykresów do wy wietlenia. .............................................................................................39

Rys. 4.21. Histogram kryteriów DD1, DD2, DD3 dla kategorii Zdrowie...................................................40

Rys. 4.22. Wykres kołowy kryterium DD1 dla kategorii Zdrowie. ............................................................40

Rys. 4.23. Histogram kryteriów DD1, DD2, DD3 dla kategorii Finanse. ..................................................41

Rys. 4.24. Wykres kołowy kryterium DD1 dla kategorii Finanse..............................................................41

Rys. 4.25. Histogram kryteriów DD1, DD2, DD3 dla kategorii Infrastruktura. ........................................42

Rys. 4.26. Wykres kołowy kryterium DD1 dla kategorii Infrastruktura. ...................................................42

Rys. 4.27. Histogram kryteriów DD1, DD2, DD3 dla kategorii Czysto . .................................................43

Rys. 4.28. Wykres kołowy kryterium DD1 dla kategorii Czysto .............................................................43

Rys. 4.29. Histogram kryteriów DD1, DD2, DD3 dla kategorii Praca. .....................................................44

Rys. 4.30. Wykres kołowy kryterium DD1 dla kategorii Praca.................................................................44

Rys. 4.31. Histogram kryteriów DD1, DD2, DD3 dla kategorii Przest pczo ..........................................45

Rys. 4.32. Wykres kołowy kryterium DD1 dla kategorii Przest pczo . ...................................................45

Rys. 4.33. Histogram kryterium DD1 dla kategorii Wszystko. ...................................................................46

Rys. 4.34. Histogram kryterium DD2 dla kategorii Wszystko. ...................................................................46

Rys. 4.35. Histogram kryterium DD3 dla kategorii Wszystko. ...................................................................47

Rys. 4.36. Wykres kołowy kryterium DD1 dla kategorii Wszystko. ...........................................................47

Rys. 4.37. Wykres kołowy kryterium DD2 dla kategorii Wszystko. ...........................................................48

Rys. 4.38. Wykres kołowy kryterium DD3 dla kategorii Wszystko. ...........................................................48

56

9. Spis tabel.

Tab. 2.1. Macierz parzystych porówna dla kryteriów z grupy rynek pracy. ............................................ 11

Tab. 2.2. Macierz parzystych porówna z wyliczonymi rangami kryteriów. ............................................ 12

Tab. 2.3. Tabela Praca............................................................................................................................... 17

Tab. 3.1. Struktura grupy Kryteria szczegółowe. ....................................................................................... 23

Tab. 3.2. Struktura grupy Macierze parzystych porówna i współczynniki wzgl dnej wa no ci kryteriów

szczegółowych. ................................................................................................................................... 23

Tab. 3.3. Struktura grupy Typy funkcji dla kryteriów szczegółowych i ich punkty kluczowe. .................... 24

Tab. 3.4. Struktura grupy Kryteria globalne.............................................................................................. 24