SNy: Biotechnologia

Studenckie Notatki Cyfrowe

www.sny.one.pl

Wrocław, 2007

Fizyka II – ćwiczenia

notatki ze studiów

na kierunku Biotechnologia

na Wydziale Chemicznym

Politechniki Wrocławskiej

Autor:
Mateusz Jędrzejewski
[e-mail]
www.jedrzejewski.one.pl

SNy: Biotechnologia

Spis treści

Informacje o kursie _____________________________________________________3

ZESTAW 0 – Prąd przemienny ____________________________________________4

ZESTAW 1 – Fale _______________________________________________________8

Kolokwium I __________________________________________________________ 15

ZESTAW 2 – Interferencja i dyfrakcja _____________________________________ 19

ZESTAW 3 – Polaryzacja________________________________________________25

Kolokwium II _________________________________________________________30

ZESTAW 4 – Efekty kwantowe___________________________________________ 31

ZESTAW 5 – Efekty kwantowe oraz rozpad promieniotwórczy ________________37

Kolokwium III ________________________________________________________45

SNy: Biotechnologia

Wstęp

otatka jest częścią projektu SNy Biotechnologia
(Studenckie Notatki Cyfrowe). Udostępniane

są one na stronie internetowej www.sny.one.pl. Każdy
może za darmo korzystać z nich w celach edukacyjnych.

a konkretna notatka dotyczy kursy FZC1004c,
czyli ćwiczeń do wykładów z Fizyki II. Notatka

zawiera przykładowe opracowanie szkiców rozwiązań
do zestawów zadań. Nie są to więc pełne rozwiązania
do zadań.

Zadania pochodzą z list omawianych

na ćwiczeniach oraz dodatkowym wykładzie. Szkice
będą, w miarę możliwości, opatrywane dodatkowymi
rysunkami i komentarzami.

Chciałbym podziękować Jakubowi Jakimiukowi

za dostarczenie treści niektórych zadań.

waga na błędy! Mimo staranności jaką włożyli
autorzy w opracowanie tej notatki mogą

zdarzyć się błędy. Więc każdy korzysta z tych notatek
na własną odpowiedzialność. Zauważone błędy proszę
zgłaszać autorowi notatki (najlepiej drogą elektroniczną).

śyczę wszystkim skutecznego korzystania z notatek.

Mateusz Jędrzejewski
(autor strony www.sny.one.pl)

Szczegółowe informacje o notatce

Nazwa pliku: e-notatka - Fizyka II - cwiczenia.pdf

Nazwa kursu: Fizyka II (FZC1004C)

Prowadzący kurs: mgr Elżbieta Trzop (ćwiczenia), doc. Krzysztof Rohleder (wykład)

Semestr/rok: 07l (rok 1, II semestr)

Kierunek: Biotechnologia

Wydział: Wydział Chemiczny

Uczelnia: Politechnika Wrocławska

Autor notatki: Mateusz Jędrzejewski

Status: tworzona

N

T

U

Studenckie Notatki Cyfrowe

SNy: Biotechnologia

www.sny.one.pl [e-mail]

Strona 3

Notatka: Fizyka II (FZC1004C) – ćwiczenia.

Utworzona:

9.03.2007 1:09

Temat: Informacje o kursie.

Zmodyfikowana: 20.03.2007 23:58

Informacje o kursie

Nazwa kursu: Fizyka II – ćwiczenia

Kod kursu: FZC1004C

Prowadzący: mgr Elżbieta Trzop

Konsultacje: poniedziałek, środa, godz. 14:30-16:30, trzeba umówić się na e-mail,

bud. A-2, pok. 413.

Przebieg zajęć: rozwiązywanie list zadań dostępnych na stronie http://ar.ch.pwr.wroc.pl

Warunki zaliczenia: trzy kolokwia na każdym dwa zadania, trzeba każde zaliczyć na 50% pkt.

kolokwium I wtorek, 3 kwietnia 2007 r. – ZESTAW 0. oraz ZESTAW 1.

kolokwium II wtorek, 15 maja 2007 r. – ZESTAW 2. oraz ZESTAW 3.

kolokwium III wtorek, 5 czerwca 2007 r. – ZESTAW 4. oraz ZESTAW 5.

Przeliczenie punktów na oceny (max. 60 pkt.)

dst 30-35

+dst 36-41

db 42-47

+db 48-53

bdb 54-58

+bdb 59-60

Zgodnie z ogłoszeniem doc. Krzysztofa Rohledera jest zwolnienie z kolokwium końcowego
z wykładu w tym semestrze (tj. semestr 07l) po zaliczeniu ćwiczeń na co najmniej db.

Studenckie Notatki Cyfrowe

SNy: Biotechnologia

www.sny.one.pl [e-mail]

Strona 4

Notatka: Fizyka II (FZC1004C) – ćwiczenia.

Utworzona:

9.03.2007 1:10

Temat: Zestaw 0 – Prąd przemienny.

Zmodyfikowana: 24.03.2007 0:30

ZESTAW 0 – Prąd przemienny

Więcej na stronie pt. „Rozdział 7 – drgania w obwodach RLC (…)”:

http://www.mif.pg.gda.pl/kfze/wyklady/WM2rozdzial7.pdf

zad. 1.

Dane:

µH

5

=

L

,

nF

20

=

C

,

V

120

max

=

U

,

30

=

N

,

Szukane:

max

Φ

,

Opór obwodu zaniedbujemy. W zadaniu mamy do czynienia z drgającym obwodem LC.
Wzór na energię całkowitą kondensatora:

2

max

2

1

U

C

E

c

⋅

=

.

Wzór na energię całkowitą cewki:

2

max

2

1

i

L

E

c

⋅

=

.

Energia „przepływa” pomiędzy jedną postacią a drugą.
Nie ma strat energii więc obywa wzory można ze sobą porównać:

L

C

U

i

i

L

U

C

max

max

2

max

2

1

2

max

2

1

=

⇒

⋅

=

⋅

Dla cewki prawdziwe jest zależność:

i

L

N

⋅

=

Φ

⋅

w szczególności:

max

max

max

max

i

i

L

N

N

L

=

Φ

⇒

⋅

=

Φ

⋅

ostatecznie:

Wb

10

26

,

1

120

6

30

10

20

10

5

max

max

max

max

max

9

6

−

⋅

⋅

⋅

⋅

=

⋅

=

Φ

=

⋅

=

=

Φ

−

−

N

LC

L

C

N

L

N

L

U

U

i

zad. 2.

Dane:

mH

2

,

1

=

L

,

µF

03

,

0

=

C

,

Szukane:

λ

,

Opór obwodu zaniedbujemy. W zadaniu mamy do czynienia z drgającym obwodem LC.

Każda fala spełnia poniższą zależność:

T

v

λ

=

gdzie:

v

– prędkość rozchodzenia się fali,

λ

– długość fali,

T

– okres fali,

W szczególności dla fali elektromagnetycznej

s

m

8

10

3

⋅

=

=

c

v

(prędkość światła w próżni)

Więc:

T

c

T

c

T

v

⋅

=

⇒

=

⇒

=

λ

λ

λ

W układzie LC okres drgań wyraża się wzorem:

LC

T

π

2

=

m

10

13

,

1

10

03

,

0

10

2

,

1

2

10

3

2

4

6

3

8

−

−

−

⋅

=

⋅

⋅

⋅

⋅

⋅

=

⋅

=

⋅

=

π

λ

π

λ

LC

c

T

c

Studenckie Notatki Cyfrowe

SNy: Biotechnologia

www.sny.one.pl [e-mail]

Strona 5

Notatka: Fizyka II (FZC1004C) – ćwiczenia.

Utworzona:

9.03.2007 1:10

Temat: Zestaw 0 – Prąd przemienny.

Zmodyfikowana: 24.03.2007 0:30

zad. 3.

Dane:

µF

16

=

C

,

Ω

=

200

R

,

V

220

=

U

,

Hz

50

=

f

,

Szukane:

Z

,

i

,

ϕ

,

C

U

,

R

U

Jest to obwód typu RC.

Opór pojemnościowy to:

C

X

C

ω

1

=

.

f

⋅

=

π

ω

2

Zawada (opór całkowy układu) to ogólnie:

(

)

2

2

L

C

X

X

R

Z

−

+

=

tu

0

=

L

X

, więc

2

2

2

2

2

2

2

2

2

4

1

1

C

f

R

C

R

X

R

Z

C

π

ω

+

=

+

=

+

=

.

Ω

=

⋅

⋅

⋅

+

=

+

=

−

1

,

282

)

10

16

(

50

4

1

200

4

1

2

6

2

2

2

2

2

2

2

π

π

C

f

R

Z

.

Prawo Ohma

R

U

i

=

, uogólnienie (opór całkowy to zawada)

Z

U

i

=

A

78

,

0

1

,

282

220

=

=

=

Z

U

i

.

Opornik oraz kondensator są połączone szeregowo więc natężenie prądu jest jakie samo
w całym obwodzie.

V

155

10

16

50

2

78

,

0

2

V

156

200

78

,

0

6

=

⋅

⋅

⋅

=

⋅

=

=

⋅

=

=

⋅

=

⋅

=

−

π

π

ω

C

f

i

C

i

X

i

U

R

i

U

C

C

R

Przesunięcie fazowy wyraża się jako:

'

51

44

995

,

0

ctg

ar

ctg

ar

ctg

ar

ctg

ar

ctg

ar

tg

200

10

16

50

2

1

2

1

2

1

1

1

6

°

=

=

=

=

=

⇒

=

=

⋅

⋅

⋅

⋅

−

π

π

π

ω

ω

ϕ

ϕ

ϕ

fCR

fCR

CR

C

C

R

R

X

zad. 4.

Dane:

V

230

=

U

,

Hz

50

=

f

,

H

5

=

L

,

Ω

=

100

R

,

Szukane:

C

,

i

,

C

U

,

Jest to obwód typu RLC.

Jeżeli występuje w nim rezonans to zachodzi wzór:

LC

T

π

2

=

F

10

03

,

2

5

50

4

1

4

1

4

1

1

4

1

2

1

6

2

2

2

2

2

2

2

2

−

⋅

=

⋅

⋅

=

=

=

⇒

=

⇒

=

⇒

=

π

π

π

π

π

L

f

C

L

f

C

LC

f

f

LC

f

T

Liczę zawadę:

Ω

=

−

⋅

⋅

+

=

−

+

=

⋅

⋅

⋅

−

100

)

50

2

5

(

100

)

(

2

50

2

10

03

,

2

1

2

2

1

2

6

π

ω

π

ω

C

L

R

Z

Studenckie Notatki Cyfrowe

SNy: Biotechnologia

www.sny.one.pl [e-mail]

Strona 6

Notatka: Fizyka II (FZC1004C) – ćwiczenia.

Utworzona:

9.03.2007 1:10

Temat: Zestaw 0 – Prąd przemienny.

Zmodyfikowana: 24.03.2007 0:30

Prawdziwy jest związek:

V

10

6

,

3

3

,

2

U

A

3

,

2

100

230

3

50

2

10

03

,

2

1

2

1

1

C

6

⋅

=

⋅

=

⋅

=

⋅

=

⋅

=

=

=

⇒

=

⋅

⋅

⋅

⋅

−

π

π

ω

f

C

C

C

i

i

X

i

i

Z

U

i

zad. 5.

Dane:

Ω

=

400

R

,

H

3

,

1

=

L

,

mF

6

,

1

=

C

,

V

230

=

U

,

Hz

50

=

f

,

Szukane:

i

,

ś

r

P

(chodzi o moc średnią, skuteczną),

s

1

16

,

314

50

2

2

=

⋅

=

⋅

=

π

π

ω

f

Zawada (opór całkowy układu) to:

(

)

2

2

L

C

X

X

R

Z

−

+

=

Gdzie:

C

C

X

ω

1

=

(opór pojemnościowy),

L

X

L

ω

=

(opór indukcyjny),

(

)

Ω

=

⋅

−

+

=

−

+

=

−

⋅

⋅

24

,

570

)

3

,

1

16

,

314

(

400

2

10

6

,

1

16

,

314

1

2

2

1

2

3

L

R

Z

C

ω

ω

A

403

,

0

24

,

570

230

=

=

=

Z

U

i

W

65

400

403

,

0

2

2

=

⋅

=

=

R

i

P

ś

r

zad. 6.

Dane:

V

127

=

U

,

Hz

50

=

f

,

Ω

=

9

R

,

W

400

=

P

,

°

=

60

δ

,

Szukane:

L

,

Treść zadania nie jest spójna (patrz komentarz na końcu rozwiązania).


I sposób rozwiązania

Wzór na przesunięcie to:

Z

R

=

δ

cos

,

Ω

=

°

=

=

⇒

=

18

60

cos

9

cos

cos

δ

δ

R

Z

Z

R

Opór indukcyjny to:

fL

L

X

L

⋅

=

=

π

ω

2

,

bo

f

⋅

=

π

ω

2

Wzór na zawadę w obwodzie RL to:

2

2

L

X

R

Z

+

=

H

050

,

0

50

2

9

18

2

2

4

2

2

2

2

2

2

2

2

2

2

2

2

=

⋅

−

=

⋅

−

=

⋅

−

=

⇒

+

=

+

=

π

π

π

π

f

R

Z

L

f

R

Z

L

L

f

R

X

R

Z

L

II sposób rozwiązania

sk

sk

sk

sk

sk

sk

sk

sk

I

U

Z

Z

U

I

U

P

I

I

U

P

=

⇒

=

⋅

=

⇒

⋅

⋅

=

δ

δ

cos

cos

Studenckie Notatki Cyfrowe

SNy: Biotechnologia

www.sny.one.pl [e-mail]

Strona 7

Notatka: Fizyka II (FZC1004C) – ćwiczenia.

Utworzona:

9.03.2007 1:10

Temat: Zestaw 0 – Prąd przemienny.

Zmodyfikowana: 24.03.2007 0:30

H

057

,

0

50

2

400

9

400

60

cos

127

cos

cos

cos

cos

cos

2

2

2

4

2

2

2

4

2

2

2

2

2

4

2

2

2

2

2

4

2

2

2

2

2

2

4

2

2

2

2

2

2

2

2

2

2

2

2

=

⋅

⋅

⋅

−

°

=

−

=

−

=

−

=

+

=

⋅

⇒

+

⋅

=

+

=

⇒

+

=

⇒

+

=

π

ω

δ

ω

δ

ω

ω

δ

ω

δ

ω

δ

ω

ω

ω

P

R

P

U

L

P

R

P

U

R

P

U

L

L

R

P

U

L

R

U

P

U

L

R

I

U

L

R

I

U

L

R

Z

sk

sk

sk

sk

sk

sk

sk

sk

sk

sk

Ten sposób poprawny merytorycznie daje inne wynik niż sposób I – też poprawny. Więc
dane w treści zadania zostały źle dobrane. Jeżeli by zmodyfikować moc

W

400

=

P

na

W

448

'

=

P

to spójność zadania będzie zachowana.

Sprawdzam:

H

050

,

0

50

2

448

9

448

60

cos

127

'

'

cos

2

2

2

4

2

2

2

4

=

⋅

⋅

⋅

−

°

=

−

=

π

ω

δ

P

R

P

U

L

sk

.

Teraz jest dobrze. Rozwiązanie ze sposobu pierwszego pokrywa się z drugim.

zad. 7.

Dane:

µF

5

,

0

=

C

,

mH

5

=

L

,

Szukane:

λ

,

Wzór na energię całkowitą kondensatora:

2

2

1

1

U

C

E

⋅

=

.

Wzór na energię całkowitą kondensatora:

2

max

2

1

U

C

E

c

⋅

=

.

Wzór na energię całkowitą cewki:

2

2

1

2

i

L

E

⋅

=

.

W każdym momencie prawdziwe jest:

2

1

E

E

E

c

+

=

(*).

Warunek z treści zadania:

2

1

E

E

=

(**)

z (*) oraz (**):

1

1

1

2

1

2E

E

E

E

E

E

c

=

+

=

+

=

1

2E

E

c

=

2

2

1

2

max

2

1

2

U

C

U

C

⋅

=

⋅

max

2

2

U

U

=

(***)

Ogólniej wzór na napięcie wyraża się:

α

sin

max

U

U

=

(****)

z (***) oraz (****):

8

2

4

2

2

sin

π

π

α

α

=

=

⇒

=

W układzie LC okres drgań wyraża się wzorem:

LC

T

π

2

=

Teraz trzeba odnieść kąt

α

do czasu t . Wiadomo, że jeden okres T odpowiada kątowi

pełnemu, czyli

π

2

rad. Więc prawdziwa jest proporcja:

s

10

93

,

3

10

5

,

0

10

5

4

8

2

8

2

2

2

5

9

3

4

4

4

−

−

−

⋅

=

⋅

⋅

⋅

=

=

=

=

=

=

=

⇒

=

π

π

π

π

π

π

π

α

α

π

LC

t

LC

LC

T

T

T

t

t

T

Studenckie Notatki Cyfrowe

SNy: Biotechnologia

www.sny.one.pl [e-mail]

Strona 8

Notatka: Fizyka II (FZC1004C) – ćwiczenia.

Utworzona:

9.03.2007 1:17

Temat: Zestaw 1 – Fale.

Zmodyfikowana: 31.03.2007 22:58

ZESTAW 1 – Fale

Wprowadzenie

Równanie fali

)

sin(

)

,

(

max

t

kx

y

t

x

y

ω

−

=

gdzie:

max

y

to maksymalne wychylenie (amplituda)

k

to liczba falowa

λ

π

2

=

k

ω

to częstość

T

π

ω

2

=

λ

to długość fali

f

v

=

λ

f

to częstotliwość

T

f

1

=

f

v

prędkość fali

k

T

T

v

f

ω

π

πλ

λ

=

=

=

2

2

T

to okres

v

T

λ

=

u

prędkość cząsteczek ośrodka (należy odróżnić ją o prędkości rozchodzenia się fali

f

v

).

)

,

(

)

,

(

)

sin(

)

cos(

2

max

2

max

t

x

y

t

x

a

t

kx

y

dt

du

a

t

kx

y

dt

dy

u

⋅

−

=

−

−

=

=

−

−

=

=

ω

ω

ω

ω

ω

Więcej na stronie pt. „Wykład 5 – drgania i fale”:

http://wazniak.mimuw.edu.pl/index.php?title=PF_Modu%C5%82_5

zad. 1.

Dane:

Hz

16

1

=

f

,

kHz

20

2

=

f

,

s

m

340

=

p

v

,

Szukane:

1

λ

,

2

λ

,

m

10

17

10

20

340

m

21

16

340

3

s

1

3

s

m

2

2

s

1

s

m

1

1

−

−

⋅

=

⋅

=

=

=

=

=

=

f

v

f

v

f

v

p

p

λ

λ

λ

zad. 2.

Dane:

m

800

=

s

,

C

20

°

=

T

,

s

78

,

1

=

∆

t

,

Szukane:

w

v

,

p

p

p

w

v

t

v

s

t

t

t

s

v

t

s

v

∆

−

=

⇒

∆

+

=

=

t

v

s

s

v

v

t

v

s

s

t

s

v

p

p

p

p

w

∆

−

=

∆

−

=

=

(*)

Studenckie Notatki Cyfrowe

SNy: Biotechnologia

www.sny.one.pl [e-mail]

Strona 9

Notatka: Fizyka II (FZC1004C) – ćwiczenia.

Utworzona:

9.03.2007 1:17

Temat: Zestaw 1 – Fale.

Zmodyfikowana: 31.03.2007 22:58

Trzeba więc znać prędkość dźwięku w powietrzu (

p

v

), żeby móc obliczyć prędkość

dźwięku w wodzie (

w

v

).

Dygresja: obliczenia prędkości dźwięku w powietrzu
Ogólnie prędkość rozchodzenia się fal w ośrodkach gazowych wyraża się:

ρ

κ

p

v

⋅

=

gdzie

v

p

c

c

=

κ

to współczynnik, którego wartość to 41

,

1

dla cząsteczek

gazu dwuatomowych, p to ciśnienie,

ρ

to gęstość, dla powierza wynosi ono

3

m

kg

29

,

1

.

Ogólnie wiadomo, że:

m

V

V

n

=

gdzie

n

to liczność,

m

V

to objętość molowa

3

dm

mol

4

,

22

.

Przy założeniu, że powietrze to gaz doskonały można skorzystać z równania Clapeyrona:

nRT

pV

=

gdzie R to stała gazowa równa

K

mol

J

314

,

8

⋅

, T to temperatura w Kelwinach,

m

m

V

RT

nV

nRT

p

V

nRT

p

=

=

⇒

=

s

m

m

mol

3

K

mol

J

m

kg

8

,

344

10

4

,

22

)

K

273

20

(

314

,

8

29

,

1

41

,

1

3

3

=

⋅

+

⋅

=

=

⋅

=

−

⋅

m

p

V

RT

p

v

ρ

κ

ρ

κ

s

m

8

,

344

=

p

v

.

Wraz więc do wzoru (*):

s

m

s

m

s

m

1481

s

78

,

1

8

,

344

m

800

m

800

8

,

344

=

⋅

−

⋅

=

∆

−

=

t

v

s

s

v

v

p

p

w

.

Gdyby przyjąć, że

s

m

343

=

p

v

wtedy:

s

m

s

m

s

m

1448

s

78

,

1

343

m

800

m

800

343

=

⋅

−

⋅

=

w

v

.

zad. 3.

Dane:

s

km

33

,

1

=

v

,

3

cm

g

8

,

0

=

ρ

,

Szukane:

κ

(współczynnik ściśliwości),

Zachodzi wzór:

ρ

B

v

=

gdzie B to moduł ściśliwości objętościowej i jest równy:

κ

1

=

B

.

więc:

N

m

10

m

kg

3

2

s

m

3

2

2

2

3

10

06

,

7

10

8

,

0

)

10

33

,

1

(

1

1

1

1

−

⋅

=

⋅

⋅

⋅

=

=

=

⇒

⋅

=

⇒

=

ρ

κ

ρ

κ

κ

ρ

ρ

v

v

v

B

v

Studenckie Notatki Cyfrowe

SNy: Biotechnologia

www.sny.one.pl [e-mail]

Strona 10

Notatka: Fizyka II (FZC1004C) – ćwiczenia.

Utworzona:

9.03.2007 1:17

Temat: Zestaw 1 – Fale.

Zmodyfikowana: 31.03.2007 22:58

zad. 4.

Dane:

cm

15

=

A

,

cm

40

=

λ

,

Hz

8

=

f

,

Szukane:

k

,

T

,

ω

,

f

v

,

)

,

(

y

x

y

,

Dla

0

=

t

oraz

0

=

x

wychylenie

A

y

=

(czyli maksymalne wychylenie). (*)

m

1

2

7

,

15

m

10

40

2

2

=

⋅

=

=

−

π

λ

π

k

s

125

,

0

Hz

8

1

1

=

=

=

f

T

s

1

3

,

50

Hz

8

2

2

=

⋅

=

⋅

=

π

π

ω

f

s

m

m

1

s

1

2

,

3

7

,

15

3

,

50

=

=

=

k

v

f

ω

Równanie fali ogólnie:

)

sin(

)

,

(

ϕ

ω

+

−

=

t

kx

A

t

x

y

gdzie:

ϕ

to przesunięcie fazowe,

z (*) wynika, że:

2

1

sin

)

0

,

0

(

sin

)

0

0

sin(

)

0

,

0

(

π

ϕ

ϕ

ϕ

ϕ

=

⇒

=

⇒

=

=

+

⋅

−

⋅

=

A

y

A

t

x

A

y

)

3

,

50

7

,

15

sin(

15

,

0

)

,

(

2

π

+

⋅

−

⋅

⋅

=

t

x

t

x

y

co jest tożsame z:

)

3

,

50

7

,

15

cos(

15

,

0

)

,

(

t

x

t

x

y

⋅

−

⋅

⋅

=

zad. 5.

Dane:

)

858

7

,

15

cos(

10

2

)

,

(

6

t

x

t

x

s

⋅

−

⋅

⋅

⋅

=

−

,

Szukane:

λ

,

f

v

,

)

003

,

0

;

05

,

0

(

s

,

v

A

(amplituda prędkości),

z równania fali

)

,

( t

x

s

wynika, że:

m

10

2

6

−

⋅

=

A

,

m

1

7

,

15

=

k

,

s

1

858

=

ω

,

m

4

,

0

7

,

15

2

2

m

1

=

=

=

π

π

λ

k

,

s

m

m

1

s

1

6

,

54

7

,

15

858

=

=

=

k

v

f

ω

m

10

433

,

0

)

003

,

0

858

05

,

0

7

,

15

cos(

10

2

)

003

,

0

;

05

,

0

(

6

6

−

−

⋅

−

=

⋅

−

⋅

⋅

⋅

=

s

A

A

v

ω

−

=

(gdzie

max

y

A

=

– patrz „Wprowadzenie”).

s

m

3

6

s

1

10

716

,

1

m

10

2

858

−

−

⋅

=

⋅

⋅

−

=

v

A

Studenckie Notatki Cyfrowe

SNy: Biotechnologia

www.sny.one.pl [e-mail]

Strona 11

Notatka: Fizyka II (FZC1004C) – ćwiczenia.

Utworzona:

9.03.2007 1:17

Temat: Zestaw 1 – Fale.

Zmodyfikowana: 31.03.2007 22:58

zad. 6.

Dane:

)

2

3

sin(

4

)

,

(

1

t

x

t

x

y

−

=

,

)

2

3

sin(

4

)

,

(

2

t

x

t

x

y

+

=

,

cm

3

,

2

=

x

,

Szukane:

x

A

(amplituda wychylenia),

położenie węzłów i strzałek,

Interferencją dwóch fal jest fala:

)

2

3

sin(

4

)

2

3

sin(

4

2

1

t

x

t

x

y

y

y

+

+

−

=

+

=

stosuję znany wzór na sumę sinusów:

2

2

cos

sin

2

sin

sin

β

α

β

α

β

α

−

+

=

+

t

x

y

t

x

t

x

t

x

t

x

2

cos

3

sin

8

cos

sin

2

4

2

2

3

2

3

2

2

3

2

3

=

⋅

=

−

−

−

+

+

−

t

x

y

2

cos

3

sin

8

=

dla

cm

3

,

2

=

x

mamy:

t

t

y

2

cos

)

9

,

6

sin(

8

2

cos

)

3

,

2

3

sin(

8

⋅

=

⋅

=

więc:

)

9

,

6

sin(

8

=

x

A

ponieważ to nie zależy od czasu i stoi przed funkcją cosinus.

cm

62

,

4

578

,

0

8

)

9

,

6

sin(

8

=

⋅

=

=

x

A

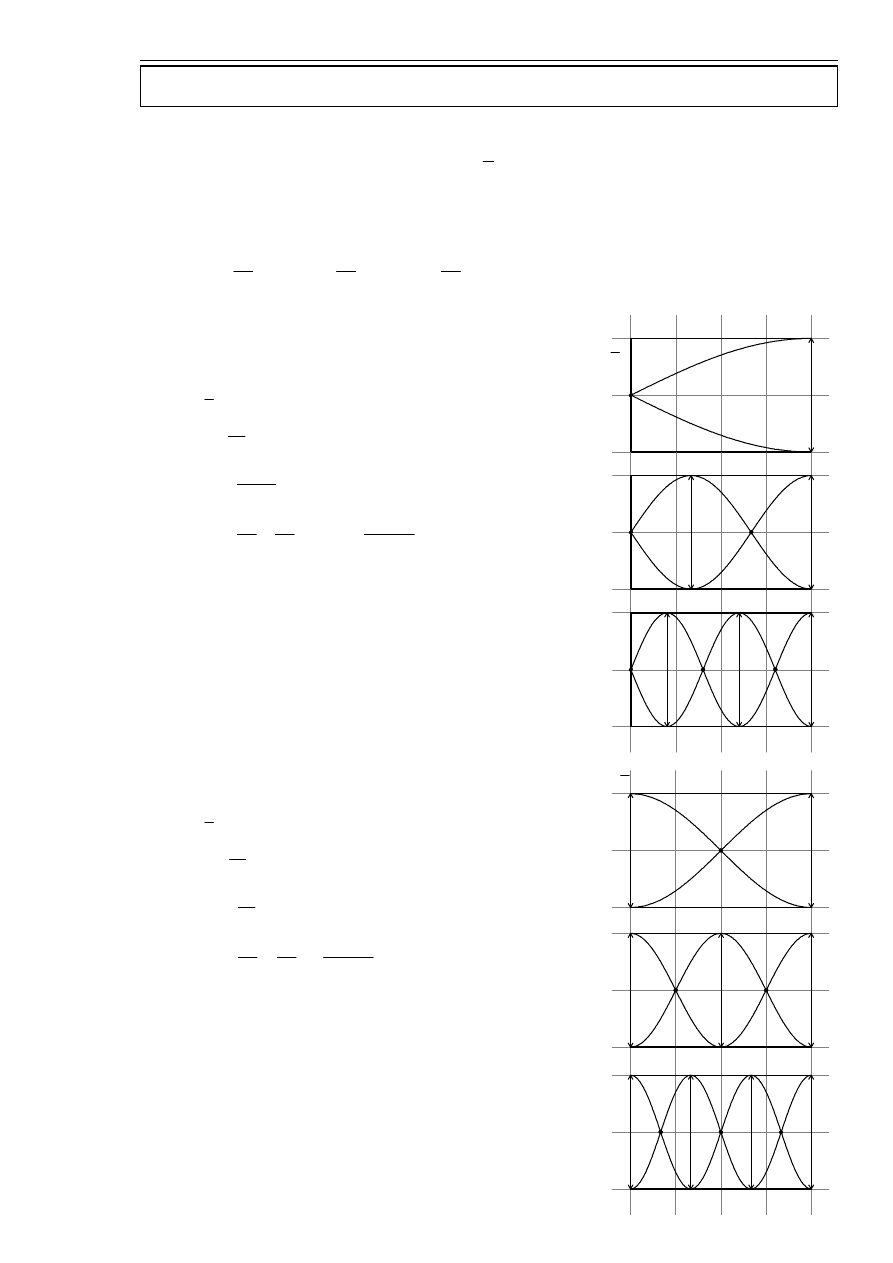
węzły fali stojącej
miejsca w przestrzeni gdzie fale wygasiły się całkowicie, więc

0

=

y

(brak wychylenia):

N

k

k

x

x

∈

∧

=

⇔

=

π

3

(

0

)

3

sin(

,

położenia węzłów:

...

,

,

,

0

3

2

3

π

π

π

=

=

=

=

x

x

x

x

strzałki fali stojącej
miejsca w przestrzeni gdzie fale wzmocniły się maksymalnie, czyli dla:

)

(

)

3

(

1

)

3

sin(

3

6

2

N

k

k

x

Z

k

k

x

x

∈

∧

+

=

⇔

∈

∧

+

=

⇔

=

π

π

π

π

położenia strzałek:

...

,

,

6

5

2

6

π

π

π

=

=

=

x

x

x

Uwaga dodatkowa:
liczba falowa tej fali to:

3

=

k

długość tej fali to:

3

2

2

π

π

λ

=

=

k

Odległości pomiędzy kolejnymi węzłami to

3

2

π

λ

=

,

odległości pomiędzy kolejnymi strzałkami to również

3

2

π

λ

=

.

Odległości pomiędzy węzłem a najbliższą strzałką to

6

4

π

λ

=

.

Studenckie Notatki Cyfrowe

SNy: Biotechnologia

www.sny.one.pl [e-mail]

Strona 12

Notatka: Fizyka II (FZC1004C) – ćwiczenia.

Utworzona:

9.03.2007 1:17

Temat: Zestaw 1 – Fale.

Zmodyfikowana: 31.03.2007 22:58

zad. 7.

Dane:

m

85

,

0

=

l

,

s

m

340

=

f

v

,

Hz

650

=

<

gr

i

f

f

,

Szukane:

i

f

(częstotliwości drgań własnych słupa powietrza w rurze),

Rozważamy tutaj fale własne, które są falami stojącymi.

i

f

i

f

f

v

f

v

f

f

v

λ

λ

λ

=

⇒

=

⇒

=

a)

rura jest zamknięta z jednej strony

Odległość między węzłem a strzałką zawsze jest taka sama i wynosi:

4

λ

.

Patrząc na rysunek widzę, że musi być nieparzysta wielokrotność

4

λ

(tak, żeby z jednej strony była strzałka, a z drugiej węzeł).

gr

i

f

i

f

i

i

i

f

f

f

f

f

i

f

i

i

i

l

v

v

f

N

i

i

l

N

i

i

l

≥

=

−

⋅

=

=

−

⋅

=

=

−

⋅

=

=

−

⋅

=

−

=

−

⋅

=

−

⋅

=

−

=

=

∈

∧

−

=

∈

∧

−

=

Hz

700

100

4

200

Hz

500

100

3

200

Hz

300

100

2

200

Hz

100

100

1

200

100

200

)

1

2

(

100

)

1

2

(

85

,

0

4

340

)

1

2

(

4

1

2

4

)

1

2

(

4

4

3

2

1

λ

λ

λ

b)

rura jest otwarta z obu stron

Odległość między węzłem a strzałką zawsze jest taka sama i wynosi:

4

λ

.

Patrząc na rysunek widzę, że musi być parzysta wielokrotność

4

λ

(tak, żeby z obu strony były strzałki).

gr

i

f

i

f

i

i

i

f

f

f

f

f

i

f

i

i

i

l

v

v

f

N

i

i

l

N

i

i

l

≥

=

⋅

=

=

⋅

=

=

⋅

=

=

⋅

=

=

=

⋅

=

=

=

∈

∧

=

∈

∧

=

Hz

800

4

200

Hz

600

3

200

Hz

400

2

200

Hz

200

1

200

200

200

85

,

0

2

340

2

2

2

4

4

3

2

1

λ

λ

λ

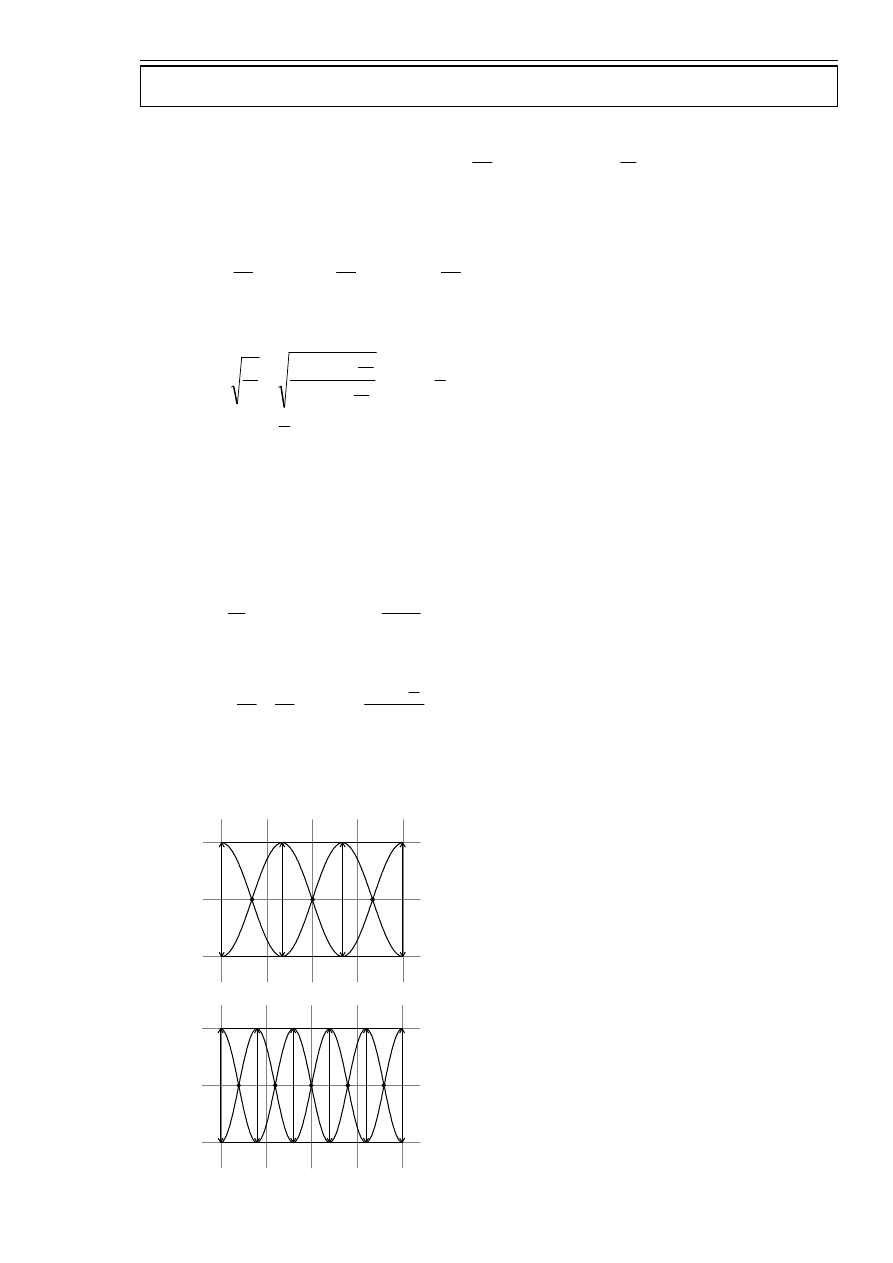
Studenckie Notatki Cyfrowe

SNy: Biotechnologia

www.sny.one.pl [e-mail]

Strona 13

Notatka: Fizyka II (FZC1004C) – ćwiczenia.

Utworzona:

9.03.2007 1:17

Temat: Zestaw 1 – Fale.

Zmodyfikowana: 31.03.2007 22:58

zad. 8.

Dane:

cm

50

=

l

,

3

cm

g

6

,

8

=

ρ

,

3

m

N

11

10

18

,

1

⋅

=

E

,

kHz

20

kHz

10

<

<

i

f

,

Szukane:

i

f

(częstotliwości drgań własnych),

Rozważamy tutaj fale własne, które są falami stojącymi.

i

f

i

f

f

v

f

v

f

f

v

λ

λ

λ

=

⇒

=

⇒

=

Jedna niewiadomą jest

f

v

, można ją wyliczyć ze wzoru

s

m

s

m

m

kg

3

m

N

11

3704

3704

10

6

,

8

10

18

,

1

3

3

=

=

⋅

⋅

=

=

f

v

E

v

ρ

Drugą niewidomą jest

i

λ

.

Fale strojące w rozważanym pręcie muszą:
1º na końcach mieć strzałki – ponieważ ta amplituda drgań ma być maksymalna,
2º w środku mieć węzeł – ponieważ pręt jest przymocowany na środku.

Z tych warunków wynika, że fale mogą mieć długości:

1

2

2

)

1

2

(

2

+

=

⇒

+

=

i

l

i

l

i

i

λ

λ

gdzie

N

i

∈

.

gr

f

i

f

i

f

f

f

f

i

i

i

l

v

v

f

≥

=

=

+

⋅

=

=

=

+

⋅

=

=

=

+

⋅

=

+

=

+

⋅

=

+

=

=

kHz

9

,

25

Hz

25928

3704

3

7408

kHz

5

,

18

Hz

18520

3704

2

7408

kHz

1

,

11

Hz

11112

3704

1

7408

3704

7408

)

1

2

(

m

5

,

0

2

3704

)

1

2

(

2

3

2

1

s

m

λ

Fala ta ma częstotliwość

1

f

,

ma trzy węzły oraz cztery strzałki.
W pręcie mieszczą się trzy połówki długości fali.

Fala ta ma częstotliwość

2

f

,

ma pięć węzłów oraz sześć strzałek.
W pręcie mieści się pięć połówek długości fali.

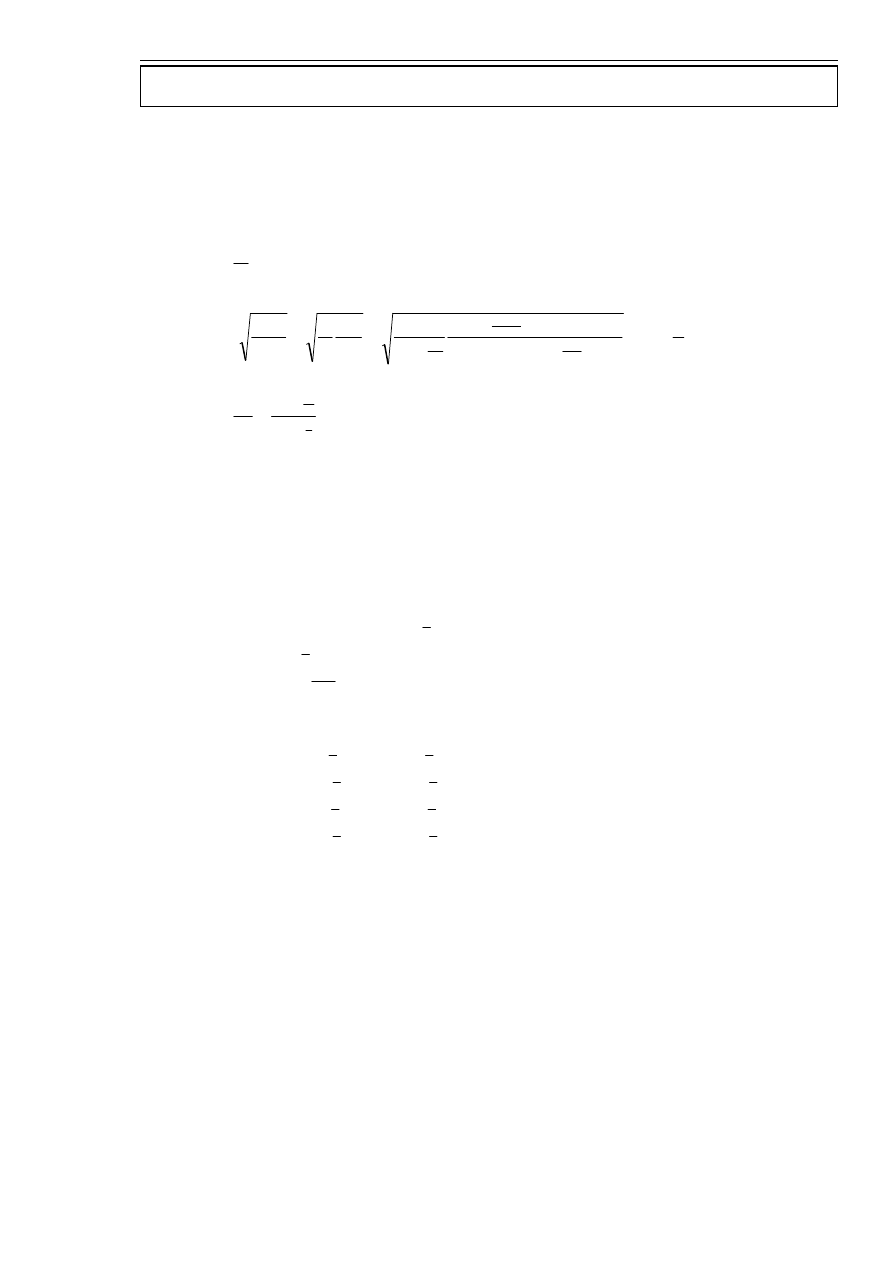
Studenckie Notatki Cyfrowe

SNy: Biotechnologia

www.sny.one.pl [e-mail]

Strona 14

Notatka: Fizyka II (FZC1004C) – ćwiczenia.

Utworzona:

9.03.2007 1:17

Temat: Zestaw 1 – Fale.

Zmodyfikowana: 31.03.2007 22:58

zad. 9.

Dane:

m

70

,

0

=

H

,

Hz

720

=

f

,

C

50

°

=

T

,

Szukane:

i

h

(wysokość słupa wody),

Rozważania można zacząć od:

f

v

=

λ

Prędkość rozchodzenia się dźwięku w powietrzu można wyliczyć ze wzoru (patrz zad. 2.)

s

m

m

mol

3

K

mol

J

m

kg

362

10

4

,

22

)

K

273

50

(

314

,

8

29

,

1

41

,

1

3

3

=

⋅

+

⋅

=

=

⋅

=

−

⋅

m

p

V

RT

p

v

ρ

κ

ρ

κ

Można więc wyznaczyć długość rozważanej fali:

m

503

,

0

720

362

s

1

s

m

=

=

=

f

v

p

λ

Oznaczenie wysokości słupa wody jako różnica wysokości naczynia oraz przestrzeni
wypełnionej powietrzem (nad powierzchnią wody do góry naczynia):

l

H

h

−

=

W rozważanej sytuacji fale stojące będą się wytwarzały na długości l wypełnionej powietrzem.
Może być wiele takich fal rezonansowych więc można przyjąć oznaczenie:

i

i

l

H

h

−

=

Należy zauważyć, że powstająca fala stojąca musi: mieć strzałkę u wylotu z naczynia oraz mieć
węzeł na powierzchni wody.
Pierwszą taką falą może być:

λ

4

1

1

=

l

(jeden węzeł i jedna strzałka),

Druga to:

λ

4

3

2

=

l

(dwa węzły i dwie strzałki),

Kolejne to:

λ

4

1

2

−

=

n

n

l

(

n

węzłów i

n

strzałek).

Można teraz przejść do obliczenia możliwych wysokości

i

h

:

m

574

,

0

m

503

,

0

m

7

,

0

4

1

4

1

1

1

=

⋅

−

=

−

=

−

=

λ

H

l

H

h

m

323

,

0

m

503

,

0

m

7

,

0

4

3

4

3

2

2

=

⋅

−

=

−

=

−

=

λ

H

l

H

h

m

071

,

0

m

503

,

0

m

7

,

0

4

5

4

5

3

3

=

⋅

−

=

−

=

−

=

λ

H

l

H

h

m

180

,

0

m

503

,

0

m

7

,

0

4

7

4

7

4

4

−

=

⋅

−

=

−

=

−

=

λ

H

l

H

h

0

4

<

h

więc nie ma to sensu fizycznego. Tym bardziej kolejne fale nie będą już dobre.

Studenckie Notatki Cyfrowe

SNy: Biotechnologia

www.sny.one.pl [e-mail]

Strona 15

Notatka: Fizyka II (FZC1004C) – ćwiczenia.

Utworzona: 31.03.2007 22:59

Temat: Kolokwium I.

Zmodyfikowana: 15.04.2007 10:31

Kolokwium I

3.04.2007 r.

Zakres tematyczny: prąd przemienny oraz fale.

Przykładowe treści zadań

zad. 1.
Jakiej długości fale można wytworzyć w obwodzie LC, w którym indukcyjność wynosi mH

4

,

a pojemność zmienia się w granicach od

pF

40

do

pF

100

? Jakie tym falom odpowiadają

częstotliwości?

Odp. długości fal zmieniają się od

m

753

do

m

1191

, a częstotliwości od

kHz

398

do

kHz

251

.

zad. 2.
Do obwodu RLC przyłożono napięcie (skuteczne)

V

220

. Spadek napięcia na cewce jest dwa

razy większy od spadku napięcia oporniku. Natomiast spadek napięcia na kondensatorze jest trzy
razy większy od spadku napięcia oporniku. Jak wartości mają te spadki napięć?

Odp.

V

67

,

36

=

R

U

,

V

33

,

73

=

L

U

,

V

110

=

C

U

.

zad. 3.
Dany jest drgający obwód typu LC, w którym indukcyjność wynosi

mH

150

. Zjawisko

rezonansu zachodzi przy częstotliwości

Hz

500

. Jaką pojemność musi mieć kondensator?

Odp.

µF

675

,

0

=

C

.

zad. 4.
Przy jakiej wysokości słupa wody powstaje fale stojąca, jeżeli cylinder z wodą ma wysokość

cm

80

,

a częstotliwość wytwarzanych fal wynosi

Hz

700

? Wysokość poziomu wody można swobodnie

zmieniać, a temperatura powietrza wynosi

C

40

°

.

Odp. możliwe poziomy wody w naczyniu:

m

673

,

0

,

m

418

,

0

,

m

164

,

0

.

zad. 5.
Dany jest obwód typu RL, w którym indukcyjność wynosi

mH

50

, a opór omowy wynosi

Ω

15

.

Przyłożono do tego obwodu napięcie (skuteczne)

V

120

. Oblicz częstotliwość drgań tego

obwodu wiedząc, że maksymalne natężenie prąd wynosi w nim A

7

.

Odp.

Hz

6

,

60

=

f

.

zad. 6.
Jaka jest częstotliwość najdłuższej fali w strunie o długości

m

5

,

0

, która rozchodzi się

z prędkością

s

m

5200

?

Odp.

Hz

5200

Studenckie Notatki Cyfrowe

SNy: Biotechnologia

www.sny.one.pl [e-mail]

Strona 16

Notatka: Fizyka II (FZC1004C) – ćwiczenia.

Utworzona: 31.03.2007 22:59

Temat: Kolokwium I.

Zmodyfikowana: 15.04.2007 10:31

Przykładowe rozwiązania zadań

zad. 1.

Dane:

mH

4

=

L

,

pF

40

min

=

C

,

pF

100

max

=

C

,

Szukane:

min

λ

,

max

λ

,

min

f

,

max

f

,

Wytwarzane fale to fale elektromagnetyczne:

T

c

f

c

⋅

=

=

λ

gdzie

s

m

8

10

3

⋅

=

c

(prędkość światła w próżni).

Okres drgań to:

LC

T

π

2

=

Więc:

s

10

51

,

2

10

40

10

4

2

2

6

m

kg

A

s

12

A

s

m

kg

3

min

min

2

2

4

2

2

2

−

⋅

⋅

−

⋅

⋅

−

⋅

=

⋅

⋅

⋅

=

=

π

π

LC

T

s

10

97

,

3

10

100

10

4

2

2

6

m

kg

A

s

12

A

s

m

kg

3

max

max

2

2

4

2

2

2

−

⋅

⋅

−

⋅

⋅

−

⋅

=

⋅

⋅

⋅

=

=

π

π

LC

T

m

753

s

10

51

,

2

10

3

6

s

m

8

min

min

=

⋅

⋅

⋅

=

⋅

=

−

T

c

λ

m

1191

s

10

97

,

3

10

3

6

s

m

8

max

max

=

⋅

⋅

⋅

=

⋅

=

−

T

c

λ

Na koniec:

T

f

1

=

kHz

251

Hz

10

251

,

0

s

10

97

,

3

1

1

6

6

max

min

=

⋅

=

⋅

=

=

−

T

f

kHz

398

Hz

10

398

,

0

s

10

51

,

2

1

1

6

6

min

max

=

⋅

=

⋅

=

=

−

T

f

zad. 2.

Dane:

V

220

=

U

,

R

L

U

U

2

=

,

R

C

U

U

3

=

,

Szukane:

R

U

,

L

U

,

C

U

,

Suma napięć na poszczególnych elementach obwodu RLC jest równa przyłożonemu napięciu:

C

L

R

U

U

U

U

+

+

=

Po podstawieniu danych z zadania:

V

110

220

3

3

3

V

33

,

73

220

2

2

2

V

67

,

36

220

6

3

2

6

1

6

1

6

1

6

1

6

1

6

1

=

⋅

⋅

=

⋅

=

=

=

⋅

⋅

=

⋅

=

=

=

⋅

=

=

⇒

=

+

+

=

U

U

U

U

U

U

U

U

U

U

U

U

U

U

R

C

R

L

R

R

R

R

R

Studenckie Notatki Cyfrowe

SNy: Biotechnologia

www.sny.one.pl [e-mail]

Strona 17

Notatka: Fizyka II (FZC1004C) – ćwiczenia.

Utworzona: 31.03.2007 22:59

Temat: Kolokwium I.

Zmodyfikowana: 15.04.2007 10:31

zad. 3.

Dane:

mH

150

=

L

,

Hz

500

=

f

,

Szukane:

C

,

Rezonans zachodzi gdy:

LC

T

π

2

=

,

gdzie T to okres drgań,

f

T

1

=

µF

675

,

0

F

10

75

,

6

10

150

500

4

1

4

1

2

1

7

3

2

2

2

2

=

⋅

=

⋅

⋅

⋅

=

=

⇒

=

−

−

π

π

π

L

f

C

LC

f

zad. 4.

Dane:

m

80

,

0

=

H

,

Hz

700

=

f

,

C

40

°

=

T

,

Szukane:

i

h

(wysokość słupa wody),

f

v

=

λ

Prędkość rozchodzenia się dźwięku w powietrzu można wyliczyć ze wzoru (patrz: Zestaw 1.):

s

m

m

mol

3

K

mol

J

m

kg

356

10

4

,

22

)

K

273

40

(

314

,

8

29

,

1

41

,

1

3

3

=

⋅

+

⋅

=

=

⋅

=

−

⋅

m

p

V

RT

p

v

ρ

κ

ρ

κ

Więc długość rozważanej fali stojącej to:

m

509

,

0

700

356

s

1

s

m

=

=

=

f

v

p

λ

Wysokość poziomu wody:

l

H

h

−

=

W rozważanej sytuacji fale stojące będą się wytwarzały na długości l wypełnionej powietrzem.
Może być wiele taki fale rezonansowych więc można przyjąć oznaczenie:

i

i

l

H

h

−

=

Należy zauważyć, że powstająca fala stojąca musi: mieć strzałkę u wylotu z naczynia oraz mieć
węzeł na powierzchni wody.
Pierwszą taką falą może być:

λ

4

1

1

=

l

(jeden węzeł i jedna strzałka),

Druga to:

λ

4

3

2

=

l

(dwa węzły i dwie strzałki),

Kolejne to:

λ

4

1

2

−

=

n

n

l

(

n

węzłów i

n

strzałek).

Można teraz przejść do obliczenia możliwych wysokości

i

h

:

m

673

,

0

m

509

,

0

m

8

,

0

4

1

4

1

1

1

=

⋅

−

=

−

=

−

=

λ

H

l

H

h

m

418

,

0

m

509

,

0

m

8

,

0

4

3

4

3

2

2

=

⋅

−

=

−

=

−

=

λ

H

l

H

h

m

164

,

0

m

509

,

0

m

8

,

0

4

5

4

5

3

3

=

⋅

−

=

−

=

−

=

λ

H

l

H

h

m

091

,

0

m

509

,

0

m

8

,

0

4

7

4

7

4

4

−

=

⋅

−

=

−

=

−

=

λ

H

l

H

h

0

4

<

h

więc nie ma to sensu fizycznego. Tym bardziej kolejne fale nie będą już dobre.

Studenckie Notatki Cyfrowe

SNy: Biotechnologia

www.sny.one.pl [e-mail]

Strona 18

Notatka: Fizyka II (FZC1004C) – ćwiczenia.

Utworzona: 31.03.2007 22:59

Temat: Kolokwium I.

Zmodyfikowana: 15.04.2007 10:31

zad. 5.

Dane:

mH

50

=

L

,

Ω

=

15

R

,

V

120

=

U

,

A

7

0

=

I

,

Szukane:

f

,

Częstotliwość można wyrazić poprzez częstość kołową drgań:

π

ω

π

ω

2

2

=

⇒

⋅

=

f

f

Napięcie maksymalne można wyznaczyć znając napięcie skuteczne:

V

7

,

169

2

120

2

2

0

0

=

⋅

=

=

⇒

=

U

U

U

U

Z praca Ohma dla prądu przemiennego można wyznaczyć zawadę:

Z

U

I

=

w szczególności zachodzi to dla wartości maksymalnych, czyli

0

0

0

0

I

U

Z

Z

U

I

=

⇒

=

Ω

24

,

24

7

7

,

169

0

0

=

=

=

I

U

Z

Opór indukcyjny to:

L

X

L

ω

=

,

Wzór na zawadę w obwodzie RL to:

2

2

L

X

R

Z

+

=

,

Hz

6

,

60

10

50

2

15

)

24

,

24

(

2

2

3

2

2

2

2

2

2

2

2

2

2

2

=

⋅

⋅

−

=

⋅

−

=

=

−

=

⇒

+

=

+

=

−

π

π

π

ω

ω

ω

L

R

Z

f

L

R

Z

L

R

X

R

Z

L

zad. 6.

Dane:

m

5

,

0

=

l

,

s

m

5200

=

v

,

Szukane:

f

,

λ

λ

v

f

f

v

=

⇒

=

W rozpatrywanym zadaniu powstają fale stojące w strunie.
Na końcach struny muszą być węzły.
Najdłuższa możliwa fala to:

l

l

2

2

=

⇒

=

λ

λ

czyli powstanie fala stojąca posiadająca dwa węzły i jedną strzałkę pomiędzy nimi.

Hz

5200

m

5

,

0

2

5200

2

s

m

=

⋅

=

=

=

l

v

v

f

λ

Studenckie Notatki Cyfrowe

SNy: Biotechnologia

www.sny.one.pl [e-mail]

Strona 19

Notatka: Fizyka II (FZC1004C) – ćwiczenia.

Utworzona: 24.03.2007 11:41

Temat: Zestaw 2 – Interferencja i dyfrakcja.

Zmodyfikowana: 27.04.2007 2:45

ZESTAW 2 – Interferencja i dyfrakcja

17.04.2007 r.

Wprowadzenie

Fala w fizyce to najogólniej zaburzenie, które podlega interferencji (superpozycji, nakładaniu).

Prawo odbicia
Kąt padania równy jest kątowi odbicia. Kąty umownie liczy się względem normalnej (prostej
prostopadłej do powierzchni).

Jeżeli fala odbija się od ośrodka gęstszego optycznie (

2

1

n

n

<

) to jej faza po odbiciu zmienia się

(przesuwa się) dokładnie o

π

. Wynika to ze wzorów Fresnela…

Prawo załamania (prawo Snelliusa)

1

2

12

sin

sin

n

n

n

=

=

β

α

gdzie

α

to kąt pod którym pada promień,

β

to kąt pod którym załamuje się promień,

12

n

to względny współczynnik załamania ośrodka 2 względem ośrodka 1,

1

n

to bezwzględny współczynnik załamania ośrodka 1.

Fala przechodząc przez granicę dwóch ośrodków ulega częściowo odbiciu, a częściowo załamaniu.
Promień padający, odbity i załamany leżą w tej samej płaszczyźnie.

Zasada Huygensa

(wymowa: hojchensa)

Każdy punkt ośrodka, do którego dotarło czoło fali można uważać za źródło nowej fali kulistej.

Doświadczenie Younga

Dotyczy to zjawiska ugięcia się fali monochromatycznej na siatce dyfrakcyjnej. Za tą siatką
ustawiony jest ekran, a którym są symetrycznie ułożone prążki.
Warunek na prążek jasny
(maksymalne wzmocnienie fal)

θ

λ

sin

d

m

=

Warunek na prążek ciemny
(maksymalne wygaszenie fal)

(

)

θ

λ

sin

2

1

d

m

=

+

gdzie:

{

}

...

,

2

,

1

,

0

∈

m

to liczba naturalna – określa ona rząd powstającego prążka, rząd ugięcia

λ

to długość fali monochromatycznej,

d

to stała siatki (suma szerokości szczeliny oraz odstępu między szczelinami),

Warunki te mogą zostać odwrócone, gdy zostanie spełniony warunek opisany w ramce powyżej.

Zasada najmniejszego działania (Zasada Fermata)
Promień biegnie od jednego do drugiego punktu zawsze w najkrótszym czasie. Promień biegnie
po najkrótszej drodze optyczne (która nie musi pokrywać się z najkrótszą drogą geometryczną).
Wynika z tego bezpośrednio prawo załamania i prawo odbicia światła.

Droga geometryczna oraz optyczna

S

– droga geometryczna, czyli zwykła odległość (Euklidesowa) na płaszczyźnie,

R

– droga optyczna, czyli taka jaką przebędzie fala w próżni w tym samym czasie co w danej substancji.

S

R

v

c

n

t

v

t

c

=

=

=

λ

λ

c

f

v

f

c

v

c

n

=

=

=

nS

R

=

Więcej na stronie pt. „Wykład 16 – zjawiska falowe”:

http://wazniak.mimuw.edu.pl/index.php?title=PF_Modu%C5%82_16

Studenckie Notatki Cyfrowe

SNy: Biotechnologia

www.sny.one.pl [e-mail]

Strona 20

Notatka: Fizyka II (FZC1004C) – ćwiczenia.

Utworzona: 24.03.2007 11:41

Temat: Zestaw 2 – Interferencja i dyfrakcja.

Zmodyfikowana: 27.04.2007 2:45

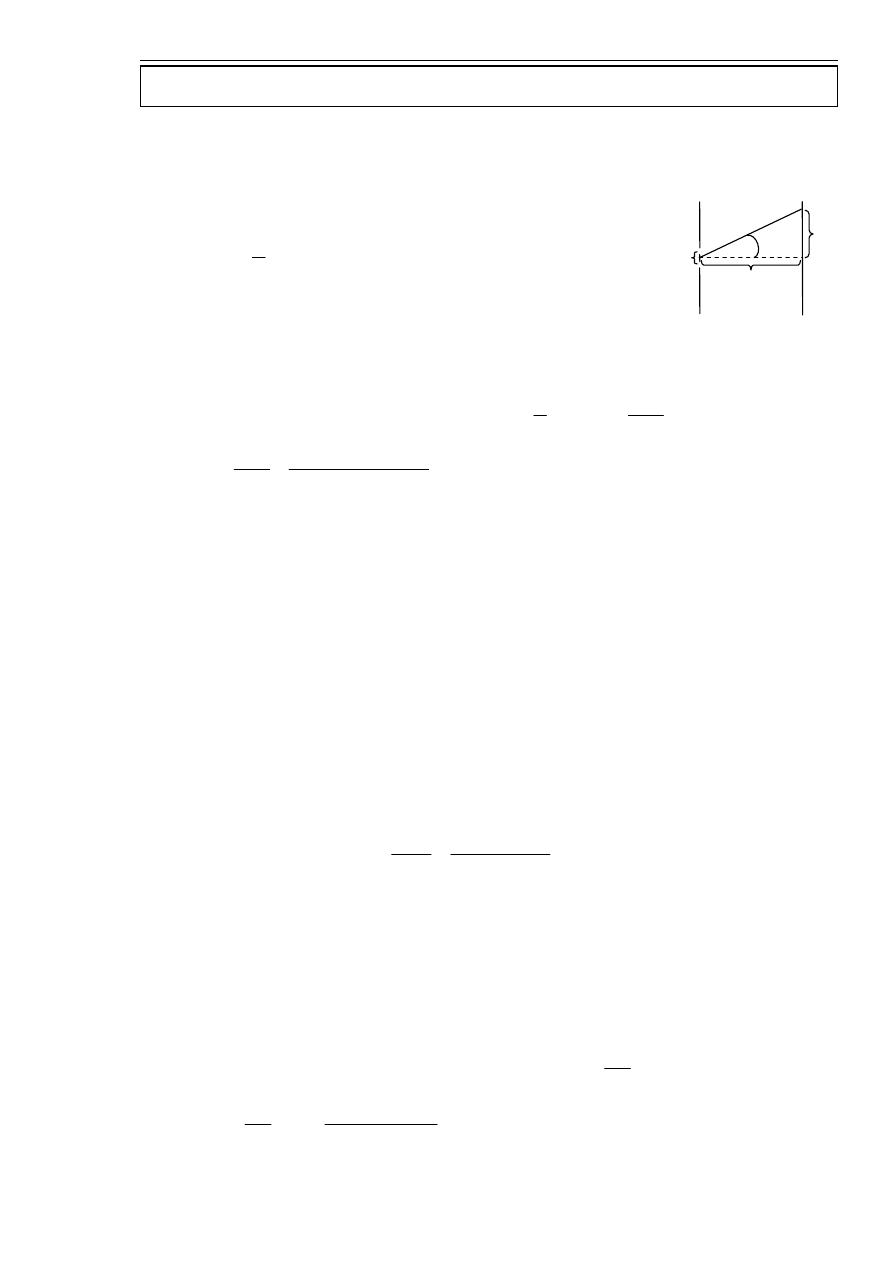
zad. 1.

Dane:

nm

680

=

λ

,

m

1

=

L

,

mm

28

=

y

,

4

=

m

(rząd prążka),

Szukane:

d

(odległość między szczelinami),

Z rysunku widać, że:

L

y

=

θ

tg

dla małych kątów w radianach można zastosować przybliżenie:

rad

sin

tg

θ

θ

θ

≈

≈

Prążek jasny powstaje gdy:

θ

λ

sin

d

m

=

gdzie

{

}

...

,

2

,

1

,

0

∈

m

(ogólnie bo w tym zadaniu

4

=

m

)

m

10

97

m

10

28

m

1

m

10

680

4

tg

sin

6

3

9

−

−

−

⋅

=

⋅

⋅

⋅

⋅

=

=

=

⇒

=

⇒

=

⇒

=

y

L

m

d

y

L

m

d

L

y

d

m

d

m

d

m

λ

λ

λ

θ

λ

θ

λ

zad. 2.

Dane:

µm

6

,

0

=

λ

,

50

,

1

=

s

n

,

Szukane:

d

(grubość płytki szklanej),

Uwaga do treści zadania: Prążek, który był zerowym powstał w miejscu piątego.

Droga optyczna:

S

n

R

⋅

=

gdzie

n

to bezwzględny współczynnik załamania światła; S to droga geometryczna,

Fala, która przechodzi przez szkoło wykonała 5 falowań więc:

5

=

N

Z jednej strony

λ

N

R

=

, z drugiej strony:

d

n

d

n

R

p

s

⋅

−

⋅

=

, czyli różnica dróg optycznych.

W tym zadaniu można przyjąć, że

1

=

p

n

(bezwzględny współczynnik załamania

powietrza), więc:

m

10

6

1

50

,

1

m

10

6

,

0

5

1

6

6

−

−

⋅

=

−

⋅

⋅

=

−

=

⇒

−

⋅

=

s

s

n

N

d

d

d

n

N

λ

λ

zad. 3.

Dane:

cm

2

=

l

,

nm

589

=

λ

,

20

=

N

,

000276

,

1

=

p

n

,

Szukane:

Cl

n

,

Należy porównać drogi optyczne dwóch promieni na odcinku o długości l oraz
uwzględnić przesunięcie o N prążków:

p

Cl

Cl

p

Cl

p

n

l

N

n

N

n

n

l

N

m

n

l

m

n

l

+

=

⇒

=

−

⋅

⇒







+

=

⋅

=

⋅

λ

λ

λ

λ

)

(

)

(

000865

,

1

000276

,

1

m

02

,

0

m

10

589

20

9

=

+

⋅

⋅

=

+

=

−

p

Cl

n

l

N

n

λ

d

y

L

θ

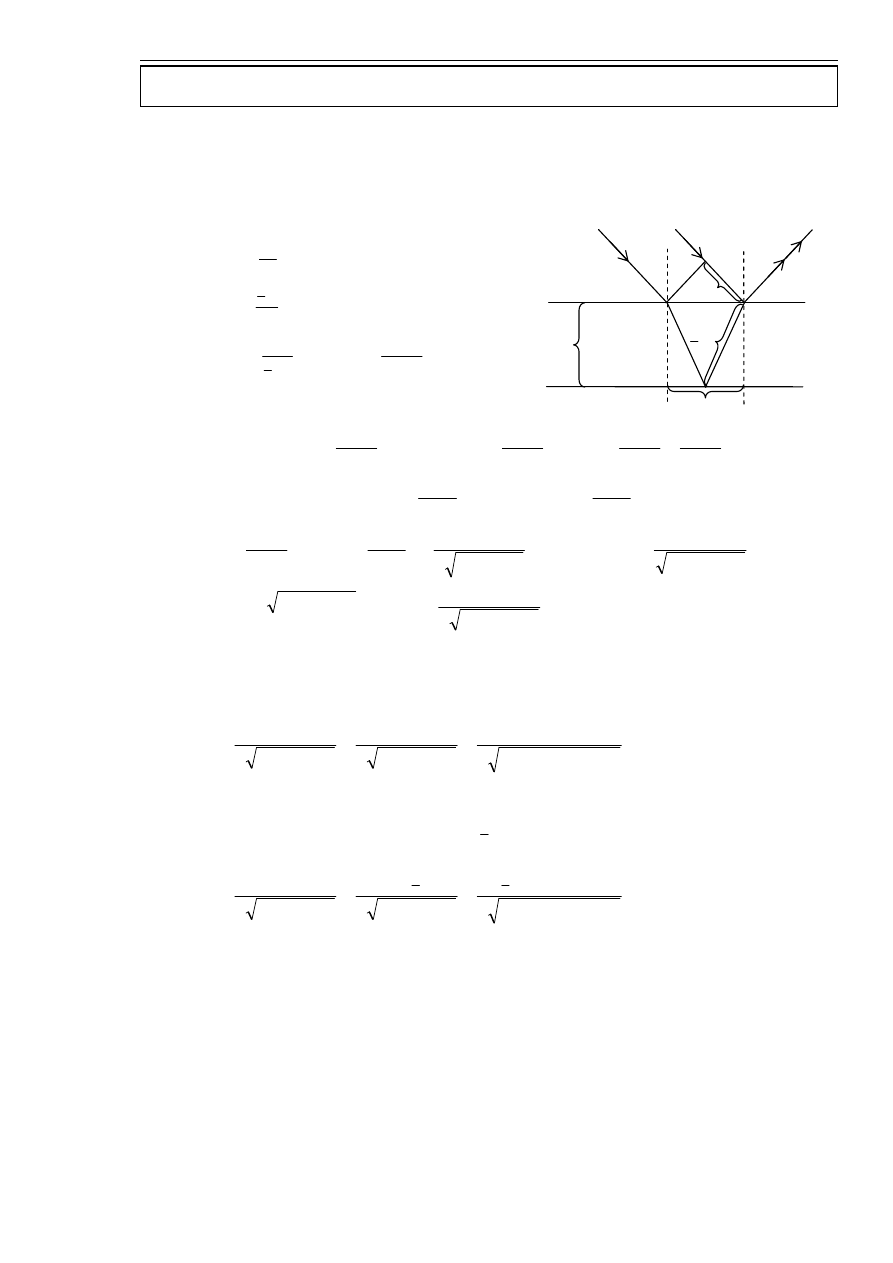
Studenckie Notatki Cyfrowe

SNy: Biotechnologia

www.sny.one.pl [e-mail]

Strona 21

Notatka: Fizyka II (FZC1004C) – ćwiczenia.

Utworzona: 24.03.2007 11:41

Temat: Zestaw 2 – Interferencja i dyfrakcja.

Zmodyfikowana: 27.04.2007 2:45

zad. 4.

Dane:

µm

6

,

0

=

λ

,

°

=

30

α

,

30

,

1

=

n

,

Szukane:

d

(grubość warstwy błony mydlanej),

Z geometrii rysunku wynika, że:

β

α

β

α

tg

sin

2

tg

sin

1

2

1

1

d

S

d

x

x

S

=

⇒












=

=

β

β

cos

2

cos

2

2

2

1

d

S

S

d

=

⇒

=

Różnica dróg optycznych pomiędzy
promieniami

oraz to:

(

)

β

α

β

β

β

α

β

β

α

β

sin

sin

cos

2

cos

sin

sin

2

cos

2

tg

sin

2

cos

2

1

1

2

−

=

−

⋅

=

−

⋅

=

⋅

−

=

∆

n

d

d

n

d

d

n

d

S

n

S

R

Korzystając z prawa Snelliusa:

n

n

α

β

β

α

sin

sin

sin

sin

=

⇒

=

.

(

)

α

α

α

α

α

β

α

α

β

2

2

2

2

2

2

2

2

2

2

2

sin

2

sin

2

sin

sin

2

sin

sin

1

2

sin

sin

cos

2

−

∆

=

⇒

−

=

∆

−

−

=

−

−

=













⋅

−

=

∆

n

R

d

n

d

R

n

n

d

n

n

d

n

n

d

R

Promień

odbijając się od powierzchni błony mydalnej zmienia fazę o

π

, więc:

Prążek ciemny powstanie gdy:

λ

m

R

=

∆

.

Szukam minimalnych wartości d , więc

1

=

m

.

m

10

25

,

0

30

sin

)

30

,

1

(

2

m

10

6

,

0

sin

2

sin

2

6

2

2

6

2

2

2

2

−

−

⋅

=

°

−

⋅

=

−

=

−

∆

=

α

λ

α

n

m

n

R

d

Maksymalne wygaszenie będzie dla grubości

µm

25

,

0

.

Prążek jasny powstanie gdy:

λ

)

(

2

1

+

=

∆

m

R

.

Szukam minimalnych wartości d , więc

0

=

m

.

m

10

125

,

0

30

sin

)

30

,

1

(

2

m

10

6

,

0

sin

2

)

(

sin

2

6

2

2

6

2

1

2

2

2

1

2

2

−

−

⋅

=

°

−

⋅

⋅

=

−

+

=

−

∆

=

α

λ

α

n

m

n

R

d

Maksymalne wzmocnienie będzie dla grubości

µm

125

,

0

.

α

β

1

S

2

2

1

S

α

β

+

d

x

Studenckie Notatki Cyfrowe

SNy: Biotechnologia

www.sny.one.pl [e-mail]

Strona 22

Notatka: Fizyka II (FZC1004C) – ćwiczenia.

Utworzona: 24.03.2007 11:41

Temat: Zestaw 2 – Interferencja i dyfrakcja.

Zmodyfikowana: 27.04.2007 2:45

zad. 5.

Dane:

nm

485

1

=

λ

,

nm

679

2

=

λ

,

32

,

1

=

olej

n

,

5

,

1

=

s

n

,

Szukane:

d

(grubość warstwy oleju),

Droga promienia:
przechodzi z powietrza do oleju, odbija się
od szkła i z powrotem wraca do powietrza.

Warunek na prążek ciemny:

λ

)

(

2

2

1

+

=

m

dn

Wiadomo, że fale o długościach

1

λ

i

2

λ

zostały

wygaszone całkowicie oraz wiadomo, że są to
dwie kolejne wygaszone fale stąd

m

oraz

1

+

m

.

2

)

485

679

(

2

679

485

3

)

(

2

3

0

)

(

2

)

)

1

((

2

1

2

2

1

2

1

1

2

3

2

2

1

1

2

3

2

2

1

2

1

2

2

1

2

1

2

3

1

2

2

1

1

2

1

=

−

−

⋅

=

−

−

=

−

−

=

−

=

−

=

−

−

+









+

=

+

+

=

λ

λ

λ

λ

λ

λ

λ

λ

λ

λ

λ

λ

λ

λ

λ

λ

λ

λ

m

m

m

m

m

m

dn

m

dn

olej

olej

Więc ostatecznie:

m

10

643

,

0

32

,

1

4

m

10

679

5

4

5

2

)

2

(

2

)

(

2

6

9

2

2

2

5

2

2

1

2

2

1

−

−

⋅

=

⋅

⋅

⋅

=

=

=

⇒

+

=

+

=

olej

olej

olej

olej

n

n

d

dn

m

dn

λ

λ

λ

λ

powietrze

olej

szkło

d

zmiana
fazy o

π

zmiana
fazy o

π

Studenckie Notatki Cyfrowe

SNy: Biotechnologia

www.sny.one.pl [e-mail]

Strona 23

Notatka: Fizyka II (FZC1004C) – ćwiczenia.

Utworzona: 24.03.2007 11:41

Temat: Zestaw 2 – Interferencja i dyfrakcja.

Zmodyfikowana: 27.04.2007 2:45

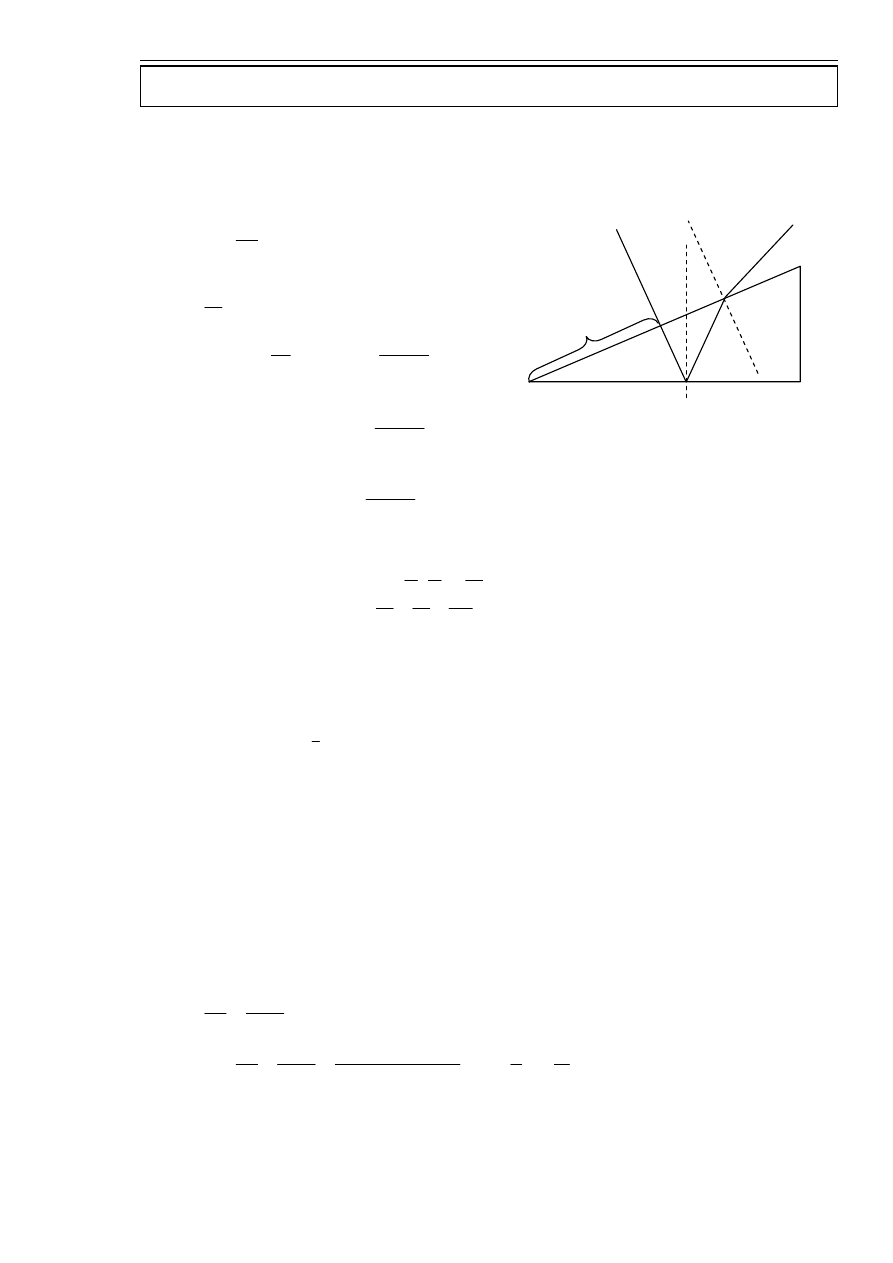
zad. 6.

Dane:

nm

582

=

λ

,

0

2

′′

=

α

,

32

,

1

=

olej

n

,

5

,

1

=

s

n

,

Szukane:

σ

(gęstość ciemnych prążków interferencyjnych),

x

m

∆

=

σ

Z geometrii rysunku wynika, że:

α

α

α

α

α

2

cos

tg

2

cos

tg

tg

2

2

1

1

1

x

S

S

S

x

S

x

S

=

⇒

=

=

⇒

=

Całkowita droga geometryczna:













+

=

+

=

α

α

2

cos

1

1

tg

2

1

x

S

S

S

Droga optyczna:













+

=

=

α

α

2

cos

1

1

tg

x

n

S

n

R

s

s

Dla małych kątów można zastosować przybliżenia.

0

2

′′

=

α

czyli 20 sekund

zamiana na stopnie:

( )

°

=

⋅

⋅

=

180

1

60

1

60

1

20

α

zamiana na radiany:

rad

10

696

,

9

rad

5

180

180

180

1

2

−

⋅

=

=

⋅

°

=

π

π

α

Kąt

α

jest mały, więc przybliżam:

α

α

α

≈

≈

tg

1

2

cos

Otrzymujemy:

x

n

R

x

n

x

n

R

s

s

s

∆

⋅

=

∆

=













+

⋅

=

α

α

α

2

2

1

1

1

Droga promienia:
wpada prostopadle do klina (nie ulega załamaniu), odbija się częściowo od spodu klina
(kąt padania równy kątowi odbicia więc kąt pomiędzy promieniem przed i po odbiciu to

α

2

) następnie wychodząc z klina załamuje się pod pewnym kątem.

Warunek na prążek ciemny

cm

1

m

1

9

5

5

500

m

10

582

10

696

,

9

5

,

1

2

2

2

2

=

=

⋅

⋅

⋅

⋅

=

=

∆

=

=

∆

=

∆

⋅

=

∆

−

−

λ

α

σ

λ

α

λ

α

λ

s

s

s

n

x

m

n

x

m

m

x

n

m

R

α

α

α

x

1

S

2

S

Studenckie Notatki Cyfrowe

SNy: Biotechnologia

www.sny.one.pl [e-mail]

Strona 24

Notatka: Fizyka II (FZC1004C) – ćwiczenia.

Utworzona: 24.03.2007 11:41

Temat: Zestaw 2 – Interferencja i dyfrakcja.

Zmodyfikowana: 27.04.2007 2:45

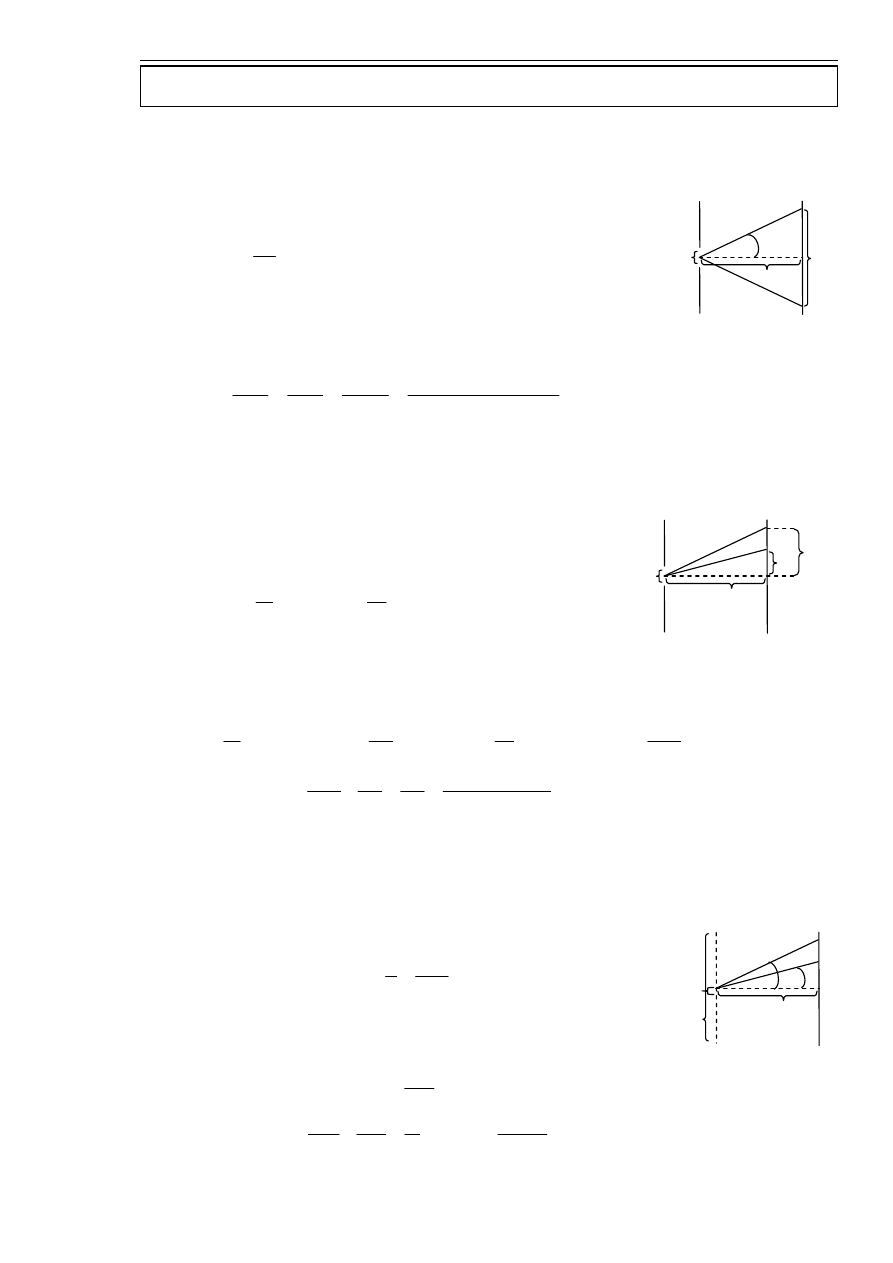
zad. 7.

Dane:

nm

546

=

λ

,

cm

3

,

82

=

L

,

mm

2

,

5

=

y

,

1

=

m

(rząd dyfrakcji),

Szukane:

a

(szerokość szczeliny),

Z geometrii rysunku:

L

y

2

tg

=

θ

dla małych kątów w radianach można zastosować przybliżenie:

rad]

[

sin

tg

θ

θ

θ

≈

≈

Jest to siatka dyfrakcyjna więc:

m

10

8

,

172

10

2

,

5

10

546

1

823

,

0

2

2

sin

sin

sin

6

3

9

−

−

−

⋅

=

⋅

⋅

⋅

⋅

⋅

=

=

=

=

=

y

Lm

m

m

a

m

a

λ

θ

λ

θ

λ

λ

θ

zad. 8.

Dane:

nm

589

=

λ

,

m

94

,

2

=

L

,

mm

16

,

1

=

a

,

Szukane:

y

∆

(odległość między dwoma pierwszymi minimami),

Z geometrii rysunku:

L

y

L

y

y

y

y

2

2

1

1

1

2

tg

tg

=

=

−

=

∆

θ

θ

dla małych kątów w radianach można zastosować przybliżenie:

rad]

[

sin

tg

θ

θ

θ

≈

≈

Jest to siatka dyfrakcyjna więc:

m

10

49

,

1

10

16

,

1

10

589

94

,

2

2

2

2

1

sin

3

3

9

1

2

2

2

1

1

−

−

−

⋅

=

⋅

⋅

⋅

=

=

−

=

−

=

∆

=

⇒

⋅

=

⋅

=

⇒

⋅

=

⋅

=

a

L

a

L

a

L

y

y

y

a

L

y

L

y

a

a

L

y

L

y

a

m

a

λ

λ

λ

λ

λ

λ

λ

λ

θ

zad. 9.

Dane:

µm

405

,

0

1

=

λ

,

µm

579

,

0

2

=

λ

,

cm

5

=

b

(szerokość siatki),

4

10

=

x

(liczba rys),

1

=

m

(rząd dyfrakcji),

Szukane:

θ

∆

(kąt między falą pierwszą a drugą),

Szerokość szczeliny to:

m

10

5

10

05

,

0

6

4

−

⋅

=

=

=

x

b

a

Z geometrii rysunku:

1

2

θ

θ

θ

−

=

∆

Jest to siatka dyfrakcyjna więc:

i

i

i

i

i

a

m

m

a

θ

λ

θ

λ

θ

≈

=

⇒

=

sin

sin

przybliżenie dla małych kątów.

(

)

(

)

°

=

=

⋅

−

⋅

=

−

=

−

=

−

=

∆

−

−

2

rad

0348

,

0

10

405

,

0

579

,

0

10

5

1

6

6

1

2

1

2

1

2

λ

λ

λ

λ

θ

θ

θ

a

m

a

m

a

m

a

y

L

θ

a

2

y

L

1

y

a

1

θ

L

b

2

θ

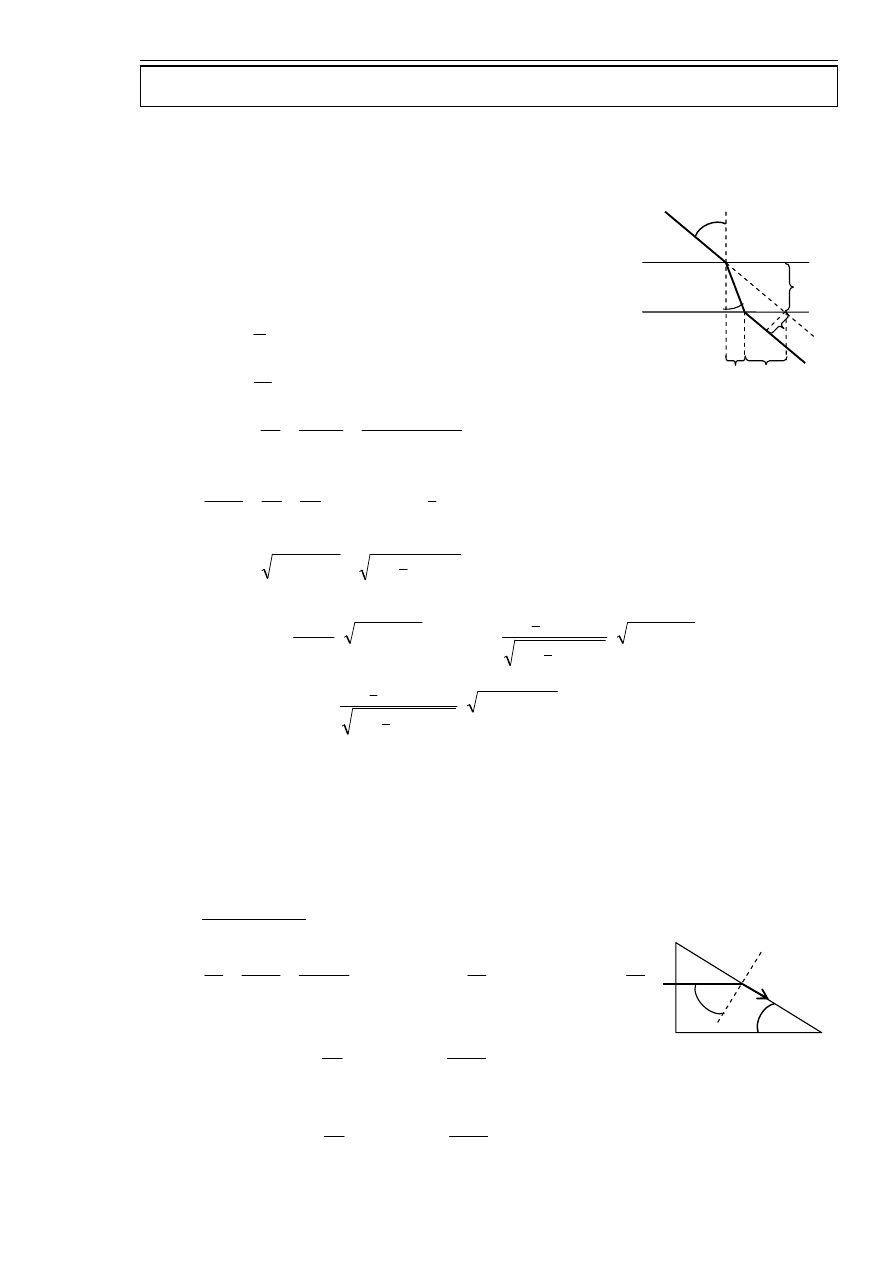
Studenckie Notatki Cyfrowe

SNy: Biotechnologia

www.sny.one.pl [e-mail]

Strona 25

Notatka: Fizyka II (FZC1004C) – ćwiczenia.

Utworzona: 26.04.2007 18:42

Temat: Zestaw 3 – Polaryzacja.

Zmodyfikowana:

9.05.2007 1:59

powietrze

szkło

powietrze

t

x

α

2

y

1

y

β

φ

gr

α

ZESTAW 3 – Polaryzacja

26.04.2007 r.

zad. 1.

Dane:

cm

2

=

t

,

°

=

30

α

,

50

,

1

=

s

n

,

Szukane:

x

,

Z geometrii rysunku:

α

β

α

β

α

α

β

β

α

α

cos

)

tg

tg

(

tg

tg

cos

tg

tg

tg

tg

1

2

1

1

2

1

−

=

⇒

−

=

−

=

=

=

⇒

=

=

⇒

=

+

=

t

x

t

t

x

y

y

x

y

x

t

y

t

y

t

y

t

y

y

y

y

Z prawa Snelliusa

α

β

β

α

sin

sin

1

5

,

1

sin

sin

3

2

=

⇒

=

=

p

s

n

n

Z jedynki trygonometrycznej:

2

3

2

2

)

sin

(

1

sin

1

cos

α

β

β

−

=

−

=

Więc:

m

10

88

,

3

30

sin

1

)

30

sin

(

1

30

sin

30

tg

02

,

0

sin

1

)

sin

(

1

sin

tg

sin

1

cos

sin

tg

3

2

2

3

2

3

2

2

2

3

2

3

2

2

−

⋅

=

°

−

















°

−

°

−

°

⋅

=

−

















−

−

=

−













−

=

x

t

t

x

α

α

α

α

α

β

β

α

zad. 2.

Dane:

520

,

1

=

s

n

,

333

,

1

=

w

n

,

Szukane:

1

φ

(dla pryzmaty w powietrzu),

2

φ

(dla pryzmatu w wodzie),

Z geometrii rysunku:

gr

gr

α

φ

α

φ

−

°

=

⇒

°

=

+

90

90

Kąt graniczny

to taki kąt padania dla którego promień jest załamany pod kątem prostym.

Z prawa Snelliusa (tutaj:

s

n

n

=

1

)

s

gr

gr

gr

n

n

n

n

n

n

2

1

2

1

2

arcsin

sin

90

sin

sin

sin

sin

=

⇒

=

⇒

°

=

=

α

α

α

β

α

Gdy pryzmat jest w powietrzu to:

1

2

=

=

p

n

n

°

=

−

°

=

−

°

=

9

,

48

520

,

1

1

arcsin

90

arcsin

90

1

s

p

n

n

φ

Gdy pryzmat jest w wodzie to:

w

n

n

=

2

°

=

−

°

=

−

°

=

7

,

28

520

,

1

333

,

1

arcsin

90

arcsin

90

2

s

w

n

n

φ

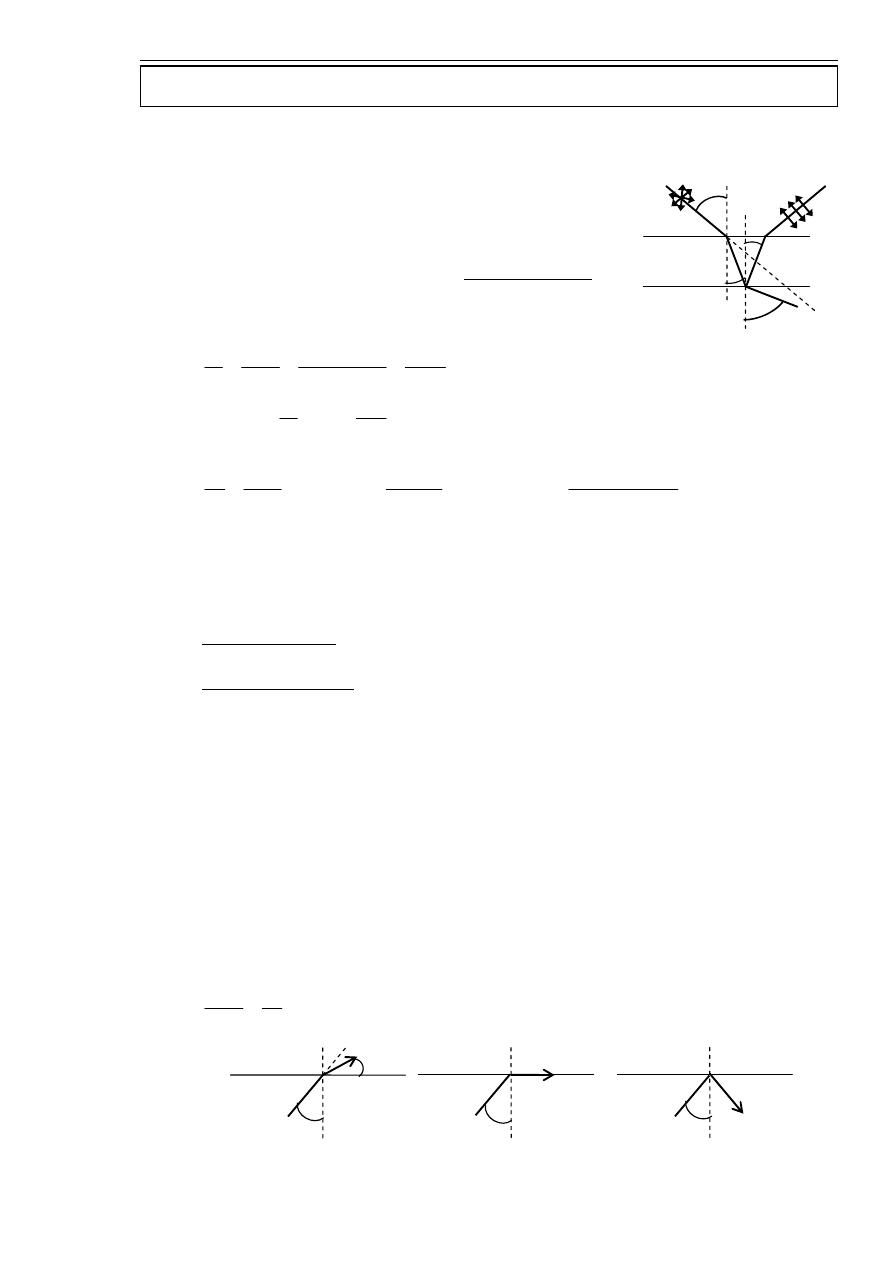
Studenckie Notatki Cyfrowe

SNy: Biotechnologia

www.sny.one.pl [e-mail]

Strona 26

Notatka: Fizyka II (FZC1004C) – ćwiczenia.

Utworzona: 26.04.2007 18:42

Temat: Zestaw 3 – Polaryzacja.

Zmodyfikowana:

9.05.2007 1:59

powietrze

ciecz

szkło

θ

α

β

α

gr

α

s

p

n

n

barwa zielona

α

s

p

n

n

barwa fioletowa

α

s

p

n

n

barwa czerwona

β

β

α

>

gr

α

α

=

zad. 3.

Dane:

33

,

1

=

c

n

,

46

,

1

=

s

n

,

Szukane:

θ

,

Należy rozpatrzeć odbicie od przeźroczystego dielektryka
przy określonym kącie takim, że:

°

=

+

90

β

α

oraz

2

1

n

n

<

.

Wtedy taki kąt padania

α

nazywamy kątem Brewstera,

ma one te własność, że promień odbity będzie całkowicie
liniowo spolaryzowany.
Rozpatrzmy sytuację na granicy cieczy i szkła:

α

α

α

α

α

β

α

tg

cos

sin

)

90

sin(

sin

sin

sin

=

=

−

°

=

=

c

s

n

n

°

=

=

=

67

,

47

33

,

1

46

,

1

arctg

arctg

c

s

n

n

α

Rozpatrzmy sytuację na granicy powietrza i cieczy:

°

=

°

⋅

=

⇒

=

⇒

=

5

,

79

1

67

,

47

sin

33

,

1

arcsin

sin

sin

sin

sin

θ

α

θ

α

θ

p

c

p

c

n

n

n

n

zad. 4.

Dane:

s

n

,

p

n

,

f

z

cz

λ

λ

λ

>

>

,

Szukane:

biegi promieni,

Dyspersją światła

nazywamy zależność bezwzględnego współczynnika załamania

światła

n

substancji od długości fali

λ

światła. Co można napisać tak:

)

(

λ

f

n

=

Dyspersją normalną

nazywamy taką dyspersję gdzie wraz ze wzrostem długości fali

λ

maleje bezwzględny współczynnik załamania

n

.

Światło wykazuje dyspersję normalną, więc:

f

z

cz

f

z

cz

s

n

n

n

f

f

f

n

<

<

⇒

<

<

)

(

)

(

)

(

:

λ

λ

λ

Wiązka światła białego pada pod kątem granicznym

gr

α

dla fali odpowiadającej barwie

zielonej, więc załamie się ona pod kątem

°

90

. Dla fali odpowiadającej barwie fioletowej

nastąpi całkowite odbicie wewnętrzne ponieważ

z

f

n

n

>

.

Natomiast fala odpowiadająca barwie czerwonej załamie pod kątem mniejszym od

°

90

,

ponieważ

z

cz

n

n

<

(*). Jednocześnie ten kąt będzie większy od

α

(kąt padania), ponieważ

fala odpowiadająca barwie czerwonej przejdzie z ośrodka gęstszego do rzadszego
optycznie (

p

s

n

n

>

), załamie się od normalnej.

(*) wynika to bezpośrednio z prawa Snelliusa, gdzie

β

to kąt załamania.

s

p

n

n

=

β

α

sin

sin

, gdy

s

n

rośnie to

β

sin

też rośnie, więc

β

rośnie. Ponieważ

const.

sin

=

gr

α

Studenckie Notatki Cyfrowe

SNy: Biotechnologia

www.sny.one.pl [e-mail]

Strona 27

Notatka: Fizyka II (FZC1004C) – ćwiczenia.

Utworzona: 26.04.2007 18:42

Temat: Zestaw 3 – Polaryzacja.

Zmodyfikowana:

9.05.2007 1:59

8.05.2007 r.

zad. 5.

Dane:

0

I

(intensywność światła niespolaryzowanego),

°

=

45

1

α

,

°

=

45

2

α

,

°

=

30

1

β

,

°

=

60

2

β

,

Szukane:

0

3

I

I

,

Rysunek poglądowy:

Pada światło niespolaryzowane na pierwszy (z lewej) polaryzator. Jego intensywność
zawsze zmniejszy się o połowę przy przechodzeniu przez idealny polaryzator.

0

2

1

1

I

I

=

Dalej będzie już to światło spolaryzowane liniowo, więc będzie można zastosować
Prawo Malusa

θ

2

0

cos

I

I

=

gdzie:

θ

to kąt pomiędzy kierunkiem polaryzacji a kierunkiem drgań wektora natężenia

pola elektrycznego

Stosując prawo Malusa:

2

2

1

2

0

2

1

2

2

2

3

1

2

0

2

1

1

2

1

2

cos

cos

cos

cos

cos

α

α

α

α

α

⋅

=

=

=

=

I

I

I

I

I

I

Więc:

125

,

0

45

cos

45

cos

cos

cos

cos

cos

2

1

2

1

2

1

2

2

2

1

2

2

1

2

2

1

0

2

2

1

2

0

2

1

0

3

=

⋅

⋅

=

°

⋅

°

=

⋅

=

⋅

=

α

α

α

α

I

I

I

I

Dla kątów

1

β

i

2

β

będzie odpowiednio (jest to inny niezależnie rozważany przypadek):

09375

,

0

60

cos

30

cos

cos

cos

cos

cos

4

1

4

3

2

1

2

2

2

1

2

2

1

2

2

1

0

2

2

1

2

0

2

1

0

3

=

⋅

⋅

=

°

⋅

°

=

⋅

=

⋅

=

β

β

β

β

I

I

I

I

zad. 6.

Dane:

°

=

34

θ

,

°

=

17

α

,

Szukane:

x

(osłabienie intensywności wiązki światła po przejściu przez układ),

Rysunek poglądowy:

Światło padające jest spolaryzowane więc stosując prawo Malusa otrzymujemy:

°

=

=

17

cos

cos

2

0

2

0

1

I

I

I

α

)

34

(

cos

)

17

(

cos

34

cos

cos

2

2

0

2

1

2

1

2

°

⋅

°

=

°

=

=

I

I

I

I

θ

(

)

%

1

,

37

%

100

)

34

(

cos

)

17

(

cos

1

%

100

)

34

(

cos

)

17

(

cos

1

%

100

1

2

2

0

2

2

0

0

2

=

⋅

°

⋅

°

−

=

=

⋅













°

⋅

°

−

=

⋅













−

=

I

I

I

I

x

0

I

1

I

2

I

°

34

°

17

0

I

1

I

2

I

3

I

°

45

°

45

Studenckie Notatki Cyfrowe

SNy: Biotechnologia

www.sny.one.pl [e-mail]

Strona 28

Notatka: Fizyka II (FZC1004C) – ćwiczenia.

Utworzona: 26.04.2007 18:42

Temat: Zestaw 3 – Polaryzacja.

Zmodyfikowana:

9.05.2007 1:59

zad. 7.

Dane:

max

1

I

I

=

,

°

=

60

α

,

max

2

1

2

I

I

=

,

Szukane:

p

np

I

I

,

β

(dla

min

3

I

I

=

),

3

1

I

I

,

Rysunek poglądowy:

W zadaniu jest obecny jeden polaryzator, który jest następnie obracany.
Padającą wiązkę światła częściowo spolaryzowanego, a częściowo nie jako dwie wiązki
i liczyć odpowiednio intensywność światła spolaryzowanego

p

I

oraz intensywność

światłą niespolaryzowanego

np

I

.

Największą intensywność dostanie się gdy kąt

θ

, czyli kąt pomiędzy kierunkiem

polaryzacji a kierunkiem drgań wektora natężenia pola elektrycznego, będzie zero.

°

=

0

θ

, bo

1

0

cos

cos

2

2

=

°

=

θ

przyjmuje maksymalną wartość, więc:

p

p

p

p

I

I

I

I

=

°

=

=

0

cos

cos

2

2

1

θ

Natomiast światło niespolaryzowane po przejściu przez polaryzator będzie spolaryzowane
i jego intensywność będzie mniejsza o połowę:

np

np

I

I

2

1

1

=

p

np

p

np

I

I

I

I

I

I

+

=

+

=

=

2

1

max

1

1

1

(*)

Gdy ten polaryzator odwrócimy o kąt

°

=

60

α

to:

p

np

p

np

I

I

I

I

I

4

1

2

1

2

2

1

2

60

cos

+

=

°

+

=

z treści zadania

max

2

1

2

I

I

=

więc:

max

2

1

4

1

2

1

I

I

I

p

np

=

+

(**)

Ostatecznie z (*) oraz (**):

np

p

p

np

p

np

p

np

p

np

p

np

p

np

I

I

I

I

I

I

I

I

I

I

I

I

I

I

I

I

I

I

=

⇒

+

=

+

⇒









+

=

+

=

⇒









+

=

+

=

2

1

2

1

2

1

max

2

1

max

4

1

2

1

max

2

1

2

1

max

(***)

Więc:

1

=

=

np

np

p

np

I

I

I

I

Kolejny obór polaryzatora, tym razem o kąt

β

(względem położenia początkowego).

Najmniejszą intensywność dostanie się gdy kąt

β

, czyli kąt pomiędzy kierunkiem

polaryzacji a kierunkiem drgań wektora natężenia pola elektrycznego, będzie

°

90

.

°

=

90

β

, bo

0

90

cos

cos

2

2

=

°

=

β

przyjmuje najmniejszą wartość, więc:

np

np

p

np

p

p

p

p

I

I

I

I

I

I

I

I

I

2

1

2

1

3

2

2

0

0

0

90

cos

cos

3

3

3

=

+

=

+

=

=

⋅

=

°

=

=

β

Więc z (*), (**) oraz (***):

3

1

2

1

2

3

2

1

2

1

2

1

2

1

2

1

2

1

3

1

min

max

=

=

+

=

+

=

+

=

=

np

np

np

np

p

np

I

I

I

I

I

I

I

I

I

I

np

I

1

np

I

p

I

1

p

I

Studenckie Notatki Cyfrowe

SNy: Biotechnologia

www.sny.one.pl [e-mail]

Strona 29

Notatka: Fizyka II (FZC1004C) – ćwiczenia.

Utworzona: 26.04.2007 18:42

Temat: Zestaw 3 – Polaryzacja.

Zmodyfikowana:

9.05.2007 1:59

zad. 8.

Dane:

655

,

1

=

s

n

,

655

,

1

0

=

n

,

485

,

1

=

e

n

,

1

=

p

n

,

°

=

30

α

,

Szukane:

γ

,

Z prawa Snelliusa

°

=

=

=

°

=

=

⇒

=

87

,

33

557

,

0

arcsin

557

,

0

30

sin

485

,

1

655

,

1

sin

sin

sin

sin

β

α

β

β

α

e

s

s

e

n

n

n

n

Z geometrii rysunku wynika, że:

°

=

°

−

°

=

−

=

87

,

3

30

87

,

33

δ

α

β

δ

Z prawa Snelliusa

5

4

5

75

,

5

1002

,

0

arcsin

1002

,

0

)

87

,

3

sin(

1

485

,

1

sin

sin

sin

sin

′

°

=

°

=

=

=

°

=

=

⇒

=

γ

δ

γ

γ

δ

p

e

e

p

n

n

n

n

α

α

β

α

δ

δ

γ

s

n

0

n

n

e

p

n

Studenckie Notatki Cyfrowe

SNy: Biotechnologia

www.sny.one.pl [e-mail]

Strona 30

Notatka: Fizyka II (FZC1004C) – ćwiczenia.

Utworzona:

9.05.2007 2:08

Temat: Kolokwium II.

Zmodyfikowana: 3.06.2007 23:23

Kolokwium II

15.04.2007 r.

Zakres tematyczny: odbicia, załamania, interferencja i dyfrakcja fal oraz polaryzacja światła.

Przykładowe treści zadań
zad. 1.
Jaki jest współczynnik załamania szkła, od którego odbija się światło, jeśli promień odbity zostaje
całkowicie spolaryzowany przy kącie załamania równym

°

30

?

Odp.

73

,

1

=

s

n

.

zad. 2.
Ile razy zmniejszy się natężenie światła niespolaryzowanego po przejściu przez dwa polaryzatory,
jeśli ich płaszczyzny polaryzacji tworzą kąt

°

63

i każdy pochłania

%

10

padającego światła?

Odp. intensywność światłą zmniejszy się 12 razy.


Przykładowe rozwiązania zadań
zad. 1.

Dane:

°

=

30

β

,

Szukane:

s

n

,

Kąt padania

α

nazywamy kątem Brewstera, jeżeli promień odbity pod tym kątem będzie

całkowicie liniowo spolaryzowany. Jest tak gdy:

°

=

+

90

β

α

gdzie:

α

to kąt padania,

β

to kąt załamania.

Rozpatrzmy sytuację na granicy powietrza (

1

=

p

n

) i szkła (

s

n

) z prawa Snelliusa:

73

,

1

30

ctg

ctg

ctg

sin

cos

sin

)

90

sin(

sin

sin

=

°

=

=

=

=

−

°

=

=

β

β

α

β

β

β

β

α

s

p

s

n

n

n

zad. 2.

Dane:

°

=

63

θ

,

9

,

0

%

90

%

10

%

100

=

=

−

=

η

,

Szukane:

2

0

I

I

,

Ogólnie:

θ

2

2

1

cos

'

p

p

np

p

I

I

I

I

=

=

W tym zadaniu:

12

63

cos

)

9

,

0

(

2

cos

2

cos

2

cos

cos

cos

2

2

2

2

2

2

2

0

2

1

2

0

2

0

2

0

2

1

2

2

1

2

0

2

1

1

=

°

=

=

=

⋅

=

⋅

=

⋅

=

⋅

=

θ

η

θ

η

θ

η

θ

η

θ

η

η

I

I

I

I

I

I

I

I

I

Studenckie Notatki Cyfrowe

SNy: Biotechnologia

www.sny.one.pl [e-mail]

Strona 31

Notatka: Fizyka II (FZC1004C) – ćwiczenia.

Utworzona: 22.05.2007 0:37

Temat: Zestaw 4 – Efekty kwantowe.

Zmodyfikowana: 2.06.2007 21:28

ZESTAW 4 – Efekty kwantowe

14.04.2007 r.

zad. 1.

Dane:

2

cm

1

=

S

,

.

min

1

=

t

,

4840

=

max

λ

Ǻ,

Szukane:

E

(wypromieniowania energia),

Przeliczenie Angstrema na metry: 1 Ǻ = 10

-10

m

c

R

– widoma (spektralna) zdolność emisyjna ciała doskonale czarnego. Służy do

ilościowego scharakteryzowania promieniowania cieplnego na jednostkę powierzchni
w danym czasie.
Zgodnie z prawem Stefana-Boltzmanna dla ciała doskonale czarnego zachodzi związek
pomiędzy całkowitą zdolnością emisyjną, a temperaturą (wyrażoną w Kelwinach).

4

T

R

c

σ

=

gdzie:

4

2

K

m

W

8

10

67

,

5

−

⋅

=

σ

jest stałą Stefana-Boltzmanna

Zgodnie z prawem przesunięć Wiena wraz ze wzrostem temperatury widmo promieniowania
ciała doskonale czasnego ulega przesunięciu w stronę krótszych długości fali.

max

max

λ

λ

C

T

T

C

=

⇒

=

gdzie:

mK

,

3

10

9

2

−

⋅

=

C

jest stałą Wiena

Wartość emitowanej energii zależy od zdolności emisyjnej ciała, jego powierzchni oraz czasu:

J

,

)

(

)

,

(

,

max

3

4

4

10

4

3

8

4

4

4

10

5

438

60

10

10

4840

10

9

2

10

67

5

⋅

=

⋅

⋅

⋅

⋅

⋅

⋅

=

⋅

⋅

=

⋅

⋅

=

⋅

⋅

=

−

−

−

−

t

S

C

t

S

T

E

t

S

R

E

c

λ

σ

σ

zad. 2.

Dane:

2

cm

1

=

S

,

s

1

=

t

,

K

2400

=

T

,

Szukane:

N

(liczba wypromieniowanych fotonów, całkowita energia do średniej),

Z treści zadania wiadomo, że średnia energia jednego kwantu promieniowania wynosi:

T

k

E

ś

r

⋅

⋅

=

75

2,

gdzie:

K

J

,

23

10

38

1

−

⋅

=

k

jest stałą Boltzmanna

Zgodnie z prawem Stefana-Boltzmanna

4

T

R

c

σ

=

gdzie:

s

K

m

W

4

2

,

8

10

67

5

−

⋅

=

σ

jest stałą Stefana-Boltzmanna

Wartość emitowanej energii zależy od zdolności emisyjnej ciała, jego powierzchni oraz czasu:

21

23

4

3

8

3

4

4

10

065

2

10

38

1

75

2

1

10

2400

10

67

5

75

2

75

2

−

−

−

−

⋅

=

⋅

⋅

⋅

⋅

⋅

⋅

=

⋅

⋅

⋅

⋅

=

⋅

⋅

⋅

⋅

⋅

=

=

⋅

⋅

=

⋅

⋅

=

,

,

,

,

,

,

k

t

S

T

T

k

t

S

T

E

E

N

t

S

T

t

S

R

E

ś

r

c

c

c

σ

σ

σ

Studenckie Notatki Cyfrowe

SNy: Biotechnologia

www.sny.one.pl [e-mail]

Strona 32

Notatka: Fizyka II (FZC1004C) – ćwiczenia.

Utworzona: 22.05.2007 0:37

Temat: Zestaw 4 – Efekty kwantowe.

Zmodyfikowana: 2.06.2007 21:28

zad. 3.

Dane:

1

T

,

%

180

1

2

⋅

=

T

T

,

nm

600

=

∆

λ

,

Szukane:

2

T

(temperatura końcowa),

Zgodnie z prawem przesunięć Wiena:

T

C

=

max

λ

gdzie:

mK

,

3

10

9

2

−

⋅

=

C

jest stałą Wiena

2

9

5

1

1

2

8

1

T

T

T

T

=

⇒

⋅

=

,

Gdy T rośnie to

λ

maleje więc:

λ

λ

λ

∆

−

=

1

2

K

,

,

7

3866

10

600

5

10

9

2

4

5

4

5

4

9

3

2

2

2

2

9

5

2

1

2

1

1

1

=

⋅

⋅

⋅

⋅

=

∆

=

∆

=

⇒

∆

=

−

⇒

=

∆

−

⇒












=

∆

−

=

−

−

λ

λ

λ

λ

λ

λ

λ

C

T

C

T

T

C

T

C

T

C

T

C

T

C

T

C

zad. 4.

Dane:

nm

275

=

red

λ

,

nm

180

=

λ

,

Szukane:

T

W

(praca wyjścia),

max

v

(maksymalna prędkość),

υ

λ

v

=

gdzie

υ

to częstotliwość,

v

to prędkość (dla fal elektromagnetycznych

równa prędkości światła w próżni

s

m

8

10

3

⋅

=

c

).

Efekt fotoelektryczny

k

T

E

W

E

+

=

gdzie

T

W

to praca wyjścia,

k

E

to energia kinetyczna fotonu.

Energia fotonu:

υ

h

E

=

gdzie

υ

to częstotliwość,

s

J

⋅

⋅

=

−

34

10

625

6,

h

jest stałą Plancka

J

,

19

9

8

34

0

0

10

23

7

10

275

10

3

10

625

6

−

−

−

⋅

=

⋅

⋅

⋅

=

=

=

=

,

c

h

h

E

W

red

T

λ

υ

Zamiana dżula na elektronowolty: 1 eV = 1 e · 1 V ≈ 1,6 · 10

-19

J

eV

,

eV

,

J

,

,

52

4

10

23

7

10

23

7

19

10

6

1

1

19

19

=

⋅

⋅

=

⋅

−

⋅

−

−

s

m

,

,

5

31

9

9

19

8

34

2

10

15

9

10

11

9

10

180

10

180

10

23

7

2

10

3

10

625

6

2

2

2

2

⋅

=

⋅

⋅

⋅

⋅

⋅

⋅

⋅

−

⋅

⋅

⋅

⋅

=

=

−

=

⇒

+

=

+

=

−

−

−

−

−

,

,

m

W

hc

v

mv

W

c

h

E

W

E

e

T

T

k

T

λ

λ

λ

gdzie masa elektronu to:

kg

,

31

10

11

9

−

⋅

=

e

m

Studenckie Notatki Cyfrowe

SNy: Biotechnologia

www.sny.one.pl [e-mail]

Strona 33

Notatka: Fizyka II (FZC1004C) – ćwiczenia.

Utworzona: 22.05.2007 0:37

Temat: Zestaw 4 – Efekty kwantowe.

Zmodyfikowana: 2.06.2007 21:28

zad. 5.

Dane:

µm

,670

0

=

red

λ

,

µm

,402

0

=

λ

,

Szukane:

U

,

E

W

T

,

Efekt fotoelektryczny

k

T

E

W

E

+

=

gdzie

T

W

to praca wyjścia,

k

E

to energia kinetyczna fotonu.

Energia fotonu:

υ

h

E

=

gdzie

υ

to częstotliwość,

s

J

⋅

⋅

=

−

34

10

625

6,

h

jest stałą Plancka

red

T

c

h

h

E

W

λ

υ

=

=

=

0

0

gdzie

red

λ

to granica długofalowa.

Energia hamowania związana jest z energią kinetyczną:

eU

mv

E

k

=

=

2

2

V

,

,

,

,

236

1

10

670

0

1

10

402

0

1

10

6

1

10

3

10

625

6

1

1

6

6

19

8

34

=













⋅

−

⋅

⋅

⋅

⋅

⋅

=

=













−

=

⇒

+

=

+

=

−

−

−

−

,

e

hc

U

eU

c

h

c

h

E

W

E

red

red

k

T

λ

λ

λ

λ

gdzie

e

to ładunek elementarny

J

,

19

10

6

1

−

⋅

=

e

,

c

to prędkości światła w próżni

s

m

8

10

3

⋅

=

c

.

%

,

,

,

60

6

0

10

670

0

10

402

0

6

6

=

=

⋅

⋅

=

=

=

−

−

red

red

T

hc

hc

E

W

λ

λ

λ

λ

zad. 6.

Dane:

nm

350

=

λ

,

nm

50

=

∆

λ

,

V

0

=

U

,

V

,59

0

=

∆

U

,

s

m

8

10

3

⋅

=

c

,

s

J

⋅

⋅

=

−

34

10

625

6,

h

,

Szukane:

e

(ładunek elementarny),

Efekt fotoelektryczny

k

T

E

W

E

+

=

gdzie

T

W

to praca wyjścia,

k

E

to energia kinetyczna fotonu.

C

,

,

)

(

19

9

9

8

34

10

604

1

10

350

1

10

300

1

59

0

10

3

10

625

6

1

1

−

−

−

−

⋅

=













⋅

−

⋅

⋅

⋅

⋅

=

=













−

∆

−

∆

=

⇒

∆

+

=

∆

−

∆

=

∆

+

=

=

∆

−

=

,

U

hc

e

U

e

hc

hc

U

e

U

U

e

E

hc

W

hc

E

k

T

λ

λ

λ

λ

λ

λ

λ

λ

λ

zadanie to jest zupełnie podobne do zadania 5.

Studenckie Notatki Cyfrowe

SNy: Biotechnologia

www.sny.one.pl [e-mail]

Strona 34

Notatka: Fizyka II (FZC1004C) – ćwiczenia.

Utworzona: 22.05.2007 0:37

Temat: Zestaw 4 – Efekty kwantowe.

Zmodyfikowana: 2.06.2007 21:28

zad. 7.

Dane:

U

U

⋅

=

5

1,

'

,

26

0,

=

∆

λ

Å,

Szukane:

U

(napięcie początkowe),

Przeliczenie Angstrema na metry: 1 Å = 10

-10

m

V

,

,

,

,

,

,

,

'

min

min

min

min

max

3

10

19

8

34

2

1

2

3

10

9

15

10

26

0

10

6

1

3

10

3

10

625

6

3

1

5

1

5

1

1

5

1

1

5

1

⋅

=

⋅

⋅

⋅

⋅

⋅

⋅

⋅

=

=

∆

=

⇒

=

∆

⇒

=

∆

⋅

−

=













∆

−

⋅

⇒















∆

−

=

⋅

=

⇒












∆

−

=

=

=

=

=

=

−

−

−

,

q

hc

U

hc

q

U

U

hc

q

qU

hc

U

hc

q

qU

hc

U

hc

q

qU

hc

c

h

qU

c

h

qU

c

h

h

qU

qU

E

h

E

e

λ

λ

λ

λ

λ

λ

λ

λ

λ

λ

υ

υ

gdzie ładunek elektronu to:

C

,

19

10

6

1

−

⋅

=

e

q

zad. 8.

Dane:

nm

,125

0

=

λ

,

°

=

45

α

,

nm

,252

0

=

d

Szukane:

możliwe kąty obrotu,

Uwaga: krystalografowie mierzą kąt padania od płaszczyzny sieciowej a nie od normalnej)

Prawo Wulfa-Braggów

λ

θ

m

d

=

sin

2

gdzie:

m

- liczba naturalna określająca kolejne płaszczyzny sieciowe,

λ

- długość fali promieniowania rentgenowskiego,

d

- odległość płaszczyzn krystalograficznych,

θ

- kąt odbłysku mierzony jako kąt między wiązką promieni padających

a płaszczyzną odbijającą

°

=

°

−

°

=

−

°

=

⋅

=

°

=

°

−

°

=

−

°

=

⋅

=

°

=

°

−

°

=

−

°

=

⋅

=

°

=

°

−

°

=

−

°

=

⋅

=

=

⋅

⋅

⋅

⋅

=

=

⇒

=

−

−

7

37

45

7

82

7

82

4

248

0

1

3

45

1

48

1

48

3

248

0

3

15

7

29

45

7

29

2

248

0

6

30

4

14

45

4

14

1

248

0

248

0

10

252

0

2

10

125

0

2

2

3

4

3

3

2

2

1

1

9

9

,

,

,

)

,

arcsin(

,

,

,

)

,

arcsin(

,

,

,

)

,

arcsin(

,

,

,

)

,

arcsin(

)

,

arcsin(

,

,

arcsin

arcsin

sin

α

θ

θ

α

θ

θ

θ

α

θ

θ

α

θ

λ

θ

λ

θ

m

m

d

m

m

d

i

i

Wykorzystano warunek na refleksy pozytywne (całkowita wielokrotność fali:

λ

m

).

Pełne wyprowadzenie (po angielsku) prawa Braggów, wraz z rysunkami znajduje się
na stronie: http://en.wikipedia.org/wiki/Bragg's_law

Studenckie Notatki Cyfrowe

SNy: Biotechnologia

www.sny.one.pl [e-mail]

Strona 35

Notatka: Fizyka II (FZC1004C) – ćwiczenia.

Utworzona: 22.05.2007 0:37

Temat: Zestaw 4 – Efekty kwantowe.

Zmodyfikowana: 2.06.2007 21:28

Zjawisko Comptona

Pełne wyprowadzenie (po angielsku) przesunięcia Comptona wraz z rysunkami znajduje
się na stronie: http://en.wikipedia.org/wiki/Compton_scattering

zad. 9.

Dane:

0

1

,

0 E

E

e

=

,

°

=

60

θ

,

Szukane:

f

λ

(długość fali fotonu rozproszonego),

0

p

(pęd fotonu padającego),

e

E

(energia elektronu odrzutu),

α

,

λ

υ

hc

h

E

=

=

Rozpatruję zderzenie idealnie sprężyste
więc jest zachowana zasada energii:

f

f

f

e

f

hc

hc

E

E

E

E

E

E

λ

λ

λ

λ

10

9

0

0

0

0

0

10

9

1

,

0

=

⇒

=

+

=

+

=

Zmianę długości fali ilościowo opisuje przesunięcie Comptona

m

10

121

,

0

10

3

10

11

,

9

2

10

625

,

6

10

2

10

2

2

)

60

cos

1

(

)

cos

1

(

10

8

31

34

10

9

0

−

−

−

⋅

=

⋅

⋅

⋅

⋅

⋅

⋅

=

=

⇒

−

=

=

°

−

=

−

=

∆

−

=

∆

c

m

h

c

m

h

c

m

h

c

m

h

c

m

h

e

f

f

f

e

e

e

e

f

λ

λ

λ

θ

λ

λ

λ

λ

Wracając do zasady zachowania energii:

eV

10

41

,

11

eV

10

825

,

1

J

10

825

,

1

10

121

,

0

9

10

3

10

625

,

6

9

3

10

6

,

1

1

15

15

10

8

34

10

9

0

0

0

19

⋅

=

⋅

⋅

=

⋅

=

=

⋅

⋅

⋅

⋅

⋅

=

=

−

=

−

=

−

=

+

=

−

⋅

−

−

−

−

f

f

f

f

f

e

e

f

hc

hc

hc

hc

hc

E

E

E

E

E

E

λ

λ

λ

λ

λ

Korzystając z hipotezy de Broglie’a (przejście ze świata cząstek do świata fal):

λ

λ

h

p

p

h

=

⇒

=

,

Więc:

s

m

kg

23

10

10

9

34

10

9

0

0

10

08

,

6

10

121

,

0

10

625

,

6

⋅

−

−

−

⋅

=

⋅

⋅

⋅

=

=

=

f

h

h

p

λ

λ

Z zasady zachowana pędu:

e

f

p

p

p

+

=

'

0

α

θ

x

y

foton
padający

foton
rozproszony

elektron
odrzutu

Studenckie Notatki Cyfrowe

SNy: Biotechnologia

www.sny.one.pl [e-mail]

Strona 36

Notatka: Fizyka II (FZC1004C) – ćwiczenia.

Utworzona: 22.05.2007 0:37

Temat: Zestaw 4 – Efekty kwantowe.

Zmodyfikowana: 2.06.2007 21:28

Pęd można rozpisać na dwie składowe poziomą

x

i pionową y :













⋅

−

⋅

=

⋅

+

⋅

=

⇒







⋅

+

⋅

−

=

⋅

+

⋅

=

α

θ

λ

α

θ

λ

λ

α

θ

α

θ

sin

sin

0

cos

cos

sin

sin

0

cos

cos

0

0

e

f

e

f

e

f

e

f

p

h

p

h

h

p

p

p

p

p

Uwaga: Nie rozwiązuje tego układu równań bo nie ma takiej potrzeby!

α

θ

λ

α

θ

λ

sin

sin

sin

sin

0

⋅

=

⋅

⇒

⋅

−

⋅

=

e

f

e

f

p

h

p

h

Wiadomo, że:

e

e

e

e

e

e

E

m

p

m

p

E

2

2

2

=

⇒

=

Więc:

°

=

=

⋅

⋅

⋅

⋅

⋅

°

⋅

⋅

=

=

⇒

⋅

=

⋅

−

−

−

−

3

,

55

822

,

0

arcsin

10

825

,

1

10

11

,

9

2

10

121

,

0

60

sin

10

625

,

6

arcsin

2

sin

sin

sin

2

sin

15

31

10

34

α

λ

θ

α

α

θ

λ

e

e

f

e

e

f

E

m

h

E

m

h

Zadania dodatkowe spoza listy:
zad. 10.
…

zad. 11.
…

Studenckie Notatki Cyfrowe

SNy: Biotechnologia

www.sny.one.pl [e-mail]

Strona 37

Notatka: Fizyka II (FZC1004C) – ćwiczenia.

Utworzona: 31.05.2007 19:32

Temat: Zestaw 5 – Efekty kwantowe oraz rozpad promieniotwórczy.

Zmodyfikowana: 2.06.2007 22:25

ZESTAW 5 – Efekty kwantowe oraz rozpad promieniotwórczy

31.05.2007 r.

zad. 1.

Dane:

708

,

0

0

=

λ

Å (długość fali padającej),

°

=

90

θ

,

Szukane:

α

,

0

E

E

e

,

λ

υ

hc

h

E

=

=

Rozpatruję zderzenie idealnie sprężyste
więc jest zachowana zasada energii:















−

=

⇒

+

=

+

=

f

e

e

f

e

f

hc

E

E

hc

hc

E

E

E

λ

λ

λ

λ

1

1

0

0

0

Zmianę długości fali ilościowo opisuje przesunięcie Comptona

m

10

732

,

0

10

708

,

0

10

3

10

11

,

9

10

625

,

6

)

90

cos

1

(

)

cos

1

(

10

10

8

31

34

0

0

0

−

−

−

−

⋅

=

⋅

+

⋅

⋅

⋅

⋅

=

+

=

⇒

−

=

=

°

−

=

−

=

∆

−

=

∆

λ

λ

λ

λ

θ

λ

λ

λ

λ

c

m

h

c

m

h

c

m

h

c

m

h

c

m

h

e

f

f

e

e

e

e

f

%

28

,

3

10

732

,

0

10

708

,

0

1

1

1

1

1

1

10

10

0

0

0

0

0

0

=

⋅

⋅

−

=

−

=















−

=















−

=

−

−

f

f

f

e

hc

hc

E

E

λ

λ

λ

λ

λ

λ

λ

λ

Z zasady zachowana pędu:

e

f

p

p

p

+

=

'

0

Pęd można rozpisać na dwie składowe poziomą

x

i pionową y :













⋅

=

⋅

=

⇒













⋅

−

⋅

=

⋅

+

⋅

=

⇒







⋅

+

⋅

−

=

⋅

+

⋅

=

α

λ

α

λ

α

θ

λ

α

θ

λ

λ

α

θ

α

θ

sin

cos

sin

sin

0

cos

cos

sin

sin

0

cos

cos

0

0

0

e

f

e

e

f

e

f

e

f

e

f

p

h

p

h

p

h

p

h

h

p

p

p

p

p

Uwaga: Nie rozwiązuje tego układu równań bo nie ma takiej potrzeby!

e

e

e

p

h

p

h

p

h

0

0

0

arccos

cos

cos

λ

α

λ

α

α

λ

=

⇒

=

⇒

⋅

=

Wiadomo, że:

23

10

10

8

34

31

0

2

10

3

,

1

10

732

,

0

1

10

708

,

0

1

10

3

10

625

,

6

10

11

,

9

2

1

1

2

2

2

−

−

−

−

−

⋅

=













⋅

−

⋅

⋅

⋅

⋅

⋅

⋅

⋅

⋅

=

=















−

=

=

⇒

=

f

e

e

e

e

e

e

e

hc

m

E

m

p

m

p

E

λ

λ

°

=

=

⋅

⋅

⋅

⋅

⋅

=

−

−

−

9

,

43

72

,

0

arccos

10

3

,

1

10

708

,

0

10

625

,

6

arccos

23

10

34

α

α

θ

x

y

foton
padający

foton
rozproszony

elektron
odrzutu

Studenckie Notatki Cyfrowe

SNy: Biotechnologia

www.sny.one.pl [e-mail]

Strona 38

Notatka: Fizyka II (FZC1004C) – ćwiczenia.

Utworzona: 31.05.2007 19:32

Temat: Zestaw 5 – Efekty kwantowe oraz rozpad promieniotwórczy.

Zmodyfikowana: 2.06.2007 22:25

zad. 2.

Dane:

µm

1

,

0

=

r

,

3

cm

g

2

=

ρ

,

1

=

λ

Å,

Szukane:

k

E

(energia kinetyczna dla O

2

),

'

k

E

(energia dla cząstki o promieniu r )

Stałe:

liczba Avogadro:

mol

1

23

10

02

,

6

⋅

=

A

N

,

masa molowa

2

O

M

:

mol

g

O

32

M

2

=

,

masa elektronu:

kg

10

11

,

9

31

−

⋅

=

e

m

,

przeliczenie Angstrema na metry: 1 Å = 10

-10

m

m

p

mv

E

k

2

2

2

2

1

=

=

Korzystając z hipotezy de Broglie’a (przejście ze świata cząstek do świata fal):

λ

λ

h

p

p

h

=

⇒

=

,

gdzie

s

J

10

625

6

34

⋅

⋅

=

−

,

h

jest stałą Plancka,

2

2

2

2

2

λ

m

h

m

p

E

k

=

=

Dla elektronu

eV

6

,

150

J

10

409

,

2

)

10

(

10

11

,

9

2

)

10

625

,

6

(

2

17

2

10

31

2

34

2

2

=

⋅

=

⋅

⋅

⋅

⋅

=

=

−

−

−

−

λ

e

k

m

h

E

Dla cząsteczki tlenu

eV

10

58

,

2

J

10

128

,

4

)

10

(

10

10

316

,

5

2

)

10

625

,

6

(

2

g

10

316

,

5

10

02

,

6

32

3

23

2

10

3

23

2

34

2

2

23

23

2

2

2

−

−

−

−

−

−

−

⋅

=

⋅

=

⋅

⋅

⋅

⋅

⋅

=

=

⋅

=

⋅

=

=

λ

O

k

A

O

O

m

h

E

N

M

m

Dla cząsteczki o promieniu r

18

3

6

3

3

4

3

3

4

10

38

,

8

)

10

1

,

0

(

10

2

'

−

−

⋅

=

⋅

⋅

⋅

⋅

⋅

=

=

=

π

π

ρ

ρ

r

V

m

eV

10

63

,

1

J

10

62

,

1

)

10

(

10

38

,

8

2

)

10

625

,

6

(

'

2

11

30

2

10

18

2

34

2

2

−

−

−

−

−

⋅

=

⋅

=

⋅

⋅

⋅

⋅

=

=

λ

m

h

E

k

zad. 3.

Dane:

mm

1

,

0

=

a

,

m

5

,

0

=

L

,

µm

8

=

d

(szerokość centralnego maksimum),

Szukane:

v

(prędkość elektronów),

Wiązkę elektronów traktujemy jak falę:
Mamy do czynienia z dyfrakcją (ugięciem) fali na pojedynczej
szczelnie. Centralne wzmocnienie będzie pomiędzy sąsiednimi
minimami (powyżej i poniżej środka ekranu). Warunek na prążek
jasny (dla

1

=

m

, gdzie

m

to rząd dyfrakcji, otrzymujemy prążek

centralny), więc:

θ

λ

λ

θ

sin

1

sin

a

m

m

a

=

⇒

=

=

Z geometrii rysunku:

L

d

L

d

2

tg

2

1

=

=

θ

a

d

L

θ

Studenckie Notatki Cyfrowe

SNy: Biotechnologia

www.sny.one.pl [e-mail]

Strona 39

Notatka: Fizyka II (FZC1004C) – ćwiczenia.

Utworzona: 31.05.2007 19:32

Temat: Zestaw 5 – Efekty kwantowe oraz rozpad promieniotwórczy.

Zmodyfikowana: 2.06.2007 22:25

Dla małych kątów w radianach można zastosować przybliżenie:

rad]

[

sin

tg

θ

θ

θ

≈

≈

Więc:

L

ad

a

a

2

tg

sin

=

=

=

θ

θ

λ

Wiązkę elektronów należy potraktować jak cząstkę:

Korzystając z hipotezy de Broglie’a:

λ

λ

h

p

p

h

=

⇒

=

,

gdzie

s

J

10

625

6

34

⋅

⋅

=

−

,

h

jest stałą Plancka,

Z drugiej strony pęd:

v

m

mv

p

e

=

=

gdzie

kg

10

11

,

9

31

−

⋅

=

e

m

to masa elektronu,

s

m

6

31

6

3

34

2

10

91

,

0

10

11

,

9

10

8

10

1

,

0

10

625

6

5

,

0

2

2

⋅

=

⋅

⋅

⋅

⋅

⋅

⋅

⋅

⋅

=

⋅

⋅

⋅

⋅

=

=

=

=

−

−

−

−

,

m

d

a

h

L

m

h

m

h

m

p

v

e

e

L

ad

e

e

λ

Zasada nieoznaczoności Heisenberga

Zasada w myśl której nie można wyznaczyć jednocześnie z dowolną dokładnością
położenia i pędu cząstki. Iloczyn błędów pomiarów dwóch wielkości sprężonych zawsze
będzie większy od h (stałej Plancka), niektórzy fizycy twierdzą, że od h („ha kreślone”).
Błędy te nie są błędami pomiarowymi wynikającymi z niedoskonałości urządzeń lub
metody pomiarowych, ale wynikają z samych teoretycznych podstaw mechaniki kwantowej.

h

≥

∆

⋅

∆

p

x

gdzie:

s

J

10

0546

1

2

34

⋅

=

=

−

·

,

h

π

h

,

x

∆

to błędność pomiaru położenia, p

∆

błędność pomiaru pędu,

Sprzężone są też ze sobą:

h

≥

∆

⋅

∆

t

E

gdzie:

E

∆

to błędność pomiaru energii, t

∆

błędność pomiaru czasu,

Nie można w innych kombinacjach sprzęgać tych wielkości fizycznych.

Metoda różniczki zupełnej

Za pomocą tej metody można określić niepewność pomiaru danej wielkości poprzez
niepewności wielkości bezpośrednio zmierzonych.
Niech

)

,

...

,

,

(

2

1

n

x

x

x

f

y

=

wtedy:

n

n

n

i

i

i

x

x

y

x

x

y

x

x

y

x

x

y

y

∆

∂

∂

+

+

∆

∂

∂

+

∆

∂

∂

=

∆

∂

∂

=

∆

∑

=

...

2

2

2

1

1

gdzie:

i

x

∆

to błędności pomiarów, wtedy y

∆

to błędność wyznaczenia wielkości y

(znane też niepewnością bezwzględną).

zad. 4.

Dane:

keV

50

,

1

=

E

,

E

E

⋅

=

∆

%

1

,

Szukane:

x

∆

(błędność położenia),

Stałe:

masa elektronu:

kg

10

9,11

31

-

e

m

⋅

=

,

J

10

6

,

1

eV

1

19

−

⋅

=

.

Zasada nieoznaczoności Heisenberga

h

≥

∆

⋅

∆

p

x

Studenckie Notatki Cyfrowe

SNy: Biotechnologia

www.sny.one.pl [e-mail]

Strona 40

Notatka: Fizyka II (FZC1004C) – ćwiczenia.

Utworzona: 31.05.2007 19:32

Temat: Zestaw 5 – Efekty kwantowe oraz rozpad promieniotwórczy.

Zmodyfikowana: 2.06.2007 22:25

Szukamy maksymalną możliwą dokładność wyznaczenia położenia, więc to będzie:

p

x

p

x

∆

=

∆

⇒

=

∆

⋅

∆

h

h

Teraz trzeba wyrazić pęd jako funkcję energii:

mv

p

=

mE

p

m

p

m

m

mv

mv

E

2

2

2

2

2

2

2

=

⇒

=

=

=

Więc:

E

m

p

e

∆

=

∆

2

Korzystamy z różniczki zupełnej:

(

)

2

2

2

01

,

0

2

2

2

2

100

1

mE

mE

mE

E

m

mE

E

m

E

mE

E

E

E

p

p

=

⋅

⋅

=

∆

=

∆

∂

∂

=

∆

∂

∂

=

∆

Więc:

m

10

001

,

1

10

6

,

1

10

50

,

1

10

9,11

2

10

0546

1

100

2

100

2

9

19

3

31

34

100

1

−

−

−

⋅

=

⋅

⋅

⋅

⋅

⋅

⋅

⋅

=

=

=

=

∆

=

∆

-

·

,

mE

mE

p

x

h

h

h

zad. 5.

Dane:

µs

01

,

0

=

τ

,

nm

600

=

λ

,

Szukane:

E

∆

,

λ

∆

,

J

10

6

,

1

eV

1

19

−

⋅

=

Zasada nieoznaczoności Heisenberga

h

≥

∆

⋅

∆

t

E

Dla

τ

=

∆

t

szukamy maksymalną dokładność wyznaczenia energii E

∆

, więc to będzie:

eV

10

6

,

6

eV

10

546

,

1

J

10

546

,

1

10

01

,

0

10

0546

1

8

10

6

,

1

1

26

26

6

34

19

−

⋅

−

−

−

−

⋅

=

⋅

⋅

=

⋅

=

⋅

=

=

∆

=

⋅

∆

−

·

,

E

E

τ

τ

h

h

Trzeba wyrazić długości fali jako funkcję energii:

E

hc

hc

h

E

=

⇒

=

=

λ

λ

ν

Korzystamy z różniczki zupełnej:

( )

m

10

91

,

1

10

01

,

0

10

3

2

)

10

600

(

2

14

6

8

2

9

2

2

2

2

2

2

2

−

−

−

⋅

=

⋅

⋅

⋅

⋅

⋅

=

⋅

=

=

∆

=

∆

∆

=

∆

=

∆

=

∆

−

=

∆













∂

∂

=

∆

∂

∂

=

∆

π

τ

π

λ

τ

λ

λ

λ

λ

λ

λ

λ

c

hc

hc

E

hc

E

E

hc

E

E

hc

E

E

hc

E

E

hc

E

E

E

hc

h

bo:

π

2

h

=

h

.

Studenckie Notatki Cyfrowe

SNy: Biotechnologia

www.sny.one.pl [e-mail]

Strona 41

Notatka: Fizyka II (FZC1004C) – ćwiczenia.

Utworzona: 31.05.2007 19:32

Temat: Zestaw 5 – Efekty kwantowe oraz rozpad promieniotwórczy.

Zmodyfikowana: 2.06.2007 22:25

Fizyka relatywistyczna

(temat nie poruszany w ramach wykładów lub/i ćwiczeń fizyka II)

zad. 6.

Dane:

c

v

9

,

0

=

,

Szukane:

błąd wyrażony w %,

Stałe:

masa (spoczynkowa) elektronu:

kg

10

9,11

31

-

e

m

⋅

=

,

prędkość światła w próżni:

s

m

8

10

3

⋅

=

c

,

Wzór na energię kinetyczną:

2

2

1

'

mv

E

k

=

Wzór na relatywistyczną energię kinetyczną:

(

)

0

1

)

(

E

v

E

k

−

=

γ

, gdzie

2

2

1

1

)

(

c

v

v

−

=

γ

,

2

0

0

c

m

E

=

Uwaga: wyprowadzenie tego wzoru znajduje się na stronie 10 w zadaniu VI w pliku
„kolko_fizyczne_szczegolna_teoria_wzglednosci.pdf” na stronie www.e-zeszyty.twoj.info

(

)

(

)

(

)

(

)

%

7

,

68

687

,

0

588

,

2

81

,

0

588

,

2

)

1

294

,

2

(

2

)

1

294

,

2

(

2

1

)

(

1

)

(

1

)

(

1

)

(

'

294

,

2

81

,

0

1

1

1

1

)

(

2

2

2

2

2

2

2

0

2

0

2

1

2

0

0

2

0

2

1

0

9

,

0

2

2

2

=

=

−

=

−

−

−

=

=

−

−

−

=

−

−

−

=

−

=

−

=

−

=

⋅

c

c

c

c

v

c

c

m

v

v

m

c

m

v

E

v

v

m

E

v

E

E

E

v

k

k

k

c

c

γ

γ

γ

γ

γ

zad. 7.

Dane:

0

3E

E

k

=

,

Szukane:

0

E

(energia spoczynkowa),

v

(prędkość protonu),

Stałe:

masa (spoczynkowa) protonu:

kg

10

672

1

27

-

p

,

m

⋅

=

,

prędkość światła w próżni:

s

m

8

10

3

⋅

=

c

,

J

10

6

,

1

eV

1

19

−

⋅

=

.

2

mc

E

=

Relatywistycznie:

2

0

2

c

m

mc

E

−

=

gdzie:

0

m

to masa spoczynkowa,

)

(v

m

m

=

to masa zależną od prędkości,

Więc, energia spoczynkowa (

0

=

v

) to:

MeV

5

,

940

eV

10

5

,

1

J

10

5

,

1

)

10

3

(

10

672

1

19

10

6

,

1

1

10

10

2

8

27

2

2

0

0

=

⋅

⋅

=

⋅

=

⋅

⋅

⋅

=

=

=

−

⋅

-

-

-

p

,

c

m

c

m

E

Wzór na relatywistyczną energię kinetyczną:

(

)

0

1

)

(

E

v

E

k

−

=

γ

, gdzie

2

2

1

1

)

(

c

v

v

−

=

γ

Uwaga: wyprowadzenie tego wzoru znajduje się na stronie 10 w zadaniu VI w pliku
„kolko_fizyczne_szczegolna_teoria_wzglednosci.pdf” na stronie www.e-zeszyty.twoj.info

Studenckie Notatki Cyfrowe

SNy: Biotechnologia

www.sny.one.pl [e-mail]

Strona 42

Notatka: Fizyka II (FZC1004C) – ćwiczenia.

Utworzona: 31.05.2007 19:32

Temat: Zestaw 5 – Efekty kwantowe oraz rozpad promieniotwórczy.

Zmodyfikowana: 2.06.2007 22:25

(

)

s

m

8

16

15

8

16

15

16

15

0

0

10

9

,

2

10

3

16

15

1

)

1

(

16

4

1

1

)

(

4

)

(

1

)

(

3

1

)

(

3

2

2

2

2

2

2

⋅

=

⋅

⋅

=

=

=

⇒

=

⇒

=

−

⇒

=

−

=

=

⇒

−

=

⇒

−

=

c

v

c

v

v

v

v

E

v

E

c

v

c

v

c

v

γ

γ

γ

γ

Wzór na masę relatywistyczną:

0

)

(

)

(

m

v

v

m

⋅

=

γ

Wzór na pęd relatywistyczny:

(

)

s

m

kg

18

2

10

3

10

9

,

2

8

27

0

0

10

89

,

1

1

10

9

,

2

10

672

,

1

1

)

(

)

(

8

8

2

2

⋅

−

⋅

⋅

−

⋅

=

−

⋅

⋅

⋅

=

−

=

⋅

⋅

=

⋅

=

c

v

v

m

v

m

v

p

v

v

m

p

γ

Defekt masy

zad. 8.

Dane:

u

013553

,

2

=

D

m

(masa deuteronu),

Szukane:

E

(energia wiązania),

Deuteron to jądro atomowe deuteru, czyli H

2

1

. Składa się z jednego protonu i jednego neutronu.

Stałe:

masa protonu:

u

007276

,

1

=

p

m

,

masa neutronu:

u

008665

,

1

=

n

m

,

prędkość światła:

s

m

8

10

3

⋅

=

c

.

kg

10

66

,

1

u

1

27

−

⋅

=

,

J

10

6

,

1

eV

1

19

−

⋅

=

.

Eksperymentalnie dowiedziono, że masa jądra danego pierwiastka jest mniejsza niż
oddzielnie suma mas nukleonów (protony i neutrony) budujących to jądro. Zjawisko
to nazywa się „defektem masy”. Ta różnica mas m

∆

daje energię wiązaniu chemicznemu:

2

mc

E

∆

=

kg

10

96

,

3

kg

10

66

,

1

10

388

,

2

u

10

388

,

2

u

013553

,

2

)

008665

,

1

u

007276

,

1

(

)

(

30

27

3

3

−

−

−

−

⋅

=

⋅

⋅

⋅

=

=

⋅

=

−

+

=

−

+

=

∆

D

n

p

m

m

m

m

MeV

23

,

2

eV

10

564

,

3

J

10

564

,

3

)

10

3

(

kg

10

96

,

3

19

10

6

,

1

1

13

13

2

s

m

8

30

=

⋅

⋅

=

⋅

=

⋅

⋅

⋅

=

−

⋅

−

−

−

E

zad. 9.

Dane:

β

N

C

0

1

14

7

14

6

−

+

=

(gdzie β

0

1

−

to elektron),

u

003242

,

14

C

=

m

,

u

003074

,

14

N

=

m

,

Szukane:

E

∆

(wydzielona energia),

Występuje tu „defekt masy”. Patrz opis zdania 8.

2

mc

E

∆

=

∆

kg

10

79

,

2

kg

10

66

,

1

10

68

,

1

u

10

68

,

1

u

003074

,

14

003242

,

14

31

27

4

4

N

C

−

−

−

−

⋅

=

⋅

⋅

⋅

=

=

⋅

=

−

=

−

=

∆

m

m

m

eV

10

157

,

0

eV

10

51

,

2

J

10

564

,

3

)

10

3

(

kg

10

79

,

2

6

10

6

,

1

1

14

13

2

s

m

8

31

19

−

⋅

−

−

−

⋅

=

⋅

⋅

=

⋅

=

⋅

⋅

⋅

=

−

E

Studenckie Notatki Cyfrowe

SNy: Biotechnologia

www.sny.one.pl [e-mail]

Strona 43

Notatka: Fizyka II (FZC1004C) – ćwiczenia.

Utworzona: 31.05.2007 19:32

Temat: Zestaw 5 – Efekty kwantowe oraz rozpad promieniotwórczy.

Zmodyfikowana: 2.06.2007 22:25

Rozpad promieniotwórczy

Szybkość rozpadu promieniotwórczego (

dt

dN

) jest proporcjonalna do liczby rozpadających

się jąder promieniotwórczych N . Współczynnikiem proporcjonalności jest stała rozpadu

β

.

Liczba jąder, które nie uległy rozpadowi maleje, więc we wzorze jest „–” (minus).

N

dt

dN

β

−

=

Szukana jest funkcja

)

(t

N

– liczba jąder N , które nie uległy rozpadowi do chwili t .

t

C

C

t

e

e

e

N

C

t

N

dt

N

dN

dt

N

dN

N

dt

dN

⋅

−

+

⋅

−

⋅

=

=

⇒

+

⋅

−

=

−

=

⇒

−

=

⇒

−

=

∫

∫

β

β

β

β

β

β

ln

Dla

0

=

t

:

0

0

0

1

N

e

e

e

e

e

e

N

C

C

C

C

=

=

⋅

=

⋅

=

⋅

=

⋅

−

β

.

Niech

0

N

będzie początkową liczbą jąder promieniotwórczych.

t

e

N

t

N

⋅

−

⋅

=

β

0

)

(

Czas połowicznego rozpadu, zaniku

τ

(litera „tau” albo

2

/

1

T

) to czas pod którym liczba

jąder zmniejszy się dwa razy. np. dla

0

2

1

N

⇒

τ

,

0

4

1

2

N

⇒

τ

,

0

8

1

3

N

⇒

τ

Ogólnie:

2

1

2

1

0

0

2

1

0

2

1

ln

=

⋅

−

⇒

=

⇒

⋅

=

⇒

=

∧

=

⋅

−

⋅

−

τ

β

τ

τ

β

τ

β

e

e

N

N

N

N

t

τ

β

2

ln

=

Więc:

τ

τ

t

N

e

N

t

N

t

−

⋅

−

⋅

=

⋅

=

2

)

(

0

2

ln

0

zad. 10.

Dane:

β

S

P

0

1

32
16

32
15

−

+

=

,

s

1

4

10

=

v

(szybkość rozpadu),

dni

3

,

14

=

τ

(czas połowicznego rozpadu),

dni

30

=

t

,

Szukane:

P

m

(masa fosforu),

)

(t

A

(aktywność w chwili t ),

Stałe:

liczba Avogadro:

mol

1

23

10

02

,

6

⋅

=

A

N

,

masa molowa P

32
15

:

mol

g

32

=

P

M

.

Aktywność promieniotwórcza to tempo, szybkość rozpadu jąder promieniotwórczych:

dt

dN

t

N

v

t

A

−

=

⋅

=

=

)

(

)

(

β

.

Jednostką aktywności (szybkości rozpadu) jest

]

[

]

[

s

1

sekundę

rozkładów

=

.

Wiadomo, że:

N

dt

dN

β

−

=

τ

β

2

ln

=

Znak „–” należy pominąć, bo interesuje na sama wartość szybkość, a nie kierunek zmiany.

2

ln

2

ln

τ

τ

β

v

N

N

N

dt

dN

v

=

⇒

=

=

=

g

10

47

,

9

32

2

ln

10

02

,

6

)

60

60

24

(

3

,

14

10

2

ln

2

ln

13

23

4

−

⋅

=

=

⋅

⋅

⋅

⋅

⋅

⋅

⋅

=

⋅

=

⋅

=

⋅

=

⋅

=

p

p

A

p

A

p

P

M

v

M

N

v

M

N

N

M

n

m

τ

τ

Studenckie Notatki Cyfrowe

SNy: Biotechnologia

www.sny.one.pl [e-mail]

Strona 44

Notatka: Fizyka II (FZC1004C) – ćwiczenia.

Utworzona: 31.05.2007 19:32

Temat: Zestaw 5 – Efekty kwantowe oraz rozpad promieniotwórczy.

Zmodyfikowana: 2.06.2007 22:25

10

13

23

0

10

78

,

1

32

10

47

,

9

10

02

,

6

⋅

=

⋅

⋅

⋅

=

=

−

p

P

A

M

m

N

N

s

rozpadów

10

0

0

7

,

2332

2

10

78

,

1

)

60

60

24

(

3

,

14

2

ln

)

30

(

2

2

ln

2

2

ln

)

(

)

(

3

,

14

30

=

⋅

⋅

⋅

⋅

⋅

⋅

=

⋅

⋅

=

⋅

⋅

=

⋅

=

−

−

−

A

N

N

t

N

t

A

t

t

τ

τ

τ

τ

β

zad. 11.

Dane:

U

235

92

,

Ra

226

88

,

Ci

1

=

A

(aktywność),

lat

10

1

,

7

8

U

⋅

=

τ

,

lat

1600

Ra

=

τ

,

Szukane:

U

m

(masa uranu),

Ra

m

(masa radu),

Aktywność: patrz opis zdania 10.
Jednostką aktywności (szybkości rozpadu) jest kiur:

s

rozpadów

10

10

7

,

3

Ci

1

⋅

=

2

ln

2

2

ln

)

0

(

2

2

ln

)

(

2

2

ln

)

(

)

(

0

0

0

A

A

t

A

N

N

t

N

t

A

t

t

⋅

=

⋅

⋅

=

⋅

⋅

=

⇒

⋅

⋅

=

⋅

=

−

−

−

τ

τ

τ

τ

β

τ

τ

τ

kg

467

10

02

,

6

2

ln

235

10

7

,

3

)

60

60

24

25

,

365

(

10

1

,

7

2

ln

23

10

8

U

U

U

0

U

U

=

⋅

⋅

⋅

⋅

⋅

⋅

⋅

⋅

⋅

⋅

=

=

⋅

⋅

⋅

=

⋅

=

⋅

=

A

A

N

M

A

M

N

N

M

n

m

τ

g

1

10

02

,

6

2

ln

226

10

7

,

3

)

60

60

24

25

,

365

(

1600

2

ln

23

10

Ra

Ra

Ra

Ra

0

Ra

Ra

=

⋅

⋅

⋅

⋅

⋅

⋅

⋅

⋅

⋅

=

=

⋅

⋅

⋅

=

⋅

=

⋅

=

N

M

A

M

N

N

M

n

m

A

τ

Więc aktywność równą 1 Ci posiada 1 gram

Ra

226

88

.

Uwaga: rok ma średnio

4

1

365

dnia.

zad. 12.

Dane:

α

Rn

Ra

4
2

219

86

223

88

+

=

,

dni

43

,

11

=

τ

,

dni

28

=

t

,

21

0

10

70

,

4

⋅

=

N

,

Szukane:

He

N

(liczba atomów helu),

Uwaga: cząstka alfa α

4
2

to jądro helu

+

2

4
2

He

.

Liczba jąder

Ra

223

88

które nie rozpadły się to:

20

21

0

10

6

,

8

2

10

70

,

4

)

28

(

2

)

(

43

,

11

28

⋅

=

⋅

⋅

=

⋅

=

−

−

N

N

t

N

t

τ

Więc liczba jąder

Ra

223

88

która rozpadła się to:

21

20

21

0

10

84

,

3

10

6

,

8

10

70

,

4

)

28

(

'

⋅

=

⋅

−

⋅

=

−

=

N

N

N

.

Tyle ile jąder

Ra

223

88

się rozpadło tyle powstało jąder

+

2

4
2

He

.

21

He

10

84

,

3

'

⋅

=

=

N

N

Studenckie Notatki Cyfrowe

SNy: Biotechnologia

www.sny.one.pl [e-mail]

Strona 45

Notatka: Fizyka II (FZC1004C) – ćwiczenia.

Utworzona: 31.05.2007 19:32

Temat: Kolokwium III.

Zmodyfikowana: 3.06.2007 23:37

Kolokwium III

5.06.2007 r.

Zakres tematyczny: ciało doskonale czarne, efekt fotoelektryczny, prawo Braggów, zjawisko
Comptona, hipoteza de Broglie’a, zasada nieoznaczoności Heisenberga.

[lista 4. cała oraz lista 5. do zadania 5. włącznie]

Przykładowe treści zadań

zad. 1.
Ciało doskonale czarne ma temperaturę

K

2900

1

=

T

. Podczas stygnięcia tego ciała długość fali,

na jaką przypada maksimum zdolności emisyjnej zmieniła się o

µm

9

=

∆

λ

. Do jakiej

temperatury ostygło ciało?

Odp.

K

290

.

Przykładowe rozwiązania zadań

zad. 1.

Dane:

K

2900

1

=

T

,

µm

9

=

∆

λ

,

Szukane:

2

T

,

Zgodnie z prawem przesunięć Wiena:

T

C

=

max

λ

gdzie:

mK

10

9

,

2

3

−

⋅

=

C

jest stałą Wiena

Z treści zadania wiadomo, że

2

1

T

T

>

bo ciało ostygło, więc:

2

1

max

max

λ

λ

<

.

1

2

1

2

max

max

max

max

λ

λ

λ

λ

λ

λ

+

∆

=

⇒

−

=

∆

K

290

10

9

,

2

10

9

2900

2900

10

9

,

2

max

max

max

max

3

6

3

1

1

1

1

1

2

1

2

2

1

2

1

1

1

2

2

1

1

=

⋅

+

⋅

⋅

⋅

⋅

=

+

∆

=

+

∆

=

+

∆

=

+

∆

=

⇒

=

+

∆

⇒












=

+

∆

=

⇒












=

=

−

−

−

C

T

CT

T

C

T

C

T

C

C

T

T

C

C

T

T

C

T

C

T

C

T

C

T

C

T

C

λ

λ

λ

λ

λ

λ

λ

λ

λ

λ

Dodatkowe zadania testowe z wykładów
…