1

WŁAŚCIWOŚCI MECHANICZNE GRUNTÓW.

WŁAŚCIWOŚCI MECHANICZNE GRUNTÓW.

ŚCIŚLIWOŚĆ GRUNTÓW 

ŚCIŚLIWOŚĆ GRUNTÓW 

MECHANIKA GRUNTÓW I FUNDAMENTOWANIE

MECHANIKA GRUNTÓW I FUNDAMENTOWANIE

Budownictwo              semestr 4

Budownictwo              semestr 4

2

Mówiąc  o  cechach  mechanicznych  gruntów  mamy  na  myśli  głównie  te 
właściwości,  które  decydują  o 

nośności

gruntu  jako  podłoża  obiektu  budowla-

nego i o jego 

odkształcalności

pod wpływem przyłożonego obciążenia.

Grunty, jako 

ośrodki rozdrobnione

, pod wpływem obciążenia odkształcają się w 

znaczniejszym  stopniu  w  porównaniu  do 

ośrodków  ciągłych

,  jak  np.  skała  lita. 

Prędkość tych odkształceń jest z kolei dużo mniejsza niż w skałach i silnie zależy 
od rodzaju gruntu: czy jest to grunt sypki, czy spoisty.

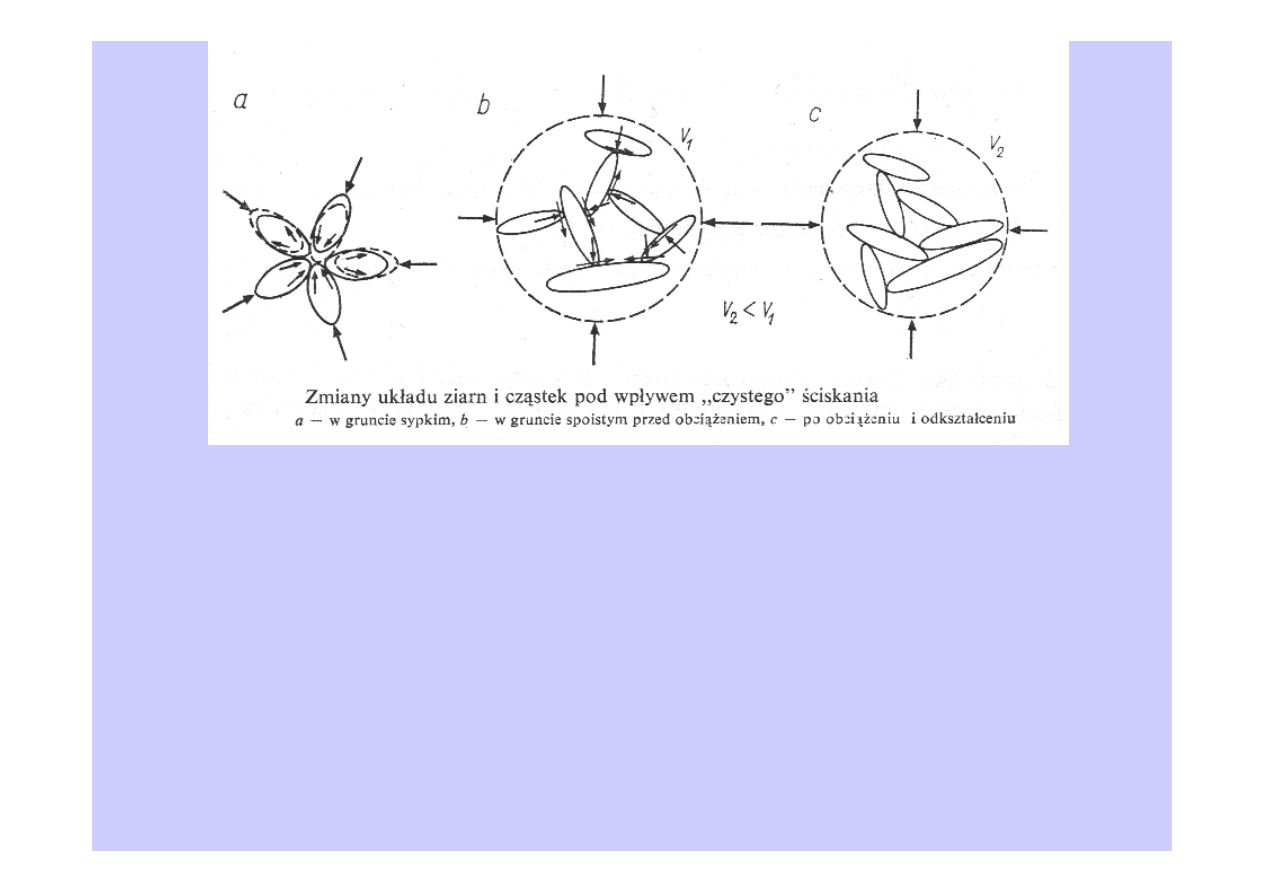
Ośrodek gruntowy (szczególnie niespoisty) charakteryzuje się ziarnistą budową. 
Pomiędzy  poszczególnymi  ziarnami  (cząstkami)  występują  pory  o  znacznych 
rozmiarach.  Obciążenia  są  przenoszone  przez  bardzo  małe  powierzchnie 
kontaktu  pomiędzy  ziarnami.  Powoduje  to  występowanie  bardzo  dużych 
naprężeń  kontaktowych. 

Efektem  obciążenia  jest  zawsze  zmniejszenie  objętości 

ośrodka gruntowego na skutek wzajemnego przemieszczenia ziaren, częściowego 
ich zniszczenia (skruszenia) oraz odkształceń samych ziaren w zakresie naprężeń 
sprężystych.

Cechą  ośrodka  gruntowego  jest  nieodwracalność  odkształceń  po 

zdjęciu działającego obciążenia. Mówimy w związku z tym, że grunt jest w tym 
zakresie ośrodkiem plastycznym. Zależność pomiędzy działającym naprężeniem 
i wywołanym przez nie odkształceniem jest zawsze krzywoliniowa.

3

Ś

ciśliwością nazywamy cechę gruntu polegającą na zmniejszania objętości pod 

wpływem  przyłożonego  obciążenia

.  Przy  rozpatrywaniu  zagadnień  związanych 

ze  ściśliwością  należy  zwrócić  uwagę  na  znaczenie  udziału  wody  znajdującej 
się  w  porach  gruntu  na  ten  proces.  Trzeba  pamiętać,  że  podstawowym 
elementem „nośnym” gruntu jest jego szkielet. Jeżeli jednak grunt podlegający 
obciążeniu jest nawodniony, to bezpośrednio po obciążeniu właśnie woda, jako 
ciecz  nieściśliwa,  przejmuje  na  siebie  praktycznie  cały  przyrost obciążenia. 
Powoduje  to  wystąpienie  gradientu  (przyrostu,  nadwyżki)  ciśnienia  wody  w 
porach  ponad  wartość  ciśnienia  hydrostatycznego,  jakie  panowało  w  porach 
przed obciążeniem. 

4

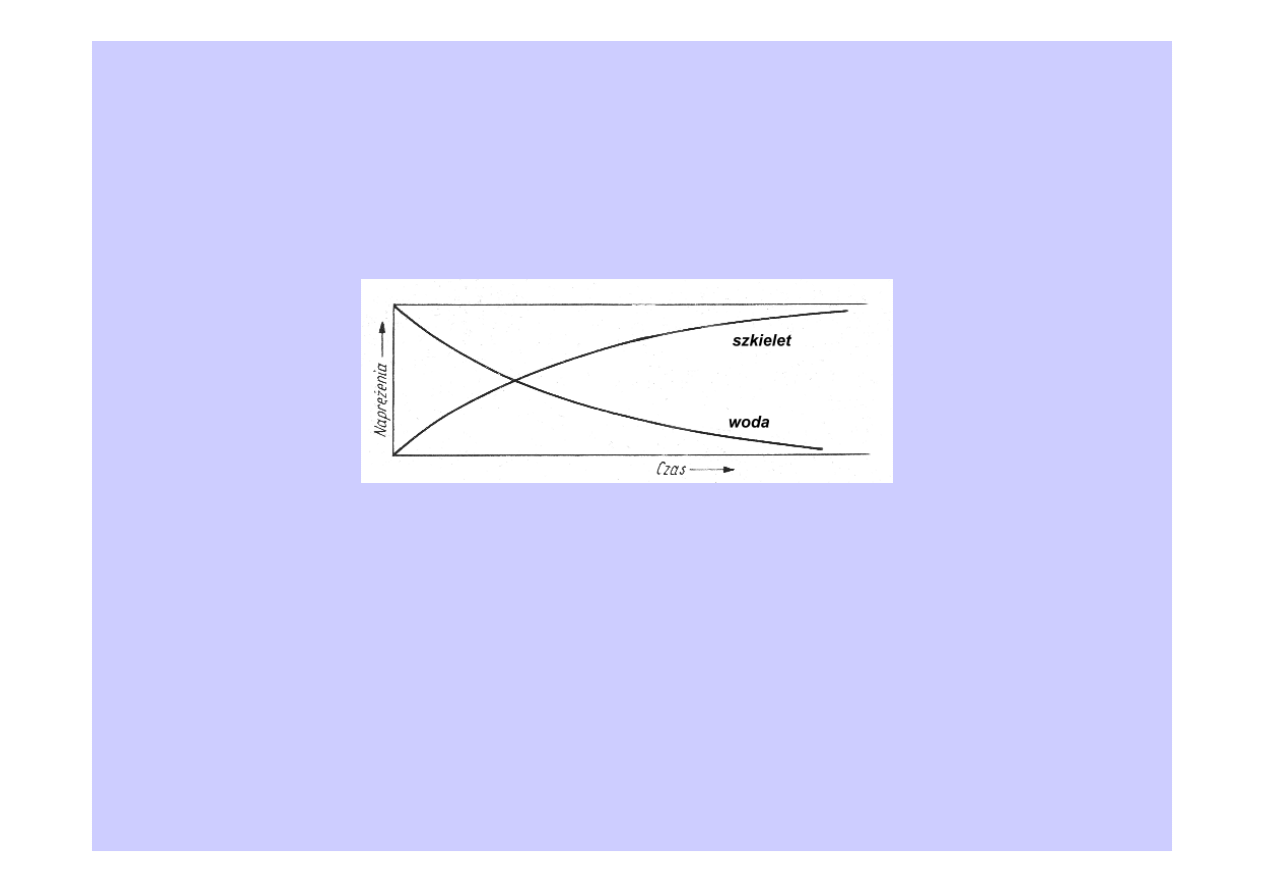
Wynikiem  wystąpienia  gradientu  ciśnienia  jest  przepływ  wody  do  miejsc  o 
niższym  ciśnieniu.  Tym  samym  wartość  ciśnienia  porowego  spada.  Równo-
cześnie następuje stopniowy wzrost naprężenia w szkielecie. W efekcie ciśnie-
nie  wody  w  porach  powraca  stopniowo  do  wartości  początkowej,  zaś całe 
obciążenie przejmuje na siebie szkielet gruntowy. 

Opisany  proces 

rozproszenia  (dyssypacji)

nadwyżki  ciśnienia  porowego 

powstałej w wyniku obciążeniem gruntu nosi nazwę 

konsolidacji

.

Czas  trwania  konsolidacji  zależy  w  największej  mierze  od  wodoprzepuszczalności 
gruntu. W gruntach sypkich, gdzie rozmiary porów są duże i istnieje łatwość przepływu 
wody,  konsolidacja  praktycznie  nie  występuje.  Odwrotnie  dzieje  się  w  gruntach 
spoistych,  gdzie  przepływ  wody  jest  bardzo  utrudniony.  Tam  proces  konsolidacji  jest 
rozciągnięty  w  czasie.  Z  tego  powodu  osiadanie  obiektów  na  podłożu  z  gruntów 
spoistych trwa jeszcze długo po zakończeniu budowy, podczas gdy  w gruntach sypkich 
osiadanie postępuje wraz ze wzrostem nacisków już w trakcie wznoszenia obiektu.

5

Jednym  ze  sposobów  analizy  zjawiska  ściśliwości  w  gruntach  jest  badanie 
próbek gruntów w 

edometrze

6

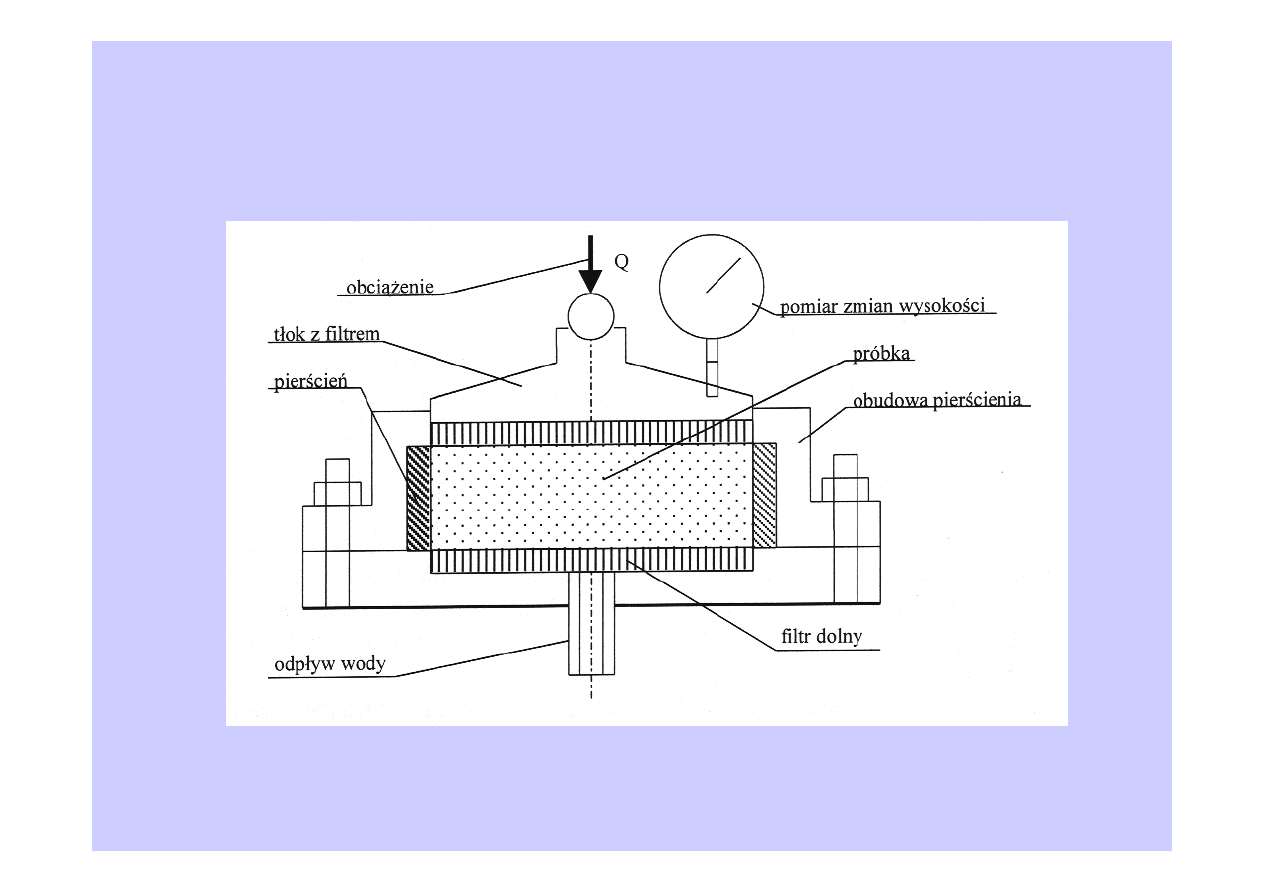
Zasadniczą  częścią  edometru  jest  metalowy  pierścień  o  średnicy  wewnętrznej 
65,0 mm oraz wysokości 20,0 mm, w którym znajduje się próbka NNS badanego 
gruntu.  Pierścień  jest  zamocowany  w  sztywnej  obudowie,  uniemożliwiającej 
poprzeczne  (poziome)  odkształcenia  pierścienia  i  próbki.  Obciążenie  jest 
przekazywane na próbkę poprzez górny tłok. Woda znajdująca się w próbce może 
się odsączać w trakcie badania przez filtry: górny i dolny. Obciążenia na próbkę 
są przykładane  kolejnymi  stopniami,  takimi,  że każdy  następny  stopień  jest  dwa 
razy większy od poprzedniego: 12,5; 25,0; 50,0; 100,0; 200,0; 400,0 i 800,0 kPa. 
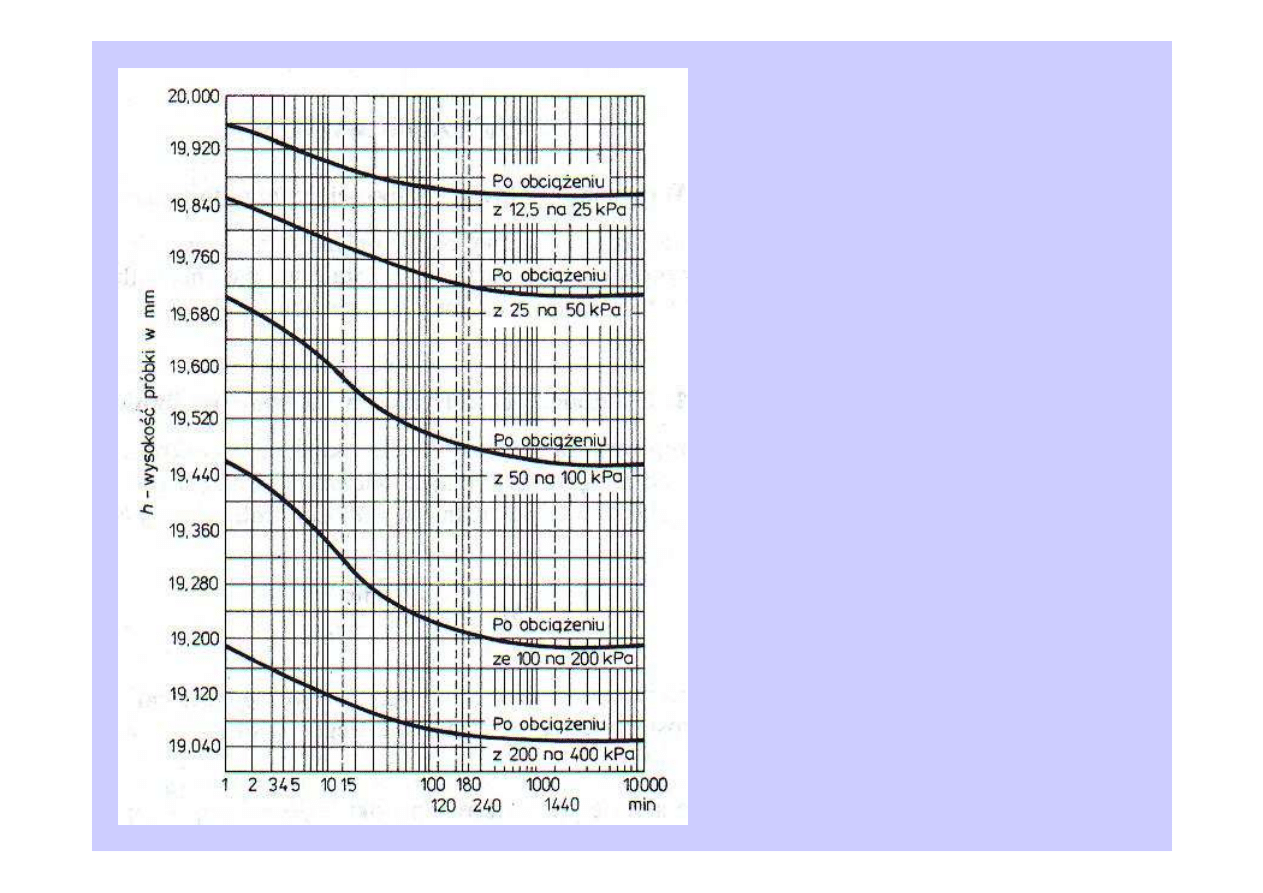
Przy każdym stopniu obciążenia są prowadzone pomiary wysokości próbki (aż do 
ustania  osiadań  – zakończenia  konsolidacji)  w  funkcji  czasu,  na  podstawie 
których  sporządza  się 

krzywe  konsolidacji

.  Te  wykresy  pozwalają  dokładnie 

prześledzić  przebieg  konsolidacji  próbki  w  czasie  trwania  obciążenia  i  ustalić 
zmianę jej wysokości. Zależność pomiędzy wysokością próbki (lub wskaźnikiem 
porowatości),  a  naprężeniem  pionowym  działającym  na  próbkę  nosi  nazwę 

krzywej  ściśliwości

.  Korzystając  z  tego  wykresu  można  zdefiniować 

edometryczne moduły  ściśliwości

,  będące  jednymi  z  parametrów  charakte-

ryzujących  ściśliwość  gruntu.  Badanie  ściśliwości  najczęściej  jest  prowadzone 
jako  badanie 

z  odciążeniem

,  tzn.  próbka  jest  najpierw  obciążana  do  wartości 

zbliżonej  do  naprężeń  pierwotnych  panujących  w  gruncie  na  głębokości 
przewidywanego  posadowienia  fundamentu,  a  następnie  odciążona  i  ponownie 
obciążona.

7

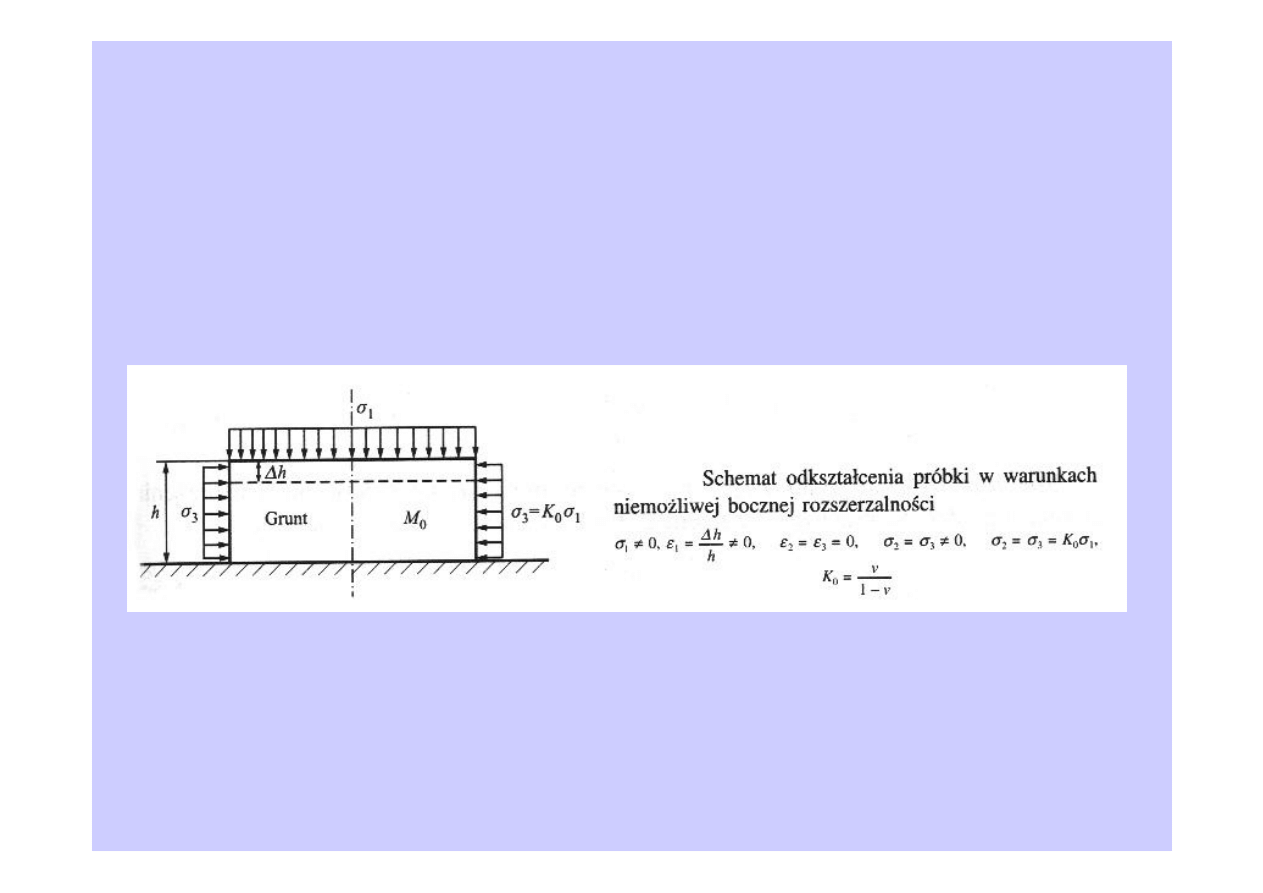
Próbka w edometrze znajduje się w 

jednoosiowym stanie odkształcenia

:

εεεε

1

> 0; 

εεεε

2

= 

εεεε

3

= 0

i w 

trójosiowym, obrotowo-symetrycznym stanie naprężenia

:

σσσσ

1

> 

σσσσ

2

= 

σσσσ

3  

> 0

K

0

- współczynnik rozporu (parcia) bocznego;  

ν

- współczynnik Poissona

8

Krzywe  konsolidacji  dla  kolejnych 
stopni obciążenia próbki

9

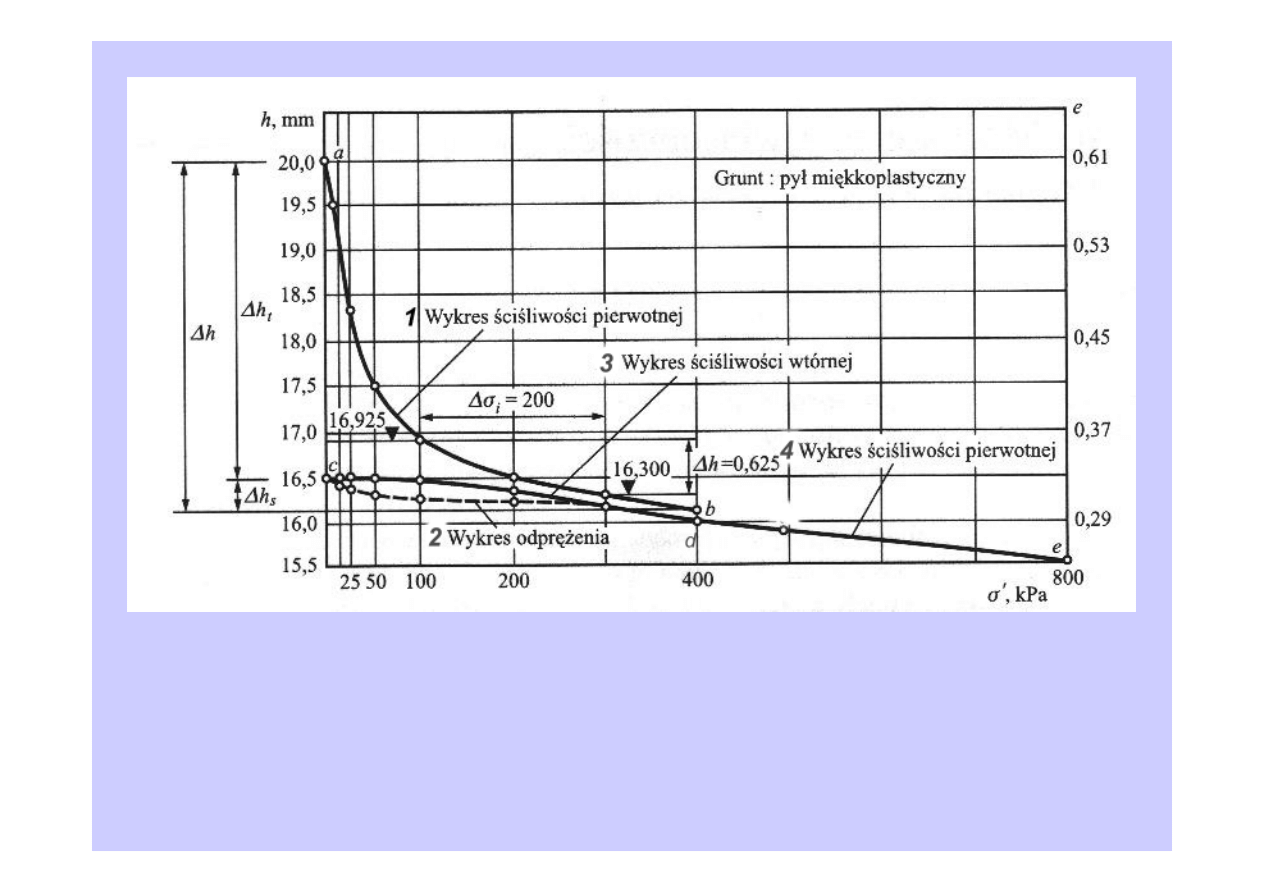
Krzywa ściśliwości dla badania z odciążeniem (z pętlą 

histerezy

)

∆∆∆∆

h - całkowite osiadanie próbki w zakresie 0 - 400 kPa, 

∆∆∆∆

h

t

- osiadanie trwałe (po odprężeniu), 

∆∆∆∆

h

s

- osiadanie sprężyste, h - wysokość próbki, e - wskaźnik porowatości

(ab)

(cd)

(bc)

(de)

10

Edometrycznym modułem  ściśliwości  (pierwotnej,  wtórnej,  odprężenia)

nazywamy stosunek przyrostu (dodatniego - dla M

0

i M, lub ujemnego – dla    ) osiowego naprężenia 

∆σ

i

do jednostkowej zmiany wysokości (odkształcenia) próbki ε

i

w warunkach niemożliwej bocznej 

rozszerzalności, po zakończeniu konsolidacji próbki

(

)

[MPa]

       

h

h

h

h

h

M

,

M

,

M

i

i

i

i

i

i

i

i

−

⋅

−

=

=

−

−

−

−

1

1

1

1

0

σσσσ

σσσσ

∆∆∆∆

σσσσ

∆∆∆∆

M

0

- edometryczny moduł  ściśliwości  pierwotnej  - odcinki  krzywej  ściśliwości  1 (a-b)  i  4  (d-e);   

M - edometryczny moduł ściśliwości wtórnej - krzywa 3 (c-d);       - edometryczny moduł odprę-
ż

enia - krzywa  2 (b-c); 

∆σ

∆σ

∆σ

∆σ

i

- przyrost  naprężenia; 

∆∆∆∆

h

i

- zmiana  wysokości  próbki; h

i-1

- wysokość 

próbki przed przyłożeniem i-tego stopnia obciążenia 

Ze  względu na  krzywoliniowy  charakter wykresu  moduły edometryczne nie  są 
wielkościami  stałymi  dla  danego  gruntu,  lecz  zależą  od  zakresu  naprężeń,  dla 
którego  zostały  wyznaczone  oraz  od  stanu  gruntu  (I

D

,  I

L

).  Dysponując  krzywą 

ś

ciśliwości można więc wyznaczyć szereg wartości modułów dla interesujących 

nas  zakresów  naprężeń.  Znając  moduły  ściśliwości  gruntów  występujących  w 
podłożu można obliczyć osiadanie fundamentu, korzystając z przekształconego 
wzoru na moduł:

M

M

h

h

s

⋅

=

=

σσσσ

∆∆∆∆

M

11

Korzystając  z  krzywej  ściśliwości  z  powyższego  wykresu  obliczmy  wartości 
edometrycznych    modułów  ściśliwości  pierwotnej  i  wtórnej  dla  przedziału 
naprężeń  100 

÷

300  kPa  (

∆σ

∆σ

∆σ

∆σ

i

=  200  kPa).  Niezbędne  wysokości  próbki  należy 

odczytać bezpośrednio z wykresu.

Edometryczny moduł ściśliwości pierwotnej:

h

i-1

= 16,925 mm; h

i

= 16,30 mm; 

∆∆∆∆

h

i

= 16,925 - 16,30 = 0,625 mm

Edometryczny moduł ściśliwości wtórnej:

h 

i-1

= 16,50 mm; h

i

= 16,20 mm;

∆∆∆∆

h

i

= 16,50 - 16,20 = 0,30 mm

Porównując wartości obu modułów widać, że obowiązuje zależność:

M

0i 

< M

i

kPa

  

5416

625

,

0

925

,

16

200

M

)

300

100

(

0

====

⋅⋅⋅⋅

====

−−−−

kPa

  

11000

30

,

0

50

,

16

200

M

)

300

100

(

====

⋅⋅⋅⋅

====

−−−−

12

Na  osi  pionowej  krzywej  ściśliwości  zwykle  są  naniesione  wysokości  próbki, 
zmieniające się w procesie obciążania/odciążania próbki. Można tam również, po 
wykonaniu 

odpowiednich 

przeliczeń, 

odczytywać 

wartości 

wskaźnika

porowatości  e.  Zależność  pomiędzy  wskaźnikiem  porowatości,  a  wysokością 
próbki w warunkach edometrycznych można wyprowadzić w następujący sposób

h

1

(e

1

)

h

0

(e

0

)

W edometrze: F = const; V

s

= const

Wskaźnik porowatości e = V

p

/V

s

, czyli

V

p

= eV

s

Na początku badania objętość próbki jest równa:

V

0

= h

0

F = V

s

+ V

p

= V

s

+e

0

V

s

= V

s

(1+e

0

)

Po zmniejszeniu wysokości do h

1

mamy:

V

1

= h

1

F = V

s

+ V

p

= V

s

+e

1

V

s

= V

s

(1+e

1

)

Po porównaniu obu wyrażeń i wyznaczeniu e

1

otrzymamy:

0

0

s

e

1

F

h

V

      

++++

⋅⋅⋅⋅

====

⇒

⇒

⇒

⇒

1

1

s

e

1

F

h

V

      

++++

⋅⋅⋅⋅

====

⇒

⇒

⇒

⇒

((((

))))

1

e

1

h

h

e

0

0

1

1

−−−−

++++

====

13

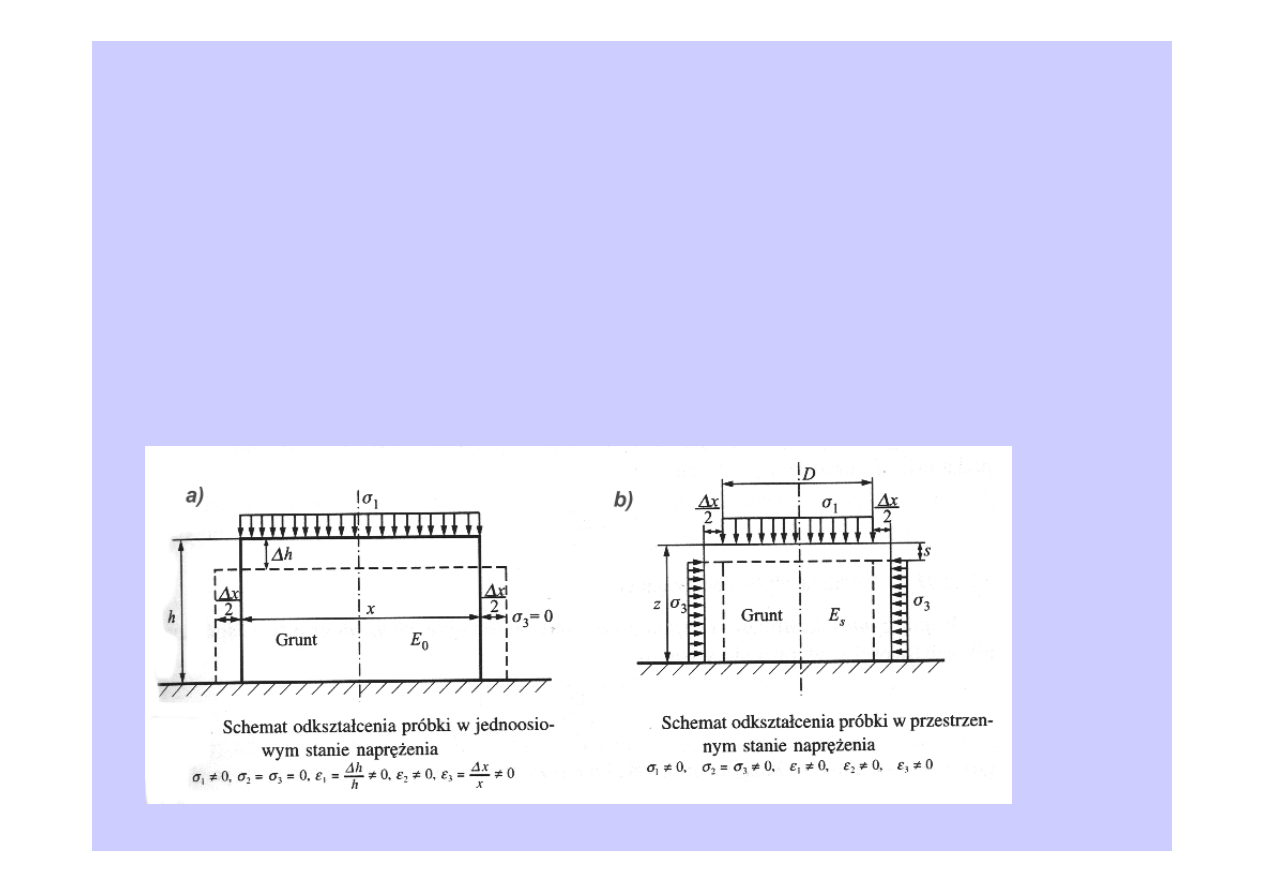
Parametry  ściśliwości  określa  się  również  dla  innych  stanów  odkształcenia  i  na-
prężenia; i tak:

-

moduły  odkształcenia  E

0

i  E

wyznacza  się  w  warunkach  możliwej  bocznej 

rozszerzalności gruntu, w jednoosiowym stanie naprężenia - rys. a;

-

moduł  podatności  podłoża  E

s

wyznacza  się  w  warunkach  ograniczonej  bocznej 

rozszerzalności  gruntu  (w  warunkach  naturalnego  zalegania  w  podłożu  boczna 
rozszerzalność  wyodrębnionego  myślowo  elementu  jest  ograniczona  przez 
elementy sąsiednie),  w  warunkach przestrzennego stanu naprężenia - rys b:

14

Pomiędzy  edometrycznymi  modułami  ściśliwości  M

0

i  M oraz  modułami 

odkształcenia E

0

i E istnieje związek:

(

) (

)

νννν

νννν

νννν

δδδδ

−

−

⋅

+

=

=

=

1

2

1

1

0

0

M

E

M

E

oraz ( 

ββββ

-

wskaźnik skonsolidowania

):

M

M

E

E

0

0

=

=

ββββ

W  praktyce  wykorzystuje  się  również  pojęcie 

współczynnika  ściśliwości  - a

, 

który wyraża stosunek zmiany 

wskaźnika porowatości gruntu - ∆e

i

,

do przyrostu 

naprężenia 

∆σ

∆σ

∆σ

∆σ

i

wywołującego tą zmianę :

]

MPa

[

e

a

i

i

1

        

σσσσ

∆∆∆∆

∆∆∆∆

=

Pomiędzy współczynnikiem ściśliwości i modułem edometrycznym istnieje zwią-
zek.  Wydzielmy  „myślowo”  z  próbki  gruntu  znajdującej  się  w  edometrze  na 
początku badania element o polu podstawy 

A = 1

oraz objętości zawartego w nim 

szkieletu 

V

s

=  1

(patrz  rysunek).  Wówczas  objętość  porów  jest  równa  wskaźni-

kowi porowatości 

e

0

zaś wysokość próbki jest 

h

0

=1 + e

0

15

Po zwiększeniu obciążenia o 

∆

σσσσ

i

objętość porów zmniejszy się o 

∆∆∆∆

e

i

= e

0

- e

i

; o 

tyle właśnie zmniejszy się wysokość elementu przy stałej objętości szkieletu, bo 

    

∆∆∆∆

h

i

= h

0

- h

i

= 

∆∆∆∆

e

i

Wykorzystując wzór na edometryczny moduł ściśliwości otrzymamy poszuki-
wany związek:

i

i

i

i

i

i

a

e

e

)

e

(

h

h

M

0

0

0

0

1

1

+

=

+

=

⋅

=

∆∆∆∆

σσσσ

∆∆∆∆

∆∆∆∆

σσσσ

∆∆∆∆

16

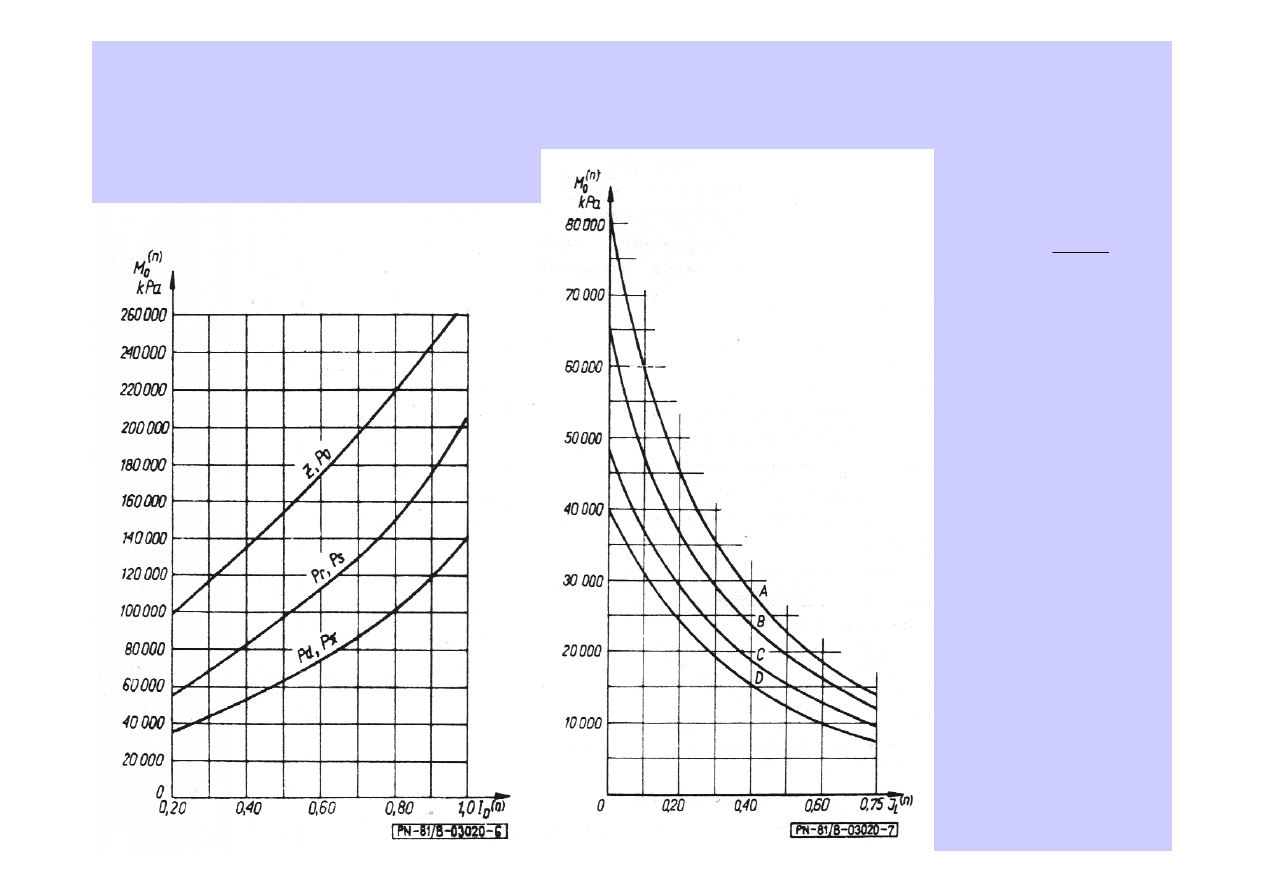
Jako  wartości  porównawcze  podaje  się,  za  normą  PN-81/B-03020,  wykresy 
edometrycznych  modułów  ściśliwości  dla  różnych  typów  gruntów  sypkich  i 
spoistych.

A - grunty  spoiste 
morenowe  skonso-
lidowane,

B - inne grunty spo-
iste skonsolidowane 
oraz spoiste moreno-
we 

nieskonsolido-

wane,

C - inne grunty spo-
iste  nieskonsolido-
wane,

D - iły,  niezależnie 
od genezy

ββββ

====

)

n

(

0

)

n

(

M

M

17

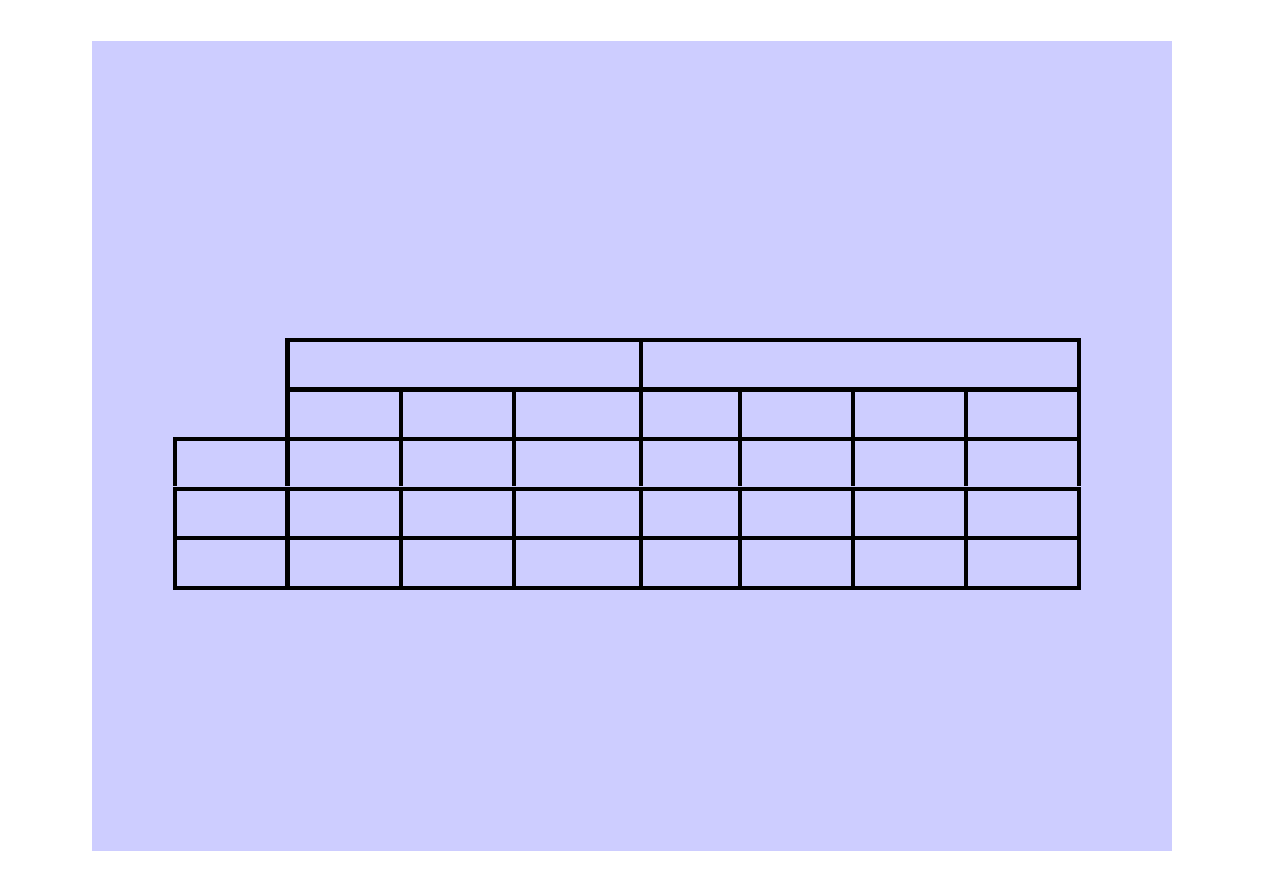
Grunty niespoiste

Grunty spoiste

Ż, Po Pr,Ps Pd,Pπ

A

B

C

D

ν

0,20

0,25

0,30

0,25

0,29

0,32

0,37

δ

0,90

0,83

0,74

0,83

0,76

0,70

0,57

β

1,0

0,90

0,80

0,90

0,75

0,60

0,80

Wartości parametrów zależne od rodzaju gruntu