ALGEBRA

1

ALGEBRA

Algebra

WYKŁAD 12

ALGEBRA

2

ALGEBRA

Definicja

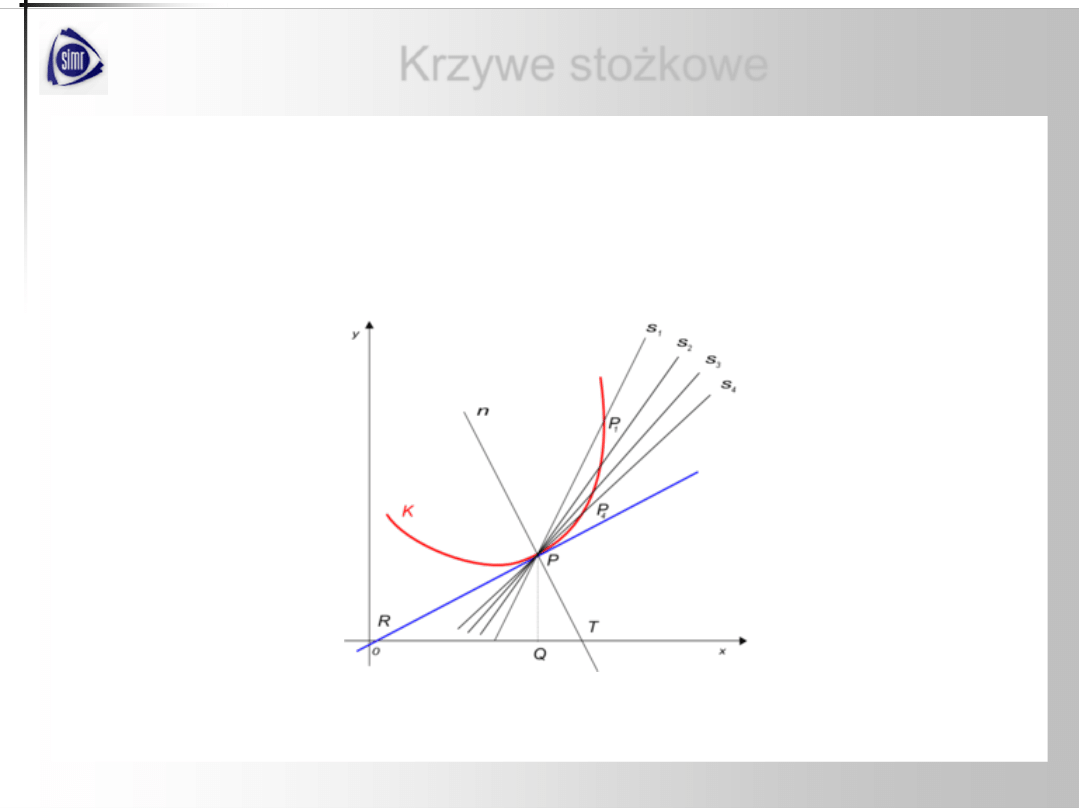
Prosta styczna

do krzywej

K

w punkcie

P

jest to prosta

,

będąca

granicznym położeniem siecznych

s

k

przechodzących przez

punkty

P

i

P

k

gdy punkt

P

k

dąży

(

zbliża się

)

do punktu

P

po krzywej

K.

Do wyznaczania równań stycznych do krzywych wykorzystuje się narzędzia
analizy matematycznej

. (

Więcej w przyszłym semestrze



.)

Krzywe stożkowe

styczna

ALGEBRA

3

Krzywe stożkowe

Równanie krzywej stożkowej

Równanie stycznej

Okrąg

Elipsa

Hiperbola

Parabola

1

)

(

)

(

2

2

0

2

2

0









b

y

y

a

x

x

2

2

0

2

0

)

(

)

(

r

y

y

x

x









1

)

(

)

(

2

2

0

2

2

0









b

y

y

a

x

x

)

(

2

)

(

0

2

0

x

x

p

y

y







2

0

0

1

0

0

1

)

)(

(

)

)(

(

r

y

y

y

y

x

x

x

x













Równania stycznych do krzywych w punkcie

P(x

1

,y

1

)

należącym do krzywej

1

)

)(

(

)

)(

(

2

0

0

1

2

0

0

1













b

y

y

y

y

a

x

x

x

x

1

)

)(

(

)

)(

(

2

0

0

1

2

0

0

1













b

y

y

y

y

a

x

x

x

x

)

)(

(

)

)(

(

0

0

1

0

0

1

x

x

x

x

p

y

y

y

y











ALGEBRA

4

ALGEBRA

Uwagi

Równanie stycznej do okręgu można wyznaczyć wykorzystując
warunki:



odległość stycznej od środka okręgu jest równa długości
promienia okręgu



styczna jest prostopadła do promienia zawierającego punkt
styczno

ści

Styczna do elipsy (lub okręgu) jest prostą mającą z krzywą
dokładnie jeden punkt wspólny (czyli układ równań opisujących
krzywą i prostą ma dokładnie jedno rozwiązanie).

Prosta (nierównoległa do osi paraboli) jest styczna do paraboli
wtedy i tylko wtedy, gdy ma z nią tylko jeden punkt wspólny.

Krzywe stożkowe

ALGEBRA

5

ALGEBRA

Równania parametryczne krzywych stożkowych

Definicja

Układ równań

x = f

1

(t)

y = f

2

(t)

gdzie

t



T



R

,

f

1,

f

2

są funkcjami ciągłymi na

T

definiuje krzywą

na

płaszczyźnie.

Równania te nazywamy równaniami parametrycznymi krzywej,
zaś

t

parametrem.

Uwaga

Ta sama krzywa może być definiowana za pomocą różnych
przedstawie

ń parametrycznych.

Krzywe stożkowe

ALGEBRA

6

Krzywe stożkowe

Równanie krzywej w postaci

kanonicznej

Równania parametryczne

krzywej

Okrąg

Elipsa

Hiperbola

Parabola

1

)

(

)

(

2

2

0

2

2

0









b

y

y

a

x

x

2

2

0

2

0

)

(

)

(

r

y

y

x

x









1

)

(

)

(

2

2

0

2

2

0









b

y

y

a

x

x

)

(

2

)

(

0

2

0

x

x

p

y

y







)

2

,

0

[

sin

cos

0

0



















t

t

r

y

y

t

r

x

x

)

2

,

0

[

sin

cos

0

0



















t

t

b

y

y

t

a

x

x

R

t

t

b

y

y

t

a

x

x

















sinh

cosh

0

0

R

t

t

y

y

p

t

x

x



















0

2

0

2

ALGEBRA

7

ALGEBRA

Definicja

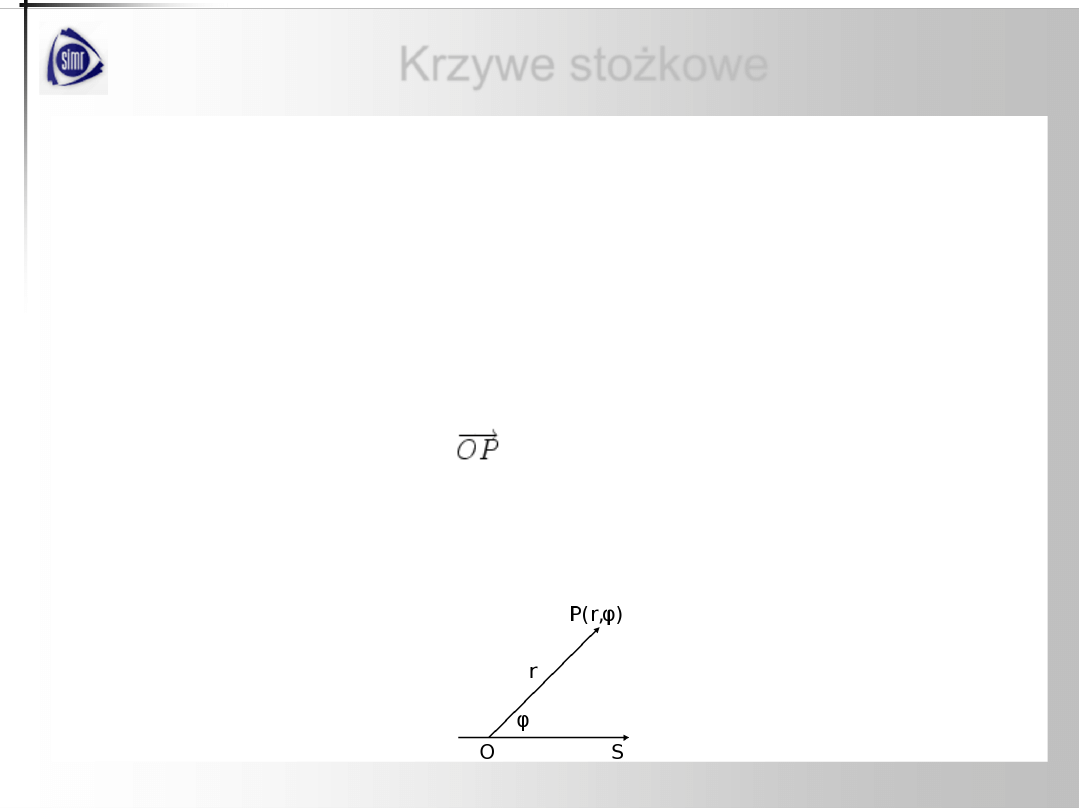
Układ współrzędnych biegunowych (polarnych) – to układ
współrzędnych na płaszczyźnie wyznaczony przez pewien punkt

O

zwany biegunem oraz

półprostą

O

S

o początku w punkcie

O

zwaną osią

biegunową, w którym każdemu punktowi

P

płaszczyzny przypisujemy

jego współrzędne biegunowe:



promień wodzący punktu

P

-

jego odległość

|OP|

od bieguna,



amplituda punktu

P

-

wartość kąta skierowanego pomiędzy

półprostą

O

S

a wektorem

.

Dla jednoznaczności przyjmuje się, że współrzędne bieguna

O

są równe

(0,0).

O amplitudzie zakładamy, że

0





<

2π

,

(

lub

- π







π

).

Krzywe stożkowe

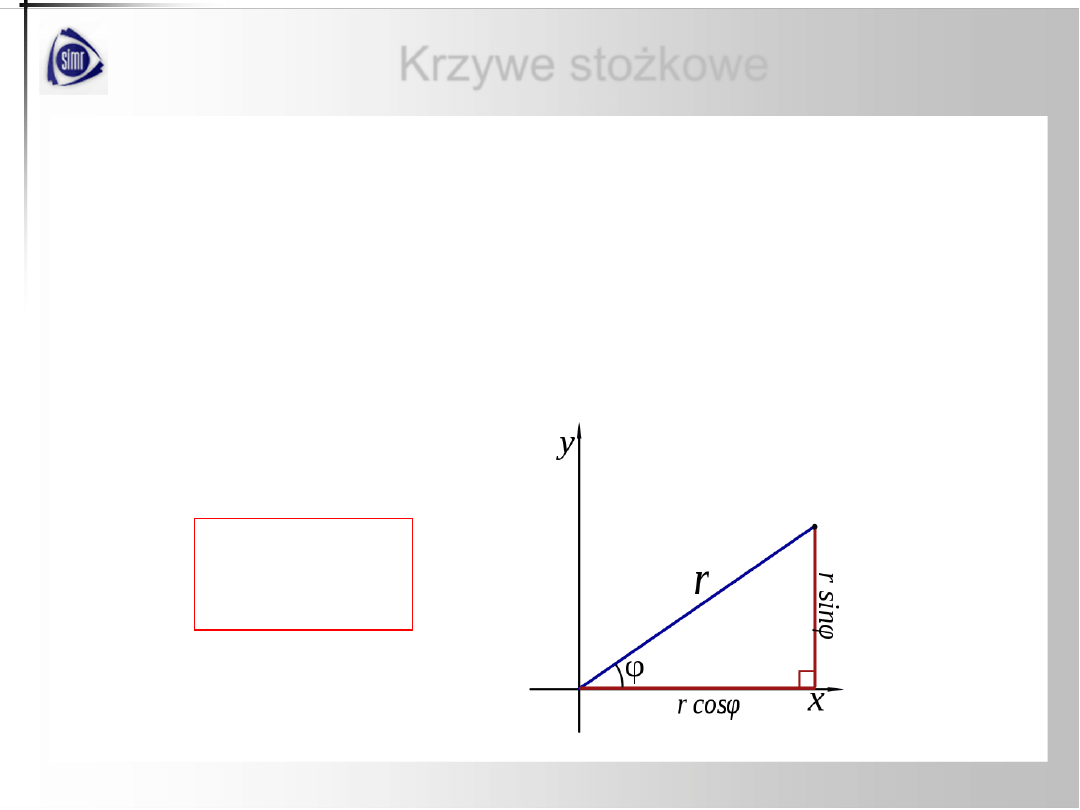
ALGEBRA

8

ALGEBRA

Definicja

Rozważmy dwa układy współrzędnych na płaszczyźnie:
układ kartezjański

Oxy

oraz układ biegunowy z biegunem

O

i osią

biegunową

Ox

.

Dla danego wektora wodzącego

r



0

i amplitudy





[0, 2π)

punktu

P

,

przejście od systemu polarnego do systemu kartezjańskiego określają
wzory

:















sin

cos

r

y

r

x

P

Krzywe stożkowe

ALGEBRA

9

ALGEBRA

R

ównanie

0

,

0

,

cos

1









e

p

e

p

r



przedstawia



okrąg dla

e = 0

,



elipsę dla

0 <

e < 1

,



parabolę dla

e = 1

,



hiperbolę dla

e > 1.

Początek układu współrzędnych jest środkiem okręgu i wspólnym
ogniskiem pozostałych stożkowych.
Na osi biegunowej leży oś wielka elipsy, oś rzeczywista hiperboli i oś
symetrii paraboli.

Stała

p

jest promieniem okręgu i półparametrem.

Stała

e

jest mimośrodem.

Krzywe stożkowe

ALGEBRA

10

Krzywe stożkowe

hiperbola

parabola

elipsa

okrąg

p

F

ALGEBRA

11

ALGEBRA

Zadanie1

znaleźć równanie stycznej do okręgu

0

10

2

2

2









y

y

x

x

w punkcie

P(2 , 0).

Krzywe stożkowe

ALGEBRA

12

ALGEBRA

Zadanie 2

Napisz równanie paraboli o wierzchołku w początku układu
współrzędnych i ognisku w punkcie

F(4 , 0).

Krzywe stożkowe

ALGEBRA

13

ALGEBRA

Zadanie 3

Dla jakich wartości parametru

m

prosta

y = mx + 2

jest styczna

do paraboli

y

2

= 4x?

Krzywe stożkowe

ALGEBRA

14

ALGEBRA

Zadanie 4

Z punktu

P(– 2 , 0)

poprowadź styczne do paraboli

y

2

= 8x

.

Krzywe stożkowe

ALGEBRA

15

ALGEBRA

Zadanie 5

Znajdź półosie i środek symetrii hiperboli:

4x

2

– y

2

– 16x – 2y – 1 = 0.

Krzywe stożkowe

ALGEBRA

16

ALGEBRA

Zadanie 6

Napisz równanie hiperboli o ogniskach leżących w wierzchołkach
osi wielkiej elipsy

16x

2

+ 25y

2

= 400

i kierownicach przechodzących przez ogniska danej elipsy.

Krzywe stożkowe

ALGEBRA

17

ALGEBRA

Zadanie 7

Elipsa jest styczna do osi

0y

w punkcie

A(0, 3)

i

przecina oś

0x

w punktach

B(3, 0)

i

C(7, 0).

Znajdź równanie tej elipsy, jeżeli jej osie są równoległe do osi układu
współrzędnych.

Krzywe stożkowe

ALGEBRA

18

ALGEBRA

Zadanie 8

Punkty

A(-6 , -4)

i

B(8 , -3)

należą do elipsy, której osiami symetrii są

osie układu. Napisz równanie tej elipsy.

Krzywe stożkowe

ALGEBRA

19