1

00510 Mechanika relatywistyczna D

TEORIA

00510

Mechanika relatywistyczna D

Stałość prędkości światła.

Dylatacja czasu, kontrakcja długości.

Równoważność masy i energii.

Energia i pęd w ujęciu relatywistycznym.

Teoria względności.

Instrukcja dla zdającego
1.

Proszę sprawdzić, czy arkusz teoretyczny zawiera 22
stron. Ewentualny brak należy zgłosić.

2.

Do arkusza może być dołączona karta wzorów i sta-
łych fizycznych. Jeśli jest, należy ją dołączyć do od-
dawanej pracy.

3.

Proszę uważnie i ze zrozumieniem przeczytać zawar-
tość arkusza.

4.

Proszę precyzyjnie wykonywać polecenia zawarte w
arkuszu: rozwiązać przykładowe zadania, wyprowa-
dzić wzory, gdy jest takie polecenie.

5.

Proszę analizować wszelkie wykresy i rysunki pod
kątem ich zrozumienia.

6.

W trakcie obliczeń można korzystać z kalkulatora.

7.

Wszelkie fragmenty trudniejsze proszę zaznaczyć w
celu ich późniejszego przedyskutowania.

8.

Uzupełniaj wiadomości zawarte w arkuszu o informa-
cje zawarte w Internecie i dostępnej ci literaturze.

9.

Znak * dotyczy wiadomości wykraczających poza
ramy programu „maturalnego”.

ś

yczymy powodzenia!

(Wpisuje zdający przed rozpoczęciem pracy)

PESEL ZDAJĄCEGO

Aktualizacja

Maj

ROK 2008

Dane osobowe właściciela arkusza

2

00510 Mechanika relatywistyczna D

TEORIA

Temat: 46

Przybliżony charakter mechaniki klasycznej.

1.

Mechanika, oparta na niutonowskich zasadach dynamiki, nazywa się mechaniką klasyczną.
Mechanika ta daje poprawny opis ruchów wszystkich ciał makroskopowych, z którymi mamy
do czynienia na Ziemi. śadnego doświadczenia ani żadnej teorii fizycznej nie można jednak
traktować jako prawdy absolutnej. Używając terminu „poprawny opis” mamy na myśli opis
pozostający w zgodzie z naszymi doświadczeniami i pomiarami dokonywanymi oczywiście
ze skończoną dokładnością.

2.

Mechanika klasyczna jest jedną z najdoskonalszych teorii fizycznych i jej stworzenie było
niewątpliwie triumfem myśli ludzkiej. Bez znajomości mechaniki klasycznej niemożliwy był-
by skok techniczny, jakiego dokonała ludzkość w ostatnich dwu stuleciach, ani też ogromny
rozwój współczesnej fizyki w wieku dwudziestym.

3.

Fakt, że mechanika klasyczna wyjaśnia tak wiele zjawisk nie tylko w świecie, w którym obra-
camy się na co dzień, ale także w skali naszego Układu Słonecznego, skłaniał dziewiętnasto-
wiecznych fizyków do przeceniania jej możliwości.. Wydawało się, że na gruncie praw me-
chaniki oraz stworzonej pod koniec XIX wieku teorii elektromagnetyzmu można będzie wyja-
ś

nić wszystkie zjawiska fizyczne poczynając od zjawisk w skali atomowej, a kończąc na zja-

wiskach w skali kosmicznej. Niektórzy wielcy fizycy wręcz uważali, że proces poznawania
podstawowych praw przyrody został w zasadzie zakończony. Tymczasem pod koniec wieku
XIX okazało się, że dwie podstawowe teorie fizyczne - mechanika i elektromagnetyzm - nie
są ze sobą zgodne. Wszystkie prawa mechaniki klasycznej mają identyczną postać we wszyst-
kich układach inercjalnych (jest to treść zasady względności Galileusza - Newtona). Nato-
miast podstawowe prawa teorii elektromagnetyzmu - równania Maxwella - nie mają tej wła-
ś

ciwości. Początkowo przypuszczano, że błąd tkwi w teorii elektromagnetyzmu. Starano się

więc tak ją zmodyfikować, by jej równania miały identyczną postać we wszystkich układach
inercjalnych. Zmodyfikowana teoria elektromagnetyzmu prowadziła jednak do wniosków
sprzecznych z doświadczeniem. Okazało się, że trzeba zmodyfikować nie teorię elektroma-
gnetyzmu, lecz pozornie doskonałą mechanikę klasyczną oraz wzory wiążące ze sobą spo-
strzeżenia obserwatorów w różnych układach inercjalnych. Wykazał to w 1905 roku Einstein.
Teorię przez niego stworzoną nazywamy szczególną teorią względności, a zmodyfikowaną w
myśl teorii względności mechanikę - mechaniką relatywistyczną.

4.

Mechanika klasyczna pozostaje w doskonałej zgodzie z mechaniką relatywistyczną, we
wszystkich układach odniesienia, w których prędkości poruszających się ciał są bardzo małe
w porównaniu z prędkością światła w próżni W zakresie prędkości ciał, porównywalnych z
prędkością światła, obie teorie prowadzą do zupełnie różnych wniosków.

Fakt ten stał się początkowo przyczyną wielu ataków na teorię względności. Przeciwnicy tej
teorii zarzucali jej brak logiki i niezgodność ze zdrowym rozsądkiem. Trudno im było uwie-
rzyć, że tak doskonała mechanika klasyczna może zostać podważona. Tymczasem to oni wy-
kazywali brak logiki i zdrowego rozsądku.

5.

Mechanika klasyczna zrodziła się z obserwacji ruchów ciał makroskopowych na Ziemi i w
Układzie Słonecznym i do opisu takich ruchów została stworzona. Brak jest jakichkolwiek
podstaw do przypuszczenia, że musi ona obowiązywać w zakresie prędkości bliskich prędko-
ś

ci światła. Trzeba sobie zdawać sprawę, że teoria względności wcale nie obala mechaniki

klasycznej, lecz jedynie kwestionuje stosowalność tej teorii w zakresie prędkości, zupełnie nie-
znanej jej twórcom.

3

00510 Mechanika relatywistyczna D

TEORIA

6.

Również próby zastosowania mechaniki klasycznej do opisu mikroświata - cząstek elemen-
tarnych, atomów i cząsteczek - skończyły się niepowodzeniem. W tym zakresie mechanika
klasyczna została zastąpiona mechaniką kwantową, której początek dali Planck i Bohr. Me-
chanika kwantowa prowadzi do wniosków równie, a może bardziej niezgodnych ze „zdrowym
rozsądkiem” niż mechanika relatywistyczna. Jednak mechanika kwantowa zastosowana do
opisu ciał makroskopowych daje zgodne wyniki z mechaniką klasyczną.

7.

Zarówno mechanika relatywistyczna, jak mechanika kwantowa są w obecnej chwili równie
dobrze ugruntowane doświadczalnie, jak mechanika klasyczna w XIX wieku. Nie da się
wręcz wyliczyć wszystkich faktów doświadczalnych, potwierdzających obie te teorie. Nie
oznacza to oczywiście, że teorie te stanowią ostatnie słowo fizyki. Można jednak z całą pew-
nością stwierdzić, że żadna doskonalsza teoria nie może ich zastąpić, a raczej obalić, podobnie
jak ani mechanika relatywistyczna ani mechanika kwantowa nie obaliły mechaniki klasycz-
nej. Każda doskonalsza teoria będzie zawierać z pewnością zarówno mechanikę klasyczną,
jak i mechanikę kwantową oraz szczególną teorię względności jako przybliżone teorie obo-
wiązujące dla określonego zakresu zjawisk. Mechanika klasyczna musi pozostać w każdej
teorii fizycznej jako przybliżona teoria ruchów ciał makroskopowych, poruszających się z
niewielkimi prędkościami.

8.

Trzeba mieć na uwadze fakt, że istnieją dwie teorie względności Einsteina: szczególna teoria
względności (skrót STW) i tak zwana ogólna teoria względności (OTW). W literaturze popu-
larnej, przez teorię względności rozumie się zazwyczaj teorię szczególną. My zajmować się
będziemy wyłącznie szczególną teorią względnością (STW) zawierającą mechanikę relatywi-
styczną, nie będziemy natomiast analizować ogólnej teorii względności (OTW), czyli teorii
grawitacji.

9.

Można by się zapytać, po co sobie głowę zawracać mechaniką relatywistyczną skoro więk-
szość prędkości z życia codziennego jest znacznie mniejsza od prędkości światła. Oto kilka
przyczyn stanowiących podsumowanie niniejszego tematu:

a)

ważnym przedmiotem badań fizyki jest światło, a światło ma prędkość v = c,

b)

teoria światła wywodzi się z teorii elektryczności. Ważne fakty elektryczne, takie jak pole
magnetyczne i indukcja elektromagnetyczna zależą od prędkości światła. Poprawne jest
stwierdzenie, że teoria elektryczności jest teorią relatywistyczną. Na przykład, najpierw trzeba
zrozumieć teorię względności, zanim można naprawdę zrozumieć teorię magnetyzmu,

c)

cząstki, którymi zajmuje się fizyka jądrowa i fizyka cząstek elementarnych, poruszają się z
prędkościami zbliżonymi (lub równymi) prędkości światła. Np. fotony i neutrina zawsze poru-
szają się z prędkością v =c,

d)

Nowoczesna astronomia ma wiele do czynienia z teorią względności. Odległe galaktyki poru-
szają się z prędkościami bliskimi prędkości światła. Nowe zjawiska, jak gwiazdy neutronowe,
pulsary, czarne dziury, wyraźnie objawiają efekty relatywistyczne,

e)

aby osiągnąć zrozumienie mechaniki kwantowej powinniśmy przedyskutować takie tematy
jak zjawisko fotoelektryczne i zjawisko Comptona, w których trzeba znać relatywistyczne
związki między energią, masą i pędem,

f)

zobaczymy, że teoria względności jawnie kłóci się ze zdrowym rozsądkiem i doświadczeniem
ż

ycia codziennego, pierwsza reakcja jest: ona nie może być prawdziwa ! Ze względów intelek-

tualnych i filozoficznych jest ważne, aby taką sytuację poddać szczególnej uwadze. Nawet
dziś jest jeszcze paru intelektualistów, którzy nie akceptują wszystkich konsekwencji tej teorii.
To jest nasz pierwszy przykład zjawisk przyrody, które otwarcie naruszają zdrowy rozsądek.

4

00510 Mechanika relatywistyczna D

TEORIA

Temat: 47

Stałość prędkości światła.

1.

Centralnym paradoksem jest to, że prędkość światła musi być taka sama dla wszystkich
obserwatorów. Na rys. 1 pokazano przykład tego, co narusza zdrowy rozsądek i jest
sprzeczne z naszym doświadczeniem.

Pojazd kosmiczny B

r

v

B

Impuls światła

r

v

impulsu

A
ZIEMIA


Rys. 1

Obserwator A na Ziemi i obserwator B w pojeździe kosmicznym jednocześnie mierzą
prędkość tego samego impulsu światła.

Przypuśćmy, że pojedynczy impuls (czyli błysk) światła mija obserwatora A stojącego na
Ziemi. W tej samej chwili obserwator B, poruszający się z prędkością

r

v

B

, przesuwa się

obok i patrzy na ten sam impuls światła. Zgodnie z tym wszystkim, czego nauczyliśmy się
dotychczas, powinien on widzieć impuls światła biegnący wolniej, z prędkością

(1)

v

v

v

imp

imp

B

'

=

−

Jednak, gdyby przeprowadzić eksperyment, to nie tylko obserwator A zmierzyłby v

imp

= c,

gdzie c = 2 998 10

8

,

⋅

m

s

,

lecz również obserwator B zmierzyłby v

imp

'

= c i to dla tego samego impulsu, i w tej samej

chwili.

Innym przykładem byłoby dwóch obserwatorów, jeden spoczywający względem odległej
gwiazdy, a drugi poruszający się szybko ku gwieździe. Obaj uzyskują ten sam wynik:

v

c

ś

wiat a

ł

=

. Głównym punktem wyjścia w teorii względności Einsteina jest to, że prędkość

ś

wiatła jest zawsze c = 2 998 10

8

,

⋅

m

s

niezależnie od prędkości obserwatora i niezależnie

od prędkości źródła światła.

Einstein wytłumaczył ten „dziwny” wynik „dziwnymi” własnościami przestrzeni i czasu.
Postulował, że przestrzeń widziana przez poruszającego się obserwatora „kurczy się” w

kierunku 1

2

2

−

v

c

razy, i że czas mierzony przez poruszającego się obserwatora „zwal-

nia” tyle samo razy. Istotnie, Einstein „zoperował” przestrzeń i czas tak, aby:

∆

∆

x

t

c

'

'

=

5

00510 Mechanika relatywistyczna D

TEORIA

dla dowolnego impulsu światła widzianego przez dowolnego obserwatora poruszającego
się ze stałą prędkością (x’ i t’ są przestrzenią i czasem mierzonymi przez poruszającego
się obserwatora).

2.

*Doświadczenie Michelsona - Morleya.

Dopóki w 1905 roku nie została ogłoszona teoria względności Einsteina, większość fizy-
ków rozumowała, że musi istnieć jakiś ośrodek, w którym rozchodzą się fale światła, po-
dobnie jak powietrze jest ośrodkiem, w którym rozchodzą się fale dźwiękowe. Ten ośro-
dek dla fal świetlnych został nazwany eterem. W takim przypadku układ odniesienia, któ-
ry by spoczywał względem eteru, byłby wyróżnionym układem odniesienia. Tylko w tym
układzie odniesienia spełniona byłaby równość:

v

c

ś

wiat a

ł

=

. Dla obserwatora mającego

prędkość v względem eteru, prędkość światła, gdy obserwator porusza się w kierunku
ź

ródła światła byłaby równa (c + v). Uważano eter za ośrodek „fizyczny”, lecz nie mający

masy - koncepcja trudna do pojęcia, łagodnie mówiąc.
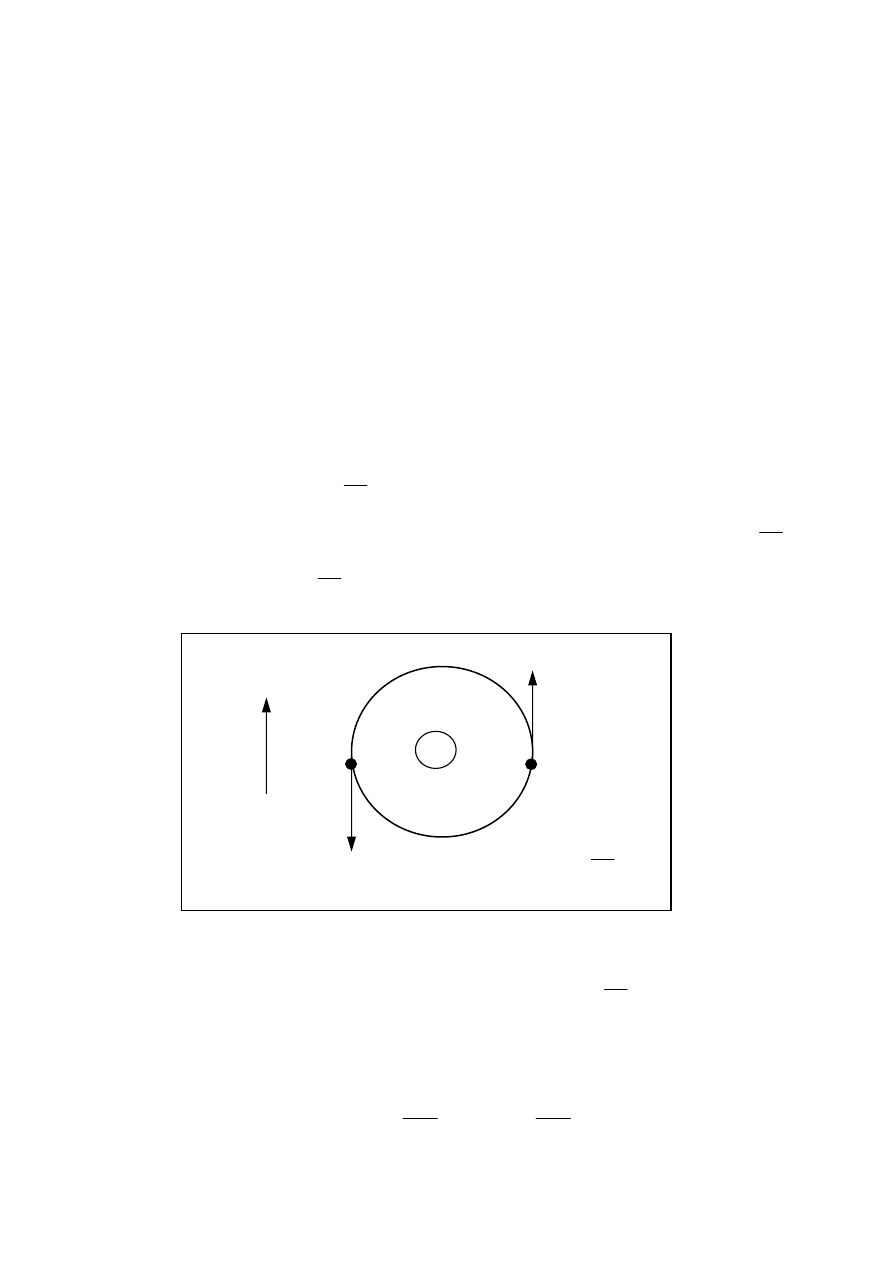
W latach osiemdziesiątych ubiegłego stulecia przeprowadzono doświadczenia, których
wyniki były spójne z zasadą, że światło biegnie z prędkością c, niezależnie od prędkości
ź

ródła lub obserwatora, a więc przeczyły hipotezie istnienia eteru. Ponieważ Ziemia poru-

sza się z prędkością v = 30

km

s

wokół Słońca, więc zwolennicy teorii eteru uważali, że

muszą być okresy w roku, kiedy Ziemia ma względem eteru prędkość co najmniej 30

km

s

(lub eter ma prędkość 30

km

s

względem Ziemi).

r

v

Z

r

v

eteru

Słońce

r

v

Z

v

Z

= 30

km

s

Rys. 2

Wówczas dla obserwatora na Ziemi (rys. 2) światło biegnące w tym samym kierunku co
eter miałoby prędkość (c + v) względem Ziemi , a światło biegnące w kierunku przeciw-

nym miałoby prędkość (c - v), gdzie v jest co najmniej równe 30

km

s

.

Zatem, zgodnie z prawem składania prędkości z punktu widzenia mechaniki Newtona,
prędkość światła będąc zmienną spowoduje, że czasy, w ciągu których promienie światła
przebędą odległość l wyniosą w obu wspomnianych przypadkach:

(1)

t

l

c

v

oraz

t

l

c

v

1

2

=

−

=

+

6

00510 Mechanika relatywistyczna D

TEORIA

A jeśli światło przebywa drogę l w kierunku prostopadłym do kierunku ruchu, to:

(2)

( )

t

c

l

v t

3

2

3

2

1

= ⋅

+ ⋅

skąd otrzymujemy

(3)

t

l

c

v

c

3

2

2

1

1

= ⋅

−

.

Sądząc, że t

1

, t

2

i t

3

są różne Michelson postanowił ujawnić te różnice obserwując obraz

interferencyjny W tym celu został skonstruowany specjalny interferometr, w którym bieg
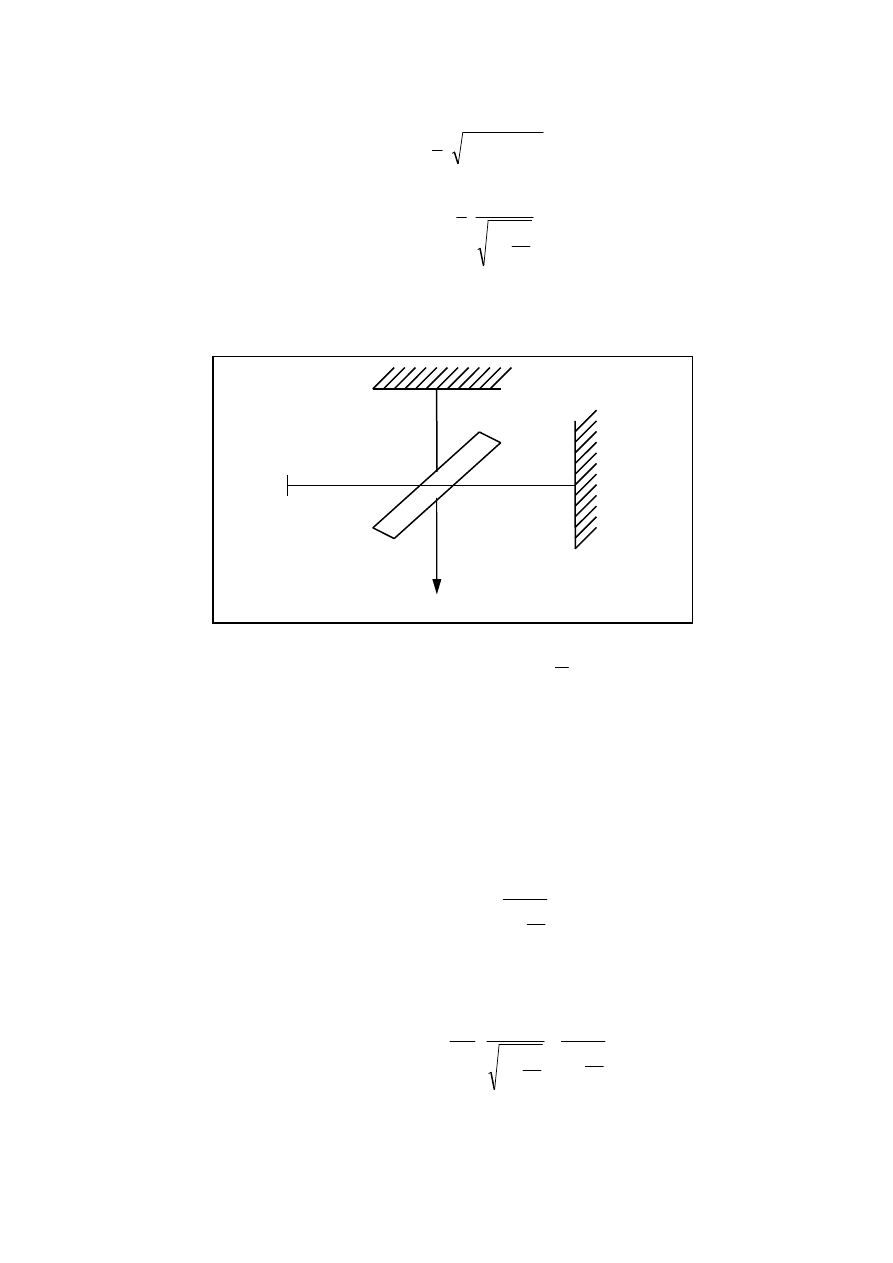
promieni wzajemnie się krzyżuje. Schemat interferometru Michelsona pokazuje rys. 3.

M’

S A M





S’
Rys. 3

Ze źródła światła S promienie świetlne padają pod kątem

π

4

na płasko - równoległościen-

ną i półprzepuszczalną płytkę A, która dzieli promienie na dwie wiązki wzajemnie prosto-
padłe. Każda z wiązek po odbiciu od płaskich zwierciadeł M i M’ ponownie pada na tę
samą płytkę. Część światła biegnie w kierunku źródła, a część trafia do punktu S’, w któ-
rym obserwuje się interferencję spowodowaną różnicą dróg przebytych przez promienie z
obu wiązek. Jeśli AM = AM’, to różnica dróg może wyniknąć tylko wskutek różnego cza-
su, w ciągu którego światło pokona te odcinki, biegnąc w jedną i drugą stronę. Obracając
interferometr, można uzyskać ustawienie jednego ramienia, np. AM równolegle do kie-
runku ruchu Ziemi. Wówczas czas, w ciągu którego światło pokona drogę AM tam i z
powrotem, według wzoru (1) , jest równy

(4)

t

t

t

l

v

c

= + =

⋅

−

1

2

2

2

2

1

Drugi promień przebędzie drogę AM’ tam i z powrotem w ciągu czasu 2 t

3

. Zatem różnica

czasów będzie wynosić:

(5)

∆

t

t

t

l

c

v

c

v

c

=

− =

⋅

−

−

−

























2

2

1

1

1

1

3

2

2

2

2

7

00510 Mechanika relatywistyczna D

TEORIA

Ponieważ ułamek

v

c

=

β

jest mały, to w przybliżeniu

(6)

∆

t

l

c

=

⋅

β

2

Po obrocie całego interferometru o kąt

π

2

znak

∆

t zmieni się i całkowite

∆

t

0

podwoi się

(7)

∆

t

l

c

0

2

2

=

⋅

β

Wówczas powinno nastąpić przesunięcie obrazu interferencyjnego o pewną część odległo-
ś

ci między maksimami. Dokładniej: zmiana czasu przebiegu światła powinna objawić się

jako zmiana obrazu interferencyjnego (amplitudy dwóch fal mogą się odjąć i dać zmniej-

szenie natężenia światła). Nawet wartość tak mała jak 30

km

s

już powinna dać wyraźnie

mierzalny efekt.
Jednak w doświadczenia Michelsona i Morleya nie udało się ujawnić żadnego przemiesz-

czenia prążków w obrazie interferencyjnym, przy obrocie przyrządu o kąt

π

2

. Ujemny re-

zultat wielokrotnie powtarzanego doświadczenia Michelsona i Morleya wykazał, że pręd-
kość światła nie zależy od stanu ruchu układu, w którym odbywa się pomiar. Wynik ten
jest sprzeczny z prawem składania prędkości w mechanice Newtona, która dla dużych
prędkości jest nieprzydatna.
Można by spodziewać się, że ta seria doświadczeń powinna mieć głęboki wpływ na Ein-
steina, gdy formułował swoje rozwiązanie problemu. Tak się jednak nie stało. Znacznie
więcej niepokoiły go niespójności między równaniami teorii elektromagnetyzmu i me-
chaniki klasycznej. Einstein z zainteresowaniem rozważał co się stanie, gdy ktoś będzie
gonił impuls świetlny i w końcu dogoni go biegnąc z prędkością v

c

≈

. Zajmował się

więc tym problemem, jakie zmiany w klasycznych pojęciach czasu i przestrzeni trzeba
wprowadzić, aby prędkość światła wydawała się jednakowa dla wszystkich obserwatorów
i aby równania teorii elektromagnetyzmu miały taką sama formę dla wszystkich obserwa-
torów poruszających się ze stałą prędkością względem siebie.

3.

Końcowe wnioski: Jak zobaczymy, rewizja pojęć przestrzeni i czasu, dokonana przez Ein-
steina, wynika wprost z dwóch podstawowych zasad:

a)

prędkość światła jest stała dla wszystkich obserwatorów, jest największą prędkością i
ż

adna cząstka z większą prędkością poruszać się nie może,

b)

musi być spełniona zasada względności Galileusza - Newtona, inaczej mówiąc - nie
może być wyróżnionego układu odniesienia ani nie istnieje sposób wyznaczenia pręd-
kości bezwzględnej.

Rzeczywiście, jeżeli zamkniemy oczy lecąc pasażerskim samolotem odrzutowym, bę-
dziemy odnosić to samo wrażenie jakbyśmy byli w spoczynku. Z zasady względności wy-
nika, ze nie ma takich doświadczeń fizycznych, które moglibyśmy przeprowadzić we-
wnątrz samolotu odrzutowego, aby wyznaczyć jego prędkość. Przez „wewnątrz samolotu”
rozumiemy całkowity brak kontaktu ze światem zewnętrznym.

8

00510 Mechanika relatywistyczna D

TEORIA

Temat: 48

Dylatacja czasu.

1.

Analizę elementów kinematyki relatywistycznej rozpoczniemy od zastosowania dwóch postu-
latów, które noszą nazwy:

◊

zasady względności Einsteina (wszystkie prawa przyrody są takie same we wszystkich in-
ercjalnych układach odniesienia),

◊

zasady stałości prędkości światła (prędkość światła w próżni jest taka sama we wszyst-
kich inercjalnych układach odniesienia i nie zależy od ruchu źródeł i odbiorników świa-
tła).

2.

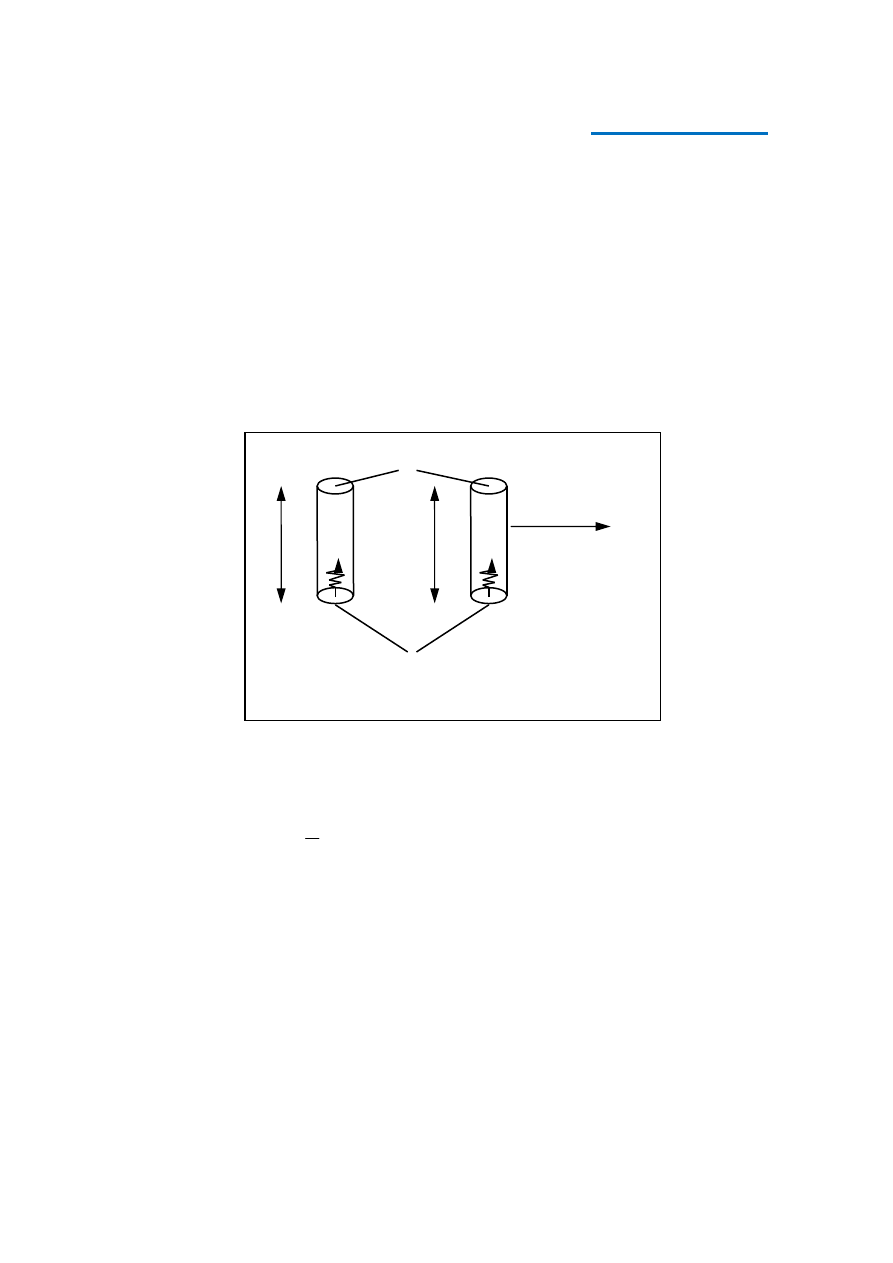
*Zrozumiemy dlaczego Einstein uważał za konieczne zmienić pojęcie czasu. Zastosujemy
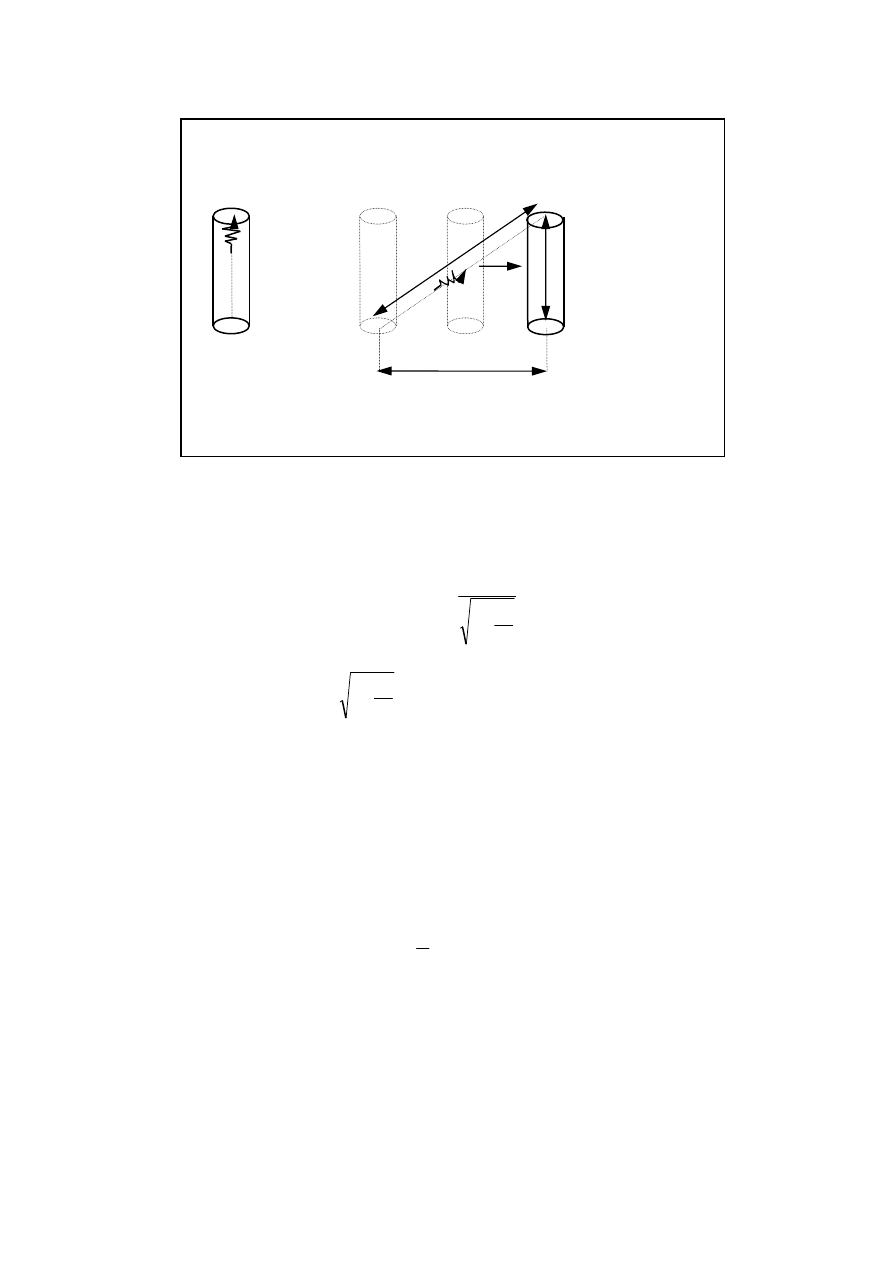
oba postulaty Einsteina do prostego rodzaju zegara zwanego „zegarem świetlnym”. Tworzą
go dwa równoległe zwierciadła, oddalone od siebie o stałą odległość L (rys. 1).

zwierciadła

t = 0

r

v

L

τ

⋅

c

A B

impulsy światła
Rys. 1

W każdym z dwóch zegarów (rys. 1) jest zamknięty impuls światła biegający tam i z powro-
tem. Niech

τ

będzie czasem potrzebnym, aby impuls światła, który wystartował z dolnego

zwierciadła, uderzył w zwierciadło górne. Za każdym razem, gdy światło uderza w zwiercia-
dło mamy „tyknięcie” zegara. Zaczynamy, gdy dwa zegary tykają synchronicznie. Czas mię-

dzy tyknięciami jest

τ

=

L

c

.

Niech teraz zegar B porusza się w prawo z prędkością

r

v ,jak na rys. 2. Najpierw możemy so-

bie postawić pytanie, czy będzie się wydawało, że poruszający się zegar ma taką samą długość
jak zegar A. Zgodnie z zasadą względności, obaj obserwatorzy są na równych prawach i obaj
powinni obserwować takie same efekty, to jest możliwe tylko wtedy, gdy dla obu obserwato-
rów oba zegary mają taką samą długość.
Pozostałą część dyskusji będziemy prowadzić z punktu widzenia obserwatora spoczywającego
względem zegara A. Taki obserwator widzi, że droga, którą impuls światła przebywa od jed-
nego końca do drugiego końca zegara B, jest dłuższa. Impuls światła B musi biec po przekąt-
nej (rys. 2) i zgodnie z zasadą stałości prędkości światła, musi poruszać się z taką samą pręd-
kością jak impuls światła w zegarze A.

9

00510 Mechanika relatywistyczna D

TEORIA

τ

sekund później

A B

c T

⋅

c

⋅

τ

r

v

v T

⋅

Rys. 2


Tak więc, aby dotrzeć do górnego zwierciadła, impuls światła B zużyje więcej czasu niż im-
puls światła A (według obserwatora A). Nazwijmy ten dłuższy czas T. Wówczas długość dro-
gi po przekątnej jest równa

c T

⋅

. Stosując twierdzenie Pitagorasa (rys. 2) otrzymamy

(1)

(

)

c T

v T

c

⋅

= ⋅

+ ⋅

2

2

2

(

)

(

)

τ

, skąd mamy

(2)

T

v

c

=

−

⋅

1

1

2

2

τ

W teorii względności czynnik

1

2

2

−

v

c

występuje tak często, że nadano mu symbol

γ

.

Według spoczywającego obserwatora, czas między tyknięciami poruszającego się zegara jest
równy T, co jest dłuższe od

τ

, czasu między tyknięciami gdy, którykolwiek zegar spoczywa.

Musimy dojść do wniosku, że każdy obserwator stwierdzi, iż poruszający się zegar tyka wol-
niej

γ

razy niż identyczny zegar spoczywający.

W równaniu (2)

τ

nazywa się czasem własnym. Jest to odstęp czasu między dwoma zdarze-

niami, które obserwator widzi tym samym punkcie przestrzeni. Wówczas T jest czasem mię-
dzy tymi zdarzeniami, zmierzonymi przez poruszającego się obserwatora (jego własnym ze-
garem).

(3)

τ

γ

= ⋅

1

T (czas własny)

Czas własny danego zegara jest czasem mierzonym przez obserwatorów, którzy poruszają się
wraz z zegarem. Obserwator poruszający się względem zegara stwierdzi, że zegar mierzy od-
stępy czasu

T

= ⋅

γ τ

według zegarów nieruchomych względem niego. Czy zegary zachowują

się w ten sposób ze względu na specjalną naturę światła ? Czy zwykłe zegary mechaniczne ,
których części poruszają się z prędkością znacznie mniejszą od prędkości światła, również
zwalniają w tym samym stosunku

γ

? Einstein powiedział, że tak, gdyż nie ma to nic wspól-

nego z naturą poszczególnego zegara - to wynika z samoistnej natury czasu.. Aby to zrozu-

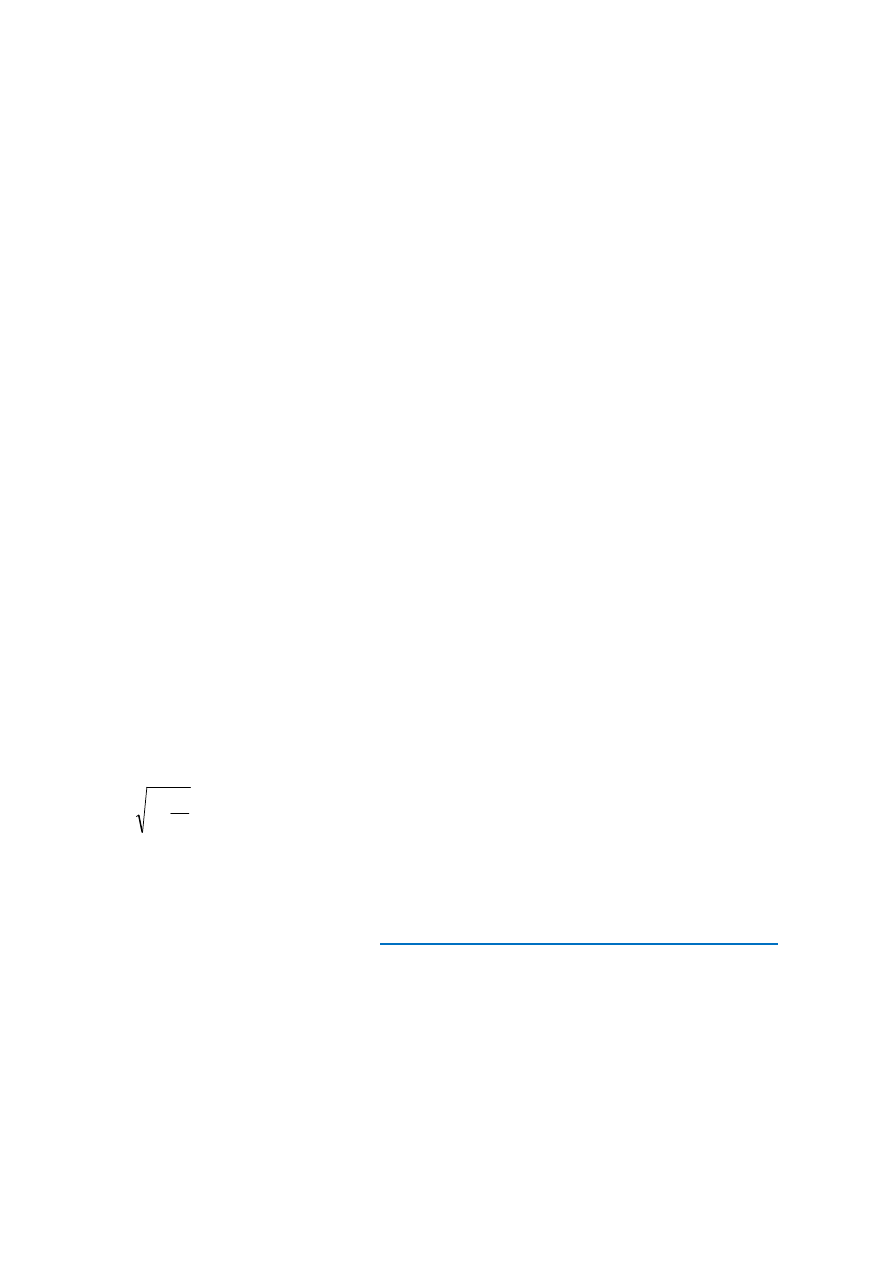
10

00510 Mechanika relatywistyczna D

TEORIA

mieć przypuśćmy, że zegar świetlny i zegarek ręczny razem podlegają przyspieszeniu, oba
wskazują identyczny czas. Później zostają pchnięte w bok z prędkością v i zegar świetlny
zwalnia, tak jak powinien, ale zegarek ręczny nie robi tego. Mielibyśmy wówczas prosty de-
tektor ruchu bezwzględnego: gdy zegary wskazują ten sam czas, są w spoczynku, gdy zegar
ś

wietlny spóźnia się - wiadomo, że są w ruchu. To oczywiście łamie zasadę względności, na

której opiera się cała nasza dyskusja.

Skoro dylatacja jest własnością samego czasu, nie tylko wszystkie poruszające się zegary
zwalniają, ale również wszystkie procesy fizyczne, jak np. reakcje chemiczne, są spowalniane,
gdy są w ruchu. Ponieważ życie polega na skomplikowanych reakcjach chemicznych, więc
ż

ycie byłoby również spowolnione w tym samym stosunku. Istotnie, gdyby starzenie się bio-

logiczne nie zwalniało w tym samym tempie, moglibyśmy przyspieszyć próbkę biologiczną,
która mierzy czas (np.. bicie serca), do prędkości poruszającego się zegara świetlnego i wtedy
zegar świetlny i bicie serca nie mierzyły jednakowo czasu, mielibyśmy detektor absolutnego
czasu, znów łamiący zasadę względności Oczywiście istota ludzka lub jakakolwiek inna for-
ma życia, w szybko poruszającym się pojeździe kosmicznym nie odczułaby ani nie zaobser-
wowała spowolnienia życia wewnątrz pojazdu kosmicznego (dalsza analiza tego przypadku
nastąpi przy temacie :Paradoks bliźniąt”).

3.

Ponieważ wszystkie procesy fizyczne zostają spowolnione, więc również czas połowicznego
zaniku próbki promieniotwórczej musi podlegać spowolnieniu w tym samym stosunku. Ta
zmiana czasu połowicznego zaniku została zaobserwowana bezpośrednio z dokładnością ok.
1 części na 10

4

, przy użyciu wiązki nietrwałych cząstek poruszających się z prędkością bliską

prędkości światła Czas połowicznego rozpadu takich cząstek wzrośnie

γ

razy.

4.

Dylatację czasu zaobserwowano nie tylko za pomocą mikroskopowych „zegarów” w postaci
nietrwałych cząstek. W 1960 roku ten efekt stwierdzono stosując tzw. zegary Mössbauera.
Urządzeniem jakie możemy zbudować przy obecnym stanie wiedzy, najbardziej stabilnie od-
mierzającym czas jest zegar wykorzystujący zjawisko Mössbauera.
„Zegary” mössbauerowskie użytkują fotony z rozpadu promieniotwórczego izotopu żelaza
zawartego w krysztale żelaza. Dwa identyczne zegary m

¬

ssbauerowskie pokazują ten sam

czas z dokładnością jednej części na 10

16

. Przesunięcie czasu ujawnia się jako wzrost tempa

zliczeń fotonów. Wielkość zmiany tempa można liczyć ilościowo. W tym doświadczeniu z
dylatacją czasu cały zegar był poddany szybkim obrotom. Stwierdzono, że zegar zwalnia

1

2

2

−

v

c

razy w stosunku do identycznego zegara mössbauerowskiego będącego w spo-

czynku.

Temat: 49

Kontrakcja długości. Jednoczesność.

1.

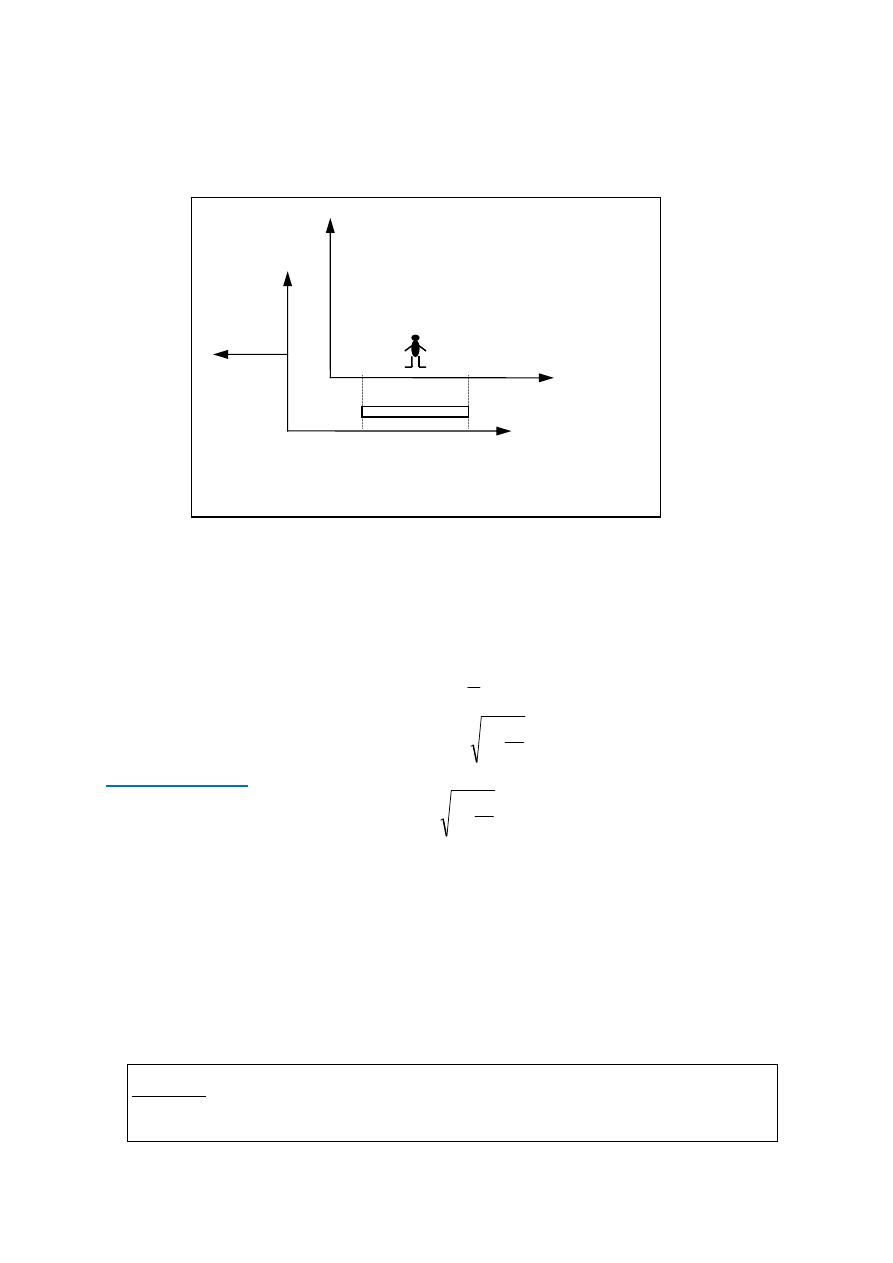
*Przypuśćmy, że pan X próbuje mierzyć długość metrowego pręta, który spoczywa w ukła-

dzie primowanym. Jego końce znajdują się w punktach

x

1

'

i

x

2

'

(rys. 1). Wtedy z transforma-

cji Lorentza wynikają równania:

(1)

x

x

v t

1

1

1

'

= ⋅ + ⋅ ⋅

γ

γ

(2)

x

x

v t

2

2

2

'

= ⋅ + ⋅ ⋅

γ

γ

11

00510 Mechanika relatywistyczna D

TEORIA

Równania (2) i (1) odejmujemy stronami

(3)

x

x

x

x

v t

t

2

1

2

1

2

1

'

'

(

)

(

)

− =

−

+ ⋅

−

γ

γ

y


y’

r

v pan X

x

1

x

2

x

x

1

'

x

2

'

x’

Rys. 1

Aby pan X mógł zmierzyć długość poruszającego się przedmiotu, uzyskując wynik, który
byłby poprawny w jego układzie odniesienia, musi dołożyć starań, aby zmierzyć położenie
jego końców w tej samej, według niego, chwili, tj. kiedy t

1

= t

2

. Wtedy poprzednie równanie

przyjmie postać:

(4)

x

x

x

x

2

1

2

1

'

'

(

)

− =

−

γ

lub

(5)

x

x

x

x

2

1

2

1

1

− =

−

γ

(

)

'

'

Czyli długość poruszającego się pręta równa się

1

2

2

−

v

c

razy długość pręta, który spoczywa:

Wzór obowiązkowy:

(6)

l

v

c

l

ruc

y

spoczywaj cy

hom

ą

=

−

⋅

1

2

2

Równanie (6) nazywa się skróceniem Fitzgeralda - Lorentza, gdyż hipotezę skrócenia poda-
li niezależnie od siebie G.F. Fitzgerald i H.A. Lorentz.
Zjawisko powyższe nazywamy również kontrakcją (skróceniem) długości.

Gdy dwóch obserwatorów mija się, każdy trzymając w kierunku ruchu identyczny pręt me-
trowy, obaj „zobaczą” pręt partnera skrócony o tyle samo razy. Napisaliśmy wyraz „zoba-
czą” w cudzysłowie, ponieważ jest ważne, aby mierzyć położenie obu końców równocze-
ś

nie, podczas gdy w rzeczywistości, jeśli patrzymy na oba końce pręta, wystąpi pewna różnica

czasu ze względu na skończony czas przelotu światła.

Przykład 1
Pręt metrowy mija cię z prędkością równą 60% prędkości światła. Jak długi ci się wyda ?

(Odp. 80 cm)

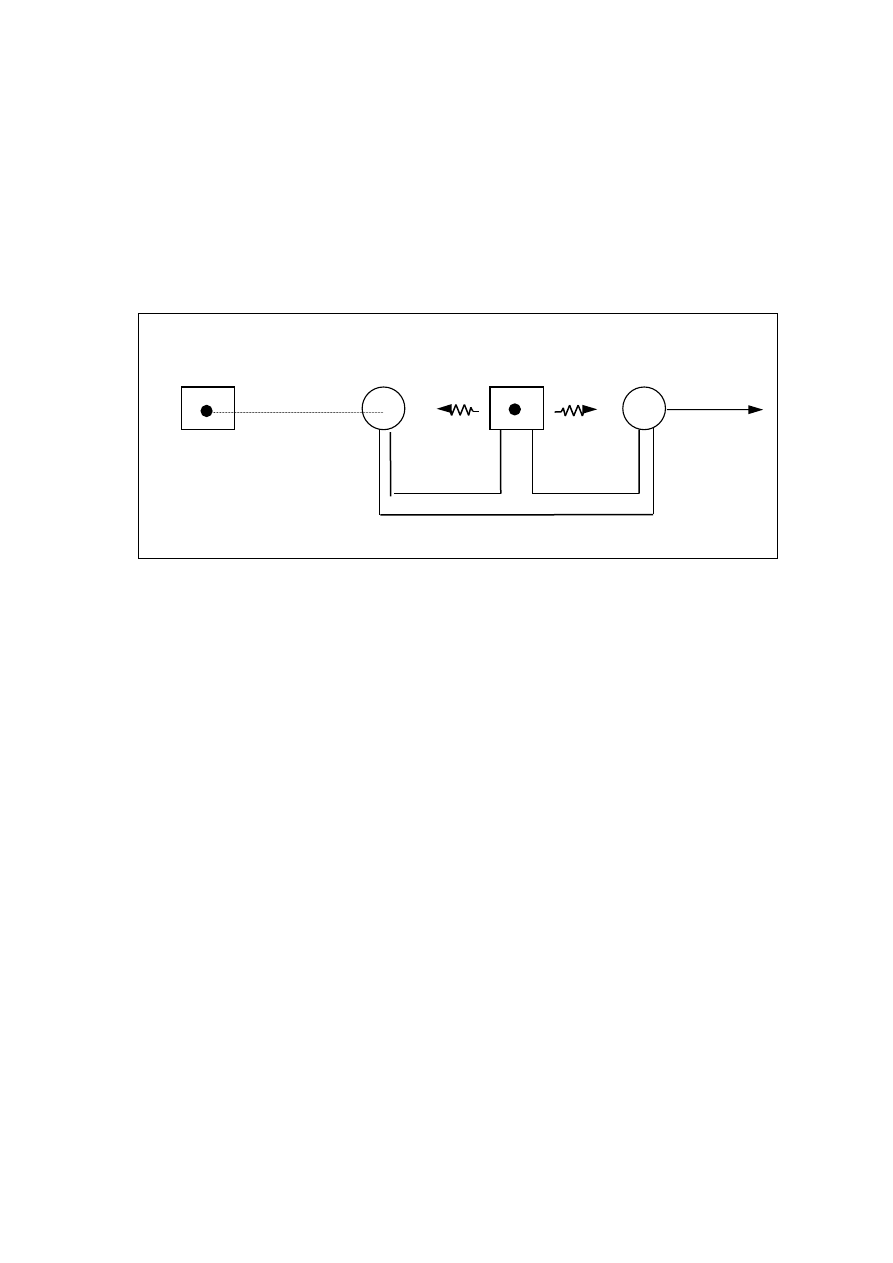
12

00510 Mechanika relatywistyczna D

TEORIA

2.

W mechanice klasycznej przestrzeń i czas są traktowane oddzielnie, niezależnie od siebie.
Newton sądził, że istnieją absolutna przestrzeń i absolutny czas. W tamtych czasach wyobra-
ż

ano sobie przestrzeń jako odnoszącą się do czegoś co zawiera przedmioty, jest stałe i nieru-

chome. O czasie Newton pisał: „Absolutny, rzeczywisty lub matematyczny czas, sam z sie-
bie , na mocy swej wewnętrznej struktury, płynie równomiernie, jednostajnie, bez odniesienia
do czegoś zewnętrznego”.

3.

Zgodnie z tym wydawało się oczywiste, że dwa zdarzenia, które są jednoczesne w jednym
układzie, są jednoczesne i w każdym innym układzie odniesienia. Bez trudu można się jednak
przekonać, że ta ostatnia teza jest sprzeczna z zasadą stałości prędkości światła.

K M K’ N

r

v

0

Rys. 2

Rozważmy ciała K i K’, które razem z odpowiednimi zegarami tworzą inercjalne układy od-
niesienia. Ciało K’ porusza się względem ciała K z prędkością

r

v

0

, skierowaną wzdłuż prostej

łączącej środki obu ciał (rys. 2). Na tej prostej umieszczone są ciała M i N, jednakowo odległe
od ciała K’ i sztywno z nim połączone. Ciała M i N poruszają się z prędkością

r

v

0

względem

ciała K, natomiast spoczywają względem ciała K’. Rozważmy w obu układach odniesienia to
samo zjawisko, polegające na emitowaniu ze środka ciała K’ sygnału świetlnego i dotarcie te-
go sygnału do ciał M i N. Prędkość światła we wszystkich kierunkach jest taka sama i równa
c. Dlatego w układzie odniesienia K’ sygnał dociera do ciał M i N w tej samej chwili czasu t’.
W układzie odniesienia K światło ma także prędkość c we wszystkich kierunkach. Ciało M
porusza się na spotkanie sygnału świetlnego. Ciało N porusza się w tę samą stronę co sygnał
ś

wietlny. Dlatego sygnał wcześniej dociera do ciała M niż do ciała N, czyli

t

t

M

N

〈

. Widzimy,

ż

e zdarzenia jednoczesne w układzie K’, nie są jednoczesne w układzie K. Wynika stąd, że

czas płynie inaczej w różnych układach odniesienia.

*Suplement:

Przestrzeń i czas są częściami jednej całości. Jednak czas różni się jakościowo od prze-
strzeni. Przejawia się to w tym, że przestrzeń czterowymiarowa różni się własnościami od
zwyczajnej przestrzeni trójwymiarowej. Zwykła przestrzeń ma metrykę euklidesową - kwa-
drat odległości

∆

l między dwoma punktami jest równy sumie kwadratów różnic współ-

rzędnych:

(a)

∆

∆

∆

∆

l

x

y

z

2

2

2

2

=

+

+

Kwadrat „odległości” między punktami świata (tę „odległość nazywamy interwałem i
oznaczamy s) jest określony wzorem:

(b)

∆

∆

∆

∆

∆

s

c

t

x

y

z

2

2

2

2

2

2

=

−

−

−

Przestrzenie, w których kwadrat odległości jest określony powyższym wzorem nazywamy
przestrzeniami pseudoeuklidesowymi.

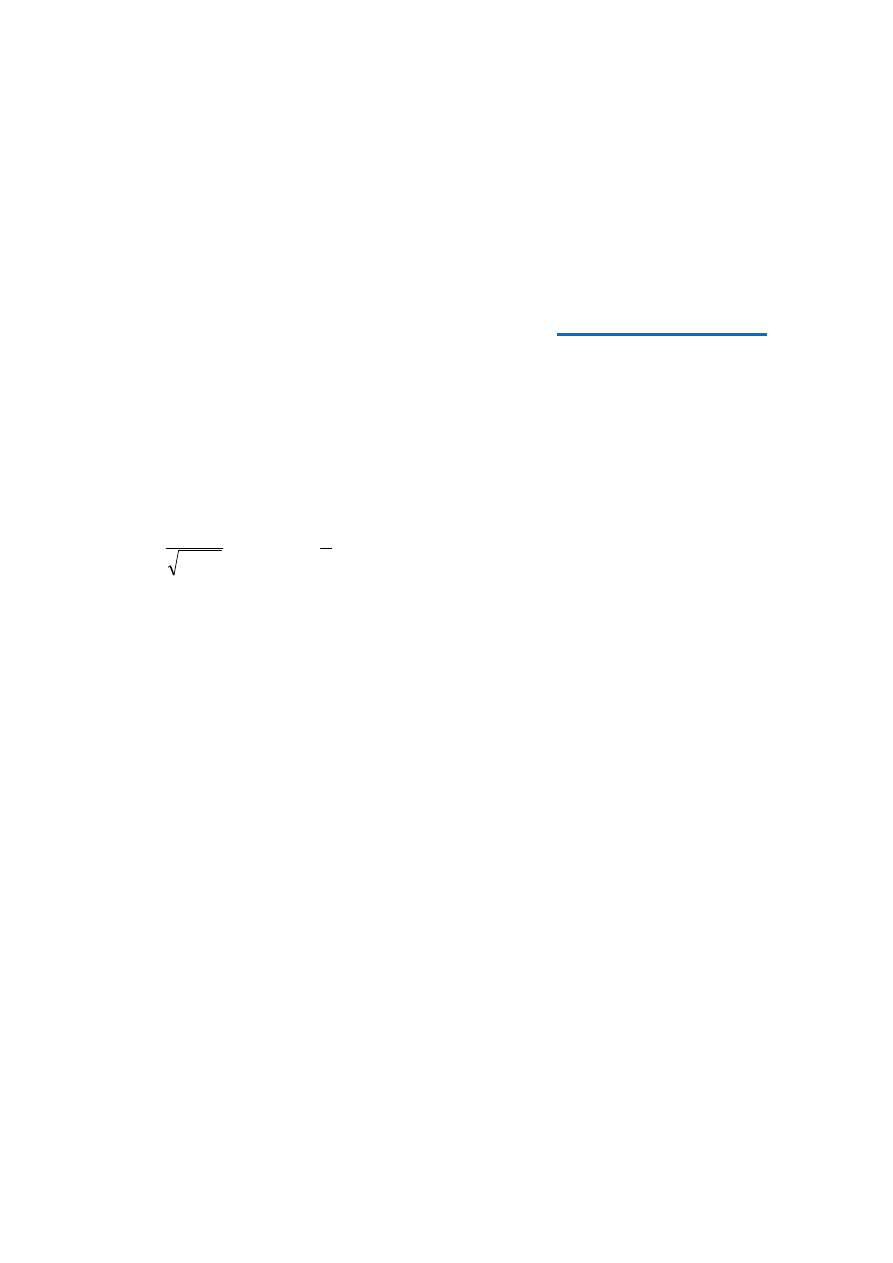
13

00510 Mechanika relatywistyczna D

TEORIA

Interwał jest niezmiennikiem względem przekształceń współrzędnych i czasu wynikają-
cych z zastąpienia jednego układu inercjalnego drugim (jego wartość jest taka sama we
wszystkich inercjalnych układach odniesienia).
Poznamy inne niezmienniki (pęd, energię) analizując elementy dynamiki relatywistycznej.

Jakościowa różnica między czasem a przestrzenią przejawia się tym, że kwadrat współ-
rzędnej czasowej i kwadraty współrzędnych przestrzennych mają w wyrażeniu (b) przeciw-
ne znaki.

Temat: 50*

Paradoks bliźniąt.

1.

Wyobraźmy sobie dwóch bliźniaków Jeden z nich (nazwiemy go A) pozostaje na Ziemi, a
drugi udaje się w kosmiczną podróż z wielką prędkością, tzn. porównywalną z prędkością
ś

wiatła c. Każdy z braci odczytuje czas na swoim zegarze: kosmonauta na zegarze statku

kosmicznego (

∆

t’), Ziemianin na zegarze ziemskim (

∆

t). Wyobraźmy sobie dalej, że ko-

smonauta wrócił na Ziemię i spotkał się ze swoim bratem. Popatrzywszy na brata wy-
krzyknął: „Jak ty się postarzałeś !”. Jeśliby bracia chcieli wyjaśnić jak długo trwała po-
dróż, to ustaliliby, że według czasu rejestrowanego przez kosmonautę trwała ona na przy-
kład 3 lata, a według czasu ziemskiego - 10 lat. Zgodnie ze wzorem

∆

∆

t

t

gdzie

v

c

=

−

=

'

,

1

2

β

β

, poruszający się zegar kosmonauty odmierzy czas krótszy,

niż zegar „nieruchomy” na Ziemi, czyli „zegar będący w ruchu opóźnia się”. W ten sposób
kosmonauta okazuje się młodszy o 7 lat od swojego brata bliźniaka Jeśli statkowi ko-
smicznemu nadamy dostatecznie dużą prędkość, to przy

∆

t’ = 30 lat możemy w zasadzie

uzyskać

∆

t = 1000 lat, czyli kosmonauta po powrocie na Ziemię zastanie odległą przy-

szłość w stosunku do pokolenia, które pozostawił na Ziemi.

2.

Od razu zauważmy, że podobna podróż w przyszłość innych ludzi, a nie w swoją własną,
nie jest sprzeczna z teorią względności i nie jest paradoksalna Na odwrót - teoria względ-
ności pokazuje jak to zrealizować. Aby

∆

t było znacznie dłuższe od

∆

t’, konieczne są

prędkości bliskie prędkości światła w próżni. Ale to już jest sprawą techniki, w zasadzie
STW nie zabrania kosmicznym statkom poruszania się z podobnymi prędkościami. Zgod-
nie z STW nie można poruszać się z prędkością większą od c, natomiast z prędkością
dowolną, mniejszą od c - można.

3.

Paradoks bliźniąt formułuje się następująco: zgodnie z STW, zresztą nie tylko STW, lecz
także z mechaniką niutonowską można wypowiedzieć dwa następujące stwierdzenia, rów-
noznaczne pod względem fizycznym:

⇒

kosmonauta porusza się, Ziemianin pozostaje w spoczynku,

⇒

kosmonauta nie porusza się, natomiast Ziemianin porusza się względem niego z taką
sama prędkością, lecz w przeciwna stronę.

Zgodnie z STW „młodnieje” poruszający się obserwator, wytwarza się zatem paradoksal-
na sytuacja: z jednej strony kosmonauta powinien być młodszy od Ziemianina, z drugiej
strony - Ziemianin młodszy od kosmonauty.

14

00510 Mechanika relatywistyczna D

TEORIA

Paradoks ten tłumaczymy w następujący sposób. Twierdzenia STW dotyczą układów in-
ercjalnych, tj. układów poruszających się cały czas jednostajnie i prostoliniowo względem
siebie. Dwaj bracia znajdujący się w różnych układach inercjalnych mogą spotkać się
„oko w oko” tylko jeden raz, przelatując jeden obok drugiego, po czym na zawsze już roz-
staną się. Aby bracia mogli ponownie się spotkać, jeden z nich, praktycznie kosmonauta,
powinien zawrócić
Nie sposób uniknąć wówczas przyspieszonego ruchu statku kosmicznego. Aby statek
mógł wrócić z powrotem, trzeba mu nadać przyspieszenie o zwrocie przeciwnym wzglę-
dem zwrotu pierwotnej prędkości. Jednak statek poruszający się z przyspieszeniem nie jest
już układem inercjalnym i w tym przypadku nie są spełnione twierdzenia szczególnej teo-
rii względności. Układ odniesienia poruszający się z przyspieszeniem (statek kosmiczny)
nie jest już pod względem fizycznym równoważny układowi nie mającemu przyspieszenia
(Ziemia). Zgodnie z ogólna teorią względności, w układzie odniesienia poruszającym się z
przyspieszeniem czas płynie wolniej. Dlatego też młodszym okaże się kosmonauta, gdyż
on właśnie porusza się z przyspieszeniem.

Praktycznie, co prawda, bardzo trudno w ten sposób zachować młodość. Wymaga to na-
dania statkowi prędkości bliskiej prędkości światła c. Aby to uzyskać musimy w długo-
trwały sposób rozpędzać statek po starcie, zatrzymać go, znowu nadać mu dużą prędkość
podczas powrotu oraz zatrzymać go przy lądowaniu na Ziemi.

Temat: 51

Dodawanie prędkości według Einsteina.

1.

*Dotychczas omawiane były ogólne własności czasu i przestrzeni. Teraz zajmować się
będziemy cząstkami materialnymi posiadającymi masę, pęd i energię. Zasady zachowania
pędu i energii nadal będą obowiązywać, ale należy zmienić klasyczne definicje pędu i
energii. Nowe, relatywistyczne definicje pędu i energii staną się oczywiście identyczne z
definicjami klasycznymi gdy v

→

0. Jedną z nowych niespodzianek będzie to, ze z każdą

masą m jest związana energia zgodnie z równaniem

E

m c

= ⋅

2

. Einstein postulował, że w

1 kg każdej substancji zawarte jest 9 10

16

⋅

J energii. To jest tak wielka ilość energii, że

mogłaby zasilać 100 W żarówkę przez 30 milionów lat.

2.

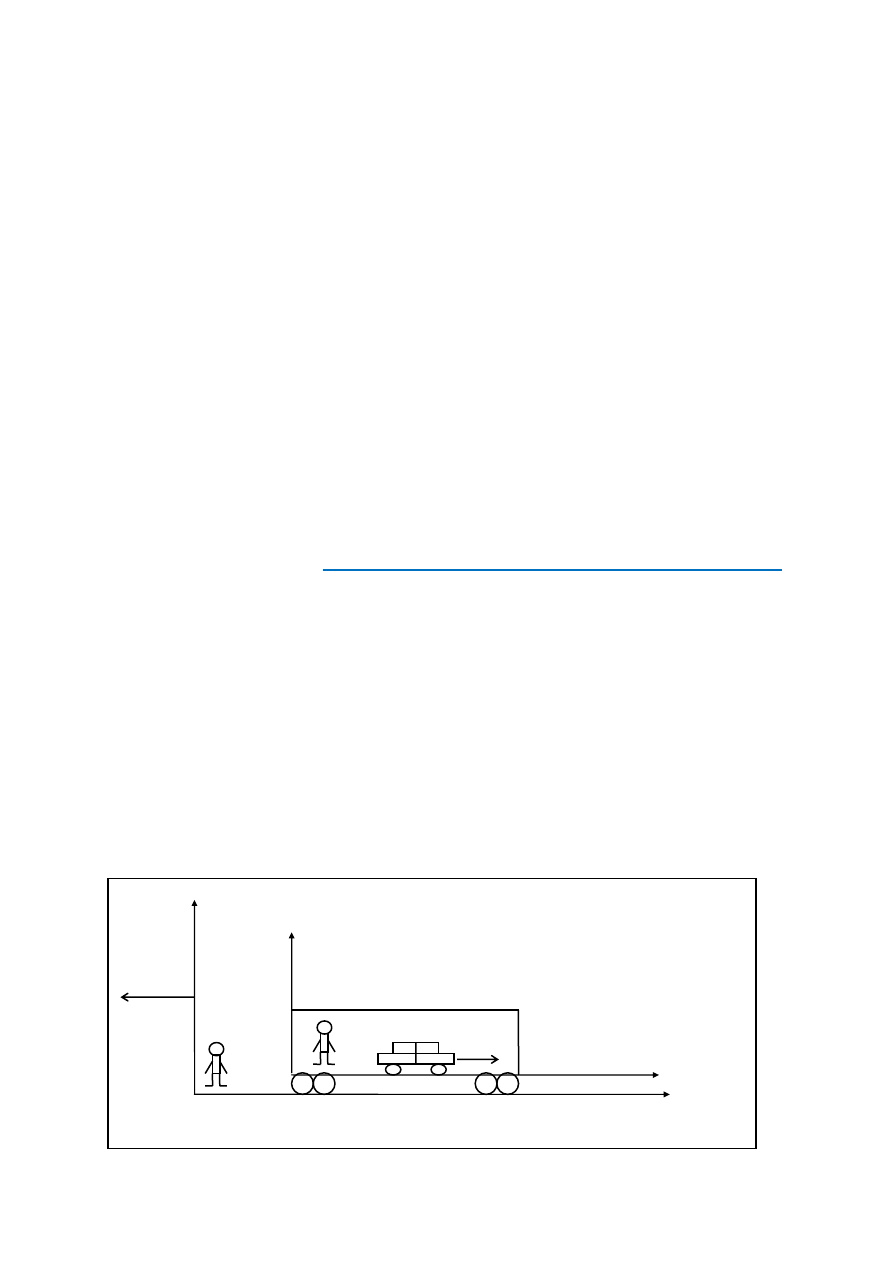
*Dotychczas mieliśmy do czynienia z cząstkami, które spoczywały w jednym układzie
odniesienia i poruszały się z prędkością v w innym układzie odniesienia. Teraz przejdzie-
my do przypadku, gdy cząstka (obiekt) ma już prędkość u

x

w jednym układzie i u

x

’ w in-

nym układzie. Przykład takiej sytuacji przedstawiono na rysunku 1.

Y’

Y

r

v

Pan X
Pan

r

u

x

Prim X

X’
Rys. 1

15

00510 Mechanika relatywistyczna D

TEORIA

Według pana X samochód ma prędkość

u

x

, a według pana Prima porusza się szybciej, z

prędkością

u

x

'

. Klasycznie

u

x

'

=

u

x

+ v. Wzory relatywistyczne uzyskamy przepisując od-

powiednie równania transformacji Lorentza w zmienionej postaci:
(1)

dx

dx

vdt

'

=

+

γ

γ

(2)

dt

dt

v

c

dx

'

=

+

⋅

γ

γ

2

Dzielimy teraz równanie (1) przez (2):

(3)

dx

dt

dx

vdt

dt

v

c

dx

dx

dt

v

v

c

dx

dt

'

=

+

+

=

+

+

⋅

2

2

1

Zastępując

dx

dt

i

dx

dt

'

'

odpowiednio przez

u

x

i u

x

'

otrzymamy:

Wzór obowiązkowy:

(4)

u

u

v

v u

c

x

x

x

'

=

+

+

⋅

1

2

Widać, że prędkość wypadkowa jest mniejsza od sumy prędkości składowych. Jednak,
gdy obie prędkości są znacznie mniejsze od prędkości światła, prędkość wypadkowa jest
bardzo bliska sumy ich obu.

3.

*Jeżeli teoria ma być w zgodności sama z sobą, równanie (4) musi wykluczać prędkości
większe od prędkości światła c. Wyobraźmy sobie cząstkę w układzie nieprimowanym,
która już porusza się z prędkością światła, czyli foton lub neutrino, mamy więc

u

x

= c.

Wówczas obserwator w układzie primowanym będzie widział

(5)

u

c

v

v c

c

c

v

c

v

c

c

'

=

+

+

⋅ =

+

+ =

1

2

.

Widzimy, że światło (lub cokolwiek innego),biegnące z prędkością c, biegnie z tą prędko-
ś

cią dla wszystkich obserwatorów, bez względu na to, z jaka prędkością oni się poruszają.

Jak już przedtem stwierdziliśmy, równania transformacji Lorentza transformują przestrzeń
i czas w taki właśnie sposób, że wiązka światła musi poruszać się z tą samą prędkością
ś

wiatła c dla wszystkich obserwatorów.

Wzór ten nazywa się wzorem Einsteina na doda-

wanie prędkości.

16

00510 Mechanika relatywistyczna D

TEORIA

Temat: 52

Równoważność masy i energii.

1.

Przewidywania Einsteina , że spoczywająca masa m powinna zawierać ogromną ilość energii

E

m c

0

2

= ⋅

, było bardzo śmiałe i miało różnego rodzaju konsekwencje praktyczne z energią ją-

drową i bombą jądrową włącznie. Einstein wyraził pogląd, że jeżeli masa spoczynkowa cząstki lub

układu cząstek zostanie zmniejszona o

∆

m, to nastąpi wyzwolenie energii

∆

∆

E

m c

=

⋅

2

.

Przykład: 1

Ile energii zawiera 1 g piasku ? ( Odp.

9 10

13

⋅

J

)

2.

*Pierwszym eksperymentalnym potwierdzeniem zależności Einsteina między masą i energią był
wynik porównania ilości energii wyzwolonej w rozpadzie promieniotwórczym z różnicą mas jądra
początkowego i produktów końcowych. Jako przykład, w jaki sposób można sprawdzić

E

m c

0

2

= ⋅

w laboratorium, rozważmy najprostszy przypadek rozpadu - rozpad swobodnego neu-

tronu. Stwierdzono, że swobodny neutron rozpada się na proton, elektron i antyneutrino (o zerowej
masie spoczynkowej)

n

p

e

→ + +

−

ϑ

Zaobserwowano, że produkty rozpadu maja całkowitą energię kinetyczną równa [J]. Zmierzono,

ż

e masa spoczynkowa neutronu jest większa od sum mas protonu i elektronu o

13 9 10

31

,

⋅

−

[kg].

Ilość energii odpowiadająca takiemu zmniejszeniu masy jest:

E =

(

)

( ,

)

,

13 9 10

3 10

1 25 10

31

8 2

13

⋅

⋅ ⋅

=

⋅

−

−

kg

J

kg

J

.

Ta ilość energii zgadza się w granicach dokładności pomiaru z zaobserwowaną energią kinetyczną

produktów rozpadu, która wynosi również

1 25 10

13

,

⋅

−

[J].

3.

Innym przykładem wielkiej energii zawartej w masie spoczynkowej jest anihilacja elektronu i
pozytonu (rys. 1). Pozyton jest dodatnim elektronem. Elektron i pozyton w zetknięciu ze sobą ani-
hilują się wzajemnie, zmieniając się w dwa fotony. Foton jest kwantem promieniowania elektro-

magnetycznego. W omawianym przypadku energia spoczynkowa

2

2

m c

e

zostaje zamieniona w

energię promieniowania elektromagnetycznego ( m

e

jest masą spoczynkową elektronu).

Naszym trzecim przykładem jest cząstka elementarna nazywająca się mionem, która rozpada się
na elektron i dwa neutrina

µ

ϑ

−

−

→

+

e

2

Mion ma masę spoczynkową 208 razy większą niż elektron z tego rozpadu. Dwa neutrina mają ze-
rową masę spoczynkową. W tym przykładzie ok. 99,5 % masy spoczynkowej jest zamienione w
energię kinetyczną elektronu i dwóch neutrin.
Proces odwrotny również zachodzi - energia kinetyczna może być zamieniona na masę spoczyn-
kową. Zwykle, gdy cząstka o dużej energii kinetycznej zderza się z jądrem atomu lub pojedyn-
czym protonem, są produkowane nowe cząstki i część energii kinetycznej jest zamieniana na masę
spoczynkową nowych cząstek. W Chicago w Narodowym Laboratorium Akcelatorowym dokona-
no zderzenia protonu o energii kinetycznej 300 GeV z będącym w spoczynku protonem w komo-
rze pęcherzykowej z ciekłym wodorem. Efektem było wyprodukowanie 22 nowych cząstek, głów-
nie pionów.

Przed .... Po... foton

e

+

e

-

Rys. 1

foton

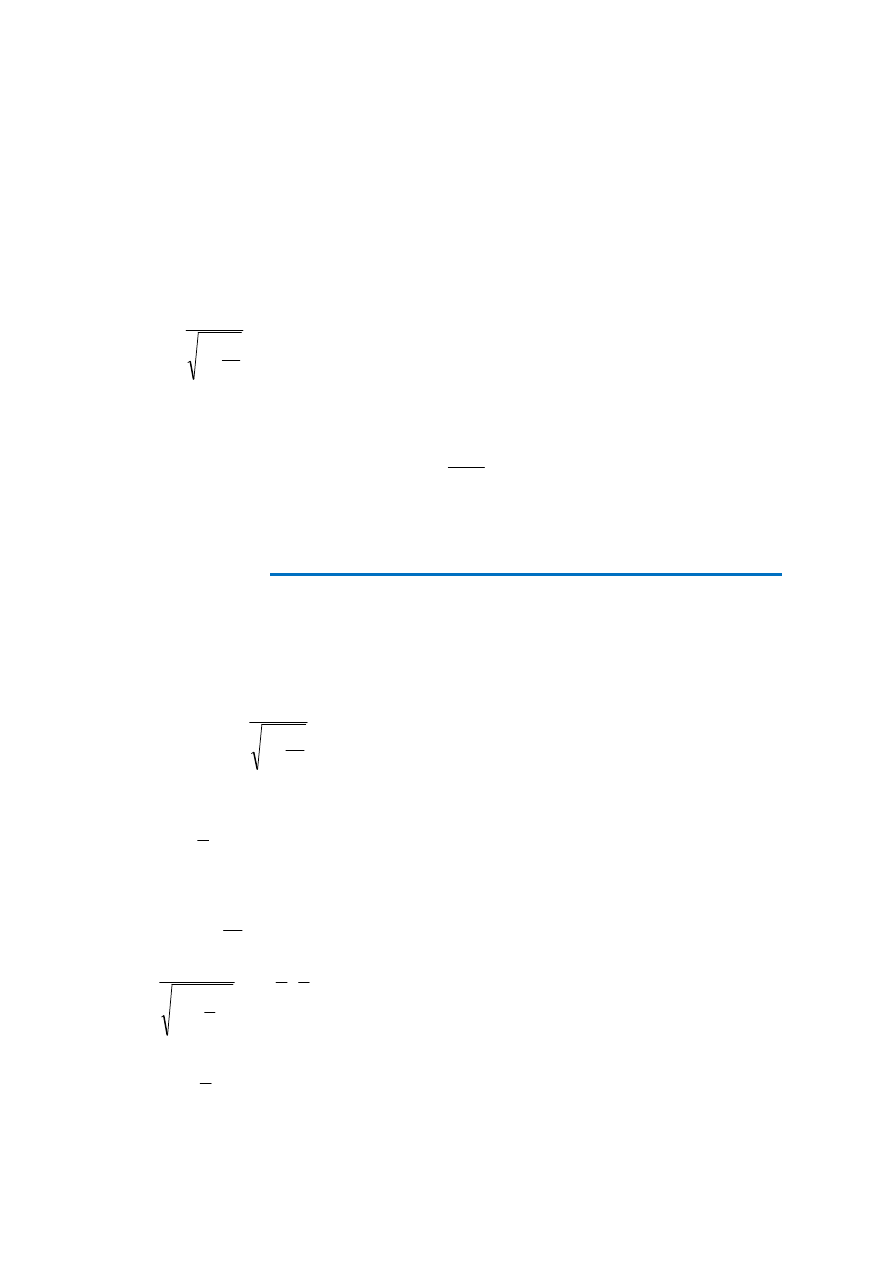
17

00510 Mechanika relatywistyczna D

TEORIA

4.

Istnieje jednak poważne ograniczenie na to, ile energii można uzyskać z konwersji (zamiany) masy
spoczynkowej. Mówi o tym podstawowe prawo natury zwane zasadą zachowania liczby bariono-
wej. Z prawa tego wynika, że całkowita liczba protonów i neutronów w próbce zwykłej materii
musi pozostawać stała. Z tego właśnie powodu nie istnieje sposób na otrzymanie z 1 g piasku

9 10

13

⋅

J

energii. Jednak w dużym jądrze, takim jak uran, można zmienić rozkład protonów i neu-

tronów tak, że masa spoczynkowa maleje ok. 0,1 %. W tym procesie zwanym rozszczepieniem ją-
drowym jądro, takie jak uran, rozpada się spontanicznie na dwa w przybliżeniu równej wielkości
jądra i na kilka neutronów. Całkowita masa spoczynkowa produktów końcowych jest ok. 0,1 %
mniejsza niż masa spoczynkowa początkowa. W niesprężystym zderzeniu dwóch cząstek lub roz-
padzie jednej cząstki, masa spoczynkowa jest oczywiście niezachowana, natomiast całkowita ener-

gia

E

m

u

c

c

j

j

=

−

⋅

∑

1

2

2

2

jest zachowana.

5.

Dla dociekliwych: Wykaż, że jeżeli podejmiemy próbę obliczenia prędkości, jaką uzyska elektron
pod działaniem napięcia przyspieszającego U = 0,5 MV, to wzór klasyczny

eU

m v

=

0

2

2

nie wystarcza. Jak ten problem rozwiązać prawidłowo ?

Temat: 53

Energia kinetyczna w ujęciu relatywistycznym.

1.

Definicja energii kinetycznej w teorii względności jest taka sama jak w mechanice kla-
sycznej : energia kinetyczna cząstki jest energią wynikającą z ruchu cząstki. Energię po-
chodzącą od ruchu cząstki swobodnej można obliczyć stosując wzór

(1)

E

m c

v

c

k

=

⋅

−

−

























0

2

2

2

1

1

1

Wzór (1) obowiązuje dla dowolnej prędkości v - zarówno dla ruchu prostoliniowego, jak i
krzywoliniowego. Wzór tren różni się od wzoru nierelatywistycznego:

(2) E

m v

k

=

1

2

0

2

Jednak dla prędkości v dużo mniejszej od prędkości światła c, relatywistyczna zależność
praktycznie przyjmuje postać wzoru, który podaje mechanika niutonowska.

Istotne, gdy

v

c

2

2

1

<<

można przyjąć, iż:

(3)

1

1

1

1

2

2

2

−











≈ +











v

c

v

c

Po podstawieniu zależności (3) do wzoru (1) otrzymamy

E

m v

k

=

1

2

0

2

czyli nierelatywistyczny wzór dla energii kinetycznej.

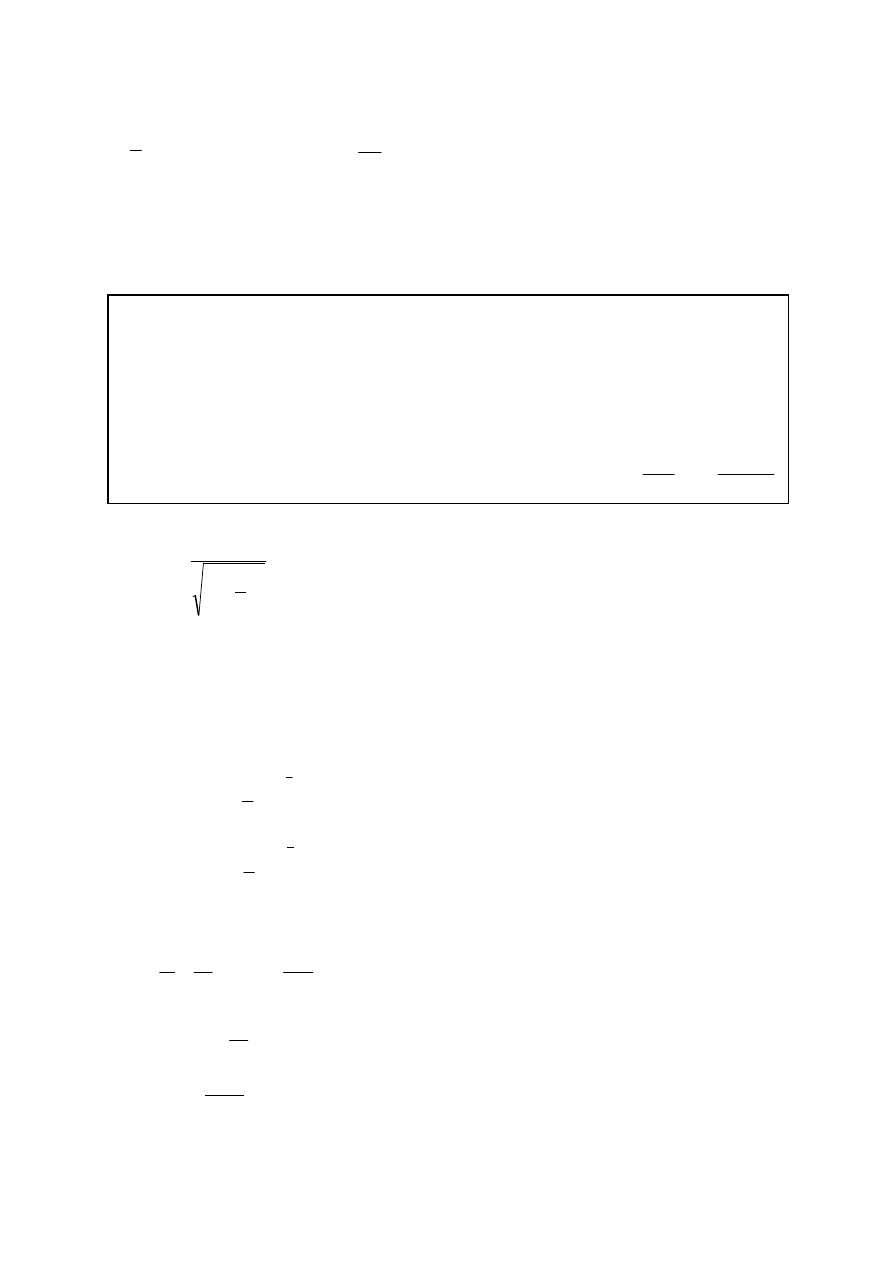
18

00510 Mechanika relatywistyczna D

TEORIA

2.

Z relatywistycznej postaci wzoru dla energii kinetycznej trzeba korzystać praktycznie, gdy

v

c

>

0 2

, , a więc gdy v > 60000

km

s

. Ciała makroskopowe poruszają się zazwyczaj z pręd-

kością równą 0.2c, dlatego też obliczając energię kinetyczną tych ciał uzyskamy dosta-
tecznie dokładny wynik, jeżeli skorzystamy ze wzoru (2). W mikroświecie natomiast wy-
stępują prędkości bliskie c, wobec tego należy w takich przypadkach posługiwać się rela-
tywistycznymi wzorami (1). Taki właśnie przypadek mamy w akceleratorach cząstek na-
ładowanych.

Przykład 1
Tak się złożyło, że jakaś cząstka ma energię kinetyczną równą swojej energii spoczynkowej. Jaka jest jej pręd-
kość?

( Odp. v = 0.866c )

Przykład: 2*
W Narodowym Laboratorium Akceleratorowym im. Fermiego w pobliżu Chicago w USA protony są przyspie-
szane do energii 400 razy większej niż ich energia spoczynkowa.

a)

jaka jest prędkość tych protonów ?

b)

jaki jest stosunek E do p·c ?

( Odp. v = 0.999997c,

c

p

E

⋅

= 1 +

1

320000

)

3.

*Wyrażenie (1) na energię kinetyczną jest różnicą dwóch wielkości :

(4) E

m c

v

c

=

−











0

2

2

1

oraz

(5) E

m c

0

0

2

=

Jak widać, wielkość E

0

, jest szczególnym przypadkiem wielkości E, gdy v = 0, a więc jest to energia nierucho-

mego ciała. Wielkość E nazywamy energią całkowitą, a wielkość E

0

- energią spoczynkową lub energią własną.

Jak widzimy, zgodnie z teorią względności nieruchome ciało swobodne, na które nie działają siły zewnętrzne, po-
siada energię spoczynkową E

0

.

4.

Teraz przypominamy relatywistyczne określenia pędu, energii i prędkości :

(6)

p

m

v

c

v

=

−























⋅

−

1

2

1

2

(7)

E

m

v

c

c

=

−























⋅

−

1

2

1

2

2

(8) E

E

m c

k

=

+

0

2

Możemy znaleźć prędkość wyrażoną przez p i E, dzieląc (6) przez (7) :

(9)

p

E

v

c

=

2

, czyli

v

pc

E

=

2

5.

Możemy uzyskać bardzo przydatną zależność między E, p i m podnosząc do kwadratu obie strony równania (7)

(10)

( )

E

v

c

mc

2

2

2

2

2

1

⋅ −











=

(10a)

E

E v

c

m c

2

2

2

2

2

4

−

=

19

00510 Mechanika relatywistyczna D

TEORIA

teraz w miejsce v podstawmy prawą stronę równania (9) :

(11) E

p c

m c

2

2

2

2

4

−

=

Przykład: 3

Energia spoczynkowa protonu jest równa 938 MeV. Załóż, ze proton porusza się z prędkością 0.5c.

a)

jaka jest jego energia kinetyczna (w MeV) według mechaniki klasycznej ?

b)

jaka jest jego energia kinetyczna według mechaniki relatywistycznej ?

Temat: 54 *Relatywistyczna postać II zasady dynamiki Newtona.

1.

Odpowiednik II zasady dynamiki Newtona w STW ma taką samą postać jak w mechanice Newtona:

(1)

dp

dt

F

r

r

=

zmiana pędu ciała w jednostce czasu jest równa sile zewnętrznej działającej na ciało.
Zasadnicza różnica jednak polega na tym, że w mechanice niutonowskiej inaczej wyraża się pęd aniżeli w mecha-
nice relatywistycznej. W pierwszej z nich pędem ciała nazywa się wielkość wektorowa równa iloczynowi masy
ciała i jego prędkości:

(2)

r

r

p

mv

=

przy czym masę traktuje się jako wielkość niezmienniczą, niezależną w szczególności od prędkości ciała.
Natomiast w teorii względności pęd ciała jest wielkością wektorową określoną w następujący sposób :

(3)

r

r

p

m v

v

c

=

−

0

2

2

1

We wzorze tym m oznacza masę ciał w układzie odniesienia, w którym ciało znajduje się w spoczynku ( jest to
tzw. masa spoczynkowa lub masa własna ciała ).

2.

Należy pamiętać, że ze wzoru (3) wynikają dwie różne interpretacje. Pierwsza z nich jest szeroko rozpowszechnio-
na w literaturze popularnonaukowej i naukowej, szkolnej oraz akademickiej. Według niej pierwiastek relatywi-
styczny znajduje się w mianowniku ułamka, którego licznikiem jest masa spoczynkowa :

(4)

m

m

=

−

0

2

1

β

, gdzie

β

=

v

c

Tak otrzymana wielkość fizyczna nazywa się masą relatywistyczną lub masą w ruchu. Zatem pęd w STW może
być formalnie określony podobnie jak w mechanice relatywistycznej, tj. jako iloczyn masy ciała i jego prędkości.
Jednakże w STW przyjmuje się, iż masa ciała zależy od jego prędkości, a więc od układu odniesienia, względem
którego rozpatruje się prędkość ciała, zgodnie ze wzorem (4).

3.

Druga interpretacja wzoru (3) występująca w literaturze naukowej z zakresu fizyki teoretycznej najlepiej odpowia-
da duchowi teorii względności. Zgodnie z nią pierwiastek relatywistyczny łączy się z wektorem prędkości, a masę
traktuje się jako wielkość niezmienniczą, równą masie spoczynkowej lub masie własnej ciała m

0

. Takie ujęcie

przyjęte jest w teorii względności, w której operuje się wielkościami wektorowymi mającymi nie trzy, lecz cztery
składowe. Są to trzy składowe przestrzenne i czwarta - składowa czasu - czyli rzut wektora na oś czasu. Takie uję-
cie prowadzi do operowania terminami czterowektorów definiowanych w przestrzeni, określanej przez fizykę teo-
retyczną jako czasoprzestrzeń lub przestrzeń Minkowskiego.

20

00510 Mechanika relatywistyczna D

TEORIA

4.

Wróćmy do II zasady Newtona. Wstawiamy do wzoru (1) wzór (2), zatem :

(5)

d mv

dt

F

(

)

r

r

=

czyli

(6)

m

dv

dt

v

dm

dt

F

r

r

r

+

=

Można ułatwić porównanie prawa relatywistycznego z nierelatywistycznym przedstawiając wielkość

dm

dt

-

zmianę relatywistycznej masy w jednostce czasu - w innej postaci. W tym celu skorzystamy z prawa Einsteina za-
leżności masy m i energii E

(7)

E

mc

=

2

Jeżeli pomnożymy

dm

dt

przez kwadrat prędkości światła w próżni (c

2

), to otrzymamy wyrażenie przedstawiające

zmianę energii ciała w jednostce czasu. Zgodnie z zasadą zachowania energii powinno być ono równe pracy źró-
dła siły zewnętrznej w jednostce czasu

(8)

d mc

dt

F v

F v

(

)

cos

2

= ⋅ = ⋅ ⋅

r r

α

gdzie

α

- kąt między kierunkami wektorów siły i prędkości. Pamiętając o tym, że

dv

dt

r

wyraża przyspieszenie

r

a

,

możemy relatywistyczny odpowiednik II zasady dynamiki Newtona zapisać w ostatecznej postaci

(9)

ma

F

v

F v

c

r

r

r

r r

= −

⋅

2

Jak widzimy podstawowe prawo mechaniki relatywistycznej w istotny sposób różni się od nierelatywistycznej II

zasady Newtona (

m a

F

0

r

r

=

).

6.

Zgodnie ze wzorem (4) masa zależy przede wszystkich od prędkości. Oznacza to, że masa ciała, tak samo jak
prędkość ciała, jest wielkością względną - zależy od układu odniesienia. Masa tego samego ciała ma różną war-
tość w różnych układach odniesienia. Niezmiennicza (niezależna od układu odniesienia) jest tylko masa spoczyn-
kowa m

0

, dlatego masa spoczynkowa nazywa się w STW masą własną ciała.

7.

Gdyby masa ciała była stała, to wskutek działania stałej siły przyspieszenie byłoby także stałe ( na podstawie II
prawa Newtona ), co prowadziłoby do nieograniczonego wzrostu prędkości z upływem czasu. Jest to oczywiście
sprzeczne z twierdzeniem STW o ograniczonej wartości prędkości światła w próżni.

Po prawej stronie równania (9) oprócz wektora siły

r

F

, znajduje się wektor

(

)

−

r

rr

v

Fv

c

2

, równoległy do prędkości

r

v

i (ogólnie mówiąc) nie równoległy do siły

r

F

. Wynika stąd wniosek, że wektor przyspieszenia w ogólnym

przypadku nie pokrywa się z kierunkiem wektora siły. Jak widać ze wzoru (9) te mają jednakowe kierunki tylko w
dwóch przypadkach :

a)

gdy

r r

F v

⋅ =

0

czyli gdy siła jest prostopadła do prędkości i

b)

gdy siła jest równoległa do prędkości

21

00510 Mechanika relatywistyczna D

TEORIA

Temat: 55

Ogólna teoria względności.

1.

Einstein całkowicie opracował szczególną teorię względności w 1905 roku, a znaczna
część ogólnej teorii w 1911 r. Ogólna teoria względności jest w istocie nowoczesną rela-
tywistyczną teorią grawitacji.

2.

W teorii grawitacji Newtona siła

F

Gm m

r

=

1

2

2

jest siłą, która działa natychmiastowo. Jeżeli

siła działa natychmiastowo, oznacza to, że sygnał lub energia mogą być przeniesione na-
tychmiastowo z masy m

1

do masy m

2

. To przeczy jednemu z podstawowych twierdzeń teo-

rii względności, że żadna z postaci energii, ani nawet żaden sygnał, nie może poruszać się
z prędkością większą od prędkości światła w próżni. A więc Einstein podjął zadanie stwo-
rzenia relatywistycznej teorii grawitacji. Postanowił, że jego nowa teoria musi spełniać za-
sadę względności jak i musi z niej bezpośrednio wynikać, że masa grawitacyjna jest zaw-
sze równoważna masie bezwładnej. Postanowienie Einsteina doprowadziło do postulatu,
który nazywa się zasadą równoważności. Z zasady tej wynika, że przebywanie w polu
grawitacyjnym jest równoważne ze znajdowaniem się w poruszającym się z przyspiesze-
niem układzie odniesienia. Na przykład, pasażer w rakiecie w czasie startu i przyspieszenia
w górę odnosi wrażenie, że to grawitacja nagle wzrosła . W rakiecie startującej z Ziemi z
przyspieszeniem a = 2g pasażerowie i wszystko inne ważyłoby trzy razy tyle co normalnie.
Ta „pseudograwitacyjna” siła jest wprost proporcjonalna do masy bezwładnej. śadne do-
ś

wiadczenie fizyczne wykonane wewnątrz rakiety, nie mogłoby wyjaśnić pasażerom, czy

to siła grawitacyjna Ziemi wzrosła trzykrotnie, czy też rakieta porusza się z przyspiesze-
niem względem Ziemi.

3.

Einstein wprowadził matematycznie zasadę równoważności do ogólnej teorii względności
stosując metody matematyczne znacznie wykraczające poza zakres tego kursu. W tym opi-
sie matematycznym każda masa „odkształca” bliski sobie obszar przestrzeni wobec tego
wszystkie poruszające się swobodnie przedmioty mają tory zakrzywiające się ku masie,
która spowodowała odkształcenia. Równania Einsteina wiążą wielkość krzywizny z mocą
(lub masą) źródła. Klasycznie powiedzielibyśmy, że każdy przedmiot poruszający się po
torze krzywoliniowym podlega przyspieszeniu i jest pod działaniem jakiejś siły. Właśnie to
przyspieszenie, które w ogólnej teorii względności jest własnością przestrzeni, jest wyja-
ś

nieniem zjawiska grawitacji. Ponieważ to przestrzeń jest „odkształcona”, więc wpływ na

wszystkie masy bezwładne jest taki sam i zasada równoważności jest automatycznie speł-
niona.

4.

Jedną z konsekwencji tej teorii jest powiększenie długości fali światła wysyłanego ze źró-
dła mającego masę. To zjawisko nazywa się grawitacyjnym przesunięciem ku czerwieni.
Przesunięcie to obserwuje się dla linii widmowych Słońca i ciężkich gwiazd. Tak więc,
tyknięcia zegara atomowego na powierzchni Słońca następują po sobie wolniej niż takiego
samego zegara atomowego na powierzchni Ziemi. Jak można się spodziewać, ogólna teo-
ria względności przewiduje, że wszystkie zegary będą chodzić wolniej w obecności pola
grawitacyjnego. Rzeczywiście, gdy dwa zegary znajdują się w pobliżu powierzchni Ziemi,
umieszczone jeden o 1 m wyżej niż drugi, to zegar niższy powinien chodzić wolniej o jed-
ną część na 10

16

. W 1960 roku zbudowano po raz pierwszy wzorce częstości dające taką

dokładność. Wykorzystano do tego fotony emitowane z promieniotwórczych jąder żelaza

22

00510 Mechanika relatywistyczna D

TEORIA

wbudowanych w kryształ. Zjawisko, które umożliwia tak dokładne pomiary częstości, na-
zywa się zjawiskiem Mössbauera.

5.

Przedtem trudno było przeprowadzić doświadczalne sprawdzenie ogólnej teorii względno-
ś

ci. Przy użyciu jednak nowych wzorców częstości wykazano w doświadczeniu laborato-

ryjnym, że grawitacja spawalnia bieg czasu. Pierwsze takie doświadczenia zostały prze-
prowadzone w 1960 r. w Uniwersytecie Harvarda w USA na wieży wysokości ok. 21 m.

6.

Innym efektem przewidzianym przez ogólną teorię względności jest zakrzywienie ku środ-
kowi Słońca wiązki światła przebiegającej w pobliżu powierzchni Słońca. Aby obliczyć si-
łę grawitacyjną między Słońcem a fotonem poruszającym się z prędkością światła jest po-
trzebna ogólna teoria względności. Tylko w czasie zaćmień Słońca można widzieć gwiaz-
dy, które mają pozorne położenie na niebie w bliskości Słońca. Zaobserwowano, że poło-
ż

enia przesuwają się o wartość przewidzianą przez Einsteina.

7.

Innym przewidywaniem ogólnej teorii względności, które aż do lat siedemdziesiątych wy-
dawało się raczej fantastyczne, było to, że w rozsądnie normalnych warunkach, gdy
gwiazda zużyje swoje paliwo energetyczne (termojądrowe), zapadnie się. To zapadnięcie
będzie tak katastrofalne, że ostatecznym rezultatem będzie „czarna dziura”. Mówiąc „czar-
na dziura” mamy na myśli, że ani światło ani inne sygnały nie mogą wyjść bardzo daleko
poza powierzchnię gwiazdy. Taka gwiazda nagle i całkowicie zniknie i nigdy już jej nie
zobaczymy. Teoria i stan badań doświadczalnych dotyczących czarnych dziur jest przed-
miotem zainteresowań astrofizyki.

8.

Jeszcze innym przewidywaniem, wynikającym z ogólnej teorii względności, jest to, że
ulegająca przyspieszeniu masa (taka jak zapadająca się gwiazda lub gwiazda w zderzeniu z
inną gwiazdą) będzie wysyłać fale grawitacyjne, podobnie jak przyspieszający ładunek
elektryczny wysyła promieniowanie elektromagnetyczne. Ostatnio zbudowano detektory
fal grawitacyjnych dostatecznie czułe, by mogły wykryć bliską supernową.

9.

Kosmologia. Ogólna teoria względności ma wiele do powiedzenia w gałęzi astrofizyki
nazwanej kosmologią. Kosmologia zajmuje się problemami pochodzenia, wielkości i
struktury Wszechświata. Niektóre z tych problemów to: czy wielkość Wszechświata jest
skończona czy nieskończona? Czy Wszechświat się rozszerza? Jak i kiedy został uformo-
wany nasz układ słoneczny i galaktyka? Ile jest galaktyk, jak są one rozłożone w prze-
strzeni? Aby zrozumieć kosmologię trzeba poznać nie tylko teorię względności, ale na-
uczyć się elementów fizyki jądrowej.