Wykład 7

Mechanika relatywistyczna

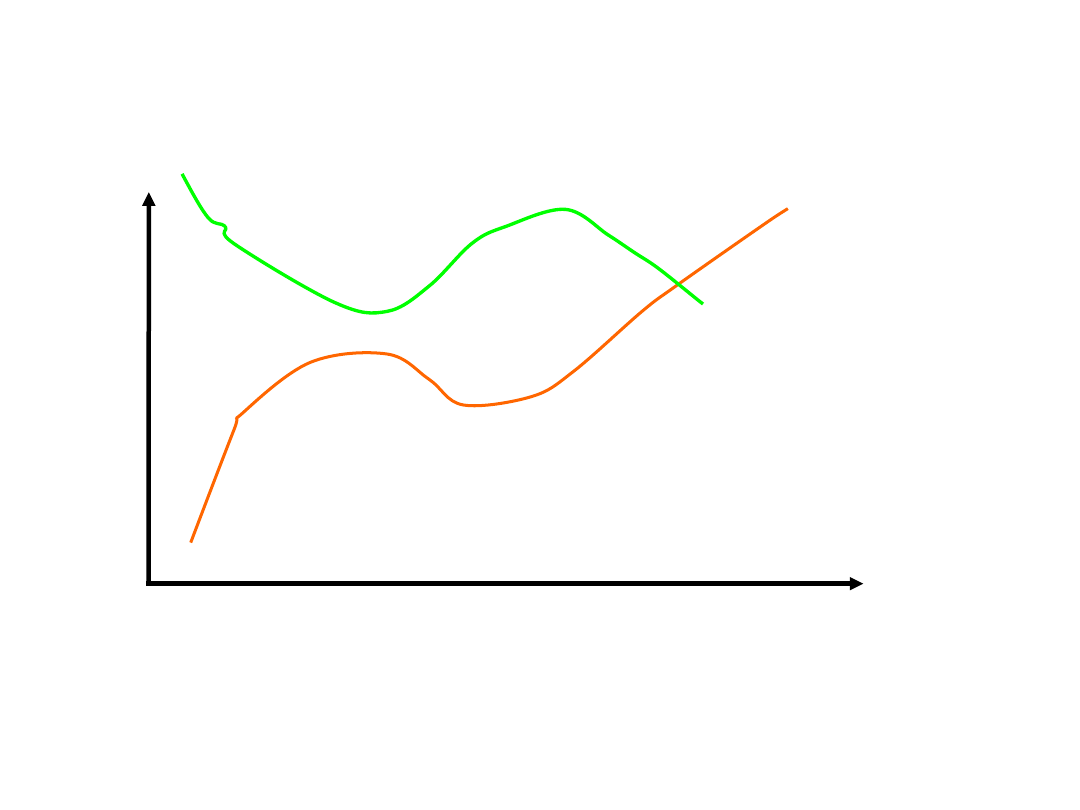
Zdarzenie w czasie i przestrzeni (klasycznie)

czas

p

o

ło

że

n

ie

• wspólny układ odniesienia

• spotkanie w tym samym miejscu, w tym samym czasie

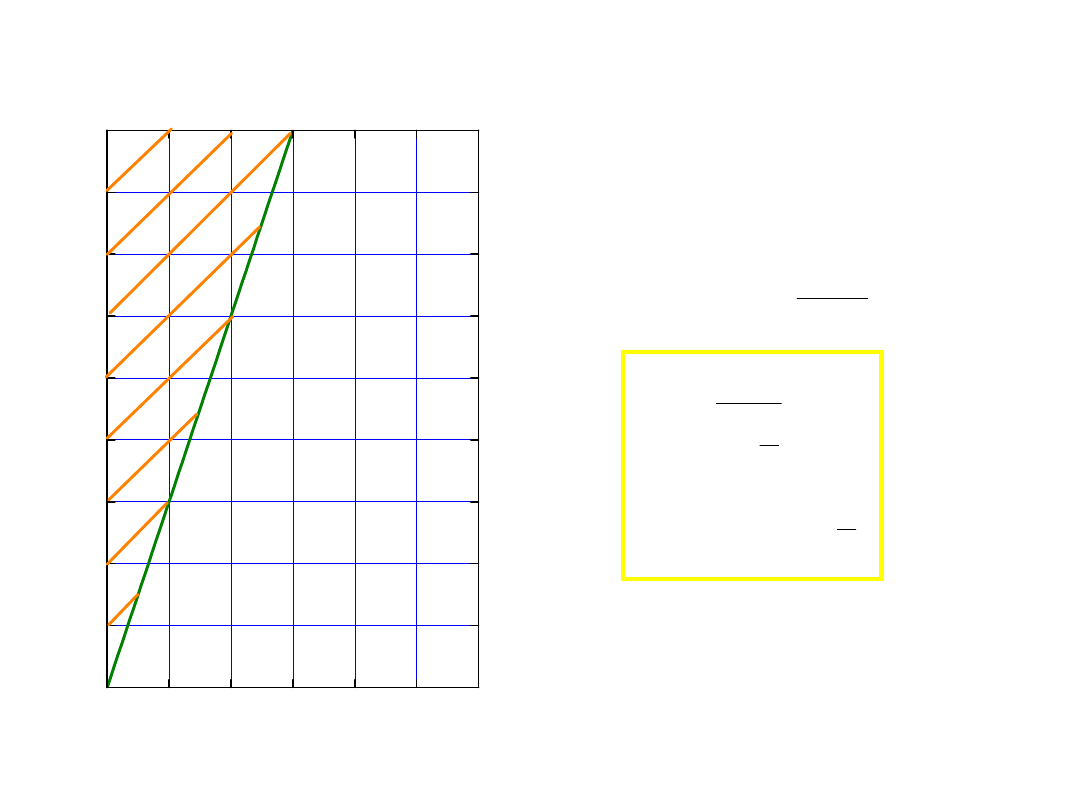
problem posłańca – list do
podróżującego

• codziennie wysyłam list, T

wys

.

• jak często dostaje go adresat?

0

1

2

3

4

5

6

7

8

9

T

wys

cz

as

, t

/T

w

ys

położenie, x

x=

ct

x=

vt

t

2

T

otrz

c

vT

T

T

otrz

wys

otrz















 







c

v

c

v

T

T

wys

otrz

wys

otrz

1

1





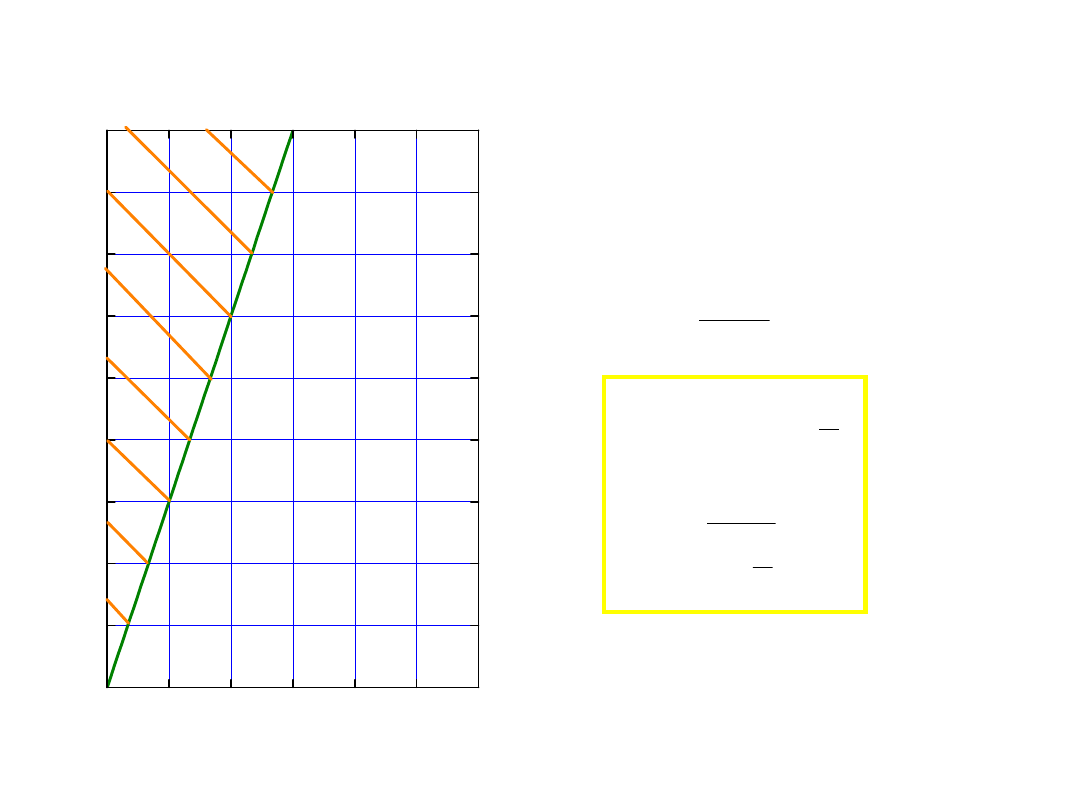
problem posłańca – list od
podróżującego

• odjeżdżający podóźny

codziennie wysyła list, T

wys

.

• jak często otrzymuje go

adresat?

0

1

2

3

4

5

6

7

8

9

T

otrz

cz

as

, t

/T

w

ys

położenie, x

x=

-ct

x=

vt

t

2

T

wys

wys

wys

otrz

T

c

vT

T





c

v

c

v

T

T

wys

otrz

wys

otrz















 



1

1





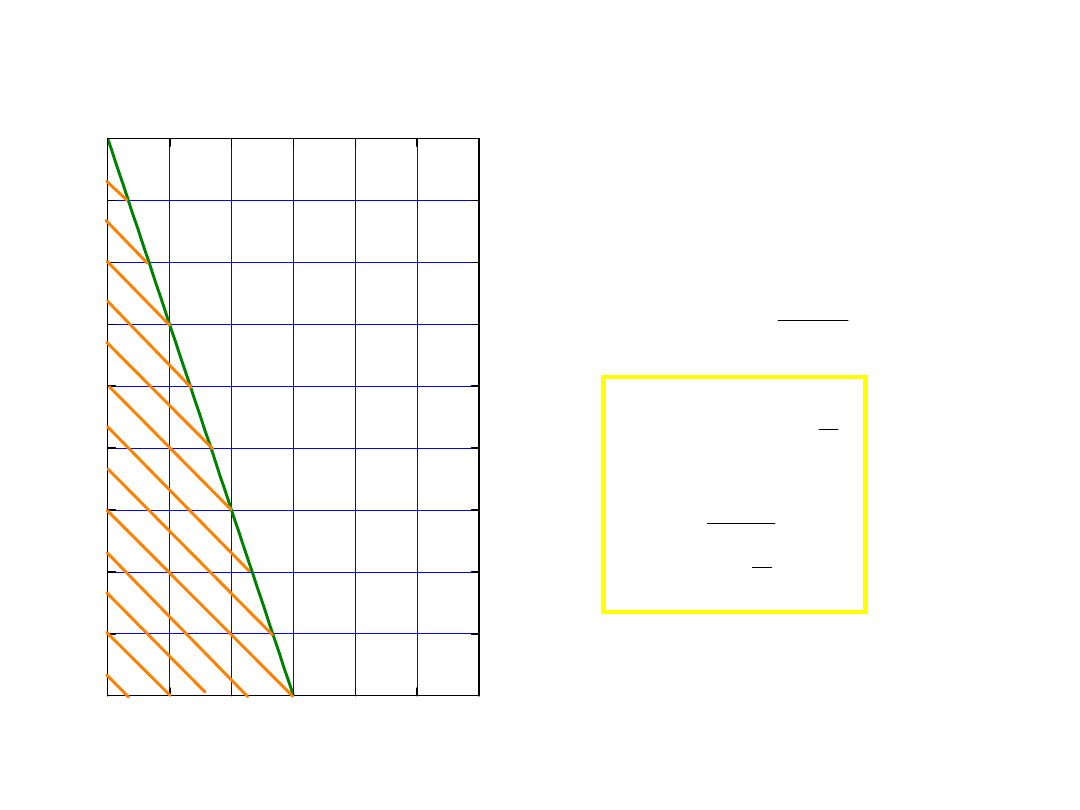
problem posłańca – list od
podróżującego

• powracający podóźny codziennie

wysyła list, T

wys

.

• jak często otrzymuje go adresat?

0

1

2

3

4

5

6

7

8

9

T

otrz

cz

as

, t

/T

w

ys

położenie, x

x=

-ct

x=

-v

t

T

wys

c

vT

T

T

wys

wys

otrz





c

v

c

v

T

T

wys

otrz

wys

otrz















 



1

1





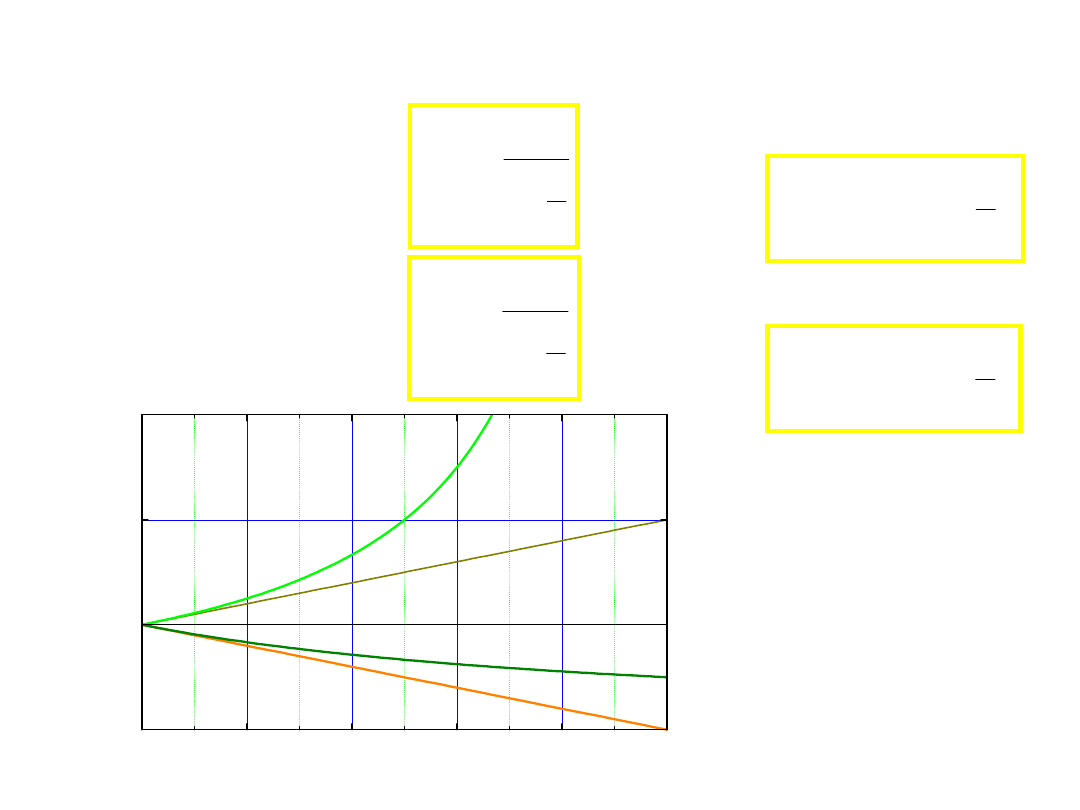
problem posłańca – 4 przypadki

• powracający podróżny

0.0

0.2

0.4

0.6

0.8

1.0

0

1

2

3

1/(1-v/c)

1+v/c

1/(1+v/c)

st

os

un

ek

o

kr

es

ów

,

T

o

tr

z

/T

w

ys

stosunek prdkości, v/c

1-v/c











 



c

v

T

T

wys

otrz

1

c

v

T

T

wys

otrz





1

• list do odjeżdżającego.

• odjeżdżający podróżny











 



c

v

T

T

wys

otrz

1

• list do wracającego.

c

v

T

T

wys

otrz





1

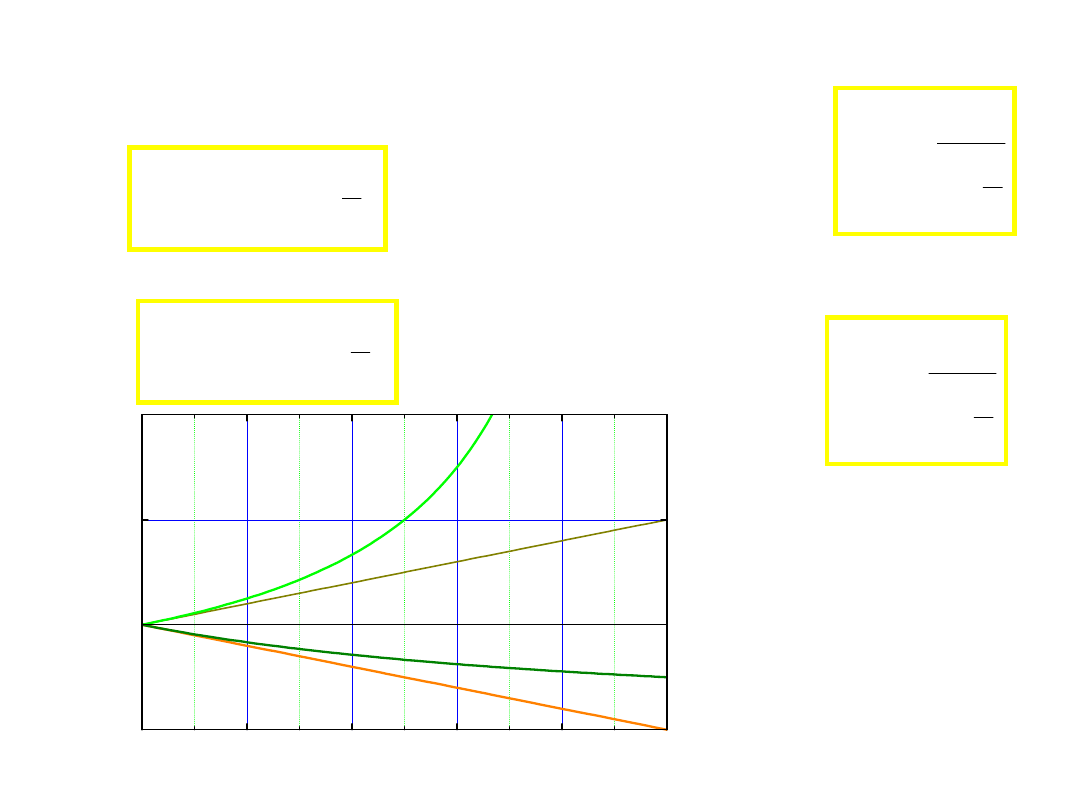
Efekt Dopplera fali akustycznej – 4
przypadki

• przybliżający się odbiorca

0.0

0.2

0.4

0.6

0.8

1.0

0

1

2

3

1/(1-v/c)

1+v/c

1/(1+v/c)

st

os

un

ek

o

kr

es

ów

,

T

o

tr

z

/T

w

ys

stosunek prdkości, v/c

1-v/c

c

v

wys

odb





1















 



c

v

wys

odb

1





• oddalające się źródło.

• oddalający odbiorca

c

v

wys

odb





1





• przybliżające się źródło.











 



c

v

wys

odb

1





Jest problem czaso-przestrzeni!

• gdy sygnał rozchodzi się w ośrodku (posłaniec,

fala akustyczna)

– różne poczucie czasu w układach poruszających się,
– niezgodność zegarów?

• gdy sygnał świetlny, DOŚWIADCZENIE:

– światło rozchodzi się w próżni!!!
– szybkość światła w każdym układzie jest taka sama!!!

• co musimy zrobić

– jeszcze raz znaleźć czynnik skalujący czas pamiętając,

że nadawca i odbiorca są sobie równoważni, ważna jest

jedynie ich wzajemna prędkość.

– szukać nowego wzoru transformującego

r,v,t

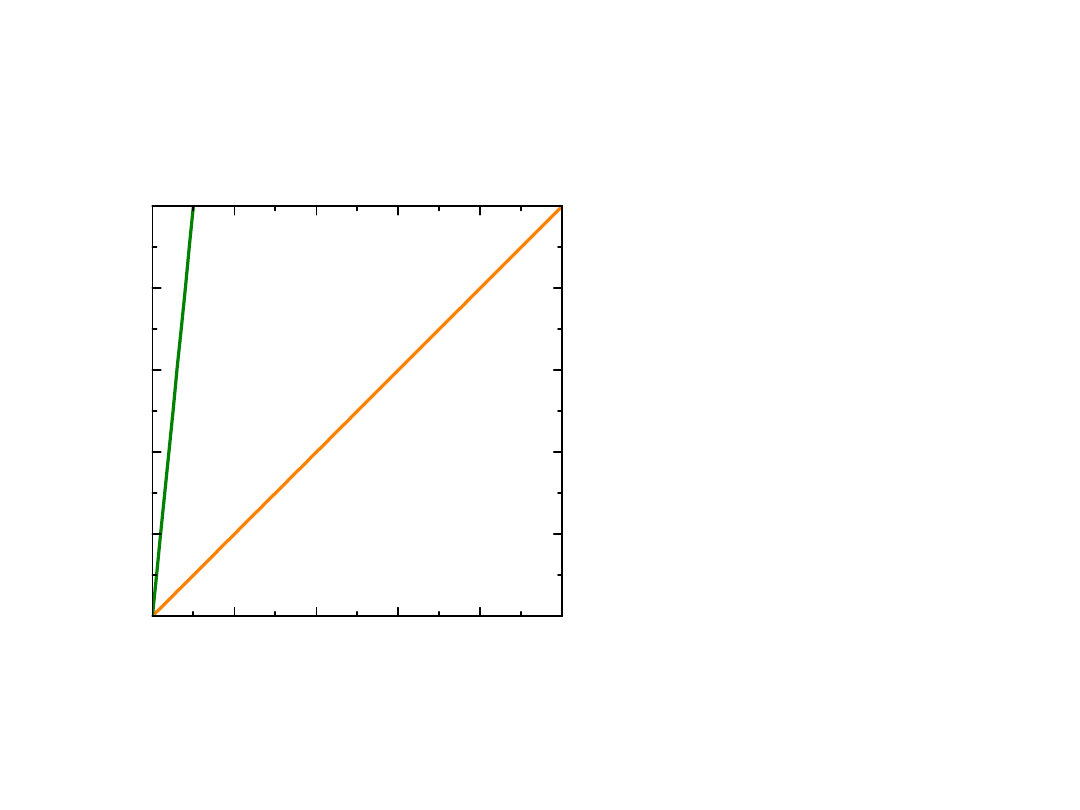
Wykres Minkowskiego, czasoprzestrzeń

0

2

4

6

8

10

0

2

4

6

8

10

cz

a

s,

c

t

położenie, x

lin

ia

św

iat

a

x=

ct

lin

ia

ś

w

ia

ta

pu

nk

tu

m

at

er

ia

ln

eg

o

x=

vt

Co to są zdarzenia
równoczesne?





ct

z

y

x

,

,

,

Cztery wymiary:

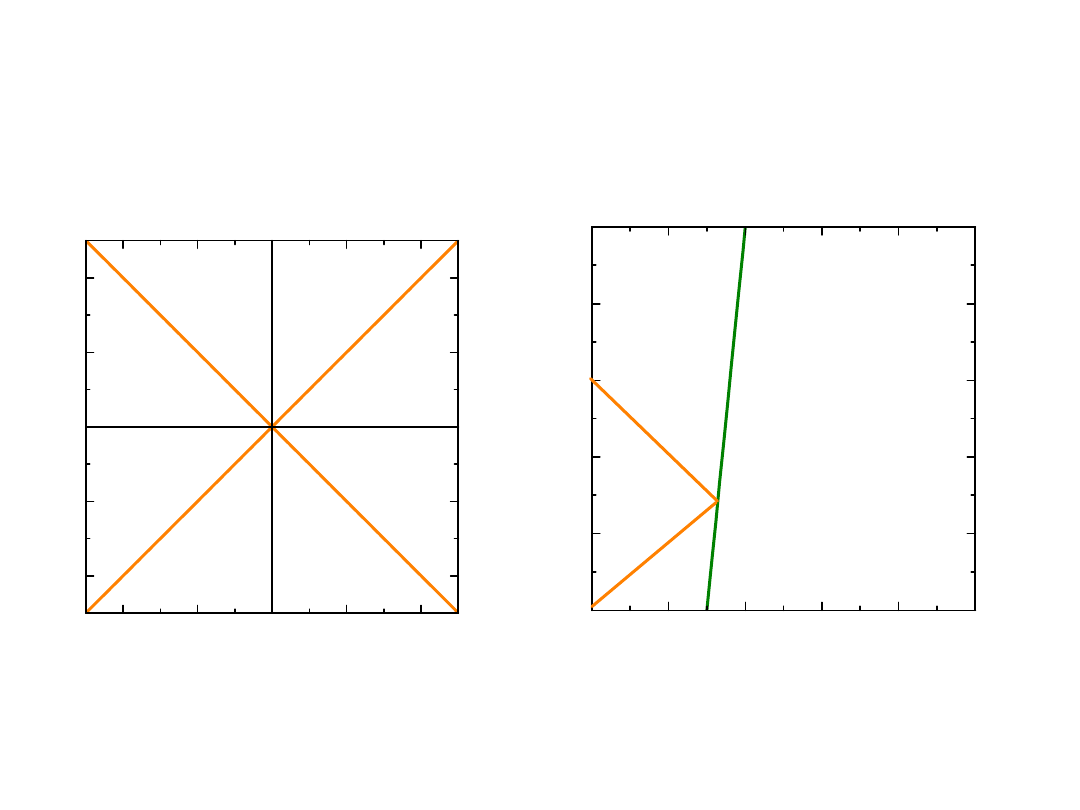
Linia świata sygnału

świetlnego

od i do obserwatora

-4

-2

0

2

4

-4

-2

0

2

4

x=

-ct

cz

a

s,

c

t

położenie, x

x=

ct

t

1

x=

-ct

cz

a

s,

c

t

położenie, x

x=

ct

x=

vt

t

2

P

radar (echo)

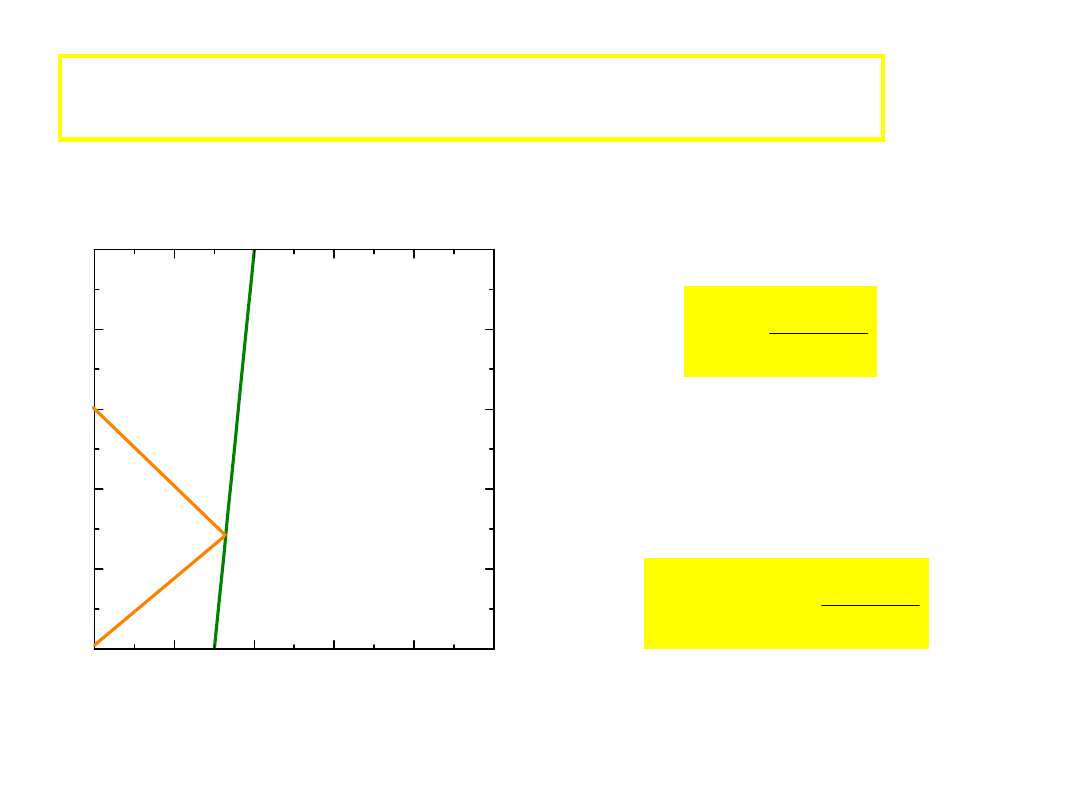
t

P

t

1

x=

-ct

cz

a

s,

c

t

położenie, x

x=

ct

t

2

P

odległość do obiektu (w pewnej chwili, P)

mierzona czasem przebiegu sygnału (echo)

 

2

1

2

t

t

c

t

x

p

P





P - zdarzenie – punkt w przestrzeni Minkowskiego

- jak obserwator wykonuje pomiar zdarzenia P

2

1

2

t

t

t

P





Czas obserwacji zdarzenia P

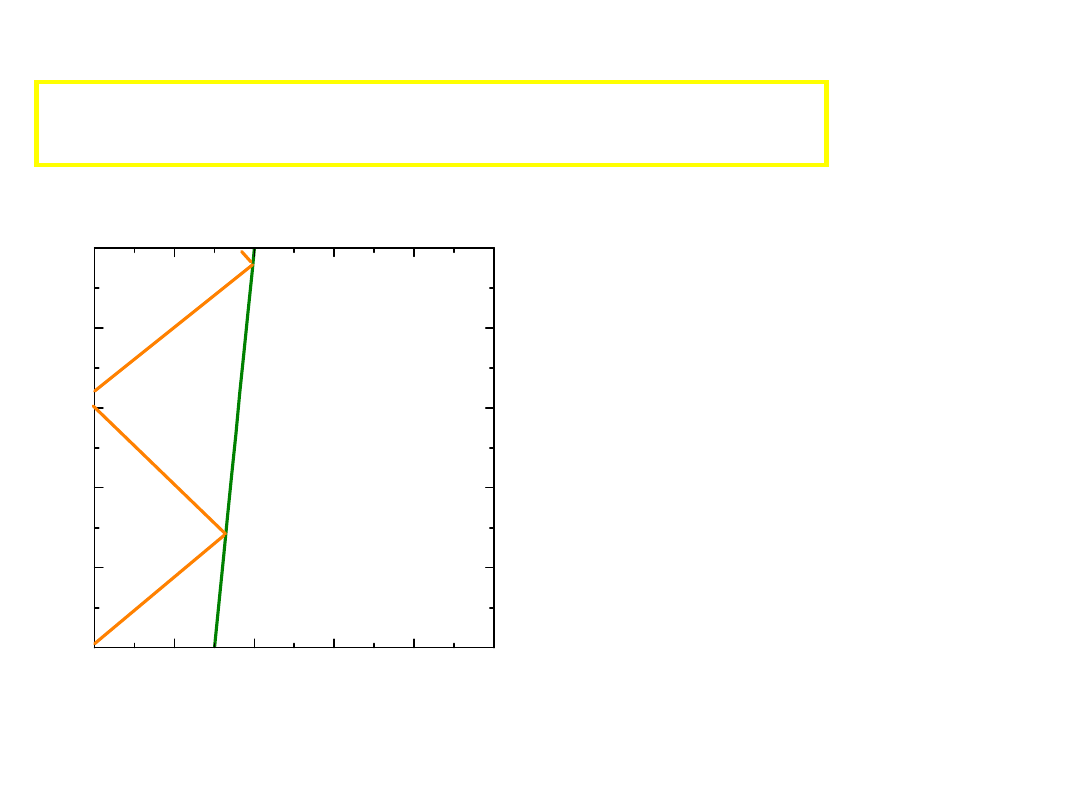
P

2

t

P

t

1

x=

-ct

cz

a

s,

c

t

położenie, x

x=

ct

x=

vt

t

2

P

1

Obserwator radarowy zbiera informacje o obiekcie:

buduje jego linie świata.

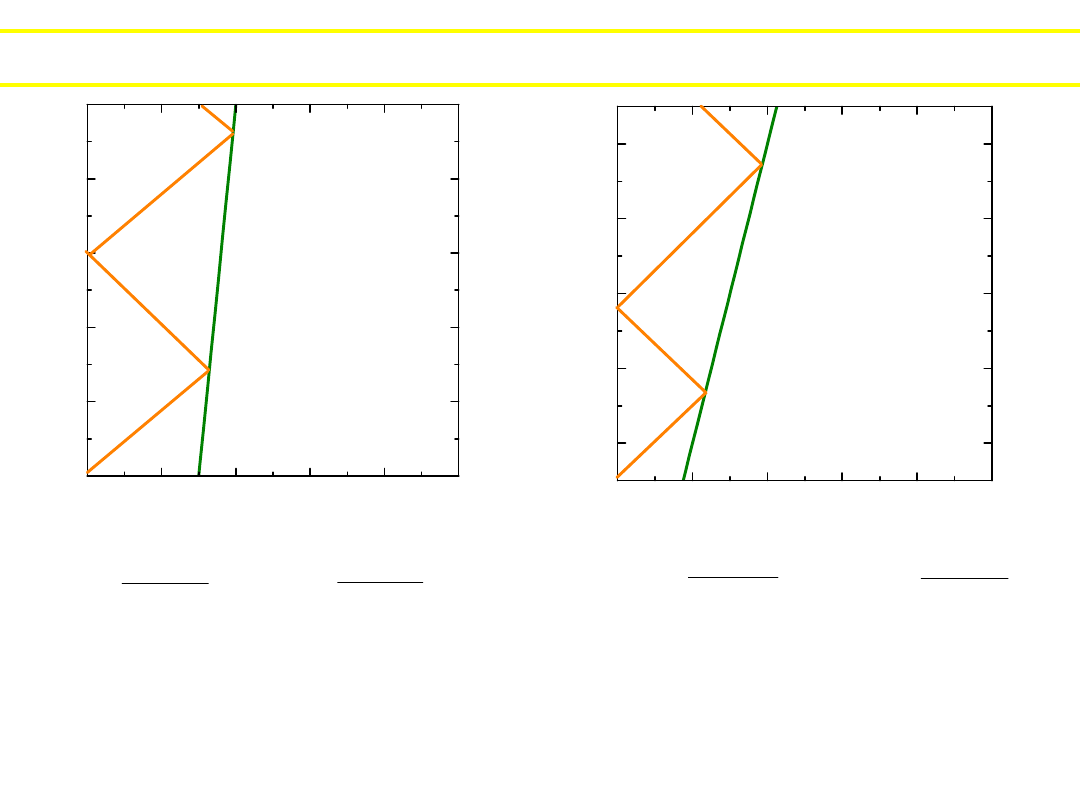
P

2

t

P

t

1

x=

-ct

cz

a

s,

c

t

położenie, x

x=

ct

x=

vt

t

2

P

1

2

1

2

t

t

c

x





Dwaj obserwatorzy zbierają informację o tym samym obiekcie

2

1

2

t

t

t

P





Jaki jest związek pomiędzy wynikami pomiarów gdy:

• układy poruszają się ruchem jednostajnym
• prędkość światła,

c

, jest stała!!!

P'

2

t'

P

t'

1

x=

-ct

cz

a

s,

c

t'

położenie, x'

x=

ct

x'

=

v'

t'

t'

2

P'

1

2

1

2

t

t

t

P











2

1

2

t

t

c

x











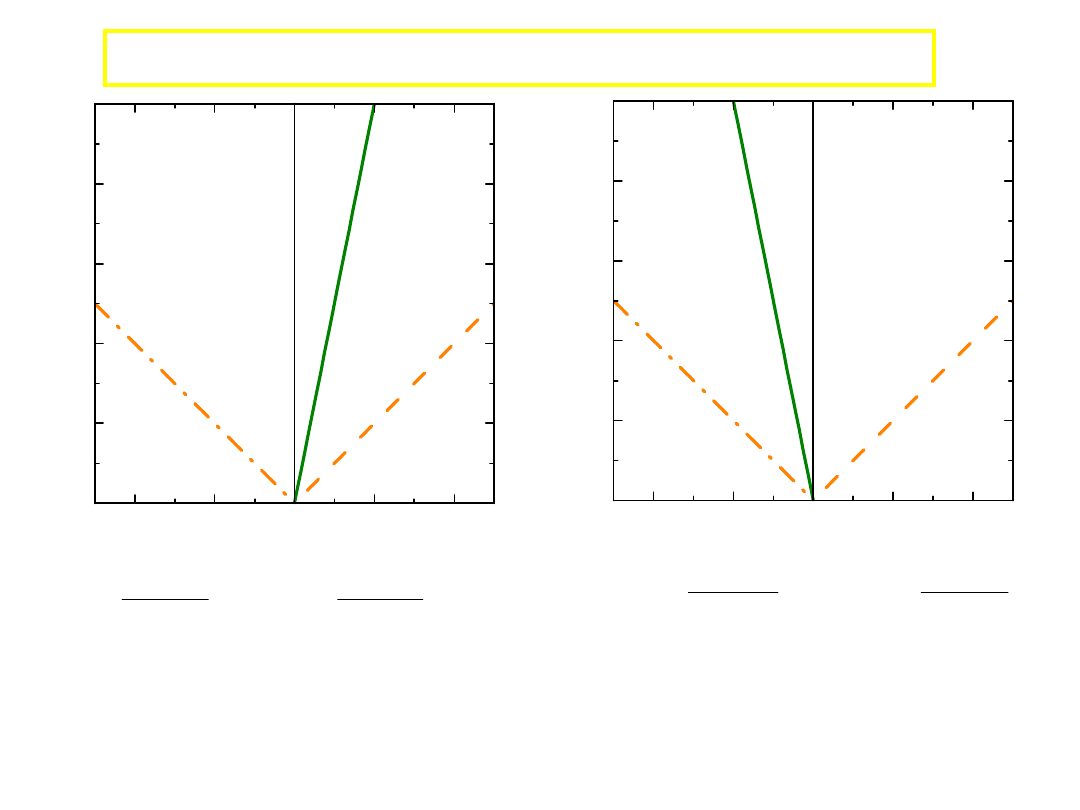
x=

-ct

cz

a

s,

c

t

położenie, x

x=

ct

x=

V

t

2

1

2

t

t

c

x





Dwaj obserwatorzy wzajemnie się obserwują

2

1

2

t

t

t

P





2

1

2

t

t

t

P











2

1

2

t

t

c

x











x'=

-ct'

cz

a

s,

c

t'

położenie, x'

x'

=c

t'

x'=

-V

t'

t

V

x

Vt

x











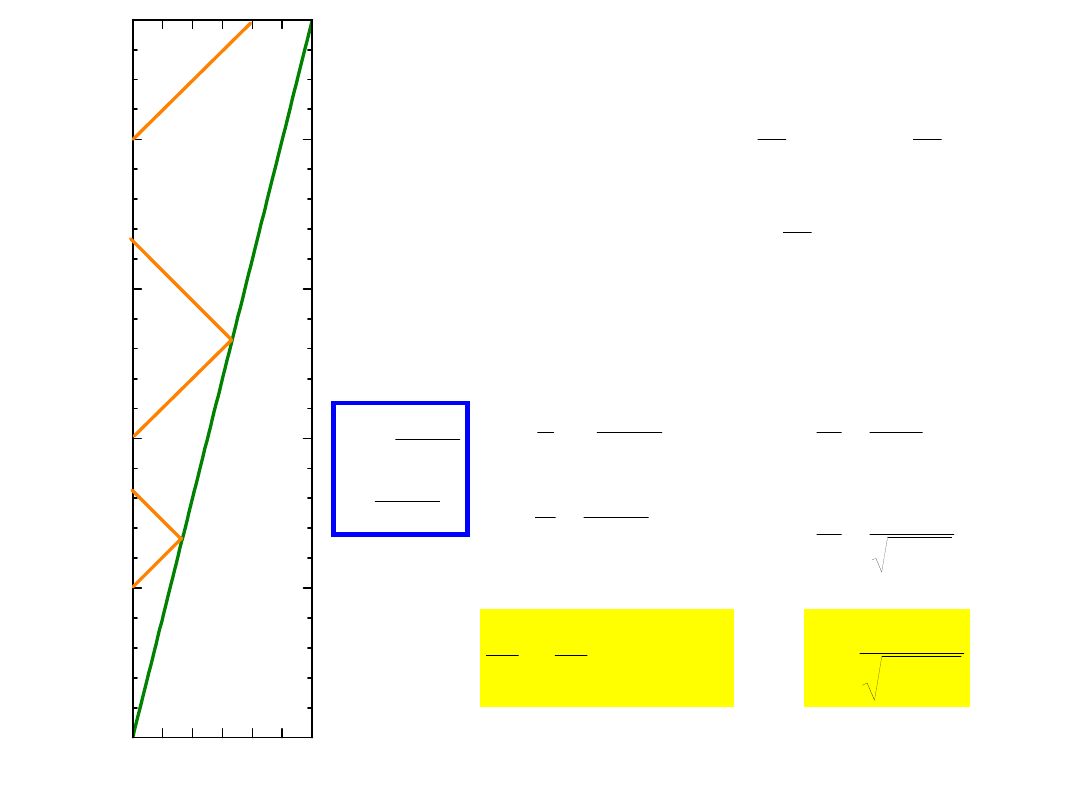
okresy mierzone przez obu
obserwatorów muszą być
wzajemnie proporcjonalne

x

--

---

--

---

>

t -->

2cT -->

cT -->

<--2cT'

<--cT'

2cT

0

-->

t'

1

x=

-ct

cz

a

s,

c

t

położenie, x

x=

ct

x'

=

v'

t'

cT

0

-->

0

T

T

const

T

T









2

0

const

T

T



2

2

0

T

T

t

T

T

c

x

o









0

T

T

T

T

c

t

x

V

o



















1

1

0

T

T

0

T

T

T

T

c

V

o











2

1

1













T

T



















1

0

T

T

T

T

2

1

1









czynnik Lorentza

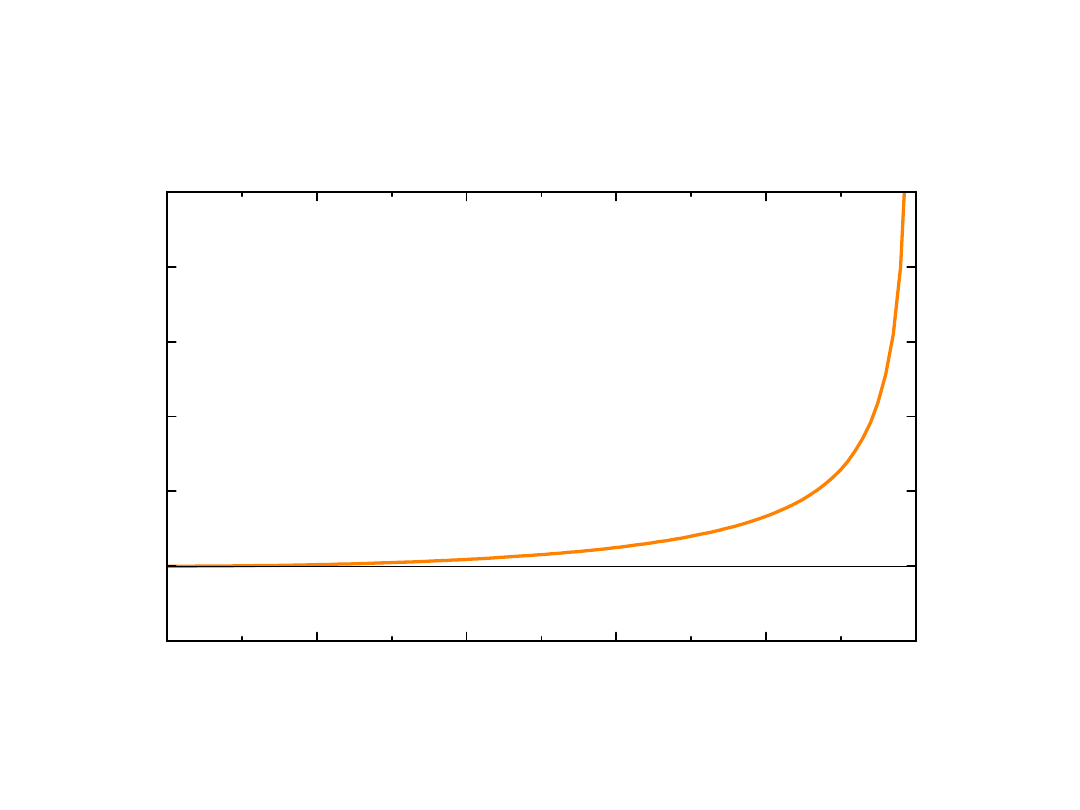
Czynnik Lorentza, 

0.0

0.2

0.4

0.6

0.8

1.0

0

1

2

3

4

5

6

C

zy

nn

ik

L

or

en

tz

a,



Stosunek prdkości, v/c

 -miara poprawki relatywistycznej

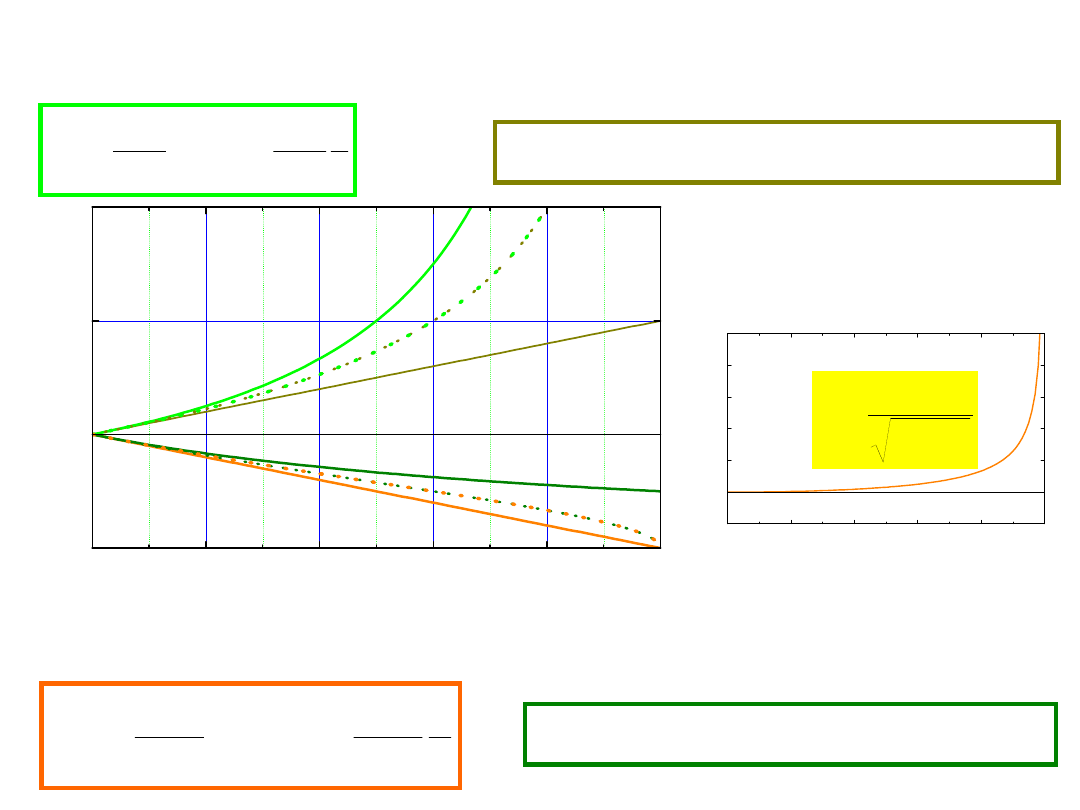
od wracającego

posłaniec sygnał

0.0

0.2

0.4

0.6

0.8

1.0

0

1

2

3

1/(1+v/c)/



(1-v/c)*



1/(1-v/c)/



(1+v/c)*



1/(1-v/c)

1+v/c

1/(1+v/c)

st

os

un

ek

o

kr

es

ów

,

T

o

tr

z

/T

w

ys

stosunek prdkości, v/c

1-v/c























1

1

wys

otrz

wys

otrz

T

T

T

T







1

1

1









wys

otrz

wys

otrz

T

T

T

T

do odjeżdżającego:
posłaniec sygnał

od odjeżdżającego
posłaniec sygnał

























1

1

wys

otrz

wys

otrz

T

T

T

T

do wracającego

posłaniec sygnał







1

1

1









wys

otrz

wys

otrz

T

T

T

T

2

1

1









0.0

0.2

0.4

0.6

0.8

1.0

0

1

2

3

4

5

6

C

zy

nn

ik

L

or

en

tz

a,



Stosunek prdkości, v/c

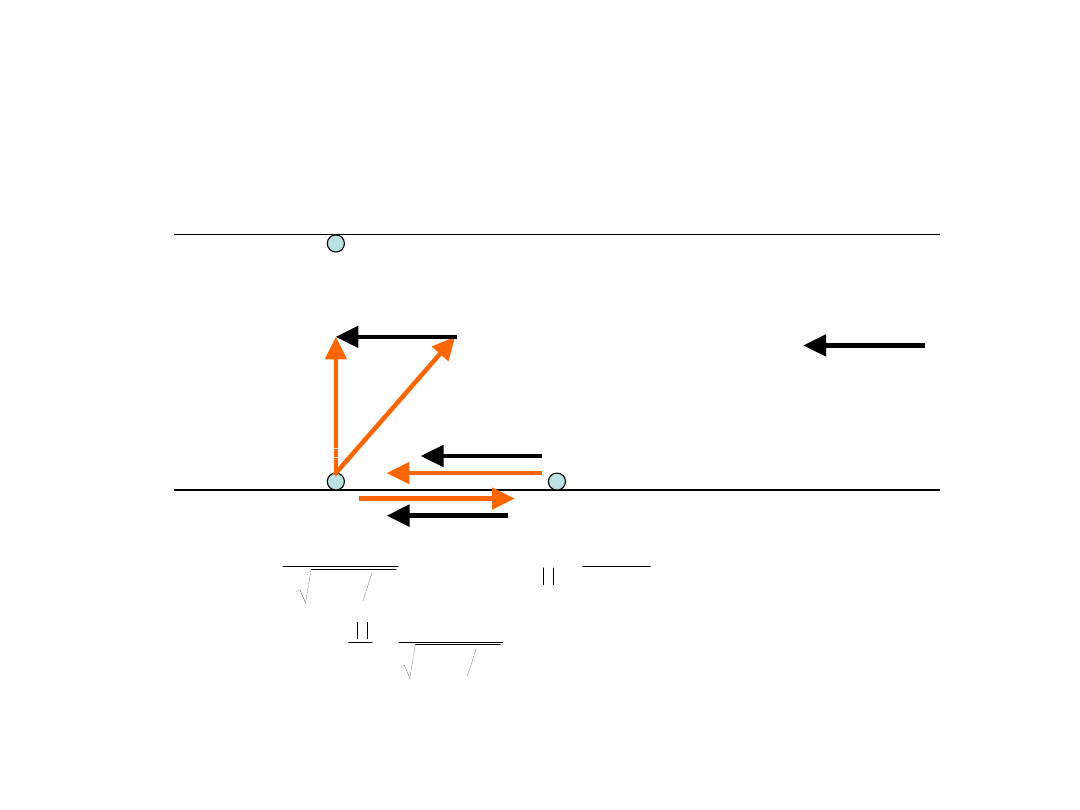
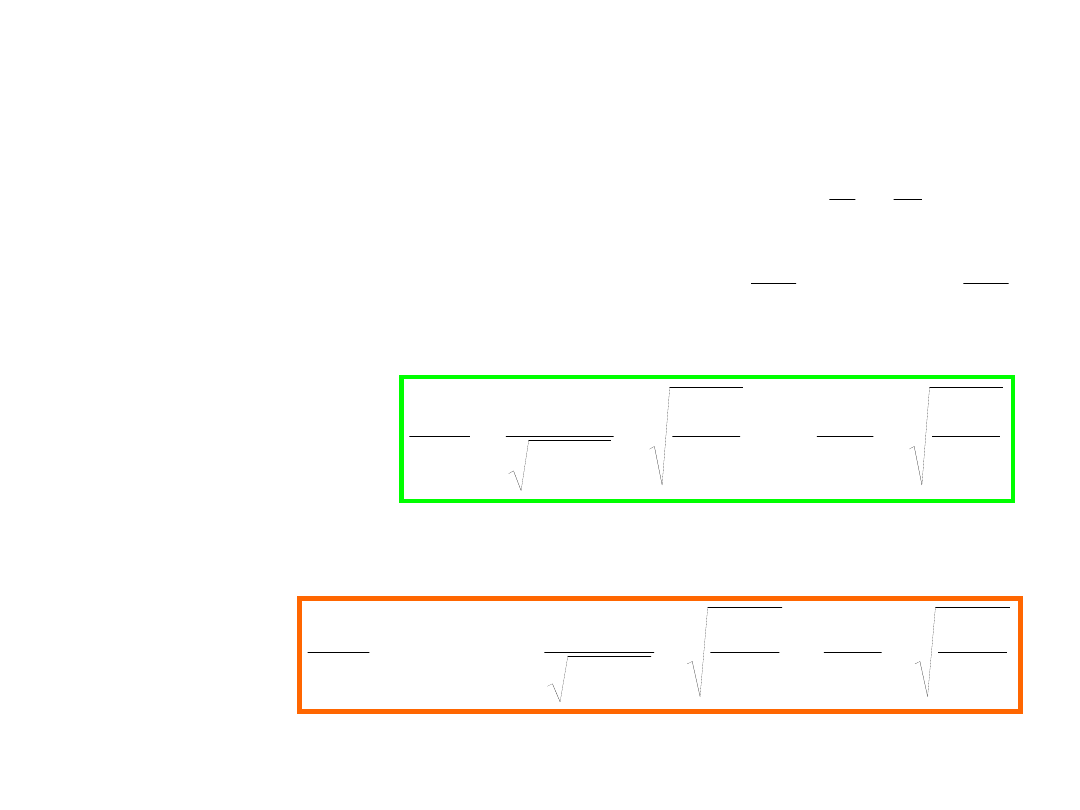
Światło, w odróżnieniu od posłańca, czy dźwięku, nie porusza

się w żadnym ośrodku!

• Wyścig pływaków w

dwu wymiarach

• Interferometr Michelsona

Tak jakby światło rozchodziło się w dodatkowym wymiarze!!!





















2

2

2

2

2

2

1

1

2

1

2

c

v

t

t

v

c

lc

t

c

v

c

l

t

v

v

c

Dylatacja czasu

• Paradoks bliźniaków
• Czas życia (rozpadu) czastek

elementarnych

– mion w spoczynku rozpada się =2.2 s
– mion rozpędzony(1.2 GeV/c) rozpada się

=26 s

• Paradoks bliźniaków

Efekt Dopplera

• 4 przypadki dla dźwieku
• 2 przypadki dla światła

– oddalanie

– przybliżanie







































1

1

1

1

1

1

2

wys

otrz

wys

otrz



















































1

1

1

1

1

1

1

2

wus

otrz

wus

otrz















2

2









k

T

T

c

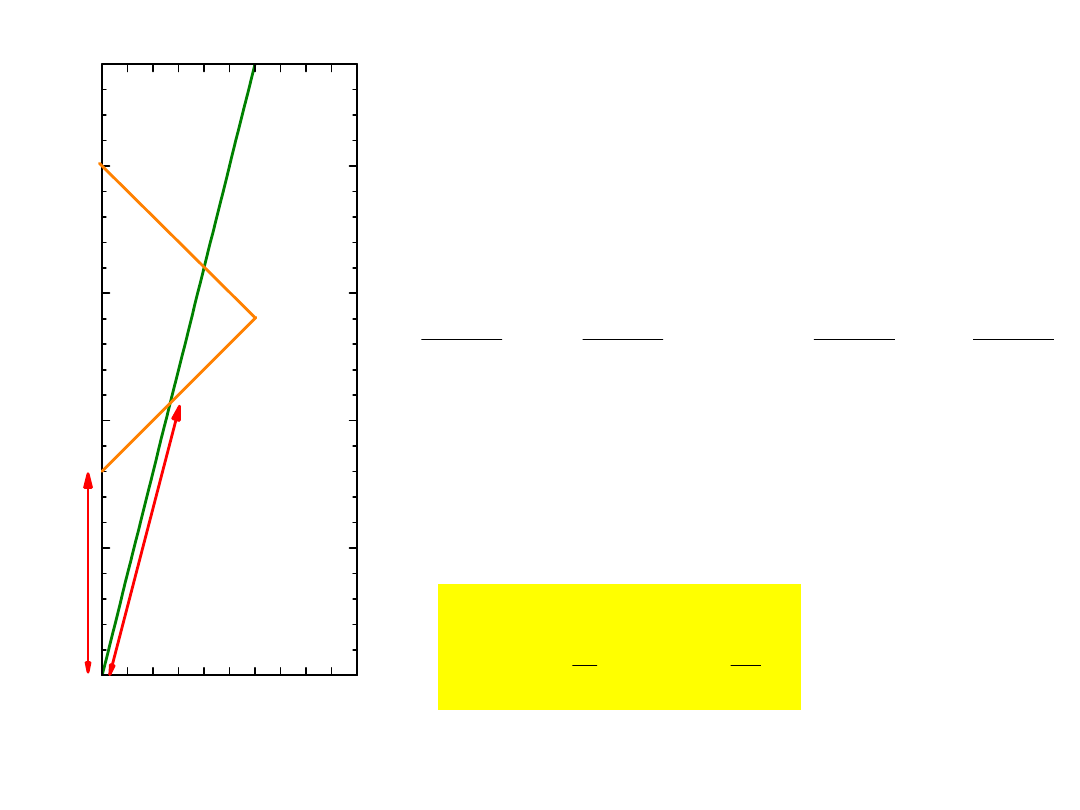
Transformacja Lorentza
(1)

Problem: jak to samo zdarzenie

(r,ct) opisuje się w dwu różnych
układach odniesienia.

cT'

cT

0

P(x,ct)

<--ct'-x'

ct -->

ct

2

=ct+x -->

cz

as

, c

t'

x

---

--

---

-->

ct

1

=ct-x -->

<--ct'+x

x=

-ct

cz

a

s,

c

t

położenie, x

x'

=

v'

t'

Obaj obserwatorzy wyznaczają

, x,t

ze wzorów

:

2

2

2

2

1

2

1

2

1

2

1

2

t

c

t

c

t

c

ct

ct

ct

t

c

t

c

x

ct

ct

x





























Pamiętamy związek interwałów czasowych:





0

1

T

T





















































x

t

c

x

ct

x

ct

x

t

c









1

1



 





















 













 















x

c

v

t

x

c

t

t

t

v

x

t

c

x

x

2













Transformacje Lorentza i Galileusza

dylatacja czasu i długości



























 



















x

c

v

t

t

z

z

y

y

t

v

x

x

2





































t

t

z

z

y

y

t

v

x

x

1

1

1

0

1

0

2

2

















c

v

c

albo

c

c

v

gdy





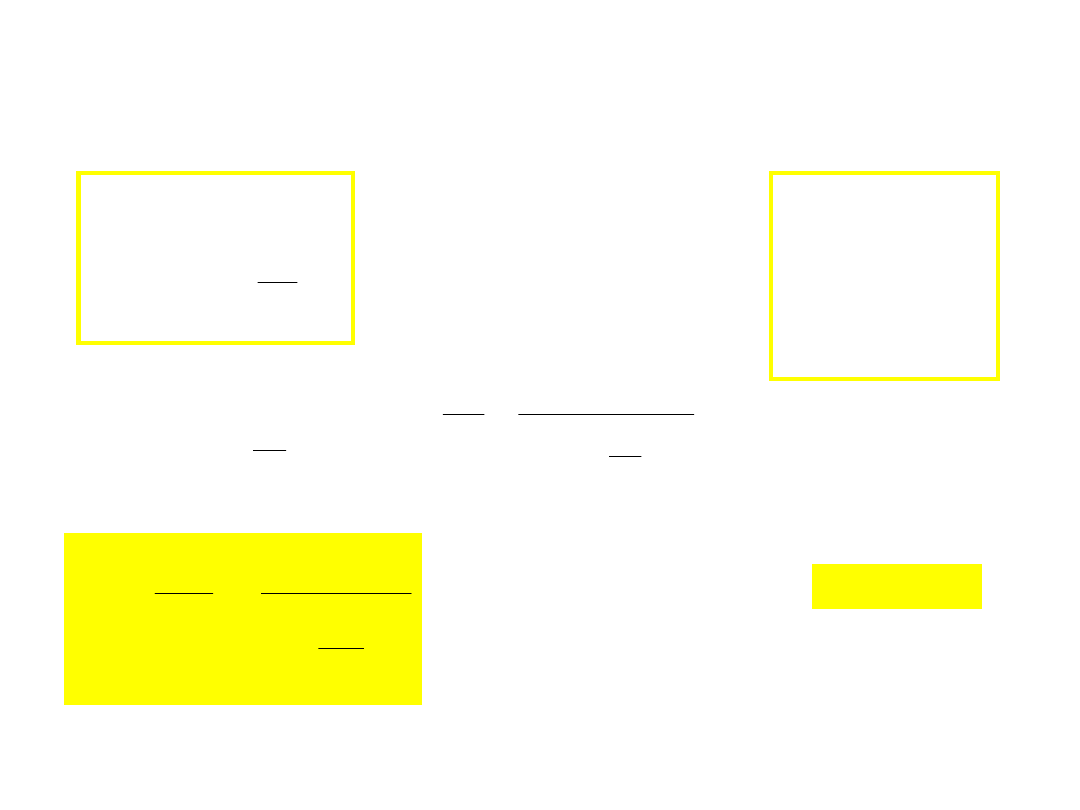
Transformacje Lorentza i Galileusza

- transformacja prędkości























 











x

c

V

t

t

t

V

x

x

2





































t

t

z

z

y

y

t

V

x

x

V

v

v





























 











dx

c

V

dt

t

d

dt

V

dx

x

d

2



















 













dx

c

V

dt

dt

V

dx

t

d

x

d

v

x

2





x

x

x

v

c

V

V

v

t

d

x

d

v

2

1













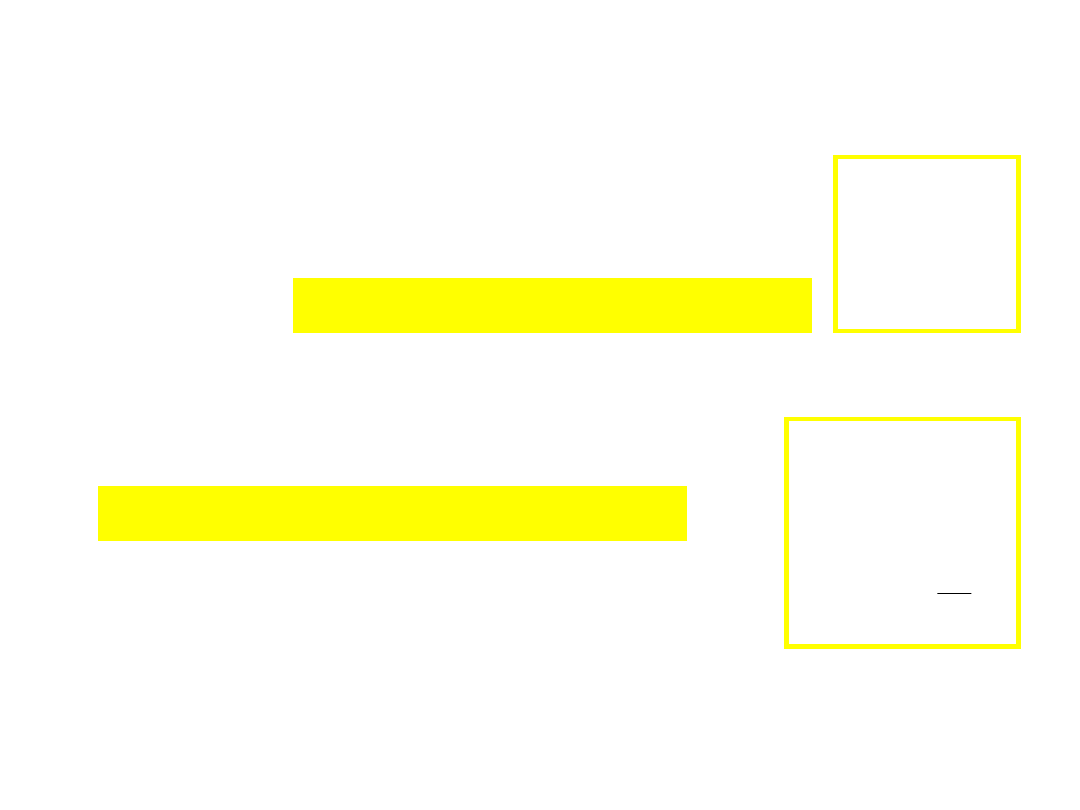
Niezmienniki
– ważne wielkości fizyczne (absolutne)

Niezmienniki transformacji Galileusza:
• czas
• odległość
• ładunek

































t

t

z

z

y

y

t

v

x

x



 

 



2

1

2

2

1

2

2

1

2

2

z

z

y

y

x

x

L







































 



















x

c

v

t

t

z

z

y

y

t

v

x

x

2





Niezmiennik transformacji Lorentza:
• interwał (miara czasoprzestrzeni)
• ładunek elektryczny



 

 



2

1

2

2

1

2

2

1

2

2

2

z

z

y

y

x

x

t

c

s















Niezmiennicze powinny być prawa fizyki!

Wielkości względne:
• czas
• odległość

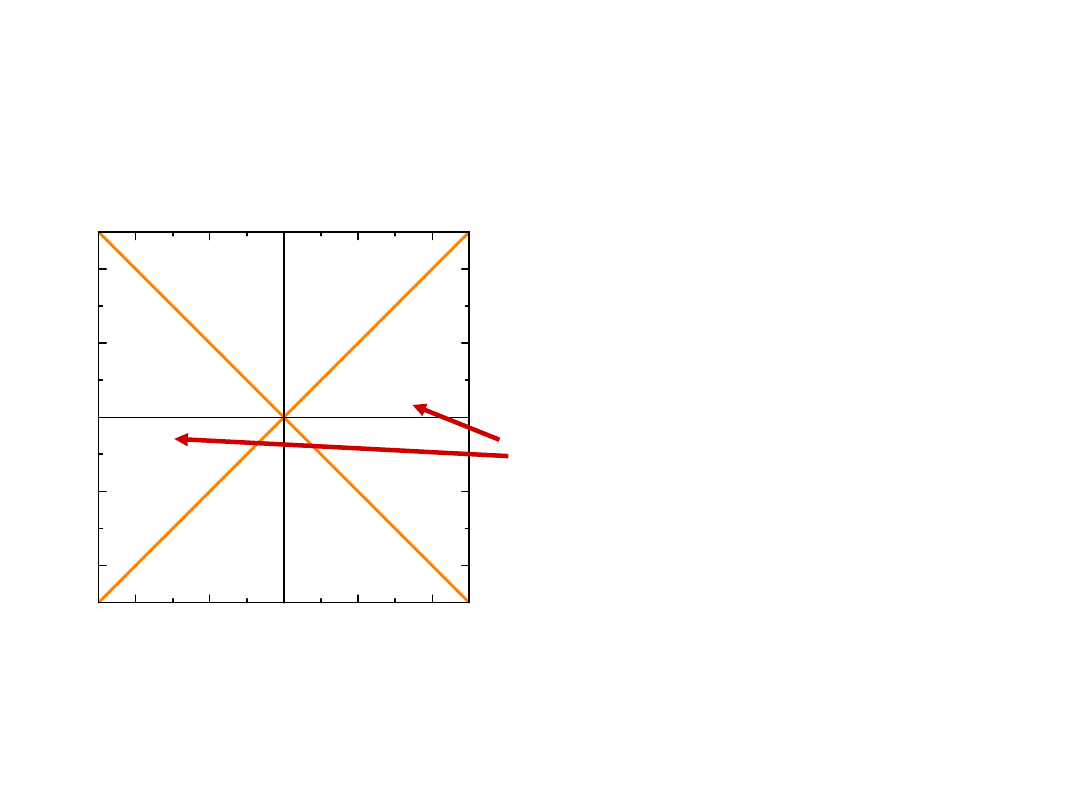
Interwały

-4

-2

0

2

4

-4

-2

0

2

4

s>0

przyszość

czasopodobny

x=

-ct

cz

a

s,

c

t

położenie, x

x=

ct

czasopodobny

przyszość

v

2

<c

2

s>0

interwał zerowy s=0

interwał przstrzennopodobny
obszar teraźniejszości s<0

stożek świetlny s>0

stożek świetlny s>0

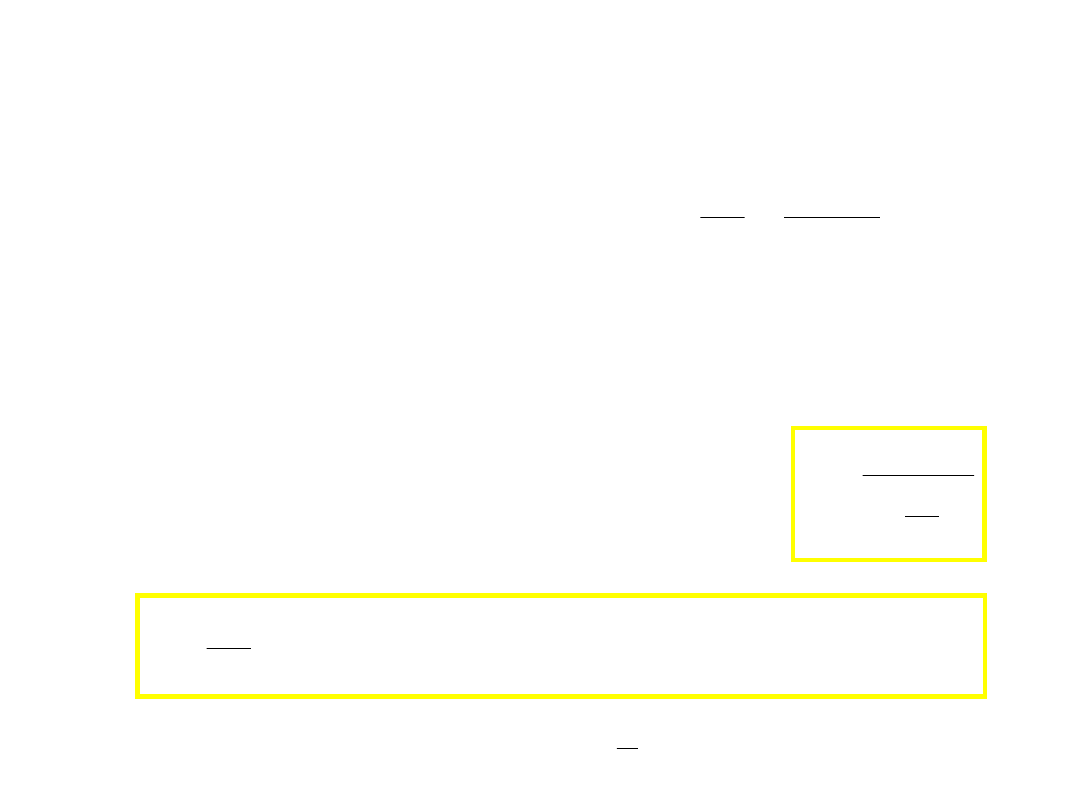
II zasada dynamiki

• Oba sformułowania niezmiennicze względem transformacji

Galileusza (stała masa)

• poszukujemy prawa niezmienniczego względem

transformacji Lorentza

– znamy zasadę transformowania prędkości (x,t)
– pozwólmy, żeby m(v)
– ma obowiązywać zasada zachowania pędu

 

dt

m

d

dt

d

czy

m

v

p

F

a

F







x

x

x

v

c

V

V

v

v

2

1







 

0

m

v

m

m

dt

d









v

p

p

F

doświadczenia masy cyklotronowej

B

m

e

c





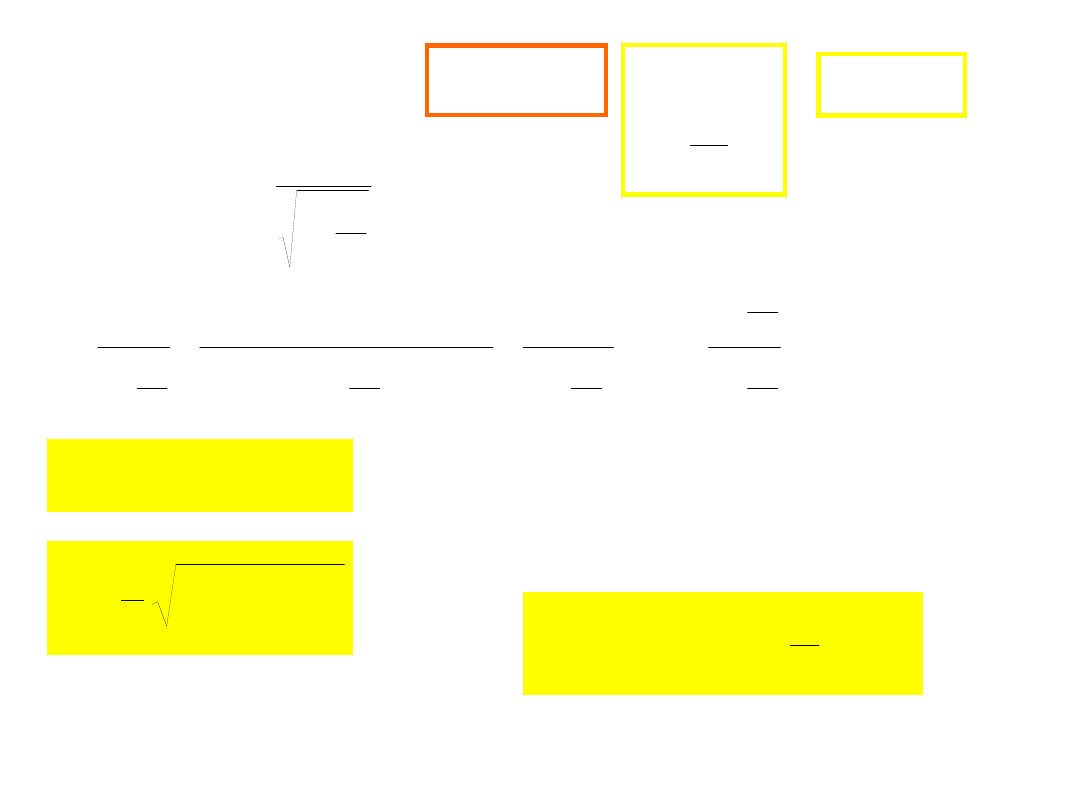
Energia i pęd

2

mc

E 

v

p

v

p

2

0

c

E

m







0

m

m





2

2

2

2

4

2

0

2

2

2

2

2

0

2

2

2

2

2

0

4

2

0

2

2

2

0

2

2

4

2

0

2

2

2

2

0

2

0

2

1

1

1

1

1

1

c

v

c

v

c

m

c

v

v

c

m

c

v

v

c

m

c

m

v

c

m

c

v

c

m

E

c

v

c

m

c

m

mc

E

































4

2

0

2

2

2

c

m

c

p

E





4

2

0

2

1

c

m

E

c

p





Bardziej ogólne wyrażenie na pęd,

c

v

c

E

p

m

dla





0

0

Foton, neutrino elektronowe i mionowe

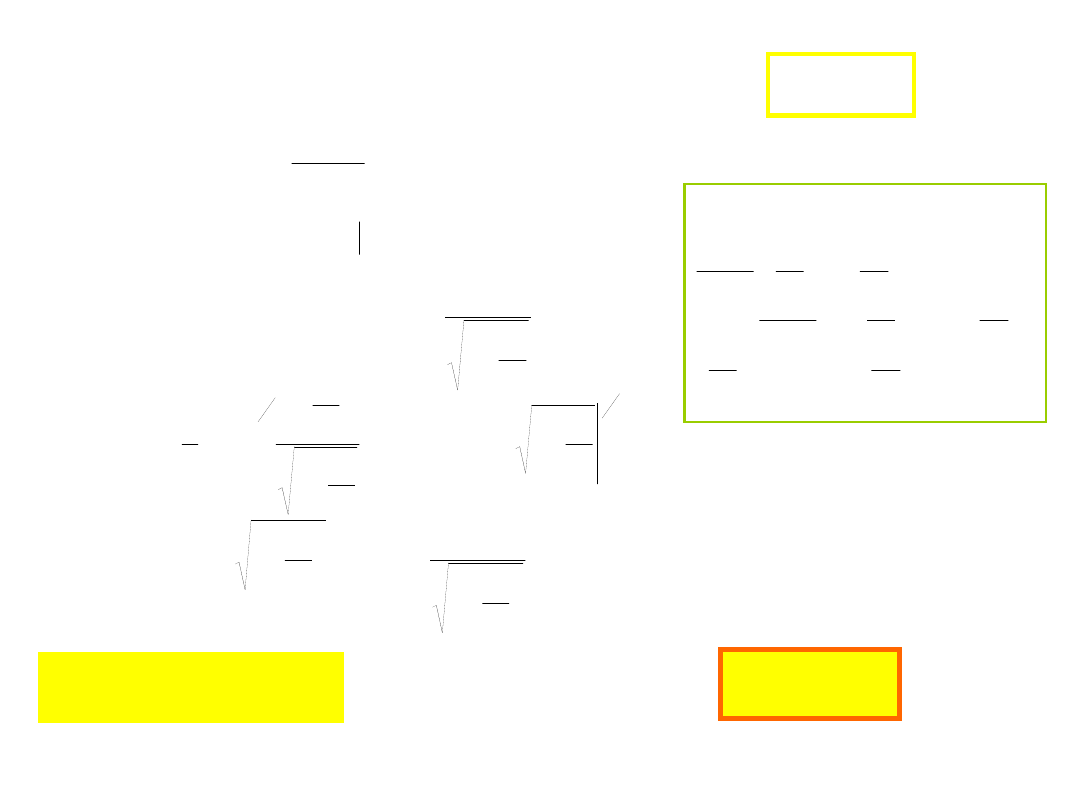
Praca wykonana przez siłę

 

 

















mv

vd

dr

dt

mv

d

Fdr

W

E

   

 

 



























V

o

V

o

k

V

V

V

k

d

c

v

m

mV

d

m

v

mV

E

d

v

m

m

m

d

W

E

0

2

2

2

0

2

0

0

0

1

v

v

v

v

v

v

v

v

v

v



całkowanie przez części

 

 

























dt

dt

dG

F

FG

dt

G

dt

dF

dt

dt

dG

F

dt

G

dt

dF

dt

dt

FG

d

FG

dt

dG

F

G

dt

dF

dt

FG

d

2

2

2

2

2

2

2

2

2

0

2

2

2

2

0

2

2

2

2

2

2

1

1

1

1

2

1

c

m

c

V

c

m

c

m

c

V

c

m

mV

E

c

v

c

m

mV

c

v

c

v

d

c

m

mV

E

o

o

o

o

k

c

V

o

c

V

o

k









































2

2

c

m

mc

E

o

k





2

mc

E 

0

m

m





Masa relatywistyczna

2

2

c

m

mc

E

o

k





2

mc

E 

0

m

m





• bezpośredni związek masy bezwładnej i energii

• przyrost energii (kinetycznej) związany jest ze wzrostem
masy

• wiązanie ciał związany jest z ubytkiem (deficytem) masy

• masa i energia to dwie miary taj samej wielkości

Przybliżenie dla małych
prędkości

2

1

...

2

1

1

1

2

2

2

2

2

2

2

2

0

2

2

mv

c

v

c

m

c

m

c

c

v

m

c

m

mc

E

o

o

o

k

































Deficyt masy

2

mc

E 

•Masa deuteronu,

E wiązaniakwant .

p+n=D+

 

 

 

     

.

.

.

0023

.

0

.

.

.

0086

.

1

.

.

.

0078

.

1

93

.

0

10

66056

.

1

12

1

.

.

.

1

2

1

1

0

1
1

1

0

1
1

27

12

6

m

j

a

D

m

n

m

H

m

m

j

a

n

m

m

j

a

H

m

GeV

kg

C

m

m

j

a





















•rozpad cząstki

nadmiar energii  kwant .

ścisła zasada zachowania energii (masy, f(v))
ścisła zasada zachowania pędu relatywistycznego

rozpad mezonu p+ na mion m+ i neutrino n