
MODEL LINII DŁUGIEJ (uzupełnienia w stosunku do podręcznika)
Jeśli zachodzi związek l<<l
gr
, to efekt związany z długością przewodnika można
pominąć. W przeciwnym razie (l=>l
gr
) w równaniach modelu badanego elementu należy
uwzględnić wzajemny wpływ pola magnetycznego i elektrycznego.
Na przykład jeśli w linii elektroenergetycznej analizowane są przebiegi zwarciowe o
częstotliwości do 20. harmonicznej (f=1000 Hz), to graniczna długość tej linii może być
oszacowana jako:
km
75
)
Hz
1000
4
(
s
km
10
3
5
gr
=
⋅
⋅
=
l
W przypadku badania zjawisk występujących podczas rozchodzenia się fali
elektromagnetycznej wywołanej uderzeniem pioruna, należy rozpatrywać znacznie większe
częstotliwości i już kilkumetrowe odcinki linii mogą wymagać zastosowania modelu o
parametrach rozłożonych. Podobnie jest w przypadku obwodów telekomunikacyjnych.
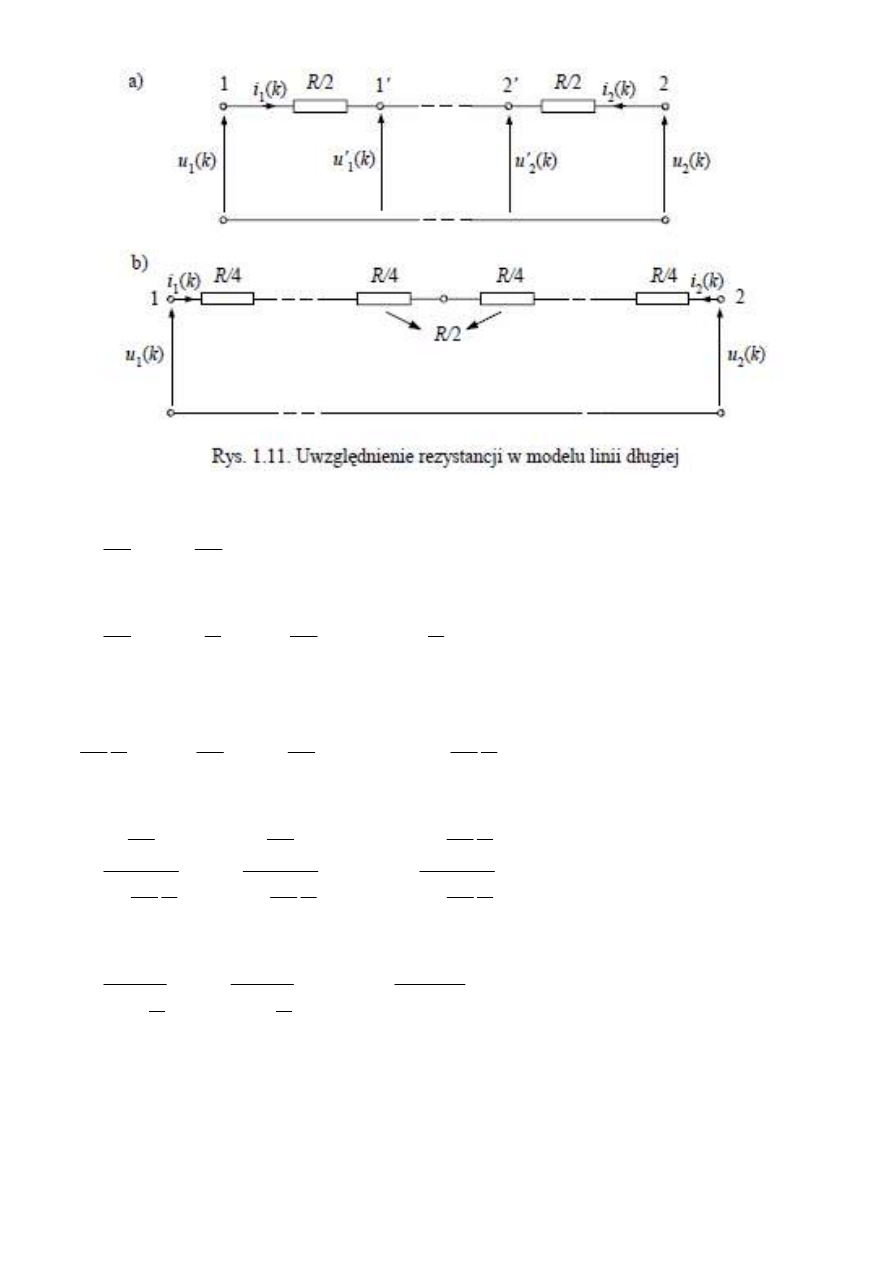
Odnosząc pierwsze z równań modelu linii długiej bezstratnej do węzłów 1’ i 2’ mamy:
)
(
)
(
1
)
(
1
)
(
2
'
2
'
1
1
m
k
i
m
k
u
Z
k
u
Z
k
i
f
f
−
−
−
−
=
Po uwzględnieniu spadków napięć na wprowadzonych rezystancjach R/2 uzyskujemy:
)
(
)
(
2
)
(
1
)
(
2
)
(
1
)
(
2
2
2
1
1
1
m
k
i
m
k
i
R
m
k
u
Z
k
i
R
k
u
Z
k
i
f
f
−
−
−
−
−
−
−
=
Przenosząc składnik z prawej strony powyższego równania zawierający prąd
i
1
(
k
) na lewą
stronę:
)
(
2
1
1
)
(
1
)
(
1
)
(
2
1
1
2
2
1
1
m
k
i
R
Z
m
k
u
Z
k
u
Z
k
i
R
Z
f
f
f
f
−
−
−
−
−
=
+
Zostawiając po lewej stronie równania
i
1
(
k
) uzyskujemy:
)
(
2
1
1
2
1
1
)
(
2
1
1
1
)
(
2
1
1
1
)
(
2
2
1
1
m
k
i
R
Z
R
Z
m
k
u
R
Z
Z
k
u
R
Z
Z
k
i
f
f
f
f
f
f
−
+
−
−
−
+
−
+
=
Po uporządkowaniu:
)
(
2
2
)
(
2
1
)
(
2
1
)
(
2
2
1
1
m
k
i
R
Z
R
Z
m
k
u
R
Z
k
u
R
Z
k
i
f
f
f
f
−
+
−
−
−
+
−
+
=
Analogicznie postępuje się z drugim równaniem modelu linii bezstratnej.
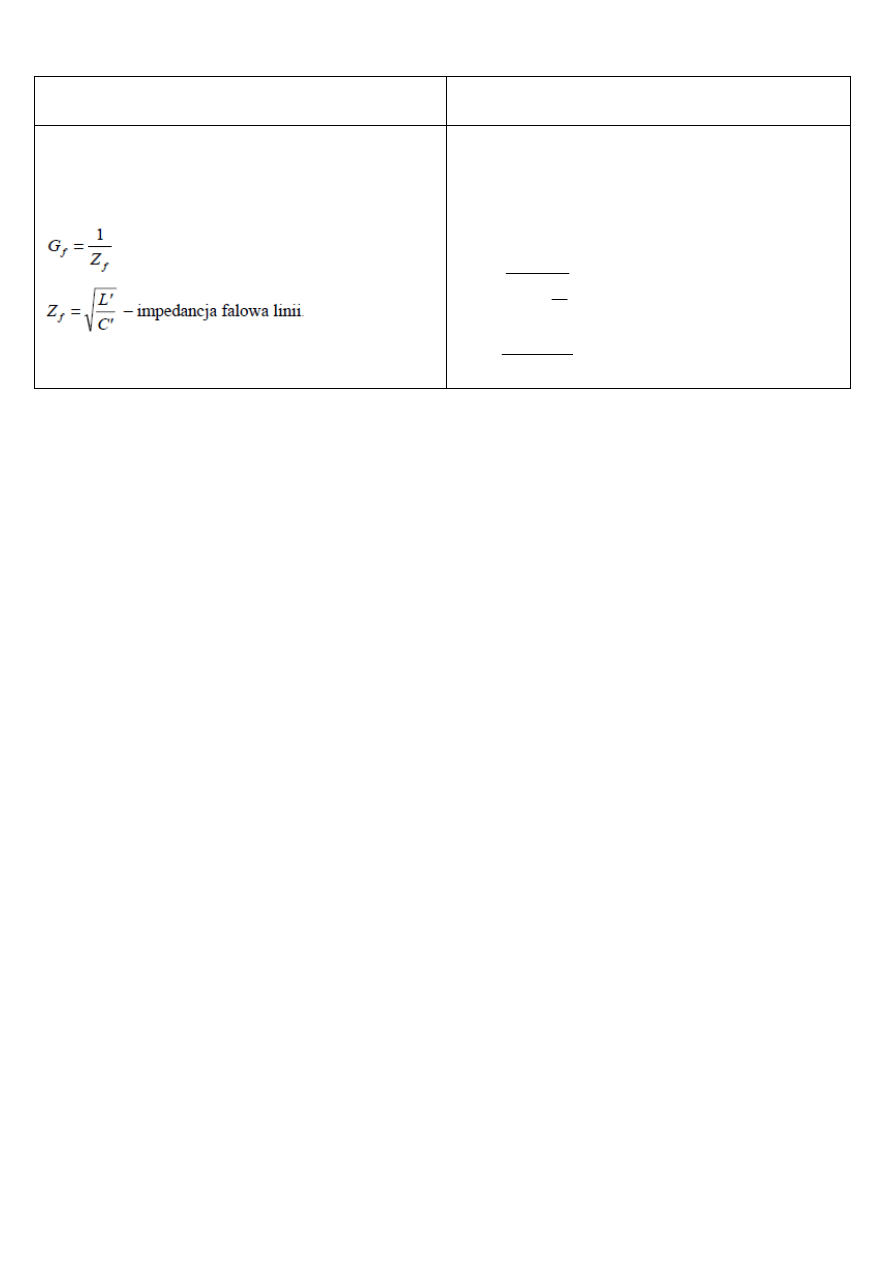
Tabela. Porównanie modeli linii długiej bezstratnej oraz z uwzględnieniem rezystancji linii
Bez uwzględnienia rezystancji linii
Z uwzględnieniem rezystancji linii jak na rys.
1.11.a
)
(
)
(
)
(
)
(
2
2
1
1
m
k
i
m
k
u
G
k
u
G
k
i
f
f
−
−
−
−
=
)
(
)
(
)
(
)
(
1
1
2
2
m
k
i
m
k
u
G
k
u
G
k
i
f
f
−
−
−
−
=
gdzie:
)
(
)
(
)
(
)
(
2
2
1
1
m
k
i
h
m
k
u
G
k
u
G
k
i
R
f
R
f
R
f
−
−
−
−
=
)
(
)
(
)
(
)
(
1
1
2
2
m
k
i
h
m
k
u
G
k
u
G
k
i
R
f
R
f
R
f
−
−
−
−
=
gdzie:
2
1
R
Z
G
f
R
f
+
=
,
R
Z
R
Z
h
f
f
R
f
+
−
=
2
2
Wyszukiwarka
Podobne podstrony:
cw8 Model linii dlugiej
11 Model linii długiej - GRĄDZKI, POLITECHNIKA LUBELSKA
Model linii długiej zadania(1)
Model linii długiej zadania
11 Model linii długiej - BŁASZCZUK, POLITECHNIKA LUBELSKA w LUBLINIE
Model linii długiej v2
Model linii elektroenergetycznej MW
Model+linii+dl
sprawko model linii elektroen
Ćwiczenie 1 - Brudnopis, Politechnika Poznańska, Elektrotechnika, Teoria pola elektromagnetycznego,
sprawko model linii elektroen
Model linii elektroenergetycznej
ip lele model linii elektr
Badanie linii długiej 3
Sprawozdanie?danie linii długiej
więcej podobnych podstron