29

Prace IMŻ 2 (2011)

Ryszard MOLENDA, Roman KUZIAK

Instytut Metalurgii Żelaza

METALOZNAWCZE PODSTAWY KSZTAŁTOWANIA

STRUKTURY I WŁAŚCIWOŚCI BLACH ZE STALI DP

W PROCESIE CIĄGŁEGO WYŻARZANIA

W artykule przeprowadzono analizę literatury metaloznawczej dotyczącej procesów zachodzących w trakcie ciągłego

wyżarzania blach cienkich. Zwrócono szczególną uwagę na proces rozpuszczania perlitu w osnowie ferrytycznej oraz

jaki wpływ wywiera on na tworzenie się austenitu, co jest istotnym elementem w procesie tworzenia struktury ferry-

tyczno-martenzytycznej stali DP. Przedstawiono zależności między strukturą a właściwościami mechanicznymi oma-

wianych stali. Omówiono kilka przemysłowych oraz laboratoryjnych linii do ciągłego wyżarzania taśm ze stali DP.

Słowa kluczowe: austenit, cementyt, ferryt, martenzyt, ciągłe wyżarzanie, stal DP

PHYSICAL METALLURGY FOUNDATIONS OF DP STEEL PLATES

STRUCTURE AND PROPERTIES FORMATION IN THE PROCESS

OF CONTINUOUS ANNEALING

The article contains analysis of physical metallurgy literature concerning the processes occurring during continuous

annealing of thin plates. Particular emphasis was put on the process of pearlite dissolution in ferrite matrix as well as

the impact it has on formation of austenite, which is a signifi cant element in the process of DP steel ferrite-martensitic

structure formation. Interrelations between the structure and mechanical properties of the concerned steels were pre-

sented. Several industrial and laboratory lines for continuous annealing of DP steel strip were described.

Key words: austenite, cementite, ferrite, martensite, continuous annealing, DP steel

1. WSTĘP

Podstawy metaloznawcze stali DP zostały sformuło-

wane i zastosowane do uruchomienia produkcji wyro-
bów płaskich i długich z tych stali w ciągu trzech ostat-
nich dekad. Duże zapotrzebowanie na wyroby z tych
stali jest wynikiem unikatowej kombinacji właściwości
mechanicznych, jakie zapewnia struktura dwufazowa,
takich jak brak wyraźnej granicy plastyczności, wyso-
ka wytrzymałość połączona z bardzo dobrą ciągliwo-
ścią, czy też bardzo dobra plastyczność technologiczna
w operacjach formowania na zimno, znacznie lepsza od
plastyczności stali HSLA, charakteryzujących się po-
równywalną wytrzymałością [1]. Z tego powodu stale
DP coraz powszechniej stosowane są w przemyśle sa-
mochodowym do wytwarzania elementów karoserii,
a także elementów o szczególnym znaczeniu; na przy-
kład zderzaków, felg, specjalnych kształtowników pod-
wyższających sztywność konstrukcji samochodu lub
zabezpieczających przed skutkami zderzenia [2–4].

Podstawowymi składnikami struktury stali DP są

dwie fazy: faza twarda (15–40%), którą jest marten-
zyt lub mieszanina martenzyt /bainit i faza miękka
– ferryt[5]. Mikrostrukturę stali DP przedstawiono
poglądowo na rysunku 1. Faza miękka – ferrytyczna,
będąca osnową, zachowuje ciągłość w objętości stali,

co powoduje, że stal wykazuje bardzo dużą ciągliwość.
Odkształcenie takiej struktury powoduje lokalizację
płynięcia plastycznego w ferrycie, co w połączeniu z od-
działywaniem z fazą twardą, daje znacznie lepszą cha-
rakterystykę umocnienia w porównaniu do umocnienia
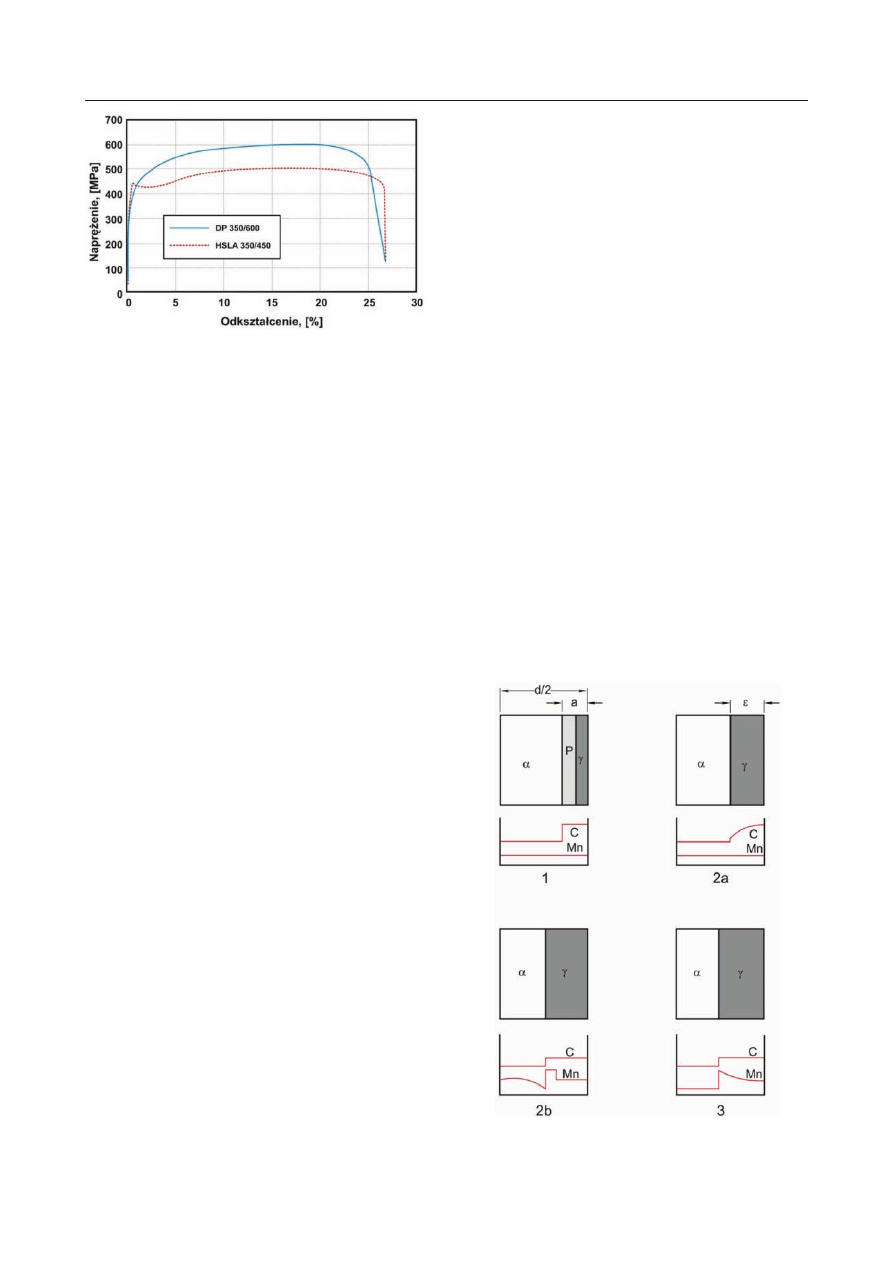
stali HSLA (rys. 2).

Rys. 1. Mikrostruktura stali DP
Fig. 1. Microstructure of DP steel

Molenda1.indd 29

25.08.2011 15:55:57

30

Prace IMŻ 2 (2011)

Ryszard Molenda, Roman Kuziak

Jednym z wyrobów wytwarzanych ze stali DP są

blachy taśmowe, których zużycie znacznie wzrosło
w ostatniej dekadzie. Blachy te stosowane są najczę-

ściej w stanie po ciągłym wyżarzaniu, które w ogólnym
zarysie polega na szybkim nagrzaniu blach cienkich po
walcowaniu na zimno do zakresu międzykrytycznego

i kontrolowanym chłodzeniu do temperatury otoczenia
lub przestarzenia. Stosowane jest również cynkowanie

zanurzeniowe bezpośrednio po procesie wyżarzania.
Wpływ profi li termicznych stosowanych w liniach cią-

głego wyżarzania i zanurzeniowego nanoszenia powłok
cynkowych na właściwości mechaniczne stali DP bada-

ny był dla zróżnicowanych składów chemicznych tych
stali w warunkach laboratoryjnych, za pomocą symu-

latorów wyżarzania i galwanizowania [6]. Badania te
dotyczyły przede wszystkim określenia wpływu tem-

peratury wyżarzania, a w zakresie międzykrytycznym,
temperatury początku przyspieszonego chłodzenia
po wygrzewaniu, szybkości chłodzenia i temperatury
przestarzenia na mikrostrukturę i właściwości me-
chaniczne blach taśmowych. Na podstawie tych badań

opracowano przemysłowe technologie wytwarzania
blach ze stali DP w liniach ciągłych do zanurzeniowego
pokrywania cynkowymi powłokami ochronnymi [7].

Przemiana struktury wyjściowej stali w austenit pod-

czas wyżarzania międzykrytycznego była przedmiotem
licznych badań. Większość z tych badań przeprowa-

dzono na blachach po walcowaniu na gorąco i auste-
nityzowaniu, w których występowała mikrostruktura
ferrytyczno-perlityczna. W tym przypadku austenit
zarodkuje na granicach rozdziału ferryt/cementyt, na

granicach ziaren ferrytu, na granicach kolonii perlitu
lub na cząstkach węglików wydzielonych w granicach
ziaren ferrytu. Podczas chłodzenia, w zależności od

hartowności stali i szybkości chłodzenia, austenit pod-
lega przemianie w martenzyt lub do postaci mieszani-
ny martenzytu z bainitem. Przy małych szybkościach
chłodzenia austenit może przemieniać się również do
ferrytu i perlitu. Podczas wyżarzania międzykrytycz-
nego obserwowano procesy segregacji manganu do
austenitu, a także w mniejszym stopniu, krzemu do
ferrytu. Stosunkowo mało uwagi poświęcono badaniom
przemian fazowych i zmian strukturalnych w blachach
walcowanych na zimno w procesie ciągłego wyżarza-
nia, który charakteryzuje się przede wszystkim krótki-
mi czasami nagrzewania i wygrzewania.

2. PODSTAWY PROCESU

WYTWARZANIA BLACH ZE STALI DP

Z WYKORZYSTANIEM WYGRZEWANIA

W ZAKRESIE MIĘDZYKRYTYCZNYM

2.1. PRZEMIANY FAZOWE PODCZAS

NAGRZEWANIA I WYGRZEWANIA

Jedną z najważniejszych cech procesu wyżarzania

blach ze stali DP w procesie ciągłym jest konieczność

dokładnego kontrolowania postępu przemian fazowych

i zmian zachodzących w strukturze zarówno podczas

nagrzewania i wygrzewania, jak również podczas chło-

dzenia tych blach. Do zmian zachodzących w struktu-

rze stali w procesie nagrzewania i wygrzewania w za-

kresie współistnienia ferrytu i austenitu w układzie

równowagi, mających istotny wpływ na właściwości

mechaniczne stali DP, zalicza się przede wszystkim:

przemianę perlitu w wysokowęglowy austenit,

–

wzrost austenitu o wysokiej zawartości węgla kosz-

–

tem ferrytu w warunkach lokalnej równowagi,

ustalanie równowagi globalnej między austenitem

–

i ferrytem poprzez dyfuzję pierwiastków i zanik se-

gregacji w tych fazach.

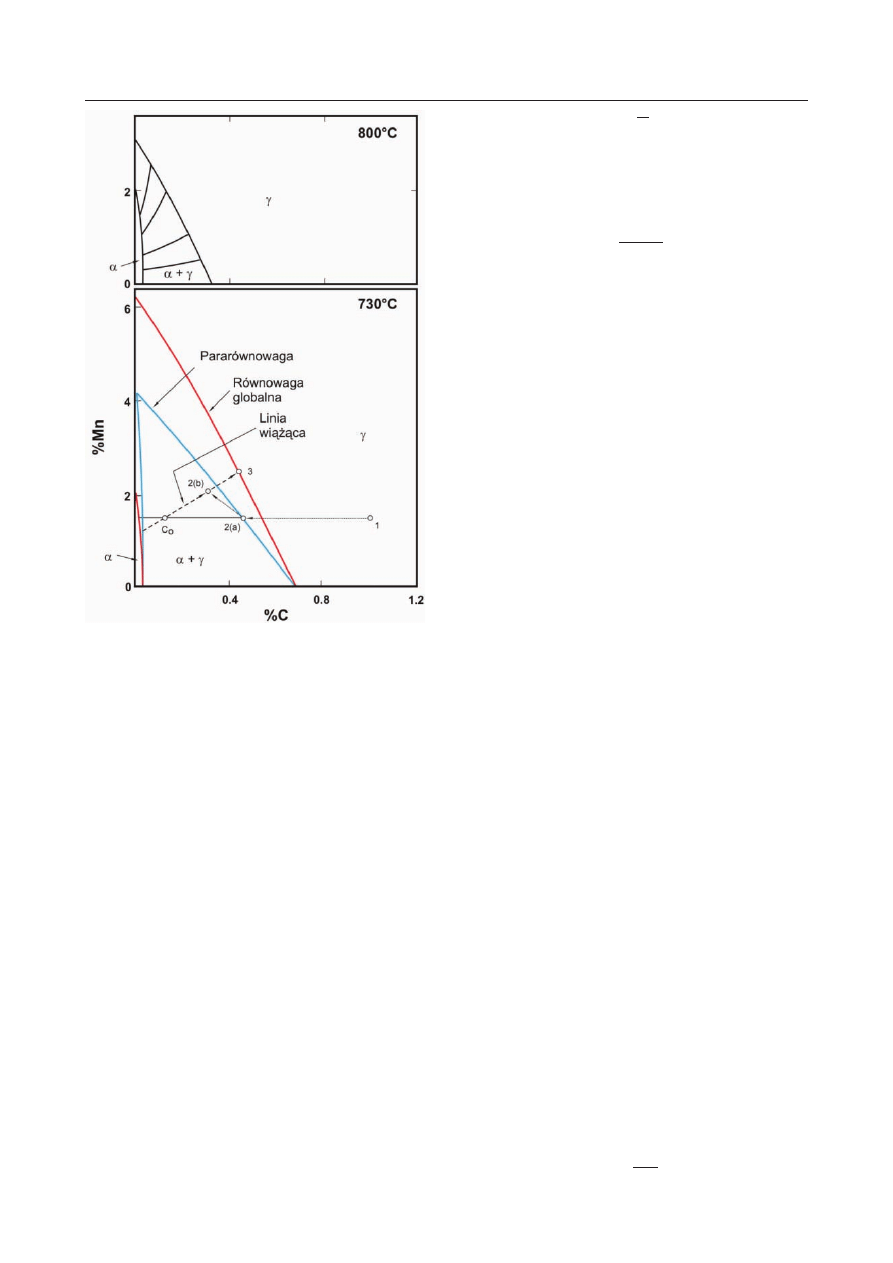
Powyższe etapy przedstawiono schematycznie na ry-

sunku 3, zaś zmiany składu chemicznego towarzyszą-

cego wspomnianym przemianom fazowym przedsta-

wiono na układzie fazowym na rysunku 4. Etap 1 na

rysunku 3 to rozpuszczanie perlitu, etap 2(a) to wzrost

austenitu w warunkach pararównowagi, etap 2(b), to

wzrost austenitu, w trakcie którego postęp przemiany

kontrolowany jest dyfuzją manganu w ferrycie, etap 3

to wyrównywanie profi lu koncentracji manganu w au-

stenicie, w wyniku czego, na końcu, uzyskuje się jed-

Rys. 2. Porównanie krzywych naprężenie – odkształcenia

stali DP i stali mikroskopowej o podwyższonej wytrzyma-

łości
Fig. 2. Comparison of stress – strain curves of DP steel and

microscope high-strength steel

Rys. 3. Zmiany zachodzące w strukturze stali wygrzewanej

w zakresie temperatur współistnienia faz [8]
Fig. 3. Changes occurring in the structure of steel soaked

in phases coexistence temperature range

Molenda1.indd 30

25.08.2011 15:56:12

31

Prace IMŻ 2 (2011)

Metaloznawcze podstawy kształtowania struktury i właściwości blach...

norodną zawartość tego pierwiastka, odpowiadającą
warunkowi równowagi.

Pierwszym procesem zachodzącym podczas wygrze-

wania stali w zakresie międzykrytycznym jest prze-
miana perlitu w wysokowęglowy austenit. Powyżej
temperatury Ac

1

następuje rozpuszczanie płytek ce-

mentytu w perlicie i wzrost zarodkującego austenitu
w kierunku perlitu. Przemiana ta jest kontrolowana
dyfuzją węgla w powierzchni rozdziału perlit/austenit,
zaś droga dyfuzji dla tej przemiany odpowiada odległo-
ści między płytkami cementytu w ferrycie (

∼0,2 μm).

Z tego powodu przemiana perlitu w austenit postępu-
je bardzo szybko. Jednak w niższych temperaturach
(

∼730°C), z uwagi na małą ruchliwość pierwiastków

stopowych, dyfuzja tych pierwiastków może być proce-
sem kontrolującym postęp przemiany perlitu w auste-
nit. Podwyższanie temperatury powoduje zmianę me-
chanizmu kontrolującego postęp przemiany z dyfuzji
pierwiastków stopowych na dyfuzję węgla, a w wyniku
tego gwałtowny wzrost szybkości postępu przemiany.
Obliczenia przeprowadzone w pracy [8] dla stali 0,06%
C – 1,5% Mn dały zmniejszenie czasu rozpuszczania
perlitu z 12 sekund przy temperaturze 740

°C do 0,11

sekundy przy 780

°C. Czas rozpuszczania obliczano za

pomocą następującego równania:

t

G

a

p

=

(1)

gdzie a jest połową grubości płytki cementytu, zaś G
jest szybkością przemieszczania się powierzchni roz-
działu.

Parametr a szacowano za pomocą następującego

wzoru:

( )

a V P d

2

V

=

(2)

gdzie V

V

(P) jest udziałem objętościowym perlitu, zaś d

jest średnicą ziarna ferrytu.

Po rozpuszczeniu się perlitu, w strukturze stali wy-

stępuje austenit wzbogacony w węgiel, który nie jest
w stanie równowagi termodynamicznej z otaczającym
go ferrytem. Z tego powodu, kolejnym etapem prze-
miany jest wzrost austenitu kosztem ferrytu. W zależ-
ności od wielkości siły napędowej przemiany, może on
zachodzić w warunkach dyfuzji lub przy braku dyfuzji
manganu. Jeśli w trakcie wzrostu nie zachodzi dyfuzja
manganu i innych pierwiastków stopowych, proces ten
zachodzi w warunkach pararównowagi. W tych warun-
kach, w początkowym etapie zawartość węgla ewoluuje
od wartości w punkcie 1 do wartości w punkcie 2(a) na
rysunku 4. Podczas długotrwałego wygrzewania, dal-
szy wzrost zachodzi w warunkach lokalnej równowagi
i może być kontrolowany dyfuzją węgla w austenicie
(przypadek 2a na rysunku 3) lub dyfuzją manganu
w ferrycie (przypadek 2b na rysunku 3). Skład chemicz-
ny austenitu ewoluuje wtedy w kierunku linii wiążącej
układu równowagi globalnej (punkt 2(b) na rysunku 4),
a następnie w kierunku punktu 3. W temperaturach
nieznacznie wyższych od Ac

3

, zachodzić może dyfuzja

manganu podczas przemieszczania się powierzchni
międzyfazowej, ponieważ szybkość dyfuzji manganu
w ferrycie jest około trzy razy większa, niż w auste-
nicie. Z tego powodu, przyjmuje się, że szybkość dyfu-
zji manganu w ferrycie początkowo kontroluje postęp
przemiany austenitu.

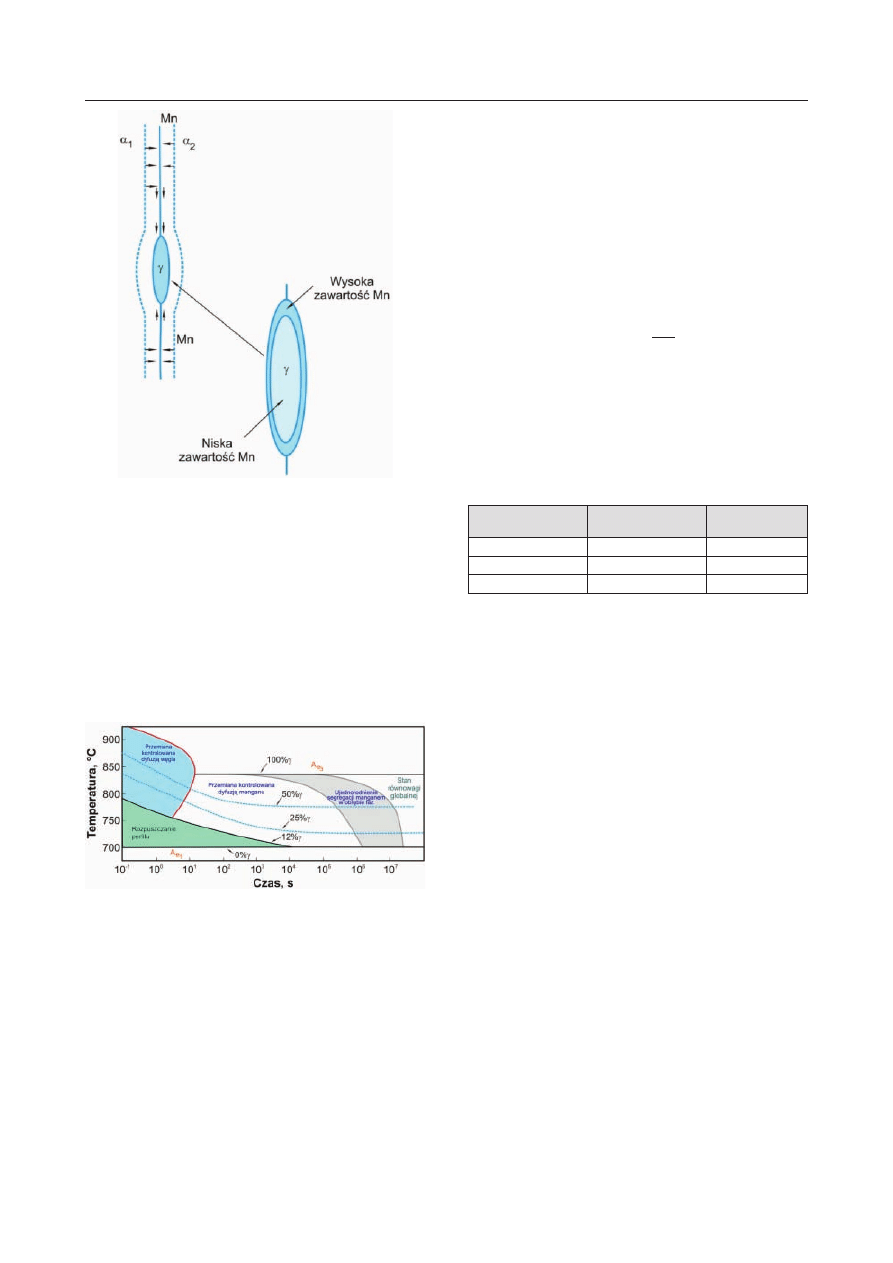
Inny model przemiany opiera się na założeniu, że dy-

fuzja manganu wzdłuż granic ziaren ferrytu zachodzi
szybciej, niż dyfuzja objętościowa. Przykładem może
być model Aarona i Aaronsona, w którym ten rodzaj
dyfuzji powoduje wzbogacenie granic ziaren w mangan
[9]. Granica ziarna w tym modelu działa, jak kolektor
gromadzący mangan (rys. 5). Jednak znaczenie tego
procesu maleje w miarę postępu przemiany.

Zarówno dyfuzja objętościowa, jak i wzdłuż granic

ziaren, powoduje tworzenie się warstwy wzbogaconej
w mangan na obrzeżu austenitu. Podczas chłodzenia,
warstwa ta tworzy rodzaj koperty wokół ziarna ferry-
tu. Przykład takiej struktury w stali DP można znaleźć
w pracy [8].

Ostatnim etapem zmian zachodzących w strukturze

stali wygrzewanej w zakresie międzykrytycznym jest
ujednorodnienie składu chemicznego austenitu. W wy-
niku, tego procesu zanikają gradienty koncentracji
pierwiastków w ferrycie i austenicie. Obliczenia mode-
lowe tego procesu prowadzi się przy założeniu jednowy-
miarowej dyfuzji ze stacjonarną powierzchnią rozdziału
o ustalonym składzie chemicznym [10]. Czas, w trakcie
którego gradient koncentracji manganu maleje o 90%
można obliczyć za pomocą następującego równania:

t

D

Mn

Mn

f

2

f

=

c

c

(3)

Rys. 4. Układ równowag fazowych Fe-Mn-C dla tempera-

tur 730 i 800

°C ilustrujący zmiany składu chemicznego faz

związane z trzyetapowym mechanizmem przemiany struk-

tury ferrytyczno-perlitycznej w austenit [8]
Fig. 4. Fe-Mn-C phase equilibrium system for temperatures:

730 and 800°C illustrating changes in chemical composi-

tion of phases related to three-stage mechanism of ferrite-

pearlite structure transformation into austenite [8]

Molenda1.indd 31

25.08.2011 15:56:12

32

Prace IMŻ 2 (2011)

Ryszard Molenda, Roman Kuziak

gdzie

f

f

jest grubością warstwy austenitu pod koniec

etapu 2(b), zaś D

M

c

jest współczynnikiem dyfuzji man-

ganu w austenicie.

Schemat zmian zachodzących w stali w trakcie prze-

miany struktury ferrytyczno-perlitycznej w austenit

podczas wyżarzania w zakresie międzykrytycznym

przedstawiono na rysunku 6.

cy [11] wykorzystując metodę Kissingera. Metoda ta
opiera się na pomiarze temperatury, przy której szyb-
kość przemiany jest najwyższa podczas nagrzewania
stali, a więc, w warunkach nieizotermicznych. Do opi-
su kinetyki przemiany zastosowano model Johnsona-
Mehl-Avramiego:

( )

exp

F t

kt

1

n

=

-

-

^ h

6

@ (4)

gdzie F(t) jest ułamkiem objętości materiału, w którym
zaszła przemiana fazowa, n jest stałą, zaś k związane
jest z energią aktywacji procesu, E, i temperaturą za
pomocą następującego równania:

exp

k k

RT

E

0

=

-

c

m (5)

Materiałem badań były stale o zawartości węgla:

0,08; 0,115 i 0,4% i w przybliżeniu stałej zawartości
manganu (0,45–0,50%) i krzemu (0,02–0,31%). Stałe
w równaniach (4) i (5) wyznaczone w badaniach poda-
no w tablicy 1.

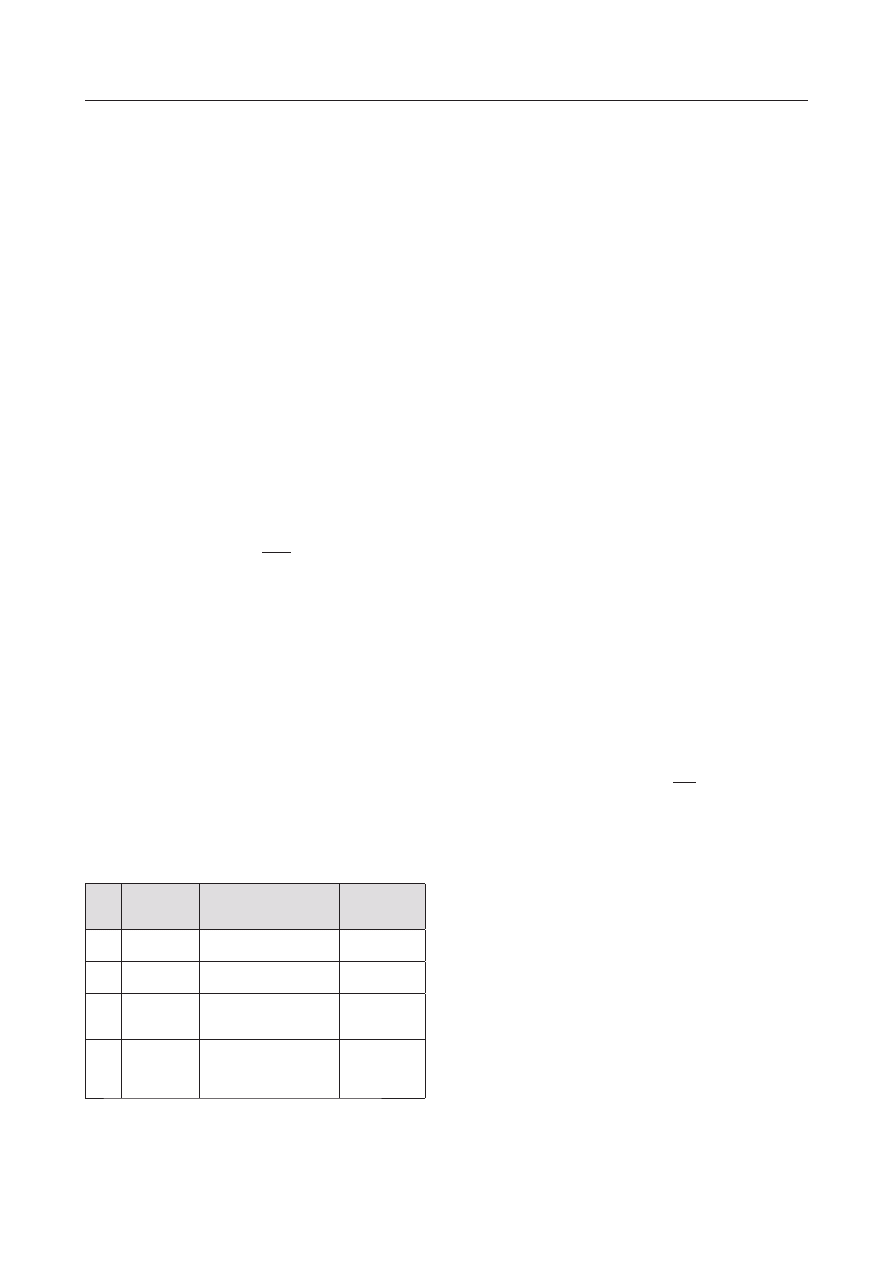
Tablica 1. Stałe w równaniach (4) i (5) dla stali badanych
w pracy [11]
Table 1. Constant in equations (4) and (5) for the examined
steels [11]

Stal

Energia aktywacji

(E), kJ/mol

n

0,08 %C

117,07

3,5

0,115 %C

113,43

3,6

0,40%C

110,21

3,8

Wartość wykładnika w równaniu (4) wskazuje, że

procesem kontrolującym postęp przemiany jest zarod-
kowanie austenitu w granicy rozdziału ferryt/cemen-
tyt. Na krzywej kalorymetrycznej stwierdzono wystę-
powanie czterech pików, które przypisano następują-
cym procesom:

przy temperaturze około 400

–

°C: odprężaniu próbki

w postaci proszkowej;
przy temperaturze 650–700

–

°C: sferoidyzacji perlitu;

przy temperaturze 800–850

–

°C: równoczesnemu roz-

puszczaniu perlitu i zarodkowaniu oraz wzrostowi
austenitu;
przy temperaturze 900–950

–

°C: wyrównaniu stężenia

węgla, zgodnie z układem równowagi.
Model opisany w pracy [11] pozwala z dużą dokład-

nością wyznaczyć wymagany czas wytrzymania izoter-
micznego do uzyskania założonego składu fazowego
stali wytrzymywanej w zakresie międzykrytycznym.
Na przykład czas wytrzymania w zakresie międzykry-
tycznym do uzyskania maksymalnego udziału austeni-
tu (13%) w stali o zawartości węgla 0,08%, przy tempe-
raturze 740

°C, wynosi 10 minut.

2.2. WPŁYW ODKSZTAŁCENIA NA ZIMNO

NA POSTĘP ZMIAN ZACHODZĄCYCH

PODCZAS WYŻARZANIA

Przedstawiony dotychczas postęp przemian zacho-

dzących podczas wyżarzania stali odnosi się do przy-
padku, gdy wyjściowa struktura jest w pełni zrekry-
stalizowana. Blachy cienkie wyżarzane są natomiast
w stanie po walcowaniu na zimno. Taki stan struktury
wyjściowej powoduje, że ziarna austenitu tworzą się
nie tylko na granicach ziaren lub powierzchniach mię-
dzyfazowych, ale również, wewnątrz zdeformowanych
ziaren [12]. Przebieg zarodkowania austenitu zależy

Rys. 5. Segregacja manganu mechanizmem dyfuzji po-

wierzchniowej podczas wygrzewania międzykrytycznego

[8]
Fig. 5. Segregation of manganese by means of surface diffu-

sion mechanism during intercritical soaking [8]

Rys. 6. Schemat zmian zachodzących w stali w trakcie

przemiany struktury ferrytyczno-perlitycznej w austenit

podczas wyżarzania w zakresie międzykrytycznym dla

stali 0,12% C – 1,5% Mn
Fig. 6. Diagram of changes occurring in steel during ferri-

te-pearlite structure transformation into austenite in the

process of annealing in the intercritical range for 0.12%C

– 1.5%Mn steel

Z rysunku 6 wynika, że proces rozpuszczania perli-

tu zachodzi bardzo wolno (15 s – 8 godzin) w przedzia-

le temperatur Ae

1

– 740

°C. W tym przypadku dalszy

wzrost austenitu kontrolowany jest dyfuzją manganu

w ferrycie. W wysokich temperaturach, w przedziale

850–900

°C, rozpuszczanie perlitu zachodzi niemal na-

tychmiast, zaś dalszy postęp przemiany kontrolowany

jest dyfuzją węgla w austenicie.

Kinetykę przemiany struktury ferrytyczno-perlitycz-

nej w austenit badano metodą kalorymetryczną w pra-

Molenda1.indd 32

25.08.2011 15:56:12

33

Prace IMŻ 2 (2011)

Metaloznawcze podstawy kształtowania struktury i właściwości blach...

zatem od rekrystalizacji ferrytu. Duży jest również

wpływ wyjściowej mikrostruktury blachy przed walco-

waniem na zimno. W przypadku, gdy przed walcowa-

niem przeprowadzono zabieg sferoidyzacji cementytu,

rekrystalizacja ferrytu poprzedza przemianę austeni-

tyczną [13]. Wtedy proces zarodkowania ferrytu ogra-

niczony jest do granic ziaren i powierzchni międzyfa-

zowych [13].

Bardzo ważnym procesem z punktu widzenia kształ-

towania tekstury zachodzącym podczas wyżarzania

blach jest rekrystalizacja. Rekrystalizacja nieciągła

obejmuje dwa procesy, mianowicie, zarodkowanie

i wzrost zarodka. Zarodek charakteryzuje się niską

gęstością dyslokacji, jego wzrost w kierunku silnie od-

kształconej osnowy powoduje obniżenie gęstości dyslo-

kacji. Zarówno zarodkowanie, jak i wzrost, wpływają

na teksturę rekrystalizacji. Uzyskanie wyróżnionych

orientacji w procesie rekrystalizacji tłumaczy się za-

równo w oparciu o mechanizm uprzywilejowanego

zarodkowania, jak również uprzywilejowanego wzro-

stu [14]. Jednak nie wszystkie zarodki rekrystalizacji

mogą rozrastać się w kierunku odkształconej osnowy.

Dla wystąpienia wzrostu konieczne jest spełnienie na-

stępujących warunków [15]:

Niestabilność termodynamiczna:

•

zarodek musi

osiągnąć wielkość krytyczną promienia, którego war-

tość można oszacować za pomocą następującego rów-

nania:

r

p

Gb

2

4

c

2

c

t

c

=

=

(6)

gdzie c jest energią napięcia powierzchniowego, p jest

energią zmagazynowaną odkształcenia plastycznego,

t

jest gęstością dyslokacji, G jest modułem odkształ-

cenia postaciowego, b jest wektorem Burgersa.

Niestabilność mechaniczna:

•

przemieszanie się

frontu rekrystalizacji (granicy zarodek/odkształcona

osnowa) możliwe jest w przypadku, gdy lokalnie nie

jest zachowana równowaga sił działających na front.

Warunek ten jest spełniony, gdy struktura dysloka-

cyjna jest silnie niejednorodna, lub gdy proces zdro-

wienia powoduje powstanie dużych podziaren.

Niestabilność kinetyczna:

•

granica zarodka musi

wykazywać dużą ruchliwość, co występuje w przy-

padku granic wysokokątowych. Wyróżnia się nastę-

pujące mechanizmy powstawania granic wysokoką-

towych:

nieciągły wzrost podziaren;

–

zarodkowanie na granicach ziaren;

–

występowanie silnej niejednorodności odkształce-

–

nia plastycznego;

zarodkowanie na dużych cząstkach wtrąceń nie-

–

metalicznych i wydzieleń;

powstawanie bliźniaków wyżarzania.

–

Trudności w jednoczesnym spełnieniu tych kryteriów

powodują występowanie silnej selekcji miejsc uprzywi-

lejowanego zarodkowania. Wyróżnionymi miejscami

zarodkowania są pasma zlokalizowanego odkształce-

nia plastycznego i granice ziaren.

Badania rekrystalizacji ferrytu i postępu przemia-

ny w austenit przeprowadzono w pracy [16] dla stali

o składzie chemicznym: Fe-0.08C-1.45Mn-0.21Si. Ki-

netykę rekrystalizacji ferrytu w tej pracy analizowano

za pomocą następującego równania:

exp

t

A

RT

Q

1

r

r

r

=

-

c

m (7)

gdzie t

r

jest czasem do uzyskania określonego ułamka

objętości zrekrystalizowanej, A

r

jest stałą, zaś Q

r

jest

energią aktywacji dla procesu rekrystalizacji.

Energia aktywacji wyznaczona w pracy [16] zależy

od wartości odkształcenia. Dla gniotu 25% wynosiła
ona 272, zaś dla gniotu 50% 225 kJ/mol. Są to wartości
zbliżone do energii aktywacji procesu samodyfuzji w
żelazie

α. Badania przeprowadzone w pracy pokazały,

że równocześnie z postępem rekrystalizacji zachodzi
proces sferoidyzacji perlitu. Przy temperaturze 700

°C

proces ten zachodzi w czasie około 20 minut. Mimo peł-
nej rekrystalizacji ferrytu, cząstki cementytu ułożone
były zgodnie z kierunkiem linii poślizgu. Zatem proces
sferoidyzacji w stanie po odkształceniu plastycznym
na zimno zachodzi znacznie szybciej w porównaniu do
stanu nieodkształconego. Jest to spowodowane częścio-
wą fragmentacją i znacznym odkształceniem płytek
cementytu.

W blachach o strukturze ferrytyczno-perlitycznej,

po odkształceniu na zimno, przemiana w austenit za-
chodzi w kilku etapach. W pierwszym etapie, austenit
zarodkuje na granicach ziaren/podziaren ferrytu, zaś
w drugim związany jest z cząstkami cementytu. Za-
rodkowanie wewnątrz ziaren ferrytu zachodzi na naj-
większych cząstkach w obszarze skupisk sferycznych
cząstek cementytu. Zarodkowanie austenitu nie zacho-
dzi na małych cząstkach, prawdopodobnie spowodowa-
ne jest to małą powierzchnią międzyfazową związaną
z tymi cząstkami. Z tego powodu małe cząstki są bar-
dzo stabilne, bardzo często hamują one rozrost ziaren
austenitu. Potwierdzają to również badania przeprowa-
dzone przez Cai i in. [17]. Badacze stwierdzili ponad-
to, że cząstki cementytu charakteryzują się znacznie
wyższą zawartością manganu w porównaniu z osnową.
Podwyższona zawartość manganu może być powodem
wolnego rozpuszczania się cząstek cementytu oraz
podwyższonej stabilności austenitu zarodkującego na
cząstkach cementytu. Pomimo różnic w wyjściowej mi-
krostrukturze badania Yanga [16] pokazały, że kinety-
ki tworzenia się austenitu w strukturze odkształconej
i nieodkształconej są zbliżone do siebie. Końcowy etap
tworzenia się austenitu w przypadku, gdy wyjściowa
struktura była odkształcona charakteryzuje się znacz-
nym spowolnieniem tego procesu. Jest to spowodowane
zarodkowaniem tej fazy na dużych cząstkach, wzboga-
conych w mangan.

2.3. PROCES PRZESTARZENIA

Celem procesu przestarzenia w linii ciągłej jest uzy-

skanie blach nie wykazujących zjawiska starzenia
zgniotowego. Starzenie zgniotowe jest utożsamiane
ze zmianą właściwości metali i stopów spowodowane
oddziaływaniem defektów punktowych z dyslokacjami
w trakcie odkształcenia (starzenie dynamiczne) lub
po odkształceniu (starzenie statyczne). W przypadku
stali największy wpływ na właściwości mechaniczne
ma oddziaływanie atomów międzywęzłowych (C i N)
z dyslokacjami. W niektórych stalach, np. BH, starze-
nie zgniotowe wykorzystuje się do podwyższenia wy-
trzymałości wyrobów fi nalnych. Jednak bardzo często,
jest to zjawisko niekorzystne, wpływające negatywnie
na stan powierzchni wyrobów. Dotyczy to na przykład
stali głębokotłocznych. W tym przypadku w linii cią-
głego wyżarzania stosuje się odkształcenie wygładza-
jące (z gniotem około 1%) przed strefą przestarzania.

Molenda1.indd 33

25.08.2011 15:56:13

34

Prace IMŻ 2 (2011)

Ryszard Molenda, Roman Kuziak

Starzenie zgniotowe może być ilościowo scharaktery-

zowane poprzez wpływ na właściwości mechaniczne.

Powoduje ono wzrost granicy plastyczności, lub nawrót

odkształcenia Lüdersa, wzrost wytrzymałości na roz-

ciąganie i obniżenie ciągliwości [18, 19]. Teorię starze-

nia po zgniocie opracowali Cottrell i Bilby [20]. Teoria

ta opiera się na założeniu, że starzenia zgniotowe za-

chodzi w przypadku, gdy spełnione są trzy warunki:

(1) w materiale występują niezakotwiczone dyslokacje;

(2) atomy międzywęzłowe mają zdolność dyfundowa-

nia do dyslokacji oraz (3) atomy międzywęzłowe mają

zdolność kotwiczenia dyslokacji. Starzenie zgniotowe

zachodzi w trzech etapach. W etapie pierwszym wy-

stępuje szybki wzrost górnej granicy plastyczności spo-

wodowany porządkowaniem się atomów międzywęzło-

wych w polu naprężeń pochodzących od dyslokacji. Jest

to tzw. efekt Snoeka [21]. Zjawisko to zachodzi w czasie

wymaganym do pojedynczego przeskoku atomu w polu

naprężeń. Drugi i znacznie wolniejszy etap to daleko-

zasięgowa dyfuzja atomów międzywęzłowych w kie-

runku rdzenia dyslokacji. W wyniku tych procesów

tworzą się tzw. atmosfery Cottrella, które efektywnie

kotwiczą dyslokacje. Proces formowania atmosfer koń-

czy się zarodkowaniem węglików żelaza. Jest to etap

trzeci procesu. Kinetykę tworzenia atmosfer Cottrella

opisuje następujące równanie:

( )

N t

n

kT

ADt

3

/

0

2 3

m

=

c

m (8)

gdzie n

o

jest całkowitą ilością atomów międzywęzło-

wych w roztworze stałym na jednostkę objętości, m jest

parametrem charakteryzującym zdolność przemiesz-

czania się rdzenia dyslokacji, A jest stałą zależną od

współczynników sprężystości, k jest stałą Boltzmanna,

D jest współczynnikiem dyfuzji atomów międzywęzło-

wych.

Proces przestarzenia blach ze stali DP powoduje

również rozpad martenzytu, co wpływa na właściwości

mechaniczne tej fazy, a równocześnie na właściwości

mechaniczne kompozytu. Procesy zachodzące w mar-

tenzycie oraz ich wpływ na właściwości mechaniczne

tej fazy scharakteryzowano w tablicy 2 [22].

Tablica 2. Charakterystyka zmian zachodzących w struk-

turze martenzytu oraz ich wpływu na właściwości mecha-

niczne w zależności od temperatury
Table 2. Characteristics of changes occurring in marten-

site structure and their impact on mechanical properties

depending on temperature

Etap

Przedział

temperatur

Proces

Wpływ na

właściwości

mechaniczne

1

100–200

°C

C

r.s.

→ węglik ε (Fe

2

C)

R

0.2

↑; R

m

↓;

ciągliwość

↑

2

200–300

°C

γ

R.

→ Fe

3

C, powstawanie

węglika Fe

5

C

2

R

0.2

↑; R

m

↓;

ciągliwość

↑

3

300–450

°C

powstawanie węglika

Fe

5

C

2

Fe

2

C

→ Fe

3

C

R

0.2

↓; R

m

↓;

ciągliwość

↑

4

450–650

°C

rozrost węglików,

powstawanie drobnych

węglików (optymalnie

przy 550

°C)

R

m

↓

Stale DP wykazują duży przyrost granicy plastycz-

ności podczas niskotemperaturowego wyżarzania po

uprzednim odkształceniu plastycznym (efekt BH).

Efekt ten jest wykorzystywany do podwyższania od-

porności elementów karoserii samochodowych na

wgniecenia. Proces starzenia po zgniocie stali DP był

badany przez Waterschoota i wsp. [23] metodą tarcia

wewnętrznego. Badania pokazały, że proces ten prze-

biega w kilku etapach obejmujących: formowanie at-

mosfer Cottrela, tworzenie się skupisk atomów węgla

w węzłach dyslokacyjnych i proces wydzieleniowy. Ba-

dania [24] wykazały, że można wyróżnić pięć etapów

przemiany martenzytu w trakcie wyżarzania stali DP

w przedziale temperatur 20–500

°C:

Poniżej 120

•

°C występuje jedynie segregacja węgla po-

wodująca nieznaczne zmiany objętości stali wynoszą-

ce około 0,05% i znaczącą redukcję tetragonalności.

Energia aktywacji tego procesu wynosi 98,9–100,6

kJ/mol, co koresponduje dobrze z energią aktywacji

dla dyfuzji objętościowej węgla.

Wydzielanie się węglika

•

h

lub f w przedziale tem-

peratur 120–200

°C. Energia aktywacji tego procesu

wynosi 121,6–123,8 kJ/mol, co sugeruje, że mechani-

zmem kontrolującym postęp procesu wydzieleniowe-

go jest dyfuzja atomów żelaza wzdłuż dyslokacji w

celu akomodacji niedopasowania sieci krystalicznych

węglików i osnowy. Proces wydzieleniowy powoduje

zmiany objętości wynoszące około 0,30% oraz obniże-

nie tetragonalności sieci krystalicznej martenzytu.

Wydzielanie węglika Hägga w przedziale temperatur

•

200–300

°C. Energia aktywacji dla tego procesu wy-

nosi 135,8 kJ/mol.

Rozpad austenitu szczątkowego, który powodu-

•

je wzrost objętości stali w przedziale temperatur

250–350

°C. Energia aktywacji tego procesu wynosi

154,7 kJ/mol.

Przemiana wszystkich węglików przejściowych w ce-

•

mentyt, która zachodzi w przedziale temperatur

290–390

°C. Energia aktywacji tego procesu wynosi

176,1 kJ/mol.

Całkowita zmiana objętości po pełnym odpuszczaniu

wynosi 0,62-0,71%. Zmiany te w pracy [24] modelowa-

no za pomocą równania Johnsona-Mehla-Avrami:

(

)

exp

f 1

n

b

=

-

-

(9)

gdzie:

( )

exp

k T t k

RT

Q t

0

b =

=

-

c

m (10)

gdzie Q jest energią aktywacji, k

0

jest stałą, T jest tem-

peraturą w skali absolutnej, t jest czasem w sekundach,

R jest stałą gazową, zaś n jest wykładnikiem, który jest

stały dla określonego mechanizmu przemiany.

W pracy Fanga i wsp. [25] badano wpływ temperatu-

ry odpuszczania na właściwości mechaniczne stali DP

o składzie chemicznym: 0,13% C, 0,85% Mn i 0,073%

Si. Stwierdzono, że ze wzrostem temperatury odpusz-

czania (T

odp

) maleje monotonicznie wytrzymałość na

rozciąganie według następującej zależności:

[

]

859 0,75

[ ]

R

T

MPa

C

m

odp

c

=

-

(11)

Podobne zachowanie wykazuje granica plastyczno-

ści, ale spadek tego parametru z temperaturą odpusz-

czania jest około dwukrotnie wolniejszy w porówna-

niu z wytrzymałością na rozciąganie. Wzrost tempe-

ratury odpuszczania powoduje monotoniczny wzrost

wydłużenia równomiernego. Natomiast, wydłużenie

całkowite rośnie monotonicznie do temperatury około

120

°C. W przedziale temperatur 120–150°C obserwu-

je się gwałtowny wzrost wydłużenia równomiernego,

po czym powyżej 150

°C wzrost ten jest bardzo wolny.

Podobny przebieg ma zależność wskaźnika charaktery-

Molenda1.indd 34

25.08.2011 15:56:13

35

Prace IMŻ 2 (2011)

Metaloznawcze podstawy kształtowania struktury i właściwości blach...

zującego podatność do zaginania końca blachy (z ang.

Hole expansion ratio) od temperatury, jednak gwałtow-

ny wzrost tego wskaźnika obserwuje się w przedziale

200–280

°C. Należy podkreślić, że badania przedsta-

wione w pracy [25] nie odzwierciedlają warunków wy-

żarzania ciągłego, bowiem zastosowany czas odpusz-

czania wynosił 1 godzinę.

3. ZWIĄZEK WŁAŚCIWOŚCI

MECHANICZNYCH ZE STRUKTURĄ

STALI DP

Większość modeli mechanicznych opisujących proces

odkształcenia stali DP przyjmuje założenie, że mikro-

struktura tych stali jest mikrokompozytem składają-

cym się z dwu faz o silnie zróżnicowanych właściwo-

ściach mechanicznych. Z przeprowadzonych badań wy-

nikają następujące cechy odkształcenia stali DP:

Do parametrów, które wpływają na proces odkształ-

•

cania stali DP zalicza się [26]:

parametry mikrostrukturalne, takie jak: udział

a)

objętościowy, średnia wielkość i kształt faz oraz

rozkład wielkości, ciągłość osnowy i fazy twardej;

stosunek (

b)

χ) naprężenia uplastyczniającego fazy

twardej i miękkiej osnowy.

Odkształcenie struktury dwufazowej zachodzi w na-

•

stępujących etapach:

Etap 1: obie fazy podlegają sprężystemu odkształce-

niu,

Etap 2: faza miękka podlega odkształceniu plastycz-

nemu, zaś faza twarda odkształca się sprę-

żyście,

Etap 3: obie fazy odkształcają się plastycznie,

Etap 4: pękanie stali, któremu towarzyszy dekohezja

w powierzchni rozdziału osnowa/faza twarda

lub mikropękanie fazy twardej.

Różnice między poszczególnymi modelami dotyczą

sposobu, w jaki dokonywany jest podział odkształce-

nia/naprężenia między ferryt i martenzyt oraz mecha-

nizmów wzajemnego wpływu każdej z tych faz na cha-

rakterystykę odkształcania się drugiej.

Teoria Ashby wykorzystująca mikromechanikę

płynięcia plastycznego opisuje wpływ twardej, nieod-

kształcającej się drugiej fazy, na umocnienie miękkiej

osnowy [27]. Ashby zakłada, że różnice w odkształceniu

się dwu faz kompensowane są poprzez wzrost gęstości

tzw. dyslokacji niezbędnych geometrycznie. Podstawo-

we założenie tej teorii, o braku odkształcenia twardej

fazy nie jest jednak spełnione w przypadku stali DP,

zwłaszcza dla dużych odkształceń [28]. Z tego powodu

obliczenia w oparciu o model Ashby zawyżają gęstość

dyslokacji, a tym samym, naprężenie płynięcia pla-

stycznego. Model Ashby został zmodyfi kowany przez

Karlsona i Lindena [29] poprzez uwzględnienie moż-

liwości odkształcenia fazy twardej oraz wpływu wiel-

kości ziarna osnowy na proces odkształcenia plastycz-

nego. Jednak model ten dał znacznie zaniżone warto-

ści naprężenia uplastyczniającego podczas obliczeń

procesu odkształcenia stali ferrytyczno-perlitycznych.

W konkluzji, autorzy stwierdzili, że wkład dyslokacji

geometrycznie niezbędnych do naprężenia uplastycz-

niającego jest niewielki, zaś istotne znaczenie może

mieć przekaz obciążenia między fazami.

Modele wykorzystujące mechanikę ośrodków cią-

głych do obliczeń wytrzymałości i zachowania się pod-

czas odkształcenia materiałów dwufazowych zaliczyć
można do dwu kategorii, mianowicie, do schematów
aproksymacyjnych oraz do analizy z wykorzystaniem
metody elementów skończonych. Schematy aproksy-
macyjne zostały opracowane do przewidywania proce-
su płynięcia plastycznego materiałów utwardzanych
dyspersyjnie [30], kompozytów elasto-plastycznych
wzmacnianych materiałami włóknistymi [31], czy też
kompozytów wykazujących nieliniowy przebieg pro-
cesu pełzania [32]. Najważniejszą wadą tych modeli,
oprócz ograniczeń związanych z rozwiązaniem proble-
mów nieliniowych, jest założenie, że fazy są ośrodkami
ciągłymi, zaś odkształcenie plastyczne składników jest
jednorodne. Zastosowanie sprężysto-plastycznego mo-
delu w analizach wykorzystujących metodę elementów
skończonych do obliczeń zachowania się układów he-
terogenicznych w zakresie odkształcenia plastycznego
daje dobre wyniki, pod warunkiem, że przyjęte zosta-
ną poprawnie wartości stałych sprężystości, granicy
plastyczności oraz charakterystyki umocnienia skład-
ników fazowych [33, 34]. Obliczenia opierające się na
metodzie elementów skończonych pozwalają prawidło-
wo opisać lokalny charakter niejednorodności płynięcia
plastycznego, jednak są bardzo złożone.

Większość badaczy do obliczeń zmian naprężenia

w funkcji udziału objętościowego drugiej fazy w stalach
DP stosowało regułę mieszanin [35, 36]:

V

V

c

f

f

v

v

v

=

+

a

a

l

l

(12a)

V

V

c

f

f

f

f

f

=

+

a

a

l

l

(12b)

gdzie: V

f

– ułamek objętościowy ferrytu, V

a

l

– ułamek

objętościowy martenzytu,

f

v

– naprężenie w ferrycie,

v

a

l

– naprężenie w martenzycie,

f

f

– odkształcenie

w ferrycie, f

a

l

– odkształcenie w martenzycie, zaś

c

v

i

c

f

są, odpowiednio, naprężeniem i odkształceniem

kompozytu.

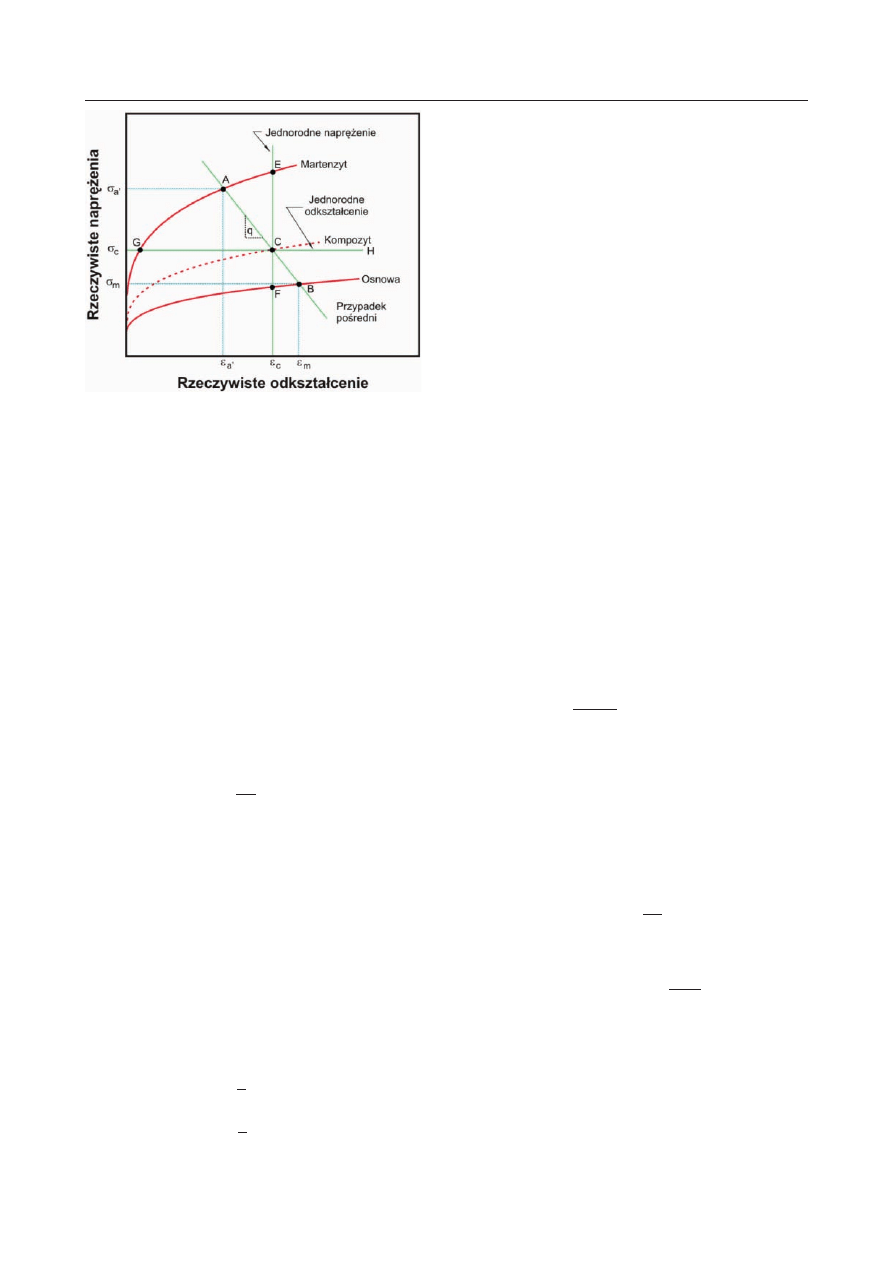
Prawo mieszanin przedstawiono grafi cznie na ry-

sunku 7. Należy podkreślić, że zależności 12(a,b) nie
pozwalają określić, jaki jest podział naprężenia i od-
kształcenia między składnikami struktury. Podział
naprężenia i odkształcenia defi niuje współczynnik na-
chylenia q linii AB:

q

f

f

f

f

v

v

=

-

-

a

a

l

(13)

Ze wzrostem q stan układu dwufazowego zbliża się

do warunków jednorodnego odkształcenia, dla których

f

f

= f

a

l

= f

c

. Z kolei małe wartości q odpowiadają wa-

runkom jednorodnego naprężenia, dla których v

f

=

v

a

l

= v

c

. Bezwzględna wartość wskaźnika q zależy od

ułamka objętości faz oraz od współczynnika podziału
naprężenia |, cech morfologicznych, charakterystyki
umocnienia składników fazowych oraz od przyłożonego
naprężenia. Dokładny charakter tej zależności nie jest
jednak znany. Małe wartości parametru q odpowiadają
dużym wartościom parametru |. W oparciu o wyniki
badań doświadczalnych, Fischmeister i Karlsson [37]
pokazali, że reguła mieszanin pozwala uzyskać dobre
wyniki dla wartości q = 4500 MPa.

Mimo dwu skrajnych i nierealistycznych alterna-

tyw, mianowicie, warunku jednorodnego naprężenia
lub jednorodnego odkształcenia w obu fazach (rys. 7),
Fischmeister and Karlsson [35] stwierdzili doświad-
czalnie oraz za pomocą obliczeń z wykorzystaniem me-

Molenda1.indd 35

25.08.2011 15:56:13

36

Prace IMŻ 2 (2011)

Ryszard Molenda, Roman Kuziak

tody elementów skończonych, że podział naprężenia
i odkształcenia dla materiału dwufazowego najlepiej
opisuje przejściowa (intermediate) reguła mieszanin.

Reguła mieszanin, wyrażona za pomocą równania

3(a,b), przedstawiona jest grafi cznie na rysunku 7.

Należy podkreślić, że równanie 12(a) i 12(b) nie de-

fi niują przekazu naprężenia i odkształcenia między
fazami. Przekaz ten jest zdefi niowany, jeśli znany jest
współczynnik nachylenia q linii AB na rysunku 7.

Wychodząc z reguły mieszanin, Razk i Bourell [38]

wyprowadzili następujące równanie na naprężenie
kompozytu uwzględniające wpływ dyslokacji tworzą-
cych się podczas przemiany martenzytycznej:

V K

C

V K

/

c

f

f

dm

a n

n

1

f

=

+

+

v

f

t

f

a

a

a

l

l

l

`

j

8

B

(14)

gdzie K

f

i K

α’

, C, a, n

f

, n

α’

są współczynnikami,a t

a

l

jest

gęstością dyslokacji powstałych w wyniku zajścia prze-
miany martenzytycznej.

Równanie (14) pokazuje, że wzrost naprężenia upla-

styczniającego stali DP nastąpić może poprzez wzrost
udziału martenzytu, wzrost wytrzymałości martenzy-
tu K

α’

i ferrytu K

f

oraz poprzez wzrost gęstości dyslo-

kacji powstałych podczas przemiany fazowej. Podział
odkształcenia między obie fazy, uzależniony jest od ich
właściwości mechanicznych.

Speich zaproponował model, który zakłada podział

odkształcenia między dwie fazy w ten sposób, że tylko
niewielki ułamek całkowitego odkształcenia przypada
na martenzyt. Przyjęcie tego założenia pozwoliło wy-
prowadzić następujące zależności [39]:

V

3

1

,

,

,

y

y f

y m

y f

m

0

0

0

v

v

v

v

=

+

-

c

m (15)

V

3

1

,

,

,

t

t f

y m

t f

m

0

0

0

=

+

v

v

v

v

-

c

m (16)

gdzie

y

v jest granicą plastyczności kompozytu,

,

y m

0

v

jest

granicą plastyczności martenzytu,

,

y f

0

v

jest granicą pla-

styczności ferrytu,

t

v

,

,

t f

0

v

są odpowiednio wytrzymało-

ścią na rozciąganie kompozytu i ferrytu.

Dla stali o zawartości 15–25% martenzytu Naresh

i wsp. opracowali model uwzględniający [40]:

efekt umocnienia składników struktury,

–

efekt indukowanej odkształceniem przemiany auste-

–

nitu w martenzyt,

efekt umocnienia osnowy ferrytu wskutek zajścia

–

przemiany martenzytycznej,

przekaz obciążenia i podział odkształcenia między

–

fazę twardą i miękką, który opisany jest zmodyfi -

kowaną regułą mieszanin zaproponowaną w pracy

[41].

Opracowany model wykorzystali do obliczeń krzy-

wych naprężenie-odkształcenie, uzyskiwanych w sta-

tycznej próbie rozciągania. Obliczenia pozwoliły przede

wszystkim określić wpływ austenitu szczątkowego na

umocnienie stali DP. Pokazały one, że najbardziej ko-

rzystną charakterystykę umocnienia stale te wykazują

w przypadku, gdy austenit charakteryzuje się umiar-

kowaną stabilnością względem odkształcenia. Duża

i mała stabilność pogarszają charakterystykę umoc-

nienia. Transfer obciążenia, którego wskaźnikiem jest

kąt nachylenia q, ma również bardzo duży wpływ na

charakterystykę umocnienia. Jeśli q maleje, wzrasta

maksymalne odkształcenie, przy którym martenzyt

wykazuje właściwości sprężyste.

W literaturze technicznej znaleźć można zależności

umożliwiające przewidywanie właściwości mechanicz-

nych stali DP z wykorzystaniem zależności typu Halla-

Petcha. Na przykład dla stali zawierającej około 0,2

martenzytu lub martenzytu z austenitem szczątkowym

(MA) zidentyfi kowano następujące zależności [42]:

,

350 18 1

(

, )

,

f

0 2

0 5

v

m

=

+

f=

-

(17)

,

d

d

40 1

(

, )

,

0 2

0 5

f

v

m

=

f=

-

(18)

gdzie m jest średnią średnicą wysp MA.

Z równań tych wynika, że dv /df rośnie szybciej niż

v

; z tego powodu rozdrobnienie cząstek MA powoduje

wzrost odkształcenia równomiernego i ogólnie wzrost

ciągliwości stali.

Odkształcenie inicjujące pękanie f

T

jest również pa-

rametrem, który bardzo często jest wykorzystywany do

scharakteryzowania plastyczności stali DP. Odkształ-

cenie to można powiązać z naprężeniem inicjującym

pękanie za pomocą następującej zależności [42]:

,

f

f

500 1420

40

75

0 2

,

fr

MA

MA

T

0 5

v

m

f

=

+

+

+

-

c

^

m

h

;

E

(19)

Z kolei naprężenie inicjujące proces pękania zależy

od parametrów mikrostruktury:

, L

L

720 24 4

,

,

fr

0 5

0 5

v

m

m

=

+

+

-

c

m

(20)

gdzie L jest średnią odległością między wyspami MA;

a zależność między L, m i f

MA

ujmuje następujące rów-

nanie:

,

,

L

f

0 87

0 98

,

MA

0 5

m

=

-

-

^

h

(21)

Do określenia zależności między granicą plastyczno-

ści, a wielkością ziarna (lub średnią drogą swobodną

dyslokacji w ferrycie) w stalach DP stosuje się równa-

nie Halla-Petcha. Podstawowym ograniczeniem w sto-

sowaniu tego równania jest zależność parametrów

0

v

i k

y

od ułamka martenzytu w strukturze. Ostatnie ba-

Rys. 7. Krzywa naprężenie – odkształcenie dla miękkiej

osnowy dla stali dwufazowej o „miękkiej” osnowie (m)

i twardej drugiej fazie (

D’). Linie EF, GH i AB odpowiadają

różnym warunkom, odpowiednio, jednorodne odkształce-

nie, jednorodne naprężenie i przypadek pośredni
Fig.7. Stress-strain curve for soft matrix for two-phase ste-

el of ”soft” matrix (m) and hard second phase (

D’). Lines

EF, GH and AB refl ect various conditions, homogeneous

strain, homogeneous stress and intermediate case

Molenda1.indd 36

25.08.2011 15:56:13

37

Prace IMŻ 2 (2011)

Metaloznawcze podstawy kształtowania struktury i właściwości blach...

dania pokazują, że problem ten można rozwiązać sto-

sując następujące równanie [43]:

( )

,

,

( )

log

log

2 8565 0 25441

y

f

v

m

=

-

(22)

gdzie m

f

jest średnią drogą dyslokacji w ferrycie struk-

tury stali DP.

W pracy [43] przeprowadzono ponadto analizę umoc-

nienia stali DP, stwierdzając występowanie następują-

cych etapów:

Etap I: jednorodne odkształcenie ferrytu poprzez

poślizg ruchliwych dyslokacji występujących

w sąsiedztwie wysp martenzytu,

Etap II: obejmuje malejące umocnienie ferrytu i prze-

mianę austenitu szczątkowego w martenzyt,

Etap III: odkształcenie ferrytu z udziałem poślizgu

poprzecznego, dynamiczne zdrowienie i od-

kształcenie martenzytu.

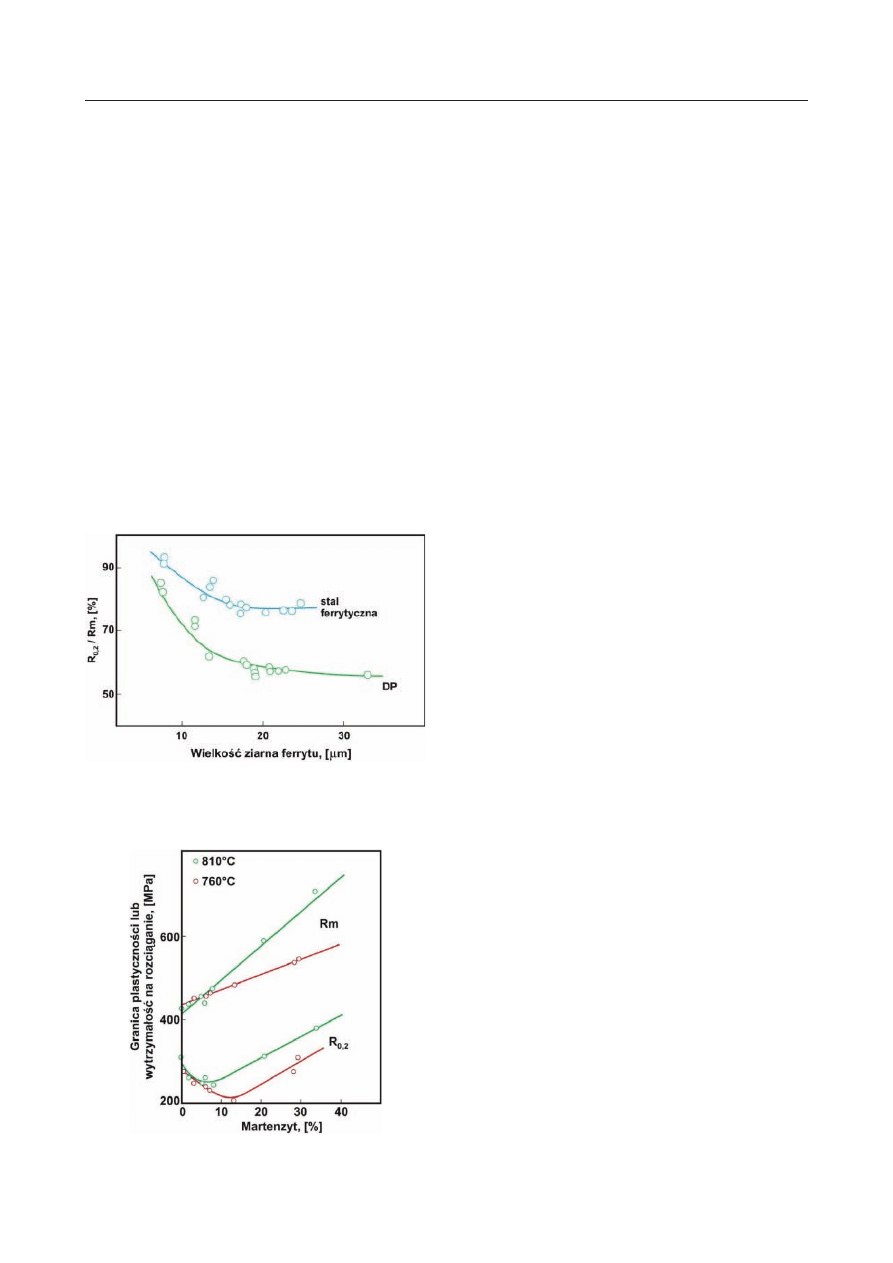
Wpływ wielkości ziarna ferrytu w stali DP oraz

w ultraniskowęglowej stali ferrytycznej na wartość

R

0,2

/R

m

przedstawiono na rysunku 8 [44]. Z rysunku

tego wynika, że wyroby ze stali DP mogą wykazywać

bardzo niską wartość tego parametru, zaś optymalna

wielkość ziarna w tych stalach jest po wyżarzaniu mię-

dzykrytycznym zależna od udziału martenzytu [44].

Z rysunku tego wynika, że wyroby ze stali DP mogą

wykazywać bardzo niską wartość tego parametru, zaś

optymalna wielkość ziarna w tych stalach jest większa

od około 12

μm.

Blachy zimnowalcowane ze stali DP po wyżarzaniu

międzykrytycznym wykazują charakterystyczną zależ-

ność granicy plastyczności od udziału objętościowego

martenzytu (rys. 9), mianowicie, wzrost udziału mar-

tenzytu w strukturze w przedziale 0–12% powoduje

obniżenie granicy plastyczności [44]. Dopiero dalszy

wzrost ułamka martenzytu powoduje wzrost granicy

plastyczności. Z kolei wytrzymałość na rozciąganie ro-

śnie ze wzrostem ułamka martenzytu w szerokim za-

kresie zmienności tego parametru.

4. PROCES CIĄGŁEGO WYŻARZANIA

BLACH CIENKICH

4.1. PRZEMYSŁOWE LINIE CIĄGŁEGO

WYŻARZANIA BLACH

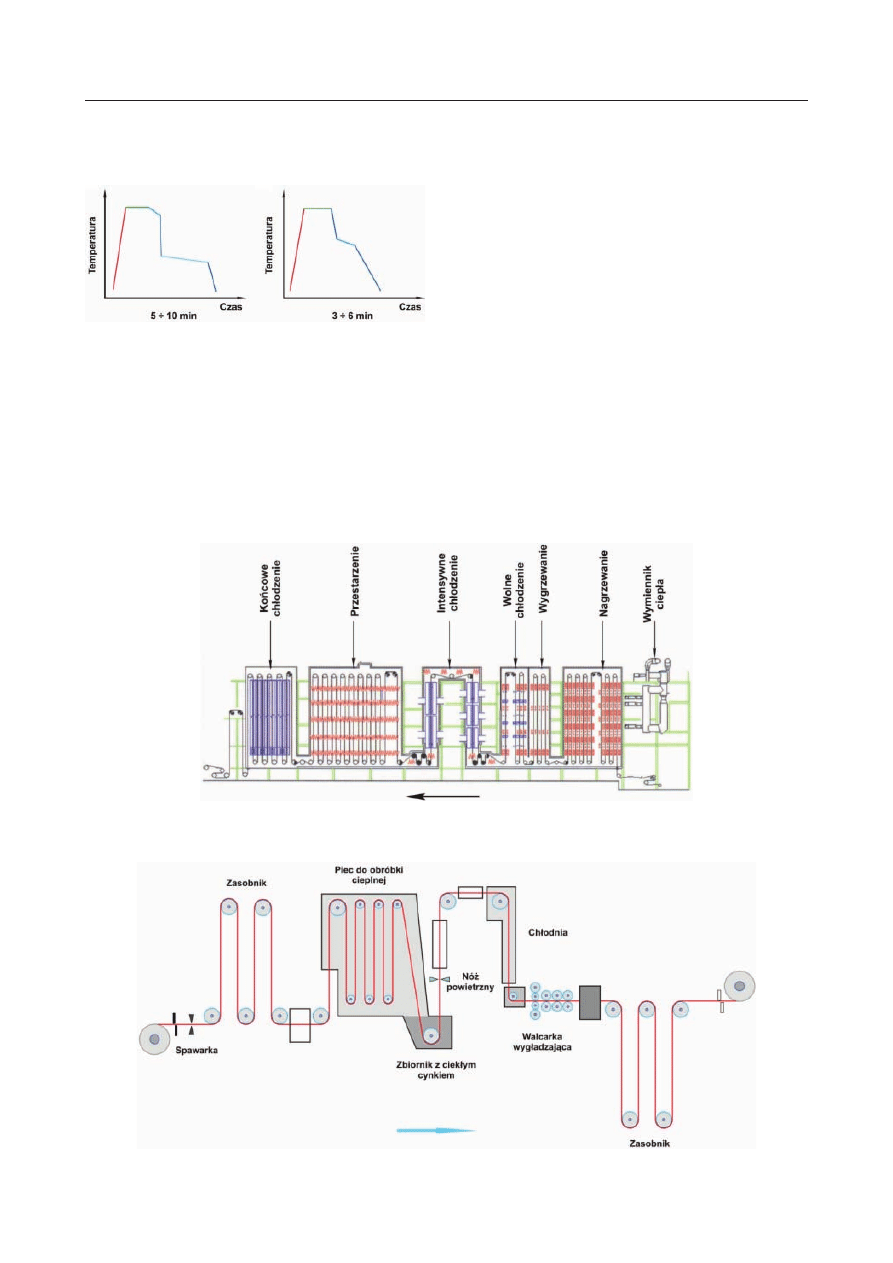
Wyżarzanie blach zimnowalcowanych przed 1950 r.

prowadzono wyłącznie w piecach kołpakowych. Cechą

charakterystyczną tego procesu, który jest stosowany

również do chwili obecnej, jest długi czas cyklu termicz-

nego, dochodzący do 50 godzin [45–47]. W latach 50.

XX wieku po raz pierwszy zastosowano wyżarzanie cią-

głe do produkcji blach taśmowych o wysokiej wytrzy-

małości i niskiej ciągliwości z przeznaczeniem do wy-

twarzania puszek konserwowych. W przeciwieństwie

do wyżarzania w piecach kołpakowych, czas cyklu ter-

micznego podczas wyżarzania ciągłego jest ograniczo-

ny do kilku minut. Systematyczne badania nad efek-

tywnym wykorzystaniem metody ciągłego wyżarzania

do kształtowania właściwości mechanicznych blach

gorąco- i zimnowalcowanych rozpoczęto w Japonii na

przełomie lat 1960–1970. W latach 70. wdrożono szereg

nowych technologii w warunkach przemysłowych. Ko-

lejnym etapem rozwoju linii ciągłych było uruchomie-

nie produkcji blach głębokotłocznych i wysokowytrzy-

małych. Obecnie, głównie z ekonomicznych powodów,

rośnie również wykorzystanie linii ciągłego wyżarzania

do wytwarzania blach taśmowych ze stali o niższej po-

datności do odkształcenia plastycznego.

Zastąpienie metody wyżarzania długookresowego

metodą ciągłego wyżarzania obniża koszty pracy o 73%

i zużycie energii o 23% w porównaniu do wyżarzania

długookresowego. Obecnie linie technologiczne ciągłe-

go wyżarzania zapewniają uzyskanie znacznie szersze-

go przedziału właściwości mechanicznych blach w po-

równaniu z technologiami bazującymi na wyżarzaniu

długookresowym. Do końca 1990 powstało 45 takich

linii o zróżnicowanej prędkości pasma od 100–300

m/min i temperaturze piku cyklu termicznego w prze-

dziale 500–850

°C.

Skrócenie czasu wyżarzania w procesie ciągłym,

w porównaniu do wyżarzania długookresowego, powo-

duje jednak wzrost wymagań odnośnie do stabilności

składu chemicznego stali i parametrów procesu. Blachy

taśmowe o niższej plastyczności wytwarza się w liniach

ciągłych poprzez zastosowanie mniej wymagających re-

żimów technologicznych, na ogół, obniżając temperatu-

rę i/lub czas cyklu. Obecnie, coraz częściej łączy się pro-

ces wyżarzania z zanurzeniowym nanoszeniem powłok

ochronnych. Porównanie typowych cykli termicznych

dla urządzeń do ciągłego wyżarzania i zanurzeniowego

Rys. 8. Wpływ wielkości ziarna na R

0.2

/R

m

w ultraniskowę-

glowej stali ferrytycznej i stali DP [44]
Fig. 8. Impact of grain size on R

0.2

/R

m

in ultra-low carbon

ferrite and DP steel [44]

Rys. 9. Zależność R

0.2

i R

m

blach ze stali wytwarzania blach

ze stali DP
Fig. 9. Dependence of R

0.2

and R

m

– DP steel plates

Molenda1.indd 37

25.08.2011 15:56:13

38

Prace IMŻ 2 (2011)

Ryszard Molenda, Roman Kuziak

nanoszenia powłok przedstawiono na rysunku 10, zaś

na rysunkach 11 i 12 przedstawiono schemat linii cią-

głego wyżarzania, za pomocą której zrealizować można

cykl przedstawiony na rysunku 10(a).

DP powoduje on odpuszczenie martenzytu lub ustale-
nie pożądanych proporcji między zawartościami mar-
tenzytu i bainitu.

Literatura dotycząca badań wpływu składu chemicz-

nego i cykli termicznych na właściwości mechaniczne
blach taśmowych ze stali DP wytwarzane w procesie
ciągłego wyżarzania lub zanurzeniowego nanoszenia
powłok ochronnych jest stosunkowo uboga. Większość
badań dotyczących przemian fazowych w stalach DP
podczas chłodzenia prowadzono ze stałą szybkością
chłodzenia do temperatury otoczenia. Na podstawie
tych badań opracowano równania pozwalające obli-
czyć krytyczną szybkość chłodzenia, której zastosowa-
nie powoduje utworzenie się martenzytu w strukturze
stali, w zależności od składu chemicznego. Tylko kilka
artykułów poświęcono badaniom przemian fazowych
w stalach DP w odniesieniu do warunków ciągłego
chłodzenia lub zanurzeniowego nanoszenia powłok
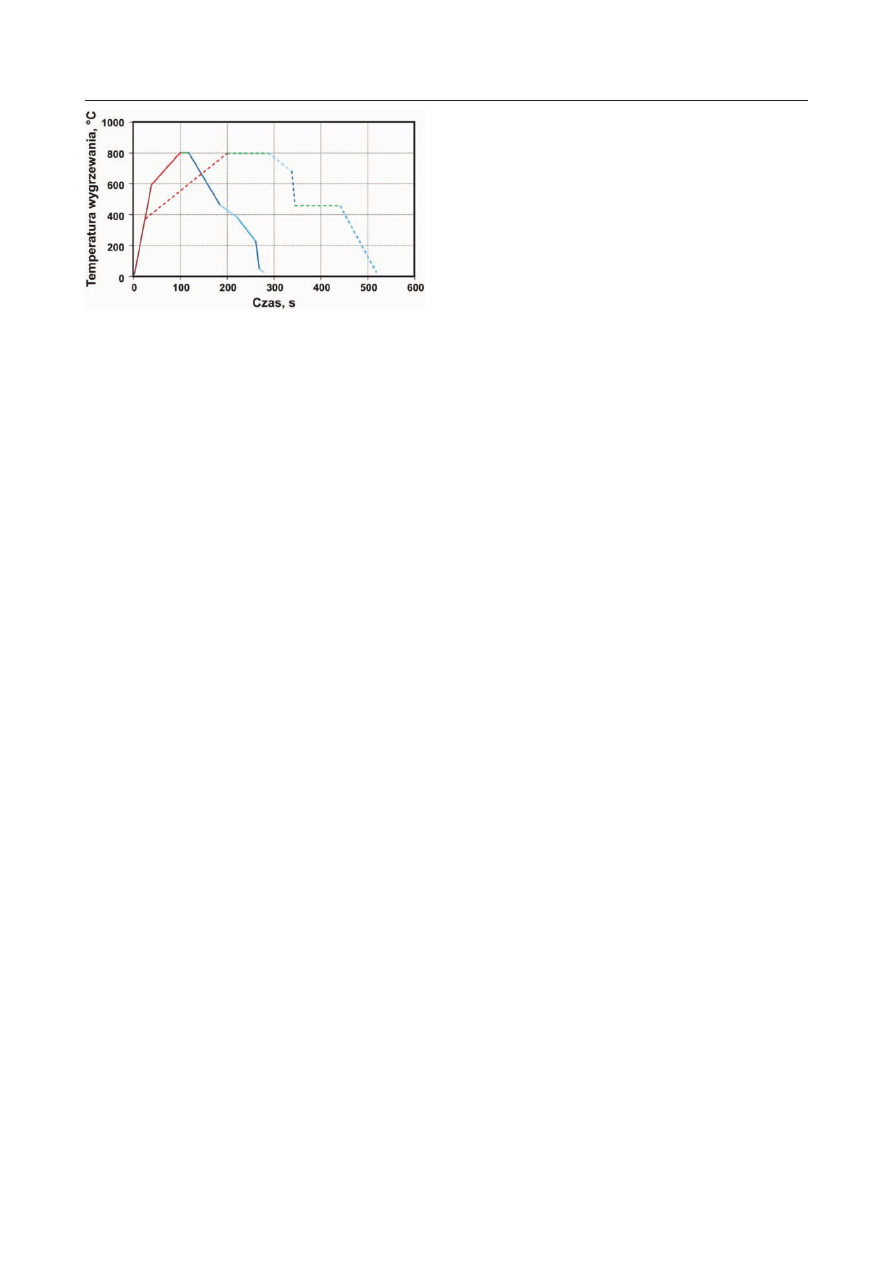
w przemysłowych liniach technologicznych. Różnice w
cyklach termicznych dla linii ciągłego wyżarzania i za-
nurzeniowego nanoszenia powłok przedstawiono na ry-
sunku 13.

Z badań [48, 49] wynika, że rozpuszczanie cemen-

tytu podczas nagrzewania stali DP jest procesem za-
chodzącym bardzo szybko, zaś udział austenitu zale-

Rys. 10. Cykl termiczny dla procesu ciągłego wyżarzania

blach taśmowych – (a) i wyżarzania połączonego z zanurze-

niowym nanoszeniem powłok ochronnych
Fig. 10. Thermal cycle for continuous metal strip an-

nealing – (a) and annealing combined with immersion

coating (protective coatings)

Rys. 12. Schemat linii technologicznej do zanurzeniowego nanoszenia powłok ochronnych
Fig. 12. Diagram of technological line for immersion coating (protective coatings)

Rys. 11. Schemat linii technologicznej do ciągłego wyżarzania blach
Fig. 11. Diagram of technological line for continuous annealing of plates

Cykl termiczny w liniach ciągłych w przypadku blach

ze stali głębokotłocznych ma nie tylko spowodować zaj-
ście rekrystalizacji ferrytu, ale również wydzielenie
węgla z roztworu stałego w postaci cząstek cementytu.
Dla blach ze stali BH, ma on również na celu regulację
zawartości węgla w roztworze stałym. Z kolei w stalach

Molenda1.indd 38

25.08.2011 15:56:13

39

Prace IMŻ 2 (2011)

Metaloznawcze podstawy kształtowania struktury i właściwości blach...

ży od maksymalnej temperatury cyklu nagrzewania.

Z tego powodu właściwości mechaniczne blach po cią-

głym wyżarzaniu silnie zależą od maksymalnej tem-

peratury nagrzewania. Badania pokazują przy tym,

że wyżarzanie przy temperaturach poniżej 760

°C nie

powoduje całkowitego rozpuszczenia cementytu w wa-

runkach nagrzewania i wygrzewania typowych dla li-

nii ciągłej. Z drugiej strony, ze wzrostem temperatury

wygrzewania uzyskuje się większy ułamek austenitu

w strukturze stali. Jednak niekoniecznie spowodować

może to wzrost udziału objętościowego martenzytu

w strukturze stali, bowiem ze wzrostem udziału auste-

nitu po wygrzewaniu wzrastać również może szybkość

postępu przemiany ferrytycznej podczas chłodzenia.

Z tego powodu, wyraźny wzrost wytrzymałości dla

niektórych gatunków stali DP możliwy jest po zasto-

sowaniu temperatury wygrzewania powodującej uzy-

skanie jednofazowej struktury austenitu. W celu uzy-

skania optymalnych właściwości mechanicznych stali

DP, w pierwszym etapie chłodzenia powinna zachodzić

przemiana ferrytyczna ze stopniowym wzbogacaniem

pozostałego austenitu w węgiel, a następnie, austenit

powinien podlegać przemianie do martenzytu. Należy

przeciwdziałać tworzeniu się perlitu i bainitu podczas

chłodzenia. Dla zapewnienia tego, należy dokładnie

ustalić szybkości chłodzenia taśmy. Małe szybkości

chłodzenia powodują występowanie perlitu i bainitu

w strukturze stali, zaś zbyt duże powodują wzrost tem-

peratury M

s

, wskutek niskiego wzbogacenia austenitu

w węgiel. Zawartość węgla w austenicie wpływa także

na kinetykę przemiany perlitycznej i bainitycznej. Ba-

dania dylatometryczne pokazują, że przemiana baini-

tyczna zachodzi z największą szybkością przy tempe-

raturze około 450

°C. Podwyższanie temperatury prze-

miany powoduje znaczący wzrost czasu przemiany, zaś

powyżej 550

°C, austenit w stalach DP może podlegać

przemianie do perlitu. Ta cecha stali DP ma wpływ na

właściwości mechaniczne blach po przestarzeniu. Ze

wzrostem temperatury przestarzenia maleją właściwo-

ści wytrzymałościowe blach. Z tego powodu, w techno-

logii produkcji taśm ze stali DP powinno stosować się

krótkie czasy przestarzenia. Ponieważ przedział tem-

peratur, w którym zachodzi proces rozpuszczania ce-

mentytu w krótkim czasie jest wąski, w urządzeniach

do wyżarzania blach karoseryjnych powinna występo-

wać strefa wygrzewania. W urządzeniach do cynko-

wania zanurzeniowego nie jest konieczne stosowanie

dużych szybkości chłodzenia, ponieważ wzbogacenie

austenitu w węgiel powoduje opóźnienie zajścia prze-

miany bainitcznej podczas wytrzymania taśmy przed

zanurzeniem w kąpieli.

4.2 LABORATORYJNE LINIE

TECHNOLOGICZNE CIĄGŁEGO WYŻARZANIA

TAŚM STALOWYCH

W pracach [50, 51] przedstawiono opisy linii labo-

ratoryjnych służących do przeprowadzania ekspery-

mentów związanych z ciągłym wyżarzaniem taśm.

Zaprojektowana i wykonana w koncernie Salzgitter

Mannesmann Forschung GmbH linia technologiczna

umożliwia nagrzewanie oporowe próbek blachy o wy-

miarach 450 mm × 250 mm × 3 mm do temperatury

1000°C z maksymalną szybkością 60°C/s. Szybkość

chłodzenia uprzednio nagrzanej próbki blachy w za-

leżności od użytego czynnika to jest :delikatnego na-

dmuchu powietrza, sprężonego powietrza, rozpylonej

wody wynosi odpowiednio: 1–20°C/s; 5–100°C/s; 100–

400°C/s. Maksymalna moc dostarczana do omawianej

linii wynosi 100 kW, ciśnienie powietrza wynosi 6 bar,

zużycie wody chłodzącej 2 m

3

/h.

Horyzontalny układ linii ciągłego wyżarzania próbek

blach stalowych o wymiarach 605 mmx200 mm przed-

stawiono w pracy [51]. Do zasadniczych podzespołów

wchodzących w skład omawianej linii technologicznej

należą:

zespół grzewczy składający się z 33 lamp halogeno-

–

wych o łącznej mocy 66 kW,

dwa piece komorowe o mocy 25 kW każdy,

–

cztery skrzynie chłodzące z dyszami powietrznymi

–

zasilanymi przez sprężarkę o poborze mocy 15 kW,

oraz

zespół dysz wodno-powietrznych.

–

Przedstawiona linia do ciągłego wyżarzania blach

stalowych umożliwia nagrzewanie próbek z maksymal-

ną szybkością 30°C/s. Maksymalna szybkość chłodze-

nia próbek o grubości 0,7 mm wynosi 100°C/s. Próbka

może przemieszczać się na linii z maksymalną szyb-

kością 2 m/s, natomiast wartość przyśpieszenia jaką

może uzyskać próbka wynosi 5 m/s

2

.

4.3 WYTWARZANIE BLACH ZE STALI DP

METODĄ WALCOWANIA NA GORĄCO

Blachy o strukturze dwufazowej wytwarzane są

również metodą walcowania na gorąco [47]. Uzyskanie

pożądanej mikrostruktury stali DP w procesie walco-

wania na gorąco wymaga stosowania złożonych sche-

matów walcowania i kontrolowanego chłodzenia po

walcowaniu (rys. 14).

Przemiany fazowe austenitu po walcowaniu w wyro-

bach ze stali DP powinny zachodzić dwuetapowo:

W etapie pierwszym pasmo jest tak chłodzone, aby

1.

w strukturze powstała wymagana ilość ferrytu

(75–80%). Z postępem przemiany ferrytycznej na-

stępuje stopniowe wzbogacenie austenitu w węgiel.

W warunkach linii walcowniczej, przemiana ferry-

tyczna powinna zachodzić bardzo szybko, co zapew-

nia stosowanie niskiej zawartość węgla w stali oraz

podwyższonej zawartość krzemu. Przemiana perli-

tyczna zostaje odsunięta w czasie w wyniku wprowa-

dzenia do stali dodatków Mo, Mn, Cr, C.

W etapie drugim stosuje się szybkie chłodzenie bla-

2.

chy z prędkościami zapewniającymi spowodowanie

Rys. 13. Porównanie cykli termicznych w linii ciągłego

wyżarzania blach (linia przerywana) i nanoszenia powłok

ochronnych (linia ciągła)
Fig. 13. Comparison of thermal cycles in the line for con-

tinuous plates annealing (broken line) and protective

coatings application (full line)

Molenda1.indd 39

25.08.2011 15:56:14

40

Prace IMŻ 2 (2011)

Ryszard Molenda, Roman Kuziak

wyłącznie przemiany martenzytycznej. Odpowiednią

stabilność austenitu kształtują pierwiastki stopowe

oraz podwyższona wskutek segregacji zawartość wę-

gla w austenicie (rys. 4). W etapie tym konieczne jest

stosowanie niskich temperatur zwijania w krąg (na

ogół, poniżej 400°C).

Krytyczna szybkość chłodzenia (K/s) dla utworzenia

struktury dwufazowej stali DP może być obliczona za

pomocą następującego równania [48]:

( )

,

,

,

,

,

log C

Mn

Si

Cr

P

5 36 2 36

1 06

2 71

4 72

>

R

-

-

-

-

(23)

lub [49],

( )

,

,

log C

Mn

5 36 2 36

R

eq

=

-

(24)

,

,

Mn

Mn

Si

Cr

P

0 45

1 15

2

eq

=

+

+

+

warunki chłodzenia blach po walcowaniu powinny być

odpowiednio zaprojektowane. Wpływ krzywych chło-

dzenia na postęp przemiany ferrytycznej przedstawio-

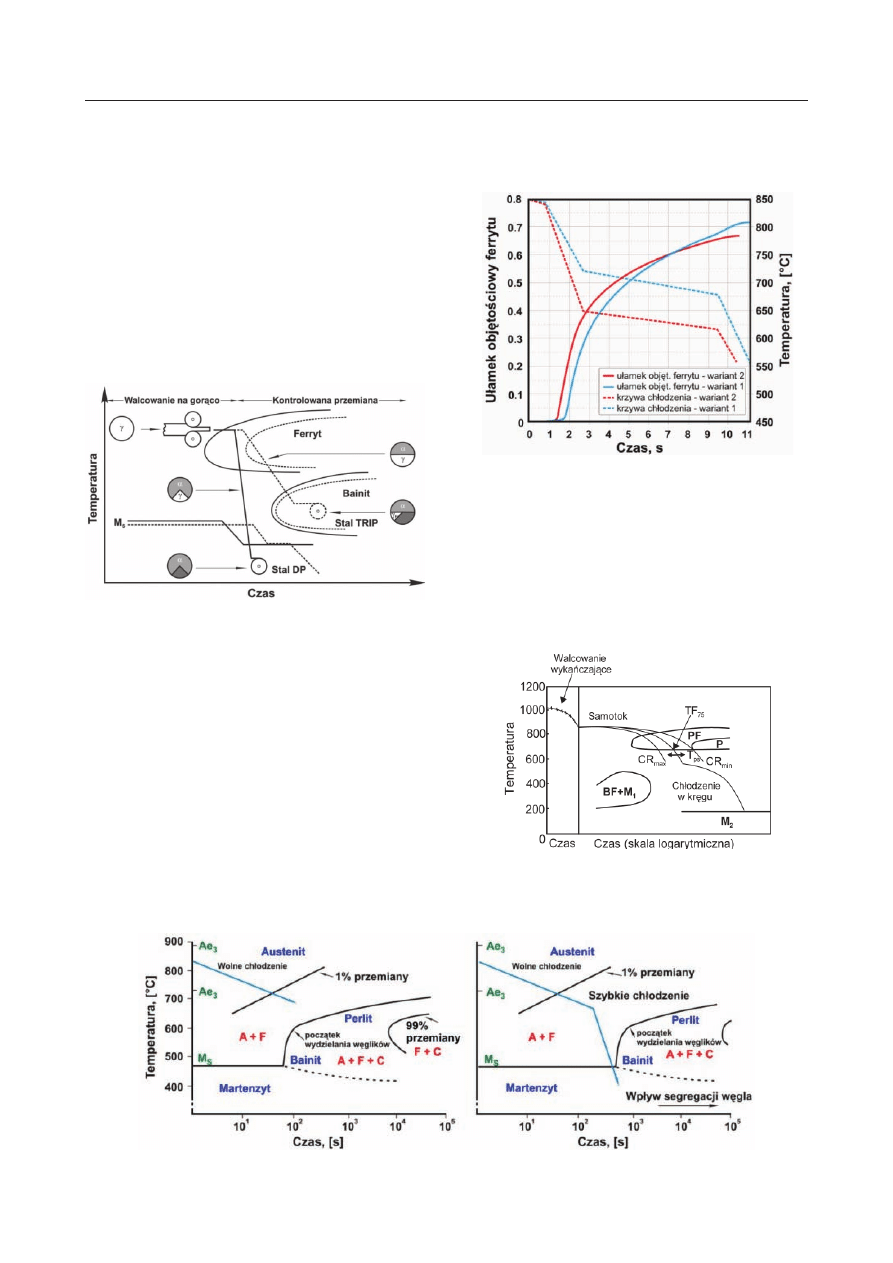
no na rysunku 16.

Rys. 14. Schemat chłodzenia blach ze stali DP praz TRIP
Fig. 14. DP and TRIP steel plates cooling diagram

Wpływ sposobu chłodzenia blach na przebieg rozpa-

du austenitu przedstawiono na rysunku 15. Rysunek

15(a) przedstawia wykres CTP

c

w przypadku chłodze-

nia próbek stali ze stałą szybkością. Przypadek ten od-

powiada konwencjonalnemu sposobowi chłodzenia pró-

bek w testach dylatometrycznych. Z kolei, na rysunku

15(b), przedstawiono sytuację, gdy początkowo próbka

chłodzona jest wolno do momentu, gdy udział ferrytu

wynosi w niej około 0,8. Następnie zastosowane jest

szybkie chłodzenie do temperatur poniżej M

s

. Postęp

przemiany ferrytycznej podczas wolnego chłodzenia

powoduje wzbogacenie austenitu w węgiel, co zwiększa

hartowność tej fazy. W wyniku tego następuje przesu-

nięcie zakresu przemiany perlitycznej i bainitycznej do

większych szybkości chłodzenia (rys. 15(b)). Z uwagi

na ograniczenia technologiczne, skład chemiczny oraz

Rys. 15. Schemat chłodzenia wyrobów ze stali DP
Fig. 15. DP steel products cooling diagram

Rys. 16. Wpływ zmian temperatury w procesie chłodzenia

blach ze stali DP na postęp przemiany ferrytycznej
Fig. 16. Impact of temperature changes in the process of

DP steel plates cooling on ferrite phase course advance

Dla uzyskania odpowiedniej stabilności właściwości

mechanicznych stali PD konieczne jest zapewnienie

szerokiego przedziału szybkości chłodzenia poprzez

odpowiednie zaprojektowanie składu chemicznego,

w którym możliwe jest uzyskanie około 75% ferrytu

w strukturze (rys. 17).

Rys. 17. Krzywa chłodzenia w procesie walcowania blach

ze stali DP
Fig. 17. Cooling curve in the process of DP steel plates rol-

ling

Molenda1.indd 40

25.08.2011 15:56:14

41

Prace IMŻ 2 (2011)

Metaloznawcze podstawy kształtowania struktury i właściwości blach...

5. WNIOSKI

W artykule przeprowadzono analizę literatury me-

1.

taloznawczej dotyczącej procesów zachodzących

w trakcie ciągłego wyżarzania blach cienkich.

Zwrócono szczególną uwagę na proces rozpuszczania

2.

perlitu w osnowie ferrytycznej oraz jaki wpływ wy-

wiera on na tworzenie się austenitu, co jest istotnym

elementem w procesie tworzenia struktury ferrytycz-

no-martenzytycznej stali DP.

Na podstawie analizy danych literaturowych oraz

3.

własnych doświadczeń związanych z procesem cią-

głego wyżarzania blach opracowano kilka wariantów

technologii, które zrealizowano za pomocą symulato-

ra Gleeble, a wyniki badań przedstawiono w kolej-

nym artykule.

LITERATURA

Liedl U., Traint S., Werner E.A.: Comp. Mater. Sci., vol. 25

1.

(2002), 122-128.

Saleh M.H., Priestner R.: J Mater. Process. Technol., vol. 113

2.

(2001) 587-593.

Bayram A., Uguz A., Ula M.: Mat. Character.; vol. 43 (1999),

3.

259-269.

Mesplont C., Watershoot T., Vandeputte S., Vanderschueren

4.

D., De Cooman B.C.: Conference Proceedings, MWSP, ISS,

vol. XXXVII, 1999, 515-524.

Sun S., Pugh M.: Mater. Sci. Eng.; A335 (2002), 298-3008.

5.

Pichler A., Hribering G., Tragl E., Angerer R., Radlmayr K.,

6.

Szinyur J., Traint S., Werner E., Stiaszny P.: Aspects of the

Production of Dual Phase and Multiphase Steel Strips, 41

st

MWSP CONF. PROC., ISS, VOL. XXXVII, 1999, 37-60.

Pichler A., Traint S., Arnolder G., Stiaszny P., Blaimschein

7.

M., Werner E.A.: I&SM, June 2003, 21-31.

Speich G.R., Demarest V.A., Miller R.L.: Metall. Trans. A,

8.

Vol. 12A, August 1981, 1419-1428.

Kinsmann K.R., Aaronson H.I.: Transformation and Harden-

9.

ability in Steels, Climax Molybdenium Corp., Ann Arbor, MI,

1967, 39-53.

Darken L.S., Gurry R.W.: Physical Chemistry of Metals,

10.

McGraw-Hill, New York, 1953, 445-449.

Nath S.K., Ray S., Mathur V.N. and Kapoor M.L.: ISIJ Int.,

11.

vol. 34 (1994), No.2, pp.191-197.

Krauss G., Matlock D.K., Cornford E.E.: in HSLA Steels Tech-

12.

nology and Applications, ed. M. Korchynsky, ASM, Metals

Park, OH, 1984, 297-327.

Garcia G.I. DeArdo A.J.: Metall. Trans. A, 1981, vol. 12A, 521-

13.

530.

Bunge H.J.: Mathematische Metoden der Textur Analyse,

14.

Akademie-Verlag, Berlin, 1969.

Gottstein G.: Physikalische Grundlagen der Materialkunde,

15.

Springer-Verlag, Berlin, 2

nd

edition, 2001.

Yang D.Z., Brown E.L., Matlock D.K., Krauss G.: Metall.

16.

Trans. A, vol. 16A, 1985, 1385-1391.

Xue-Ling Cai, Carrat-Reed A.J., Owen W.S.: Metall. Trans. A,

17.

vol. 16A, 1985, 543-557.

Leslie W.C.: The Physical Metallurgy of Steels, McGraw-Hill,

18.

New York, NY, 1981, 79-90.

Low J.R., Gensamer M.: Trans. AIME, vol. 158, 1944, 207-

19.

249.

Cottrell A.H., Bilby B.A.: Proc. Phys. Cos., 1949, 49-62.

20.

Bailey F.D., Foley R.P., Matlock D.K.: Proceedings on High-

21.

Strength Steels for the Automotive Industry, ed. R. Pradhan,

Iron & Steel Society, Baltimore, MD, 1994, 119-133.

Waterschoot T., De S. A.K.: Vandeputte and B.C. de Cooman;

22.

Metall. Trans. A. vol. 34A, 2003, 781.

Waterschoot T., De S. A.K.: Vandeputte and B.C. de Cooman;

23.

Z. Metallkd., vol. 94, 2003, 424.

Waterschoot T., Verbeken K., De Cooman B.C.: ISIJ Interna-

24.

tional, vol. 46 (2006), No.1, 138-146.

Fang X., Fan Z., Ralph B., Evans P., Underhill R.: Mat. Proc.

25.

Technol., vol. 132 (2003), 215-218.

Fischmeister H., Karlsson B.: Z. Metallkde, vol. 68(5), 1977,

26.

311.

Asby M.F.: Phil. Mag., vol. 21, 1970, 399.

27.

Korzekwa D.A., Lawson R.D., Matlock D.K., Krauss G.: Scrip-

28.

ta Met., vol. 14, 1980, 1023.

Karlsson B., Linden G.: Mat. Sci. Eng., vol. 17, 1975, 209.

29.

Tomota Y., Kuroki K., Mori T., Tamura I.: Mat. Sci. Eng., vol.

30.

24, 1976, 85.

Dvorak G.J., Bahei-El-Din Y.A.: J. Mech. Phys. Of Solids, vol.

31.

27, 1979, p.51.

Chen I.W., Argon A.S.: Acta Metall., vol. 27, 1979, 789.

32.

Karlson B., Sundstrom B.O.: Mat. Sci. Eng., vol. 16, 1974,

33.

161.

Sundstrom B.O.: Mat. Sci. Eng., vol. 12, 1977, 265.

34.

Davies R.G.: Metall. Trans. A, 1978, vol. 9A, 671.

35.

Thomas G. and Koo J.Y.: Structure and Properties of Dual

36.

Phase Steels, eds. R.A. Kot and J.W. Morris, TMS-AIME, New
York, NY, 1979, 183.

Fisher H., Karlsson B.: Z. Metallkde, vol. 68(5), 1977, 311.

37.

Rizk, Bourel D..: Scripta Metall., vol. 16, 1982, 1321-1324.

38.

Speich G.R.: Proc. Conf. „Fundamentals of Dual Phase Steels”,

39.

TMS-AIME, Chicago, IL, February 1981, 4-46.

Naresh C., Goel C., Sangal S., Tangri K.: Metall. Trans. A;

40.

16A, 1985, 2013-2021.

Tomota Y., Tamura I.: Trans. ISIJ, vol. 22, 1982, 665.

41.

Physical Metallurgy Handbook, ed. A. K. Sinha, 2003, 15.45.

42.

Bag A., Ray K.K., Dwarakadasa E.S.: Metall. Mat. Trans. A,

43.

vol. 30A, May 1999, 1193.

Ginzburg V.B.: Steel – Rolling Technology, Theory and Prac-

44.

tice, Marcel Dekker,

Zalecki W., Skraba M.: Opracowanie nowego sterowania pra-

45.

cą pieców kołpakowych w walcowni blach karoseryjnych HTS
oraz optymalizacja procesów wyżarzania blach. Sprawozdanie

z pracy badawczej IMŻ, Nr – B-884/2, 1992 – niepublikowane

Pichler A. i inni: 41 ST Mechanical Working and Steel Pro-

46.

cessing Conference Proceedings, Baltimore,October, 1999, 37-
59.

Turczyn S.: Inżynieria wytwarzania płaskich wyrobów walco-

47.

wanych na gorąco,AGH Uczelniane wydawnictwo naukowo
techniczne, Kraków 2008.

Abe M.: Mater. Sci. Techno., vol. 7, 1992, 285.

48.

Furukawa T. i in.: Trans. Iron Steel Inst. Jpn., vol. 21, 1981,

49.

812.

De Paepe, Elogoyhen C. i in.: Prediction on the micro-struc-

50.

ture development in HHS- grades during.continuous anneal-
ing and the resulting of mechanical properties. European
Commision ,Technical steel research, 2007.,

Niemeyer M., Schulz T. i in.: Steel Research Int. 79 , No.5

51.

2008, 396.

Recenzent: prof. dr hab. Józef Paduch

Molenda1.indd 41

25.08.2011 15:56:14