X L V I I I K O N F E R E N C J A N AU K O W A

KOMITETU INŻ YNIERII LĄ DOWEJ I WODNEJ PAN

I KOMITETU NAUKI PZITB

Opole – Krynica

2002

Szczepan WOLIŃ SKI

1

PROBABILISTYCZNE WYMIAROWANIE ELEMENTÓ W

Ż ELBETOWYCH Z UWZGLĘDNIENIEM TRWAŁ OŚCI

1. Wprowadzenie

Konstrukcje i elementy żelbetowe powinny być tak zaprojektowane, aby przez cały przewi-
dywany okres użytkowania w określonych warunkach środowiskowych i dla założonej strategii
utrzymania mogły być uznane za niezawodne, to znaczy, aby z należytym prawdopodobieństwem
spełniały wymagania dotyczące stateczności, nośności i użytkowalności [1, 2]. Nośność i użyt-
kowalność konstrukcji w okresie eksploatacji zależą zarówno od obciążeń i oddziaływań
pośrednich, jak i od destrukcyjnego wpływu czynników środowiskowych na konstrukcję,
definiowanych ogólnie jako korozja: chemiczna, mrozowa, karbonatyzacja, korozja wewnętrzna
betonu, i inne [3]. Zalecenia dotyczące zapewnienia niezawodności konstrukcji w okresie użyt-
kowania są formułowane w normach projektowania jako warunki stanów granicznych, oraz
ilościowe i jakościowe wymagania odnośnie: jakości betonu i stali zbrojeniowej, składu,
sposobów układania, zagęszczania i pielęgnacji mieszanki betonowej, grubości otuliny i roz-
mieszczenia prętów zbrojeniowych, oraz inne zalecenia ustalone na podstawie doświadczeń prak-
tycznych. We współczesnej literaturze z zakresu konstrukcji betonowych, trwałość konstrukcji
jest definiowana jako zdolność do zachowania wymaganej nośności i użytkowalności w prze-
widywanym okresie eksploatacji, określoną z uwzględnieniem destrukcyjnych oddziaływań
środowiskowych [4]. W zależności od sposobu uwzględnienia wpływu czynników destrukcyj-
nych można wyróżnić dwie metody postępowania: pośrednią, w której zapewnienie wymaganej
trwałości polega na spełnieniu zaleceń normowych, bez uzasadnienia obliczeniowego, i bezpo-
średnią, polegającą na ilościowej ocenie wpływu czynników destrukcyjnych na konstrukcję w
okresie jej użytkowania.

Półprobabilistyczna metoda stanów granicznych nie jest przystosowana do analizy

niezawodności w sytuacjach, kiedy odporność konstrukcji zależy od czasu. Z kolei
probabilistyczne projektowanie konstrukcji metodami analitycznymi i numerycznymi jest trudne i
pracochłonne, a efektywność obliczeń radykalnie maleje ze wzrostem liczby losowych
zmiennych stanu [5, 6]. W referacie przedstawiono możliwości zastosowania symulacji Monte
Carlo do probabilistycznego wymiarowania elementów żelbetowych z uwzględnieniem wpływu
zależnej od czasu destrukcji betonu i stali zbrojeniowej. Podano przykład probabilistycznego
wymiarowania zbrojenia i oceny ugięcia płyty żelbetowej z uwzględnieniem rozwijających się w
czasie użytkowania uszkodzeń betonu i stali zbrojeniowej.

1

Dr hab. inż., prof PRz, Wydział Budownictwa i Inżynierii Środowiska Politechniki Rzeszowskiej

270

2. Metody wymiarowania

Z punktu widzenia oceny bezpieczeństwa konstrukcji metody wymiarowania można
podzielić na: półprobabilistyczne (m.in. częściowych współczynników bezpieczeństwa),
uproszczone probabilistyczne (m.in. wskaźnika niezawodności

b

) i w pełni probabi-

listyczne. Najczęściej stosowanym sposobem uwzględnienia wpływu czynników destrukcyj-
nych na nośność konstrukcji wymiarowanych metodami półprobabilistycznymi, jest korekta
częściowego współczynnika bezpieczeństwa

R

g

[7]

M

P

D

Ro

R

j

j

j

g

g

=

(1)

gdzie:

Ro

g

– podstawowy częściowy współczynnik bezpieczeństwa,

D

j

,

M

P

j

j

,

– współ-

czynniki korekcyjne zwią zane z: rozważanym procesem lub czynnikiem destrukcyjnym,
przewidywanymi zabezpieczeniami i strategią utrzymania konstrukcji. Podobnie można
skorygować podstawowy wskaźnik niezawodności

b

, wymiarują c konstrukcję uproszczoną

metodą probabilistyczną

2

2

2

)

(

/

)

(

S

R

M

P

D

S

R

M

P

D

m

m

s

s

j

j

j

j

j

j

b

+

-

=

(2)

gdzie:

S

R

m

m ,

- wartości oczekiwane nośności (odporności) konstrukcji i efektu działania

obcią żeń,

S

R

s

s

,

- odchylenia standardowe nośności (odporności) konstrukcji i efektu

działania obcią żeń.

Projektowanie i wymiarowanie konstrukcji z wykorzystaniem współczynników

korekcyjnych wymaga ścisłego powią zania ich wartości z rozważanymi stanami granicznymi
i zróżnicowanymi poziomami niezawodności, co powoduje, że oszacowanie wielkości tych
współczynników jest bardzo ucią żliwe i niepewne.

Jeżeli rozważany mechanizm degradacji odporności konstrukcji można wyrazić w

postaci zależności intensywności uszkodzeń od czasu użytkowania, to możliwe jest
bezpośrednie zastosowanie jednej z uproszczonych metod probabilistycznych lub metody w
pełni probabilistycznej. Odporność lub nośność konstrukcji w czasie użytkowania R(t)
można wówczas zapisać w formie wzoru

R(t) = g(t) R

0

= g(t) R

0

(X

1

, X

2

,...,X

n

) (3)

gdzie: g (t) – funkcja degradacji, R

0

– począ tkowa odporność konstrukcji, X

i

, i = 1, 2, ...,n –

zmienne losowe uwzględnione w obliczeniach.

Wpływ zabiegów i środków powodują cych złagodzenie i zapobieganie skutkom

degradacji konstrukcji można wyrazić przez zróżnicowanie czasu inicjacji uszkodzeń, a
naprawy i działania zwią zane z utrzymaniem konstrukcji można uwzględnić przez
modyfikacje począ tkowej odporności. Stosowanie metod probabilistycznych jest zwią zane z
poważnymi ograniczeniami, w szczególności jeśli warunki wyrażają ce stany graniczne są
silnie nieliniowe. Analityczne obliczenia prawdopodobieństwa P

f

przekroczenia stanów

granicznych lub obliczenie ilości zbrojenia bą dź wymiarów przekroju niezbędnych aby
wartość P

f

nie przekroczyła wartości dopuszczalnej P

fd

, są możliwe tylko w szczególnych

przypadkach, a całkowanie numeryczne jest efektywne jeśli warunek graniczny zawiera nie
więcej niż 5 – 6 zmiennych losowych i obszar całkowania jest z góry znany.

271

ò

£

=

FA

fd

f

P

dz

z

f

P

)

(

(4)

gdzie: FA – obszar zniszczenia określony przez warunek stanu granicznego, f (.) – funkcja
gęstości rozkładu prawdopodobieństwa, z – wektor m zmiennych losowych. W innych
sytuacjach przybliżone rozwią zania można uzyskać metodami symulacyjnymi. Po losowym
wygenerowaniu N wektorów z, zgodnie z oryginalnymi lub założonymi funkcjami gęstości
prawdopodobieństwa, równanie (4) można zapisać w postaci

fd

N

i

f

P

z

N

P

£

=

å

=

1

)

(

1

d

(5)

gdzie: N – liczba symulacji,

)

(z

d

= 1 jeśli

FA

z

Î

, lub

)

(z

d

= 0 jeśli

FA

z

Ï

.

Procedurę wymiarowania elementu konstrukcyjnego z założonym prawdopodobień-

stwem przekroczenia rozważanego stanu granicznego, za pomocą symulacji Monte Carlo,
można przedstawić w następują cy sposób: (a) założyć liczbę symulacji N, (b) wygenerować
cią gi N liczb losowych lub pseudolosowych o rozkładach prawdopodobieństwa zgodnych z
rozkładami wejściowych zmiennych losowych z

j ,

j = 1, 2,..., m, w rozważanych zakresach

zmienności, (c) z warunku granicznego dla rozpatrywanego stanu granicznego elementu
obliczyć wartości poszukiwanej zmiennej wyjściowej (np. pola przekroju zbrojenia) dla
wszystkich N zbiorów wartości zmiennych wejściowych, (d) zbudować histogram częstości
rozkładu zmiennej wyjściowej i obliczyć poszukiwaną wartość (kwantyl), której zaniżenie
jest możliwe z prawdopodobieństwem P

f

£

P

fd

.

3. Opis destrukcji elementó w ż elbetowych w czasie uż ytkowania

Ilościowy opis destrukcji elementów żelbetowych spowodowanej oddziaływaniami
środowiska zewnętrznego w czasie użytkowania, wymaga rzetelnego rozeznania procesów
chemicznych i towarzyszą cych im zjawisk fizycznych zachodzą cych w betonie i zbrojeniu.
Klasy środowiska, opisy jego charakterystyk, przyczyny, skutki i objawy różnych rodzajów
korozji betonu i stali zbrojeniowej są przedstawione w normach i obszernej literaturze
przedmiotu, m. in. [1-5, 7]. Informacje te mają jednak z reguły, charakter jakościowy w
dużym stopniu nieprecyzyjny, a modele matematyczne opisują ce procesy destrukcji są
zazwyczaj zależnościami statystycznymi, których ekstrapolacja jest bardzo niepewna.

Zagadnienia poprawności i dokładności opisu wpływu destrukcji elementów

żelbetowych w okresie użytkowania konstrukcji, spowodowanej przez korozję betonu i
zbrojenia nie są przedmiotem niniejszego referatu. Zależności przyjęte w przykładzie są
oparte na sugestiach zawartych w literaturze i dotyczą szczególnego przypadku korozji
[4, 5, 7]. W obliczeniach uwzględniono wpływ karbonatyzacji betonu powodują cej zmniej-
szenie wysokości strefy ściskanej przekrojów elementu, inicjację korozji rozcią ganej stali
zbrojeniowej i redukcję pola przekroju rozcią ganego zbrojenia.

Rozwój karbonatyzacji betonu w czasie można opisać za pomocą prostej zależności [4]:

t

t

d

c

´

=

a

)

(

(6)

gdzie: d

c

– grubość warstwy betonu skorodowanej w wyniku karbonatyzacji,

a

– współ-

czynnik karbonatyzacji określany doświadczalnie, t – czas użytkowania elementu.

272

Zakładają c, że miarą korozyjnego uszkodzenia zbrojenia jest redukcja począ tkowego

pola przekroju zbrojenia A

s

, wynik rozwoju korozji można przedstawić w formie zależności

}

]

/

)

[(

1

/{

)

(

2

t

t

t

A

t

t

A

krb

s

krb

s

-

-

=

>

(7)

gdzie:

2

)

/

(

a

c

t

krb

=

- czas karbonatyzacji otuliny o grubości c.

4. Przykłady obliczeń probabilistycznych

4.1. Wymiarowanie zginanej płyty ż elbetowej z uwzględnieniem wpływu korozji

Rozważane zadanie polega na obliczeniu pola przekroju rozcią ganego zbrojenia A

s

w

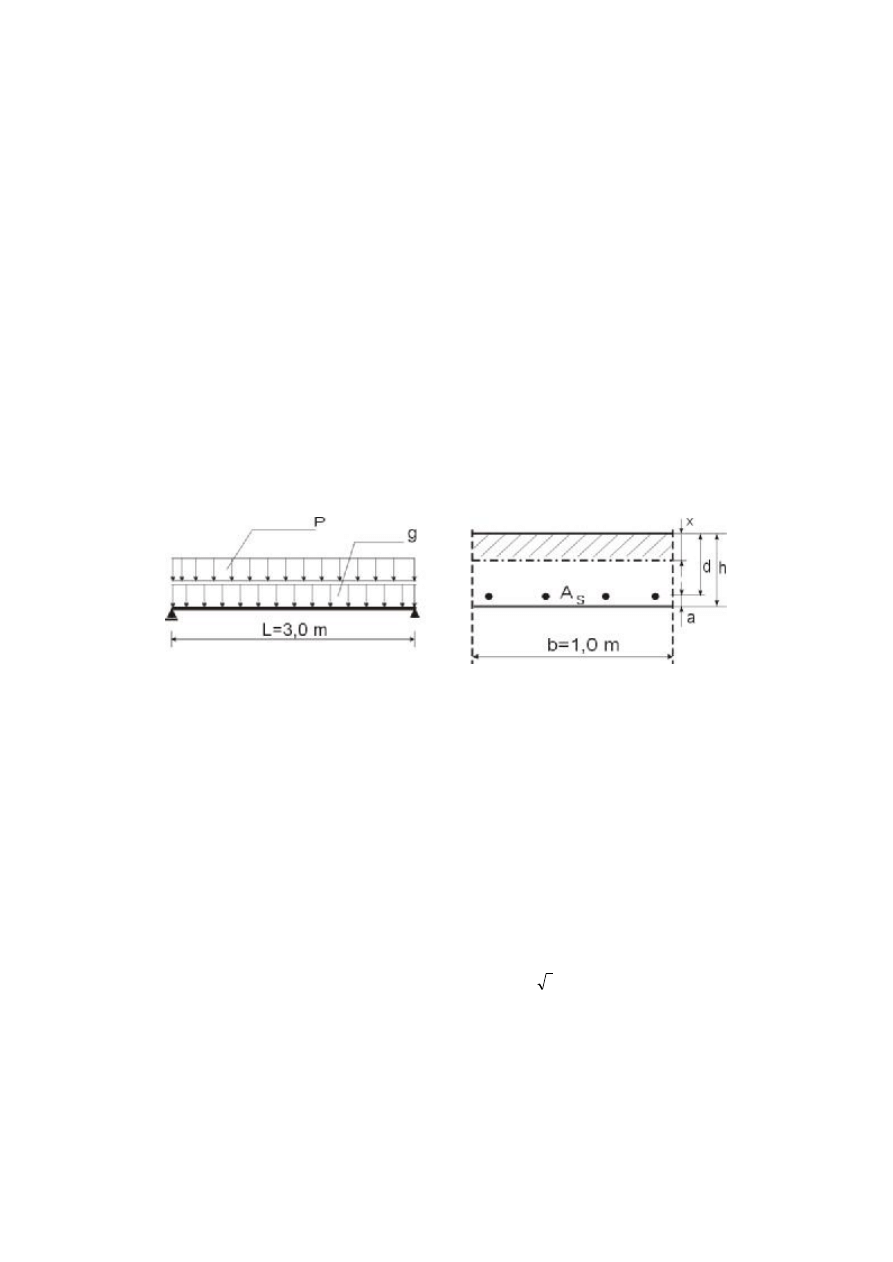
przekroju krytycznym swobodnie podpartej płyty żelbetowej (rys. 1), tak, żeby
prawdopodobieństwo zniszczenia elementu P

f

nie przekroczyło, po 50 latach użytkowania

płyty, założonej wartości P

fd

= 7,2

´

10

–5

(odpowiadają cej wskaźnikowi niezawodności

b

= 3,80).

Rys. 1. Schemat statyczny i przekrój poprzeczny płyty żelbetowej

Obliczenia wykonano przy założeniu zasady płaskich przekrojów, według metody ogólnej
podanej w normie PN-B-03264:1999 [1], z uwzględnieniem wpływu karbonatyzacji betonu i
korozji rozcią ganego zbrojenia w czasie użytkowania na nośność graniczną elementu,
wyrażonych za pomocą zależności (6) i (7).

( )

(

)

[

]

{

}

2

/

1

/

t

t

t

A

t

A

krb

s

s

-

-

=

(8)

(

)

(

)

b

d

f

f

A

y

c

s

´

´

´

´

=

x

/

85

.

0

21

/

17

(9)

x

Þ

(

)

(

)

(

)

0

)

85

,

0

/(

21

/

17

98

/

33

2

2

=

´

´

´

+

´

-

´

c

f

d

b

M

x

x

(10)

(

)

2

125

,

0

L

p

g

M

´

+

´

=

(11)

( )

2

/

a

c

t

krb

=

,

( )

t

d

t

d

´

-

=

a

(12)

Przyjęto następują ce rozkłady i parametry zmiennych losowych uwzględnionych w

obliczeniach:

273

- wytrzymałość betonu na ściskanie f

c

Þ

LN (f

cm

= 28,

s

c

= 4.86) MPa,

- granica plastyczności stali zbrojeniowej f

y

Þ

LN (f

ym

= 462,

s

y

= 35.7) MPa,

- wysokość użyteczna przekroju d

Þ

N (d

m

= 130,

s

d

= 6.5) mm,

- grubość otuliny betonowej zbrojenia c

Þ

N (c

m

= 30,

s

a

= 3) mm,

- współczynnik karbonatyzacji

a

Þ

LN (

a

m

= 4.0,

a

s

= 0.82) mm/rok,

- obcią żenia stałe g

Þ

N (g

m

= 5.0,

s

g

= 0.5) kN/m,

- obcią żenia zmienne p

Þ

G

(p

m

= 5.0,

s

p

= 1.75) kN/m,

- pozostałe zmienne uznano za zdeterminowane i do obliczeń przyjęto ich wartości nominalne,
gdzie: LN, N,

G

– zmienne losowe o rozkładach: logarytmo-normalnym, normalnym

i gamma, x

m

– wartość oczekiwana,

s

– odchylenie standardowe rozważanej zmiennej

losowej, c = a –

f

/2 – otulina prętów zbrojenia o średnicy

f

. Parametry rozkładów

obcią żeń dobrano w taki sposób, że wartości których zawyżeniu odpowiada
prawdopodobieństwo 0.001 są równe g

d

= 5,75 kN/m i p

d

= 11,7 kN/m, czyli odpowiadają

wartościom obliczeniowym tych obcią żeń przyjmowanych w metodzie półprobabilistycznej.

Obliczenia wykonano metodą symulacji Monte Carlo za omocą programu

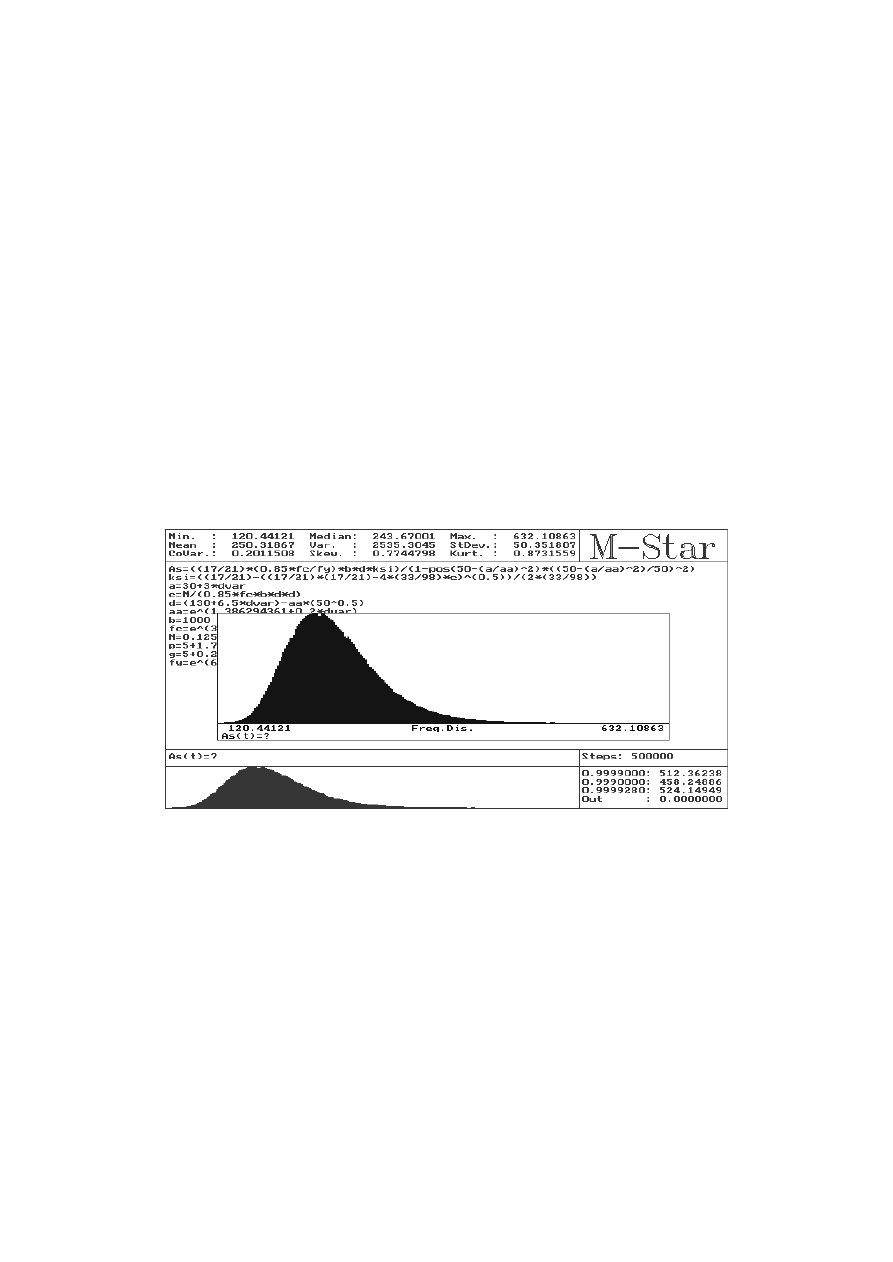
komputerowego M-Star [6, 8]. Na rys. 2 przedstawiono wyniki obliczeń zbrojenia A

s

po

wykonaniu 500 000 symulacji.

Rys. 2. Wyniki obliczeń zbrojenia rozcią ganego w płycie metodą symulacji Monte Carlo

Pole przekroju rozcią ganego zbrojenia niezbędnego w przekroju krytycznym płyty, aby

nie uległa ona zniszczeniu w okresie 50 lat użytkowania, z prawdopodobieństwem 1 – P

f

³

1 – P

fd

=1 – 7,2

´

10

–5

= 0.999928, wynosi A

s

= 524 mm

2

. Przyjęcie większego

dopuszczalnego prawdopodobieństwa zniszczenia powoduje zmniejszenie niezbędnego
przekroju zbrojenia, na przykład: jeśli P

fd

= 0.0001, to A

s

= 512 mm

2

, jeśli P

fd

= 0.001, to

A

s

= 458 mm

2

.

Ze względu na niekorzystny wpływ oddziaływań środowiskowych na nośność płyty,

przekrój zbrojenia niezbędny z założonym stałym prawdopodobieństwem, zwiększa się w
czasie użytkowania. Na rys. 3 przedstawiono wykresy zależności niezbędnego przekroju
zbrojenia płyty w zależności od okresu użytkowania, od 0 do 50 lat, oraz od dopuszczalnego
prawdopodobieństwa zniszczenia: P

fd

= 7.2

´

10

–5

i P

fd

= 10

–3

.

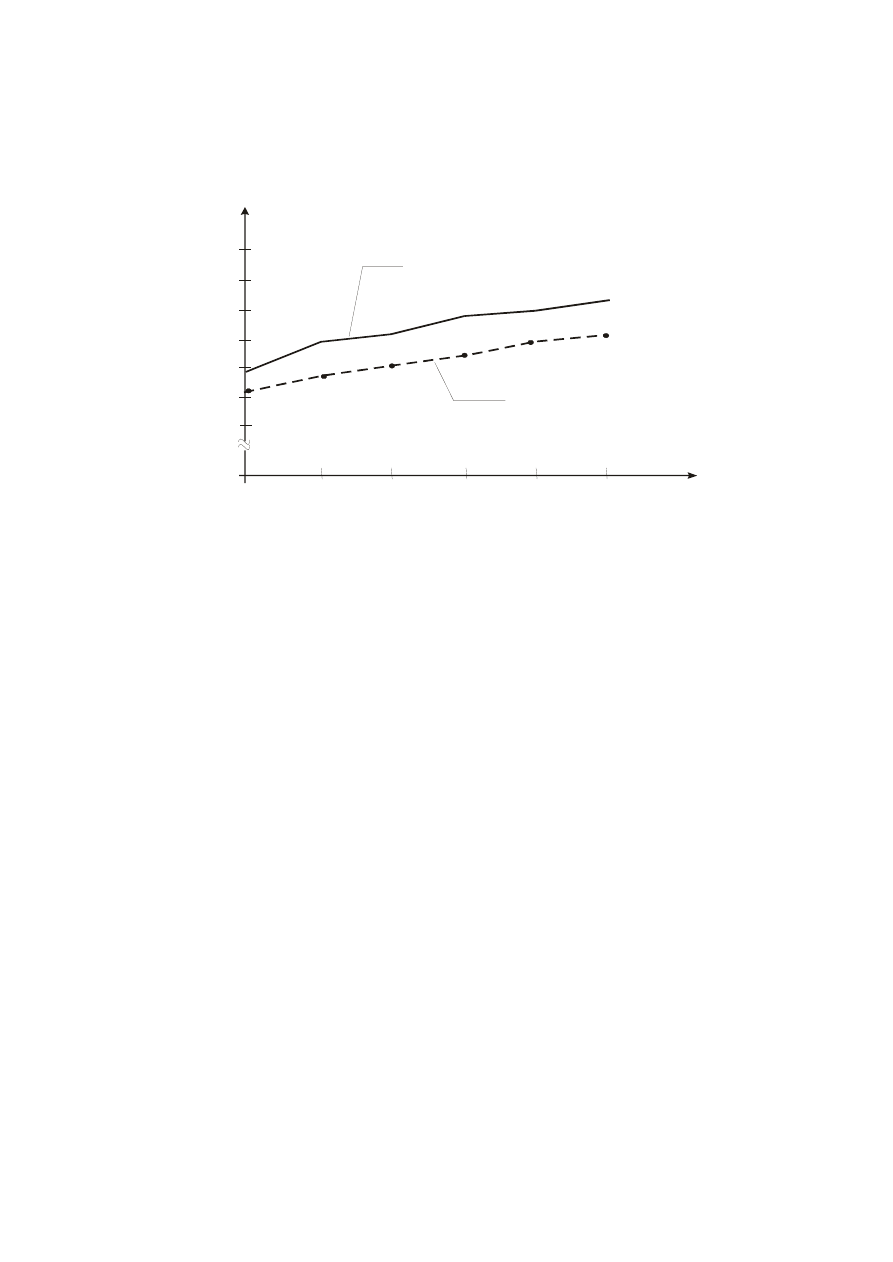
274

x

x

x

x

x

0 10 20 30 40 50

300

400

500

600

(398)

(445)

(477)

(490)

(524)

x

(454)

(353)

(389)

(407)

(424)

(440)

(451)

t

[lata]

A

S

[mm ]

2

P =10

-3

f

P =7,2 x 10

f

-5

Rys. 3. Zależność przekroju zbrojenia płyty od okresu użytkowania

i prawdopodobieństwa zniszczenia elementu

4.2. Weryfikacja ugięcia płyty ż elbetowej w czasie uż ytkowania

Zadanie polega na weryfikacji ugięcia płyty żelbetowej zwymiarowanej w p. 4.1, poddanej
obcią żeniom stałym i części długotrwałej obcią żeń zmiennych q = g + 0,8 p. W obliczeniach
uwzględniono wpływ uszkodzeń spowodowanych oddziaływaniami środowiska w czasie
użytkowania elementu. Przyjęto jednakowy sposób opisu wpływu uszkodzeń i zmiennych
losowych uwzględnionych podczas wymiarowaniu zbrojenia płyty i w obliczeniach ugięć.
Wytrzymałość betonu na rozcią ganie f

ct

i moduł sprężystości betonu E

c

obliczono jako

funkcję wytrzymałości betonu na ściskanie f

c

, według zależności podanych w PN-B-

03264:1999 [1]. Moduł sprężystości stali zbrojeniowej E

s

= 200 GPa, i końcowy

współczynnik pełzania betonu,

to

,

¥

F

= 2,55, obliczony dla wieku obcią żenia betonu t

0

= 28

dni , wilgotności względnej RH = 65% i miarodajnego wymiaru elementu 14,5 mm, uznano
za wielkości zdeterminowane. Ugięcie zginanej płyty obliczono zgodnie z zaleceniami
PN-B-03264:1999, według wzorów

(

) (

)

2

/

48

/

5

L

B

M

f

´

´

=

(13)

(

) (

)

[

]

I

II

s

sr

II

cef

J

J

J

E

B

B

/

1

/

1

/

2

2

1

-

´

´

-

´

=

=

¥

s

s

b

b

(14)

gdzie: J

I

, J

II

- sprowadzone momenty bezwładności przekroju płyty w fazie I (niezarysowany) i

w fazie II (zarysowany),

s

sr

s

s

,

- naprężenia w zbrojeniu w przekroju przez rysę, dla obciążenia

powodującego zarysowanie i obciążenia powodującego ugięcie,

1

b

= 1,0 – dla prętów

żebrowanych,

2

b

= 0,5 – dla obciążeń długotrwałych, E

cef

= E

c

/ (1+

to

,

¥

F

) – efektywny moduł

sprężystości betonu. Zakładając pole przekroju zbrojenia A

s

= 524 mm

2

, niezbędne dla

zapewnienia nośności płyty na zginanie w okresie użytkowania równym 50 lat, obliczono ugięcie

275

elementu, które nie zostanie przekroczone w okresie 50 lat z założonym prawdopodobieństwem
P

f

= 0,0686 (odpowiadającym wskaźnikowi niezawodności

b

= 1,50). Obliczenia wykonano za

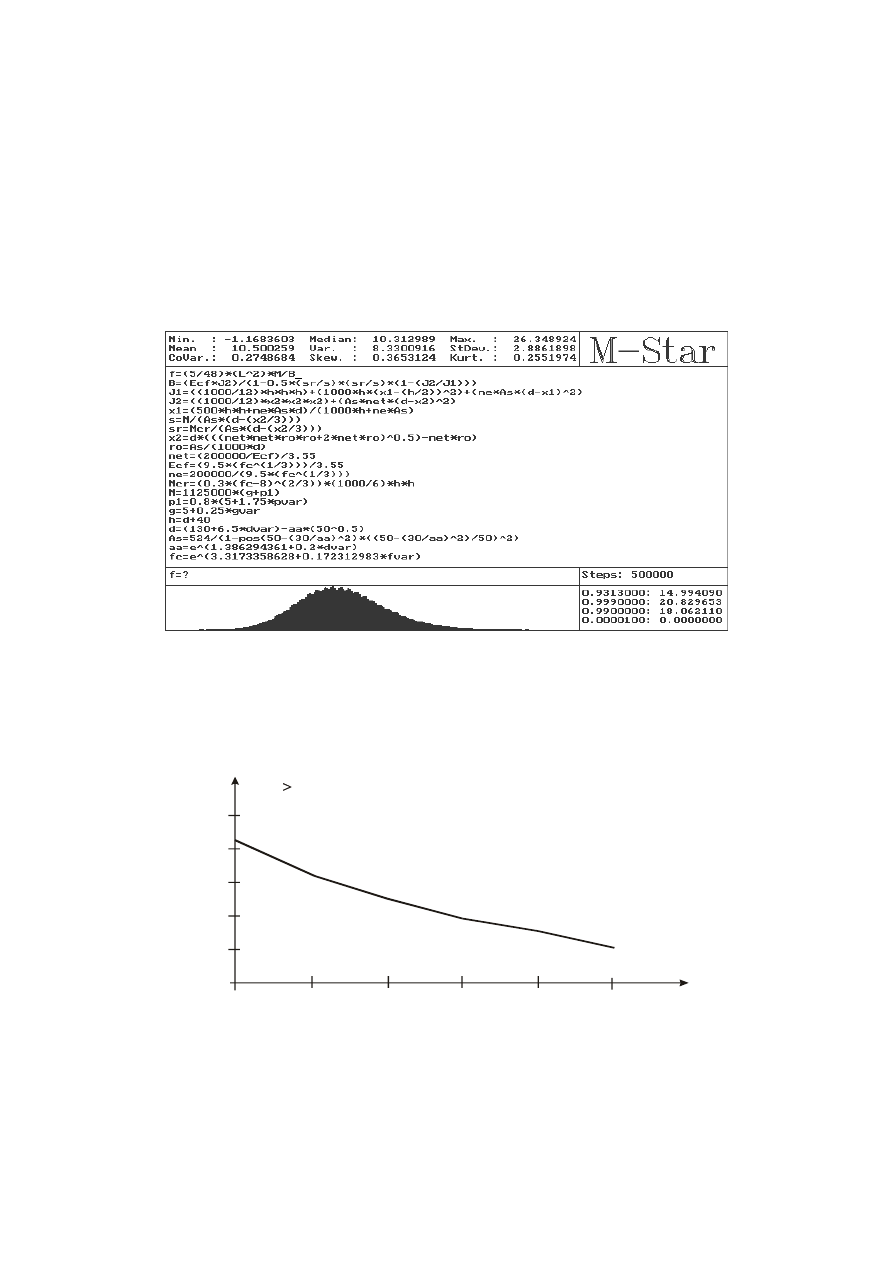
pomocą programu komputerowego M-Star [8], dla 500 000 symulacji. Na rys. 4 przedstawiono
plik wejściowy i wyniki obliczeń w postaci histogramu ugięcia płyty i wartości ugięć, które nie
będą przekroczone z zadanym prawdopodobieństwem, np. f (P

fd

= 1 – 0,9313 = 0.0687) =

= 14,99 mm, f (P

fd

= 1- 0.999 = 0.001) = 20,83 mm.

Rys. 4. Wyniki obliczeń ugięć płyty metodą Monte Carlo

Prawdopodobieństwo przekroczenia dopuszczalnego ugięcia płyty f

lim

= L/200=15 mm

w okresie 50 lat użytkowania elementu zwiększa się z upływem czasu z powodu postępów
korozji. Na rys. 5 przedstawiono wykres zależności P

f

(t > 15 mm) w czasie t = 0-50 lat, dla

A

s

=524 mm

2

.

x

x

x

x

x

x

0 10 20 30 40 50

10

10

10

10

10

-5

-4

-3

-2

-1

t

[lata]

(5,5 x 10 )

-5

(5 x 10 )

-4

(2,5 x 10 )

-3

(0,01)

(0,028)

(0,0687)

A

S

= 524 mm

2

P (f 15mm)

f

Rys. 5. Wykres zależności P

f

(f > 15 mm) w okresie użytkowania płyty

276

5. Podsumowanie

Destrukcyjny wpływ środowiska zewnętrznego na trwałość konstrukcji żelbetowych
powinien być uwzględniony już w fazie projektowania. Postulat ten jest realizowany
współcześnie w sposób pośredni. Projektant jest zobowią zany do przestrzegania zaleceń
dotyczą cych doboru materiałów konstrukcyjnych, określenia klasy środowiska, przyjęcia
odpowiednich grubości otuliny betonowej prętów zbrojenia, ograniczenia obliczeniowych
szerokości rys i ewentualnego zastosowania zabezpieczeń antykorozyjnych.

Ocena wpływu destrukcyjnego oddziaływania środowiska na trwałość, czyli nośność i użyt-

kowalność konstrukcji w okresie eksploatacji, wymaga sformułowania ilościowych zależności
wielkości uszkodzeń od czasu i uzależnienia przyjętych miar niezawodności od czasu. Jest to
możliwe w ramach probabilistycznych metod projektowania. Praktyczne możliwości wykorzys-
tania tych metod są jednak poważnie ograniczone ze względu na trudności obliczeniowe,
szczególnie w przypadku poszukiwania rozwiązań metodami analitycznymi i numerycznymi.
Trudności te eliminuje zastosowanie metod symulacyjnych. Przykłady przedstawione w referacie
ilustrują możliwości ich zastosowań do analizy wpływu zmiennych w czasie, losowych
uszkodzeń korozyjnych elementów żelbetowych na prawdopodobieństwo przekroczenia stanów
granicznych nośności i użytkowalności w okresie eksploatacji tych elementów.

Literatura

[1] PN-B-03264:1999. Konstrukcje betonowe, ż elbetowe i spręż one. PKN, styczeń 1999.
[2] Eurocode 2. Design of concrete structures – part 1: general rules and rules for

buildings. EN 1992 – 1 : 2001 (Final draft).

[3] Ściślewski Z., Ochrona konstrukcji ż elbetowych. Warszawa, Arkady, 1999.
[4] CEB Bulletin d’Information No. 238, New approach to durability of reinforced concrete.

An example for carbonation induced corrosion. ECS, January 2000.

[5] Thoft-Christensen P., Modeling of the deterioration of reinforced concrete structures.

Proc. 9

th

IFIP WG 7.5 Working Conf. on Reliability and Optimization of Structural

Systems. Ann Arbor, University of Michigan, 2000, s. 15-26.

[6] Marek P., Brozzetti J., Gustar M., editors, Probabilistic Assessment of Structures using

Monte Carlo Simulation. Praha, ITAM Czech Academy of Sciences, 2001.

[7] Faber M., Melchers R., Aspects of safety in design and assessment of deteriorating structures.

Conf. Report, Int. Conf. on Safety, Risk and Reliability. Malta, March 2001, s. 161-166.

[8] Marek P., Gustar M., Monte Carlo simulation programs for PC: M-Star. Prague, 1999.

PROBABILISTIC DIMENSIONING OF REINFORCED CONCRETE

STRUCTURAL ELEMENTS CONSIDERIG DURABILITY

Summary

The problem of probabilistic simulation-based dimensioning of reinforced concrete structural
elements for durability is considered in this paper. It is proposed that modeling of
deterioration of concrete and reinforcing steel should be based on the reliable relationships
between the measures of damage affected by different indirect effects, e.g. chemical and
physical attack, and the time. Using illustrative examples, the potential of simulation-based
probabilistic method of structural dimensioning is demonstrated.