
Wybrane zagadnienia z Mechaniki Płynów
1/32
Wybrane zagadnienia
z Mechaniki Płynów
Wojciech Sobieski
Uniwersytet Warmińsko-Mazurski
Wydział Nauk Technicznych
Katedra Mechaniki i Podstaw Konstrukcji Maszyn
10-957 Olsztyn, ul. M. Oczapowskiego 11.
tel.: (89) 5-23-32-40
fax: (89) 5-23-32-55
wojciech.sobieski@uwm.edu.pl
Niniejszy dokument może być dowolnie kopiowany, udostępniany
rozprowadzany w wersji oryginalnej. Autor nie zezwala na zmianę treści
dokumentu ani na jego modyfikacje.
Olsztyn 2001

Wybrane zagadnienia z Mechaniki Płynów
2/32
S P I S T R E Ś C I
1.
PODSTAWOWE WIADOMOŚCI O PŁYNACH...................................................... 3
2.
PODSTAWOWE WŁAŚCIWOŚCI PŁYNÓW.......................................................... 6
3.
NAPÓR HYDROSTATYCZNY ................................................................................. 8
4.
PŁYWANIE CIAŁ .................................................................................................... 10
5.
PRAWO EULERA .................................................................................................... 11
6.
PRAWO PASCALA .................................................................................................. 12
7.
RÓWNANIE EULERA W HYDROSTATYCE....................................................... 13
8.
KINEMATYCZNY WARUNEK CIĄGŁOŚCI RUCHU PŁYNU ŚCIŚLIWEGO W
PRZEPŁYWACH NIEUSTALONYCH........................................................................... 15
9.
RÓWNANIE BERNOULIEGO ................................................................................ 18
10.
RÓWNANIE NAVIERA-STOCKES’A ................................................................... 19
11.
RUCH ELEMENTU PŁYNU ................................................................................... 27
12.
GRADIENT SKALARA ........................................................................................... 31
Wybrane zagadnienia z Mechaniki Płynów
3/32
1.
PODSTAWOWE WIADOMOŚCI O PŁYNACH
Dwóm stanom materii – cieczom i gazom - można przypisać cechy płynności i ciągłości.
Jeżeli w określonych warunkach cechy te są możliwe do zaakceptowania, to zarówno
ciecz jak i gaz będziemy nazywali płynami.
Z punktu widzenia molekularnej teorii budowy materii zarówno ciecz jak i gaz jest
zbiorowiskiem chaotycznie poruszających się molekuł, pomiędzy cieczą a gazem istnieją
jednak pewne różnice (rys. 1.).
Rys. 1. Ruch molekuł w cieczy (z lewej) i w gazie (z prawej).
Ciecz – ruch molekuł jest ruchem drgającym dookoła średniego położenia oraz ruchem
przeskoku molekuł w coraz to nowe miejsce „życia osiadłego”
τ
0
. Przyjmijmy, że średnia
droga przeskoku wynosi l
0
.
Gaz – ruch molekuł jest ruchem chaotycznym, bez możliwości „życia osiadłego”.
W ruchu chaotycznym molekuły zderzają się, zmieniając w ten sposób swoją prędkość.
Drogi pomiędzy kolejnymi zderzeniami są różne – jednak średnia droga l
0
pomiędzy
kolejnymi zderzeniami jest znacznie dłuższa od średniej drogi przeskoku w stanie
ciekłym.
Charakterystyczne wymiary liniowe odnoszące się do molekuł można zdefiniować
następująco:
dla stanu ciekłego
dla stanu gazowego
•
wymiar
charakteryzujący
wielkość
molekuły
•
ś
rednia odległość między molekułami
•
ś
rednia amplituda drgań
•
ś
rednia droga przeskoku
•
wymiar
charakteryzujący
wielkość
molekuły
•
ś
rednia odległość między molekułami
•
ś
rednia droga swobodna
Inne cechy
•
zachowuje kształt naczynia
•
mało ściśliwy
•
nie zachowuje kształtu
•
bardzo ściśliwy
Wybrane zagadnienia z Mechaniki Płynów
4/32
Płynność. Gdy czas działania t siły odkształcającej jest bardzo długi w porównaniu z
czasem życia osiadłego
τ
0
, wtedy odkształcenie jest możliwe dzięki wymuszonej przez tę
siłę zmianie układu molekuł w przestrzeni. Można się spodziewać proporcjonalności
między działającą siłą a odkształceniem – nawet mała siła odkształcająca wywołuje
skończoną prędkość odkształcenia. Jeżeli czas działania siły jest porównywalny bądź też
krótszy od życia osiadłego molekuł, nie zdążą się one dostosować do sił deformujących
(zjawisko takie zachodzi np. podczas szybkiego odkształcania smoły -
τ
0
≈
1 s – ulega
ona wówczas pękaniu, jak ciało stałe).
Proporcjonalność pomiędzy prędkością odkształcenia (płynięciem) a siłą odkształcającą
jest cechą określoną jako płynność. Z powyższego rozumowania wynika ograniczenie tej
cechy. Jeżeli
0
τ
t
>>1,
to cieczom można przypisać cechę płynności. Jeżeli zaś
0
τ
t
<1,
to mamy sytuację podobną do tej, jaka panuje w ciele stałym.
Jest rzeczą oczywistą, że w gazach, dla których
τ
0
= 0, cecha płynności nie ulega
ograniczeniom.
Ciągłość. Jest to cecha oznaczająca możliwość traktowania materii jako ośrodka
wypełniającego przestrzeń w sposób ciągły. Jest to możliwe tylko wtedy, gdy wymiary
liniowe L ciał opływanych cieczą lub gazem są znacznie większe od l
0
. Tak więc i tu
pojawia się ograniczenie tej cechy. Jeżeli
0
l
L
>>1,
to cieczom i gazom można przypisać cechę ciągłości. Jeżeli zaś
0
l
L
<1,
to założenie ciągłości nie stanowi dobrego modelu fizycznego.

Wybrane zagadnienia z Mechaniki Płynów
5/32
Ponieważ wartość l
0
jest znacznie większa dla gazów, można oczekiwać naruszenia tej
cechy przede wszystkim w gazach. Istotnie, gazy rozrzedzone dla wymiarów ciał
porównywalnych z l
0
nie mogą być rozpatrywane jako ośrodek ciągły.
Liczba Knudsena. Aby ocenić stopień zgodności przyjętego modelu płynu (ciągły -
nieciągły) wprowadzono parametr zwany liczbą Knudsena
L
l
Kn
0
=
.
Dla liczb Knudsena < 0,01 przyjmuje się model ośrodka ciągłego.
Płyn doskonały (idealny) – płyn, który jest nieściśliwy, nielepki, nie ulega
rozszerzalności termicznej, nie „poddaje się” rozciąganiu, ściskaniu, ścinaniu.
Płyn rzeczywisty – powyższe założenia nie obowiązują.
Modele płynów. W zależności od związków pomiędzy prędkością deformacji a
naprężeniami stycznymi, przyjmuje się różne modele płynów rzeczywistych:
płyn Newtona
– płyn, w którym naprężenie styczne jest proporcjonalne do
prędkości deformacji (woda. powietrze, olej, benzyna, itp)
płyn Binghama
– płyn, w którym naprężenie styczne jest niejednorodną funkcją
deformacji (pasty, zaprawy)
płyn pseudoplastyczny – płyn, w którym naprężenie styczne maleje wraz z prędkością
deformacji (ciekły kauczuk, roztwory mydlane)
płyn tiksotropowy
– płyn, w którym przy stałej prędkości deformacji, naprężenia
styczne maleją w czasie (farby, lakiery)
płyn Hooke’a
– płyn, który ulega tylko odkształceniu objętościowemu (???)
płyn z pamięcią
– ??? (farma emulsyjna)

Wybrane zagadnienia z Mechaniki Płynów
6/32
2.
PODSTAWOWE WŁAŚCIWOŚCI PŁYNÓW
1. Ciśnienie.
dA
dP
A
P
p
A
=
∆
∆
=
→
∆
0
lim
2
m
N
2. Gęstość.
dV
dm
V
m
V
=
∆
∆
=
→
∆
0
lim
ρ
3
m
kg
ρ =
m
V
3. Ciężar właściwy.
dV
dG
V
G
V
=
∆
∆
=
→
∆
0
lim
γ
3
m
N
γ =
G
V
γ ρ
= ⋅
g
4. Objętość właściwa.
ρ
1
v
=
kg
m
3
5. Rozszerzalność objętościowa.
dT
dV
V
1
⋅
=
α
1
K
T
1
0
T
∆
+
=
α
ρ
ρ
(
)
T
V
V
∆
+
=
α
1
1
2
T
V
V
1
∆
=
∆
α
6. Ściśliwość.
dp
dV
V
1
B
⋅
−
=
N
m
2
p
B
1
0
p
∆
−
=
ρ
ρ
(
)
p
B
1
V
V
1
2
∆
−
=
p
B
V
V
1
∆
−
=
∆
7. Lepkość dynamiczna.
dn
dV
⋅
−
=
µ
τ
dT = ±
τ
.
dA
⋅
=
s
m
kg
µ
1P
g
cm s
=
⋅
8. Lepkość kinematyczna.
ρ
µ
ν
=
=
s
m
2
υ
=
s
cm
St
2
1
9. Równanie stanu (tylko dla gazów idealnych).
mRT
pV
=
lub
RT
p
ρ
=

Wybrane zagadnienia z Mechaniki Płynów
7/32
Oznaczenia symboli:
P – siła
G - ciężar
m - masa
V - objętość (prędkość w punkcie 7)
v - objętość właściwa
µ
- dynamiczny współczynnik lepkości (czasami oznacza się
η
)
ν
−
współczynnik lepkości kinematycznej
P - Poise – jednostka lepkości ( jednostka mniejsza 1cP = 1P
.
10
-2
)
St – Stockes - jednostka lepkości ( jednostka mniejsza 1cSt = 1St
.
10
-2
)
B - współczynnik ściśliwości (
B=1/E)
E - moduł Younga
R - indywidualna stała gazowa

Wybrane zagadnienia z Mechaniki Płynów
8/32
3.
NAPÓR HYDROSTATYCZNY
Siła naporu hydrostatycznego, wywieranego przez ciecz na płaską ścianę o dowolnym
konturze wynosi
P =
ρ
·g·
z dA
A
⋅
∫
.
( 1 )
Wyrażenie
z dA
A
⋅
∫
jest momentem statycznym, zatem
z dA
A
⋅
∫
= z
s
·A,
gdzie z
s
oznacza głębokość zanurzenia środka geometrycznego ściany o polu
powierzchni równym A. Wobec tego napór cieczy na dowolną figurę płaską można
wyrazić następującym wzorem:
P =
ρ
·g·z
s
·A =
γ
·z
s
·A.
( 2 )
Jeżeli na ciecz działa dodatkowo ciśnienie p., to
P = (p +
γ
·z
s
)·A
( 3 )
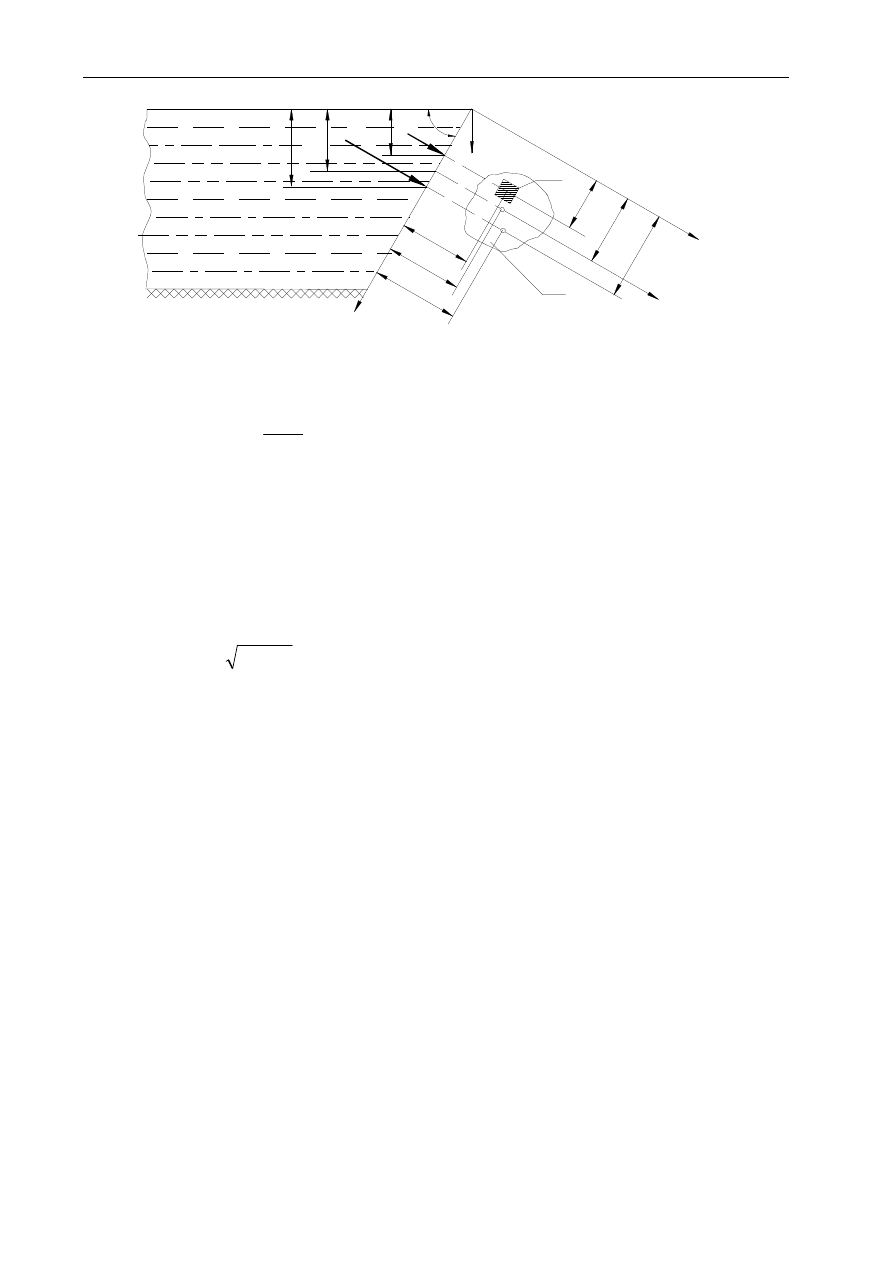
Współrzędne położenia środka naporu, tj. punktu C, w którym przyłożony jest wektor
siły naporu, działającej na rozpatrywany wycinek ściany o polu powierzchni równym A,
wyznaczamy z następujących zależności:
x
c
=
xy
s
I
A y
⋅
y
c
=
x
s
I
A y
⋅
= y
s
+
0
x
I
A y
s
⋅
( 4 )
z
c
= z
s
+
0
x
I
A z
s
⋅
·sin
2
α
y
s
, z
s
- współrzędne środka ciężkości,
I
x
- moment bezwładności względem osi x,
I
xy
- moment dewiacyjny względem osi x i y,
I
xo
- moment bezwładności względem osi x
0
przechodzącej przez środek ciężkości S.
Wybrane zagadnienia z Mechaniki Płynów
9/32
x
0
x
x
s
x
c
y
y
y
s
y
c
dA
s
c
z
A
z
z
s
z
c
P
dP
α
x
Dla ściany prostopadłej do zwierciadła cieczy
α = 90
°
z
c
= z
s
+
0
x
I
A z
s
⋅
( 5 )
Ze wzorów ( 4 ) i ( 5 ) wynika, że środek naporu znajduje się zawsze poniżej środka
ciężkości. Punkty C i S pokrywają się tylko wówczas, gdy A jest wycinkiem ściany
płaskiej, równoległej do zwierciadła cieczy.
Wypadkowy napór hydrostatyczny cieczy na ściankę zakrzywioną
P =
x
z
P
P
2
2
+
Składowa pozioma P
x
równa jest parciu wywieranemu na rzut powierzchni zakrzywionej
na płaszczyznę prostopadłą do rozpatrywanego kierunku. Linia działania składowej
poziomej przechodzi przez środek naporu rzutu rozważanej powierzchni.
Składowa pionowa naporu P
z
równoważona jest ciężarem „bryły ciekłej” ograniczonej
rozpatrywaną powierzchnią zakrzywioną i tworzącymi pionowymi, które łączą jej kontur
ze zwierciadłem cieczy. Kierunek działania naporu pionowego przechodzi przez środek
ciężkości rozpatrywanej „bryły”. Natężenie składowej pionowej P
z
nie zależy przy tym
od tego, czy nad ścianą zakrzywioną wznosi się aż do zwierciadła realny słup cieczy, czy
też nie.
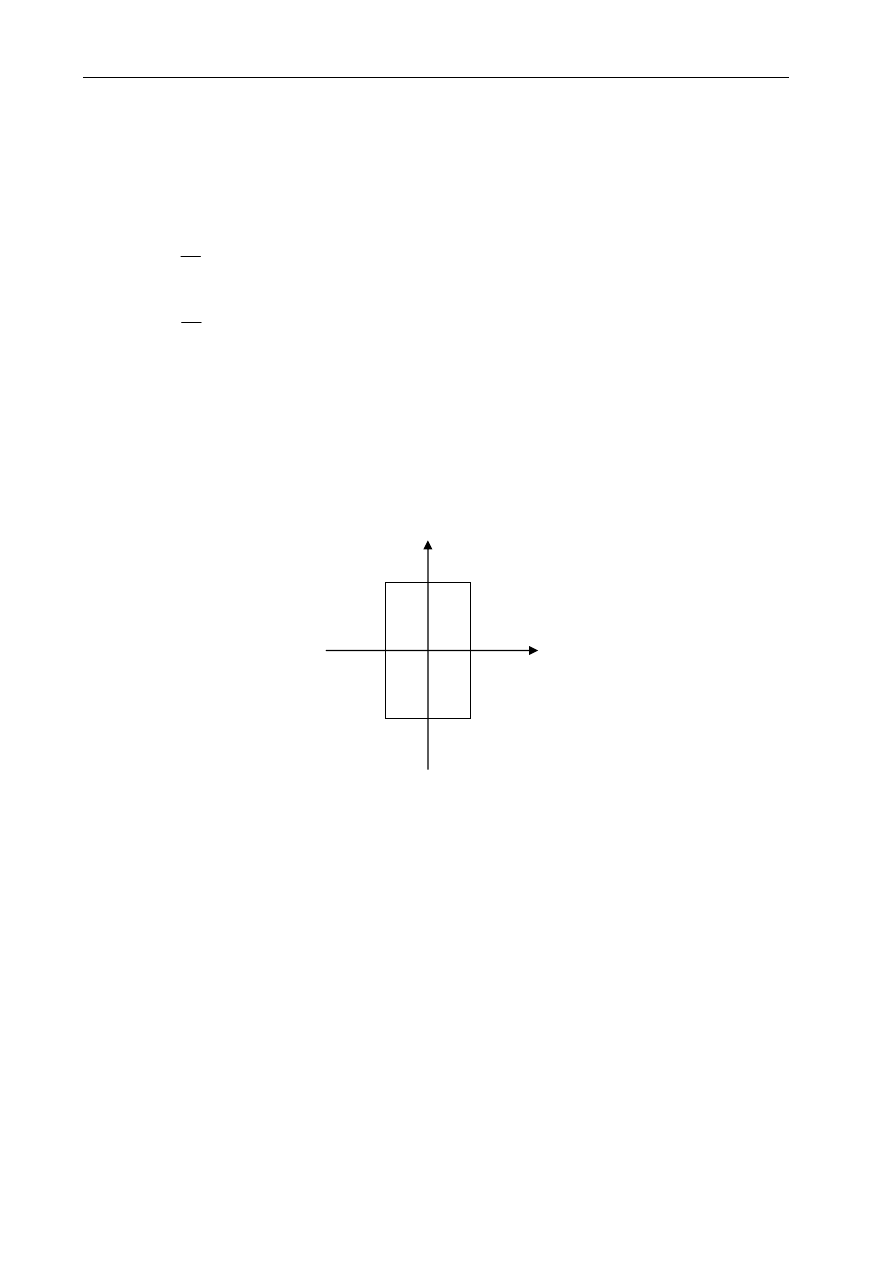
Wybrane zagadnienia z Mechaniki Płynów
10/32
4.
PŁYWANIE CIAŁ
Stateczność określa się na podstawie tzw. wysokości metacentrycznej z następujących
zależności:
a
V
I
m
z
x
x
±
=
- stateczność względem osi x,
a
V
I
m
z
y
y
±
=
- stateczność względem osi y.
gdzie
V
z
- objętość zanurzona,
I
x
, I
y
- momenty bezwładności pola przekroju pływania względem osi x i y,
a
- odległość między środkiem ciężkości ciała i środkiem wyporu (ujemna wartość a
występuje wówczas, gdy środek ciężkości znajduje się powyżej środka wyporu).
Do badania stateczności bierze się ten kierunek, dla którego wartość momentu
bezwładności jest mniejsza.
m > 0 - stateczność stała,
m < 0 - stateczność chwiejna,
m = 0 - stateczność obojętna.
x
y

Wybrane zagadnienia z Mechaniki Płynów
11/32
5.
PRAWO EULERA
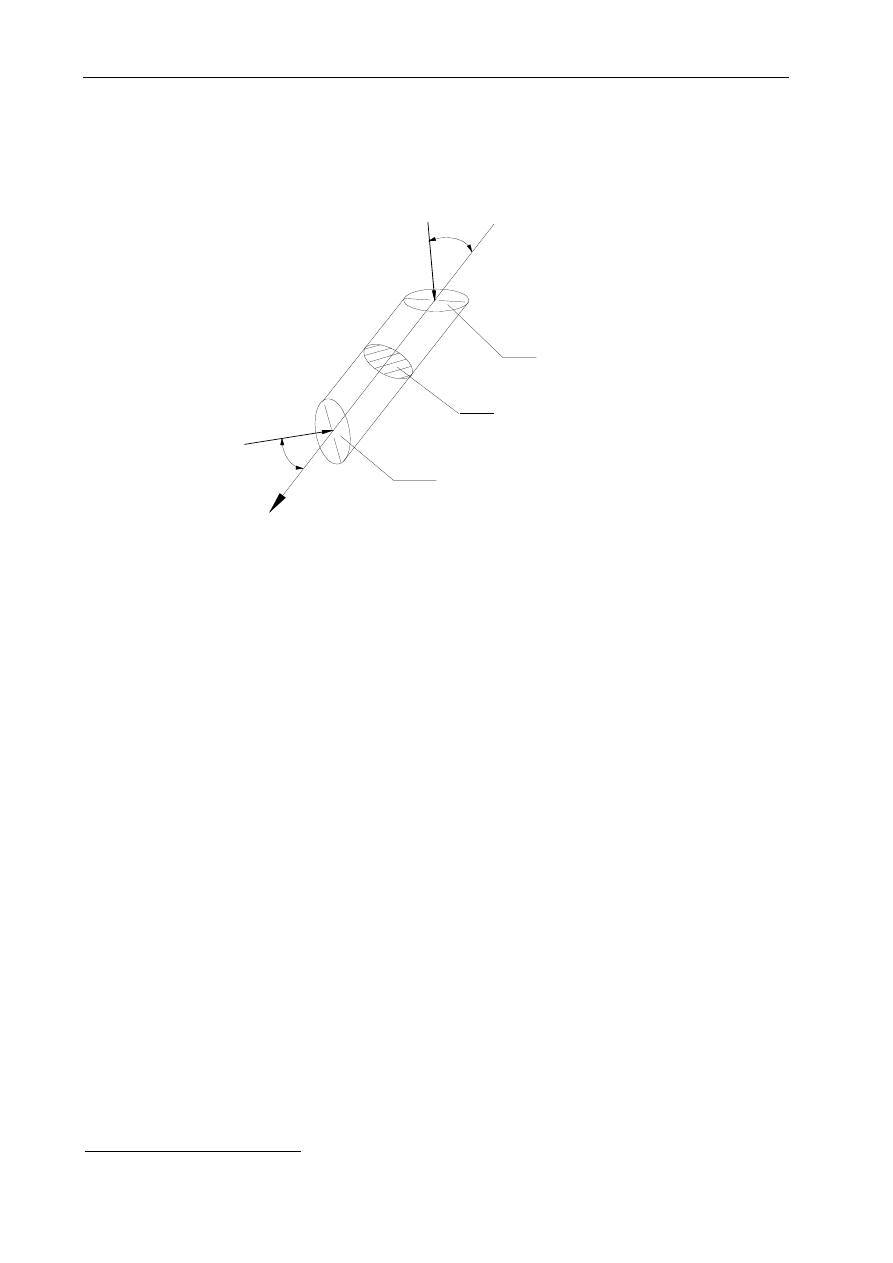
Prawo Eulera - wartość ciśnienia nie zależy od orientacji (położenia) elementu
powierzchniowego, do którego „wektor” ciśnienia jest prostopadły.
P
x
z
y
p
x
p
y
p
z.
α
β
γ
dx
dz
dy
dAx
dAz
dAy
Aby układ był w stanie równowagi:
p
x
.
dAx - p
.
dA
.
cos
α
= 0
p
y
.
dA
y
- p
.
dA
.
cos
β
= 0
(1)
p
z
.
dA
z
- p
.
dA
.
cos
γ
= 0
ponieważ
dA
.
cos
α
= dA
x
dA
.
cos
β
= dA
y
dA
.
cos
γ
= dA
z
równanie (1) otrzyma postać
p
x
.
dAx - p
.
dA
x
= 0
p
y
.
dA
y
- p
.
dA
y
= 0
(2)
p
z
.
dA
z
- p
.
dA
z
= 0
po uproszczeniu zaś
p
x
= p
p
y
= p
(3 )
p
z
= p
czyli
p
x
= p
y
= p
z
= p.
(4)
Wybrane zagadnienia z Mechaniki Płynów
12/32
6.
PRAWO PASCALA
Prawo Pascala - jeżeli na płyn działają tylko siły powierzchniowe, to ciśnienie w każdym
punkcie płynu jest takie samo
1
.
P
1
P
2
α
2
α
1
z
dA
1
dA
2
dA
Aby układ był w stanie równowagi:
iz
P
∑
=
0
czyli
1
1
1
2
2
2
0
p dA
p dA
⋅
⋅
− ⋅
⋅
=
cos
cos
α
α
(1)
ponieważ
1
1
dA
dA
⋅
=
cos
α
2
2
dA
dA
⋅
=
cos
α
więc
1
2
0
p dA
p dA
⋅
− ⋅
=
1
2
0
p
p
− =
(2 )
Ogólnie zaś
1
2
p
p
p
n
=
= =
K
.
(3)
1
Prawo to nie uwzględnia ciśnienia słupa cieczy.
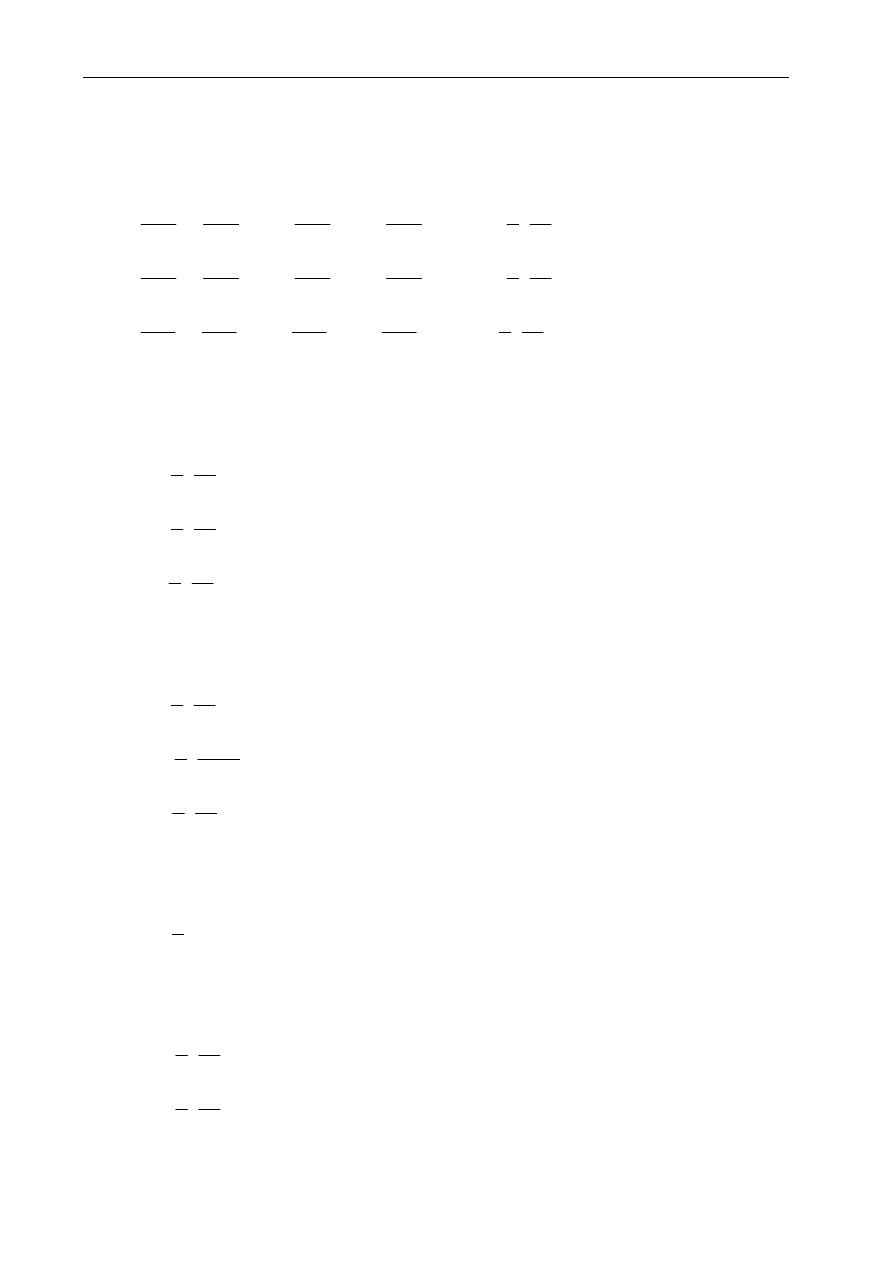
Wybrane zagadnienia z Mechaniki Płynów
13/32
7.
RÓWNANIE EULERA W HYDROSTATYCE
Pełna postać równania Eulera:
∂
∂
Vx
t
+
∂
∂
Vx
x
·Vx +
∂
∂
Vx
y
·Vy +
∂
∂
Vx
z
·Vz = X -
1
ρ
·
∂
p
dx
∂
∂
Vy
t
+
∂
∂
Vy
x
·Vx +
∂
∂
Vy
y
·Vy +
∂
∂
Vy
z
·Vz = Y -
1
ρ
·
∂
p
dy
(1)
∂
∂
Vz
t
+
∂
∂
Vz
x
·Vx +
∂
∂
Vz
y
·Vy +
∂
∂
Vz
z
·Vz = Z -
1
ρ
·
∂
p
dz
Jeżeli element płynu jest w stanie spoczynku, to w równaniu Eulera nie ma członu
prędkości, przyjmie ono postać
X -
1
ρ
·
∂
p
dx
= 0
Y -
1
ρ
·
∂
p
dy
= 0
(2)
Z -
1
ρ
·
∂
p
dz
= 0
Lub we współrzędnych cylindrycznych
q
r
-
1
ρ
·
∂
∂
p
r
= 0
q
ϑ
-
1
ρ
·
∂
∂ϑ
p
r
⋅
= 0
(3)
q
z
-
1
ρ
·
∂
∂
p
z
= 0
Zapis wektorowy równania ( 1.1 ) ma postać
r
F
gradp
= ⋅
1
ρ
(4)
Równanie ( 1.1 ) można przekształcić do innej postaci
X =
1
ρ
·
∂
p
dx
/·dx
Y =
1
ρ
·
∂
p
dy
/·dy
Wybrane zagadnienia z Mechaniki Płynów
14/32
Z =
1
ρ
·
∂
p
dz
/·dz
X·dx =
1
ρ
·
∂
p
dx
·dx
Y·dy =
1
ρ
·
∂
p
dy
·dy
(5)
Z·dz =
1
ρ
·
∂
p
dz
·dz
Dodając stronami równania ( 1.4 ) otrzymamy
X·dx + Y·dy + Z·dz =
1
ρ
·(
∂
p
dx
·dx +
∂
p
dy
·dy +
∂
p
dz
·dz)
gdzie P = f(x, y, z)
dp =
∂
p
dx
·dx +
∂
p
dy
·dy +
∂
p
dz
·dz
więc
X·dx + Y·dy + Z·dz =
1
ρ
·dp
(6)
Równanie ( 1.4 ) stanowi drugą postać równania hydrodynamiki Eulera.
Dla powierzchni ekwipotencjalnej dp = 0 wówczas
X·dx + Y·dy + Z·dz = 0
(7)
Równanie ( 1.4 ) można zapisać w układzie współrzędnych cylindrycznych
q
r
·dr + q
ϑ
·r·d
ϑ
+ q
z
·dz =
1
ρ
·dp
(8)
Równanie powierzchni ekwipotencjalnej we współrzędnych cylindrycznych
q
r
·dr + q
ϑ
·d
ϑ
+ q
z
·dz = 0.
(9)
Wybrane zagadnienia z Mechaniki Płynów
15/32
8.
KINEMATYCZNY WARUNEK CIĄGŁOŚCI RUCHU PŁYNU
ŚCIŚLIWEGO W PRZEPŁYWACH NIEUSTALONYCH
Przyjmijmy kontrolną objętość dx
.
dy
.
dz w układzie kartezjańskim, przez którą przepływa
strumień płynu ściśliwego o gęstości
ρ
. W przypadku ruchu ustalonego, strumień masy
wpływający do objętości (zgodnie z warunkiem stałości ilości materii) musi być równy
strumieniowi wypływającemu, rozpatrywanemu w tej samej jednostce czasu (zerowy
przyrost
masy).
W układzie nie mogą występować chwilowe lokalne zagęszczenia lub rozrzedzenia masy
(lokalne kompresje i ekspansje) – zjawisko takie stanowi właściwość przepływów
nieustalonych.
Rys. 1. Strumienie wpływający i wypływający do objętości dx
.
dy
.
dz w kierunku x
(w celu zwiększenia czytelności rysunku strumienie na kierunkach y i z nie są opisane).
W przypadku ruchu ustalonego całkowity przyrost masy płynu przepływającego przez
powierzchnie ograniczające objętość kontrolną dx
.
dy
.
dz można zapisać jako
( )
( )
( )
=
∂
∂
+
−
+
+
∂
∂
+
−
+
+
∂
∂
+
−
0
dxdydt
dz
z
V
V
dxdydt
V
dxdzdt
dy
y
V
V
dxdzdt
V
dydzdt
dx
x
V
V
dydzdt
V
z
z
z
y
y
y
x
x
x
ρ
ρ
ρ
ρ
ρ
ρ
ρ
ρ
ρ
.
(1)
Po uproszczeniu otrzymamy
( )
( )
( )
0
=
∂
∂
+
∂
∂
+
∂
∂
dxdydzdt
z
V
dxdydzdt
y
V
dxdydzdt
x
V
z
y
x
ρ
ρ
ρ
,
(2)
x
z
y
ρ
⋅ ⋅ ⋅ ⋅
Vx dy dx dt
(
)
ρ
∂ ρ
∂
∂
⋅
+
⋅
⋅
⋅ ⋅ ⋅
Vx
Vx
x
x
dy dx dt
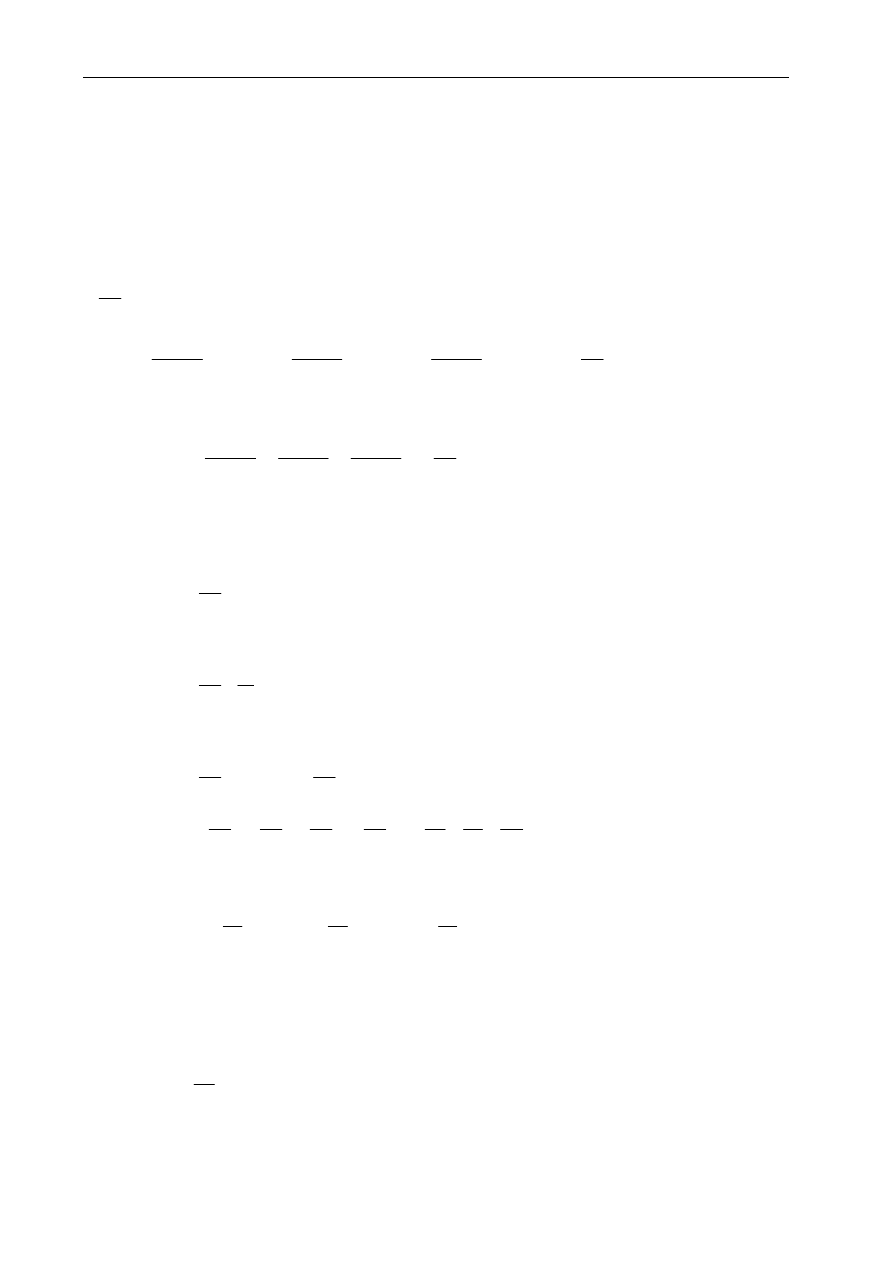
Wybrane zagadnienia z Mechaniki Płynów
16/32
W przypadku przepływu nieustalonego, w obszarze objętości kontrolnej, w czasie dt,
mogą pojawić się zmiany gęstości wywołane ściśliwością płynu. Konsekwencją tego
będzie niezerowa wartość przyrostu masy w obszarze rozpatrywanej objętości kontrolnej.
Ustalając, że strumień masy wypływającej z objętości ma znak dodatni (podczas
ekspansji), zaś wpływającej znak ujemny (podczas kompresji), przyrost ten będzie równy
-
t
∂
∂
ρ
dxdydzdt. Formuła (2) przyjmie wówczas postać
( )
( )
( )
dxdydzdt
t
dxdydzdt
z
V
dxdydzdt
y
V
dxdydzdt
x
V
z
y
x
∂
∂
−
=
∂
∂
+
∂
∂
+
∂
∂
ρ
ρ
ρ
ρ
.
(3)
W odniesieniu do jednostki objętości i czasu otrzymamy
( )
( )
( )
t
z
V
y
V
x
V
z
y
x
∂
∂
−
=
∂
∂
+
∂
∂
+
∂
∂
ρ
ρ
ρ
ρ
,
(4)
Lewa strona powyższego wyrażenia stanowi dywergencję strumienia masy
V
s
ρ
,
równanie (4) można więc zapisać wektorowo
( )
0
=
+
∂
∂
V
div
t
r
ρ
ρ
,
(5)
lub w ogólnej postaci kartezjańskiej jako
( )
0
=
∂
∂
+
∂
∂
i
V
i
t
ρ
ρ
,
gdzie i = x, y, z.
(6)
Rozwijając dalej równanie (5) otrzymamy
( )
∂
∂
+
∂
∂
+
∂
∂
+
∂
∂
+
∂
∂
+
∂
∂
+
∂
∂
=
=
+
+
∂
∂
=
+
∂
∂
z
w
y
v
x
u
z
w
y
v
x
u
t
V
div
grad
V
t
V
div
t
ρ
ρ
ρ
ρ
ρ
ρ
ρ
ρ
ρ
ρ
r
r
r
.
(7)
Wobec tego, iż
t
x
u
∂
∂
=
,
t
y
v
∂
∂
=
,
t
z
w
∂
∂
=
,
(8)
pierwsze cztery człony równania stanowią pochodną zupełną (substancjonalną) gęstości
względem czasu, a suma pochodnych cząstkowych w nawiasie – dywergencję wektora
prędkości, otrzymamy
0
=
+
V
div
dt
dp
r
ρ
.
(9)
Jest to inna forma równania ciągłości w najogólniejszym przypadku ruchu nieustalonego
płynu ściśliwego.

Wybrane zagadnienia z Mechaniki Płynów
17/32
Przypadki równania ciągłości:
- ruch nieustalony płynu ściśliwego
( )
0
=
+
∂
∂
V
div
t
r
ρ
ρ
;
(10)
- ruch ustalony płynu ściśliwego
( )
0
=
V
div
r
ρ
;
(11)
- ruch ustalony płynu nieściśliwego
0
=
V
div
r
.
(12)
Warto zwrócić uwagę, iż warunek (12) oznacza niezmienność objętości.
Równanie ciągłości obowiązuje zarówno dla płynów nielepkich jak i lepkich.
Wybrane zagadnienia z Mechaniki Płynów
18/32
9.
RÓWNANIE BERNOULIEGO
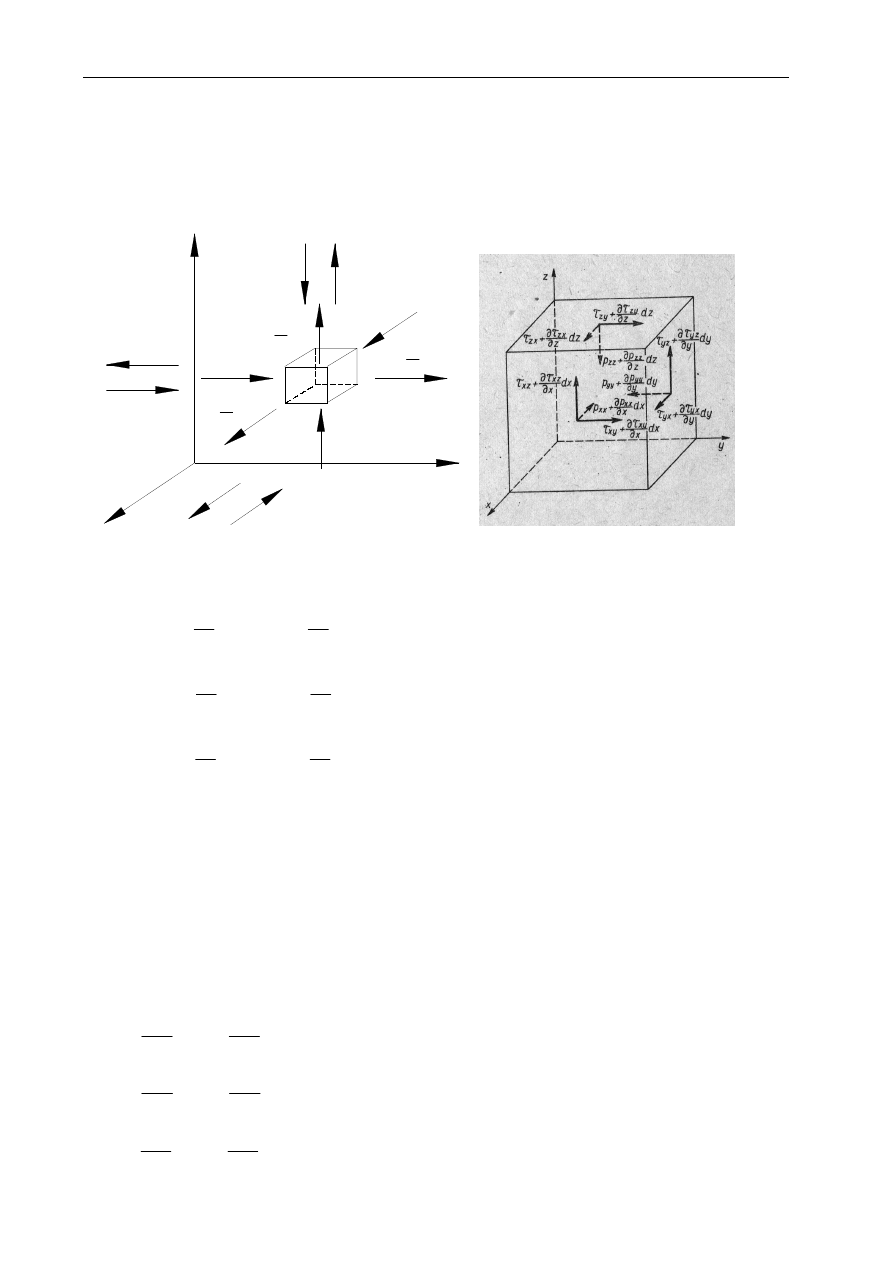
Rozważmy przepływ przez kanał o zmiennym przekroju elementu płynu o stałej masie m
i objętości V. Przez c oznaczmy prędkość średnią elementu płynu.
Całkowita energia zawarta w płynie nie może ulec zmianie, mamy więc
const
E
E
E
cakowita
=
=
=
2
1
.
(1)
W układzie jak na rysunku mamy trzy rodzaje energii:
- energię kinetyczną
2
2
mc
;
- energię potencjalną
mgh
;
- energię ciśnienia
pV
.
Dla położeń 1 i 2 możemy więc zapisać
V
p
mgh
mc
V
p
mgh
mc
2
2
2
2
1
1
2
1
2
2
+
+
=
+
+
.
(2)
Równanie (2) można przekształcić do postaci
m
V
p
gh
c
m
V
p
gh
c
2
2
2
2
1
1
2
1
2
2
+
+
=
+
+
a następnie
g
V
m
p
h
g
c
g
V
m
p
h
g
c
2
2
2
2
1
1
2
1
2
2
+
+
=
+
+
.
(3)
Uwzględniając, że
ρ
=
V
m
a
γ
ρ
=
g
otrzymamy
γ
γ
2
2
2
2
1
1
2
1
2
2
p
h
g
c
p
h
g
c
+
+
=
+
+
(4)
lub ogólnie
.
2
2
const
p
h
g
c
=
+
+
γ
(5)
Wzór (5) stanowi najbardziej znaną postać równania Bernouliego.
c
c
h
h
p
p
Wybrane zagadnienia z Mechaniki Płynów
19/32
10.
RÓWNANIE NAVIERA-STOCKES’A
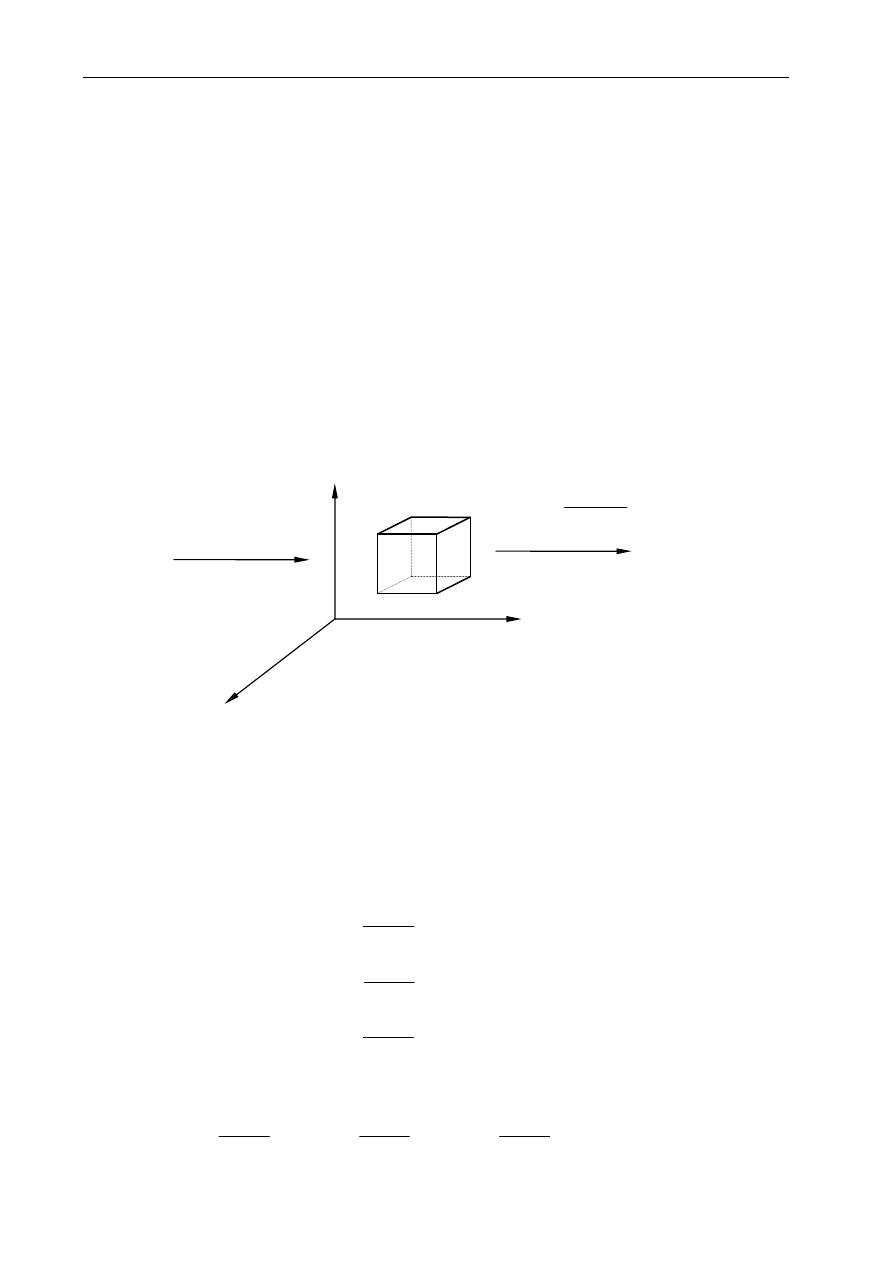
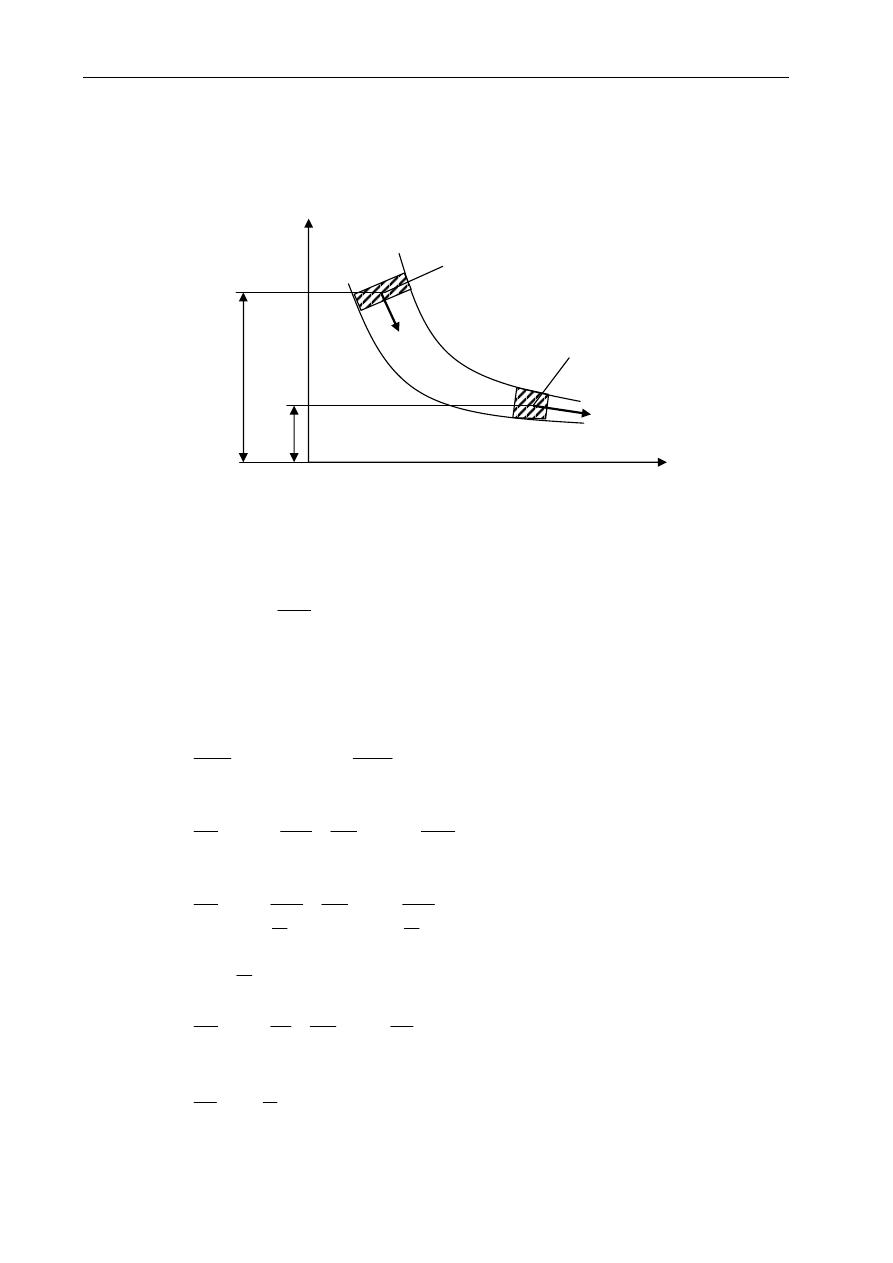
Przyjmijmy kontrolną objętość dx
.
dy
.
dz w układzie kartezjańskim, przez którą przepływa
strumień płynu ściśliwego o gęstości
ρ
i lepkości
µ
.
z
x
y
P
P
P
P
P
x
dx
+
⋅
∂
∂
P
P
y
dy
+
⋅
∂
∂
P
P
z
dz
+
⋅
∂
∂
Fx
Fy
Fz
Bx
By
Bz
Na element płynu działają następujące siły:
1.
Siły wywołane ciśnieniem
P
x
=
dxdydz
x
p
dydz
dx
x
p
p
p
∂
∂
−
=
∂
∂
−
−
P
y
=
dxdydz
y
p
dxdz
dy
y
p
p
p
∂
∂
−
=
∂
∂
−
−
(1)
P
z
=
dxdydz
z
p
dxdy
dz
z
p
p
p
∂
∂
−
=
∂
∂
−
−
2.
Siły masowe
dxdydz
X
Xdm
F
x
ρ
=
=
dxdydz
Y
Ydm
F
y
ρ
=
=
(2)
dxdydz
Z
Zdm
F
z
ρ
=
=
3.
Siły bezwładności – przy założeniu, że element porusza się zgodnie z kierunkami osi
układu, wartość sił bezwładności będą miały znak ujemny
B
x
=
dxdydz
dt
dVx
dm
dt
dVx
ρ
−
=
−
B
y
=
dxdydz
dt
dVy
dm
dt
dVy
ρ
−
=
−
(3)
B
z
=
dxdydz
dt
dVz
dm
dt
dVz
ρ
−
=
−

Wybrane zagadnienia z Mechaniki Płynów
20/32
4.
Siły styczne – w znakowaniu pierwszy symbol oznacza oś, do której jest prostopadły
dany element powierzchni, drugi zaś kierunek składowej naprężeń
dxdy
dz
z
dxdz
dy
y
dydz
dx
x
p
p
p
zx
zx
zx
yx
yx
yx
xx
xx
xx
∂
∂
+
+
−
+
∂
∂
+
+
−
+
∂
∂
−
−
τ
τ
τ
τ
τ
τ
dxdy
dz
z
dxdz
dy
y
p
p
p
dydz
dx
x
zy
zy
zy
yy
yy
yy
xy
xy
xy
∂
∂
+
+
−
+
∂
∂
−
−
+
∂
∂
+
+
−
τ
τ
τ
τ
τ
τ
(4)
dxdy
dz
z
p
p
p
dxdz
dy
y
dydz
dx
x
zz
zz
zz
yz
yz
yz
xz
xz
xz
∂
∂
−
−
−
+
∂
∂
+
+
−
+
∂
∂
+
+
−
τ
τ
τ
τ
τ
τ
po uproszczeniu
dxdydz
z
y
x
p
zx
yx
xx
∂
∂
+
∂
∂
+
∂
∂
−
τ
τ
dxdydz
z
y
p
x
zy
yy
xy
∂
∂
+
∂
∂
−
∂
∂
τ
τ
(5)
dxdydz
z
p
y
x
zz
yz
xz
∂
∂
−
∂
∂
+
∂
∂
τ
τ
Aby element płynu był w równowadze
ix
P
∑
= P
x
+ F
x
+ B
x
= 0
iy
P
∑
= P
y
+ F
y
+ B
y
= 0
(6)
iz
P
∑
= P
z
+ F
z
+ B
z
= 0
więc
dxdydz
x
p
∂
∂
−
+
dxdydz
X
ρ
-
dxdydz
dt
dVx
ρ
+
dxdydz
z
y
x
p
zx
yx
xx
∂
∂
+
∂
∂
+
∂
∂
−
τ
τ
= 0
dxdydz
y
p
∂
∂
−
+
dxdydz
Y
ρ
-
dxdydz
dt
dVy
ρ
+
dxdydz
z
y
p
x
zy
yy
xy
∂
∂
+
∂
∂
−
∂
∂
τ
τ
= 0
(7)
dxdydz
z
p
∂
∂
−
+
dxdydz
Z
ρ
-
dxdydz
dt
dVz
ρ
+
dxdydz
z
p
y
x
zz
yz
xz
∂
∂
−
∂
∂
+
∂
∂
τ
τ
= 0
Ponieważ wektor
(
)
t
z
y
x
V
V
,
,
,
r
r
=
, to każda ze składowych wektora
V
r
też jest funkcją tych
samych zmiennych:
(
)
t
z
y
x
V
V
x
x
,
,
,
r
r
=
,
(
)
t
z
y
x
V
V
y
y
,
,
,
r
r
=
,
(
)
t
z
y
x
V
V
z
z
,
,
,
r
r
=
(8)
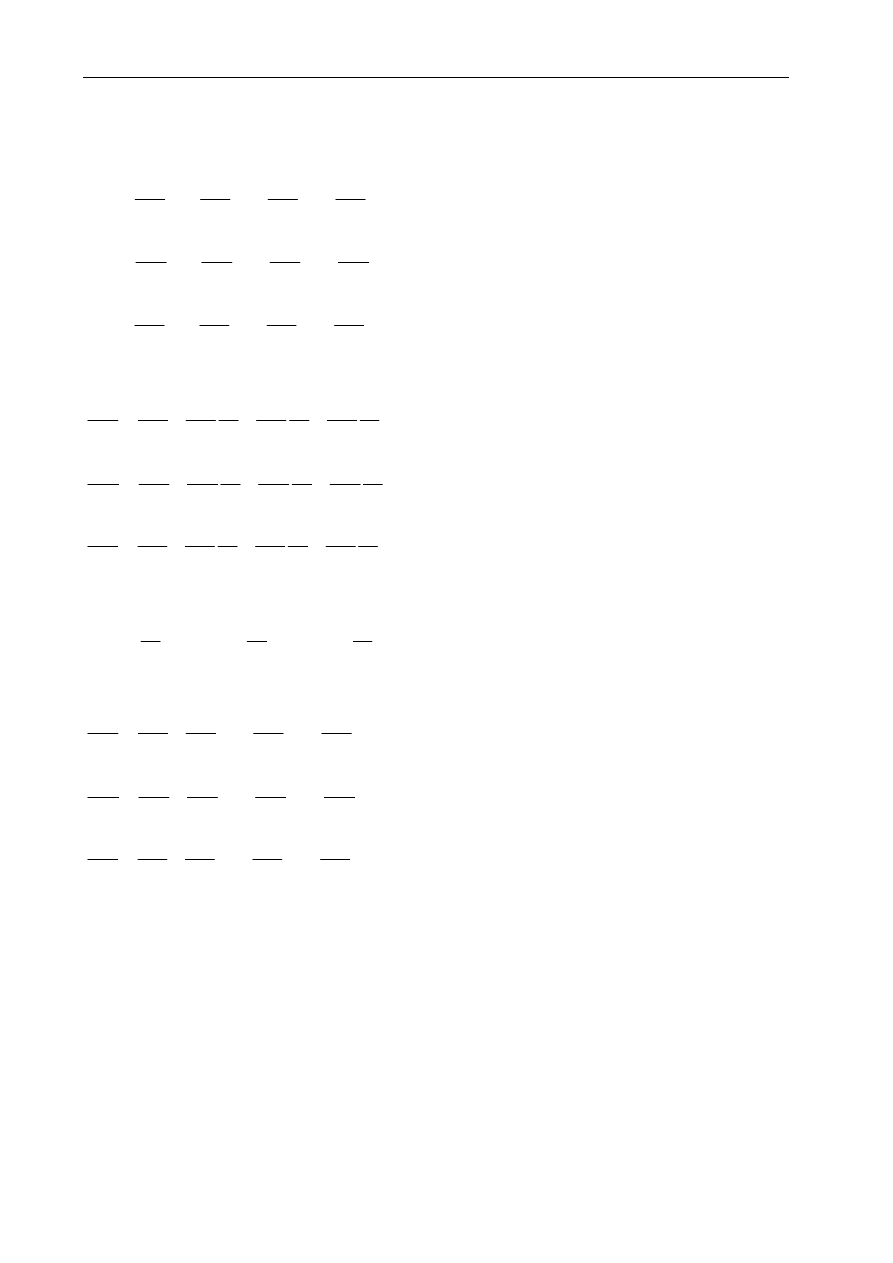
Wybrane zagadnienia z Mechaniki Płynów
21/32
Funkcje te są ciągłe i różniczkowalne, można więc różniczkę zupełną przedstawić w
postaci sumy różniczek cząstkowych:
dz
z
V
dy
y
V
dx
x
V
dt
t
V
dV
x
x
x
x
x
∂
∂
+
∂
∂
+
∂
∂
+
∂
∂
=
dz
z
V
dy
y
V
dx
x
V
dt
t
V
dV
y
y
y
y
y
∂
∂
+
∂
∂
+
∂
∂
+
∂
∂
=
(9)
dz
z
V
dy
y
V
dx
x
V
dt
t
V
dV
z
z
z
z
z
∂
∂
+
∂
∂
+
∂
∂
+
∂
∂
=
lub (po podzieleniu przez dt)
dt
dz
z
V
dt
dy
y
V
dt
dx
x
V
t
V
dt
dV
x
x
x
x
x
∂
∂
+
∂
∂
+
∂
∂
+
∂
∂
=
dt
dz
z
V
dt
dy
y
V
dt
dx
x
V
t
V
dt
dV
y
y
y
y
y
∂
∂
+
∂
∂
+
∂
∂
+
∂
∂
=
(9)
dt
dz
z
V
dt
dy
y
V
dt
dx
x
V
t
V
dt
dV
z
z
z
z
z
∂
∂
+
∂
∂
+
∂
∂
+
∂
∂
=
Ponieważ
x
V
dt
dx
=
,
y
V
dt
dy
=
,
z
V
dt
dz
=
(10)
więc
z
x
y
x
x
x
x
x
V
z
V
V
y
V
V
x
V
t
V
dt
dV
∂
∂
+
∂
∂
+
∂
∂
+
∂
∂
=
z
y
y
y
x
y
y
y
V
z
V
V
y
V
V
x
V
t
V
dt
dV
∂
∂
+
∂
∂
+
∂
∂
+
∂
∂
=
(11)
z
z
y
z
x
z
z
z
V
z
V
V
y
V
V
x
V
t
V
dt
dV
∂
∂
+
∂
∂
+
∂
∂
+
∂
∂
=
Wzór (11) przedstawia tzw. pochodne zupełne (substancjonalne) eulerowskiej metody
analizy lokalnej, składające się z dwu części: pochodnej lokalnej reprezentującej zmiany,
jakie zachodzą z upływem czasu dt w danym punkcie pola prędkości (w przepływach
ustalonych pochodna ta jest równa zeru) oraz pochodnej konwekcyjnej, obrazującej
zmiany, jakie zachodzą przy przesunięciu w czasie dt elementu płynu z punktu x, y, z do
nieskończenie blisko położonego punktu x+dx, y+dy, z+dz.
Wybrane zagadnienia z Mechaniki Płynów
22/32
Zależność (11) podstawiamy do równania (7)
dxdydz
x
p
∂
∂
−
+
dxdydz
X
ρ
+
∂
∂
−
∂
∂
−
∂
∂
−
∂
∂
−
z
x
y
x
x
x
x
V
z
V
V
y
V
V
x
V
t
V
dxdydz
ρ
+
dxdydz
z
y
x
p
zx
yx
xx
∂
∂
+
∂
∂
+
∂
∂
−
τ
τ
=0
dxdydz
y
p
∂
∂
−
+
dxdydz
Y
ρ
+
∂
∂
−
∂
∂
−
∂
∂
−
∂
∂
−
z
y
y
y
x
y
y
V
z
V
V
y
V
V
x
V
t
V
dxdydz
ρ
+
dxdydz
z
y
p
x
zy
yy
xy
∂
∂
+
∂
∂
−
∂
∂
τ
τ
= 0
dxdydz
z
p
∂
∂
−
+
dxdydz
Z
ρ
+
∂
∂
−
∂
∂
−
∂
∂
−
∂
∂
−
z
z
y
z
x
z
z
V
z
V
V
y
V
V
x
V
t
V
dxdydz
ρ
+
dxdydz
z
p
y
x
zz
yz
xz
∂
∂
−
∂
∂
+
∂
∂
τ
τ
= 0
Po odniesieniu do jednostki objętości (dzieląc przez dxdydz) otrzymamy
x
p
∂
∂
−
+
ρ
X
ρ
ρ
ρ
ρ
z
x
y
x
x
x
x
V
z
V
V
y
V
V
x
V
t
V
∂
∂
−
∂
∂
−
∂
∂
−
∂
∂
−
+
∂
∂
+
∂
∂
+
∂
∂
−
z
y
x
p
zx
yx
xx
τ
τ
= 0
y
p
∂
∂
−
+
ρ
Y
ρ
ρ
ρ
ρ
z
y
y
y
x
y
y
V
z
V
V
y
V
V
x
V
t
V
∂
∂
−
∂
∂
−
∂
∂
−
∂
∂
−
+
∂
∂
+
∂
∂
−
∂
∂
z
y
p
x
zy
yy
xy
τ
τ
= 0
(13)
z
p
∂
∂
−
+
ρ
Z
ρ
ρ
ρ
ρ
z
z
y
z
x
z
z
V
z
V
V
y
V
V
x
V
t
V
∂
∂
−
∂
∂
−
∂
∂
−
∂
∂
−
+
∂
∂
−
∂
∂
+
∂
∂
z
p
y
x
zz
yz
xz
τ
τ
= 0
lub przekształcając (przenosząc i dzieląc przez (–1))
ρ
ρ
ρ
ρ
z
x
y
x
x
x
x
V
z
V
V
y
V
V
x
V
t
V
∂
∂
+
∂
∂
+
∂
∂
+
∂
∂
x
p
∂
∂
+
=
z
y
x
p
zx
yx
xx
∂
∂
+
∂
∂
+
∂
∂
−
τ
τ
+
ρ
X
ρ
ρ
ρ
ρ
z
y
y
y
x
y
y
V
z
V
V
y
V
V
x
V
t
V
∂
∂
+
∂
∂
+
∂
∂
+
∂
∂
y
p
∂
∂
+
=
z
y
p
x
zy
yy
xy
∂
∂
+
∂
∂
−
∂
∂
τ
τ
+
ρ
Y
(14)
ρ
ρ
ρ
ρ
z
z
y
z
x
z
z
V
z
V
V
y
V
V
x
V
t
V
∂
∂
+
∂
∂
+
∂
∂
+
∂
∂
z
p
∂
∂
+
=
z
p
y
x
zz
yz
xz
∂
∂
−
∂
∂
+
∂
∂
τ
τ
+
ρ
Z
Dla płynu ściśliwego gęstość
ρ
nie jest stałe, musi więc wejść pod znak różniczki
( ) (
)
(
)
(
)
z
V
V
y
V
V
x
V
V
t
V
z
x
y
x
x
x
x
∂
∂
+
∂
∂
+
∂
∂
+
∂
∂
ρ
ρ
ρ
ρ
x
p
∂
∂
+
=
z
y
x
p
zx
yx
xx
∂
∂
+
∂
∂
+
∂
∂
−
τ
τ
+
ρ
X

Wybrane zagadnienia z Mechaniki Płynów
23/32
( ) (
) (
) (
)
z
V
V
y
V
V
x
V
V
t
V
z
y
y
y
x
y
y
∂
∂
+
∂
∂
+
∂
∂
+
∂
∂
ρ
ρ
ρ
ρ
y
p
∂
∂
+
=
z
y
p
x
zy
yy
xy
∂
∂
+
∂
∂
−
∂
∂
τ
τ
+
ρ
Y
(15)
(
) (
)
(
)
(
)
z
V
V
y
V
V
x
V
V
t
V
z
z
y
z
x
z
z
∂
∂
+
∂
∂
+
∂
∂
+
∂
∂
ρ
ρ
ρ
ρ
z
p
∂
∂
+
=
z
p
y
x
zz
yz
xz
∂
∂
−
∂
∂
+
∂
∂
τ
τ
+
ρ
Z
Przyjmując odpowiednio, że
X = b
x
,
Y = b
y
,
Z = b
z
(16)
oraz
p
xx
=
τ
xx,
p
yy
=
τ
yy
,
p
zz
=
τ
zz
(17)
powyższe równania można zapisać symbolicznie w postaci skróconej
i
c
ij
ij
j
i
i
b
j
p
V
V
j
V
t
ρ
τ
δ
ρ
ρ
+
∂
∂
=
+
∂
∂
+
∂
∂
)
(
)
(
)
(
(18)
gdzie i, j = x, y, z (dla jednego równania i jest stałe, zaś j przyjmuje wartości x, y, z).
W postaci wektorowej równanie (16) przyjmie postać
b
div
)
I
p
V
V
div(
V
t
cakowite
r
t
t
r
r
r
ρ
τ
ρ
ρ
∂
∂
+
=
+
⊗
+
)
(
)
(
.
(19)
Można wykazać, że w istocie stan napięcia w każdym punkcie przestrzeni wypełnionej
płynem lepkim określony jest liczbową wartością, nie dziewięciu, a sześciu naprężeń.
Równanie momentów względem osi x ma następującą postać (kierunek dodatni od osi y
do z)
0
2
1
2
1
2
1
2
1
2
1
2
1
2
1
2
1
=
∂
∂
+
−
+
∂
∂
+
−
−
∂
∂
+
+
−
∂
∂
+
+
+
∂
∂
+
+
−
∂
∂
+
−
dxdydz
dz
z
dy
dxdy
p
dy
dxdy
dz
z
p
p
dxdzdy
dy
y
dz
dxdz
p
dz
dxdz
dy
y
p
p
dy
dydz
dx
x
dy
dydz
dz
dydz
dx
x
dz
dydz
zy
zy
zz
zz
zz
yz
yz
yy
yy
yy
xz
xz
xz
xy
xy
xy
τ
τ
τ
τ
τ
τ
τ
τ
τ
τ
(20)
Po uproszczeniu i pominięciu małych czwartego rzędu
(
)
0
=
−
dxdydz
zy
yz
τ
τ
skąd
0
=
−
zy
yz
τ
τ
.
(21)
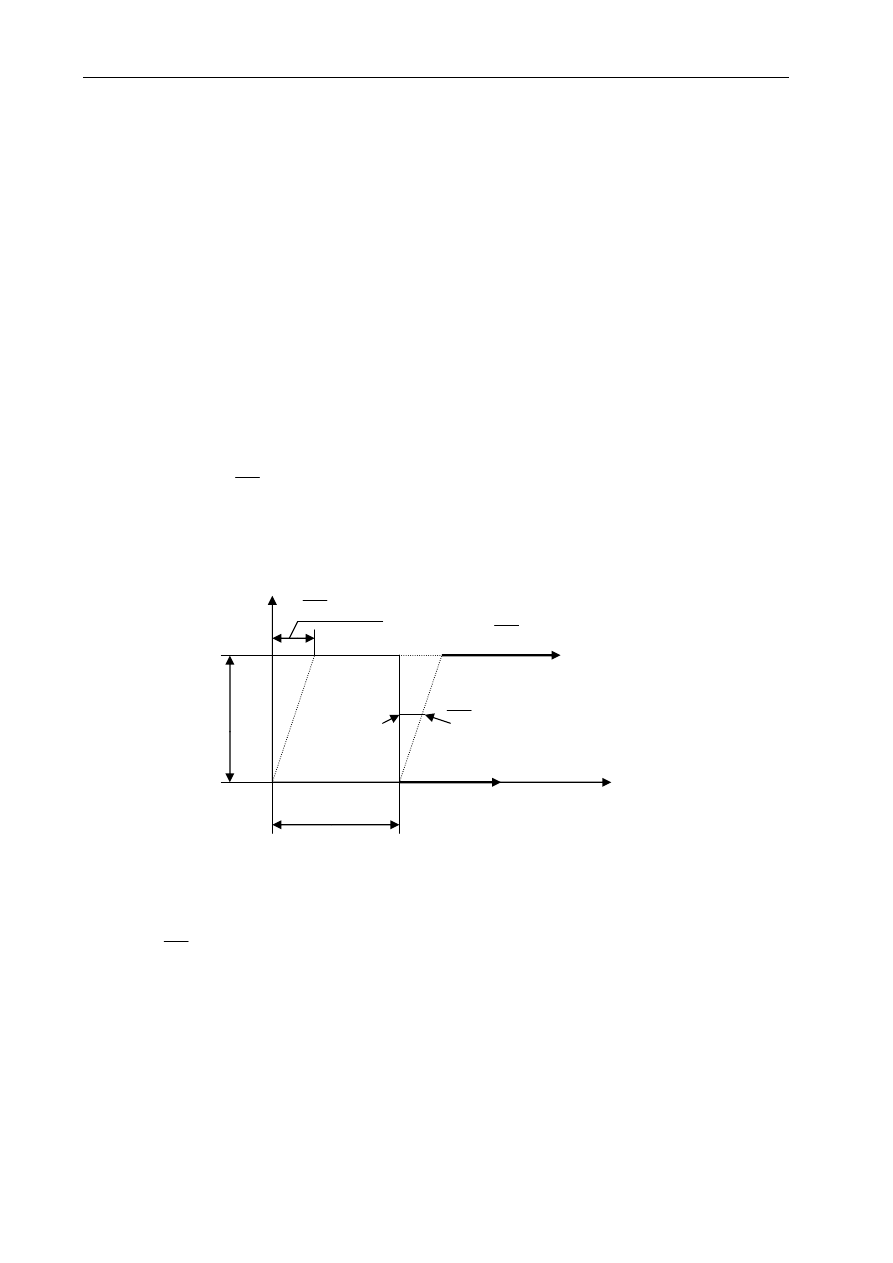
Wybrane zagadnienia z Mechaniki Płynów
24/32
Podobnie
0
=
−
xz
zx
τ
τ
,
0
=
−
yx
xy
τ
τ
.
Tak więc naprężenia styczne zbieżne na tej samej krawędzi są sobie równe (istnieje
symetria naprężeń stycznych).
Podstawowym
założeniem,
pozwalającym
związać
ilościowo
stan
naprężeń
powierzchniowych z polem prędkości, jest założenie proporcjonalności tych naprężeń do
odkształceń. Wzór podany przez Newtona na naprężenie styczne w przypadku przepływu
płaskiego stanowi najprostsze sformułowanie tego założenia
n
V
∂
∂
=
µ
τ
.
(22)
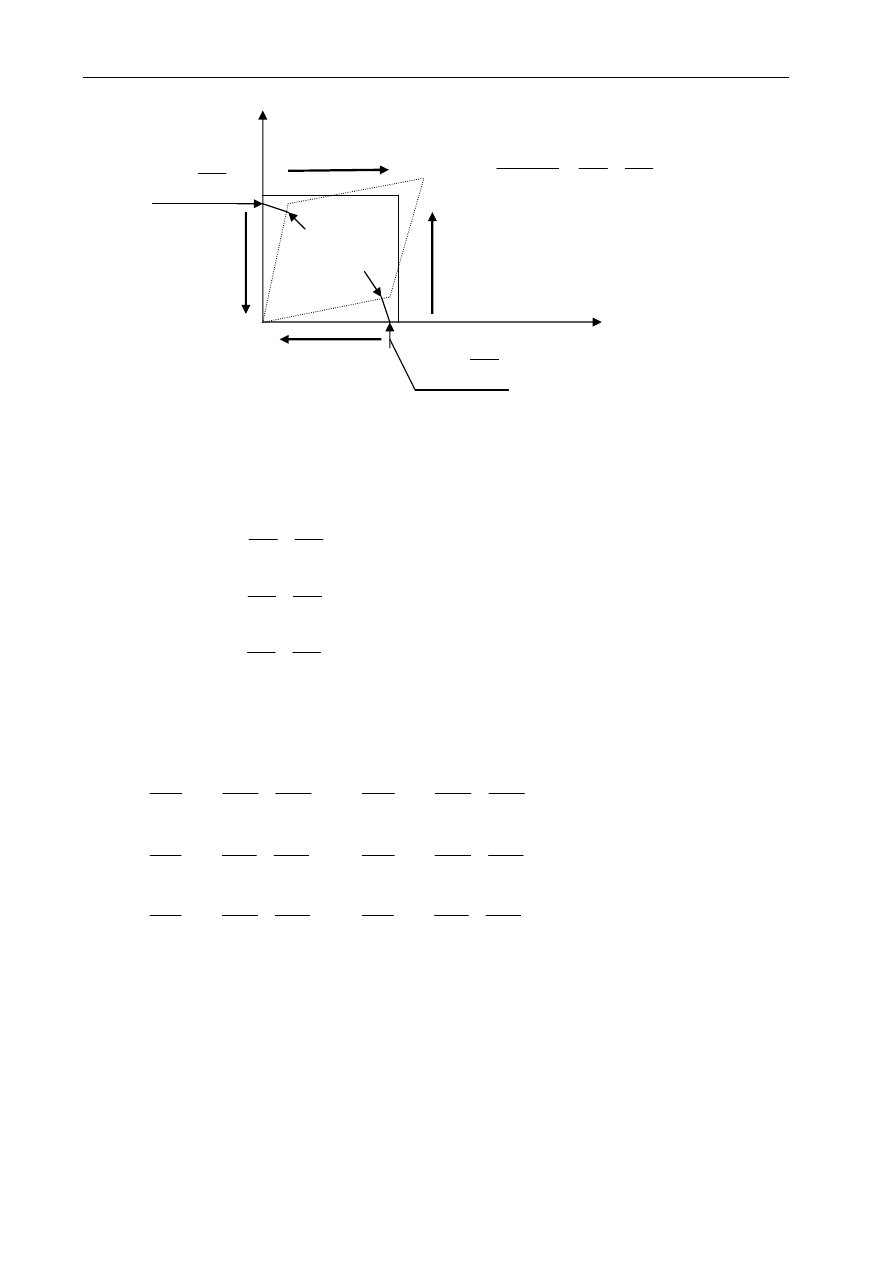
Współczynnik proporcjonalności
µ
wskazuje, jak duży będzie przyrost prędkości na
kierunku n, w jednostce czasu dt, w warstwach płynu oddalonych od siebie o odległość
dn (rys. 1.).
Rys. 1. Odkształcenie kątowe elementu płynu.
Wartość
n
V
∂
∂
stanowi prędkość odkształcenia kątowego elementu dnds. Naprężenia
powierzchniowe styczne mogą wystąpić tylko w przypadku odkształceń kątowych
elementu płynu.
dn
n
V
V
∂
∂
+
dndt
n
V
∂
∂
V
s
n
ds
d
dt
n
V
∂
∂
Wybrane zagadnienia z Mechaniki Płynów
25/32
Rys. 2. Odkształcenia elementu płynu w układzie kartezjańskim na ściance dxdy.
W układzie kartezjańskim zależności te przyjmą następującą formę (rys. 2):
∂
∂
+
∂
∂
=
=
∂
∂
+
∂
∂
=
=
∂
∂
+
∂
∂
=
=
x
V
z
V
z
V
y
V
y
V
x
V
z
x
xz
zx
y
z
zy
yz
x
y
yx
xy
µ
τ
τ
µ
τ
τ
µ
τ
τ
,
(23)
według której można obliczyć pochodne cząstkowe poszczególnych składowych
naprężeń
∂
∂
∂
+
∂
∂
∂
=
∂
∂
∂
∂
∂
+
∂
∂
∂
=
∂
∂
∂
∂
∂
+
∂
∂
∂
=
∂
∂
x
z
V
x
x
V
x
z
y
V
z
z
V
z
x
y
V
x
x
V
x
x
z
xz
z
y
zy
x
y
xy
2
2
2
2
2
2
µ
τ
µ
τ
µ
τ
,
∂
∂
∂
+
∂
∂
∂
=
∂
∂
∂
∂
∂
+
∂
∂
∂
=
∂
∂
∂
∂
∂
+
∂
∂
∂
=
∂
∂
z
x
V
z
z
V
z
y
z
V
y
y
V
y
y
x
V
y
y
V
y
z
x
zx
y
z
yz
y
x
yx
2
2
2
2
2
2
µ
τ
µ
τ
µ
τ
.
(24)
Do dalszych rozważań wykorzystane będzie równanie (14) z uwzględnieniem warunku
(17)
dt
y
V
d
x
∂
∂
=
β
dt
x
V
d
y
∂
∂
=
α
x
y
ττττ
y
ττττ
x
ττττ
yx
+d
ττττ
y
ττττ
xy
+d
ττττ
x
y
V
x
V
dt
d
d
x
y
∂
∂
+
∂
∂
=
+
β
α

Wybrane zagadnienia z Mechaniki Płynów
26/32
+
∂
∂
−
∂
∂
+
∂
∂
=
∂
∂
+
∂
∂
+
∂
∂
+
∂
∂
+
∂
∂
+
∂
∂
+
∂
∂
−
∂
∂
=
∂
∂
+
∂
∂
+
∂
∂
+
∂
∂
+
∂
∂
+
∂
∂
+
∂
∂
+
∂
∂
−
=
∂
∂
+
∂
∂
+
∂
∂
+
∂
∂
+
∂
∂
ρ
τ
τ
ρ
ρ
ρ
ρ
ρ
τ
τ
ρ
ρ
ρ
ρ
ρ
τ
τ
ρ
ρ
ρ
ρ
Z
z
p
y
x
z
p
V
z
V
V
y
V
V
x
V
t
V
Y
z
y
p
x
y
p
V
z
V
V
y
V
V
x
V
t
V
X
z
y
x
p
x
p
V
z
V
V
y
V
V
x
V
t
V
zz
yz
xz
z
z
y
z
x
z
z
zy
yy
xy
z
y
y
y
x
y
y
zx
yx
xx
z
x
y
x
x
x
x
(25)
lub krócej jako
∂
∂
−
∂
∂
+
∂
∂
+
=
∂
∂
+
∂
∂
+
∂
∂
−
∂
∂
+
=
∂
∂
+
∂
∂
+
∂
∂
+
∂
∂
−
=
∂
∂
+
z
p
y
x
Z
z
p
dt
dV
z
y
p
x
Y
y
p
dt
dV
z
y
x
p
X
x
p
dt
dV
zz
yz
xz
z
zy
yy
xy
y
zx
yx
xx
x
τ
τ
ρ
ρ
τ
τ
ρ
ρ
τ
τ
ρ
ρ
(26)
Po podstawieniu odpowiednich różniczek cząstkowych wg zależności (24) otrzymamy
∂
∂
−
∂
∂
∂
+
∂
∂
∂
+
∂
∂
∂
+
∂
∂
∂
+
=
∂
∂
+
∂
∂
∂
+
∂
∂
∂
+
∂
∂
−
∂
∂
∂
+
∂
∂
∂
+
=
∂
∂
+
∂
∂
∂
+
∂
∂
∂
+
∂
∂
∂
+
∂
∂
∂
+
∂
∂
−
=
∂
∂
+
z
p
y
z
V
y
y
V
x
z
V
x
x
V
Z
z
p
dt
dV
z
y
V
z
z
V
y
p
x
y
V
x
x
V
Y
y
p
dt
dV
z
x
V
z
z
V
y
x
V
y
y
V
x
p
X
x
p
dt
dV
zz
y
z
x
z
z
z
y
yy
x
y
y
z
x
y
x
xx
x
2
2
2
2
2
2
2
2
2
2
2
2
µ
µ
ρ
ρ
µ
µ
ρ
ρ
µ
µ
ρ
ρ
Po przekształceniach
∂
∂
∂
+
∂
∂
∂
+
∂
∂
∂
+
∂
∂
∂
+
∂
∂
−
=
∂
∂
+
∂
∂
∂
+
∂
∂
∂
+
∂
∂
∂
+
∂
∂
∂
+
∂
∂
−
=
∂
∂
+
∂
∂
∂
+
∂
∂
∂
+
∂
∂
∂
+
∂
∂
∂
+
∂
∂
−
=
∂
∂
+
y
z
V
y
y
V
x
z
V
x
x
V
z
p
Z
z
p
dt
dV
z
y
V
z
z
V
x
y
V
x
x
V
y
p
Y
y
p
dt
dV
z
x
V
z
z
V
y
x
V
y
y
V
x
p
X
x
p
dt
dV
y
z
x
z
zz
z
z
y
x
y
yy
y
z
x
y
x
xx
x
2
2
2
2
2
2
2
2
2
2
2
2
µ
ρ
ρ
µ
ρ
ρ
µ
ρ
ρ

Wybrane zagadnienia z Mechaniki Płynów
27/32
11.
RUCH ELEMENTU PŁYNU
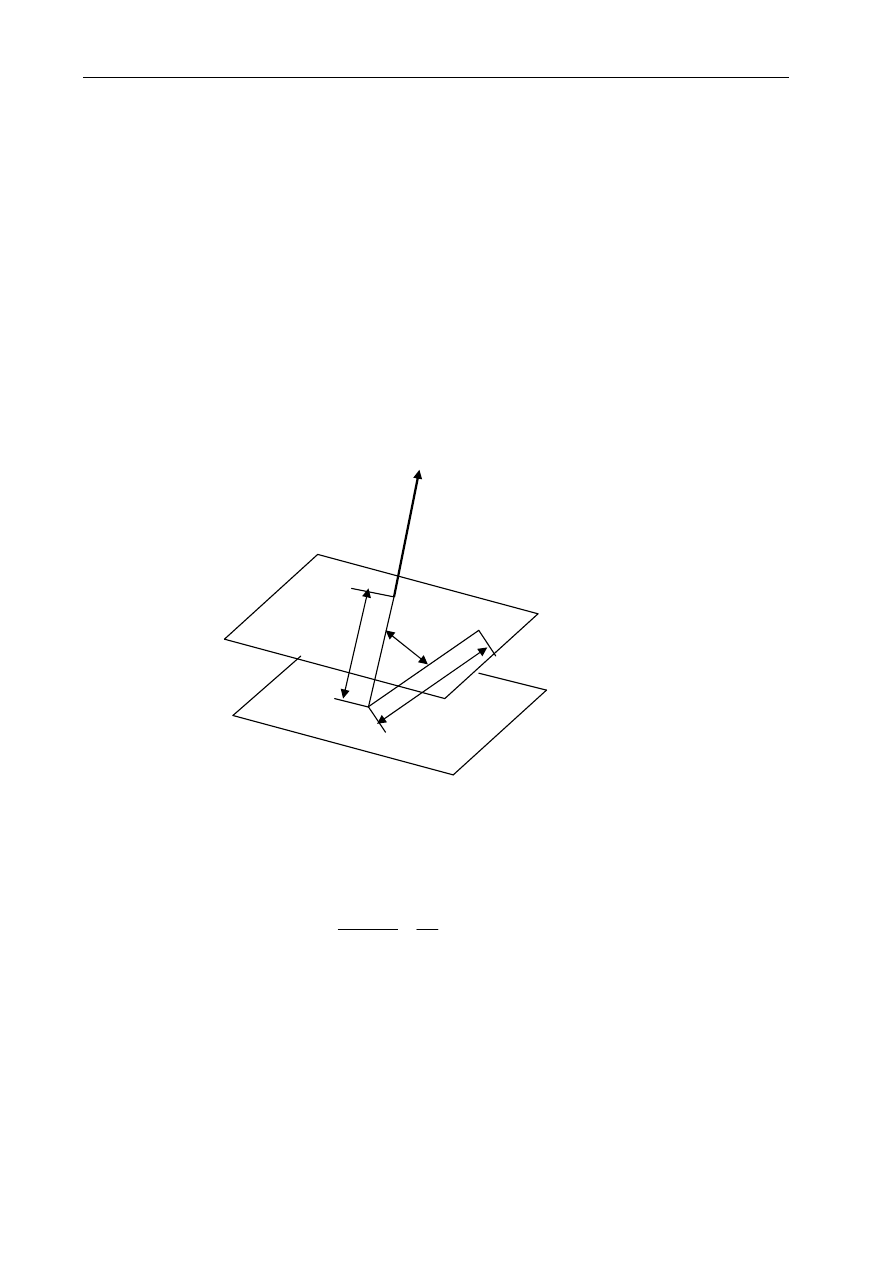
Rozpatrzmy element płynu pozostający w ruchu, jak poglądowo pokazuje to rysunek.
Sytuacja pokazana jest w chwili ustalonej t
0
. Stąd wewnątrz elementu odległości od
punktu 0 (dowolnie obrany punkt) oznaczone będą symbolem
r
∂
. Punkt 0 nazwiemy
biegunem. Punkt A jest dowolnym punktem wewnątrz elementu, różnym od bieguna.
Mamy więc relację:
r
r
r
A
∂
+
=
0
.
(1)
Jeżeli powyższy związek zróżniczkujemy względem czasu, to otrzymamy
( )
dt
r
d
dt
dr
dt
dr
A
∂
+
=
0
(2)
Relację tę można zapisać
( )
dt
r
d
u
u
A
∂
+
=
0
(3)
Z drugiej strony, wektor prędkości w punkcie A może być zapisany jako
u
u
u
A
∂
+
=
0
.
(4)
Stąd wynika, iż
( )
u
dt
r
d
∂
=
∂
.
(5)
Związek między wektorami
∂
u i
∂
r można zapisać jako
r
r
u
u
∂
∂
∂
=
∂
.
(6)
Podstawiając powyższą zależność do wzoru (4) otrzymamy
r
r
u
u
u
A
∂
∂
∂
+
=
0
(7)
∂
u
u
0
u
0
r
0
r
A
0
A
∂
r
u
A
t
0
x
y
z

Wybrane zagadnienia z Mechaniki Płynów
28/32
Tensor
∂
u/
∂
r można przedstawić w postaci dwóch tensorów – symetrycznego D
i niesymetrycznego A - poprzez następujące przekształcenie:
+
∂
∂
+
−
∂
∂
=
∂
∂
gradu
r
u
gradu
r
u
r
u
2
1
2
1
(8)
lub
D
A
r
u
+
=
∂
∂
(9)
gdzie
−
∂
∂
=
gradu
r
u
A
2
1
(10)
+
∂
∂
=
gradu
r
u
D
2
1
(11)
Ponieważ
uk
uj
ui
u
∂
+
∂
+
∂
=
∂
,
(12)
zk
yj
xi
r
∂
+
∂
+
∂
=
∂
.
mamy więc
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
=
∂
∂
z
u
y
u
x
u
z
u
y
u
x
u
z
u
y
u
x
u
r
u
z
z
z
y
y
y
x
x
x
(13)
Gradient u można otrzymać jako wynik iloczynu diadycznego gradientu i wektora u:
(
)
k
u
j
u
i
u
k
z
j
y
i
x
gradu
z
y
x
+
+
∂
∂
+
∂
∂
+
∂
∂
=
,
(14)
skąd po wykonaniu działań otrzymamy
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
=
z
u
z
u
z
u
y
u
y
u
y
u
x
u
x
u
x
u
gradu
z
y
x
z
y
x
z
y
x
.
(15)

Wybrane zagadnienia z Mechaniki Płynów
29/32
Na podstawie wzorów (12) i (15) można obliczyć składowe tensorów A i D:
∂
∂
−
∂
∂
∂
∂
−
∂
∂
−
∂
∂
−
∂
∂
−
∂
∂
−
∂
∂
∂
∂
−
∂
∂
∂
∂
−
∂
∂
−
=
0
2
1
2
1
2
1
0
2
1
2
1
2
1
0
z
u
y
u
x
u
z
u
z
u
y
u
y
u
x
u
x
u
z
u
y
u
x
u
A
y
z
z
x
y
z
x
y
z
x
x
y
(16)
∂
∂
∂
∂
+
∂
∂
∂
∂
+
∂
∂
∂
∂
+
∂
∂
∂
∂
∂
∂
+
∂
∂
∂
∂
+
∂
∂
∂
∂
+
∂
∂
∂
∂
=
z
u
y
u
z
u
x
u
z
u
y
u
z
u
y
u
x
u
y
u
x
u
z
u
x
u
y
u
x
u
D
z
z
y
z
x
z
y
y
y
x
z
x
y
x
x
2
1
2
1
2
1
2
1
2
1
2
1
(17)
Po uwzględnieniu rozbicia tensora
∂
u/
∂
r wzór (7) otrzyma ostateczną postać
r
D
r
A
u
u
A
∂
+
∂
+
=
0
0
0
(18)
gdzie wszystkie pochodne w tensorach A i D są wyznaczane dla punktu 0, co zostało
oznaczone indeksami A
0
i D
0
.
Wzór (18) stanowi zapis pierwszego twierdzeniu Helmholtza, które mówi, że prędkość
dowolnego punktu elementu płynu składa się z trzech prędkości:
- prędkości postępowej punktu obranego za biegun u
0
;
- prędkości obrotowej dookoła osi przechodzącej przez biegun z prędkością kątową
ω
0
, której wektor wyznacza oś obrotu;
- prędkości deformacji elementu płynu D
0
∂
r.

Wybrane zagadnienia z Mechaniki Płynów
30/32
Składowe tensora A stanowią wartości prędkości kątowych
ω
względem osi x, y, z
−
−
−
=
0
0
0
x
y
x
z
y
z
A
ϖ
ϖ
ϖ
ω
ω
ϖ
Tensor deformacji D można rozłożyć na dwa tensory – tensor deformacji liniowych oraz
tensor deformacji kątowych:
∂
∂
+
∂
∂
∂
∂
+
∂
∂
∂
∂
+
∂
∂
∂
∂
+
∂
∂
∂
∂
+
∂
∂
∂
∂
+
∂
∂
+
∂
∂
∂
∂
∂
∂
=
0
2
1
2
1
2
1
0
2
1
2
1
2
1
0
0
0
0
0
0
0
y
u
z
u
x
u
z
u
y
u
z
u
x
u
y
u
x
u
z
u
x
u
y
u
z
u
y
u
x
u
D
z
y
z
x
z
y
y
x
z
x
y
x
z
y
x
Wybrane zagadnienia z Mechaniki Płynów
31/32
12.
GRADIENT SKALARA
W polu skalarnym L = F(x,y,z,t), w założeniu, że funkcja F jest ciągła i mająca pochodną
we wszystkich punktach pola, istnieją zawsze pewne powierzchnie (dla pola ustalonego
zawsze te same, dla pola nieustalonego – w danej chwili t) określone równaniem L =
F(x,y,z) = const, na których wartość danego skalara jest stała. Mogą to być powierzchnie
równych ciśnień, temperatur, gęstości, itd.
Istnieje pewna wielkość stanowiąca nowe pole, zależne od danego pola skalarnego,
charakteryzująca zmienność skalara przy przejściu od jednej powierzchni stałej jego
wartości L = C
1
do sąsiedniej L = C
2
.
Najkrótszą drogą przejścia od pewnego punktu A powierzchni L = C
1
do powierzchni L
= C
2
jest odcinek normalnej
n
r
, poprowadzonej w punkcie A, zawarty między tymi
dwiema powierzchniami. Wyrażenie
dn
dL
AB
C
C
AB
=
−
→
1
2
)
lim
(1)
określa wielkość zwaną gradientem skalara. Gradient skalara jest wektorem, którego
kierunek w każdym punkcie określa orientację elementu powierzchni L = const
obejmującego dany punkt. Wektor ten jest skierowany zgodnie z normalną
odpowiedniego elementu powierzchni L = const. Dodatni zwrot gradientu skalara
przyjmuje się zazwyczaj w stronę rosnących wartości skalara.
A
B
dn
L = C
1
L = C
2
C
ds
β

Wybrane zagadnienia z Mechaniki Płynów
32/32
Nowy wektor oznaczmy literą G
n
dn
dF
z
y
x
gradF
n
dn
dL
gradL
G
r
r
r
=
=
=
=
)
,
,
(
(2)
Wartość pochodnej
dn
dF
dn
dL
=
stanowi tutaj moduł gradientu G.
W polu ustalonym lub w danej chwili t w polu nieustalonym
dz
z
F
dy
y
F
dx
x
F
dF
dL
∂
∂
+
∂
∂
+
∂
∂
=
=
.
(3)
Jeżeli dx, dy, dz oznaczają składowe dowolnego przesunięcia ds z danej powierzchni
L = C
1
do powierzchni L = C
2
(na przykład od punktu A do C, jeżeli AC
→
0), to
β
cos
ds
dL
dn
dL
G
=
=
(4)
skąd
β
cos
G
ds
dL
=
,
(5)
β
cos
Gds
dL
=
.
(6)
Wzory (4-6) dowodzą, że różnica wartości pomiędzy dwiema powierzchniami o stałej
wartości pola L, nie zależy od położenia punktów na tych powierzchniach, a tylko od
odległości tych powierzchni.
Wyszukiwarka
Podobne podstrony:
Mechanika Plynow Lab, Sitka Pro Nieznany
Mechanika płynów na kolosa z wykładów
Mechanika płynów zaliczenie wykładów
Równanie równowagi płyny, mechanika plynów
pyt.4 gr 1, Semestr III, Mechanika Płynów
sciaga MP, INŻYNIERIA ŚRODOWISKA WGGiIŚ AGH inżynierskie, SEMESTR 3, Mechanika Płynów
wyznaczanie współczynnika strat liniowych, studia, V semestr, Mechanika płynów
spr 2 - wizualizacja, ☆☆♠ Nauka dla Wszystkich Prawdziwych ∑ ξ ζ ω ∏ √¼½¾haslo nauka, mechanika płyn
Lab. mech. płynów-Wizualizacja opływu walca w kanaliku, Mechanika Płynów pollub(Sprawozdania)
Czas wypływu, mechanika plynów
Newton jest jak Herkules z bajki, Księgozbiór, Studia, Mechanika Płynów i Dynamika Gazów
mechanika płynów
PLYNY4~1, Księgozbiór, Studia, Mechanika Płynów i Dynamika Gazów
tabela do 2, inżynieria środowiska agh, mechanika plynow
Mechanika Płynów Lab, Sitka N19
spawko mechanika plynow nr 3 mf
Mechanika płynów sprawozdanie 1 współczynnik lepkościs
Mechanika Płynów wzorcowanie manometrów
więcej podobnych podstron