301

DYSKRETNY UKŁAD PUNKTÓW

MATERIALNYCH

ŚRODEK MASY
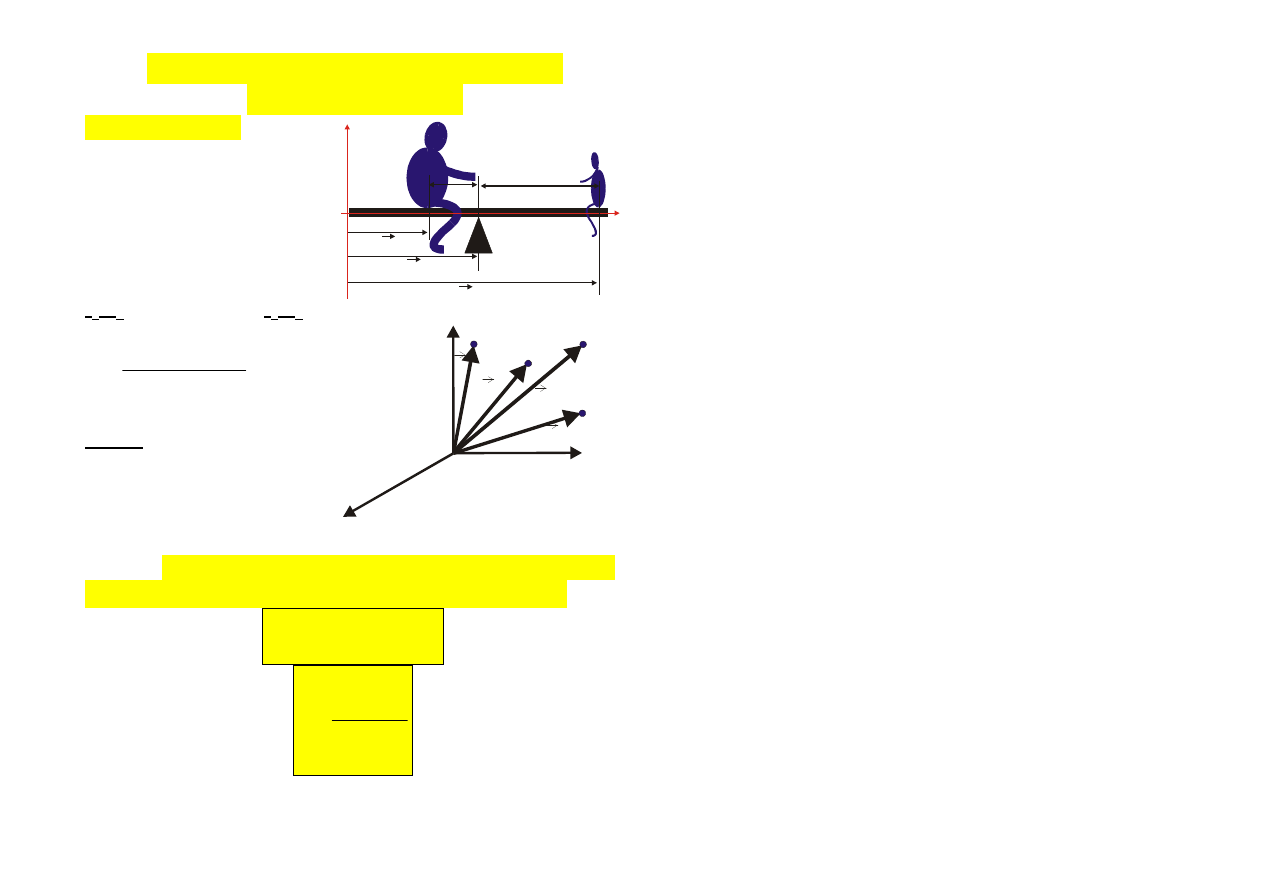
Przykład intuicyjny -
gdzie znajduje się
środek masy. ukł?

a

1

m

1

=

a

2

m

2

w ukł. współż. XY:
(r

s

- r

1

) m

1

= (r

2

- r

s

) m

2

r

s

m

1

- r

1

m

1

= r

2

m

2

- r

s

m

2

r

s

m

1

+ r

s

m

2

= r

1

m

1

+ r

2

m

2

2

1

2

2

1

1

s

m

m

m

r

m

r

r

⋅

+

⋅

+

⋅

=

.

Dane:
dyskretny ukł. pp mater.
m

1

, m

2

, m

3

, ... , m

n

,

1

r

r

,

2

r

r

,

3

r

r

, ... ,

n

r

r

,

Tw.: Środkiem masy ukł. pp materialnych nazywamy
punkt, którego wektor wodzący

s

r

r

spełnia równanie:

∑

∑

=

=

⋅

=

⋅

n

1

i

i

i

n

1

i

i

s

r

m

m

r

r

r

,

∑

∑

∑

∑

∑

∑

∑

∑

=

==

=

=

==

=

⋅⋅⋅⋅

====

n

1

i

i

n

1

i

i

i

s

m

r

m

r

r

r

.

X

Y

Z

r

r

r

r

1

1

2

n

2

s

s

n

m

m

m

m

m

a

r

r

r

a

1

1

2

s

1

2

2

X

Y

302

X

Y

Z

r

s

s

r

dm

dV=dx dy dz

. .

Ponieważ:

∧

∧

∧

∧

∧

∧

∧

∧

∧

∧

∧

∧

⋅⋅⋅⋅

++++

⋅⋅⋅⋅

++++

⋅⋅⋅⋅

====

k

z

j

y

i

x

r

s

r

r

v

r

∑

∑

∑

∑

∑

∑

∑

∑

=

==

=

=

==

=

⋅⋅⋅⋅

====

n

1

i

i

n

1

i

i

i

m

x

m

x

,

∑

∑

∑

∑

∑

∑

∑

∑

=

==

=

=

==

=

⋅⋅⋅⋅

====

n

1

i

i

n

1

i

i

i

m

y

m

y

,

∑

∑

∑

∑

∑

∑

∑

∑

=

==

=

=

==

=

⋅⋅⋅⋅

====

n

1

i

i

n

1

i

i

i

m

z

m

z

Dla ciągłego rozkładu masy:

∫∫∫∫

∫∫∫∫

∫∫∫∫

⋅⋅⋅⋅

====

⋅⋅⋅⋅

====

M

M

M

s

dm

r

M

1

dm

dm

r

r

r

r

r

W praktyce trudno całkować po masie
dm → dV,

dV

dm

V

M ====

====

ρρρρ

→

dV

dm

⋅⋅⋅⋅

ρρρρ

====

∫∫∫∫

⋅⋅⋅⋅

⋅⋅⋅⋅

ρρρρ

====

V

s

dV

r

M

1

r

r

r

∫∫∫∫

⋅⋅⋅⋅

⋅⋅⋅⋅

ρρρρ

====

V

s

dV

x

M

1

x

∫∫∫∫

⋅⋅⋅⋅

⋅⋅⋅⋅

ρρρρ

====

V

s

dV

y

M

1

y

∫∫∫∫

⋅⋅⋅⋅

⋅⋅⋅⋅

ρρρρ

====

V

s

dV

z

M

1

z

∫∫∫

⋅

⋅

ρ

=

z

,

y

,

x

s

dxdydz

x

M

1

x

.

Dla ρ=Const

∫

⋅

ρ

=

V

s

dV

r

M

r

r

r

.

303

RUCH ŚRODKA MASY

z def. ś.m.:

∑

∑

∑

∑

=

==

=

⋅⋅⋅⋅

====

⋅⋅⋅⋅

n

1

i

i

i

s

r

m

M

r

r

r

dt

d

/

∑

∑

∑

∑

=

==

=

⋅⋅⋅⋅

====

⋅⋅⋅⋅

====

n

1

i

i

i

s

s

v

m

v

M

dt

r

d

M

r

r

r

pęd środka masy = sumie pędów

∑

∑

∑

∑

=

==

=

====

n

1

i

i

s

p

p

r

r

∑

∑

∑

∑

=

==

=

⋅⋅⋅⋅

====

⋅⋅⋅⋅

n

1

i

i

i

s

v

m

v

M

r

r

/dt zróżniczkujmy

(

)

∑

=

⋅

=

n

1

i

i

i

s

dt

v

m

d

dt

v

d

M

r

r

s

s

a

M

dt

v

d

M

r

r

⋅

=

,

(

)

∑

∑

∑

=

=

=

=

=

⋅

n

1

i

i

n

1

i

i

n

1

i

i

i

F

dt

p

d

dt

v

m

d

r

r

r

R-nie ruchu ś.m.:

∑

∑

=

=

=

=

=

⋅

=

n

1

i

i

n

1

i

i

s

s

s

dt

p

d

F

dt

p

d

a

M

F

r

r

r

r

r

Suma wektorowa sił przyłożonych do poszczególnych
punktów materialnych.
Rodzaje sił działających na p. mat.:
1. siły zewn.

Zi

F

r

2. siły wewn.

Wi

F

r

Równanie ruchu ś.m. można zatem zapisać:

304

∑

∑

∑

∑

∑

∑

∑

∑

=

==

=

=

==

=

++++

====

⋅⋅⋅⋅

n

1

i

Wi

n

1

i

Zi

s

F

F

a

M

r

r

r

Siły wewn. to siły wzajemnego oddziaływania punktów na
siebie. Jeśli pogrupujemy je w pary (dwójki), to zgodnie z
III ZDN będą się parami znosić, a więc:

0

F

n

1

i

Wi

====

∑

∑

∑

∑

=

==

=

r

czyli:

∑

∑

∑

∑

=

==

=

====

⋅⋅⋅⋅

n

1

i

Zi

s

F

a

M

r

r

∑

∑

=

=

=

=

=

⋅

=

n

1

i

i

n

1

i

Zi

s

s

s

dt

p

d

F

dt

p

d

a

M

F

r

r

r

r

r

To jest II ZDN dla dyskretnego układu punktów

materialnych (II ZDN DUPM)

305

ZSADA ZACHOWANIA PĘDU (ZZP)

wynika wprost z II ZDN:

((((

))))

dt

v

m

d

dt

p

d

F

r

r

r

⋅⋅⋅⋅

====

====

Gdy

F

→

= 0

, to

d p

dt

→

= 0

, czyli

p

Const

→

=

.

Zasada zachowania pędu (ZZP):

ZZP: pęd punktu materialnego, na który nie działa
żadna siła jest wielkością stałą.

306

ZASTOSOWANIE ZASADY ZACHOWANIA PĘDU

ZDERZENIA
ZZP obowiązuje w każdym procesie fizycznym, zarówno
w makro-świecie (zjawiska galaktyczne) jak i mikro-
świecie (procesach jądrowych) i nie znane są odstępstwa.

Najłatwiejszymi

przykładami

ilustrującymi

ZZP

są

zderzenia:

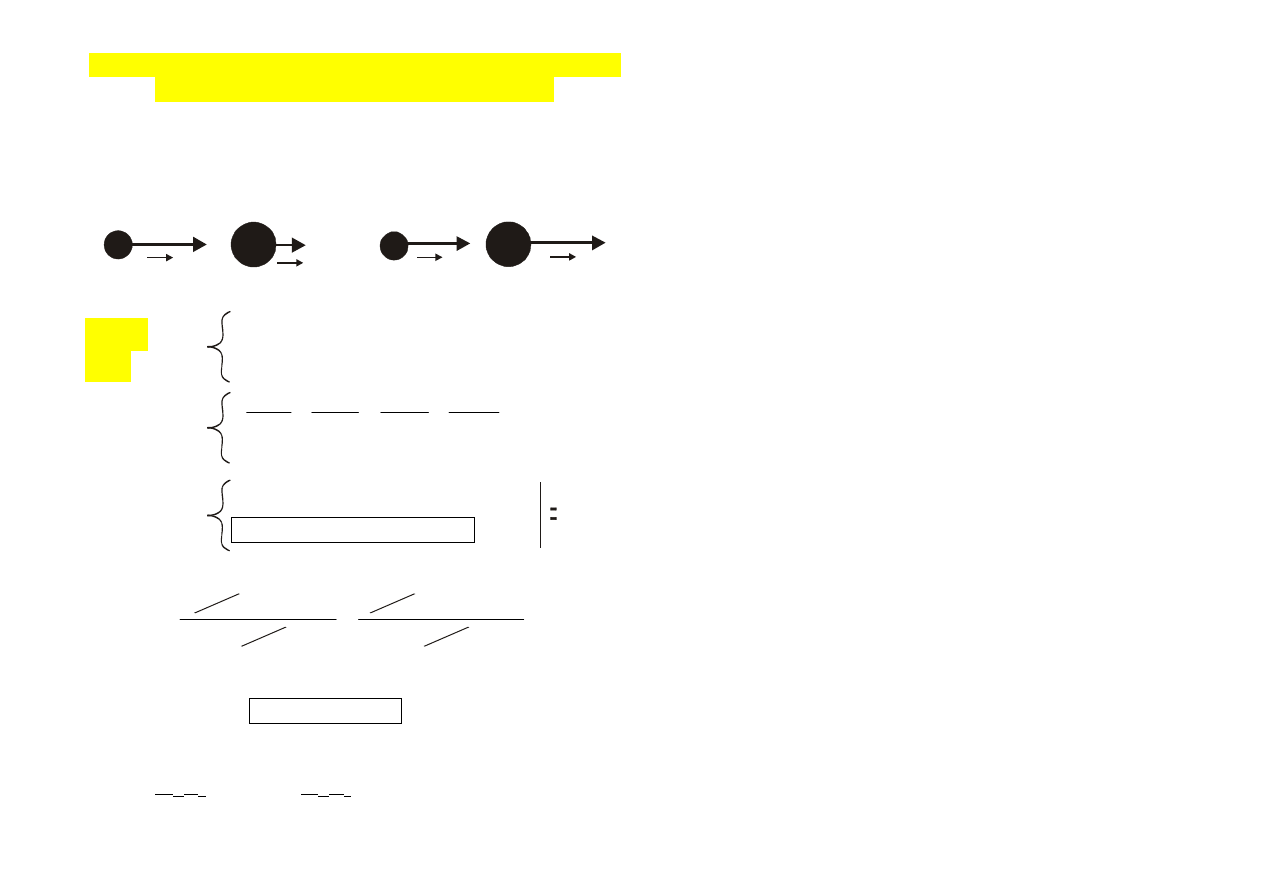
Zderzenia można podzielić:
(I). ze względu na trajektorie ruchu na:

a). centralne - gdy środki kul poruszają się po tej
samej prostej,
b). niecentralne,

(II). ze względu na spełnienie ZZEM na:

a). doskonale sprężyste - gdy cała energia

mechaniczna zderzenia zamienia się na energię
mechaniczną - spełnione są ZZEM + ZZP (+ZZE)

b). niesprężyste - spełnione są ZZP (+ZZE), a nie jest

spełniona ZZEM

c). doskonale niesprężyste - ciała po zderzeniu

poruszają się razem - spełnione są ZZP (+ZZE), a
nie jest spełniona ZZEM.

307

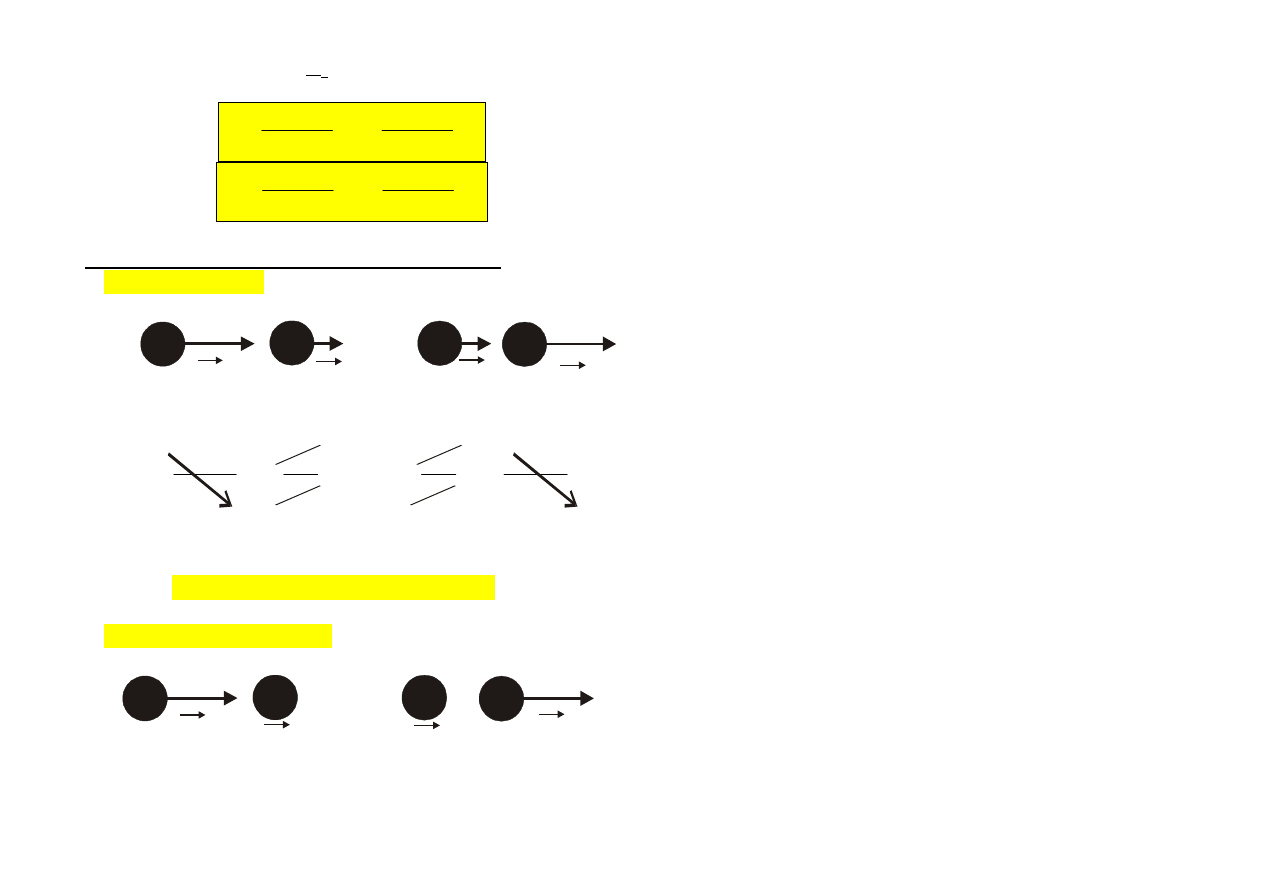
ZDERZENIA CENTRALNE, DOSKONALE SPRĘŻYSTE

W PRZESTRZENI JEDNOWYMIAROWEJ

Dane: masy kul m

1

i m

2

, prędkości przed zderzeniem v

1

i

v

2

. Obl.: prędkości kul po zderzeniu v'

1

i v'

2

?

przed zderzeniem:

po zderzeniu:

v

1

v'

1

v

2

v'

2

Stosujemy:
ZZEM:

∑

∑

=

'
k

k

E

E

,

ZZP:

∑ ∑

=

'

p

p

r

r

.

ZZEM

2

'

v

m

2

'

v

m

2

v

m

2

v

m

2
2

2

2

1

1

2
2

2

2

1

1

+

=

+

, /·2

ZZP: m

1

v

1

+ m

2

v

2

= m

1

v'

1

+ m

2

v'

2

.

Przenieśmy m

1

z lewej strony równań, a m

2

z prawej:

)

v

'

v

(

m

)

'

v

v

(

m

2
2

2
2

2

2

1

2

1

1

−

=

−

,

m

1

(v

1

– v'

1

) = m

2

(v'

2

– v

1

). (*)

Dzieląc ww. równania stronami otrzymujemy:

)

v'

-

(v

)

v'

(v

)

v'

-

(v

)

v'

-

(v

)

v'

(v

)

v'

-

(v

2

2

2

2

2

2

1

1

1

1

1

1

+

⋅

=

+

⋅

,

v

1

+ v'

1

= v

2

+ v'

2

,

a po uporządkowaniu

v'

2

= v

1

+ v'

1

– v

2

(**)

Obl v'

1

odstawiając równanie ** do *:

m

1

(v

1

– v'

1

) = m

2

(v

1

+ v'

1

– v

2

– v

2

),

m

1

v

1

– m

1

v'

1

= m

2

v

1

+ m

2

v'

1

– 2 m

2

v

2

,

308

v

1

(m

1

– m

2

) + 2 m

2

v

2

= v'

1

(m

1

+ m

2

).

Ostatecznie otrzymujemy:

2

2

1

2

1

2

1

2

1

1

v

m

m

m

2

v

m

m

m

m

'

v

⋅

+

⋅

+

⋅

+

−

=

,

2

2

1

1

2

1

2

1

1

2

v

m

m

m

m

v

m

m

m

2

'

v

⋅

+

−

+

⋅

+

⋅

=

.

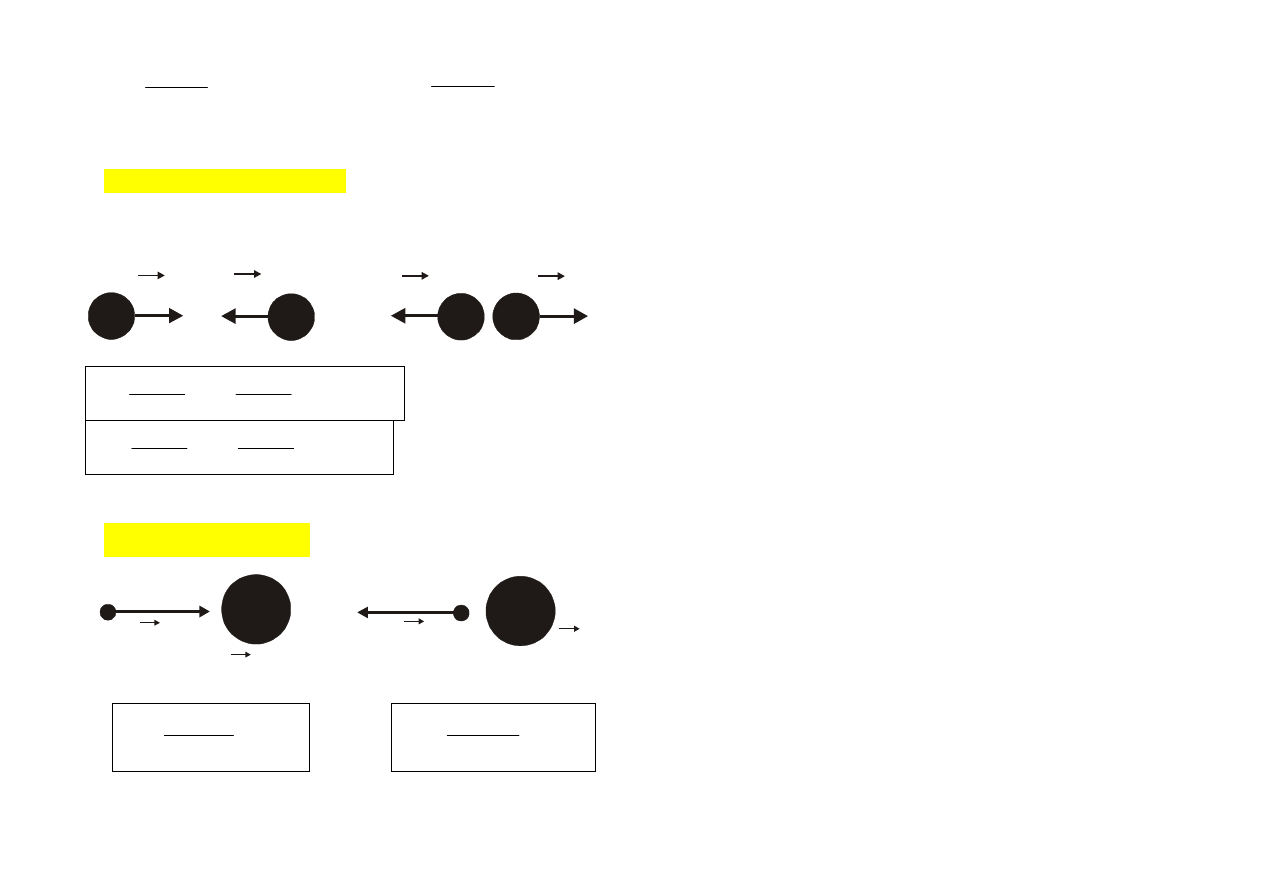
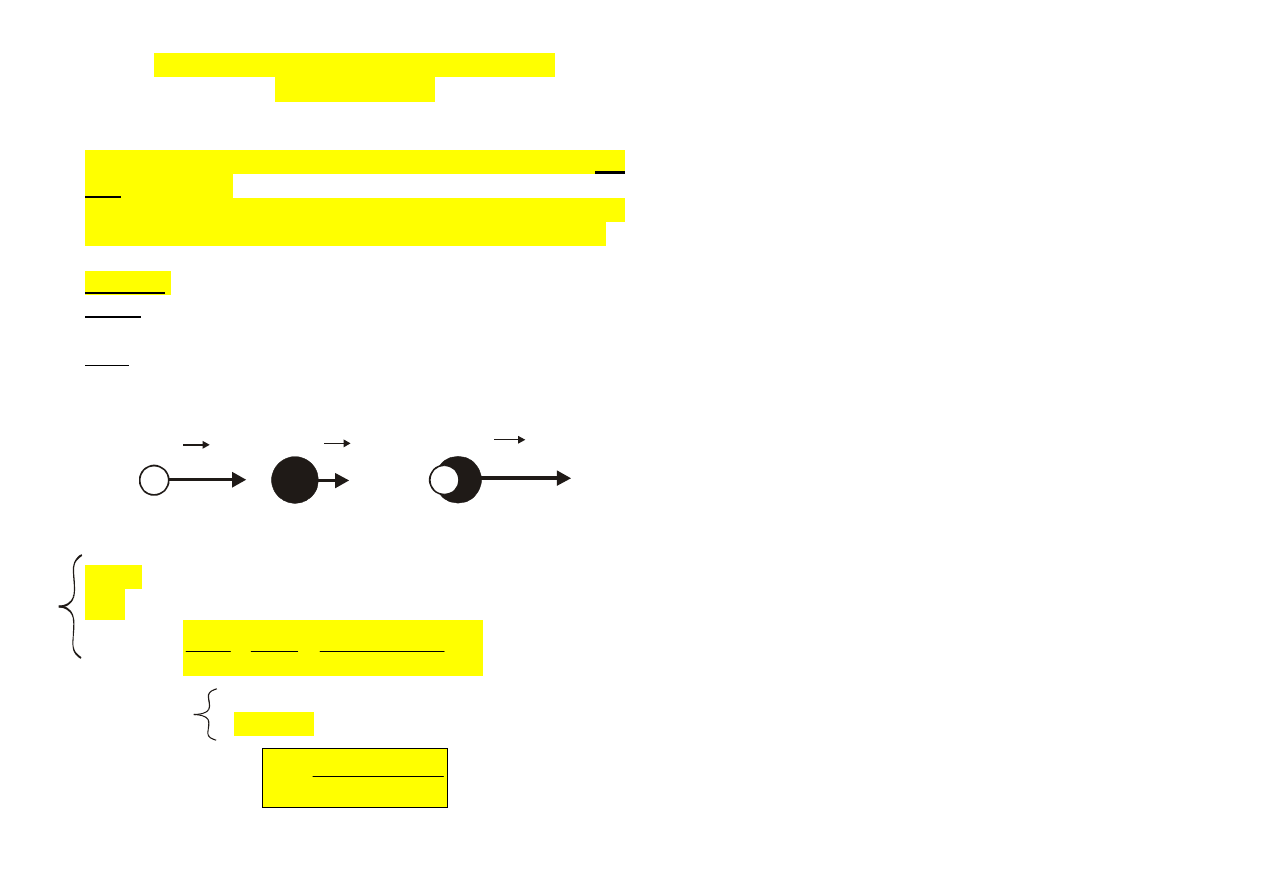
Rozpatrzmy kilka przypadków szczególnych:
● gdy m

1

= m

2

= m

v

1

v'

1

v

2

przed zderzeniem:

po zderzeniu:

v'

2

1

V

r

2

V

r

'

1

V

r

'

2

V

r

2

1

'

1

v

m

2

m

2

v

m

2

m

m

v

+

−

=

,

2

1

'
2

v

m

2

m

m

v

m

2

m

2

v

−

+

=

.

v'

1

= v

2

oraz v'

2

= v

1

czyli cząstki wymieniły się prędkościami.

● gdy m

1

= m

2

= m i v

2

= 0 (obydwa ww. przypadki): 1 stoi

v

1

v'

1

v

2

przed zderzeniem:

po zderzeniu:

v'

2

=0

=0

=0

=0

309

( )

0

v

m

m

m

m

'

v

1

1

⋅

+













+

−

=

oraz

( )

0

v

m

m

m

2

'

v

1

2

⋅

+













+

=

v'

1

= 0 oraz v'

2

= v

1

(wymiana prędkości)

● gdy m

1

= m

2

= m i v

2

=-v

1

(kule uderzają w siebie z

jednakowymi prędkościami skierowanymi przeciwnie):

v

1

v'

1

v

2

przed zderzeniem:

po zderzeniu:

v'

2

(

)

1

1

1

1

v

v

m

m

m

2

v

m

m

m

m

'

v

−

=

−

⋅

+

⋅

+

⋅

+

−

=

,

(

)

1

1

1

2

v

v

m

m

m

m

v

m

m

m

2

'

v

=

−

⋅

+

−

+

⋅

+

⋅

=

.

odbicie z przeciwnymi prędkościami (wymiana prędkości).

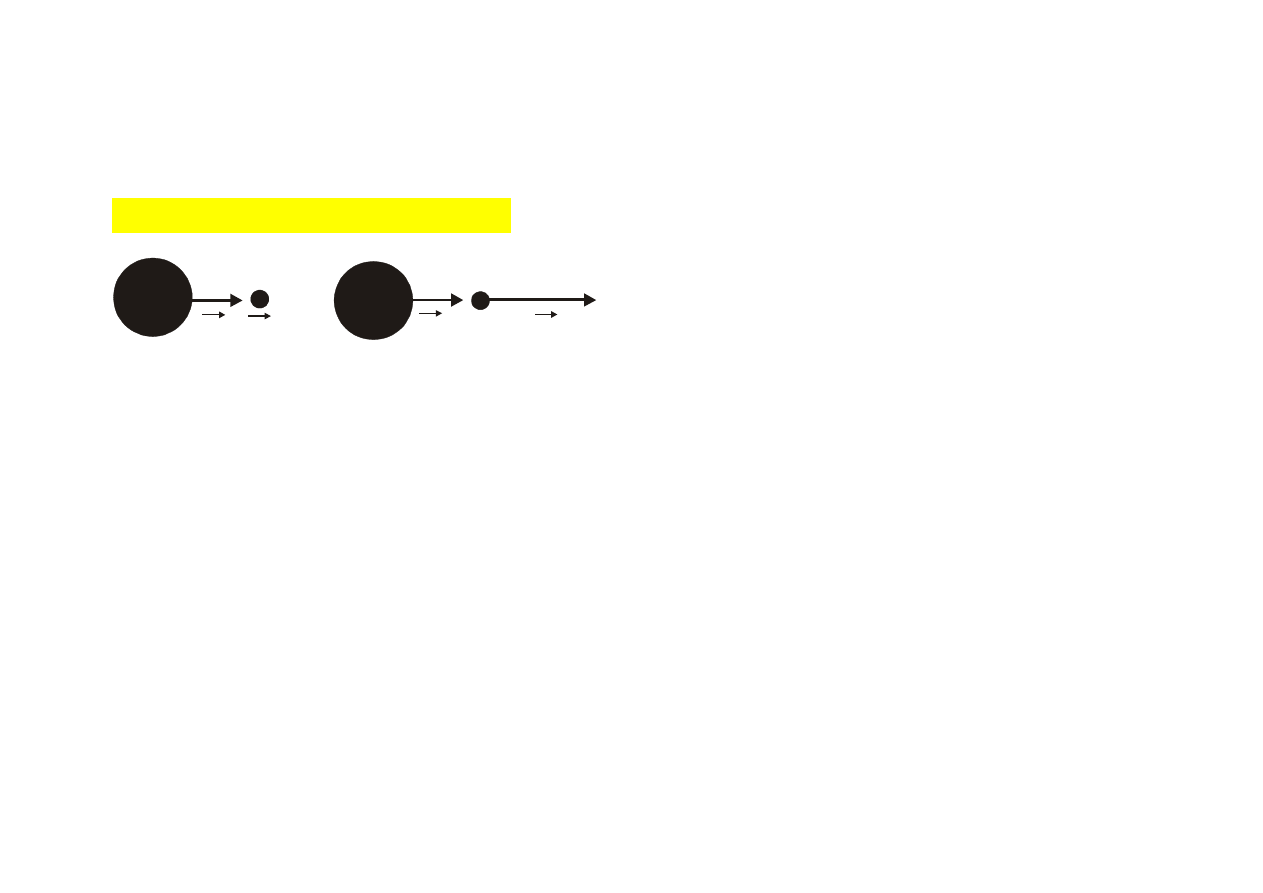
● gdy v

2

=0 i

m

2

>> m

1

(duża nieruchoma masa)

v

1

v'

1

przed zderzeniem:

po zderzeniu:

v'

2

v

2

=0

=0

0

v

m

m

'

v

1

2

1

m

2

1

m

1

+

⋅

+

−

=

, oraz

0

v

m

'

v

1

2

1

m

1

m

2

2

+

⋅

+

=

v'

1

≅

– v

1

oraz

v'

2

≅

0

310

odbicie m

1

od nieruchomego olbrzyma ("zderzenie

pijanego ze ścianą")
Taka sytuacja zachodzi np. przy zderzeniu cząstki
lekkiej z bardzo ciężką (spoczywającą) np. piłka
uderza o ścianę.

•

gdy v

2

=0, ale sytuacja odwrotna m

2

<<

m

1

,

v

1

v'

1

przed zderzeniem:

po zderzeniu:

v'

2

v

2

=0

v'

1

≅

v

1

oraz

v'

2

≅

2 v

1

.

Prędkość cz. ciężkiej (padającej) prawie się nie
zmienia.

311

ZDERZENIA CENTRALNE, DOSKONALE

NIESPRĘŻYSTE

W PRZESTRZENI JEDNOWYMIAROWEJ.

Przy zderzeniach

niesprężystych

energia kinetyczna

nie

jest

zachowana.

Różnica energii kinetycznej (początek – koniec) jest
zamieniana w ciepło lub energię potencjalną deformacji.

Przykład.

Dane: dwie kule z

plasteliny

o masach:

m

1

i

m

2

,

poruszające się z prędk. przed zderzeniem

v

1

i

v

2

.

Obl.: (a). prędkości kul po zderzeniu

v'

1

=

? i

v'

2

=

?

(b). zmianę energii kinet. ∆E

k

= ?

przed zderzeniem:

po zderzeniu:

v

m

m

m + m

1

1

2

2

1

v'

1

v

2

2

Stosujemy:
ZZEM:

nie jest spełniona

ZZP:

∑ ∑

=

'

p

p

r

r

ZZE:

Q

2

'

v

)

m

m

(

2

v

m

2

v

m

2

12

2

1

2
2

2

2

1

1

+

⋅

+

=

+

m

1

v

1

+ m

2

v

2

= (m

1

+ m

2

)

v'

12

Q = ∆E

M

= E

k1

+ E

k2

–E'

k12

2

1

2

2

1

1

12

m

m

v

m

v

m

'

v

+

⋅

+

⋅

=

312













+

⋅

+

⋅

−

⋅

+

⋅

⋅

=

∆

2

1

2

2

2

1

1

2
2

2

2

1

1

M

m

m

)

v

m

v

m

(

v

m

v

m

2

1

E

,

(

)

(

)













+

+

−

+

+

+

⋅

=

∆

2

1

2

2

2

1

1

2
2

2

1

2

2

1

2

1

1

M

m

m

)

v

m

v

m

(

v

m

m

m

v

m

m

m

2

1

E













++++

−−−−

⋅⋅⋅⋅

−−−−

⋅⋅⋅⋅

++++

⋅⋅⋅⋅

⋅⋅⋅⋅

++++

⋅⋅⋅⋅

⋅⋅⋅⋅

++++

⋅⋅⋅⋅

⋅⋅⋅⋅

====

∆

∆

∆

∆

2

1

2

1

2

1

2
2

2
2

2
2

2

1

2

1

2

1

2

1

2

1

M

m

m

...

v

m

v

m

v

m

m

v

m

m

v

m

2

1

E













⋅⋅⋅⋅

⋅⋅⋅⋅

⋅⋅⋅⋅

⋅⋅⋅⋅

−−−−

⋅⋅⋅⋅

−−−−

...

v

v

m

m

2

v

m

...

2

1

2

1

2
2

2
2

Q

)

v

v

(

m

m

m

m

2

1

E

2

2

1

2

1

2

1

M

≡

−

⋅

+

⋅

⋅

=

∆

.

Rozpatrzmy przypadek szczególny:

•

gdy m

1

= m

2

= m

oraz v

1

= –v

2

i zał. v

1

= v (czyli v

2

= –v),

Obl. v'

12

=? oraz ∆E

M

=?

przed zderzeniem:

po zderzeniu:

v

m

m

2m

1

v' =0

1

v

2

2

0

m

2

v

m

v

m

m

m

v

m

v

m

'

v

2

1

2

2

1

1

12

=

⋅

−

⋅

=

+

⋅

+

⋅

=

zatem v'

12

= 0 czyli kule zatrzymają się,

∆E

M

= m v

2

A co to znaczy?

2

2

2

v

m

2

1

v

m

2

1

v

m

Q

⋅

+

⋅

=

⋅

=

lub inaczej Q = (E

k

1 kulki) + (E

k

2 kulki)

313

Wniosek:

"Energia mechaniczna kul całkowicie

zamieniła się w ciepło"

ZDERZENIA W TRZECH WYMIARACH 3-D

Aby rozwiązać zagadnienie 3D musimy rozwiązać

układ równań składający się z:
ZZEM

∑

∑

=

k

k

'

E

E

,

ZZP (kier X)

∑

∑

=

x

x

'

p

p

,

ZZP (kier Y)

∑

∑

=

y

y

'

p

p

,

ZZP (kier Z)

∑

∑

=

z

z

'

p

p

.

ZASADA ZACHOWANIA PĘDU DLA

DYSKRETNEGO UKŁADU PUNKTÓW

MATERIALNYCH (ZZP DUPM)

Wychodząc z II ZDN dla DUPM:

∑

=

=

=

n

i

1

i

s

zi

dt

p

d

F

r

r

,

gdy

∑

=

=

=

n

i

1

i

zi

0

F

r

to

0

dt

p

d

s

=

r

, a zatem

.

Const

p

s

=

r

ZZP:
Gdy na dyskretny układ punktów materialnych nie
działają żadne siły zewnętrzne, lub siły te równoważą
się, to pęd środka masy układu odosobnionego jest
stały.

314

ZASADA ZACHOWANIA PĘDU DLA UKŁADU

ZE ZMIENNĄ MASĄ - NAPĘD ODRZUTOWY

Dotychczas zajmowaliśmy się układami o stałej masie.

Obecnie zajmiemy się układami, których masa zmienia
się podczas obserwacji.

= 0

V

K

V

U

V

Ł

Idea - ZZP:

L

L

K

K

v

m

v

m

r

r

⋅⋅⋅⋅

====

⋅⋅⋅⋅

(gdzie Ł - łódka, K - "Student")
np:

1. odrzut karabinu,
2. samolot odrzutowy (wyrzut sprężonych, produktów

spalania: paliwa i powietrza),

3. napęd rakietowy (j.w., ale rakieta wiezie ze sobą

utleniacz O

2

).

315

Przykład (K.R. 2.33)

Opisać:
a) zmianę masy rakiety w czasie

m

r

(t)=?

oraz

b) zmianę prędkości rakiety lecącej pionowo w górę

v

r

(t)=?

,

jeżeli dane są:

m

ro

- masa początkowa rakiety,

u

- względna w stosunku do rakiety prędkość

wyrzucanych produktów spalania,

µ

- szybkość zużycia produktów spalania = szybkości

zmiany (ubytku) masy rakiety µ = dm

r

/dt [kg/s].

Założyć, że prędkość produktów spalania

v

s

= v

r

– u

jest

stała w czasie

v

s

(t)=Const

. Pominąć opór powietrza.

Przyjmijmy oznaczenia:

r

- rakieta,

s

- produkty spalania

(spaliny).

(a)

. Jeżeli w pewnym przedziale czasowym

dt

z rakiety wyrzucona zostaje masa

dm

s

z

prędkością

u

to masa rakiety maleje o

dm

r

,

przy czym

t

d

m

d

t

d

m

d

r

s

−

=

=

µ

t

m

t

dt

dm

m

)

t

(

m

m

0

r

r

0

r

r

r

⋅

µ

−

=

⋅

−

=

=

(b).

Obl

v

r

(t) = ?

F

r

= F

s

– F

G

(*) (inaczej

∑

= 0

F

i

r

)

Obl.:

F

r

=?, F

s

=?, F

G

=?

F

G

F

s

s

v

s

dm

316

)

v

m

(

dt

d

)

p

(

dt

d

F

r

r

r

r

⋅

=

=

dt

dv

m

v

dt

dm

F

r

r

r

r

r

++++

⋅⋅⋅⋅

====

)

p

(

dt

d

F

s

s

−

=

znak (-) bo

s

F

r

↑ w górę, a

s

v

r

↓ w dół

=

⋅

−

=

)

v

m

(

dt

d

F

s

s

s

,

ale v

s

=Const oraz v

s

= v

r

– u

dt

dm

)

u

v

(

dt

dm

v

F

r

r

s

s

s

−

⋅

−

−

=

⋅

−

=

dt

dm

)

u

v

(

F

r

r

s

⋅

−

=

g

m

F

r

G

⋅

=

Podstawiając w.w. składniki do (*) (

F

r

= F

s

– F

G

):

g

m

dt

dm

)

u

v

(

dt

dv

m

v

dt

dm

r

r

r

r

r

r

r

⋅

−

⋅

−

=

⋅

+

⋅

,

g

m

dt

dm

u

dt

dm

v

dt

dv

m

v

dt

dm

r

r

r

r

r

r

r

r

⋅

−

⋅

−

⋅

=

⋅

+

⋅

,

II ZDN dla ruchu rakiety:

g

m

dt

dm

u

dt

dv

m

r

r

r

r

⋅

−

⋅

−

=

⋅

g

m

dt

dm

u

dt

dv

m

r

r

r

r

⋅

−

⋅

−

=

⋅

/·dt/m

r

dt

g

m

dm

u

dv

r

r

r

⋅

−

⋅

−

=

, /

∫

∫

∫

∫

⋅

−

⋅

−

=

=

t

0

m

m

r

r

v

0

r

r

dt

g

m

dm

u

dv

v

r

0

r

r

,

t

0

m
m

r

r

]

t

g

)]

m

ln(

u

v

r

r

0

⋅

−

⋅

−

=

,

317

)

t

(

v

t

g

m

m

ln

u

v

r

0

r

r

r

=

⋅

−













⋅

−

=

,













=













−

r

0

r

0

r

r

m

m

ln

m

m

ln

oraz

t

m

m

0

r

r

µ

−

=

.

R-nie ruchu rakiety:

t

g

t

m

m

ln

u

)

t

(

v

0

r

0

r

r

⋅⋅⋅⋅

−−−−













⋅⋅⋅⋅

µ

µµ

µ

−−−−

⋅⋅⋅⋅

====

.

Przeanalizujmy to r-nie (warunki brzegowe):

dla t=0

0

0

g

m

m

ln

u

)

0

t

(

v

0

r

0

r

r

====

⋅⋅⋅⋅

−−−−













⋅⋅⋅⋅

====

====

(

0

1

ln

a

a

ln

=

=













)

dla t ↑

t

g

t

m

m

ln

u

)

t

(

v

0

r

0

r

r

⋅⋅⋅⋅

−−−−













⋅⋅⋅⋅

µ

µµ

µ

−−−−

⋅⋅⋅⋅

====

1 składnik - r-nie typu:













−

=

x

1

1

ln

y

2 składnik - r-nie liniowe:

x

a

y

⋅

=

RAZEM:

x

a

x

1

1

ln

y

⋅

−













−

=

318

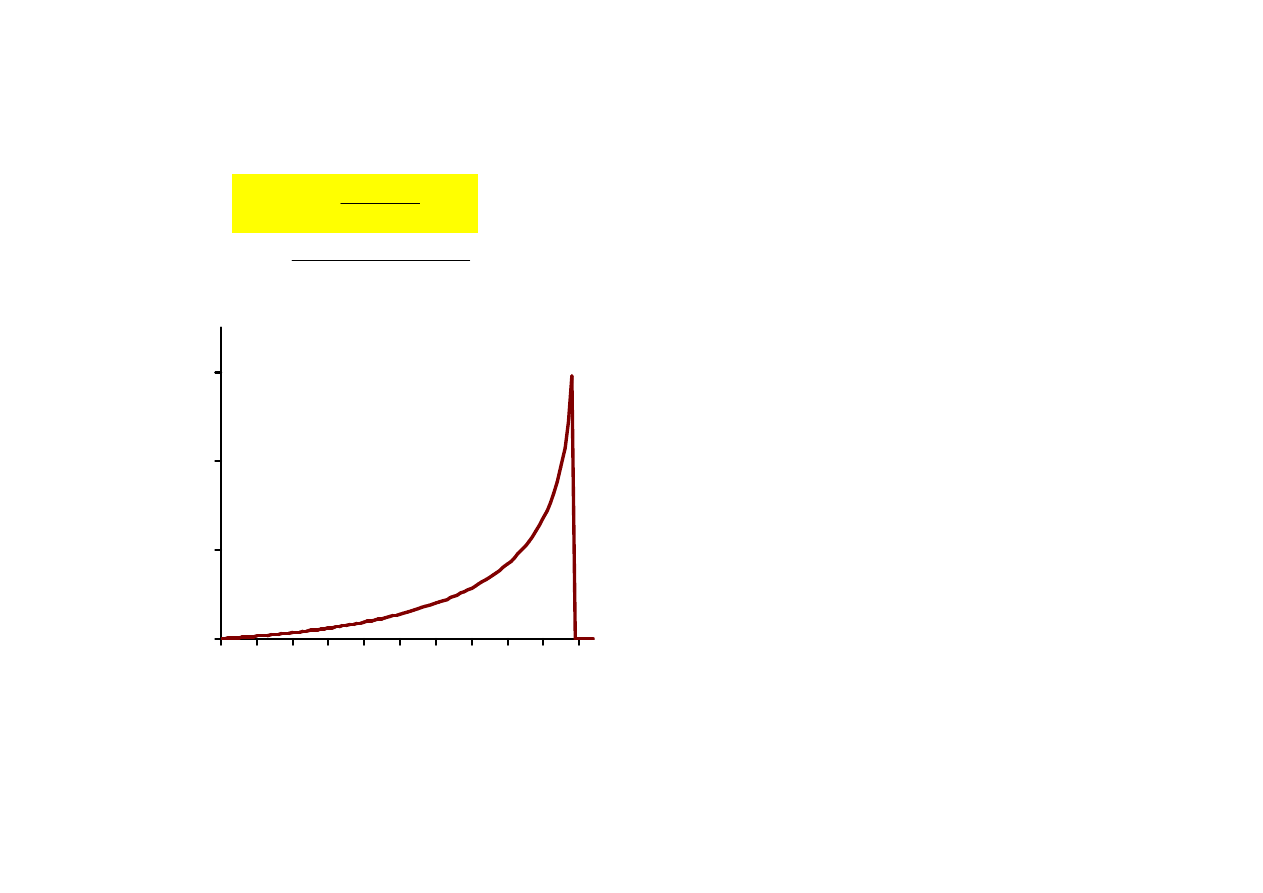
Przykład

Obl.

prędkość

rakiety

o

masie

początkowej

m

r0

=15 000 kg

, gdy szybkość spalania paliwa wynosi

µ=150 kg·s

-1

, a prędkość wyrzucania gazów względem

rakiety jest równa

u=1500 m·s

-1

.

t

g

t

m

m

ln

u

)

t

(

v

0

r

0

r

r

⋅⋅⋅⋅

−−−−













⋅⋅⋅⋅

µ

µµ

µ

−−−−

⋅⋅⋅⋅

====

t

s

m

81

,

9

t

s

kg

150

kg

15000

kg

15000

ln

s

m

1500

)

t

(

v

2

1

1

r

⋅

⋅

−













⋅

⋅

−

⋅

⋅

=

−

−

−

0

2000

4000

6000

1

21

41

61

81

101

t [s]

v

r(

t)

[

m

/s

]

319

CZY TO JEST POPRAWNE?

Przecież rakieta musi posiadać swoją masę własną, np.:
m

rw

=5000 kg

powinno być:

t

m

m

t

dt

dm

m

m

)

t

(

m

m

rw

0

r

r

rw

0

r

r

r

⋅

µ

−

−

=

⋅

−

−

=

=

t

g

m

m

m

ln

u

)

t

(

v

rw

0

r

r

r

⋅

−













−

⋅

−

=

t

g

t

m

m

m

m

ln

u

)

t

(

v

rw

0

r

rw

0

r

r

⋅

−













⋅

µ

−

−

−

⋅

=

t

s

m

81

,

9

t

s

kg

150

kg

5000

kg

15000

kg

5000

kg

15000

ln

s

m

150

)

t

(

v

2

1

1

r

⋅

⋅

−













⋅

⋅

−

−

−

⋅

⋅

=

−

−

−

0

2000

4000

6000

1

21

41

61

81

101

t [s]

v

r(

t)

[

m

/s

]