
Gaz
Gaz
najprostszy stan materii
najprostszy stan materii
nie ma kształtu, objętości ani swobodnej
nie ma kształtu, objętości ani swobodnej
powierzchni
powierzchni
wypełnia przestrzeń
wypełnia przestrzeń
cząsteczki gazu s
cząsteczki gazu są
ą znacznie od siebie
znacznie od siebie
oddalone
oddalone
oddalone
oddalone
poruszają się niezależnie po torach w
poruszają się niezależnie po torach w
niewielkim stopniu zaburzonych prze
niewielkim stopniu zaburzonych przez
z
oddziaływania
oddziaływania
międzycząsteczkowe
międzycząsteczkowe
i temperaturę
i temperaturę T
T

Stan gazu
Stan gazu
Stan gazu
Stan gazu –
– jest
jest określony przez parametry
określony przez parametry
stanu:
stanu:
objętość
objętość V
V, liczbę moli
, liczbę moli n
n, ciśnienie
, ciśnienie p
p i temperaturę
i temperaturę
objętość
objętość V
V, liczbę moli
, liczbę moli n
n, ciśnienie
, ciśnienie p
p i temperaturę
i temperaturę
T
T
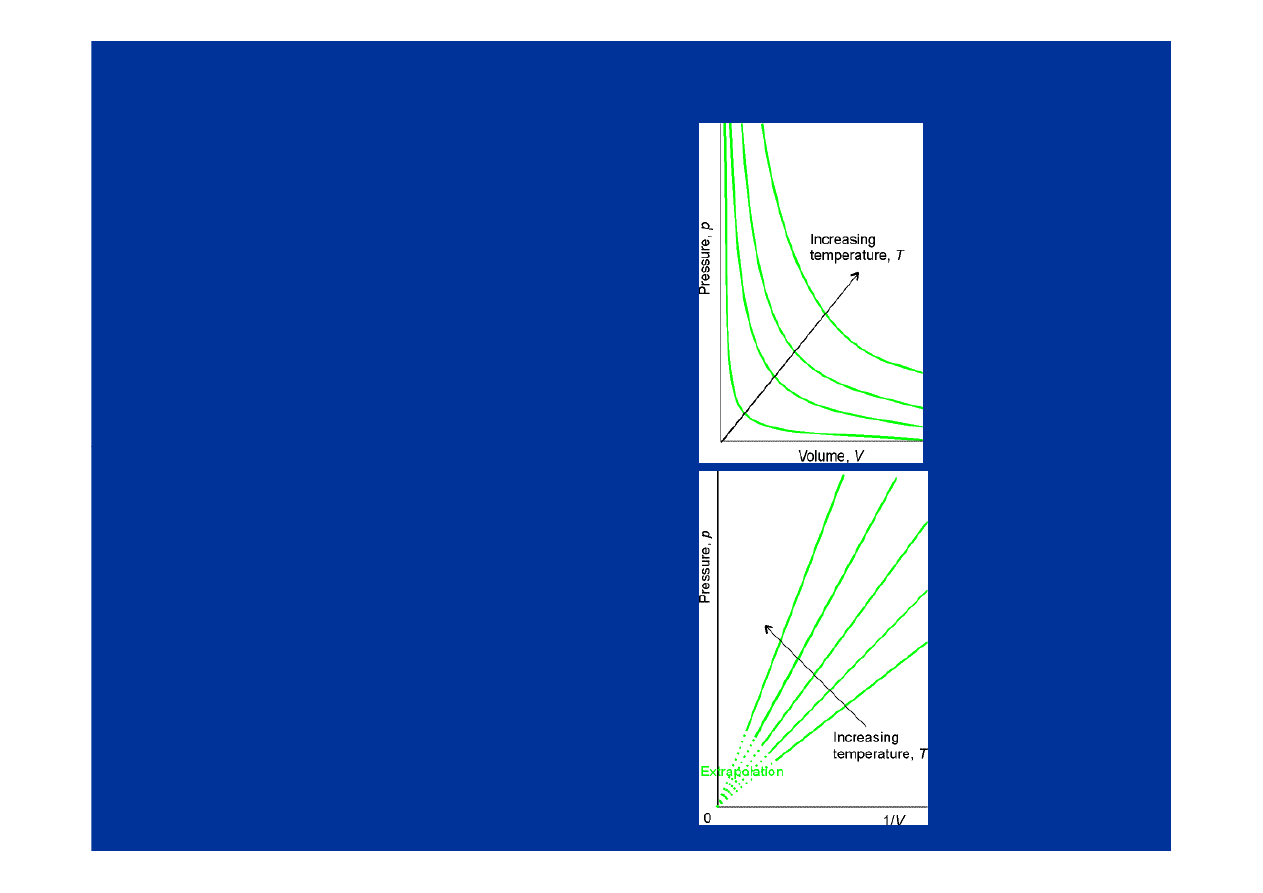
Prawa gazowe
Prawa gazowe
Prawo Boyle’a
Prawo Boyle’a
p V = const
p V = const
gdy T = const
gdy T = const
gdy T = const
gdy T = const
V/m
V/m –
– objętość właściwa
objętość właściwa
gazu
gazu

Prawo Charlesa
Prawo Charlesa
V=const *T (pod stałym
V=const *T (pod stałym
ciśnieniem)
ciśnieniem)
Alternatywa parwa
Alternatywa parwa
Charlesa:
Charlesa:
Charlesa:
Charlesa:
p=const *T(przy stałej
p=const *T(przy stałej
objętości)
objętości)
Konkluzja wynikająca z
Konkluzja wynikająca z
rawa Avogadra:
rawa Avogadra:
V=const*n
V=const*n

Równanie stanu gazu doskonałego
Równanie stanu gazu doskonałego
p V = n RT
p V = n RT
R
R –
– uniwersalna stała gazowa
uniwersalna stała gazowa
8,314 J/mol.K lub 1,986
8,314 J/mol.K lub 1,986
cal/mol.K
cal/mol.K
Gdy: p = 1 atm, T = 273 K, to
1 mol gazu zajmuje 22,4 dm3

Oblicz pracę wykonaną przez 1 mol gazu
Oblicz pracę wykonaną przez 1 mol gazu
doskonałego, rozprężającego się izotermicznie od
doskonałego, rozprężającego się izotermicznie od
V
V
p
p
do V
do V
k
k
∫
=
Vk
Vp
pdV
W
dla n=1 mamy p = (RT)/V
dla n=1 mamy p = (RT)/V
p
k
Vk
Vp
V
V
RT
V
dV
RT
W
ln
∫
=
=
Uwaga: przy rozprężaniu – praca jest dodatnia
przy sprężaniu – praca jest ujemna

Ciśnienie
Ciśnienie
(siła
(siła
wywierana
wywierana na jednostkę powierzchni)
na jednostkę powierzchni)
jednostka (SI) 1
jednostka (SI) 1 Pa
Pa = 1 N/m
= 1 N/m
2
2
pomiar
pomiar -- manometry cieczowe, membranowe
manometry cieczowe, membranowe
pomiar
pomiar -- manometry cieczowe, membranowe
manometry cieczowe, membranowe
ciśnienie standardowe p
ciśnienie standardowe p
0
0
=10
=10
5
5
Pa=1000 hPa
Pa=1000 hPa
≅≅
1
1 aatm
tm
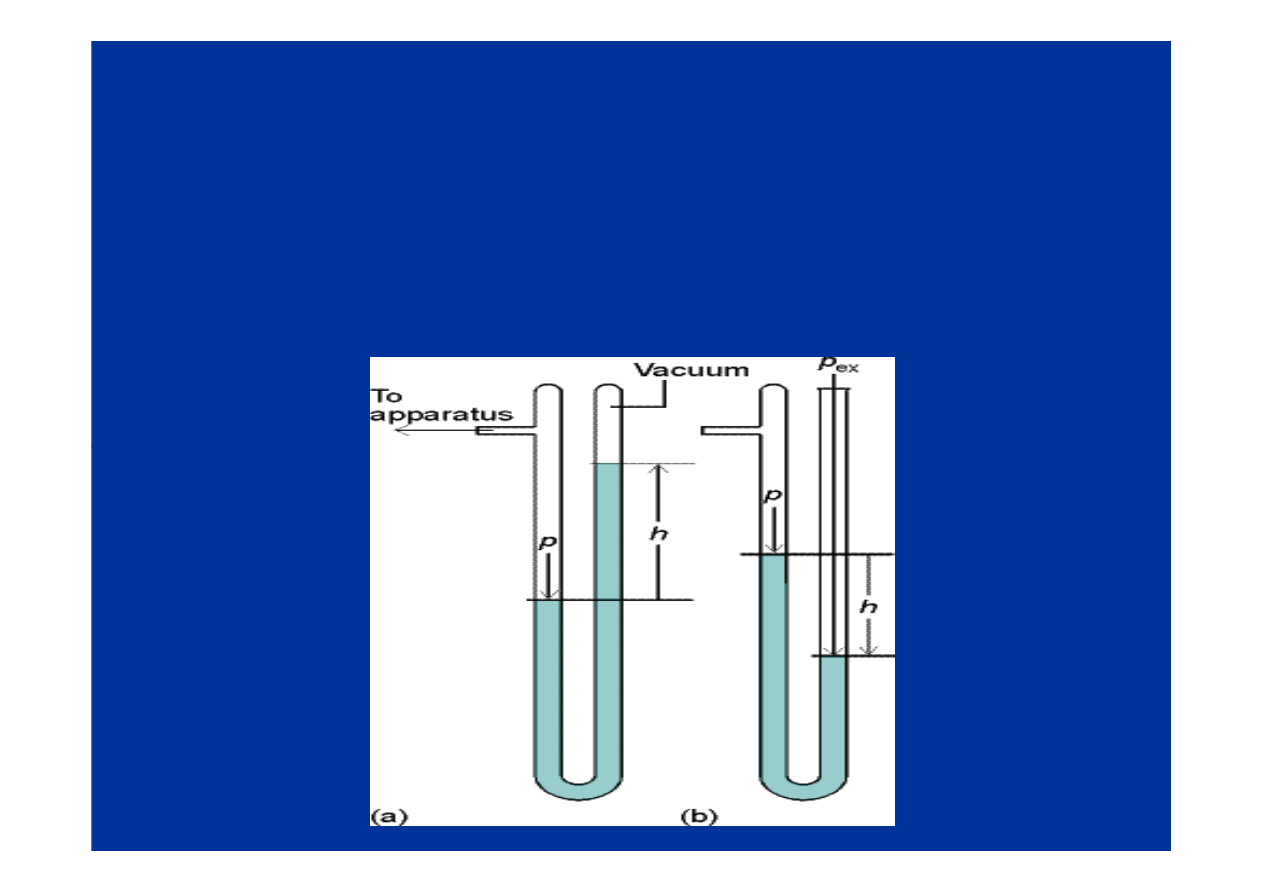
Pomiar ciśnienia
• manometry cieczowe hydrostatyczne,
•manometry hydrauliczne,
•sprężynowe, membranowe
•rurka Bourdona,
•elektryczne, próżniomierze jonizacyjne i in.

Wybrane jednostki ciśnienia
Wybrane jednostki ciśnienia
1 bar = 10
1 bar = 10
5
5
Pa = 1,02 at
Pa = 1,02 at
= 0,99 atm
= 0,99 atm
1 at
1 at = 1 kG/cm
= 1 kG/cm
2
2
1 atm = 760 Tr = 760 mm Hg
1 atm = 760 Tr = 760 mm Hg
1 psig = 1 funt/cal
1 psig = 1 funt/cal
2
2
1 psia = 1
1 psia = 1 funt/cal
funt/cal
2
2
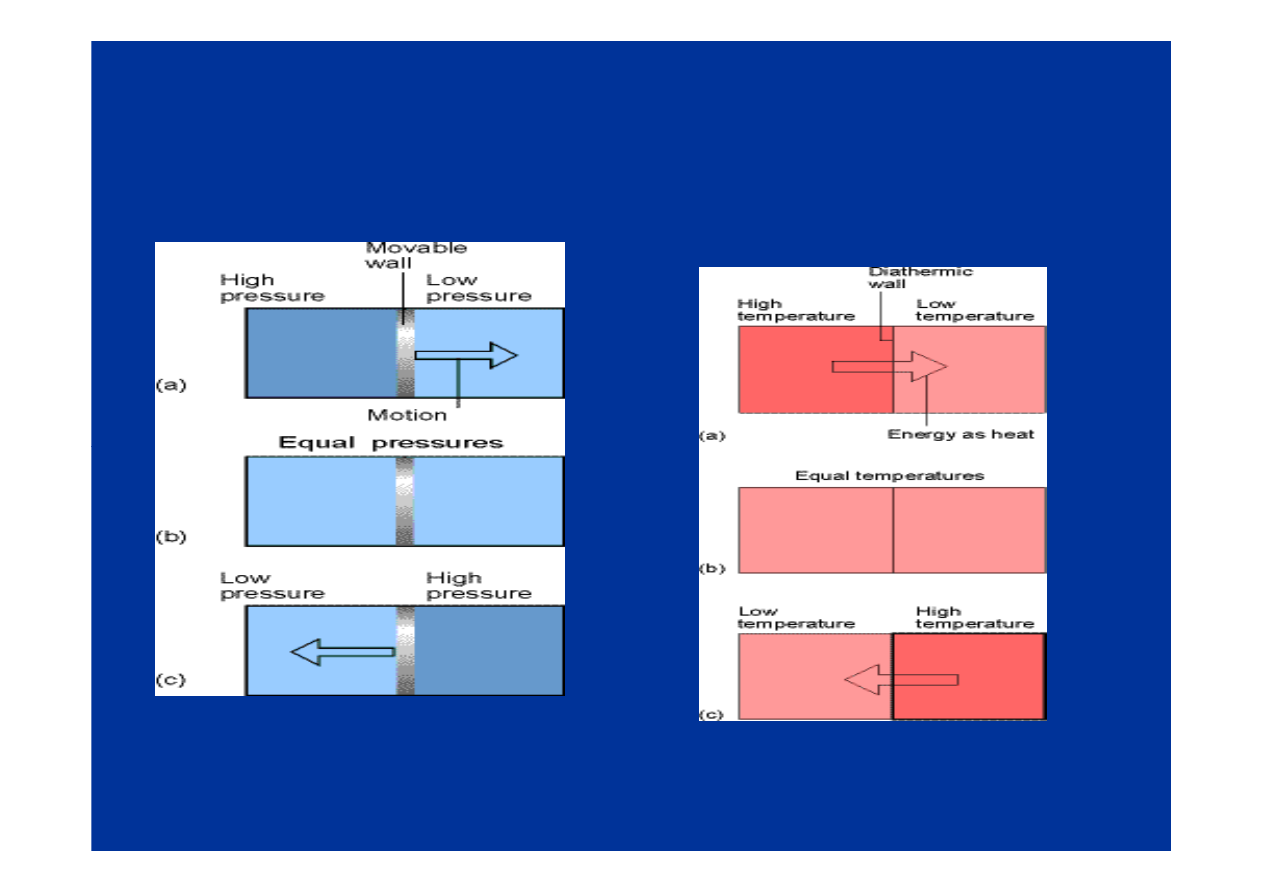
Równowaga mechaniczna - równość ciśnień
•
dowód - na podstawie II zasady termodynamiki
Równowaga termiczna - równość temperatur
Temperatura - z (obserwacji) - określa kierunek przepływu
ciepła (dokładna definicja I i II zasady termodynamiki)

Zerowa zasada termodynamiki
T
A
=T
B
& T
A
= T
C
⇒
T
B
= T
C
Jeżeli ciało A jest w termicznej
równowadze z ciałem B, a B jest
w termicznej równowadze
w termicznej równowadze
z ciałem C, to ciało A jest w
Równowadze termicznej z ciałem C
(tzw. gazowa skala temperatury)
Skale temperatury:
Termodynamiczna -
K
Celsjusza -
0
C
Fahrenheita
-
0
F
T (K) = t (
o
C) + 273,15
t (
o
C) = 5/9 [T(
o
F) – 32]

Mieszaniny gazów
Prawo Daltona:
Ciśnienie wywierane przez mieszaninę gazów doskonałych jest sumą
ciśnień cząstkowych wywieranych przez poszczególne składniki
mieszaniny
V
RT
n
V
RT
n
V
RT
n
p
p
p
B
A
B
A
=
+
+
=
+
+
=
K
K
n
n
x
x
x
n
n
n
i
i
B
A
B
A
=
=
+
+
=
+
+
,
1
,
K
K
ułamki molowe
n
x
x
x
n
n
n
i
B
A
B
A
=
=
+
+
=
+
+
,
1
,
K
K
ułamki molowe
p
x
p
J
J
=
słuszne również dla gazów rzeczywistych

Ułamki molowe i ciśnienia cząstkowe
Ułamki molowe i ciśnienia cząstkowe
Ułamek molowy x
Ułamek molowy x
JJ
w mieszaninie
w mieszaninie –
– jest to ilość (liczba moli) cząsteczek J
jest to ilość (liczba moli) cząsteczek J
wyrażona jako ułamek całkowitej ilości cząsteczek w próbce
wyrażona jako ułamek całkowitej ilości cząsteczek w próbce
xx
J
J
=n
=n
JJ
/n; n= n
/n; n= n
A
A
+ n
+ n
B
B
+…
+…
Przykład:
Przykład:
W mieszaninie zawierającej 1.0 mol N
W mieszaninie zawierającej 1.0 mol N
2
2
i 3mole H
i 3mole H
2
2
, ułamek molowy N
, ułamek molowy N
2
2
wynosi
wynosi
0.25, a H
0.25, a H
2
2
wynosi 0.75.
wynosi 0.75.
xx
A
A
+ x
+ x
B
B
+…=1
+…=1
Wyszukiwarka
Podobne podstrony:
prawa gazowe, chemia - liceum
Prawa gazowe 2 id 385360 Nieznany
chemia ogólna quiz ekolokwium e kolokwium, prawa gazowe, prawa gazowe
prawa gazowe
wyklad 1 prawa gazowe
prawa gazowe (2)
cw prawa gazowe
Prawa gazowe
cw. 2. Prawa gazowe, Pielęgniarstwo, farmakologia, Nauka
Egzamin - sciagi, 27. Prawa gazowe i termodynamika, 27
Prawa gazowe, INNE PRAWA DOTYCZĄCE GAZÓW
04 Podstawowe prawa gazowe
3 prawa gazowe
prawa gazowe, chemia - liceum
Prawa gazowe 2 id 385360 Nieznany
więcej podobnych podstron