2. Opis teoretyczny:
Prawo powszechnego ciążenia:
Dwa punkty materialne o masach m1 i m2 przyciągają się wzajemnie siłą proporcjonalną do iloczynu ich mas i odwrotnie proporcjonalną do kwadratu odległości między nimi r.
m ⋅ m
m 2
F = G 1 2 gdzie G jest stałą grawitacji i wynosi: G=6,67⋅10−11[ N
] .
r 2
kg 2
Powyższe prawo zostało sformułowane przez Izaaka Newtona w 1687r. Wynika ono z obserwacji astronomicznych oraz z wielu eksperymentów przeprowadzonych na ziemi. Stała grawitacji nie zależy od rodzaju ciał jest uniwersalna.
Ciała rozciągłe o skończonych rozmiarach traktujemy jako układ punktów materialnych. Siły przyciągania między takimi ciałami oblicza się przez całkowanie prawa powszechnego ciążenia dla punktów materialnych. Mówi się, że:
Jednorodne ciała kuliste oraz ciała złożone z jednorodnych warstw kulistych, przyciągają się tak
jak punkty materialne umieszczone w ich środkach.
Sposób wyznaczenia stałej grawitacji:
Słynny fizyk Cavendish uważał, że potrafi wyznaczyć stałą G o wiele dokładniej niż zrobił to Newton. Potrzebował do tego jedynie układu, za pomocą którego będzie mógł udowodnić, że wszystkie ciała przyciągają się do siebie siłą grawitacyjną niezależnie od masy i gęstości Ziemi.
Taką możliwość dał mu układ pomiarowy zwany wagą Cavendisha.
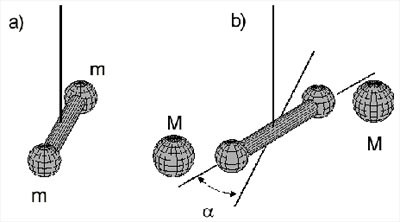
Pierwotnie była to równoważnia zawieszona na linie z włókna kwarcowego, na jej obu końcach umieszczone były stosunkowo małe masy (kule). Wykorzystał on fakt, że siła potrzebna do skręcenia długiego, cienkiego włókna kwarcowego o kilka stopni jest bardzo mała.
Cavendish najpierw wykalibrował włókna, a następnie zawiesił na nich pręt z dwiema małymi kulkami ołowianymi na końcach (rysunek_a). Następnie w pobliżu każdej z kulek umieścił większą kulę ołowianą i zmierzył precyzyjnie kąt o jaki obrócił się pręt (rysunek_b).
Ważenie Ziemi
Mając już godną zaufania wartość G, Cavendish wyznaczył masę Ziemi z równania: gR 2
M =
z
z
G
Wynik pomiaru jest równie dokładny jak wyznaczenia stałej G.
Cavendish wyznaczył też masę Słońca, Jowisza i innych planet, których satelity zostały zaobserwowane. Np. niech M. będzie masą Słońca, a m masą planety krążącej wokół Słońca np.
Ziemi. Wtedy:
GM
M =
z
z
FR 2
gdzie R- to odległość Ziemi od Słońca.
1
1. Odczytałam położenie plamki świetlnej na skali wychyleń, następnie poprosiłam prowadzącego zajęcia o przesunięcie kul na pierwsze skrajne położenie.
2. W odstępach 30-sekundowych zapisywałam kolejne położenia plamki na skali wychyleń.
Pomiarów dokonywałam w czasie 30 minut.
3. Poprosiłam prowadzącego zajęcia o przesunięcie kul na drugie skrajne położenia i również w ostępach 30-sekundowych zapisywałam kolejne położenia plamki w czasie 30 minut.
4. Obliczenia:
We wszystkich poniższych obliczeniach korzystam z wykresu zawartego w sprawozdaniu oraz z tabeli pomiarowej zawartej na pierwszej stronie.
b + b
1
3 + b
Korzystam ze wzoru:
2
b
b
b
2
b
1
2
3
=
=
+
+
aby obliczyć położenie środka wahań b01 i
01
2
4
2
4
b02, dla pierwszego i drugiego ustawienia dużych kul.
Obliczyłam położenie środka dla pierwszego skrajnego położenia: 24,8 21,0
24,2
b =
=22,75 cm
01
4
2
4
b1 = 24,8 cm, b2 = 21,0 cm, b3 = 24,2 cm, gdzie b1,b2, b3 są wartościami minimalnymi i maksymalnymi wychylenia dla pierwszego skrajnego położenia. Odczytałam te wartości z wykresu.
Obliczyłam położenie środka dla drugiego skrajnego położenia: 22,1 19,5 21,7
b =
=20,7 cm
02
4
2
4
b1 = 22,1 cm, b2 = 19,5 cm, b3 = 21,7 cm, gdzie b1,b2, b3 są wartościami minimalnymi i maksymalnymi wychylenia dla drugiego skrajnego położenia. Odczytałam te wartości z wykresu.
Obliczyłam różnice ze wzoru: b01 – b02 = ∆b
∆ b=22,75−20,7=2.05 cm .
A⋅ ∆b
π 2⋅ r 2⋅ d
Następnie stosując wzór G=
, gdzie A=
przystąpiłam do obliczenia stałej
T 2
M⋅ L
grawitacji przyjmując, że:
r = 0, 047 m (odległość pomiędzy środkami mas M i m) d = 0,05 m (odległość małej kulki m od osi obrotu) Δb = 0,0205 m (środek wahań)
M = 1,5 kg (masa dużej kuli M)
T = 10 min = 600 s (można go odczytać z wykresu oraz tabeli) L = 0, 86 m (odległość zwierciadełka od ekranu) 2
π 2⋅ r 2⋅ d⋅ ∆b Podstawiając A do wzoru na G: G=
.
M⋅ L⋅ T 2
0,002209⋅9,8696⋅0,05⋅0,0205
Otrzymałam: G=
=7,81236761⋅10−11 N⋅ m 2
1,5⋅360000⋅0,86
kg 2
Następnie obliczyłam masę Ziemi na podstawie otrzymanej przeze mnie stałej grawitacji: gR 2
m
M =
z
gdzie: g = 9,81
, R =6,37⋅106 m , G=7,81236761⋅10−11 N⋅ m 2
z
z
G
s 2
kg 2
9,81⋅6,37⋅1062
M =
=5,14⋅1024 kg
z
.
7,81236761⋅1011
5. Analiza błędu:
Na podstawie wykresu drgań wahadła oszacowałam niepewność wyznaczenia okresu u(T) oraz oszacowałam dokładność z jaką można wyznaczyć poszczególne wartości b1, b2, b3 (na podstawie punktów w najbliższym otoczeniu maksimów i minimów) i następnie obliczyłam niepewność wyznaczenia wartości u(∆b).
b1 – b6 były wyznaczane z dokładnością 0, 1 cm zatem u(∆b)=2∙0,1=0,2 cm Okres T odczytywany z wykresu oraz tabeli wynosił T = 10 min = 600 s z dokładnością u(T) = 30s.
Zakładając że: M, L, d, r – są stałe i nie mają wpływu na moje obliczenia, wyliczyłam niepewność u(G) ze wzoru:
u G u ∆b
u T
u T
=
2
==> u G= G⋅ u ∆b2
.
G
∆b
T
∆b
T
Podstawiając otrzymane dane otrzymuje niepewność: 30
u G=7,81236761⋅1011 0,002 2
=1,543418967⋅10−11 N⋅ m 2
0,0205
600
kg 2
Ostatecznie uzyskałam wynik: G=7±2⋅10−11 N⋅ m 2 .
kg 2
6. Wnioski:
Uzyskałam wynik na stałą grawitacji: G=7±2⋅10−11 N⋅ m 2 i obliczyłam na jej podstawie masę kg 2
9,81⋅6,37⋅1062
Ziemi: M =
=5,14⋅1024 kg
z
.
7,81236761⋅1011
Otrzymane przeze mnie wyniki są bardzo dobre ponieważ wartości w tablicach fizycznych: m 2
Mz = 5,98 · 1024 kg oraz G=6,67⋅10−11[ N
] znajdują się w zakresie niepewności
kg 2
wyznaczonej wartości.
Jakiekolwiek błędy przy pomiarach mogły wyniknąć z faktu, że moją skalą wahań była linijka wisząca na nitkach, której dotknięcie mogło spowodować jej przesunięcie.
3
Wyszukiwarka
Podobne podstrony:
19 sprawko, Studia, Pracownie, I pracownia, 19 Pomiar stałej grawitacyjnej G (ważenie Ziemi), 19 - n
wazenie ziemi
Zew pole grawitacyjne ziemi, Geodezja, Geodezja Wyzsza, Sciagi II
Fiz-pola grawitacyjne, Pierwsza prędkość kosmiczna jest to prędkość jaką należy nadać ciału wyżucone
faza stala, ^ Wydział Nauk o Ziemi UŚ Geografia ZGS, Gleboznawstwo
grawitacja i elementy astronomii bliskie i nieco dluzsze kosmiczne sasiedztwo ziemi
KLIMATY ZIEMI
Na przekor grawitacji
Biomy Ziemi
wyk8 grawitacja
ochrona powierzchni ziemi ppt
Moduł III cz 2 stała i stopien dysocjacji, zobojetnianie
grawitacyjne zageszczanie osado Nieznany
Perły ziemi Swiętokrzyskiej swiętokrzyska przyroda
11 Stała szybkości utleniania
16 Człowiek zmienia powierzchnię Ziemi
więcej podobnych podstron