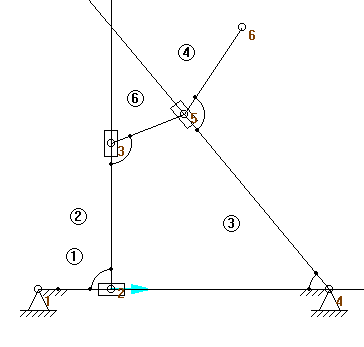
2.Analiza kinematyczna mechanizmu: Dla tego mechanizmu założyłem przyspieszenie członu napędzającego: a=20mm/ s 2

W związku z tym prędkość będzie się zmieniać w funkcji czasu zgodnie ze wzorem: v= a⋅ t=20⋅ t mm / s Przemieszczenie członu napędzającego wyniesie: a⋅ t 2 20⋅ t 2

x=

=

=10⋅ t 2 mm

2

2

Podczas analizy mechanizmu metodą grafo-analityczną badam parametry członów oraz punktów charakterystycznych mechanizmu w chwili t=5s .

Dla tej chwili:

a=20mm/ s 2

v=100mm / s

x=250mm

,gdzie x jest odległością punktu A od początku przyjętego układu współrzędnych, natomiast początkowa prędkość członu napędzającego jest równa zero.

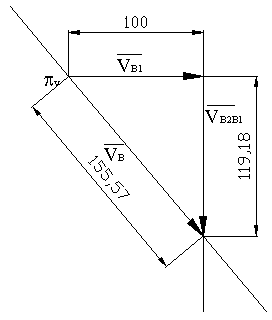
Plan prędkości w mechanizmie:

V A – znany kierunek, znana wartość V B2B1 -znany kierunek, nieznana wartość V B – znany kierunek, szukana wartość V = V

C

B

V = V = V

D

C

B

Plan prędkości został wykreślony przy użyciu pakietu oprogramowania AutoCad2002

LT

Na podstawie następującego równania wektorowego:



V = V   

V

B

B2B1

B1

Dzięki temu nie było nawet konieczne wprowadzanie podziałki.

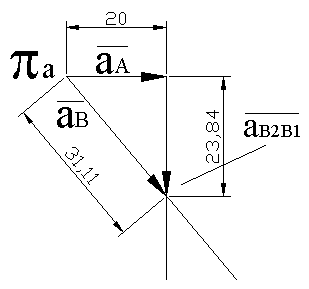
Plan przyspieszeń przedstawia się analogicznie do planu prędkości ponieważ nie występuje tu żaden ruch obrotowy.

Plan przyspieszeń w mechanizmie:

a A – znany kierunek, znana wartość a B2B1 -znany kierunek, nieznana wartość a B – znany kierunek, szukana wartość a = a

C

B

a = a = a

D

C

B

Plan został zrealizowany na podstawie następującego równania:



a = a



B

 B2B1



a B1

Wyznaczone przez program AutoCad wartości odpowiednich prędkości i przyspieszeń mogą być obarczone błędem zaokrągleń przyjętych przez program, jednak błąd ten jest małego rzędu.

Wyznaczenie przyspieszeń i prędkości metodą analityczną.

Metoda analityczna pozwala na wyznaczenie prędkości w dowolnej chwili czasu, a nie tylko w danym położeniu mechanizmu.

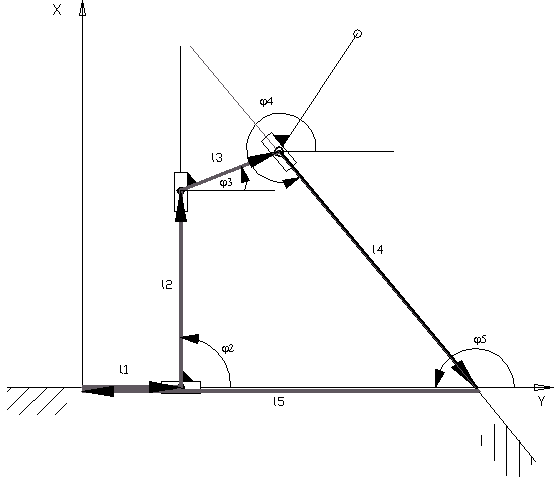
Wrysowując w mechanizm zamknięty wielobok wektorowy otrzymuję równania rzutów poszczególnych wektorów na osie przyjętego układu współrzędnych.

Długości poszczególnych wektorów

l  t=10⋅ t 2

1

l  t= ?

2

l  t=269,2 mm= const 3

l  t = ?

4

l  t=1008,4 mm= const 5

wartości kątów:  =0 o

=90 o

=22 o

=310 o

1

2

3

4

Dwa równania rzutów wektorów na osie pozwolą na wyznaczenie niewiadomych l 2

oraz l 4 ponieważ jest to układ dwóch równań z dwiema niewiadomymi.

 l 1 l 2 l 3 l 4 l 5=0

⇒ Rzut na oś odciętych OX:

l 1 l 3⋅cos3 l 4⋅cos4 – l 5=0

⇒ Rzut na oś odciętych OY:

l 2 l 3⋅sin 3 l 4⋅sin 4=0

Z pierwszego równania mogę bezpośrednio wyznaczyć długość wektora l 4 : l

l = 5 – l 1 t  – l 3⋅cos 3

4

cos 4

Teraz na podstawie równania drugiego wyznaczam długość l 2 : l 2=− l 3⋅sin 3 – l 4⋅sin 4

dl

dl

V = 4 =− 1⋅ 1

B

dt

dt cos 4

dl sin 

V

= 1⋅

4

B2B1

dt cos 4

d l

d l

a = 2 4 =− 2 1⋅ 1

B

dt 2

dt 2 cos 4

d

d

sin 

a

= 2 l 2 = 2 l 1⋅

4

B2B1

dt 2

dt 2 cos 4

Po wstawieniu odpowiednich wartości dla chwili czasu t=5s otrzymuję następujące wyniki: V =−155,57 mm/ s

B

V

=−119,17 mm/ s

B2B1

a =−31,11 mm/ s 2

B

a

=−23,83 mm/ s 2

B2B1

Wyniki niewiele różnią się od tych ktore otrzymałem w metodzie analityczno wykreślnej.

Dodatkowo wykonana symulacja w programie SAM 4.2 potwierdza poprawność wyników

Model mechanizmu w programie SAM 4.2

Podsumowanie wyników:

SAM 4.2

m. analityczno wykreślna

m. analityczna

V B

156mm/s

155,57 mm/ s

155,57 mm/ s

V B2B1

120mm/s

119,18 mm/ s

119,17 mm/ s

a B

-

31,11 mm/ s 2

31,11 mm/ s 2

a

-

B2B1

23,84 mm/ s 2

23,83 mm / s 2