Po
P li
l t
i e
t chn
h ik
i a
k
a Ślą
l s
ą k
s a
k
a w Gli
l w
i ic
i ac
a h
Me
M cha
h n
a ika
k
a Pł
P y
ł nów
Wykład nr 15
„Prz
P e
rz pł
p y
ł w
w cieczy
z prz
p e
rz z
z dłu
d gie kan
a ał
a y
ł .”
„Przepływ cieczy przez długie kanały.”
Wykład 15
Potrzeby techniczne sprawiają konieczność uproszczonych metod obliczeń, w których stosuje się prosty model przepływu, a wszystkie założone zjawiska uwzględnia się wprowadzając korekty empiryczne. Modelem dla przepływu cieczy i gazu w kanałach jest przepływ jednowymiarowy ustalony. Do obliczeń stosuje się równanie z przepływu idealnych, najczęściej w postaci równania Bernoull’ego: 2
2
v
p
v
p
1
1
2
+
+ z =
+
+ z + z .
(15.1)
1
2
str
g
2
γ
g
2
γ
zstr – straty mocy w przepływach rzeczywistych oblicza się ze wzoru :
l v2
z
= λ .
(15.2)
str
d g
2
Czasami zstr wyraża się poprzez ciśnienie :
∆
= β p
z
.
str
µ
(15.3)
Równania te są typowymi przedstawicielami równań mechaniki płynów zwanej hydrauliką. Powszechnie stosowana w obliczeniach rurociągów i najstarszym działaniem mech. płynów.
Takie techniczne układy jak: dysze, dyfuzory zalicza się do działu hydrauliki i stosuje się uproszczone metody obliczeń.
W obliczeniach kanałów i długich przewodów stosuje się :
1. obliczanie strumienia masy lub objętości przy znanej różnicy ciśnień, lub obliczenie potrzebnej różnicy ciśnień dla danego strumienia masy.
•
dm
•
m =
, ∆p = f m .
(15.4)
dt
2. obliczanie średnicy kanału dla danego strumienia lub objętości dla różnej różnicy ciśnień.
•
d = f m, ∆p .
(15.5)
w w w . c h o m i k u j . p l / M a r W a g 9 8 7
„Przepływ cieczy przez długie kanały.”
Wykład 15
METODA OBLICZEŃ PRZEPŁYWU CIECZY W DŁUGICH KANAŁACH
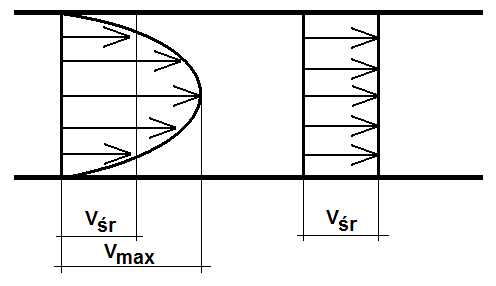
Wiemy, że dla cieczy lepkiej rozkład prędkości obiega od wartości średniej. W tej sytuacji jako prędkość przepływu jednowymiarowego przyjmuje się jako prędkość przepływu prędkość średnią.
Rys. 1
Należy rozważyć jaki błąd się popełnia przy przepływie przez kanały opartych o równanie Bernulli’ego.
Rzeczywista energia płynu przepływającego przez dany przekrój kanału w jednostce czasu czyli rzeczywisty strumień energii rzeczywistej w postaci różniczkowej.
•
1
•
1
•
2
2
d E =
d m V =
d
ξ V v
(15.6)
2
2
•
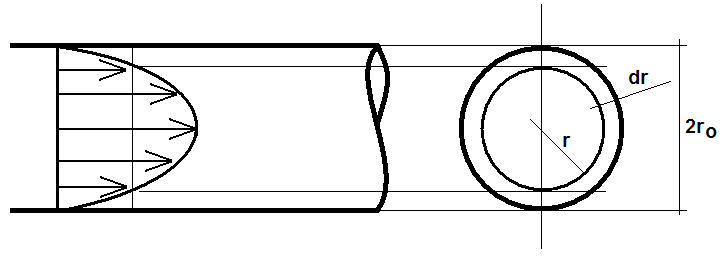
Elementarny strumień objętości d V o przekroju kołowym ϕ = r 2
obliczamy na
0
podstawie poniższego rysunku :
w w w . c h o m i k u j . p l / M a r W a g 9 8 7
„Przepływ cieczy przez długie kanały.”
Wykład 15
Rys. 2
•
d V = 2 r
π *dr * v .
(15.7)
ro
•
2
V = 2π∫ rdr * v = r
π v .
(15.8)
sr
o
sr
0
Gdybyśmy założyli prędkość zależną od promienia r czyli v(r) to wydatek objętości:
•
0
r
V = 2π∫ r(v(r) d
) r .
(15.9)
0
15.7 → 15.6
•
1
3
d E =
ξ2 r
π drv .
(15.10)
2
•
ro
E = πξ
π ∫ 3
rv dr .
(15.11)
0
Gdy strumień energi kinetycznej odniesiemy do prędkości średniej vśr
•
1 •
1
•
2
E =
m v
=
d
ξ V v .
(15.12)
sr
sr
2
2
•
v 2
'
E = π r2 sr
ξ
π
.
(15.13)
2
•
Gdzie V można wyliczyć : (strumień objętościowy)
•
V = A * v .
(15.14)
sr
w w w . c h o m i k u j . p l / M a r W a g 9 8 7
„Przepływ cieczy przez długie kanały.”
Wykład 15
A – przekrój rury
Zatem
•
V
v
=
.
(15.15)
sr
A
Uwzględniając zależność (15.6) można napisać :
r
r
o
o
2π∫ v rdr
2∫ v(r r
) dr
sr
(15.16)
0
0
v
=
=
.
sr
2
2
r
π
r
0
o
Podstawiając vsr do wzoru (15.10) otrzymujemy że :
3
r0
4
πξ
π
∫ v(r r)dr
∫
•
(15.17)
0
'
E =
.
4
ro
•
Otrzymano dwa wyrażenia: jedno E (15.8) dla rzeczywistego rozkładu prędkości i
•
strumień energii '
E dla przyjętego rozkładu prędkości vsr.
Iloraz tych strumieni energii jest nazywany współczynnikiem Coriolisa :
•
α = E
(15.18)
•
'
E
r
r
0
0
4
3
3
r πξ
π ∫rdrv
∫rdrv
2
r
0
0
0
d =
=
3
3
(15.19)
r
r
0
4
0
4
πξ
π ∫ v(r r
) dr
∫
∫ v(r r)dr
∫
0
0
•
Stosunek rzeczywistego strumienia energii kinetycznej E do strumienia energii
•
kinetycznej '
E wynikającej z obliczeń prędkości średniej vśr nosi nazwę wsp. Coriolisa i dla przekroju kołowego wynosi zgodnie z wzorem (15.16) widzimy, że α jest zawsze większa od jedności.
w w w . c h o m i k u j . p l / M a r W a g 9 8 7
„Przepływ cieczy przez długie kanały.”
Wykład 15
Dla ruchu laminarnego α =2
(15.20)
Dla ruchu turbulentnego α =1.1
W przypadku obliczeń pożądane jest uwzględnienie tego współczynnika, gdyż rzeczywista energia kinetyczna wyrażona poprzez prędkość średnią vśr wynosi : v 2
E
= α* sr
(15.21)
rz
2
α
Praktycznie współczynnik
jest uwzględniony tylko wtedy gdy wartość energii kinetycznej jest porównywalny z wartością strat podczas przepływu. W długich kanałach nie mogą być pomijane opory przepływu i stosując równanie bilansu Bernulli’ego piszemy jego postać pół-empiryczną jak to podano wzorami (15.1).
2
2
v
p
v
p
1
1
2
+
+ z =
+
+ z + z .
(15.22)
1
2
str
g
2
γ
g
2
γ
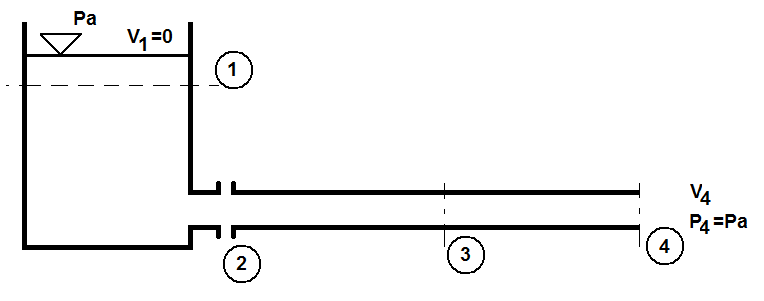
Kanał pojedynczy: najprostszym przykładem przepływu długi kanał o stałym przekroju (często kołowym) ciesz wypływa z zbiornika przez poziomy kanał o Ø=d i dł.=l, na swobodnej powierzchni cieczy ciśnienia pa. Zakłada się w obliczeniach, że w powierzchnia zbiornika A1 jest znacznie większa od przekroju Au wobec czego V1 w zbiorniku przyjmujemy równe 0. Schemat można przedstawić następująco: Rys. 3
Równanie przyjmuje postać:
2
2
v
p
v
p
1
1
2
0 =
+
+ z =
+
+ z + z .
(15.23)
1
2
str
g
2
γ
g
2
γ
w w w . c h o m i k u j . p l / M a r W a g 9 8 7
„Przepływ cieczy przez długie kanały.”
Wykład 15
Otrzymujemy wyrażenie, że poziomu w zbiorniku cieczy : 2
v4
z =
+ z ,
(15.24)
1
str
g
2
l v2
z
4
= λ
.
(15.25)
str
d g
2
Uwzględniając wsp. Coriolisa
v2
l v2
z
4
4
= α
+ λ
.
(15.26)
1
g
2
d g
2
Odnośnie współczynnika λ są różne reguły wyznaczania tego współczynnika, który jest funkcją najczęściej liczby Reynolds’a względnie można go uzyskać na podstawie odpowiednich wykresów, które można znaleźć w podręcznikach hydrauliki dotyczących obliczeń kanałów: np. wzór
0 1
, 6
λ =
.
(15.27)
4 Re
Przepływy laminarne i turbulencyjne – współczynnik strat
– liczba Blasiusa
Prawo Hagena-Poiseuille’a
π
p
∆
4
Q =
*
* d ,
(15.28)
128µ
l
(strata energii) po przekształceniu:
p
∆
64
l
v
h
∆ =
*
* śr
=
,
(15.29)
r
Re
d
2g
v d
Re
śr
=
,
(15.30)
v
v2 l
h
= R
.
(15.31)
str
g
2 d
w w w . c h o m i k u j . p l / M a r W a g 9 8 7
„Przepływ cieczy przez długie kanały.”
Wykład 15
Współczynnik strat na tarcie λ
• dla ruchu laminarnego
64
λ =
,
(15.32)
Re
• dla ruchu turbulentnego λ określa się doświadczalnie wg wzoru Blausiusa
0,316
λ =
,
(15.33)
4 Re
• ogólny wzór laminarnego
bn
1
64
λ = ∑K
=
.
(15.34)
n Re
Re
vd
Istnieje pewna krytyczna wartość Re =
poniżej której ruch kształtuje się jako
v
laminarny a powyżej turbulentny.
Laminarny Rekr1
Laminarny lub Turbulentny Rekr2 Turbulentny Rekr1 = 2340
Rekr2 = 50 000
Współczynnik strat dla ruchu laminarnego są 2 razy mniejsze (dla przepływu laminarnego lub turbulentnego) – przyjmuje się wyższe.
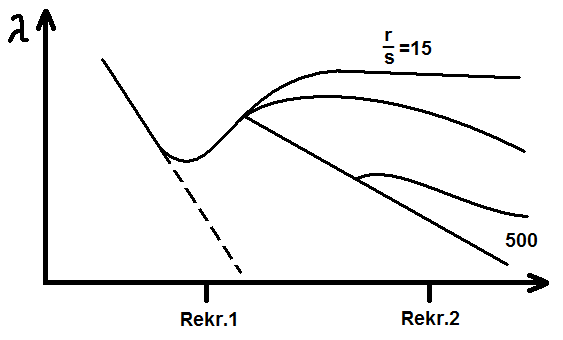
Szorstkość:
• Wzór Nikuradusa
1
λ =
.
2
v
(15.35)
2lg + 174
s
Przy każdej szorstkości ustala się wartość współczynnika strat λ wg tabeli lub z wykresu (rys.4 ).
• Wzór Misesa
k
2
λ = 0
,
0 096 + 4
+ 7,2
.
(15.36)
r
Re
w w w . c h o m i k u j . p l / M a r W a g 9 8 7
„Przepływ cieczy przez długie kanały.”
Wykład 15
k - liczba (wymiar długości charakterystycznej).
Rys. 4
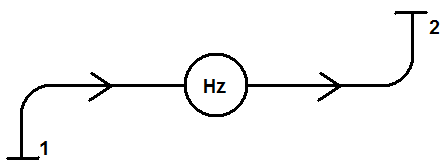
Obliczanie wydajności pomp.
Jeżeli na drodze przepływu strugi
znajduje się źródło energii, to w tym
miejscu następuje przyrost lub ubytek
energii cieczy. Znajduje to odbicie w
równaniu Bernoulliego.
Rys. 5
2
2
v
p
v
p
1
1
2
2
+
+ z =
+
+ z + h + H .
(15.37)
1
2
str
z
g
2
λ
g
2
λ
Hz – wys. hydrauliczna źródła energii
H = h
∆ + h
∆ + h
∆ − h ,
z
v
p
z
str
(15.38)
N = γ Q H .
(15.39)
z
W praktyce przyjmujemy że przy długich rurociągach straty lokalne są małe w stosunku do strat wzdłuż przewodu i można ja zaniedbać. Cała energia strumienia zużyta zostaje na pokonanie tarcia.
w w w . c h o m i k u j . p l / M a r W a g 9 8 7
„Przepływ cieczy przez długie kanały.”
Wykład 15
v2 l
h
= ~ λ
.
(15.40)
str
g
2 d
2g h
d
v
str
=
.
(15.41)
λ l
d4
π
Q =
v .
(15.42)
4
Przyjmując λ w przybliżeniu obliczamy vI,
następnie
v d
Re
I
=
,
(15.43)
v
oraz z wzoru Blausiasa
0,316
λ =
,
(15.44)
4 Re
następnie II przybliżenie, czyli dla vII liczymy ze wzoru (15.43) Re i wyznaczamy λ ze wzoru (15.44).
Przewody rozgałęzione
Rys. 6
H – efektywna różnica ciśnień
2
2
v
l
v
l
1
1
2
2
H
= h
+ h
= λ
+ λ
AB
str1
str 2
1
2
(15.45)
2g d
2g d
1
2
2
2
v
l
v
l
1
1
3
3
H
= h
+ h
= λ
+ λ
AC
str1
str 3
1
3
(15.46)
2g d
2g d
1
3
2
2
2
Q = Q + Q = v d = v d + v d (15.47)
1
3
1
1
2
2
3
3
w w w . c h o m i k u j . p l / M a r W a g 9 8 7
Wyszukiwarka
Podobne podstrony:
Przepływ cieczy przez długie kanały
Przepływ cieczy przez długie kanały wersja na rzutnik
Przepływ cieczy przez duży otwór
Ustalony przepływ cieczy przez duży otwór
Ćwiczenie nr 7 ?danie przepływu cieczy przez poziome rurki
Przepływ cieczy przez duży otwór3
Przepływ cieczy przez duży otwór2
Przeplyw czynnika przez kanaly dolotowe i wylotow
Przepływ energii przez ekosystem
Pomiar natężenia przepływu cieczy roboczej w układach hydrauliki siłowej - sprawko, Uczelnia, Hydrau
Analiza przepływu wody przez przekrój mostowy (FM)
przepływ cieczy pod ciśnieniem, BUDOWNICTWO, Inżynierka, semestr 3, Hydraulika i hydrologia, hydraul
wyznaczanie współczynnika strat lokalnych energi przy przepływie cieczyw ukaładach hydraulicznych
Opór liniowy podczas przepływu płynu przez przewód
Wspolczynnik przeplywu cieczy 3
więcej podobnych podstron