Równanie stanu.
-HVWWR]DOH*QRüSRPL G]\QS9L7GDQDSU]H]SHZQ IXQNFM
f(n,p,V,T)=0
:QLRVNLZ\QLNDMFH]LVWQLHQLDUyZQDQLDVWDQXEH]]QDMRPRFLMHJRSRVWDFL
3U]\NáDG]DOH*QRüPL G]\ZVSyáF]\QQLNDPLUR]V]HU]DOQRFL
1)
V
∂
≡ 1
α
- ZVSyáF]\QQLNREM WRFLRZHMUR]V]HU]DOQRFLFLHSOQHMRNUHODZ]JO GQ
V T
∂ p
]PLDQ REM WRFLFLDáDSU]\RJU]DQLXJRR0K
-H*HOLWHPSHUDWXU Z\UD]LüZVWRSQLDFK&HOVMXV]DWRW>&@ 7>.@-2730 2F]\ZLFLHG7 GW
1 V
∂
α
, V
0 =
0 – REM WRüZWHPSHUDWXU]H0C
V 0 t
∂ p
-H*HOLSU]\Mü*HZSHZQ\P]DNUHVLHWHPSHUDWXUα
to
0 = const
V
α
∂
V =
= const ⇒ V = V 1 + α
0
0
0 (
t
0 )
t
∂ p
2)
p
∂
= 1
β
- ZVSyáF]\QQLNWHPSHUDWXURZ\FLQLHQLD
p T
∂ V
3)
1 V
∂
κ = − - ZVSyáF]\QQLNFLOLZRFLL]Rtermicznej.
V
p
∂ T
=QDNPLQXV]RVWDáZ\EUDQ\DE\ZVSyáF]\QQLNκ > 0 gdy p ↑, V ↓
0R*QDSRND]Dü*H]VDPHJRLVWQLHQLDUyZQDQLDVWDQXZ\QLND
∂ V ∂ T ∂
p
= −1
∂ T
p
V
p ∂
V ∂ T
:VWDZLDMFGRWHJRUyZQDQLDGHILQLFM ZVSyáF]\QQLNyZα,β,κ dostajemy
(
1
1
V
α ) −
= −1⇒ α = βκ p
β p κ V
1
5yZQDQLHVWDQXJD]XGRVNRQDáHJRU&ODSH\URQD
pV=nRT
gdzie:
n – liczba moli gazu,
J
R = (8,314510 ± 0,00007)
- VWDáDJD]RZD
Kmol
p – FLQLHQLHZ>3D@9– REM WRüZ>
3
m ], T – temperatura w [K].
Dla jednego mola gazu mamy:
pV=RT
0R*HP\UyZQDQLHJD]XGRVNRQDáHJRZ\]QDF]\ü]UR]ZD*D IL]\NLVWDW\VW\F]QHM
5R]ZD*P\JD]ZVWDQLHUyZQRZDJL1LHFK & f ( v ) E G]LHUR]NáDGHPSU GNRFLF]VWHNWM
&
f ( v ) jest OLF]ERZRUyZQHVWRVXQNRZLOLF]E\F]VWHNSRVLDGDMF\FKSU GNRFLZSU]HG]LDOH
[ v , v + dv ]×[ v , v + dv ]× [ v , v + dv ] ≡ U GRRJyOQHMOLF]E\F]VWHNSRG]LHORQHMSU]H]
x
x
x
y
y
y
z
z
z
ÄREM WRü´WHJRSU]HG]LDáX
&
&
1
( )
&
&
f ( v )
dN v
=
,
dN ( v) = Nf ( v ) dv dv dv N dv dv dv
x
y
z
x
y
z
3 &
Oznaczmy d v ≡ dv dv dv 2F]\ZLFLH
x
y
z
∫∫∫ & &
f ( v ) 3
d v = 1
JG]LHFDáNRZDQLHRGE\ZDVL SRZV]\VWNLFKSU GNRFLDFK
=
9
$
:\]QDF]P\LOHF]VWHNSRUXV]DMF\FKVL ]
SU GNRFL & v XGHU]DZFLDQ $ZF]DVLHF]DVX
dt.
dV=Avzdt –REM WRüZNWyUHMZV]\VWNLHF]VWNi
SRUXV]DMFHVL ]SU GNRFL & v ZHZQWU]G9
Y GW
]
XGHU]ZSRZLHU]FKQL $
2
/LF]EDWDNLFKF]VWHNZ\QLHVLHGODXSURV]F]HQLDSLV]HP\
&
dN ≡ dN ( v) ):
dV
& 3&
dN = N
f ( v ) d v , gdzie V –FDáNRZLWDREM WRü]DMPRZDQDSU]H]XNáDG
V
.D*GDF]VWNDRGELWDSU]HND]XMHFLDQLHS GPY =PLDQDS GXGODG1F]VWHNQDMHGQRVWN
z
F]DVXLQDSU]HG]LDáSU GNRFLZ\QRVL
2
& 3& Adt
dp = 2 mv dN = 2 Nmv f
=
z
z
( v) d v
dF dt
V
A
VWGVLáDSRFKRG]FDRGF]VWHNRSU GNRFLDFK]SU]HG]LDáX8
2
& 3&
dF = 2 Nmv f
A
z
( v)
A
d v V
zatem ciQLHQLH
+∞
+∞
+∞
1
N
&
p =
dF =
dv
dv
dv f v
mv
∫
∫ ∫ ∫
A
x
y
z
( )
2
2
z
A
V −∞
−∞
0
*D]MDNRFDáRüMHVWZVSRF]\QNXF]\OLUR]NáDGSU GNRFLMHVWL]RWURSRZ\0R*QDZL F
]DVWSLü &
f ( v) przez f ( v) , gdzie 2
2
2
v ≡ v
+ v + v .
x
y
z
Ponadto:
+∞
+∞
∫ dv
dv
z = 1 ∫
2
z
0
−∞
Tak wL FPR*HP\PQR*FSRZ\*V]FDáN VWURQDPLSU]H]9QDSLVDü
∞ ∞ ∞
pV = mN ∫ ∫ ∫ dv dv dv f ( v) v 2 mN
f ( v) v 2 dv
x
y
z
z
=
∫∫∫
z
−∞−∞−∞
v
DFDáND
2
2
2
2
f ( v) v dv = v
= v
= v
∫∫∫
z
z
y
x
v
3RQLHZD*
1 &
2
2
2
2
2
2
v = v
+ v + v → v
=
v
VWGRWU]\PXMHP\
x
y
z
z
3
1 & 2
2
pV = mN
v
= N E
k
3
3
gdzie E
-UHGQLDHQHUJLDNLQHW\F]QDF]VWHN
k
3RUyZQXMFWRUyZQDQLH]IHQRPHQRORJLF]Q\PUyZQDQLHP&ODSH\URQDPDP\
2
pV = RT → RT =
N
E
A
k
3
3 R
E
=
T
k
2 N A
3
E
= kT
k
2
gdzie k –VWDáD%ROW]PDQQD1
23
−
=
⋅
A – liczba Avogadro
1
022137
,
6
10 mol
Dla warunków normalnych mamy:
=
N
p
01325
,
1
⋅ 5
10
1 atm
0
=
2
m
atm ⋅ m 3
R = 08206
,
0
K ⋅ kmol
T =
15
,
273
K
0
= 0 C
m 3
V =
4138
,
22
-REM WRüGODJD]XGRVNRQDáHJR
0
kmol
'ODJD]yZU]HF]\ZLVW\FKQLHMHVWWRSUDZGPR*QD]URELüQDVW SXMF\Z\NUHV
1,4
pV
N 2
RT
1,2
He
1,0
Ar
0,8
CH 4
0,6
p/p0
0,4
100
200
300
400
500
Rys.1
RównDQLH&ODSH\URQDQLHRSLVXMHGRNáDGQLHJD]yZU]HF]\ZLVW\FK]ZáDV]F]DSU]\GX*\FK
FLQLHQLDFKLQLVNLFKWHPSHUDWXUDFK
4
Równanie stanu gazów rzeczywistych 5yZQDQLHVWDQXGODPRODJD]XGRVNRQDáHJRPR*QD]DSLVDüQDVW SXMFR
pV =1
RT
Aby uwzJO GQLüRGG]LDá\ZDQLDPL G]\F]VWHF]NDPLJD]XPR*QD]URELüQDVW SXMF
PRG\ILNDFM
pV
B( T ) C( T ) D( T )
= 1 +
+
+
+ ... (1)
2
3
RT
V
V
V
lub
pV =1+ B (′ T) p + C (′ T) 2
p + D (
′ T ) 3
p + ...
RT
↑
6WRW]ZUR]ZLQL FLDZLULDOQHUyZQDQLDVWDQyZU]HF]\ZLVW\FK
%7%¶7VWRZVSyáF]\QQLNLZLULDOQH–PR*QDMHZ\]QDF]\ü]HNVSHU\PHQWXOXE
PHWRGDPLIL]\NLVWDW\VW\F]QHMF]\QLFRGSRZLHGQLH]DáR*HQLDGRW\F]FHVSRVREX
RGG]LDá\ZDQLDF]VWHNJD]X
Równanie van der Waalsa (1873 rok).
2
n′
p + a
( V − n b
′ )= n RT
′
V
gdzie a, b – parametry empiryczne, charakterystyczne dla danej substancji, n’MHVWOLF]EPROL
V –REM WRFLD7–WHPSHUDWXU7RVDPRUyZQDQLHGODOLF]E\PROLQ’ = 1:
a
p +
2 ( V − b) = RT
V
5yZQDQLHWRXZ]JO GQLDFKDUDNWHURGG]LDá\ZDQLDSRPL G]\F]VWHF]NDPL
9
U
Rys. 2. OdG]LDá\ZDQLHYDQGHU:DDOVD
5
♦ &]VWHF]NRPSU]\SLVXMHVL VNRF]RQHUR]PLDU\2EM WRüGRVW SQDGODLFKUXFKXMHVW
PQLHMV]DRGREM WRFL9]ELRUQLND0R*QDSRND]Dü*H b = 4 N
, gdzie Ω jest
A Ω
REM WRFLF]VWHF]NLSU]\]DáR*HQLX*HMHVWRQDWZDUGNXON >üZLF]HQLD@
♦ 1DZL NV]\FKRGOHJáRFLDFKF]VWHF]NLJD]XRGG]LDáXMQDVLHELHSU]\FLJDMFR:JD]LH
SRMDZLDVL GRGDWNRZHFLQLHQLHZHZQ WU]QHS 0R*QDSRND]Dü*H
w
a
p =
>üZLF]HQLD@
w
2
V
:DUWRFLSDUDPHWUyZDLEGODNLONu substancji.
4
Nm
3
m
substancja
2
a
10 −
⋅
6
b
10−
⋅
2
mol
mol
He
0,34
23,41
H2
2,48
26,61
Ar
13,2
30,32
O2
13,8
32,58
N2
13,6
38,52
CO2
40,1
42,64
H2O
54,8
30,52
3RSU]HNV]WDáFHQLDFKRWU]\PXMHP\UyZQDQLHYDQGHU:DDOVDZSRVWDFLZLULDOnej:
−1
pV
a
ab
b
= 1−
+
1 −
2
RT
VRT
V RT
V
gdzie:
−1
2
3
b
b
b
b
1 −
= 1 + +
+
+ ...
2
3
V
V
V
V
MHVWUR]ZLQL FLHPZV]HUHJ7D\ORUD3RSRGVWDZLHQLXPDP\
pV
a 1
2
1
3
1
= 1+ b −
+ b
+ b
+ ...
2
3
(2)
RT
RT V
V
V
3RUyZQXMFUR]ZLQL FLHZLULDOQH]RWU]\PXMHP\Z]RU\QDZVSyáF]\QQLNLZLULDOQH
B( T )
a
= b −
, C( T )
2
= b , D( T )
3
= b
RT
Równanie van der Waalsa jest równaniem 3-VWRSQLDZ]JO GHP]PLHQQHM9
RT
a
ab
3
2
V −
+ b V + V −
= 0
(3)
p
p
p
D]DWHPPDZRJyOQRFLWU]\Uy*QHUR]ZL]DQLDZ]DOH*QRFLRGZDUWRFLZVSyáF]\QQLNyZ
a) V
VU]H
1 , V2 i V3
czywiste
b) V1 rzeczywiste , V2 , V3 zespolone
6
'ODSU]\SDGNXDUyZQDQLHPR*QD]DSLVDüQDVW SXMFR
( V − V V − V V − V =
1 )(
2 )(
) 0
3
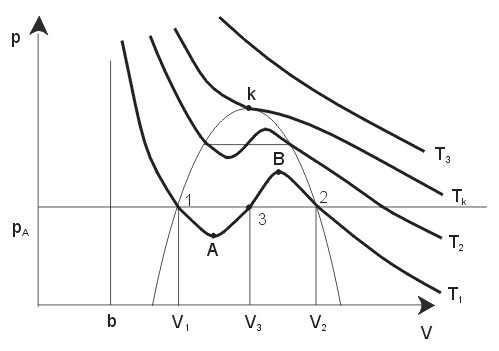
'ODXVWDORQ\FKZDUWRFL7 FRQVWS FRQVWUyZQDQLHSRVLDGDUR]ZL]DQLHGODUy*Q\FK
REM WRFLSDWU]Z\NUHVSRQL*HM&]\PDMone sens fizyczny?
Rys.3
2ND]XMHVL *HW\ONR9
PDMVHQVIL]\F]Q\SU]\F]\P
1 i V2
- V R]QDF]DREM WRüPRODFLHF]\SU]\GDQ\FKSL7
1
- V REM WRüPRODSDU\QDV\FRQHMSU]\GDQ\FKSL7
2
5R]ZL]DQLH93 nie ma realnego znaczenia fizycznego.
Gdy WHPSHUDWXUDJD]XURQLH]EOL*DMFVL GRSHZQHMZDUWRFLNU\W\F]QHM7 UR]ZL]DQLD9
k
1
i V ]EOL*DMVL GRVLHELH'OD7
ZWHG\UyZQDQLHPR*QD
2
k mamy V1 = V2 = V3 = Vk
SU]HSLVDüZSRVWDFL
( V − V
V
V V
V V
V
k )3 = 0
3
→
− 3
2
k
+ 3 2
3
k
− k = 0
Z porównania z (3) otrzymujemy
8 a
a
V = b
3 , T =
p =
>üZLF]HQLD@
k
k
27 bR
k
2
27 b
lub odwrotnie :
V
8 p V
k
b =
,
2
a = 3 p V ,
k
k
R =
3
k
k
3 Tk
:LHONRFL7k, pk i Vk nazywamy odpowiednio temperaturFLQLHQLHPLREM WRFLNU\W\F]Q
7
QRVLQD]Z VWDQXNU\W\F]QHJR
k , pk , Tk
:DUWRFLSDUDPHWUyZNU\W\F]Q\FKGODNLONXVXEVWDQFML
p
m 3
p V
k
k
k
T
V
k [ K ]
k
p
mol
RT
0
k
He
5,2
2,26
57,8
0,306
H2
33,24
12,8
65
0,305
N2
126,25
33,54
90,1
0,292
O2
154,78
50,14
78
0,308
CO2
304,19
72,85
94,04
0,274
H2O
647,3
218,39
56
0,230
Hg
1460±30
1640±50
48
0,65
Li
3200±600
680
66
0,17
Dla T>Tk równanie (3) ma dla dowolnych waUWRFLSGZDSLHUZLDVWNL]HVSRORQHLW\ONRMHGHQ
U]HF]\ZLVW\3RQLHZD*UR]ZL]DQLD]HVSRORQH9VQLHIL]\F]QH]DWHPGODS FRQVWLVWQLHMH
W\ONRMHGQDREM WRüMDNPR*H]DMPRZDüPROJD]XZWHPSHUDWXU]H7
5R]SDWU]P\WHPSHUDWXU 71 < Tk - dla ustalonego p1 mamy V1 < V3 < V2 (patrz rys.3).
1LHFKWHUD]VLáD]HZQ WU]QDVSU *DJD]OXEFLHF]]PQLHMV]DMFGRVW SQREM WRü9
• na lewo od (1) –VSU *DQLHFLHF]\SURZDG]LGRGX*HJRZ]URVWXFLQLHQLD→PDáD
FLOLZRüFLHF]\
• na prawo od (2) –VSU *DQLHSDU\QLHQDV\FRQHMZ\ZRáXMH]QDF]QLHPQLHMV]\Z]URVW
FLQLHQLD
• SRPL G]\-QDVW SXMH]MDZLVNRVNUDSODQLDSDU\SU]HMFLHJD]→ ciecz
&]\PR*QDRVLJQüSXQNW\$L%"2Wy*WDN–PDWRPLHMVFHZQDVW SXMF\FKSURFHVDFK
-SU]HMFLH– (B) – izotHUPLF]QHVSU *DQLHSDU\QLH]DZLHUDMFHMRURGNyZNRQGHQVDFML
MRQ\S\áNL– powstaje para przesycona
-SU]HMFLH– (A) –L]RWHUPLF]QHUR]SU *DQLHFLHF]\SR]EDZLRQHM]DQLHF]\V]F]H
LZQDF]\QLXRZ\SROHURZDQ\FKFLDQNDFK– powstaje ciecz przegrzana 2EDWHVWDQ\VQLHWUZDáHLQLHZLHONLH]DEXU]HQLHPR*HSURZDG]LüGRZU]HQLDZSU]\SDGNX
cieczy przegrzanej lub skraplania (para przesycona).
8
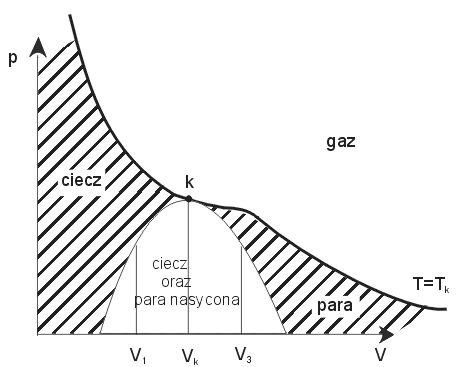
0R*QD]URELüQDVW SXMF\Z\NUHVREUD]XMF\REV]DU\S7ZNWyU\FKLVWQLHMHGDQ\VWDQ
(faza):
Rys.4
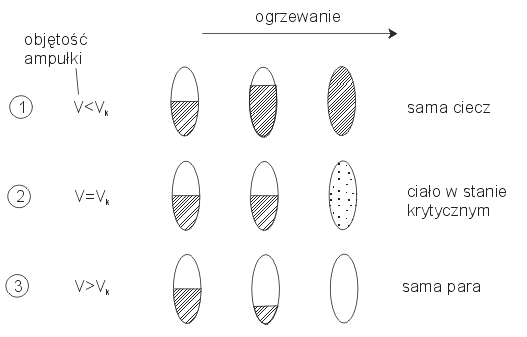
-HOLZDPSXáFHRREM WRFL9]DPNQLHP\SHZQLORüFLHF]\L]DF]QLHP\MRJU]HZDüWR
PR*OLZHVQDVW SXMFHSU]\SDGNL
Rys.5
9
Wyszukiwarka
Podobne podstrony:
Wyk 02 Pneumatyczne elementy
02 OperowanieDanymiid 3913 ppt
02 Boża radość Ne MSZA ŚWIĘTAid 3583 ppt
OC 02
PD W1 Wprowadzenie do PD(2010 10 02) 1 1
02 Pojęcie i podziały prawaid 3482 ppt
WYKŁAD 02 SterowCyfrowe
02 filtracja
02 poniedziałek
21 02 2014 Wykład 1 Sala
Genetyka 2[1] 02
02 czujniki, systematyka, zastosowania
auksologia 13 02 2010
02 MAKROEKONOMIA(2)id 3669 ppt
Sys Inf 03 Manning w 02
więcej podobnych podstron