PRZYKŁAD 1
Wyznaczyć odpowiedź skokową członu opisanego poniższym równaniem, dla zerowych warunków początkowych: dy
dx
T
+ y = K
dt
dt
Rozwią zanie
Wyznaczamy transmitancję:
Y ( s)
G
S =
= Ks
X ( s)
Ts + 1
Z transmitancji wynika:
Ks
Y ( s) =
X ( s) (*)
Ts + 1
Skoro sygnałem wejściowym jest skok jednostkowy, to: 1
x t
( )
t
(
1 ) ⇒
=
X ( s) =
s
Podstawiając do (*):
Ks
1
K
1
Y ( s) =
⋅ =
Ts + 1 s
T
1
s + T
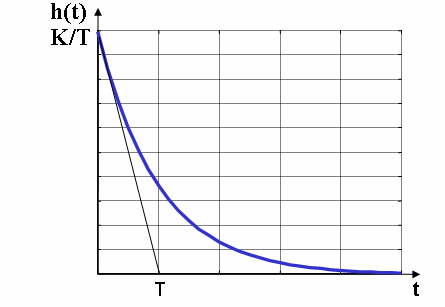
Z tablicy transformat wynika:
K
t
h( t) =
−
y( t) =
e T ⋅ (
1 t)
T
Co możemy zilustrować:
_________________________________________________
1 _
_______________________________________________
Powered by xtoff®
lalik.krzysztof@wp.pl
Wyznaczyć odpowiedź skokową oraz impulsową członu opisanego poniższym równaniem, dla zerowych warunków początkowych: d 2
2
y
T
+ y = Kx
dt 2
Rozwią zanie
Wyznaczamy transmitancję:
Y ( s)
G
S =
=
K
X ( s)
2
2
T s + 1
Z transmitancji wynika:
K
Y ( s) =
X ( s) (**)
2
2
T s + 1
Skoro sygnałem wejściowym jest skok jednostkowy, to: 1
x t
( )
t
(
1 ) ⇒
=
X ( s) =
s
Podstawiając do (**):
K
1
K
1
Y ( s) =
⋅ =
2
2
T s + 1
2
s
T
2
1
s( s +
)
2
T
Rozkładając powyższą zależność na ułamki proste, otrzymujemy: K
s
Y ( s) =
− K
s
1
2
s +
2
T
Z tablicy transformat wynika:
K
Y ( s)
⇒
=
y( t) = K ⋅ (
1 t)
s
s
1
Y ( s) = − K
⇒ y( t) = − K ⋅ cos( t)
2
1
T
s +
2
T
Stąd:
1
h( t) = y( t) = K ⋅ (
1 t) − K ⋅ cos( t) ⋅ (
1 t)
T
_________________________________________________
2 _
_______________________________________________
Powered by xtoff®
lalik.krzysztof@wp.pl
Stosując twierdzenie o pochodnej h(t)otrzymano wzór na odpowiedź impulsową, dzięki czemu nie trzeba jeszcze raz przeliczać transmitancji (tym razem dla x(t)= δ(t)): d
g( t) =
[ h( t)]
dt
Czyli:
K
1
K
1
g( t) = h (
′ t) = 0 + ⋅sin( t) ⋅ (
1 t) =
⋅sin( t) ⋅ (
1 t)
T
T
T
T
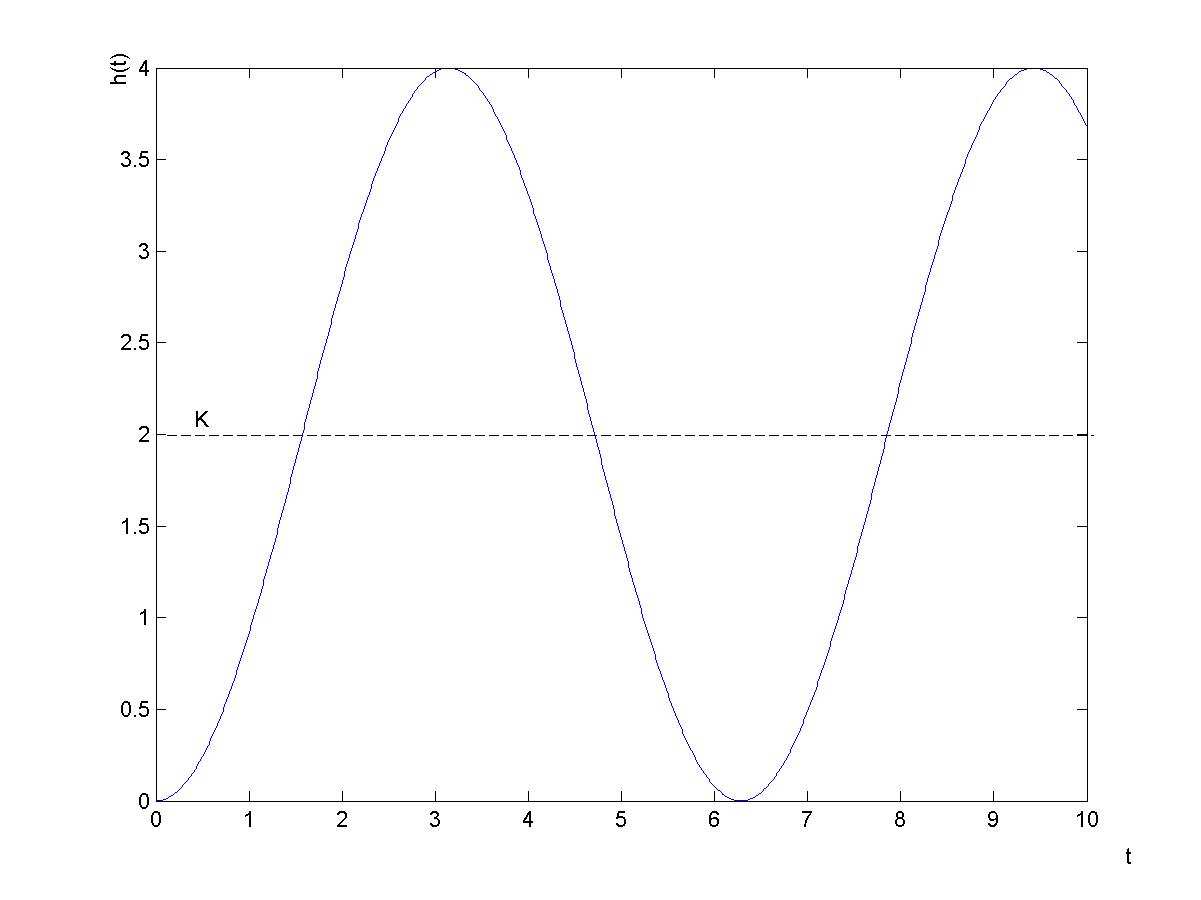
Jak widać odpowiedź skokowa jest wykresem odbicia względem x cosinusa, przesuniętym o wektor [0,K] i o amplitudzie K, oraz okresie T
π
2
.
K
Odpowiedź impulsowa jest wprost sinusem o tym samym okresie i amplitudzie T
Odpowiedź skokowa została wykreślona poniżej: _________________________________________________
3 _
_______________________________________________
Powered by xtoff®
lalik.krzysztof@wp.pl
Wyszukiwarka
Podobne podstrony:
zadania i rozwiazania z przekrojów 2
,projektowanie materiałów inżynierskich, zadania i rozwiązania Umocnienie roztworowe
K05 pf08L zadania rozwiazania
Zadania z rozwiazaniami ZaiP zadanie 3
belki proste zadania z rozwiaza Nieznany (2)
Obliczanie pochodnych Zadanie Rozwiazanie zadania domowego id
ARYT ZADANIA i rozwiazania
K03 pf08L zadania rozwiazania Nieznany
Matematyka finansowa zadania z rozwiązaniami 2
Zadania z rozwiązaniami 1 8
Zadania z rozwiazaniami ZaiP, zadanie 1 rozwiazanie
Matematyka finansowa - zadania z rozwiązaniami
zadania z rozwiazaniami, ZADANIA Z ROZWIĄZANIAMI:
przykładowe zadania i rozwiazania
III etap zadania rozwiazania id Nieznany
więcej podobnych podstron