MECHANIKA BUDOWLI
semestr zimowy
1 |
S t r o n a
mgr inż. Hanna Weber
0,5EI
q=8kN/m
P=24kN
6
4
1,5
EI
2
0,5EI
0,5EI
0,5EI
I
EI
X
1
X
2
X
2
L =6
L =4
1,5
X
1
X
0
X
3
L
1
*
2
3
Rozwiązywanie belki statyczne niewyznaczalnej Metodą Trzech Momentów
Polecenie: Narysuj wykres sił wewnętrznych w belce. Zadanie rozwiąż metodą trzech momentów.
Określenie stopnia statycznej niewyznaczalności układu:
𝑛
𝑠
= 𝑙
𝑟
− 𝑙
𝑝
− 3 = 5 − 0 − 3 = 2 — układ dwukrotnie statycznie niewyznaczalny.
Schemat podstawowy metody trzech momentów:
Układ równań metody trzech momentów:
Wzór na długość sprowadzoną „i-tego” elementu:
; gdzie za porównawczy moment bezwładności elementu przyjęto :
𝐼
𝑝
= 𝐼
Wyznaczenie długości sprowadzonych poszczególnych elementów:
20
3
3
3
2
2
2
1
10
2
2
2
1
1
1
0
6
'
)
'
'
(
2
'
6
'
)
'
'
(
2
'
p
p
EI
L
X
L
L
X
L
X
EI
L
X
L
L
X
L
X
i
p
i
i
I
I
L
L
'
0
'
1
1
1
1
*
I
L
I
I
L
L
p
m
I
I
I
I
L
L
p
6
6
'
2
2
2
m
I
I
I
I
L
L
p
8
5
,
0
4
'
3
3
3
MECHANIKA BUDOWLI
semestr zimowy
2 |
S t r o n a
mgr inż. Hanna Weber
q=8kN/m
P=24kN
-
40
24
32
13,75
18,25
12
9
64
T
0
M
0
1
EI
X =1
2
L =6
L =4
1,5
X =1
2
L
1
*
2
3
0,5EI
0,5EI
I
1
2
0kN
40kN
45,75kN
30,25kN
+
-
+
+
EI
X =1
1
L =6
L =4
1,5
X =1
1
L
1
*
2
3
0,5EI
0,5EI
I
M
1
M
2
EI
L =6
L =4
1,5
L
1
*
2
3
0,5EI
0,5EI
I
Rozwiązanie 1:
Przy ustalaniu lewej strony drugiego równania układu pominięto wpływ obciążenia q na wsporniku, przyjmując
X
3
=0, natomiast moment od obciążenia uwzględniono przy rysowaniu wykresu M
0
i liczeniu
𝛿
10
i
𝛿
20
.
Układ równań po wprowadzeniu wyznaczonych długości sprowadzonych i momentu X
3
:
Po przekształceniu :
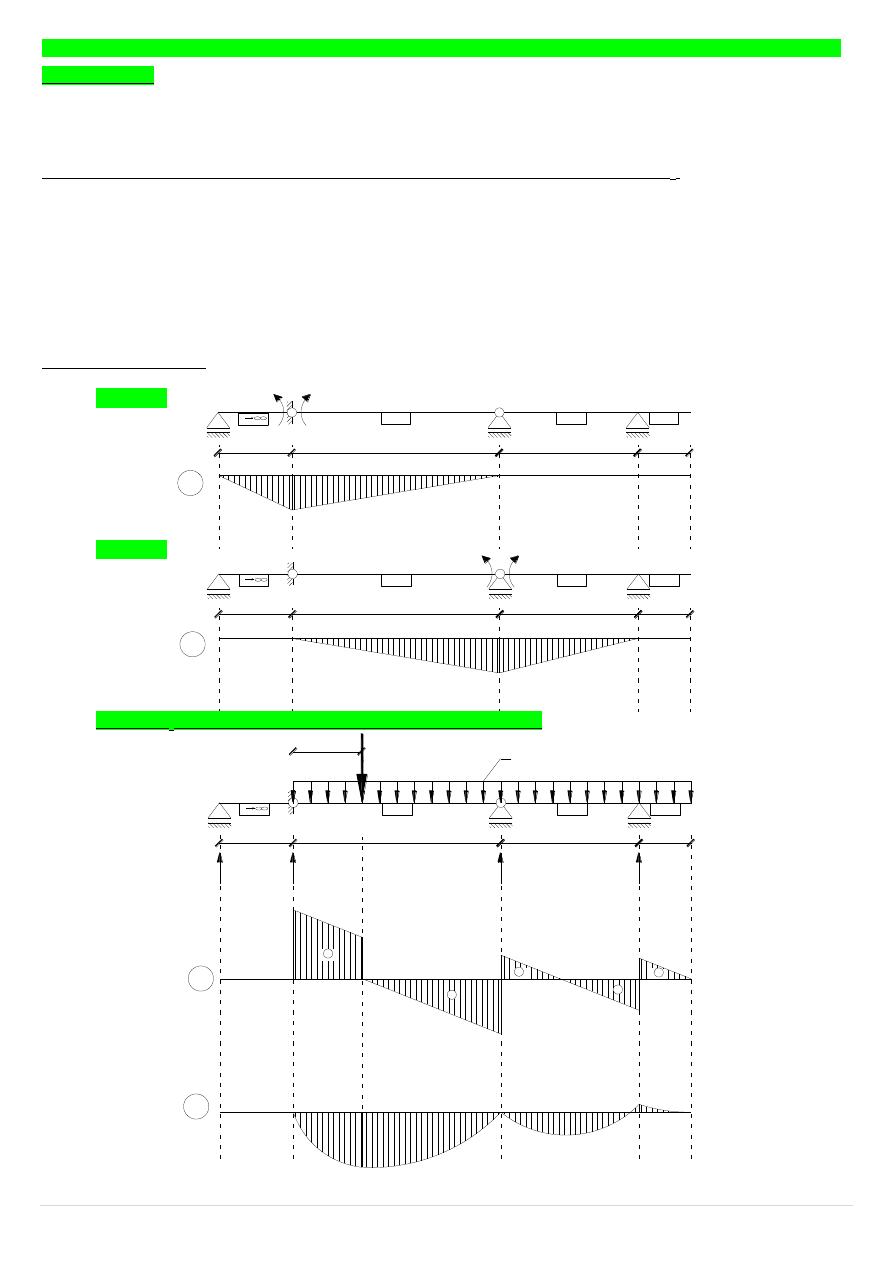
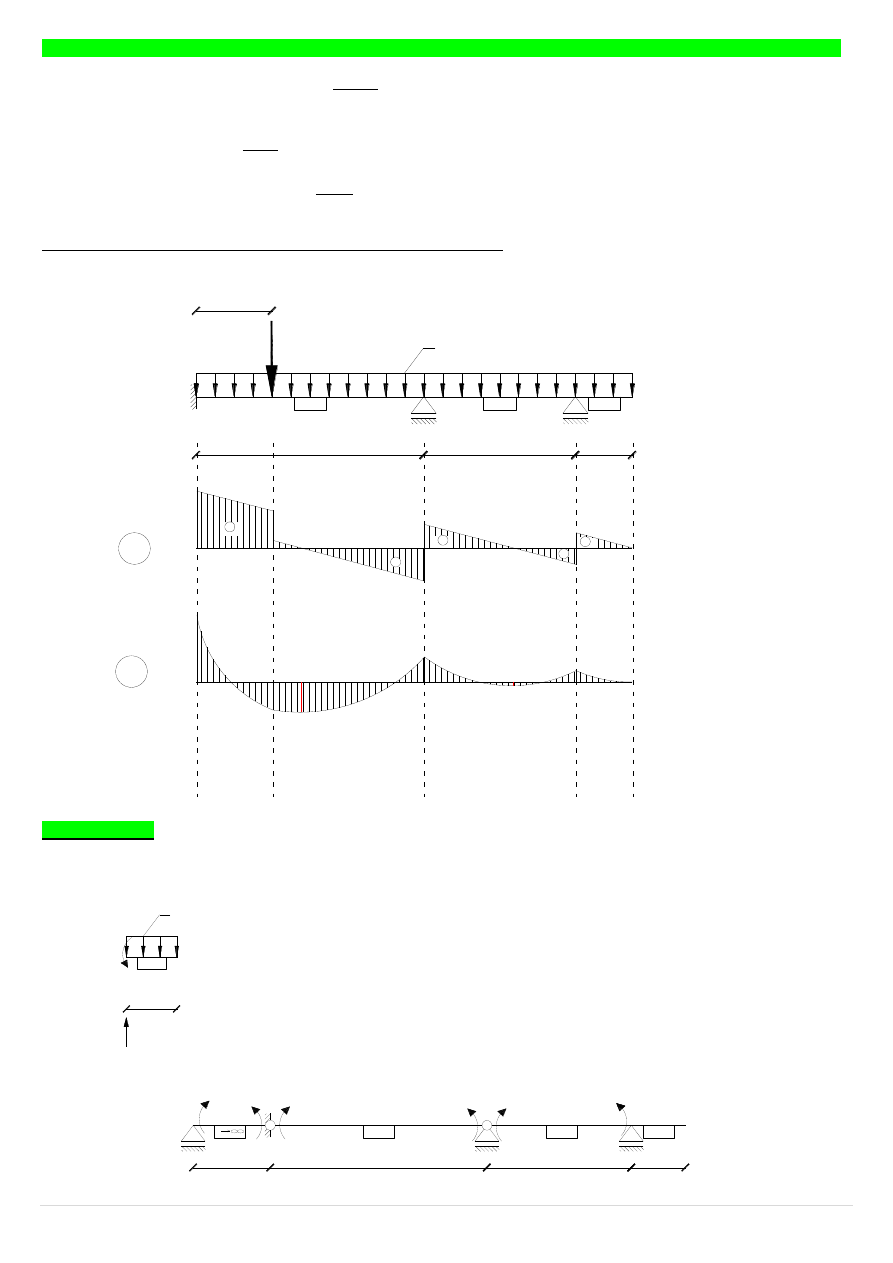
Wykresy jednostkowe:
stan X
1
=1
stan X
2
=1
Wykres M
0
(moment zginający od obciążenia zewnętrznego):
20
2
1
10
2
1
0
6
8
0
)
8
6
(
2
6
6
6
)
6
0
(
2
0
EI
X
X
EI
X
X
X
20
2
1
10
2
1
6
28
6
6
6
12
EI
X
X
EI
X
X
MECHANIKA BUDOWLI
semestr zimowy
3 |
S t r o n a
mgr inż. Hanna Weber
q=8kN/m
P=24kN
-
40
24
32
13,75
18,25
12
9
64
T
0
M
0
2
3
1
3
1
EI
X =1
2
L =6
L =4
1,5
X =1
2
L
1
*
2
3
0,5EI
0,5EI
I
1
2
0kN
40kN
45,75kN
30,25kN
+
-
+
+
EI
X =1
1
L =6
L =4
1,5
X =1
1
L
1
*
2
3
0,5EI
0,5EI
I
M
1
M
2
EI
L =6
L =4
1,5
L
1
*
2
3
0,5EI
0,5EI
I
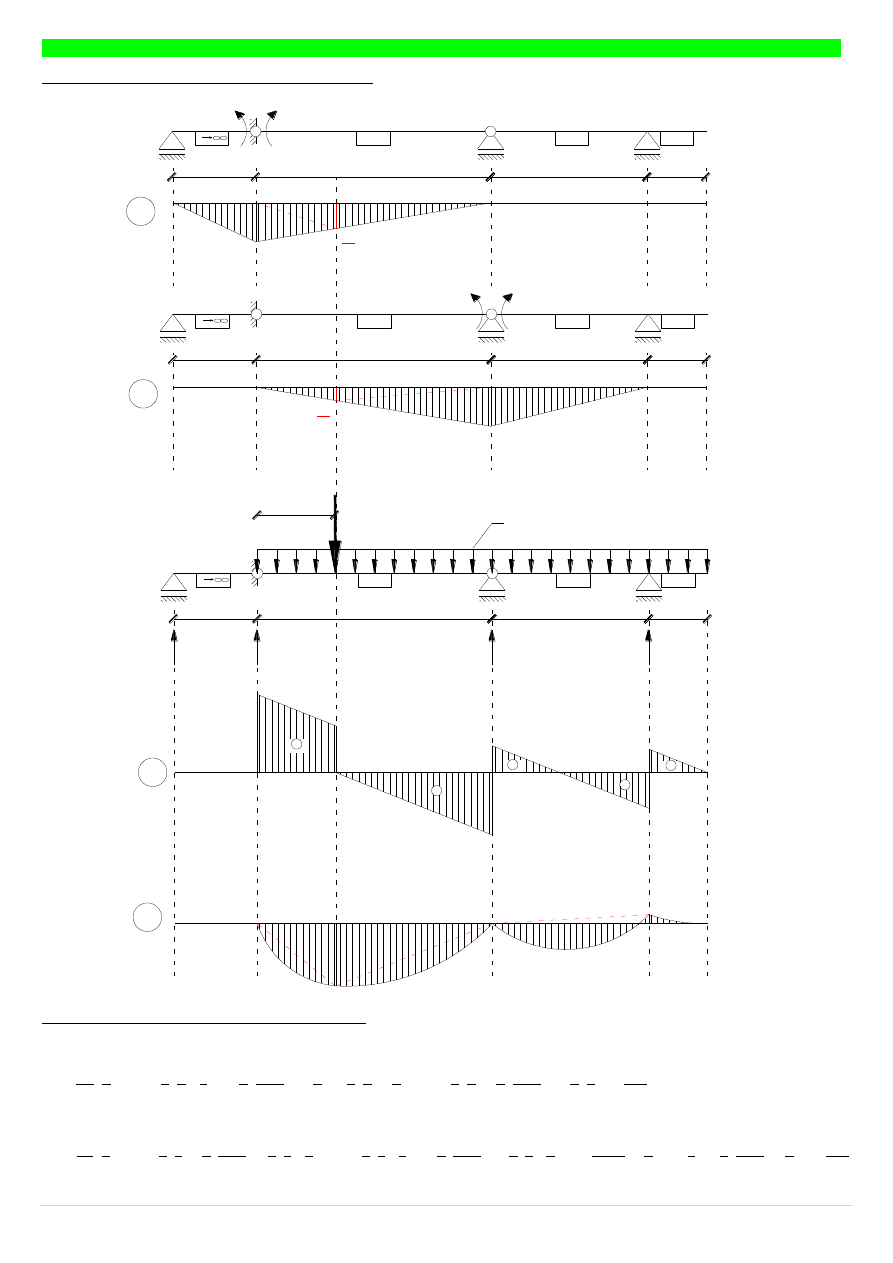
Podział wykresów momentów do całkowania:
Współczynniki prawej strony układu równań:
10
-
całkujemy wykres M
1
z M
0
EI
EI
3
376
3
2
2
1
4
8
4
8
3
2
3
2
3
2
4
64
2
1
3
2
2
1
1
2
1
2
8
2
8
3
2
1
3
1
3
2
3
2
2
64
2
1
1
2
2
10
20
-
całkujemy wykres M
2
z M
0
EI
EI
EI
3
436
1
2
1
4
8
4
8
3
2
1
3
1
4
9
2
1
5
,
0
1
1
2
1
3
1
2
1
4
8
4
8
3
2
1
3
1
3
1
3
2
4
64
2
1
3
1
2
1
2
8
2
8
3
2
3
1
3
2
2
64
2
1
1
2
2
2
20
MECHANIKA BUDOWLI
semestr zimowy
4 |
S t r o n a
mgr inż. Hanna Weber
4
4
1,5
EI
2
0,5EI
A
B
C D
E F
G
0,5EI
13,29kN
9kNm
9kNm
19,84kNm
19,84kNm
18,71kN
26,52kN
26,52kN
18,71kN
13,29kN
45,48kN
x
1
x
2
45,23kN
25,29kN
0,5EI
q=8kN/m
P=24kN
4
4
1,5
EI
2
0,5EI
52,75kNm
q=8kN/m
q=8kN/m
12kN
12kN
Układ równań metody trzech momentów:
Podstawiając otrzymane wartości do układu równań:
EI
EI
X
X
EI
EI
X
X
3
436
6
28
6
3
376
6
6
12
2
1
2
1
Rozwiązanie układu równań:
kNm
X
kNm
X
84
,
19
75
,
52
2
1
Wyznaczenie wartości momentów w poszczególnych punktach na podstawie wzoru:
𝑀
𝑖
= 𝑀
𝑖1
∙ 𝑋
1
+ 𝑀
𝑖2
∙ 𝑋
2
+ 𝑀
𝑖0
𝑀
𝐴
= 1 ∙ (−52,75) + 0 ∙ (−19,84) + 0 = −52,75 𝑘𝑁𝑚
𝑀
𝐵
=
2
3
∙ (−52,75) +
1
3
∙ (−19,84) + 64 = 22,22 𝑘𝑁𝑚
𝑀
𝐶
= 0 ∙ (−52,75) + 1 ∙ (−19,84) + 0 = −19,84 𝑘𝑁𝑚
𝑀
𝐷
= 0 ∙ (−52,75) + 1 ∙ (−19,84) + 0 = −19,84 𝑘𝑁𝑚
𝑀
𝐸
= 0 ∙ (−52,75) + 0 ∙ (−19,84) − 9 = −9 𝑘𝑁𝑚
𝑀
𝐹
= 0 ∙ (−52,75) + 0 ∙ (−19,84) − 9 = −9 𝑘𝑁𝑚
𝑀
𝐺
= 0 ∙ (−52,75) + 0 ∙ (−19,84) + 0 = 0 𝑘𝑁𝑚
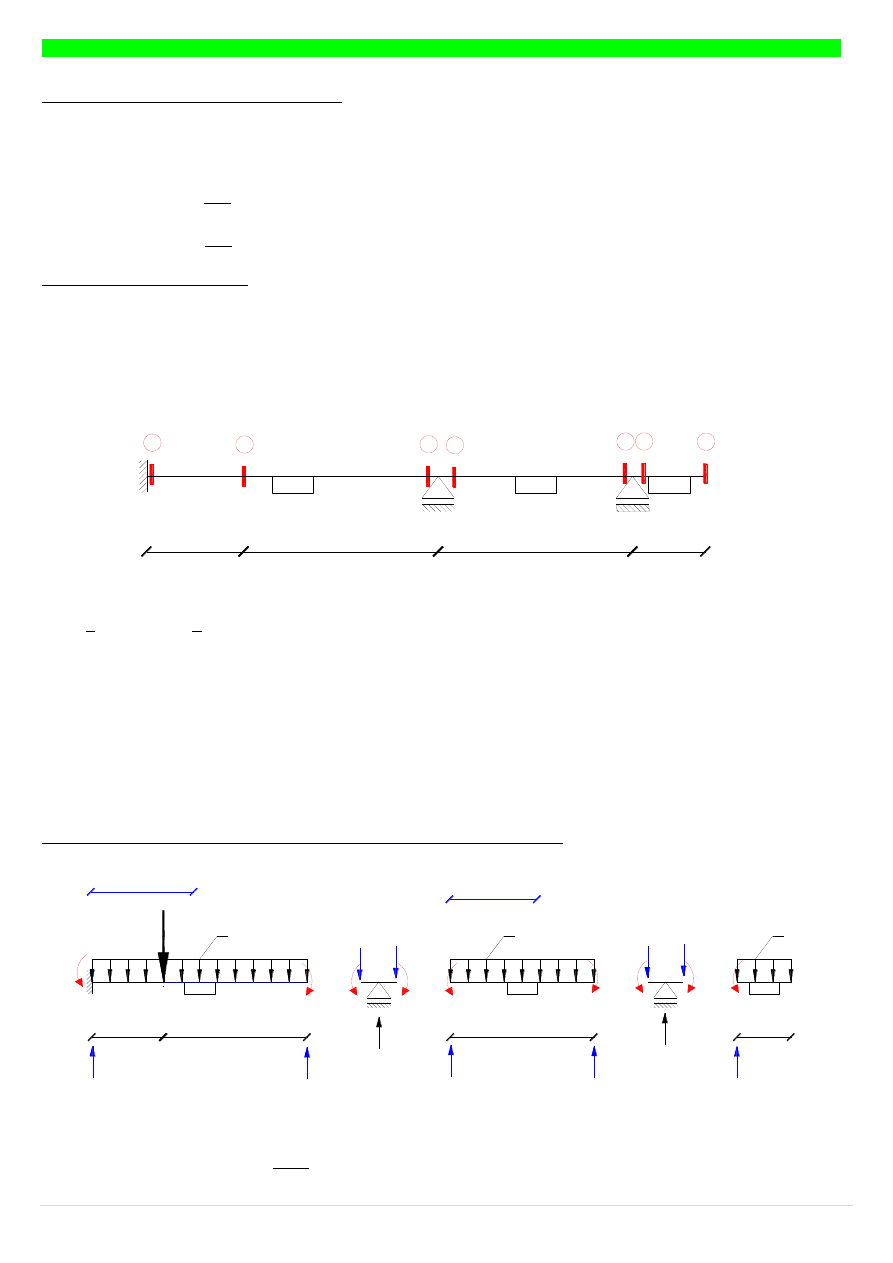
Wyznaczenie wartości sił tnących przez rozbicie układu na belki proste:
Wyznaczenie ekstremum (dla skrajnej części belki po lewej stronie):
m
x
x
x
T
685
,
2
8
48
,
21
0
24
8
48
,
45
)
(
1
1
1
20
2
1
10
2
1
6
28
6
6
6
12
EI
x
x
EI
x
x
MECHANIKA BUDOWLI
semestr zimowy
5 |
S t r o n a
mgr inż. Hanna Weber
0,5EI
q=8kN/m
P=24kN
6
4
1,5
EI
2
0,5EI
-
45,48
-
+
+
+
29,48
5,48
26,52
18,71
13,29
12
52,75
22,22
24,09
19,84
2,04
9
T
[kN]
M
[kNm]
1,5
0,5EI
q=8kN/m
12kN
9kNm
0,5EI
0,5EI
I
EI
X
1
X
2
X
2
L =6
L =4
1,5
X
1
X
0
X
3
L
1
*
2
3
kNm
m
x
M
09
,
24
2
685
,
2
24
2
685
,
2
8
685
,
2
48
,
45
75
,
52
)
685
,
2
(
2
1
Wyznaczenie ekstremum (dla środkowej belki):
m
x
x
x
T
34
,
2
8
71
,
18
0
8
71
,
18
)
(
1
2
2
kNm
m
x
M
04
,
2
2
34
,
2
8
34
,
2
71
,
18
84
,
19
)
34
,
2
(
2
2
Wykresy sił wewnętrznych w belce statycznie niewyznaczalnej:
Rozwiązanie 2:
Przy ustalaniu lewej strony drugiego równania układu przyjęto X
3
równe momentowi od obciążenia q na
wsporniku.
𝑀 = 8 ∙ 1,5 ∙ 0,75 = 9𝑘𝑁𝑚
↓
𝑋
3
= −9𝑘𝑁𝑚
MECHANIKA BUDOWLI
semestr zimowy
6 |
S t r o n a
mgr inż. Hanna Weber
EI
X =1
1
L =6
L =4
1,5
X =1
1
L
1
*
2
3
0,5EI
0,5EI
I
1
EI
X =1
2
L =6
L =4
1,5
X =1
2
L
1
*
2
3
0,5EI
0,5EI
I
1
M
1
M
2
EI
L =6
L =4
1,5
L
1
*
2
3
0,5EI
I
q=8kN/m
P=24kN
2
64
M
0
2
3
1
3
ql /8=8 4 /8=16kNm
2
Układ równań metody trzech momentów przyjmuje postać:
Po przekształceniu :
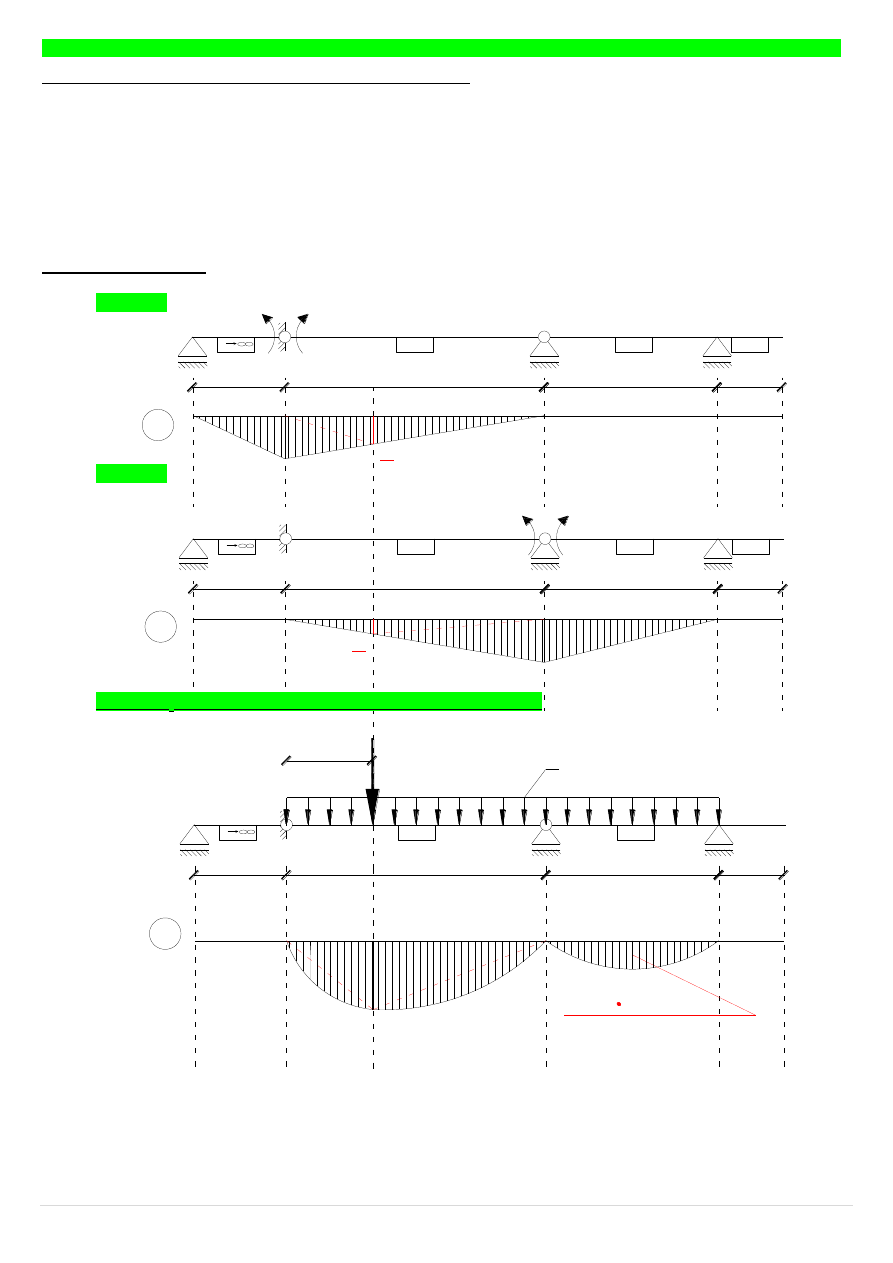
Wykresy jednostkowe:
stan X
1
=1
stan X
2
=1
Wykres M
0
(moment zginający od obciążenia zewnętrznego):
Ponieważ do układu równań został już wprowadzony moment od obciążenia q na wsporniku w postaci
𝑋
3
= −9𝑘𝑁𝑚 , pominięto wpływ tego obciązenia przy rysowaniu wykresu M
0
i w konsekwencji przy liczeniu
delt.
20
2
1
10
2
1
0
6
8
9
)
8
6
(
2
6
6
6
)
6
0
(
2
0
EI
X
X
EI
X
X
X
72
6
28
6
6
6
12
20
2
1
10
2
1
EI
X
X
EI
X
X

MECHANIKA BUDOWLI
semestr zimowy
7 |
S t r o n a
mgr inż. Hanna Weber
Współczynniki prawej strony układu równań:
10
-
całkujemy wykres M
1
z M
0
EI
EI
3
376
3
2
2
1
4
8
4
8
3
2
3
2
3
2
4
64
2
1
3
2
2
1
1
2
1
2
8
2
8
3
2
1
3
1
3
2
3
2
2
64
2
1
1
2
2
10
20
-
całkujemy wykres M
2
z M
0
EI
EI
EI
3
472
1
2
1
4
16
3
2
5
,
0
1
1
2
1
3
1
2
1
4
8
4
8
3
2
1
3
1
3
1
3
2
4
64
2
1
3
1
2
1
2
8
2
8
3
2
3
1
3
2
2
64
2
1
1
2
2
20
Podstawiając otrzymane wartości do układu równań:
72
3
472
6
28
6
3
376
6
6
12
2
1
2
1
EI
EI
X
X
EI
EI
X
X
Rozwiązanie układu równań:
kNm
X
kNm
X
84
,
19
75
,
52
2
1
Dalszy tok obliczeniowy analogiczny jak w rozwiązaniu 1. Należy pamiętać, że moment w pkt. E i F jest równy
X
3
, ponieważ z sumy wykresów moment ten wychodzi równy 0, gdyż został on uwzględniony wcześniej w
postaci
𝑋
3
= −9𝑘𝑁𝑚.
Wyszukiwarka
Podobne podstrony:
metoda trzech momentow styczen 2011 id 291566
Mechanika budowli Metoda trzech momentów
Metoda 3 momentów belka
Linie wpływu Metoda przemieszczeń mmp belka lw
Pomiary parametrów dwójników pasywnych metodą trzech woltomierzy
PROTOKOL3 METRO ELEK Pomiary parametrów dwójników metodą trzech woltomierzy
metoda trzech mom - zad II, obc p -temp-osiad-styczeń 2011
SPRAWOZDANIE3 METRO ELEK Pomiary parametrów dwójników metodą trzech woltomierzy
Metoda trzech wałeczków
Metoda trzech równań podsumowanie
Ćw3 Pomiary parametrów dwójników pasywnych metodą trzech woltomierzy
metoda trzech mom zad II obc p temp osiad styczeń 2011
Metoda sił, projekt-belka
Metoda sił projekt belka
Linie wpływu Metoda przemieszczeń mmp belka lw
Metoda trzech woltomierzy
więcej podobnych podstron