Konspekt jest współfinansowany przez Unię Europejską
w ramach Europejskiego Funduszu Społecznego
w projekcie:
"Innowacyjna dydaktyka bez ograniczeń
- zintegrowany rozwój Politechniki Łódzkiej zarządzanie Uczelnią,
nowoczesna oferta edukacyjna
i wzmacniania zdolności do zatrudniania,
także osób niepełnosprawnych".
Materiały pomocnicze do przedmiotu
Obwody Elektryczne 3
Przedmowa
Materiały pomocnicze do przedmiotu Obwody Elektryczne 3 są przeznaczone głównie dla
studentów studiów niestacjonarnych. Mają ułatwić samodzielną naukę praktycznego
wykorzystania metod analizy obwodów poznawanych w ramach przedmiotu Obwody
Elektryczne 3. Materiały nie są typowym zbiorem zadań, nie zawierają propozycji zadań do
samodzielnego rozwiązania lecz zadania o niezbyt dużym stopniu trudności, których
rozwiązania są dokładnie opisane. Ma to służyć lepszemu zrozumieniu problemów analizy
obwodów, szczególnie w zakresie podstaw tej dziedziny. Opanowanie analizy obwodów w
zakresie przewidzianym przez zajęcia ćwiczeniowe z Obwodów Elektrycznych 3 wymaga
opanowania zagadnień zawartych w odpowiednich rozdziałach podręcznika: TEORIA
OBWODÓW, ZADANIA opracowanego pod redakcją profesora M.Tadeusiewicza.
2
Zadanie 1
Wyznacz opis łańcuchowy czwórnika przedstawionego na rys.1.1.
2
’
1
Z
2
Z
1
1
’
2
Rys.1.1
Rozwiązanie
Do opisu czwórników wykorzystuje się cztery wielości związane z czwórnikiem: napięcie na
zaciskach wejściowych, prąd wejściowy, napięcie na zaciskach wyjściowych oraz prąd
wyjściowy. Są one przedstawione na rys.1.2.
1
’
czwórnik
i
1
u
2
2
2
’
1
i
2
u
1
Rys.1.2. Wielkości używane w opisach czwórników
Do analizy układu, w którym występują dowolne sygnały nieokresowe może być
wykorzystane przekształcenie Laplace’a. Do opisu czwórników wykorzystane zostaną zatem
wielkości operatorowe, które oznaczane są w następujący sposób:
( )
( )
( )
( )
2
2
2
2
1
1
1
1
i
s
I
u
s
U
i
s
I
u
s
U
=
=
=
=
(1.1)
Równania łańcuchowe czwórnika są jednymi z sześciu rodzajów wykorzystywanych do opisu
czwórników. Zależność (1.2) przedstawia równania łańcuchowe:
a
a
u
+
=
(1.2)
( )
( )
2
22
2
21
1
2
12
2
11
1
i
a
u
a
i
i
u
−
+
=
−
Postać macierzowa tych równań to:
(1.3)
−
=
2
2
1
1
i
u
i
u
A
gdzie:
(1.4)
=
22
21
12
11
a
a
a
a
A
3
Współczynniki wiążące napięcia i prądy wejściowe oraz wyjściowe, które są elementami
macierzy A mogą zostać wyznaczone poprzez analizę układu czwórnika w dwóch różnych
stanach, np. w stanie zwarcia zacisków wyjściowych (rys.1.3) oraz w stanie jałowym, czyli w
stanie rozwarcia zacisków wyjściowych (rys.1.4).
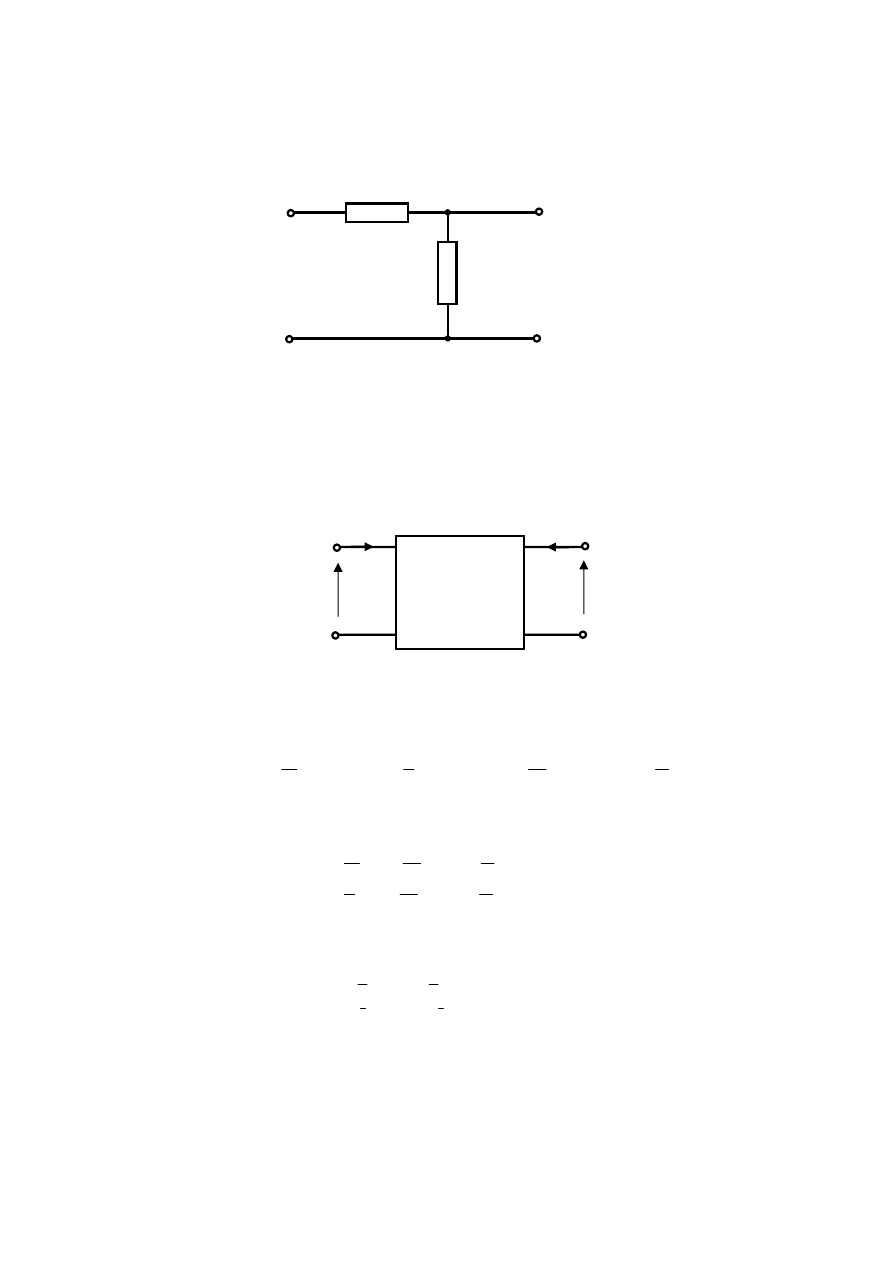
Rys.1.3. Czwórnik w stanie zwarcia zacisków wyjściowych
Rys.1.4. Czwórnik w stanie rozwarcia zacisków wyjściowych
Analiza zależności (1.2) pozwala na wyznaczenie sposobu wyznaczenia wyrazów macierzy
łańcuchowej. Wyrazy
oraz
zostaną wyznaczone na podstawie analizy stanu
rozwarcia zacisków wyjściowych
11
a
21
a
2
1
2
1
0
21
0
11
2
2
u
i
u
u
i
i
a
a
=
=
=
=
(1.5)
Odpowiada to następującemu stanowi analizowanego czwórnika:
1
1
i
czwórnik
0
2
=
i
1
u
2
u
1
2
i
1
i
czwórnik
1
u
0
2
=
u
1
i
0
2
=
i
1
u
2
u
Z
1
Z
2
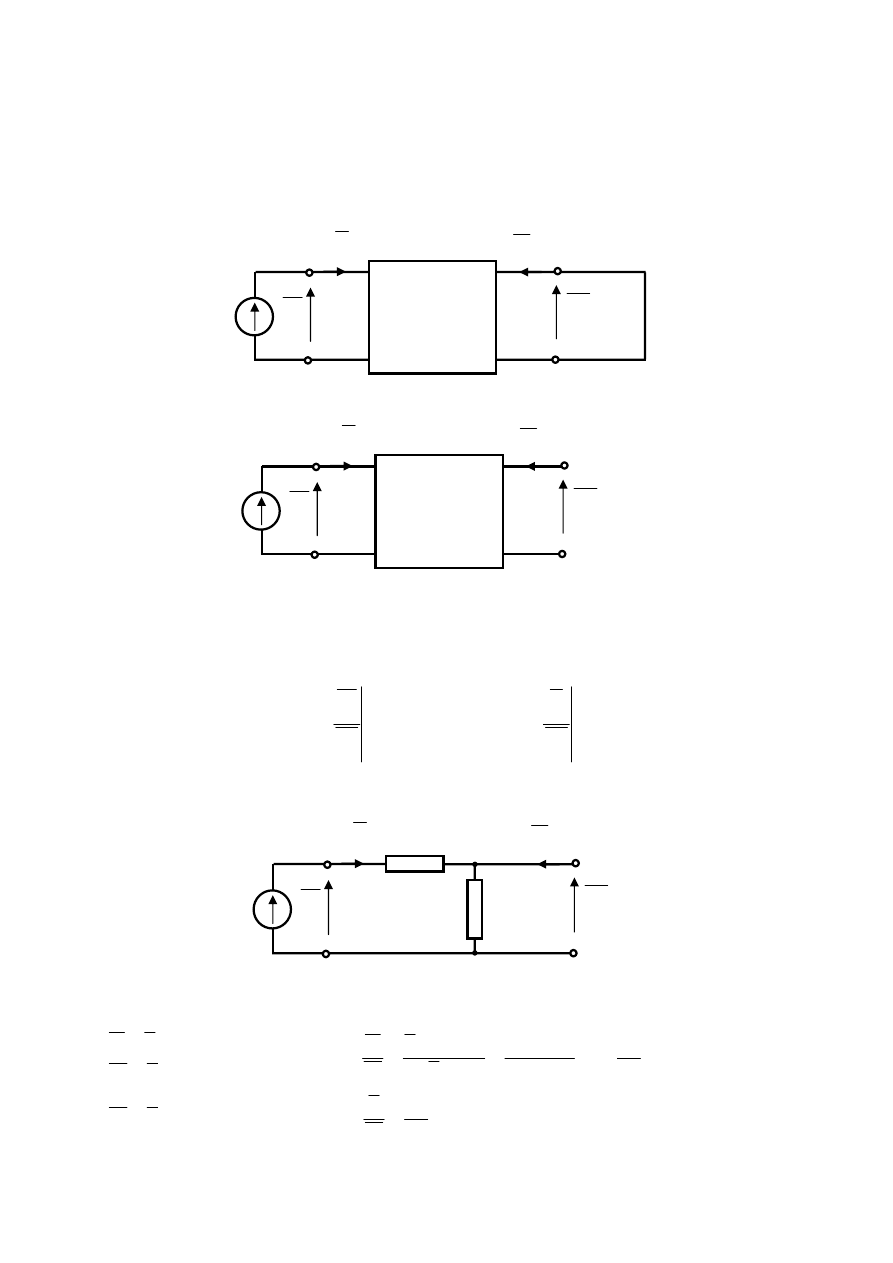
Rys.1.5. Stan rozwarcia zacisków wyjściowych analizowanego czwórnika
Na podstawie rys.1.5 można sformułować równania:
(
)
(
) (
)
2
2
1
21
2
1
2
2
1
2
2
1
2
1
2
1
1
2
1
11
2
1
2
2
1
1
1
1
1
Z
u
i
a
Z
i
u
Z
Z
Z
Z
Z
Z
i
Z
Z
i
u
u
a
Z
i
u
Z
Z
i
u
=
=
⇒
=
+
=
+
=
+
=
=
⇒
=
+
=
4
Wyrazy
oraz
a
zostaną wyznaczone na podstawie analizy stanu zwarcia zacisków
wyjściowych czwórnika
12
a
22
2
1
2
1
0
22
0
12
2
2
i
i
i
u
u
u
a
a
−
−
=
=
=
=
(1.6)
Odpowiada to następującemu stanowi analizowanego czwórnika:
2
i
1
i
1
u
0
2
=
u
Z
1
Z
2
Rys.1.6. Stan zwarcia zacisków wyjściowych analizowanego czwórnika
Na podstawie rys.1.6 można sformułować równania:
1
2
1
22
1
2
1
1
1
1
2
1
12
1
2
1
1
1
=
−
=
⇒
−
=
=
=
−
=
⇒
−
=
=
i
i
a
i
i
Z
i
Z
i
i
u
a
i
i
Z
i
u
Poszukiwana macierz łańcuchowa czwórnika to:
+
=
1
1
1
2
1
2
1
Z
Z
Z
Z
A
Zadanie 2
Wyznacz opis admitancyjny czwórnika typu Π przedstawionego na rys.2.1.
Y
1
2
’
1
Y
2
Y
1
1
’
2
Rys.2.1
Rozwiązanie
5
Opis admitancyjny czwórnika przedstawiają równania (2.1) ÷ (2.3).
(2.1)
2
22
1
21
2
2
12
1
11
1
u
y
u
y
i
u
y
u
y
i
+
=
+
=
W postaci macierzowej:
(2.2)
=
2
1
2
1
u
u
i
i
Y
gdzie:
(2.3)
=
22
21
12
11
y
y
y
y
Y
Podobnie, jak w zadaniu 1, wyrazy macierzy Y zostaną wyznaczone przez analizę dwóch
różnych stanów czwórnika. Z zależności (2.1) wynika, że najwygodniejszym sposobem
wyznaczenia poszukiwanych parametrów będzie analiza czwórnika ze zwartymi zaciskami
wyjściowymi, tzn. dla
oraz ze zwartymi zaciskami wejściowymi, tzn. przy
0
2
=
u
0
1
=
u
.
Pierwszy z tych stanów przedstawia rys.2.2.
1
i
2
i
1
u
0
2
=
u
Y
1
Y
1
Y
2
Rys.2.2. Analizowany czwórnik przy zwartych zaciskach wyjściowych
Dla
u
zależności (2.1) przyjmują postać
0
2
=
1
21
2
1
11
1
u
y
i
u
y
i
=
=
Wynikają z nich następujące wartości dwóch poszukiwanych parametrów:
0
1
2
21
0
1
1
11
2
2
=
=
=
=
u
u
u
i
y
u
i
y
Analiza obwodu z rys.2.2 pozwala na sformułowanie następujących równań, z których
wynikają poszukiwane parametry:
(
)
2
0
1
2
21
1
2
2
2
1
0
1
1
11
1
2
1
1
2
1
1
1
2
2
Y
u
i
y
u
Y
i
Y
Y
u
i
y
u
Y
Y
u
Y
u
Y
i
u
u
−
=
=
⇒
⋅
=
−
+
=
=
⇒
+
=
⋅
+
⋅
=
=
=
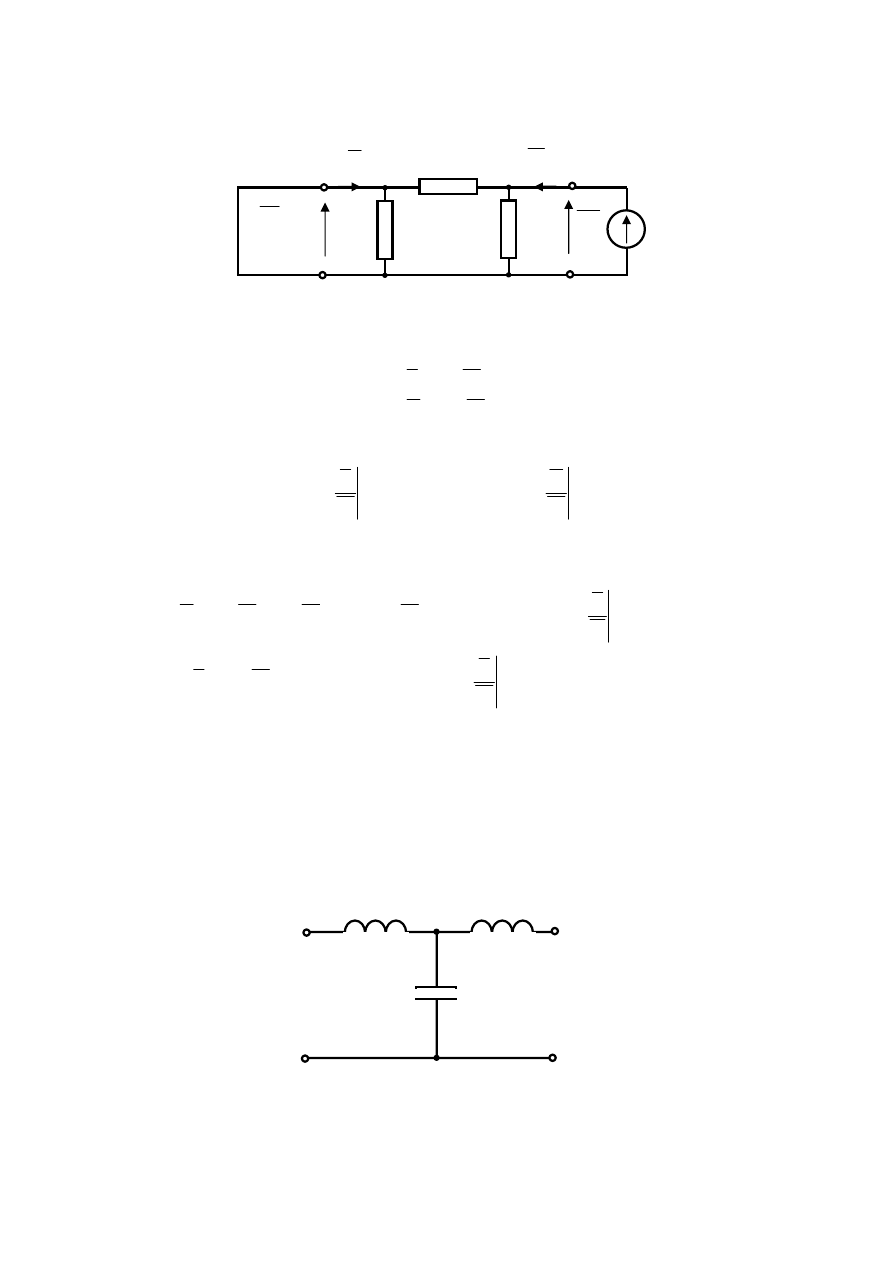
Drugi z analizowanych stanów to stan zwarcia zacisków wejściowych czwórnika,
0
1
=
u
.
Stan ten przedstawiony jest na rys.2.3
6
2
i
1
i
0
1
=
u
2
u
Y
1
Y
1
Y
2
Rys.2.3. Analizowany czwórnik przy zwartych zaciskach wejściowych
Dla
u
zależności (2.1) przyjmują postać:
0
1
=
2
22
2
2
12
1
u
y
i
u
y
i
=
=
Wynikają z nich następujące wartości dwóch poszukiwanych parametrów:
0
2
2
22
0
2
1
12
1
1
=
=
=
=
u
u
u
i
y
u
i
y
Analiza obwodu z rys.2.3 pozwala na sformułowanie następujących równań, z których
wynikają poszukiwane parametry:
(
)
2
0
2
1
12
2
2
1
2
1
0
1
1
22
2
2
1
2
2
2
1
2
2
2
Y
u
i
y
u
Y
i
Y
Y
u
i
y
u
Y
Y
u
Y
u
Y
i
u
u
−
=
=
⇒
⋅
=
−
+
=
=
⇒
+
=
⋅
+
⋅
=
=
=
Poszukiwana macierz admitancyjna to:
+
−
−
+
=
2
1
2
2
2
1
Y
Y
Y
Y
Y
Y
Y
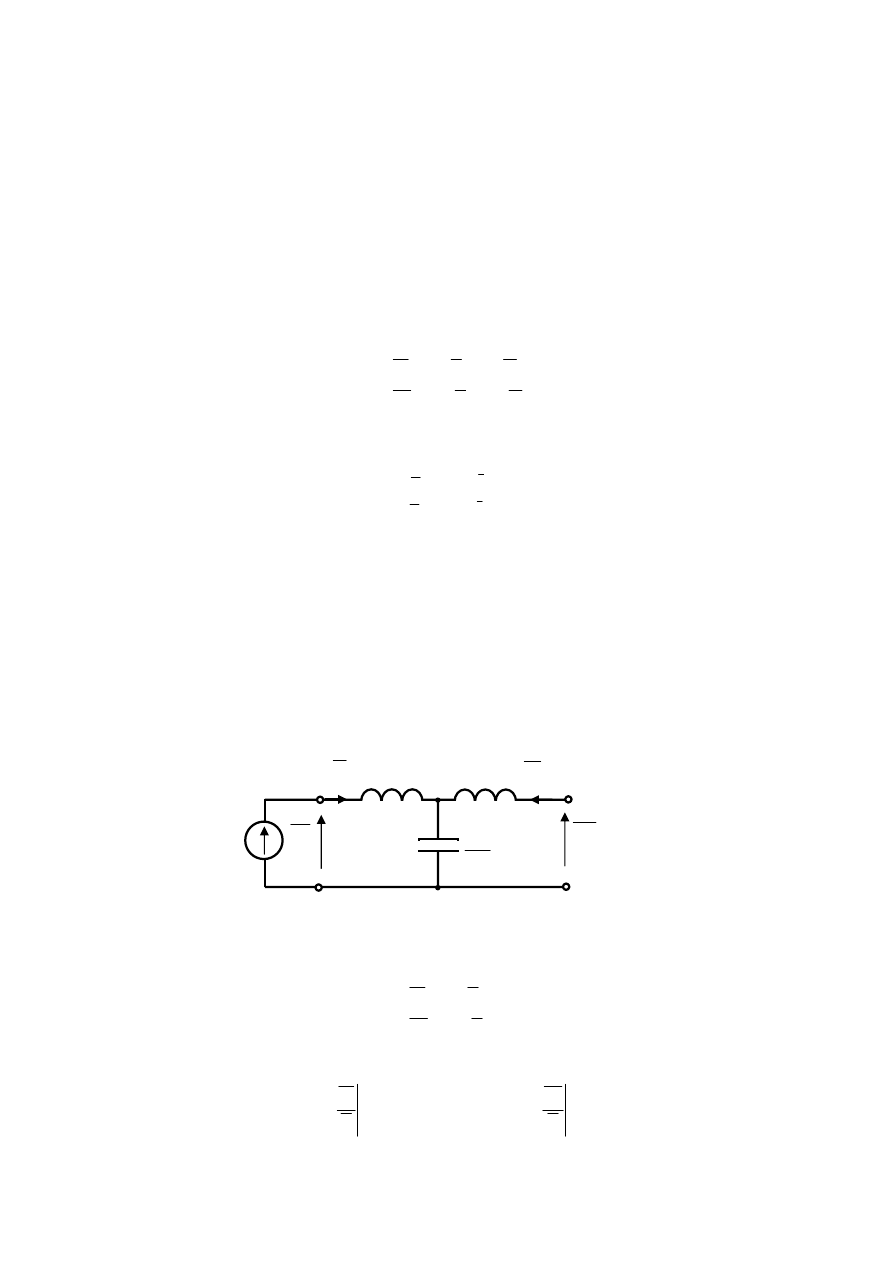
Zadanie 3
L
2
’
1
C
L
1
’
2
Rys.3.1
7
1. Wyznacz opis impedancyjny czwórnika typu T przedstawionego na rys.3.1 na
podstawie analizy dwóch wybranych jego stanów.
2. Wyznacz opis hybrydowy czwórnika korzystając z wyznaczonego w punkcie 1 opisu
impedancyjnego.
Rozwiązanie
Punkt 1
Opis impedancyjny czwórnika przedstawiają równania (3.1) ÷ (3.3).
(3.1)
2
22
1
21
2
2
12
1
11
1
i
z
i
z
u
i
z
i
z
u
+
=
+
=
W postaci macierzowej:
(3.2)
=
2
1
2
1
i
i
u
u
Z
gdzie:
(3.3)
=
22
21
12
11
z
z
z
z
Z
Podobnie, jak w zadaniu 1, wyrazy macierzy Z zostaną wyznaczone przez analizę dwóch
różnych stanów czwórnika. Z zależności (3.1) wynika, że najwygodniejszym sposobem
wyznaczenia poszukiwanych parametrów będzie analiza czwórnika z rozwartymi zaciskami
wyjściowymi, tzn. dla
i
oraz z rozwartymi zaciskami wejściowymi, tzn. przy
0
=
0
2
1
=
i
.
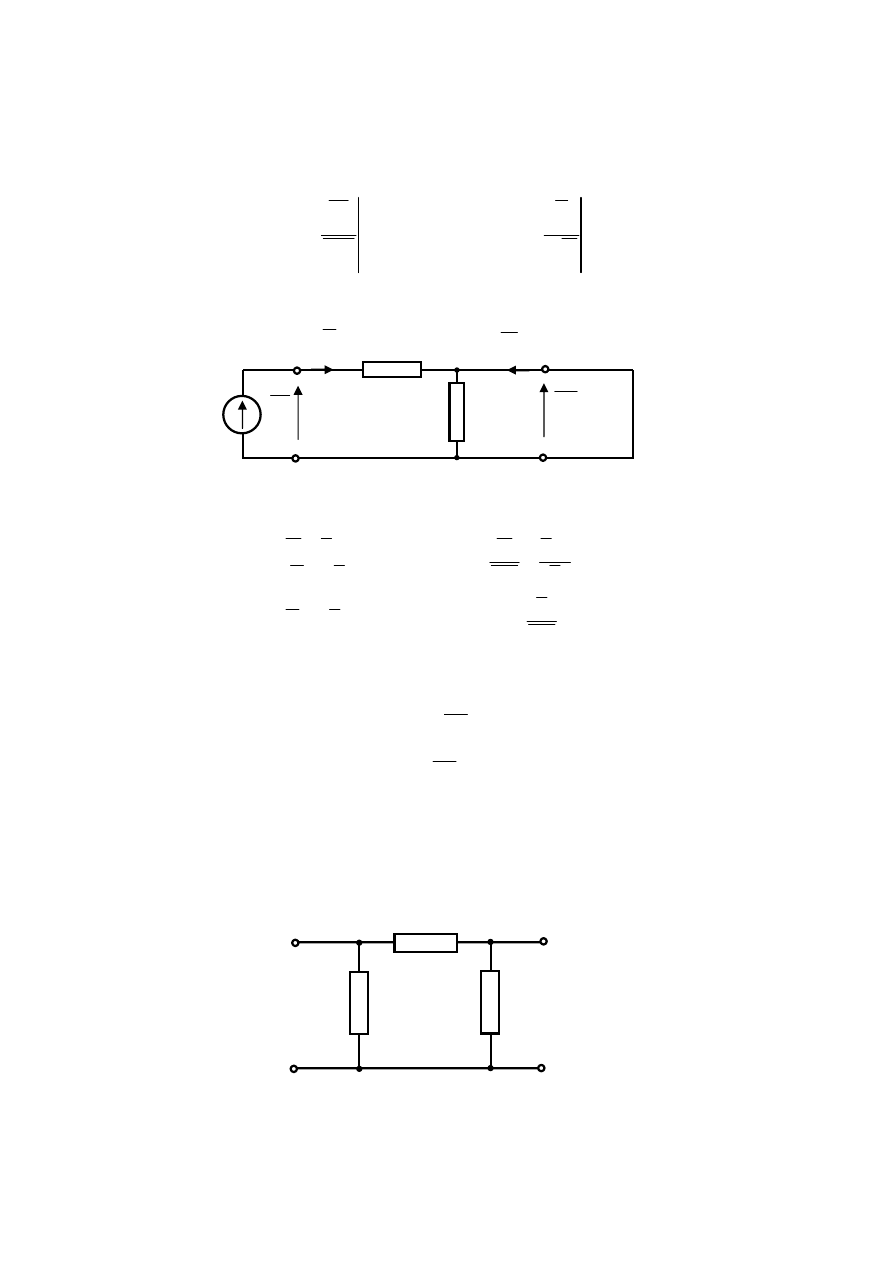
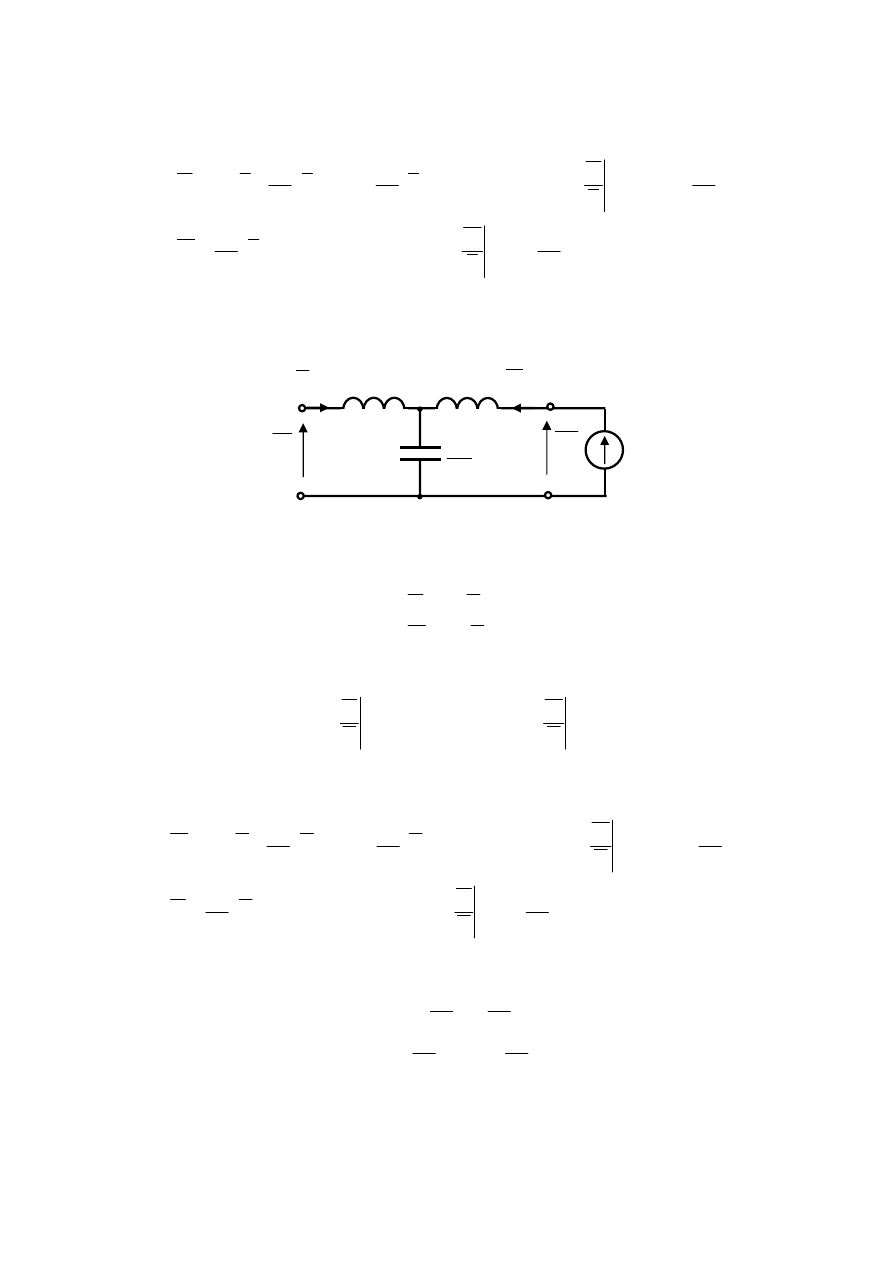
Pierwszy z tych stanów przedstawia rys.3.2.
1
i
0
2
=
i
1
u
2
u
sC
1
sL
sL
Rys.3.2. Analizowany czwórnik przy rozwartych zaciskach wyjściowych
Dla
i
zależności (3.1) przyjmują postać
0
2
=
1
21
2
1
11
1
i
z
u
i
z
u
=
=
Wynikają z nich następujące wartości dwóch poszukiwanych parametrów:
0
1
2
21
0
1
1
11
2
2
=
=
=
=
i
i
i
u
y
i
u
z
8
Analiza obwodu z rys.3.2 pozwala na sformułowanie następujących równań, z których
wynikają poszukiwane parametry:
sC
i
u
z
i
sC
u
sC
sL
i
u
z
i
sC
sL
i
sC
i
sL
u
i
i
1
1
1
1
1
0
1
2
21
1
2
0
1
1
11
1
1
1
1
2
2
=
=
⇒
⋅
=
+
=
=
⇒
+
=
⋅
+
⋅
=
=
=
Drugi z analizowanych stanów to stan rozwarcia zacisków wejściowych czwórnika,
0
1
=
i
.
Stan ten przedstawiony jest na rys.3.3.
2
i
0
1
=
i
2
u
sL
sC
1
sL
1
u
Rys.3.3. Analizowany czwórnik przy rozwartych zaciskach wejściowych
Dla
i
zależności (3.1) przyjmują postać:
0
1
=
2
22
2
2
12
1
i
z
u
i
z
u
=
=
Wynikają z nich następujące wartości dwóch poszukiwanych parametrów:
0
2
2
22
0
2
1
12
1
1
=
=
=
=
i
i
i
u
z
i
u
z
Analiza obwodu z rys.3.3 pozwala na sformułowanie następujących równań, z których
wynikają poszukiwane parametry:
sC
i
u
z
i
sC
u
sC
sL
i
u
z
i
sC
sL
i
sC
i
sL
u
i
i
1
1
1
1
1
0
2
1
12
2
1
0
2
2
22
2
2
2
2
1
1
=
=
⇒
⋅
=
+
=
=
⇒
+
=
⋅
+
⋅
=
=
=
Poszukiwana macierz impedancyjna to:
+
+
=
sC
sL
sC
sC
sC
sL
1
1
1
1
Z
Punkt 2
Równania hybrydowe czwórnika przedstawiają zależności (3.4) ÷ (3.6)
9
(3.4)
2
22
1
21
2
2
12
1
11
1
u
h
i
h
i
u
h
i
h
u
+
=
+
=
W postaci macierzowej:
(3.5)
=
2
1
2
1
u
i
i
u
H
gdzie:
(3.6)
=
22
21
12
11
h
h
h
h
H
Poszukiwane parametry zostaną wyznaczone przez rozwiązanie równań (3.1) o znanych
współczynnikach względem napięcia
oraz prądu
. Pierwsze z równań (3.4) jest
związkiem napięć
oraz prądu . Z równań (3.1) należy zatem wyeliminować prąd
i
.
Pomnożenie drugiego z równań przez
1
u
2
i
2
1
u
,
u
1
i
2
22
12
z
z
−
a następnie dodanie stronami obu równań
pozwala na osiągnięcie tego celu.
2
12
1
22
21
12
2
22
12
2
12
1
11
1
i
z
i
z
z
z
u
z
z
i
z
i
z
u
−
−
=
−
+
=
Po dodaniu stronami i uporządkowaniu otrzymanego równania zgodnie z pierwszym
równaniem (3.4) otrzymuje się:
2
22
12
1
22
21
12
11
2
22
12
1
22
21
12
1
11
1
1
22
21
12
1
11
2
22
12
1
u
z
z
i
z
z
z
z
u
z
z
i
z
z
z
i
z
u
i
z
z
z
i
z
u
z
z
u
+
−
=
+
−
=
−
=
−
Porównanie ostatniej zależności z pierwszym równaniem (3.4) prowadzi do równań:
22
12
12
22
21
12
11
11
z
z
h
z
z
z
z
h
=
−
=
Przekształcenie drugiego równania (3.1) do postaci zgodnej z drugim równaniem (3.4) daje
następujący wynik:
2
22
1
22
21
2
2
22
1
21
2
1
u
z
i
z
z
i
i
z
i
z
u
+
−
=
+
=
Porównanie ostatniego równania z drugim równaniem (3.4) prowadzi do następujących
wyników:
10
22
22
22
21
21
1
z
h
z
z
h
=
−
=
Poszukiwana macierz hybrydowa to:
−
−
=
22
22
21
22
12
22
21
12
11
1
z
z
z
z
z
z
z
z
z
H
Po uwzględnieniu wyznaczonych w punkcie wartości elementów macierzy Z otrzymuje się:
(
)
(
)
(
)
(
)
(
)
+
+
−
+
+
+
=
+
=
+
=
=
+
−
=
−
=
+
=
=
+
+
=
+
−
+
=
+
⋅
−
+
=
−
=
1
1
1
1
1
1
2
1
1
1
1
1
1
1
1
1
2
1
1
1
1
1
1
1
2
2
2
2
2
2
22
22
2
22
21
21
2
22
12
12
2
2
2
2
22
21
12
11
11
LC
s
sC
LC
s
LC
s
LC
s
LC
s
sL
LC
s
sC
sC
sL
z
h
LC
s
z
z
h
LC
s
z
z
h
LC
s
LC
s
sL
LC
s
sC
sC
LC
s
sC
sL
sC
sC
sC
sL
z
z
z
z
h
H
Zadanie 4
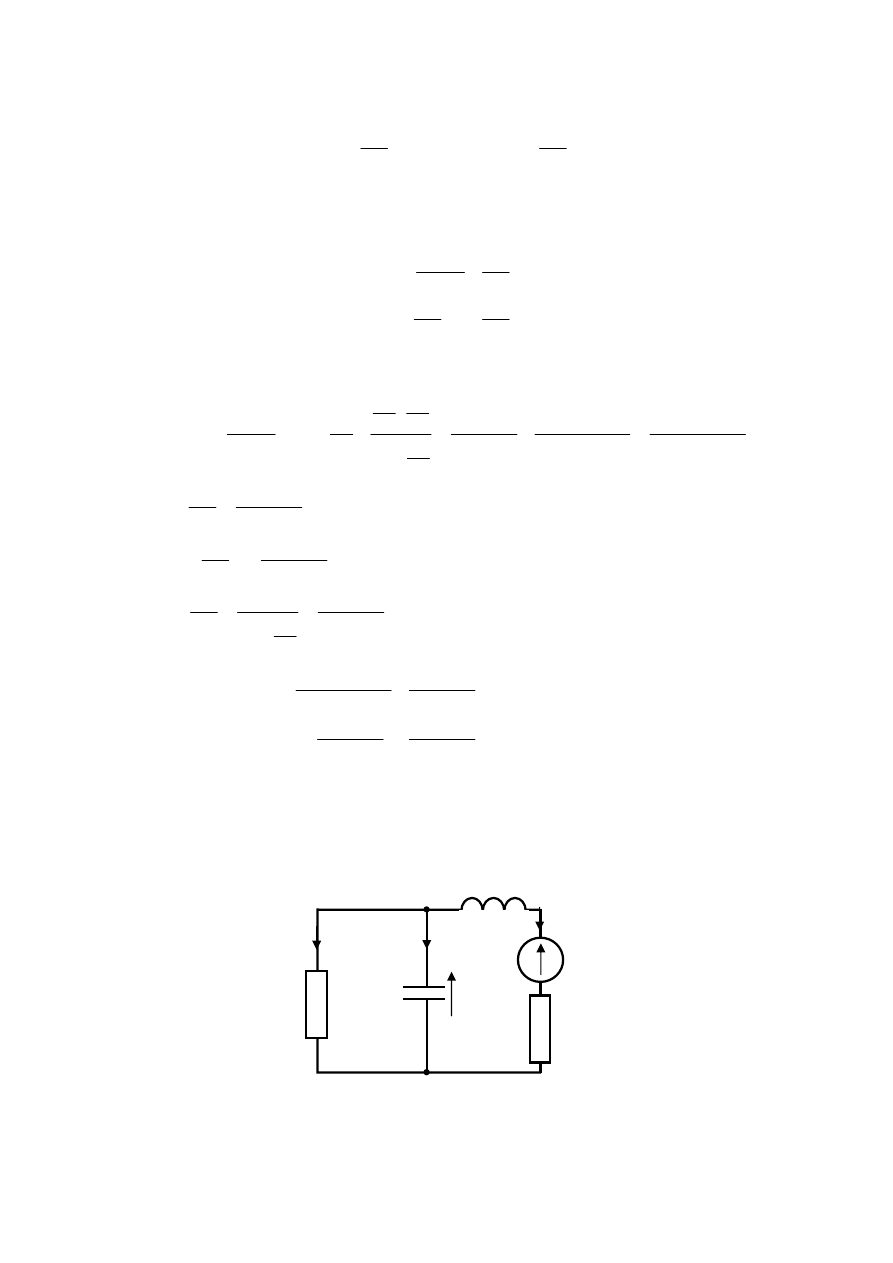
Wyznacz opis stanowy obwodu przedstawionego na rys.4.1.
L
i
L
i
R
Rys.4.1
C
e
u
C
i
C
R
2
R
1
11
Rozwiązanie
Opis stanowy układu liniowego ma postać:
(4.1)
( )
t
t
b
Ax
x
+
=
d
d
gdzie:
(4.2)
[ ]
n
n
ij
a
×
=
A
jest macierzą stanu,
(4.3)
[
]
T
1
n
x
x K
=
x
jest wektorem stanu, jego składowe
n
,
i
x
i
K
1
;
=
to zmienne stanu,
n jest rzędem obwodu a
(4.4)
( )
( )
[
]
T
1
t
b
t
b
n
K
=
b
to wektor źródłowy. Wektor
(4.5)
T
1
d
d
d
d
d
d
=
t
x
t
x
t
n
K
x
jest wektorem pochodnych zmiennych stanu. Zależność (4.1) przedstawia
n równań
następującej postaci :
( )
( )
( )
t
b
x
a
x
a
x
a
t
x
t
b
x
a
x
a
x
a
t
x
t
b
x
a
x
a
x
a
t
x
n
n
nn
n
n
n
n
n
n
n
+
+
+
+
=
+
+
+
+
=
+
+
+
+
=
K
M
K
K
2
2
1
1
2
2
2
22
1
21
2
1
1
2
12
1
11
1
d
d
d
d
d
d
(4.6)
Cechą charakterystyczną równań (4.6) jest to, że po lewej stronie każdego równania
występuje pochodna zmiennej stanu, w każdym równaniu innej, po prawej stronie mogą
występować wszystkie zmienne stanu z odpowiednimi współczynnikami oraz elementy
wektora źródłowego.
Obwód z rys.4.1 jest układem drugiego rzędu. Jako zmienne stanu przyjęte zostają: napięcie
na kondensatorze
( )
t
C
u
oraz prąd płynący przez cewkę
( )
t
i
L
. W przypadku prostych
obwodów, takich jak przedstawiony na rys.4.1, równania stanu można sformułować
posługując się prawami Kirchhoffa oraz zależnościami elementarnymi.
Prądowe prawo Kirchoffa dla każdego z dwóch węzłów obwodu ma postać:
0
=
+
+
L
C
R
i
i
i
Wielkość
( )
t
i
L
jest zmienną stanu,
( )
t
C
i
- pochodną zmiennej stanu. Z równania należy
zatem wyeliminować tylko prąd
( )
t
i
R
zastępując go wyrażeniem zależnym wyłącznie od
zmiennych stanu oraz ewentualnie prądu
( )
t
i
C
. Podstawiając:
2
R
u
i
C
R
=
12
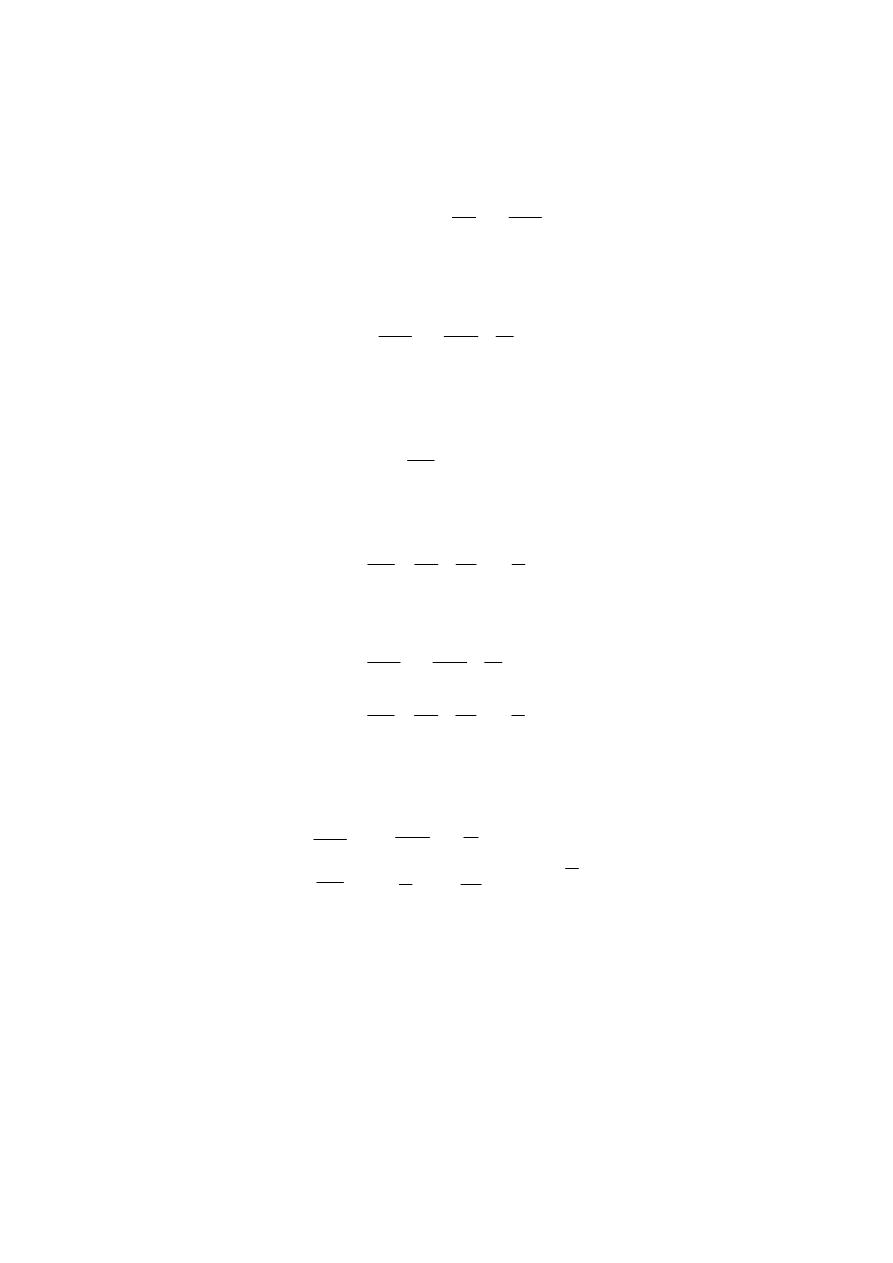
otrzymuje się zależność, która nie zawiera żadnych wielkości obwodowych poza zmiennymi
stanu oraz pochodną jednej z nich. Jest to zatem równanie stanu w nieuporządkowanej jeszcze
formie.
0
d
d
0
2
=
+
+
⇒
=
+
+
L
C
C
L
C
R
i
t
u
C
R
u
i
i
i
Wynikiem uporządkowania ostatniego równania zgodnie z formatem zależności (4.6) jest
pierwsze z równań stanu:
C
i
CR
u
t
u
L
C
C
−
−
=
2
d
d
W celu wyznaczenia drugiego równania stanu sformułowane zostaje napięciowe prawo
Kirchhoffa dla prawego oczka obwodu z rys.4.1.
0
d
d
1
=
−
−
−
R
i
e
t
i
L
u
L
L
C
Jest to równanie stanu, które wymaga uporządkowania zgodnie z zależnością (4.6).
L
e
i
L
R
L
u
t
i
L
C
L
−
−
=
1
d
d
Poszukiwany opis stanowy to:
L
e
i
L
R
L
u
t
i
C
i
CR
u
t
u
L
C
L
L
C
C
−
−
=
−
−
=
1
2
d
d
d
d
lub w postaci macierzowej:
−
+
−
−
−
=
L
e
i
u
L
R
L
C
CR
t
i
t
u
L
C
L
C
0
1
1
1
d
d
d
d
1
2
Zadanie 5
Na rys.5.1 przedstawiony jest obwód dynamiczny zawierający cewki i kondensatory.
Wyznacz rząd tego obwodu.
Rozwiązanie
Rząd obwodu jest najmniejszą liczbą warunków początkowych niezbędnych do
jednoznacznego określenia stanu obwodu w dowolnej chwili.
13
R
1
L
7
j
9
i
7
L
5
C
4
C
3
e
8
R
2
L
6
u
3
i
6
i
5
u
4
Rys.5.1
Dla obwodów zawierających niezależne źródła napięciowe i prądowe oraz elementy R, L i C
(bez źródeł sterowanych) rząd obwodu jest równy liczbie cewek i kondensatorów obecnych w
obwodzie pomniejszonej o liczbę pętli CE (pętli zawierających wyłącznie kondensatory oraz
idealne źródła napięciowe) oraz liczbę przekrojów LJ (przekrojów zawierających wyłącznie
gałęzie z cewkami oraz idealnymi źródłami prądowymi).
(5.1)
CE
LJ
C
L
n
n
n
n
n
−
−
+
=
gdzie: n jest rzędem obwodu, n
L
– liczbą cewek w obwodzie, n
C
– liczbą kondensatorów w
obwodzie, n
LJ
– liczbą przekrojów LJ a n
CE
– liczbą pętli CE.
Przedstawiony obwód zawiera 2 kondensatory oraz 3 cewki. Pierwszym przybliżeniem rzędu
obwodu jest liczba 5 (suma cewek i kondensatorów. Rząd obwodu ulega jednak obniżeniu o
liczbę pętli CE oraz liczbę przekrojów LJ. Na rys.5.2 przedstawione zostały znalezione pętle
CE oraz przekroje LJ.
j
9
C
3
e
8
L
7
R
1
R
2
C
4
L
6
L
5
u
3
i
5
i
6
i
7
u
4
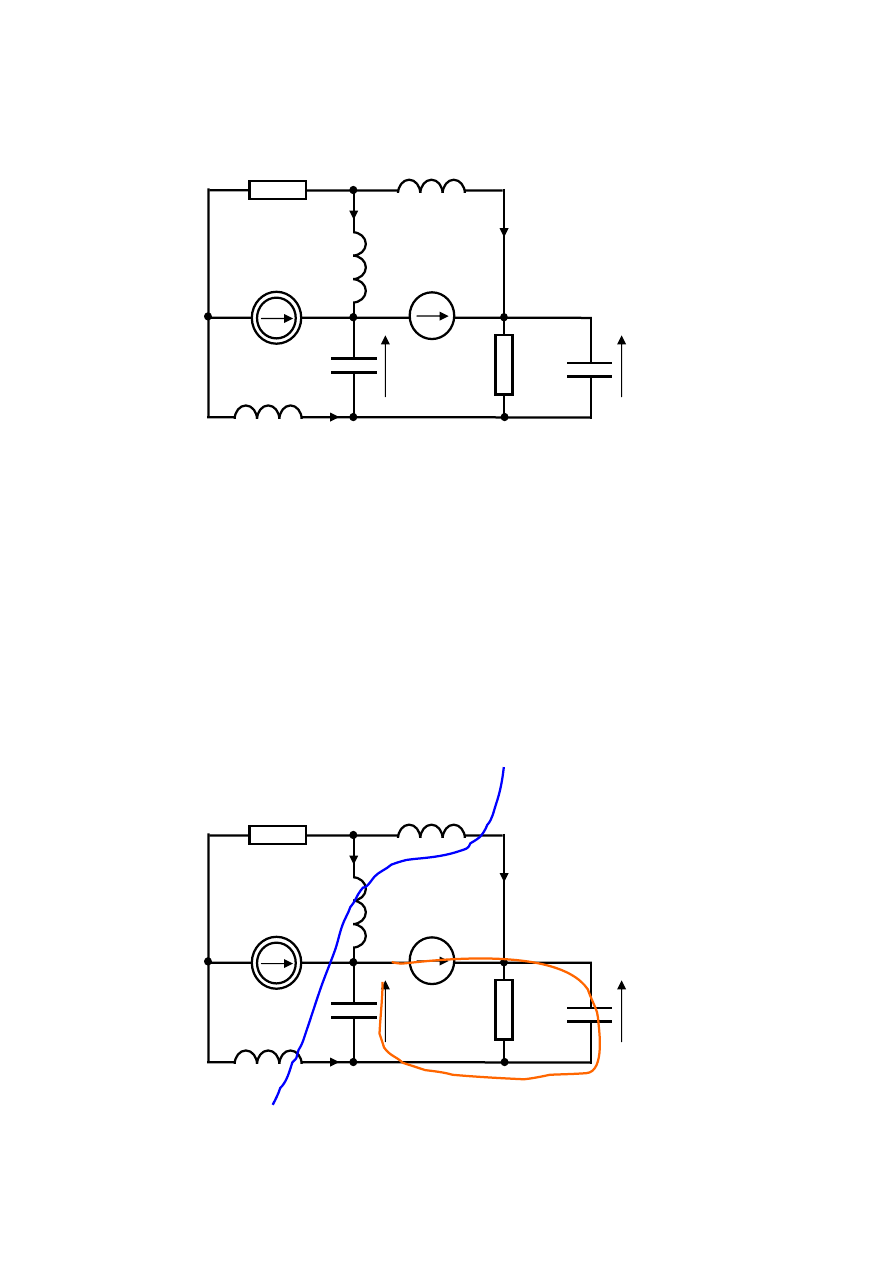
Rys.5.2. Znalezione w obwodzie pętle CE oraz przekroje LJ.
14
W obwodzie jest jedna pętla CE, oznaczona kolorem czerwonym na rys.5.2 oraz jeden
przekrój LJ oznaczony na niebiesko na rys.5.2. Można sformułować zatem dwa równania. Dla
pętli CE – napięciowe prawo Kirchhoffa:
0
4
8
3
=
−
+
u
e
u
oraz dla przekroju LJ – prądowe prawo Kirchhoffa
0
7
6
9
5
=
+
+
+
i
i
j
i
Pierwsze równanie pozwala na wyznaczenie jednego z napięć na kondensatorach u
3
lub u
4
jeżeli znamy wartość drugiego. Jeden z warunków początkowych dla napięć na
kondensatorach staje się zbyteczny a rząd obwodu obniża się o 1. Drugie równanie pozwala
na obliczenie jednego z prądów cewek: i
5,
i
6
lub i
7
gdy znamy wartości dwóch pozostałych.
Jeden z warunków początkowych dla prądów staje się niepotrzebny a rząd obwodu ulega
obniżeniu o 1. Rząd obwodu wynosi zatem 3.
Zadanie 6
Na rys.6.1 przedstawiony jest obwód dynamiczny zawierający cewki i kondensatory.
Wyznacz opis stanowy tego obwodu. Jako zmienne stanu przyjmij prąd cewki
L
i
oraz
napięcia na kondensatorach:
i u
.
1
C
u
2
C
u
C1
j
R
1
R
2
R
3
R
4
R
5
i
L
L
C
1
C
2
u
C2
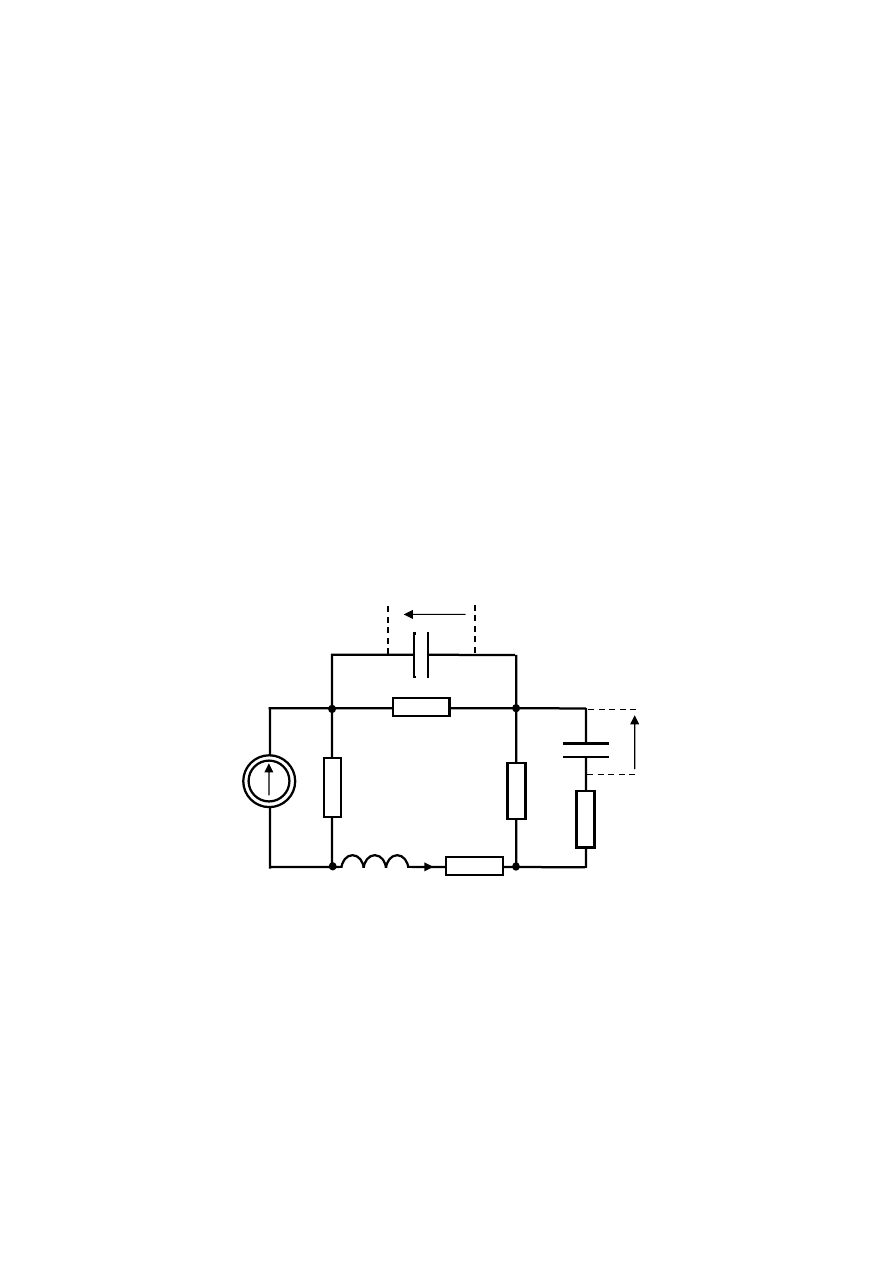
Rys.6.1
Rozwiązanie
Do rozwiązania problemu zostanie zastosowana następująca koncepcja wyznaczania opisu
stanowego. Kolejność postępowania jest następująca:
1. zastąpienie kondensatorów źródłami napięcia o wartościach napięć źródłowych
równych napięciom na kondensatorach (są to zmienne stanu) oraz zastąpieniu cewek
źródłami prądu o wartościach prądów źródłowych równych prądom płynącym przez
cewki (są to też zmienne stanu)
2. rozwiązanie otrzymanego w ten sposób obwodu rezystancyjnego względem prądów
kondensatorów oraz napięć na cewkach
3. wprowadzenie do otrzymanych równań zależności:
15
(6.1)
t
i
L
u
t
u
C
i
L
L
C
C
d
d
d
d
=
=
4. podzielenie równań przez C lub odpowiednio L, co kończy formułowanie równań
stanu
Realizacja punktu 1 polega na zastąpieniu kondensatorów C
1
oraz C
2
idealnymi źródłami
napięciowymi o napięciach źródłowych:
i u
oraz zastąpieniu cewki L idealnym
źródłem prądowym o prądzie źródłowym
1
C
u
2
C
L
i
. Prowadzi to do otrzymania obwodu
rezystancyjnego przedstawionego na rys.6.2.
i
C1
R
1
R
2
R
3
R
4
R
5
i
L
u
C2
j
u
C1
u
L
i
C2
Rys.6.2. Obwód rezystancyjny otrzymany po wprowadzeniu źródeł
zastępujących kondensatory oraz cewkę
Otrzymany obwód zostanie rozwiązany względem prądów płynących przez źródła napięciowe
zastępujące kondensatory:
oraz
i napięcia panującego na zaciskach źródła prądowego
zastępującego cewkę
1
C
i
2
C
i
L
u
. Zastosowana będzie metoda superpozycji. Wyniki analiz
poszczególnych obwodów, w których obecne są kolejno różne źródła będą oznaczane
górnymi indeksami.
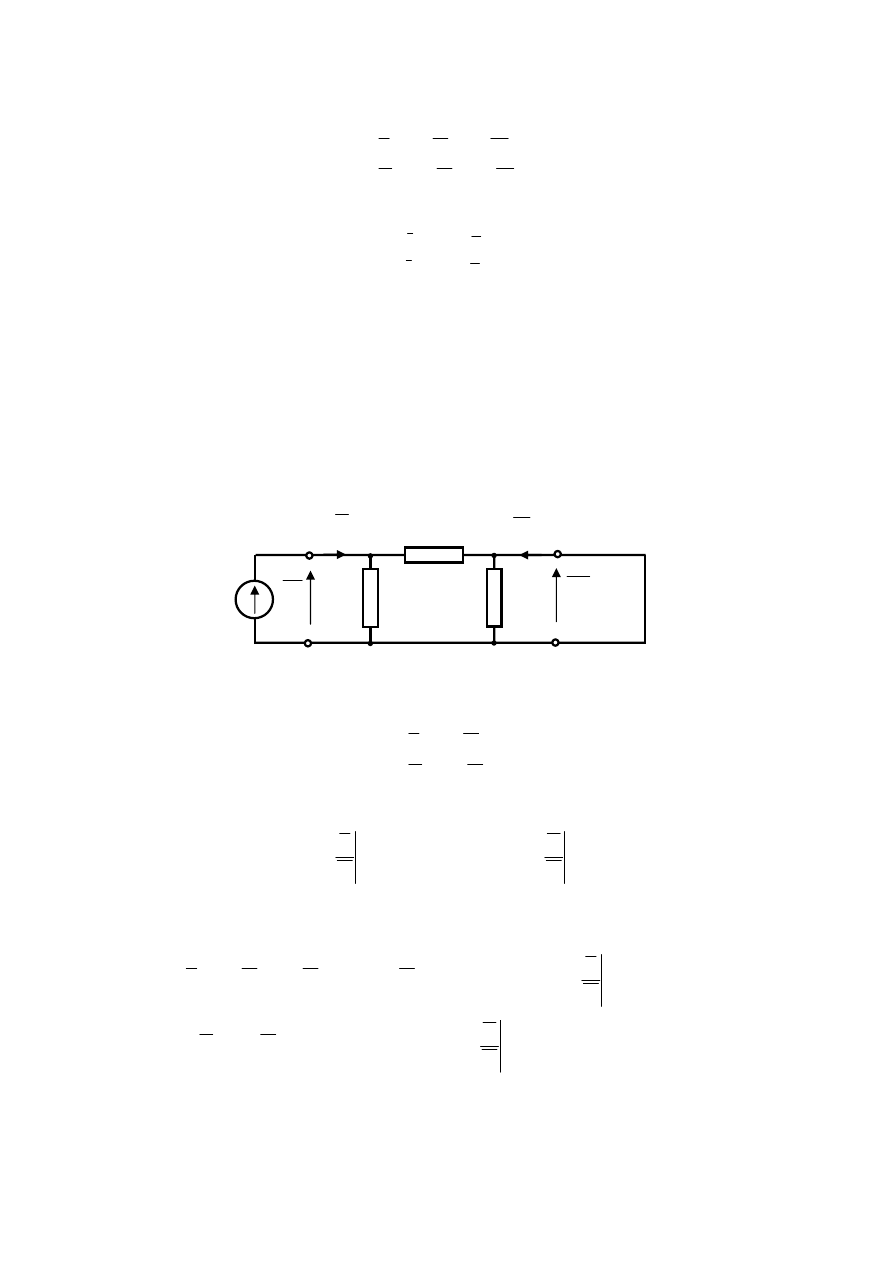
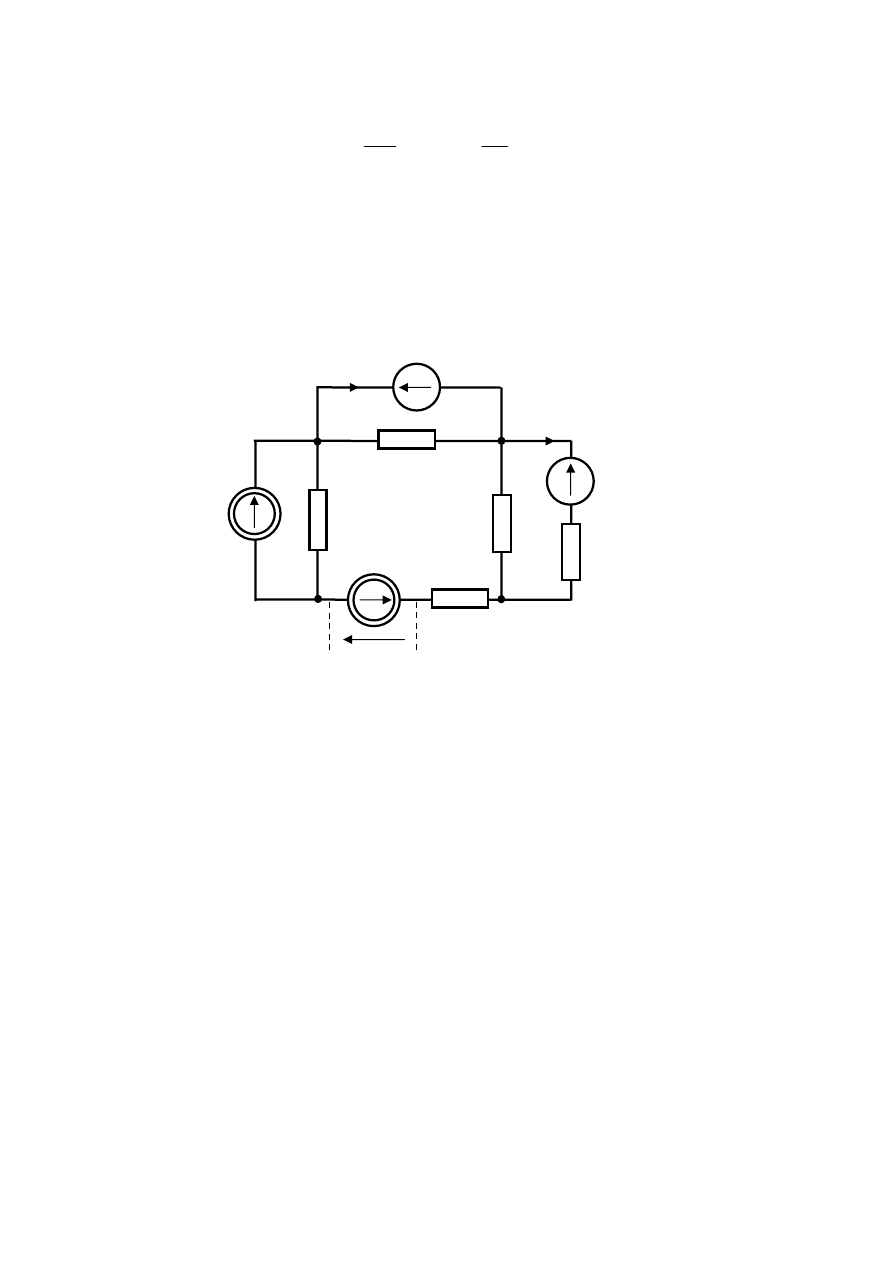
Pierwszym analizowanym obwodem będzie przedstawiony na rys.6.3. Powstał on przez
usunięcie źródeł zastępujących kondensatory i cewkę oraz pozostawienie w obwodzie jedynie
źródła prądowego j. Usunięcie z obwodu źródeł napięciowych związane jest ze zwarciem
zacisków tych źródeł, usunięcie źródła prądowego wymaga pozostawienia jego zacisków
rozwartych.
W obwodzie z rys.6.3 prąd płynie tylko przez opornik R
1
. Jest to prąd źródłowy j. Prądy w
obu gałęziach, w których znajdowały się kondensatory są równe 0.
(6.2)
0
0
1
2
1
1
=
=
)
(
C
)
(
C
i
i
Płynący przez opornik R
1
prąd źródła powoduje powstanie napięcia, które jest równe napięciu
na zaciskach usuniętego źródła prądowego. Jego wartość wynika z prawa Ohma.
(6.3)
1
1
R
j
u
)
(
L
⋅
−
=
16
i
C1
(1)
R
1
R
2
R
3
R
4
j
u
L
(1)
i
C2
(1)
R
5
Rys.6.3. Pierwszy z analizowanych obwodów zbudowany na mocy zasady superpozycji
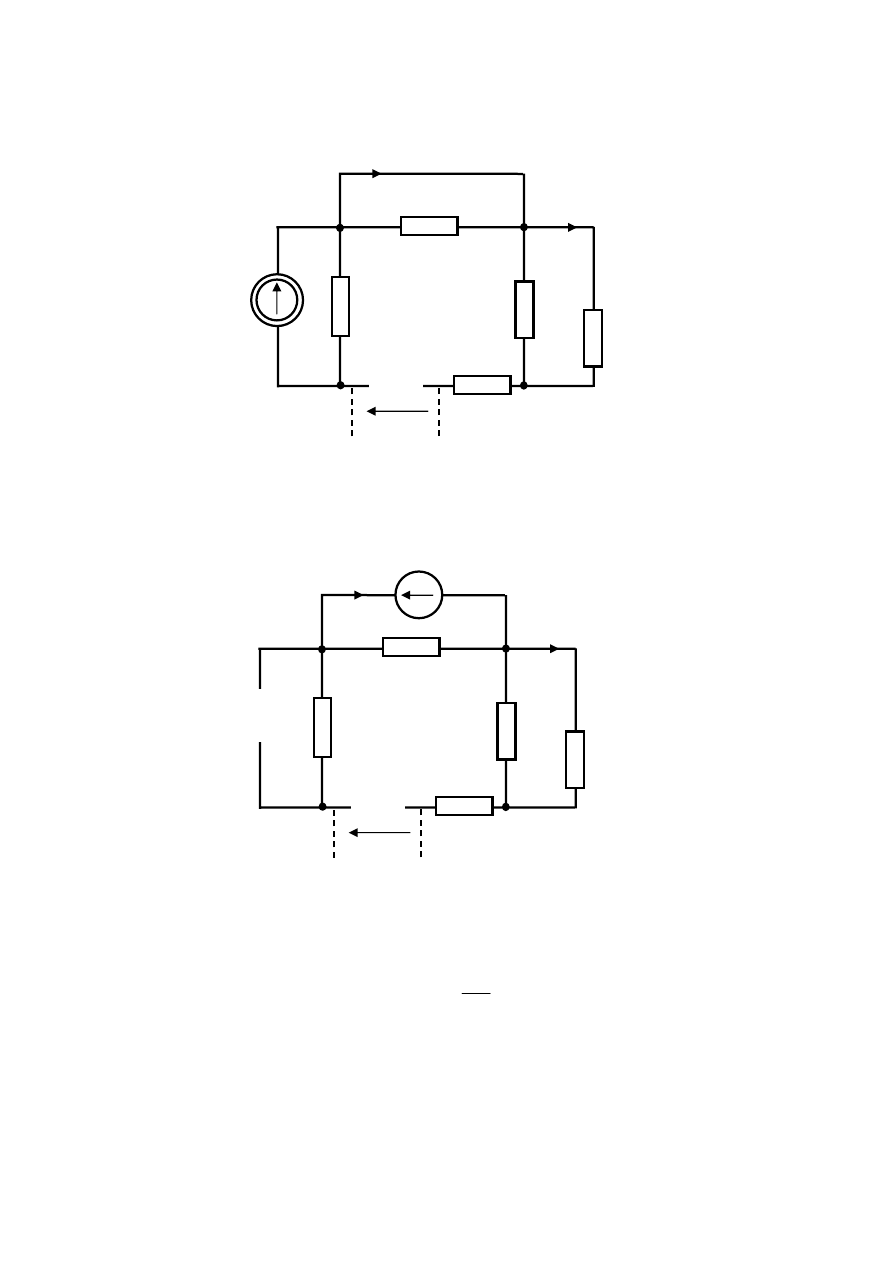
W drugim z analizowanych obwodów pozostawione zostanie źródło napięciowe
. Inne
źródła zostają usunięte. Otrzymany w ten sposób obwód przedstawiony jest na rys.6.4.
1
C
u
u
C1
i
C1
(2)
R
1
R
2
R
3
R
4
u
L
(2)
i
C2
(2)
R
5
Rys.6.4. Drugi z analizowanych obwodów zbudowany na mocy zasady superpozycji
W obwodzie z rys.6.4 źródło
wywołuje przepływ prądu przez opornik R
1
C
u
2
. Jego wartość
wynika z prawa Ohma.
2
1
2
1
R
u
i
C
)
(
C
−
=
(6.4)
Drugi z prądów w gałęziach z kondensatorami to
0 (6.5)
2
2
=
)
(
C
i
17
Ponieważ przez rezystory R
1
oraz R
4
nie płynie prąd, napięcia na ich zaciskach są równe 0.
Napięcie na rozwartych zaciskach źródła prądowego
L
i
jest równe napięciu źródłowemu
.
1
C
u
(6.6)
1
2
C
)
(
L
u
u
=
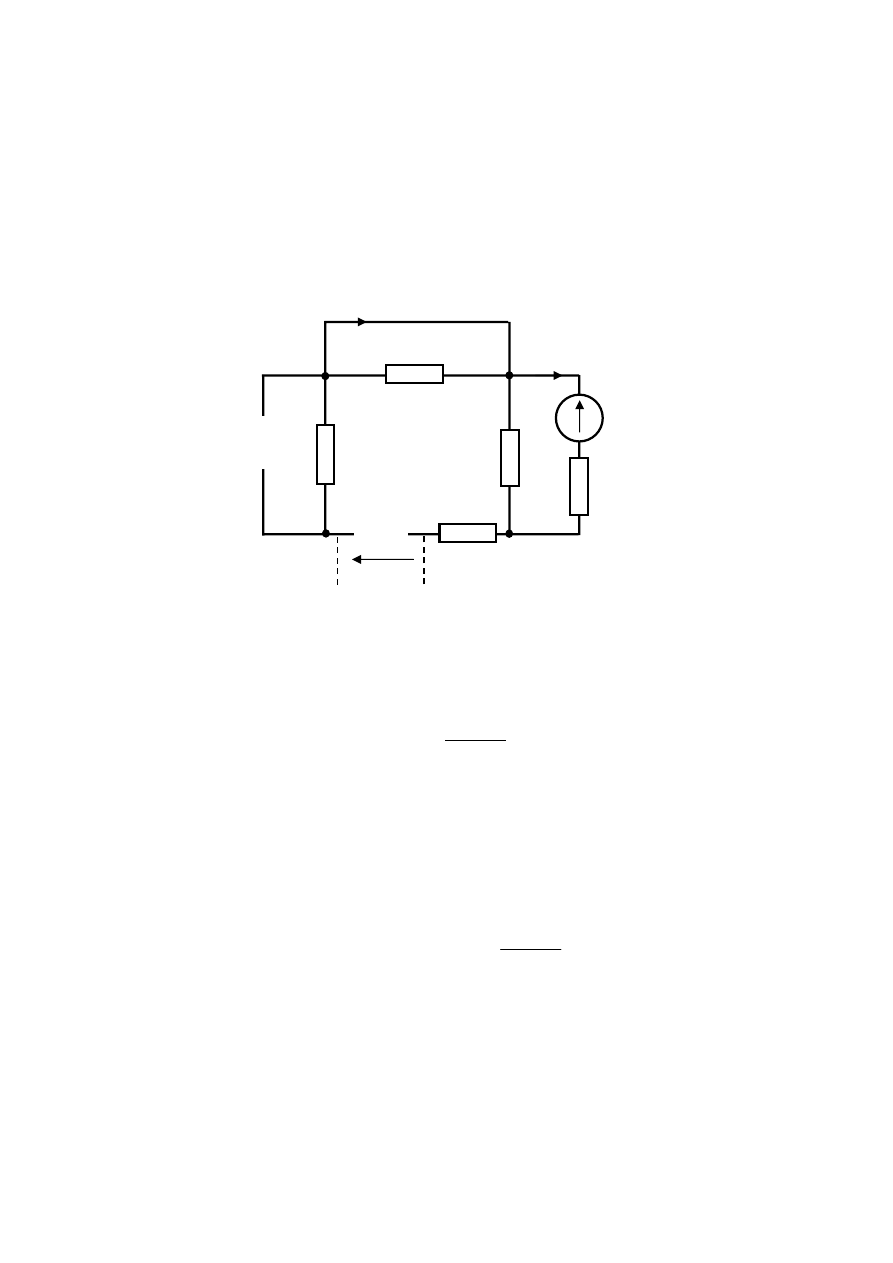
Trzeci z analizowanych obwodów zawierający jedynie źródło
przedstawiony jest na
rys.6.5.
2
C
u
u
C2
i
C1
(3)
R
1
R
2
R
3
R
4
R
5
u
L
(3)
i
C2
(3)
Rys.6.5. Trzeci z analizowanych obwodów zbudowany na mocy zasady superpozycji
W obwodzie z rys.6.5 źródło
wywołuje przepływ prądu przez oporniki R
2
C
u
4
oraz R
5
. Jego
wartość wynika z prawa Ohma.
5
4
2
3
2
R
R
u
i
C
)
(
C
+
−
=
(6.7)
Drugi z prądów w gałęziach z kondensatorami to
(6.8)
0
3
1
=
)
(
C
i
Ponieważ przez rezystory R
1
, R
2
oraz R
3
nie płynie prąd, napięcia na ich zaciskach są równe 0.
Napięcie na rozwartych zaciskach źródła prądowego
L
i
jest równe napięciu panującemu na
zaciskach rezystora R
4
. Wynosi ono:
5
4
4
2
4
3
2
3
R
R
R
u
R
i
u
C
)
(
C
)
(
L
+
=
⋅
−
=
(6.9)
Ostatni z analizowanych obwodów zawierający jedynie źródło prądowe
L
i
przedstawiony
jest na rys.6.6. Prąd źródła
L
i
płynie przez rezystor R
3
, połączony szeregowo ze źródłem,
następnie przez równoległe połączenie oporników R
4
oraz R
5
, przez bezoporową zworę
łączącą zaciski rezystora R
2
i przez opornik R
1
. Prądy w gałęziach, w których były
umieszczone kondensatory wynoszą:
(6.10)
L
)
(
C
i
i
−
=
4
1
18
i na podstawie zależności obowiązującej dla dzielnika prądowego:
5
4
4
4
2
R
R
R
i
i
L
)
(
C
+
−
=
(6.11)
i
L
i
C1
(4)
R
1
R
2
R
3
R
4
u
L
(4)
i
C2
(4)
R
5
Rys.6.6. Czwarty z analizowanych obwodów zbudowany na mocy zasady superpozycji
Napięcie na źródle prądowym
L
i
wynosi zgodnie z napięciowym prawem Kirchhoffa:
+
+
+
−
=
1
5
4
5
4
3
4
R
R
R
R
R
R
i
u
L
)
(
L
(6.12)
Podsumowanie otrzymanych wyników analizy czterech układów dla trzech poszukiwanych
wielkości, przedstawionych przez zależności (6.2) ÷ (6.12) prowadzi do następujących
wzorów:
+
+
+
−
+
+
+
⋅
−
=
+
+
+
=
+
−
+
−
+
=
+
+
+
=
−
+
−
=
+
+
+
=
1
5
4
5
4
3
5
4
4
2
1
1
4
3
2
1
5
4
4
5
4
2
4
2
3
2
2
2
1
2
2
2
1
4
1
3
1
2
1
1
1
1
0
0
0
0
R
R
R
R
R
R
i
R
R
R
u
u
R
j
u
u
u
u
u
R
R
R
i
R
R
u
i
i
i
i
i
i
R
u
i
i
i
i
i
L
C
C
)
(
L
)
(
L
)
(
L
)
(
L
L
L
C
)
(
C
)
(
C
)
(
C
)
(
C
C
L
C
)
(
C
)
(
C
)
(
C
)
(
C
C
(6.13)
Uwzględnienie zależności (6.1) prowadzi do równań stanu:
(
)
(
)
(
)
L
R
R
R
R
R
R
i
L
R
R
R
u
L
u
L
R
j
t
i
C
R
R
R
i
C
R
R
u
t
u
C
i
R
C
u
t
u
L
C
C
L
L
C
C
L
C
C
1
1
d
d
d
d
1
d
d
1
5
4
5
4
3
5
4
4
2
1
1
2
5
4
4
2
5
4
2
2
1
2
1
1
1
+
+
+
−
+
+
+
⋅
−
=
+
−
+
−
=
−
−
=
(6.14)
19
Postać macierzowa tych równań to:
(
)
(
)
(
)
⋅
−
+
⋅
+
+
+
−
+
+
−
+
−
−
−
=
L
R
j
i
u
u
L
R
R
R
R
R
R
L
R
R
R
L
C
R
R
R
C
R
R
C
R
C
t
i
t
u
t
u
L
C
C
L
C
C
1
2
1
1
5
4
5
4
3
5
4
4
2
5
4
4
2
5
4
1
2
1
2
1
0
0
1
1
1
0
1
0
1
d
d
d
d
d
d
(6.15)
Zadanie 7
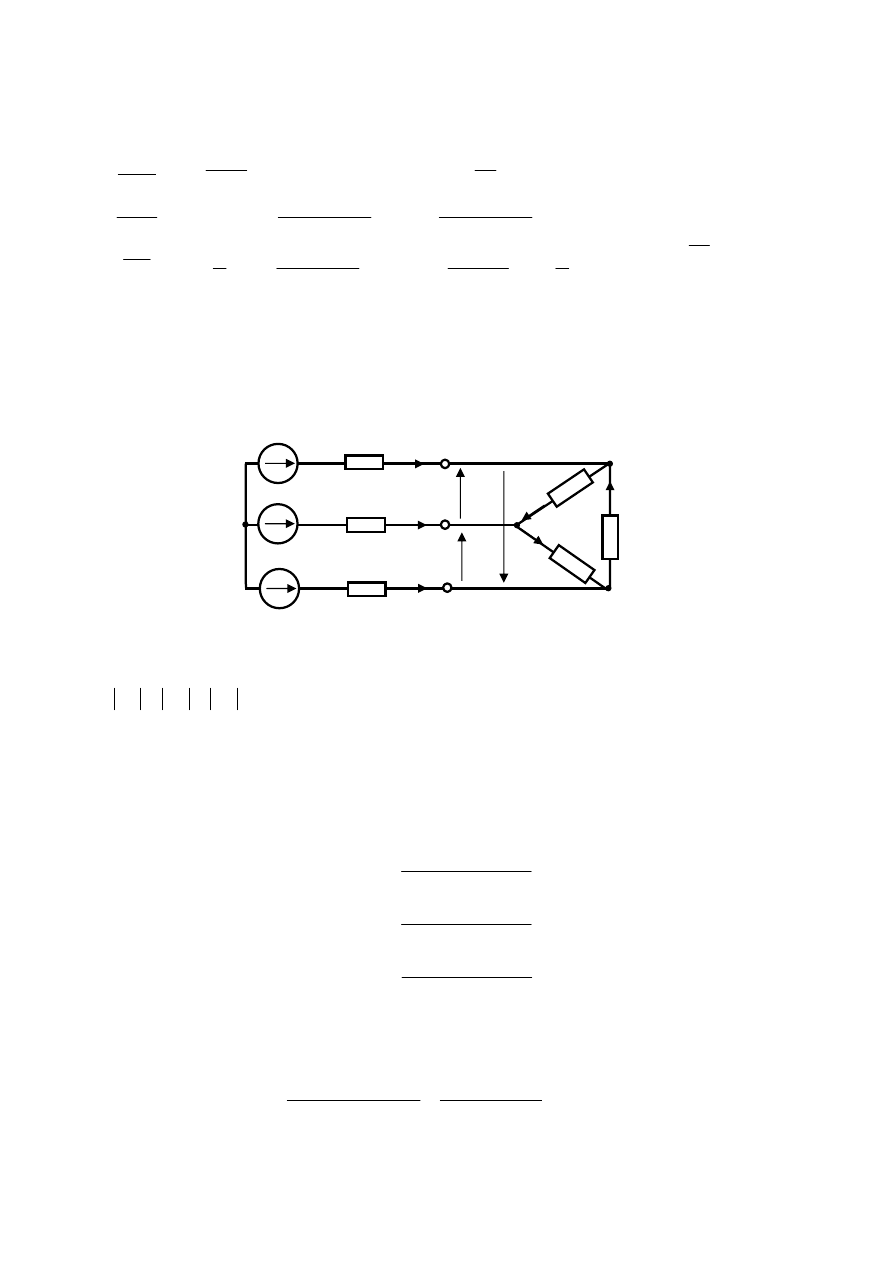
W układzie przedstawionym na rys.7.1 oblicz prądy fazowe i przewodowe oraz
narysuj wykres wskazowy. Generator jest symetryczny.
Z
CA
Z
AB
Z
BC
Z
p
Z
p
C
B
Z
p
A
U
AB
U
BC
I
C
I
B
I
A
E
C
E
A
E
B
I
CA
I
BC
U
CA
I
AB
Rys.7.1
Dane:
(
)
(
Ω
+
=
=
Ω
=
Ω
+
=
=
=
=
50
50
;
100
;
20
10
;
230
j
Z
Z
Z
j
Z
V
E
E
E
CA
BC
AB
p
C
B
A
)
Rozwiązanie
Odbiornik połączony jest w trójkąt. W celu wyznaczenia prądów przewodowych oraz
fazowych należy zamienić trójkąt obciążenia na równoważną gwiazdę zgodnie z
zależnościami podanymi poniżej.
CA
BC
AB
BC
CA
C
CA
BC
AB
AB
BC
B
CA
BC
AB
CA
AB
A
Z
Z
Z
Z
Z
Z
Z
Z
Z
Z
Z
Z
Z
Z
Z
Z
Z
Z
+
+
=
+
+
=
+
+
=
(7.1)
Po wprowadzeniu do zależności (7.1) wartości liczbowych określających impedancje trójkąta
otrzymuje się:
(
) (
)
Ω
+
=
+
+
=
+
+
=
10
30
100
200
50
50
100
j
j
j
Z
Z
Z
Z
Z
Z
CA
BC
AB
CA
AB
A
20
(
) (
)
Ω
+
=
+
+
=
+
+
=
10
30
100
200
50
50
100
j
j
j
Z
Z
Z
Z
Z
Z
CA
BC
AB
AB
BC
B
(
)(
) (
)
Ω
+
=
+
+
+
=
+
+
=
20
10
100
200
50
50
50
50
j
j
j
j
Z
Z
Z
Z
Z
Z
CA
BC
AB
BC
CA
C
Z
p
E
A
0’
A
B
Z
p
Z
p
U
A
U
B
C
U
C
Z
B
Z
A
Z
C
I
C
I
B
I
A
E
C
E
B
0
U
0
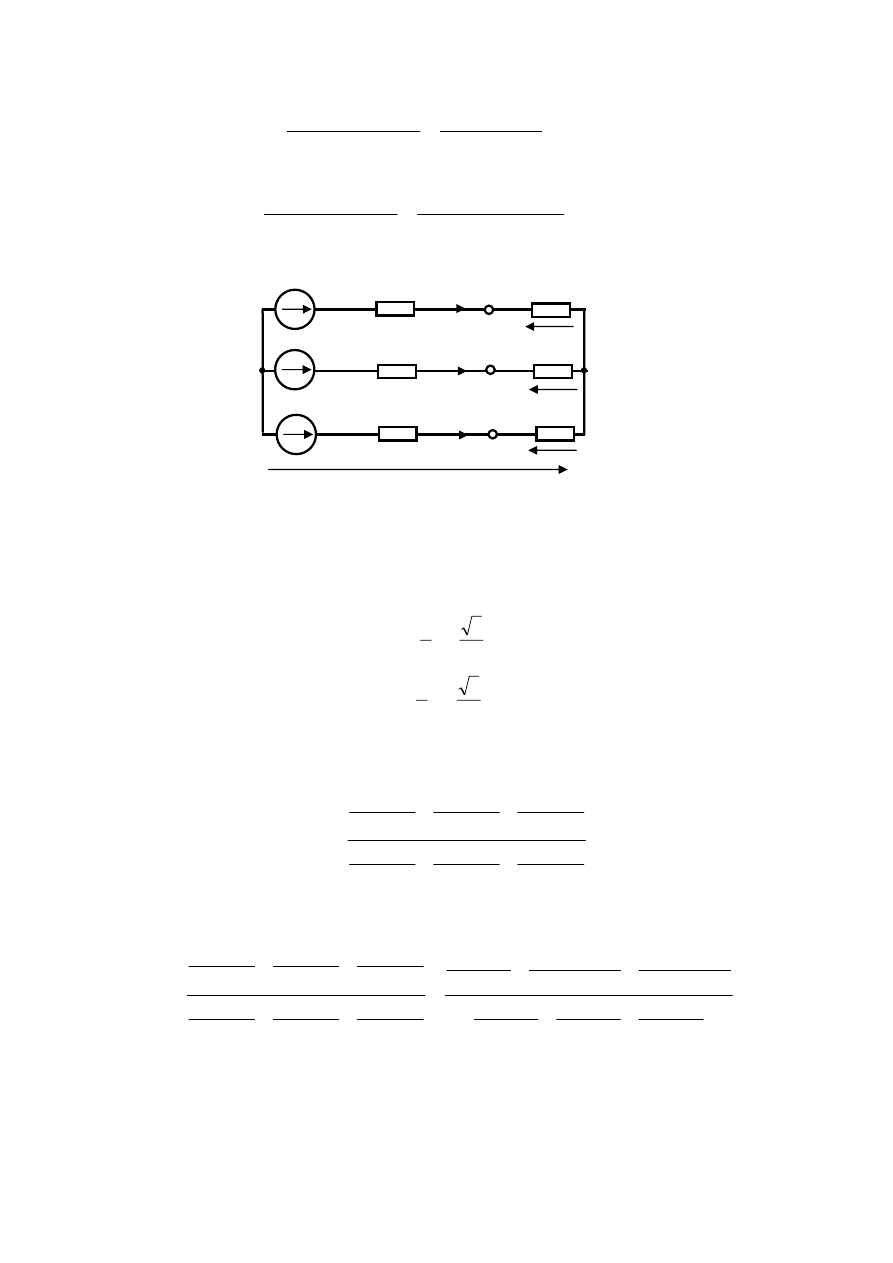
Rys.7.2. Analizowany obwód po zamianie obciążenia trójkątowego na gwiazdę
Do dalszej analizy układu założona zostaje zerowa faza początkową
A
E
. Stąd:
V
E
A
230
=
(
V
j
j
a
E
E
A
B
199
115
2
3
2
1
230
2
−
−
=
−
−
=
=
)
(7.2)
(
)
V
j
j
a
E
E
A
C
199
115
2
3
2
1
230
+
−
=
+
−
=
=
Początkiem analizy układu z rys.7.2 jest wyznaczenie napięcia
pomiędzy punktami
gwiazdowymi generatora i odbiornika. Określa je zależność (7.3).
0
U
p
C
p
B
p
A
p
C
C
p
B
B
p
A
A
Z
Z
Z
Z
Z
Z
Z
Z
E
Z
Z
E
Z
Z
E
U
+
+
+
+
+
+
+
+
+
+
=
1
1
1
0
(7.3)
Podstawienie wartości liczbowych daje w wyniku:
(
)
V
,
j
,
j
j
j
j
j
j
j
j
Z
Z
Z
Z
Z
Z
Z
Z
E
Z
Z
E
Z
Z
E
U
p
C
p
B
p
A
p
C
C
p
B
B
p
A
A
03
24
21
29
40
20
1
30
40
1
30
40
1
40
20
199
115
30
40
199
115
30
40
230
1
1
1
0
+
=
=
+
+
+
+
+
+
+
−
+
+
−
−
+
+
=
+
+
+
+
+
+
+
+
+
+
=
21
Wyznaczona wartość napięcia U pozwala na obliczenie prądów przewodowych. Zależności
pozwalające na obliczenie tych prądów otrzymuje się na podstawie napięciowego prawa
Kirchhoffa dla pętli utworzonych przez przewód każdej fazy oraz domkniętych strzałką
napięcia U .
0
0
(
)
(
)
(
)
p
C
C
C
p
C
C
C
p
B
B
B
p
B
B
B
p
A
A
A
p
A
A
A
Z
Z
U
E
I
U
Z
Z
I
E
Z
Z
U
E
I
U
Z
Z
I
E
Z
Z
U
E
I
U
Z
Z
I
E
+
−
=
⇒
=
−
+
−
+
−
=
⇒
=
−
+
−
+
−
=
⇒
=
−
+
−
0
0
0
0
0
0
0
0
0
(7.4)
Po podstawieniu do zależności (7.4) wartości liczbowych otrzymuje się prądy przewodowe.
(
)
(
)
(
)
A
,
j
,
j
,
j
,
j
Z
Z
U
E
I
A
,
j
,
j
,
j
,
j
Z
Z
U
E
I
A
,
j
,
j
,
j
,
Z
Z
U
E
I
p
C
C
C
p
B
B
B
p
A
A
A
63
4
06
2
40
20
03
24
21
29
199
115
84
1
98
4
30
40
03
24
21
29
199
115
79
2
92
2
30
40
03
24
21
29
230
0
0
0
+
=
+
−
−
+
−
=
+
−
=
−
−
=
+
−
−
−
−
=
+
−
=
−
=
+
−
−
=
+
−
=
Znajomość prądów przewodowych pozwala na wyznaczenie napięć fazowych odbiornika
połączonego w trójkąt. Można je wyznaczyć z równań sformułowanych na podstawie
napięciowego prawa Kirchhoffa dla dwóch impedancji odbiornika z rys.7.2:
A
A
C
C
CA
C
C
B
B
BC
B
B
A
A
AB
Z
I
Z
I
U
Z
I
Z
I
U
Z
I
Z
I
U
−
=
−
=
−
=
(7.5)
Druga możliwość wyznaczenia napięć odbiornikowych to napięciowe prawa Kirchhoffa
napisane dla generatorów oraz napięć na impedancjach przewodów dwóch faz. Równania te
mogą być formułowane zarówno dla układu z rys.7.3 jak też z rys.7.4.
A
p
C
p
A
C
CA
C
p
B
p
C
B
BC
B
p
A
p
B
A
AB
I
Z
I
Z
E
E
U
I
Z
I
Z
E
E
U
I
Z
I
Z
E
E
U
+
−
−
=
+
−
−
=
+
−
−
=
(7.6)
Podstawiając do zależności (7.5) wyznaczone wartości prądów przewodowych otrzymuje się
napięcia U
odbiornika:
CA
,
BC
AB
U
U
,
(
)
(
)
(
)
V
j
,
,
j
,
,
j
Z
I
Z
I
U
V
,
j
,
j
j
Z
I
Z
I
U
V
,
j
,
j
,
j
,
Z
I
Z
I
U
A
A
C
C
CA
C
C
B
B
BC
B
B
A
A
AB
142
5
187
5
54
5
115
5
87
72
5
192
59
5
87
72
105
131
5
50
5
246
105
131
5
54
5
115
+
−
=
+
−
+
−
=
−
=
−
−
=
−
+
−
−
=
−
=
+
=
+
+
−
=
−
=
Znajomość napięć fazowych odbiornika pozwala na wyznaczenie prądów fazowych
odbiornika połączonego w trójkąt.
CA
,
BC
AB
I
I
,
I
22
(
)
(
)
(
)
A
,
j
,
j
j
,
Z
U
I
A
,
j
,
j
,
j
Z
U
I
A
,
j
,
,
j
,
Z
U
I
CA
CA
CA
BC
BC
BC
AB
AB
AB
30
3
46
0
50
50
142
5
187
34
1
52
2
50
50
5
192
59
51
0
47
2
100
5
50
5
246
+
−
=
+
+
−
=
=
−
−
=
+
−
−
=
=
+
=
+
=
=
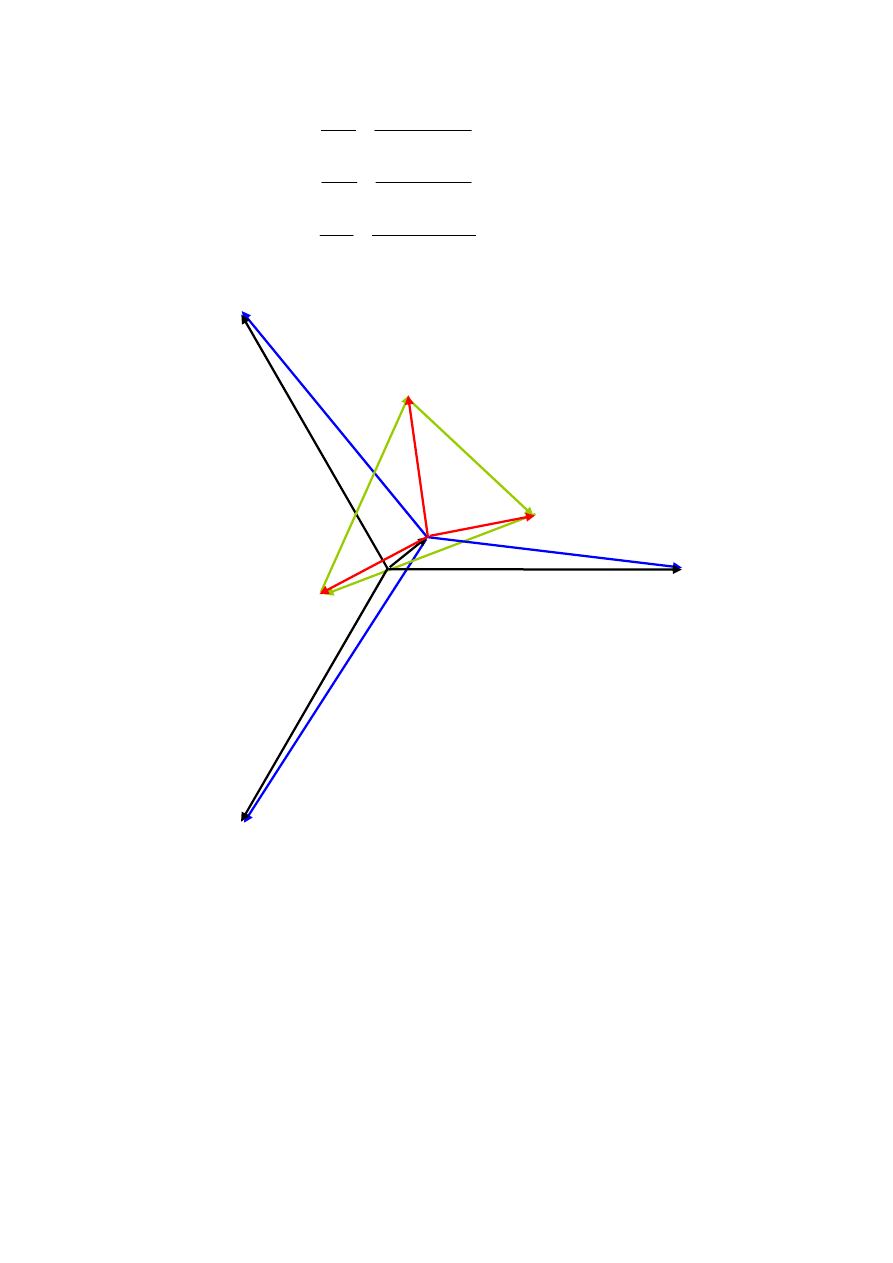
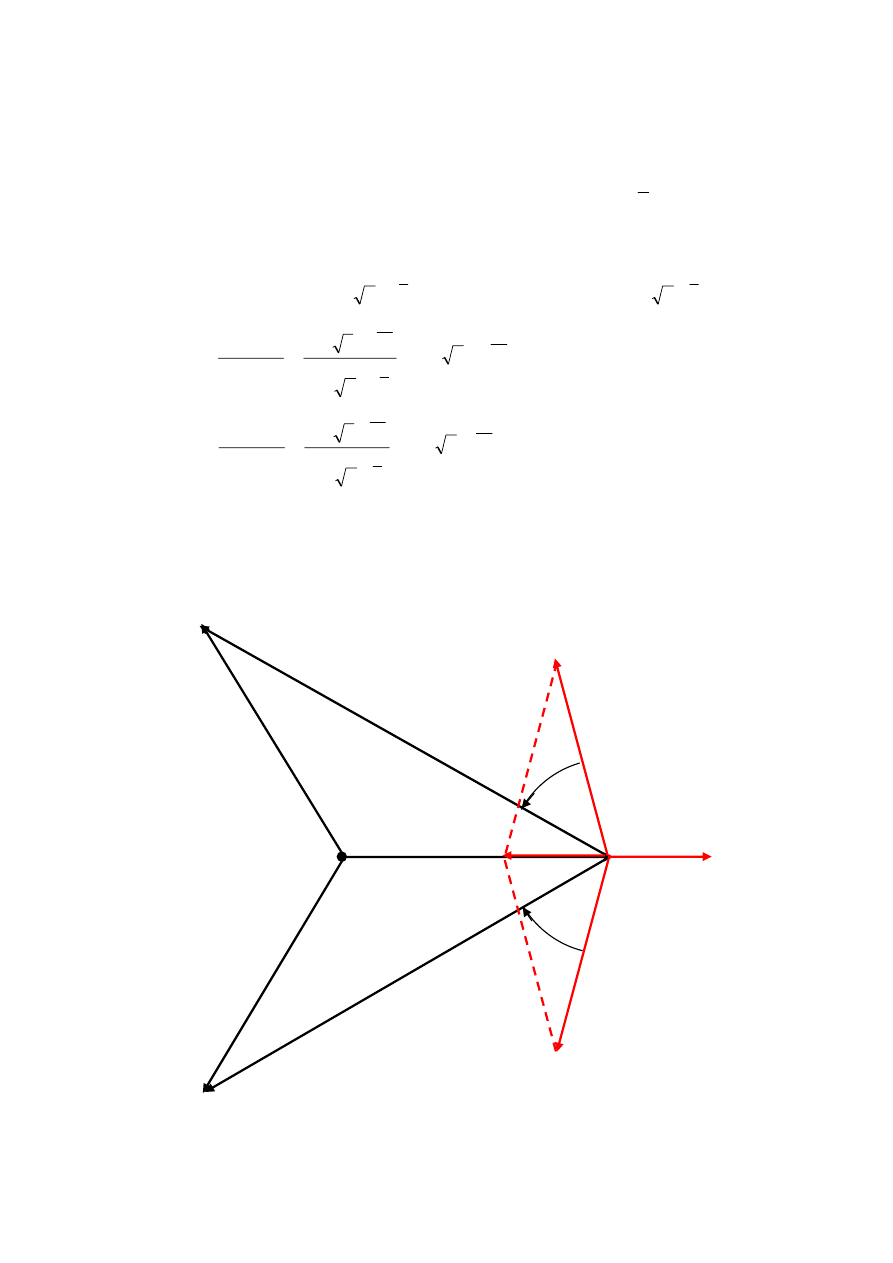
Wykres wskazowy prądów i napięć analizowanego obwodu przedstawiony jest na rys.7.3.
U
0
I
CA
0
0’
I
C
I
AB
I
BC
U
A
+I
A
Z
p
I
A
E
C
E
B
E
A
U
B
+I
B
Z
p
I
B
U
C
+I
C
Z
p
Rys.7.3. Wykres wskazowy prądów i napięć analizowanego obwodu
Kolorem czerwonym oznaczone są prądy fazowe, zielonym – prądy przewodowe. Prądy
przewodowe są różnicą odpowiednich prądów fazowych.
Kolorem niebieskim oznaczone są napięcia na impedancjach połączenia gwiazdowego oraz
impedancjach przewodów w każdej fazie układu z rysunku 7.2. Punkt 0’ oraz napięcie
istnieje tylko w układzie z rys.7.2.
0
U
Rysowanie wykresu rozpoczyna się od symetrycznej gwiazdy napięć generatora
.
Przy jej rysowaniu należy uwzględnić poczynione założenie, zależności (7.2). Z punktu
początkowego narysowanych napięć generatorów wykreśla się napięcie U , którego wartość
została wyznaczona zgodnie ze wzorem (7.3). Koniec wskazu napięcia
jest punktem
gwiazdowym 0
C
B
A
E
,
E
,
E
0
U
0
’
zastępczego odbiornika (rys.7.2). Wskazy, których początkiem jest punkt 0
’
a
końcami są zakończenia wskazów napięć generatora są napięciami panującymi na fazach
23
odbiornika gwiazdowego oraz impedancjach przewodów w odpowiednich fazach. Prądy
przewodowe są ilorazem tych napięć oraz impedancji fazowych odbiornika gwiazdowego
powiększonych o impedancje przewodów. Na wykresie są umieszczone wskazy prądów
fazowych odbiornika trójkątowego (kolor czerwony) oraz prądy przewodowe (kolor zielony),
wykreślone jako różnice odpowiednich prądów fazowych.
Zadanie 8
W układzie z rys.8.1 wyznacz prądy przewodowe. Narysuj wykres wskazowy. Generator jest
symetryczny.
U
A
0
’
0
Uc
U
B
U
0
Z
B
Z
A
=0
Z
C
I
C
I
B
I
A
E
C
E
A
E
B
Rys.8.1
Dane:
(
)
(
Ω
+
=
Ω
−
=
=
=
=
=
100
100
;
100
100
;
0
V;
230
j
Z
j
Z
Z
E
E
E
C
B
A
C
B
A
)
Rozwiązanie:
Układ badany jest niesymetrycznym układem trójprzewodowym ze zwarciem w fazie A.
Analiza układu rozpoczyna się od wyznaczenia napięcia
na podstawie zależności (7.3).
W obliczeniach należy uwzględnić, że impedancja fazy A jest zerowa, tzn.
0
U
∞
→
A
Y
. Na
potrzeby rozwiązania zostaje poczynione również założenie:
V
E
A
A
230
=
=
E
.
A
A
A
C
A
B
A
A
A
C
C
A
B
B
A
A
A
C
B
A
C
C
B
B
A
A
E
E
Y
Y
Y
Y
Y
Y
Y
Y
E
Y
Y
E
Y
Y
E
Y
Y
Y
Y
E
Y
E
Y
E
U
=
=
+
+
+
+
=
+
+
+
+
=
1
0
Znajomość napięcia
umożliwia obliczenie napięć odbiornikowych w analizowanym
układzie:
0
U
V
e
E
E
E
U
E
U
V
e
E
E
E
U
E
U
U
E
U
j
CA
A
C
C
C
j
BA
A
B
B
B
A
A
6
5
0
6
5
0
0
3
230
3
230
0
π
π
−
=
=
−
=
−
=
=
=
−
=
−
=
=
−
=
24
Prądy fazowe odbiornika, które w tym przypadku są także prądami przewodowymi, są
ilorazami wyznaczonych napięć odbiornikowych oraz impedancji fazowych odpowiednich
faz. Dla fazy A nie można wykorzystać podanego sposobu obliczenia prądu, ponieważ po
podstawieniu wartości napięć i impedancji fazy A otrzymujemy symbol
0
0
. Dla faz B oraz C
odbiornika wyznaczone zostają następujące wartości prądów (są to jednocześnie prądy
fazowe i przewodowe):
(
)
(
)
(
)
(
)
A
,
j
,
A
e
,
e
e
Z
U
E
I
A
,
j
,
A
e
,
e
e
Z
U
E
I
e
j
Z
e
j
Z
j
j
j
C
C
C
j
j
j
B
B
B
j
C
j
B
721
2
729
0
6
15
1
2
100
3
230
721
2
729
0
6
15
1
2
100
3
230
2
100
100
100
2
100
100
100
12
7
4
6
5
0
12
7
4
6
5
0
4
4
+
−
=
=
=
−
=
−
−
=
=
=
−
=
Ω
=
+
=
Ω
=
−
=
π
π
π
π
−
π
−
π
−
π
π
−
Prąd fazy A zostaje wyznaczony na podstawie prądowego prawa Kirchhoffa dla punktu 0’
odbiornika:
(
)
A
,
I
I
I
I
I
I
C
B
A
C
B
A
458
1
0
=
+
−
=
⇒
=
+
+
U
B
U
C
φ
B
φ
C
-I
A
I
C
I
B
0’
0
E
A
=U
0
E
B
E
C
I
A
Rys.8.2. Wykres wskazowy układu z rys.8.1
25
Sposób rysowania wykresu jest następujący. Zaczyna się od symetrycznej gwiazdy napięć
generatora:
. Następnie z punktu, który jest początkiem wskazów napięć
generatora (punkt 0) wykreślone zostaje napięcie
(na podstawie obliczeń). Jego koniec
wyznacza położenie punktu 0’. Wskazy mające początek w punkcie 0’, a końce w punktach
będących końcami wskazów napięć generatora to napięcia fazowe odbiornika. Prądy faz B i C
są przesunięte względem napięć o kąty fazowe impedancji znajdujących się w fazach B i C.
Prąd fazy A wynika z PPK. Jego konstrukcja polega na znalezieniu sumy wskazów prądów
, która jest równa
C
B
A
E
,
E
,
E
0
U
C
B
I
,
I
A
I
−
a następnie znalezieniu wskazu przeciwnego do niego.
Zadanie 9
Obliczyć wskazania mierników w układzie przedstawionym na rys.9.1 oraz narysować
wykres wskazowy dla dwóch przypadków:
1. wyłącznik w
1
jest zamknięty a wyłącznik w
2
otwarty,
2. wyłącznik w
1
jest otwarty a wyłącznik w
2
zamknięty.
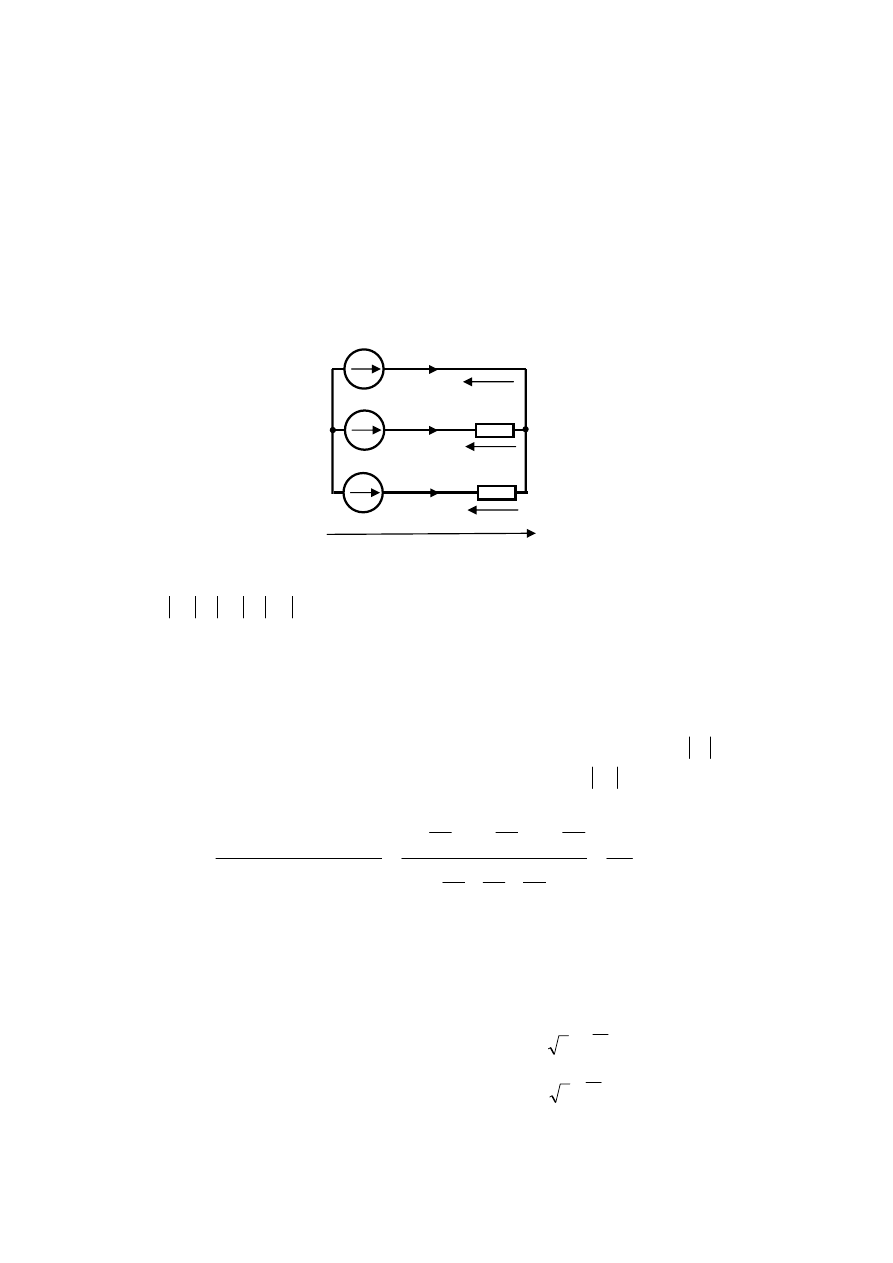
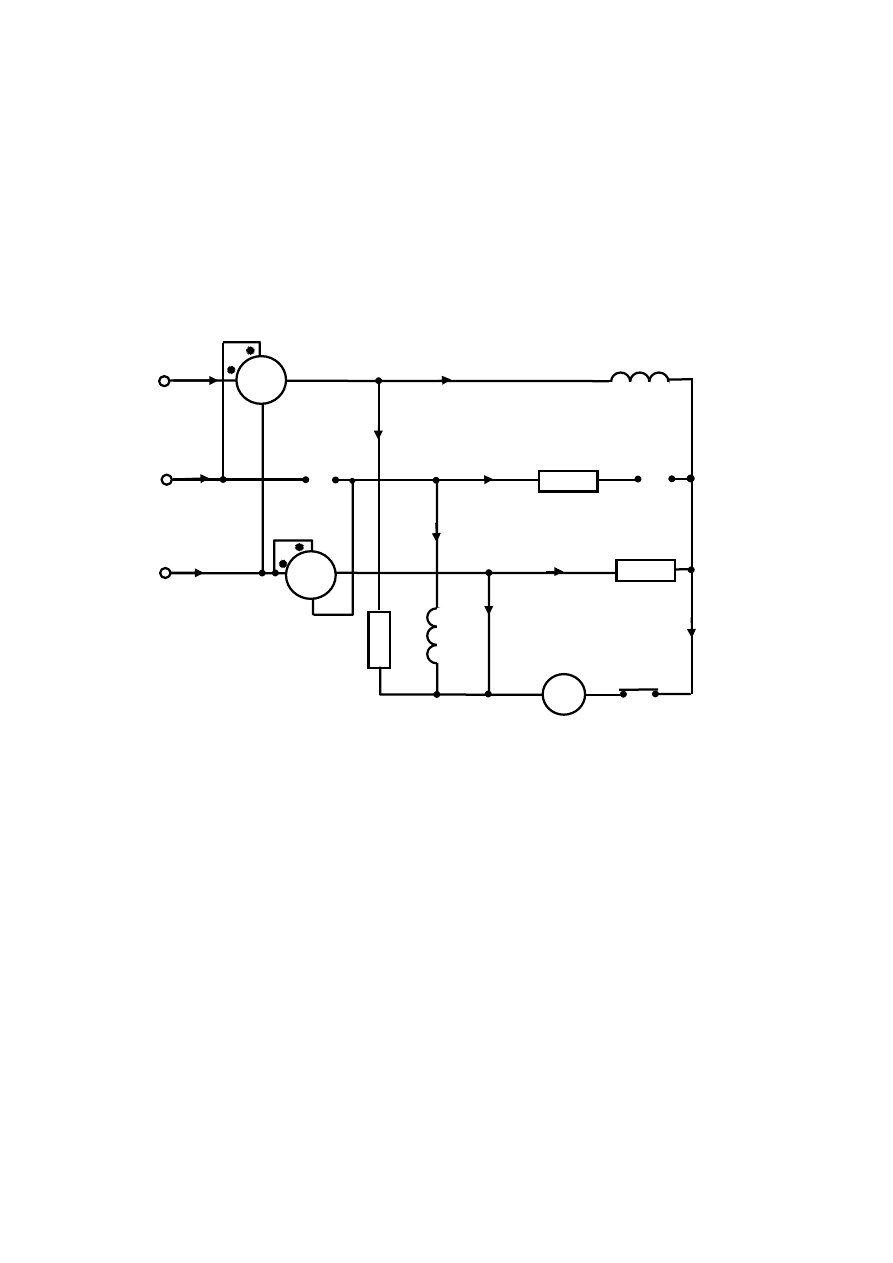
Rys.9.1
W
2
W
1
L
A
w
2
C
R
L
I
B
I
A
I
C
R
R
A
C
L
w
1
B
L
C
Dane:
R=ωL=1/ωC=20Ω, |U
p
|=400V, zasilanie symetryczne o zgodnej kolejności faz,
impedancja przewodów jest pomijana
Rozwiązanie
Punkt 1:
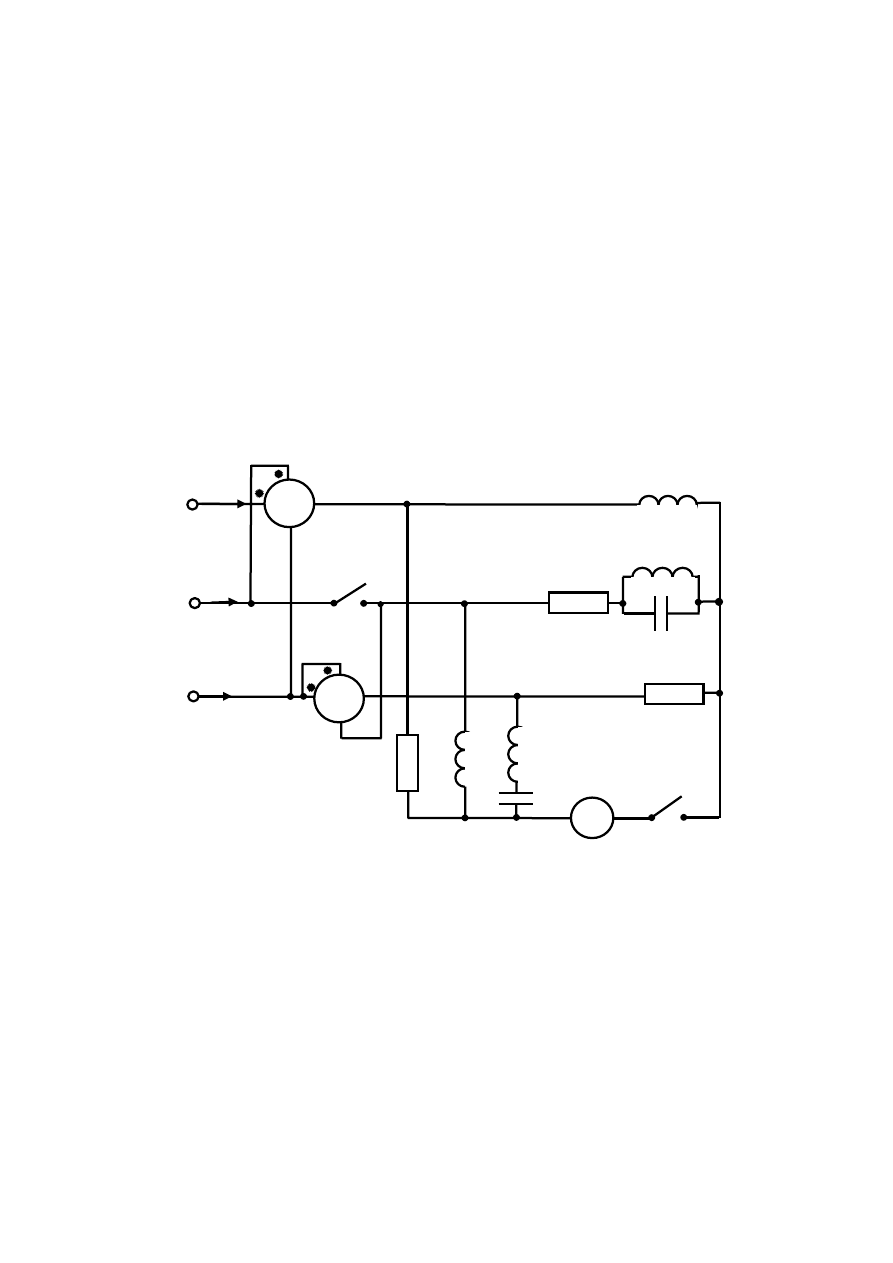
Na rysunku 9.2 przedstawiony został układ, który powstał po zamknięciu wyłącznika w
1
oraz
otwarciu wyłącznika w
2
. Zamknięcie wyłącznika w
1
zapewnia symetryczne zasilanie całego
układu (wszystkie fazy zasilania są doprowadzone do odbiornika). Otwarcie wyłącznika w
1
spowodowało rozdzielenie części odbiorczej układu trójfazowego na dwa niezależne
odbiorniki połączone w gwiazdę, których punkty gwiazdowe (zerowe) są rozłączone.
Powoduje to powstanie ogólnie różnych napięć między punktem zerowym generatora oraz
punktami zerowymi każdego z układów.
26
B
w
1
L
C
A
R
R
I
C
I
A
I
B
L
R
w
2
0’
W
2
A
I
C
’
I
C
’’
I
A
’
I
B
’
I
B
’’
I
A
’’
W
1
0’’
Rys.9.2. Analizowany układ w konfiguracji połączeń odpowiadającej punktowi 1
Oznaczenia punktów zerowych obu układów oraz ich prądów fazowych są na rys.9.2 różne
(odróżniają je różne dodatki do symboli: ‘ lub ‘’. W porównaniu do rys.9.1 rys.9.2 zawiera
jeszcze dwie zmiany. Połączenie równoległe elementów L i C w fazie B odbiornika z
punktem zerowym 0’’ zostało zastąpione przerwą, ponieważ admitancja tego połączenia jest
równa 0 (równe moduły reaktancji elementów L oraz C). W połączeniu tym zachodzi
rezonans prądów. Szeregowe połączenie elementów L i C występujące w fazie C odbiornika z
punktem zerowym 0’ zostało zastąpione zwarciem ponieważ impedancja tego połączenia
równa jest 0 (równe moduły reaktancji elementów L oraz C). Prądy każdego z dwóch
odbiorników układu z rys.9.2 są niezależne od siebie, są rezultatem dwóch różnych napięć
punktów zerowych względem punktu zerowego generatora.
W przewodzie łączącym punkty zerowe 0’ oraz 0’’ jest przerwa (wyłącznik w
2
jest otwarty,
nie przewodzi prądu) a więc wskazanie amperomierza
0
=
amp
I
. Napięcie U
0
’ obliczone
zostaje w oparciu o zależność 7.3. Zostaje założona zerowa wartość fazy początkowej
napięcia generatora w fazie A,
V
230
=
A
E
. Ze względu na zwarcie w fazie C pierwszego
odbiornika (na rys.9.2 jest on umieszczony w dolnej części schematu)
∞
→
C
Y
napięcie jego
punktu gwiazdowego względem punktu gwiazdowego generatora wynosi:
V
3
400
1
3
2
0
π
j
C
C
C
C
C
B
C
A
C
C
C
C
B
B
C
A
A
C
B
A
C
C
B
B
A
A
'
e
E
E
Y
Y
Y
Y
Y
Y
Y
E
Y
E
Y
E
Y
Y
Y
Y
E
Y
E
Y
E
U
=
=
=
+
+
+
+
=
+
+
+
+
=
Y
Y
Y
Obliczona wartość napięcia
pozwala na wyznaczenie prądów odbiornika pierwszego.
Wyznaczenie prądów w fazach A oraz C następuje na podstawie zależności (7.4).
'
U
0
27
(
)
A
20
20
400
A
10
32
17
A
20
20
400
6
6
−
=
−
=
−
=
−
=
=
=
−
=
−
−
j
j
L
ω
j
E
E
I
j
,
e
e
R
E
E
I
C
B
'
B
π
j
π
j
C
A
'
A
Prąd fazy zwartej, fazy C wyznaczony zostaje na podstawie prądowego prawa Kirchhoffa:
(
)
(
)
(
)
A
10
68
2
20
10
3
10
j
,
j
I
I
I
'
B
'
A
'
C
+
=
−
−
−
=
+
−
=
0’
I
C
I
A
I
B
0
E
A
E
C
=
U
0
’
E
B
U
B
U
A
Rys.9.3. Wykres wskazowy pierwszego odbiornika
Układ z punktem gwiazdowym 0’’ to układ z przerwą w fazie B, w której występuje rezonans
prądów cewki L i kondensatora C. Przy otwartym wyłączniku w
2
obowiązuje równanie:
0
=
+
+
''
C
''
B
''
A
I
I
I
Prąd I
B
’’=0. Wynika stąd, że:
''
C
''
A
''
C
''
A
I
''
C
''
B
''
A
I
I
I
I
I
I
I
''
B
−
=
⇒
=
+
=
+
+
⇒
=
0
0
0
Zatem słuszne jest napięciowe prawo Kirchhoffa:
(
)
L
ω
j
R
I
U
R
I
L
ω
j
I
U
''
A
AC
''
C
''
A
AC
+
=
⇒
=
+
−
0
Prądy w drugim odbiorniku to:
(
)
A
66
13
66
3
A
2
10
20
20
400
12
5
6
,
j
,
e
j
e
L
ω
j
R
U
I
I
π
j
π
j
AC
''
C
''
A
−
=
=
+
=
+
=
−
=
−
−
28
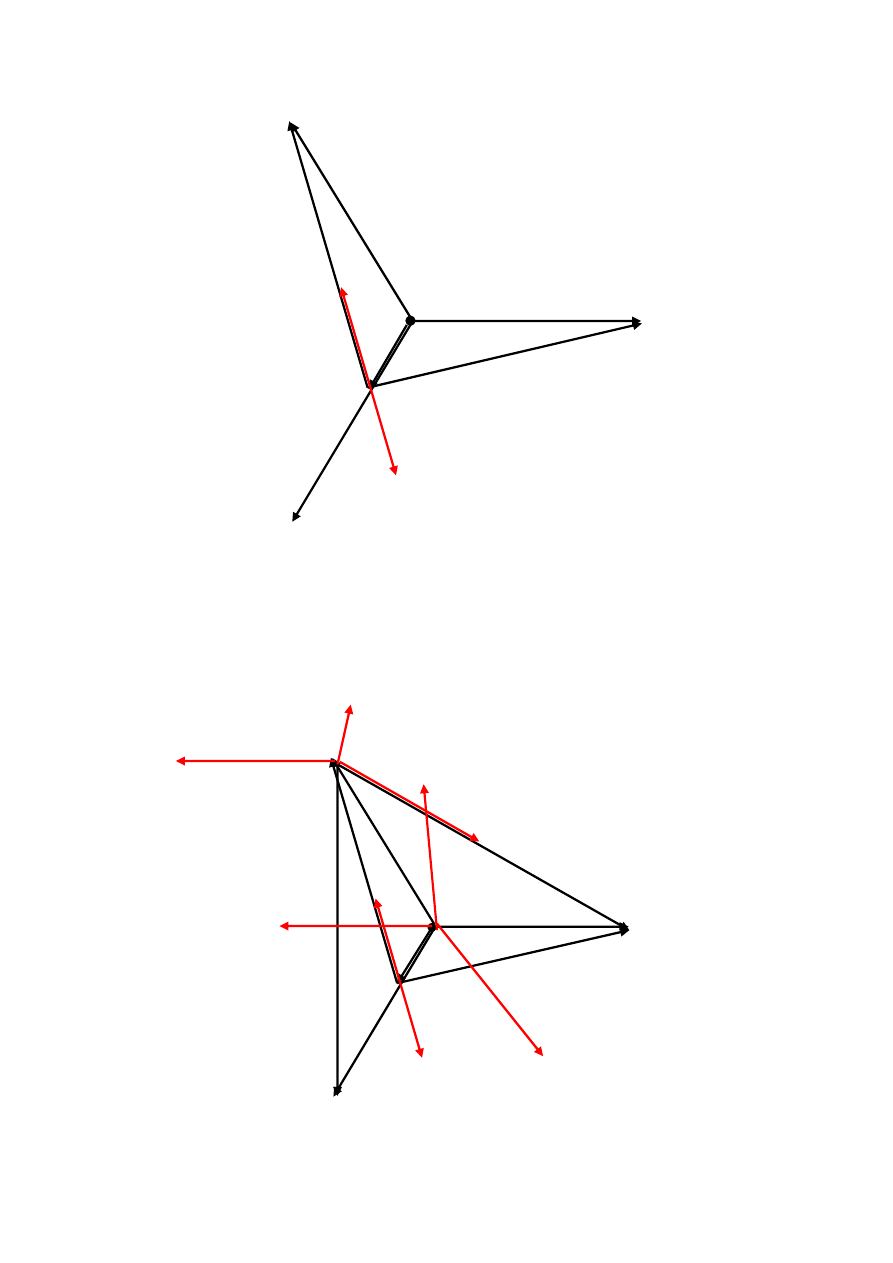
0’’
I
C
’’
I
A
’’
U
A
’’
U
0
’’
0
E
A
E
C
E
B
U
C
’’
Rys.9.4. Wykres wskazowy drugiego odbiornika
Prądy przewodowe faz A oraz C całego układu niezbędne do wyznaczenia wskazań
watomierzy znajduje się jako sumy prądów fazowych obu odbiorników.
(
)
(
)
A
66
23
98
0
66
13
66
3
10
68
2
A
66
23
98
20
66
13
66
3
10
32
17
,
j
,
,
j
,
j
,
I
I
I
,
j
,
,
j
,
j
,
I
I
I
''
C
'
C
C
"
A
'
A
A
+
−
=
+
−
+
=
+
=
−
=
−
+
−
=
+
=
E
A
U
A
’
I
A
I
B
I
C
’’
I
A
’’
I
C
’
I
A
’
I
B
’
0
E
C
=
U
0
’
I
C
E
B
U
B
’
U
C
’’
U
A
’’
U
0
’’
Rys.9.5. Wykres wskazowy całego układu dla przypadku 1
29
Wskazania watomierzy obliczane są na podstawie znanych zależności:
{
}
(
)
{
}
{
}
(
)
{
}
W
9464
66
23
98
0
400
W
9464
66
23
98
20
400
2
1
=
−
−
=
=
=
+
−
=
=
∗
∗
,
j
,
j
I
U
Re
P
,
j
,
j
I
U
Re
P
C
CB
W
A
BC
W
Punkt 2:
Układ przedstawiony na rys.9.6 składa się z dwóch odbiorników, z których każdy połączony
jest w gwiazdę.
W
2
W
1
I
A
’’
I
B
’’
I
C
’
I
B
’
I
A
’
I
C
’’
A
w
2
R
L
I
B
I
A
I
C
R
R
0’
A
C
L
w
1
B
0’’
I
amp
Rys.9.6. Analizowany układ w konfiguracji połączeń odpowiadającej punktowi 2
Punkty gwiazdowe obu odbiorników 0
’
oraz 0
’’
posiadają wspólny potencjał, ponieważ są
połączone przewodem bezoporowym (wyłącznik w
2
jest zamknięty). Zatem:
0
0
0
U
U
U
''
'
=
=
Otwarty wyłącznik w
1
powoduje przerwę w fazie B. Prądy fazowe obu odbiorników w tej
fazie i prąd całego układu są zatem równe 0:
0
=
=
=
B
''
B
'
B
I
I
I
W fazie C pierwszego odbiornika jest w dalszym ciągu zwarcie. Obliczona w punkcie 1
wartość napięcia U
0
’
pozostaje nadal aktualna.
C
''
'
E
U
U
U
=
=
=
0
0
0
Przez opornik R umieszczony w fazie C drugiego odbiornika prąd nie płynie bo napięcie na
tym elemencie jest zerowe.
0
=
''
C
I
30
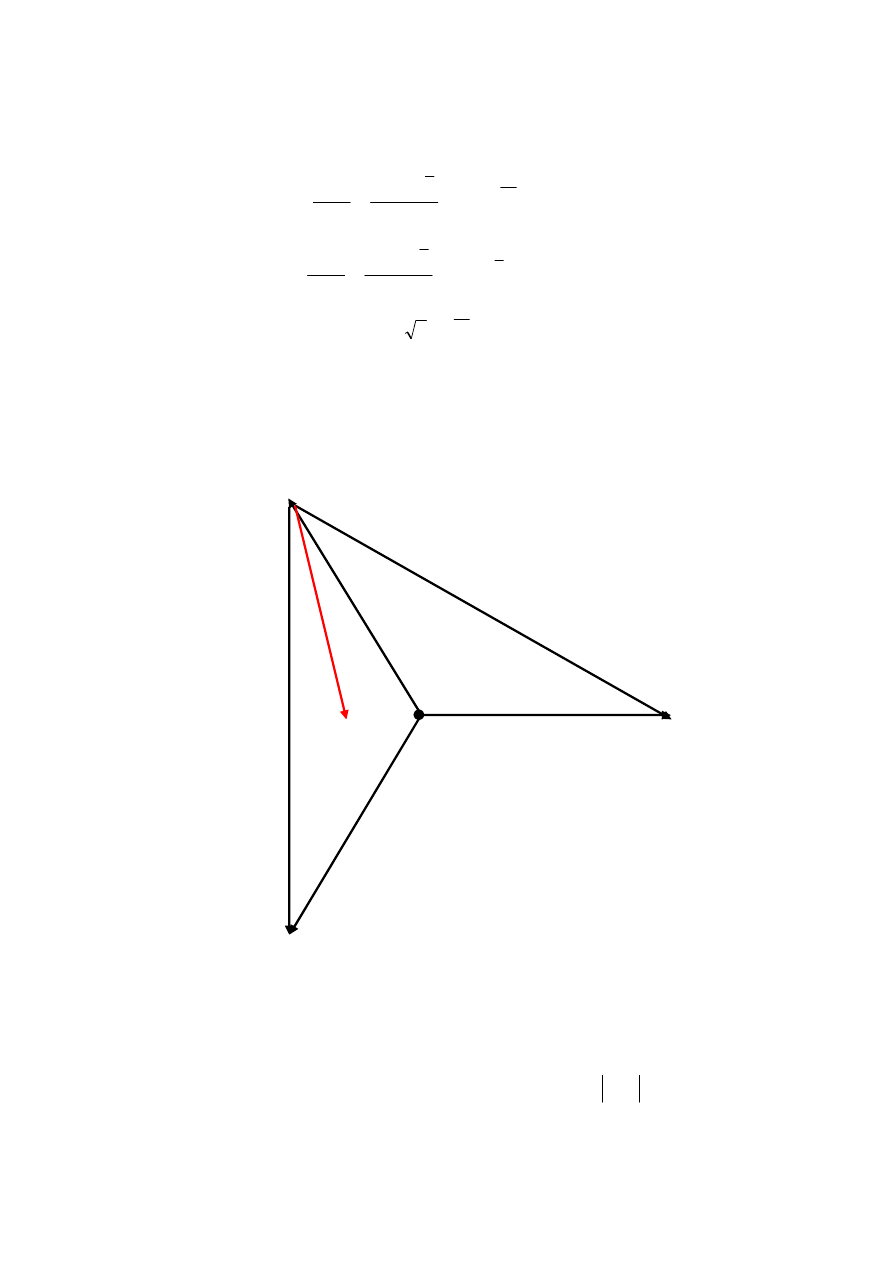
Wyznaczone napięcie U
0
pozwala na obliczenie prądów w fazie A obu odbiorników oraz
całego układu.
(
)
A
32
27
32
7
2
20
A
20
20
400
A
20
20
400
12
5
6
6
3
2
6
,
j
,
A
e
''
I
'
I
I
e
e
R
U
'
I
e
j
e
L
ω
j
U
''
I
π
j
A
A
A
π
j
π
j
AC
A
π
j
π
j
AC
A
−
=
=
+
=
=
=
=
=
=
=
−
−
−
−
−
Ponieważ w fazie B jest przerwa to prąd całego układu w fazie B nie płynie. Zatem
A
C
C
A
I
C
B
A
I
I
I
I
I
I
I
B
−
=
⇒
+
+
⇒
=
+
+
=
0
0
0
E
C
= U
0
’
=
U
0
’’
U
B
’
I
A
=
-
I
C
0’=0’’
U
A
’
0
E
A
E
B
Rys.9.7. Wykres wskazowy całego układu dla przypadku 2
Prądy w fazach B oraz C drugiego odbiornika nie płyną. Wynika stąd wartość prądu
amperomierza. Przez amperomierz płynie następujący prąd:
A
20
0
=
⇒
=
⇒
=
=
amp
amp
''
A
''
C
''
B
I
I
I
I
I
31
Wskazanie watomierza W
1
wynika z zależności, która posłużyła do wyznaczania wskazań
watomierzy w punkcie 1.
{
}
(
)
{
}
W
10928
32
27
32
7
400
1
=
+
−
=
=
∗
,
j
,
j
I
U
Re
P
A
BC
W
Wskazanie watomierza W
2
wynika z zerowej wartości napięcia panującego na jego cewce
napięciowej. Początek cewki napięciowej jest zwarty z jej końcem przez cewkę prądową
watomierza, na której panuje zerowe napięcie, zwartą fazę C pierwszego odbiornika oraz
cewkę L znajdującą się w fazie B pierwszego odbiornika, przez którą nie płynie prąd gdyż
jeden z jej końców jest dołączony do punktu, który nie jest połączony z żadnym innym
elementem układu.
(
)
0
0
2
2
=
=
W
W
U
P
32