1

Statystyka
opisowa

Wykład 8.

2

Analiza danych „na oko”

Człowiek nie myśli liczbami



Przy porównaniu nie stosuje punktów



Przy ocenianiu nie stawia oceny

Otaczający nas świat daje nam
liczby



Liczba to dana



Liczba z interpretacją to informacja

Człowiek musi interpretować liczby

3

Statystyka opisowa

Wstępne opracowanie wyników

pomiarów
Prezentacja poglądowa wyników

pomiarów
Nie stosujemy rachunku

prawdopodobieństwa
Nie wyciągamy wniosków

dotyczących całej populacji

4

Elementy statystyki
opisowej

Miary tendencji centralnej
Miary rozproszenia
Wykresy statystyczne

Korelacje

5

Miary tendencji centralnej

Liczby opisujące skupienie danych
(gdzie i jak się skupiają)



Średnia arytmetyczna



Mediana



Kwartyle (decyle, centyle)



Moda

6

Średnia arytmetyczna

Suma wartości podzielona przez
liczebność próbki:

n

X

X

n

i

i







1

7

Własności średniej
arytmetycznej

Jest wrażliwa na wyniki ekstremalne
Suma odchyleń od średniej jest

równa zero
Jest taką liczbą, dla której suma

kwadratów odchyleń od tej liczby

przyjmuje wartość minimalną
Średnia może nie występować w

zestawie danych

8

Przykład

Średnia arytmetyczna próbki

0, 1, 11

jest równa 4

Średnia arytmetyczna próbki

3, 4, 5

jest równa 4

Wniosek: samotna średnia arytmetyczna nie

jest dobrą charakteryzacją zestawu danych.

9

Mediana

Wartość środkowa



Liczba znajdująca się pośrodku

uporządkowanego zestawu danych

Obliczanie mediany w zestawie n danych



Porządkujemy zestaw danych niemalejąco



Jeżeli n jest nieparzyste to medianą jest

liczba stojąca na (n +1)/2 miejscu



Jeżeli n jest parzyste to medianą jest średnia

arytmetyczna liczb stojących na miejscach

n/2 i n/2+1

10

Przykład

Zestaw danych

4, 8, 9, 1, 6, 5, 6

mediana 6 (bo 1 4 5

6

6 8 9 )

Zestaw danych

8, 2, 8, 1, 2, 0, 5, 7

mediana 4 (bo 0 1 3

3 5

7 8 8 i

(3+5)/2=4)

11

Wrażliwość średniej i
mediany

Średnia

arytmetyczna

1, 3, 4, 5, 7



średnia 4

1, 3, 4, 5,

42



średnia

11

1,

2

,

5

, 5, 7



średnia 4

Mediana

1, 3, 4, 5, 7



mediana 4

1, 3, 4, 5,

42



mediana 4

1,

2

,

5

, 5, 7



mediana

5

12

Własność mediany

Mediana minimalizuje wartość
bezwzględną odchyleń



Mediana jest liczbą, dla której suma
wartości bezwzględnych odchyleń od
tej liczby jest najmniejsza

13

Przykład

Średnia arytmetyczna = 6

Suma wartości bezwzględnych odchyleń:

|1-6|+|2-6|+|3-6|+|7-6|+|8-6|+|9-6|+|12-6|=24

Suma kwadratów odchyleń:

(1-6)

2

+(2-6)

2

+(3-6)

2

+(7-6)

2

+(8-6)

2

+(9-6)

2

+(12-6)

2

=100

Zestaw danych: 1, 2, 3, 7, 8, 9, 12

Mediana = 7

Suma wartości bezwzględnych odchyleń:

|1-7|+|2-7|+|3-7|+|7-7|+|8-7|+|9-7|+|12-7|=23

Suma kwadratów odchyleń:

(1-7)

2

+(2-7)

2

+(3-7)

2

+(7-7)

2

+(8-7)

2

+(9-7)

2

+(12-7)

2

=107

14

Kwartyle

Liczby dzielące uporządkowany zestaw

danych na 4 (równe) grupy



Pierwszy kwartyl to (najmniejsza) liczba, od której

co najmniej ¼ wszystkich danych jest niewiększa



Drugi kwartyl to (najmniejsza) liczba, od której co

najmniej ½ wszystkich danych jest niewiększa



Trzeci kwartyl to (najmniejsza) liczba, od której co

najmniej ¾ wszystkich danych jest niewiększe

Uwaga: kwartyle nie rozdzielają równych

wartości

15

Przykład

Uporządkowany zestaw danych

0,0,1,1,1,2,2,2,2,5,6,7,8,8,9,9



Pierwszy kwartyl: 1



Drugi kwartyl: 2



Trzeci kwartyl: 7

Mamy więc podział według kwartyli

0,0,1,1,1 2,2,2,2 5,6,7 8,8,9,9

16

Decyle, centyle

Jak kwartyle ale podział nie na 4



Decyle – na 10



Pierwszy decyl oddziela co najmniej 0.1
danych, drugi 0.2, itd.



Centyle – na 100



Pierwszy centyl oddziela co najmniej 1%
danych, drugi 2%, itd.

17

Moda (dominanta)

Liczba najczęściej występująca w
zestawie danych
Można traktować jako najbardziej
typowy wynik
W przeciwieństwie do średniej
arytmetycznej i mediany zawsze
występuje w zestawie danych

18

Wielomodalność

Moda nie jest wyznaczana jednoznacznie
Gdy jest jedna moda to zestaw
nazywamy

jednomodalnym

Gdy są dwie mody to zestaw nazywamy

bimodalnym

Gdy mamy więcej niż dwa typowe wyniki
to zestaw nazywamy

wielomodalnym

19

Miary rozproszenia

Liczby opisujące jak rozrzucone są
dane



Rozstęp danych



Odchylenie średnie



Wariancja



Odchylenie standardowe

20

Rozstęp danych

Zakres zmienności
Różnica między największą i
najmniejszą wartością w zestawie
danych

21

Odchylenie średnie

Średnia wartość bezwzględna
odchylenia od średniej arytmetycznej

n

X

X

n

i

i







1

|

|

22

Wariancja

Średnie odchylenie kwadratowe populacji

Średnie odchylenie kwadratowe
próbki

1

)

(

1

2

2











n

X

X

S

n

i

i

n

X

X

n

i

i









1

2

2

)

(



23

Obliczanie wariancji

Wzór ułatwiający obliczanie wariancji,
gdy mamy dane zsumowane























































n

X

X

n

S

n

i

i

n

i

i

2

1

1

2

2

1

1

24

Odchylenie standardowe

Pierwiastek z wariancji (średniego
odchylenia kwadratowego)

1

)

(

1

2











n

X

X

S

n

i

i

25

Wykresy statystyczne

Diagramy



Słupkowe



Kołowe

Histogram
Wykres pudełkowy



Z wąsami



Bez wąsów

Wykres łodygowy (łodygowo-liściowy)

26

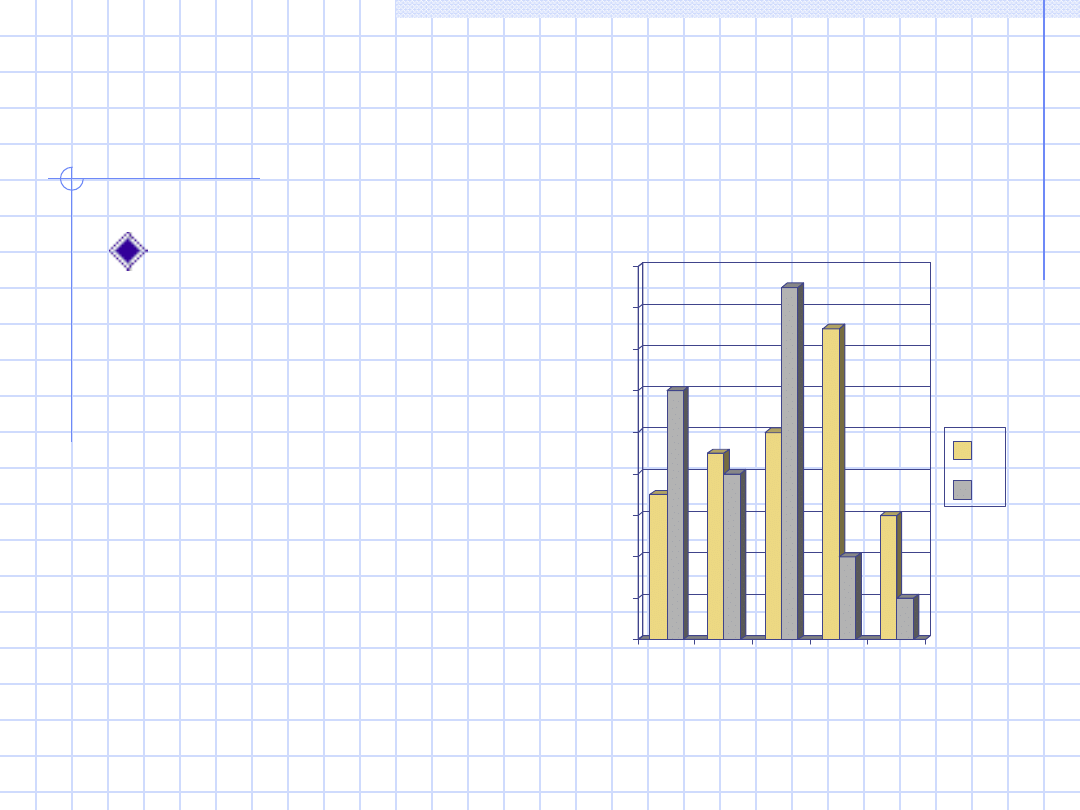
Diagram słupkowy

Dla każdej wartości,
lub zakresu wartości
mamy słupek,
którego wysokość
odpowiada liczbie
takich wartości w
zestawie danych. Im
wyższy słupek tym
częściej dana
wartość występuje w
zestawie danych.

0

2

4

6

8

10

12

14

16

18

1

2

3

4

5

A
B

27

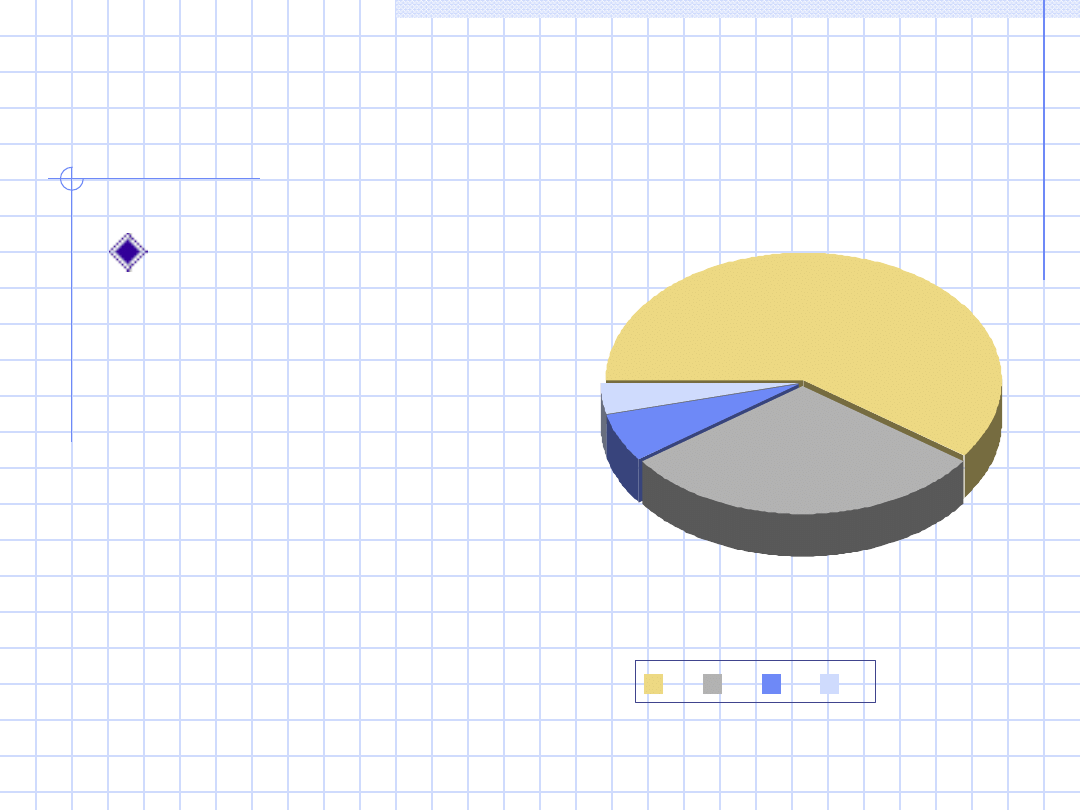
Diagram kołowy

Koło przedstawia
wszystkie dane
(100% danych)
każda wartość ma
przydzielony wycinek
koła proporcjonalny
do liczby wystąpień
danej wartości w
całym zestawie
danych

60%

30%

6%

4%

A

B

C

D

28

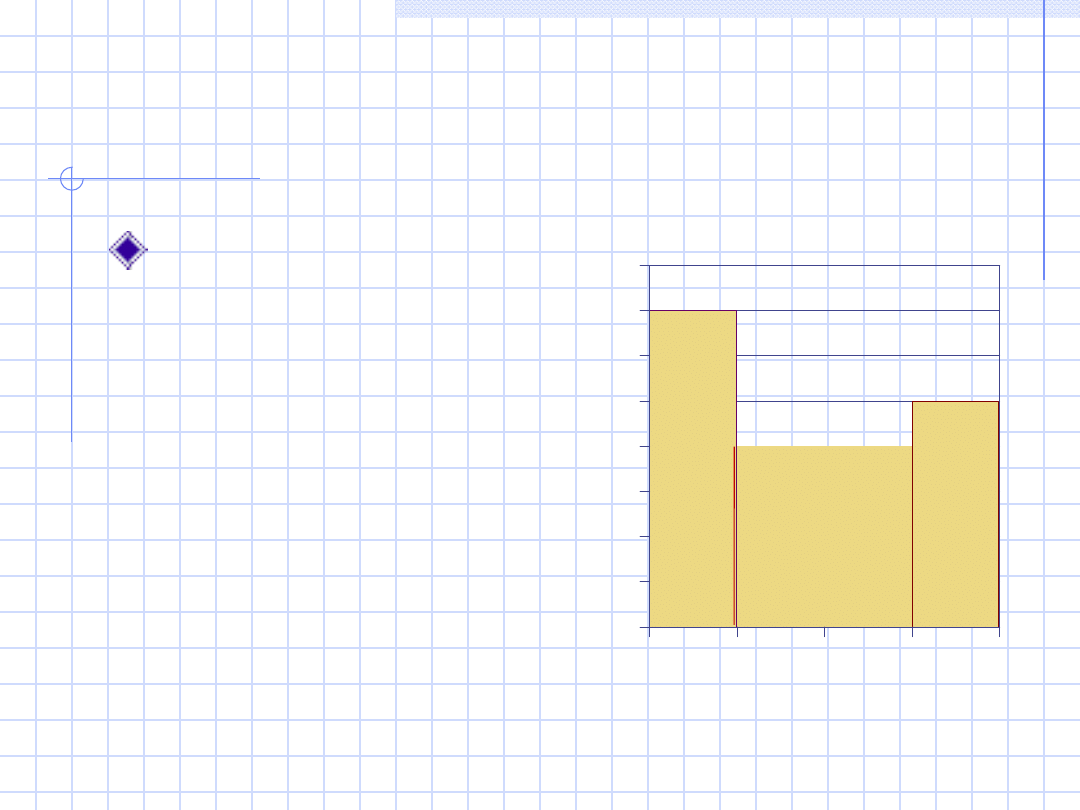
Histogram

Podobny do wykresu

słupkowego ale



Nie ma przerw między

danymi (wszystkie

wartości na osi są

przypisane do jakiegoś

„słupka”)



Rozmiary przedziałów

na osi mogą być różne



Powierzchnia słupka jest

proporcjonalna do liczby

danych mieszczących

się w przedziale

opisującym słupek

0

5

10

15

20

25

30

35

40

1

3

4

29

Wykres pudełkowy

Prostokąt od pierwszego (Q1) do

trzeciego (Q3) kwartyla
Kreska w miejscu mediany
Wąsy



X=1.5 * (Q3-Q1)



„Wąs lewy” od Q1-X



„Wąs prawy” do Q3+X

Wartości odległe, tzn. poza przedziałem

od Q1-X do Q3+x zaznaczone jako

pojednyncze punkty

30

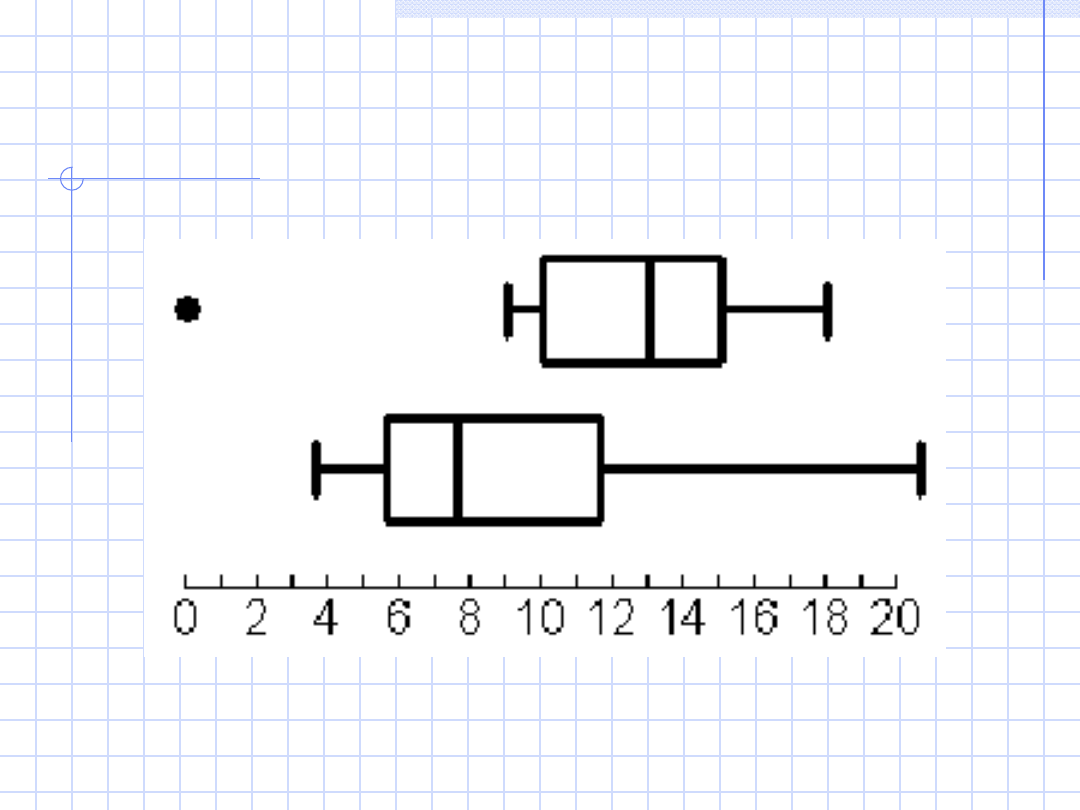
Przykład

31

Zróbmy pudełko (1)

Zestaw danych

9, 9, 2, 11, 2, 10, 5, 8,11, 3,

5, 8, 4, 10, 8, 2, 11, 3, 6, 21

32

Zróbmy pudełko (2)

Porządkujemy dane

9, 9, 2, 11, 2, 10, 5, 8,11, 3,

5, 8, 4, 10, 8, 2, 11, 3, 6, 21

2 2 2 3 3

4 5 5 6

8 8

8 9 9 10 10

11 11 11 21

Mediana=8, Q1=3, Q4=10, X=1.5*(10-3)=10.5
Lewy wąs: od 3-10.5=-7.5 czyli od 2
Prawy wąs: do 10+10.5=20.5 czyli do 11
Wartość odległa: 21 z prawej

33

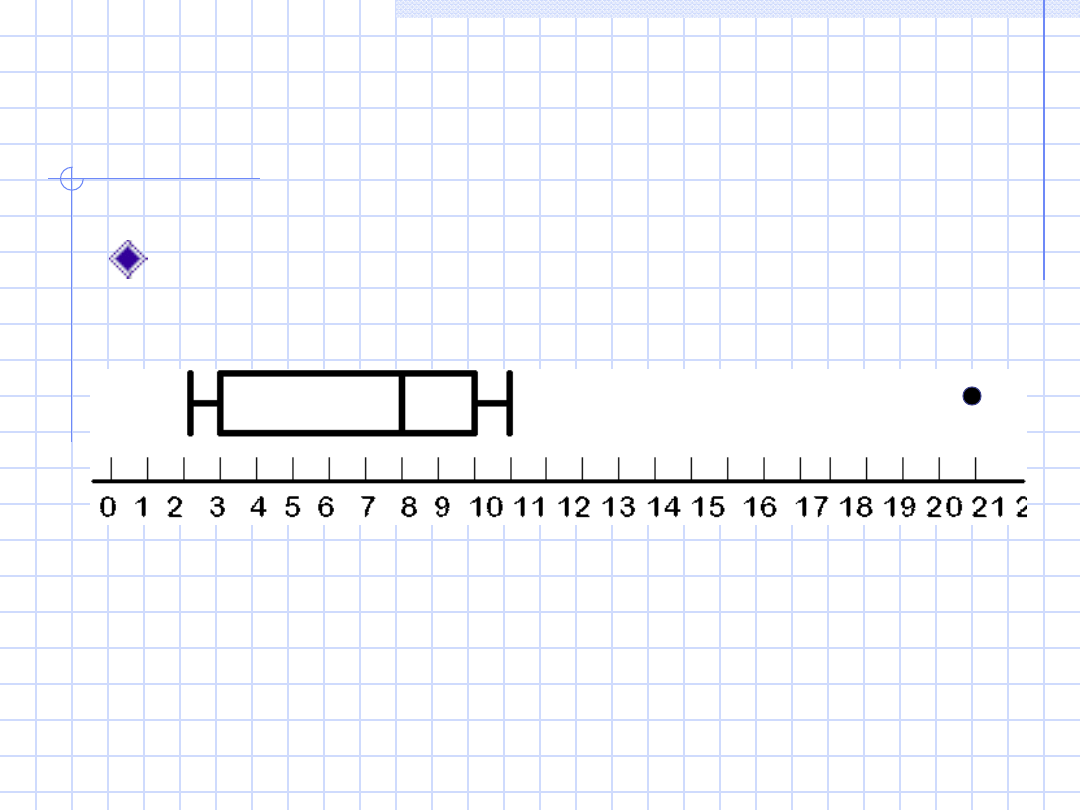
Zróbmy pudełko (3)

Wykres

34

Wykres łodygowo-liściowy

Dane dzielimy na dwie części (np. część całkowitą
i ułamkową) łodygę i liść (łodyga ważniejsza)
Wypisujemy w kolumnie łodygi w porządku
rosnącym
Po prawej rysujemy kreskę
Po kresce dopisujemy odpowiednie liście do
każdej łodygi
Gdy za dużo liści to odpowiednio dzielimy tę grupę
(tworzymy nową łodygę)
Trzeba zapisać zasadę podziału!

35

Przykład

Zestaw danych

28, 19, 89, 26, 9, 1,

90, 45, 19, 19, 53,
3, 83, 8, 20, 43, 8,

94, 16, 82

Zasada podziału:
cyfra dziesiątek
łodyga, cyfra
jedności liść

Diagram

0 9 1 3 8 8
1 9 9 9 6
2 8 6 0
4 5 3
5 3
8 9 3 2
9 0 4

36

Korelacja

Korelacja to związek dwóch mierzonych

w tym samym czasie wielkości
Korelacja jest pozytywna (dodatnia)

jeżeli wzrost zmiennej niezależnej

powoduje wzrost zmiennej zależnej
Korelacja jest negatywna (ujemna) jeżeli

wzrost zmiennej niezależnej powoduje

zmniejszenie zmiennej zależnej
Może nie być żadnej korelacji

37

Współczynnik korelacji

Współczynnik korelacji jest miarą korelacji:



Współczynnik bliski 1: korelacja dodatnia



Współczynnik bliski –1: korelacja ujemna



Współczynnik bliski 0: brak korelacji

Współczynnik Pearsona:





































n

i

j

n

i

i

n

i

i

i

y

y

x

x

y

y

x

x

r

1

2

1

2

1

38

Współczynnik korelacji -
przykład

Dane:

x

3

4

9

12 13 15

y

13 19 30 42 48 51

Współczynnik Pearsona: r =
0,99

0

10

20

30

40

50

60

3

4

9

12

13

15

39

Korelacja rang

Korelacja ocen (sędziowskich) dla dwóch
wielkości.
Najpierw trzeba dane zanotowane dla
dwóch obserwowalnych zmiennych
zamienić na oceny. W obu przypadkach
postępujemy tak samo: najmniejszej
wartości nadajemy ocenę 1 (najniższą),
następnej 2, itd. aż do końca.
Badamy korelację ocen, a nie wartości
zmiennych

40

Korelacja rang -
współczynnik

Do oceny korelacji rang używamy współczynnika

korelacji rang Spearman’a:

Gdzie d są różnicami ocen przyznanych odpowiadającym

sobie (mierzonym jednocześnie) wartościom badanych

zmiennych; n liczba obserwowanych par wartości.

)

(

1

6

1

2

1

2











n

n

d

r

n

i

i

s

41

Korelacja rang - przykład

Dane:

 

Obiekt

A

B

C

D

E

F

Ocena I 7

4

9

6

5

2

Ocena II 9

0

7

5

4

1

Współczynnik Spearmana: 0,886