teoria



Ważnym zagadnieniem w wytrzymałości
materiałów, oprócz obliczeń
wytrzymałościowych, odkształcalności jest
stateczność układu. Równowaga jest stateczna,
jeżeli dowolne niewielkie odkształcenie układu
wywołuje siły przywracające mu postać
pierwotną. Jeżeli siła ściskająca P pręt będzie
wzrastać, to przy pewnej jej wartości P kr
minimalny impuls ( Q = 0) spowoduje, że pręt
nie wróci do prostoliniowego stanu równowagi
przy krzywoliniowej postaci pręta



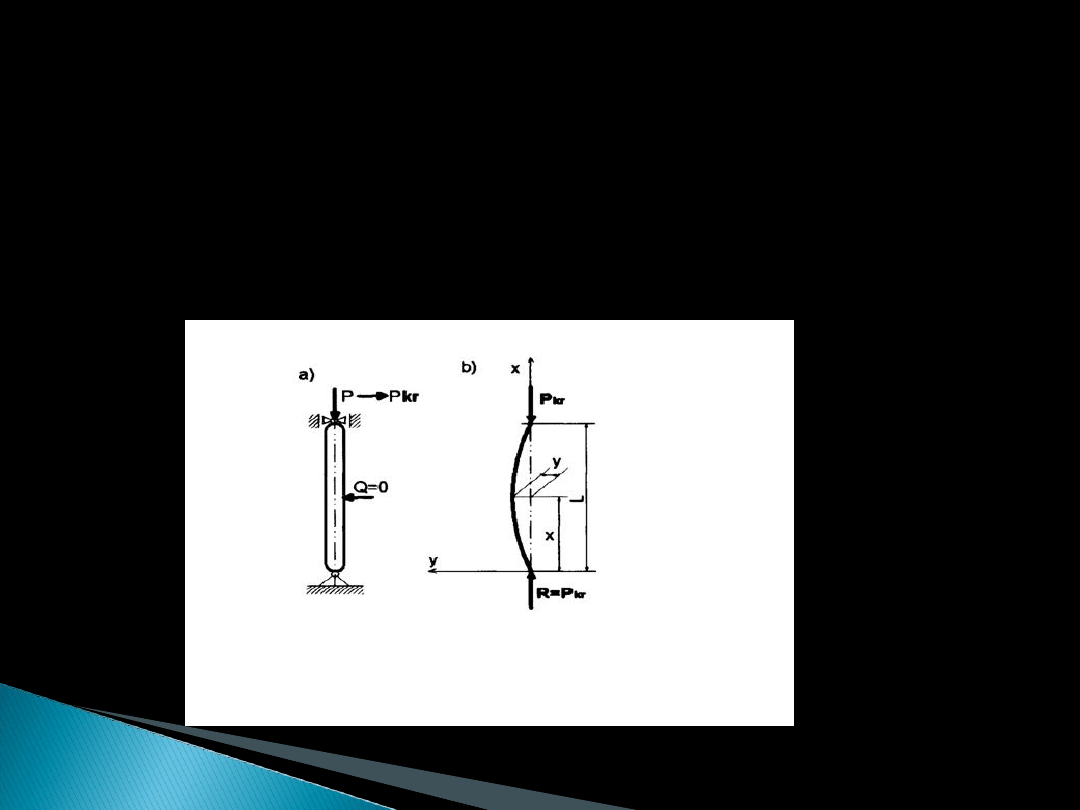
Jest to stan gdzie oprócz ściskania siłą P. powstaje również zginanie pręta momentem
Mg = P kr. Co może spowodować zniszczenie pręta nawet przy niewielkim wzroście
siły ściskającej. Przejście układu ze stanu równowagi chwiejnej lub obojętnej
( krzywoliniowa postać równowagi pręta ) nazywamy utratą stateczności układu, a
siłę powodującą zmianę stanu równowagi nazywamy siłą krytyczną P



Wykorzystując równanie różniczkowe linii
ugięcia można uzyskać równanie linii
ugięcia pręta ściskanego siłą krytyczną, a
stąd najmniejszą wartość siły krytycznej,
która dla pręta ściskanego między dwoma
przegubami wynosi:



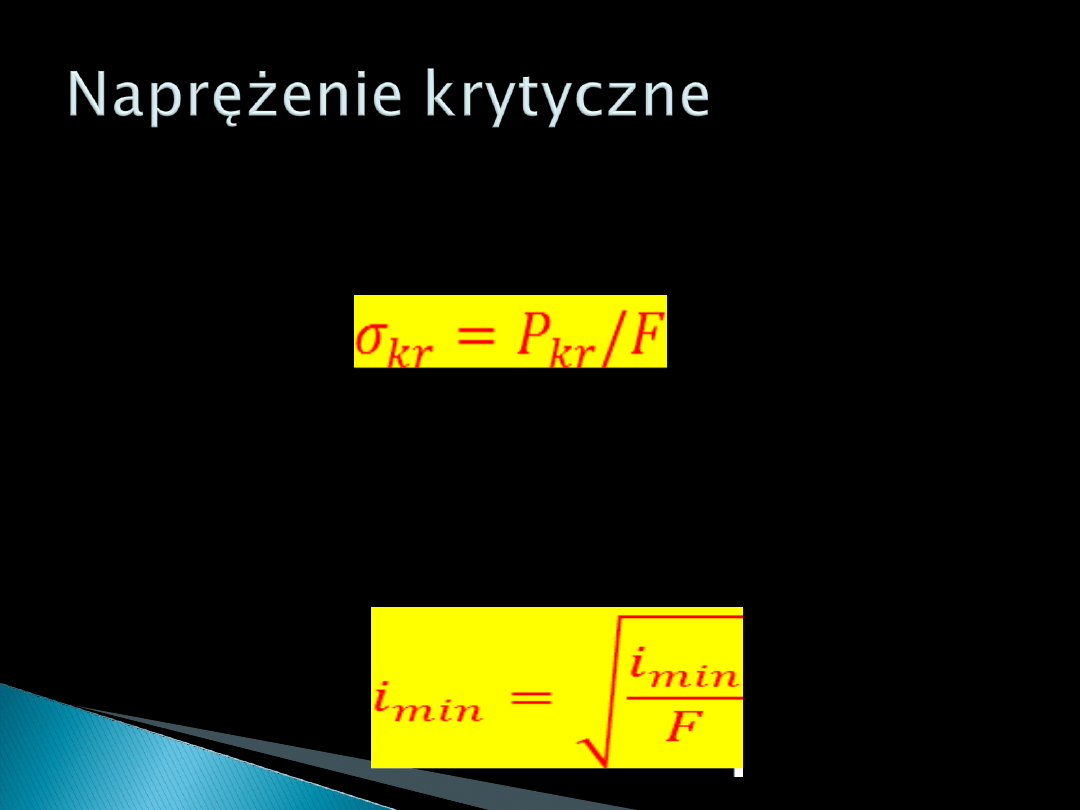
Jeżeli wyznaczymy siłę krytyczną, to
oczywiście uzyskamy naprężenie krytyczne



Przy których następuje utrata stateczności
pręta ściskanego.



Wprowadzone pojęcie minimalnego
promienia bezwładności przekroju

**



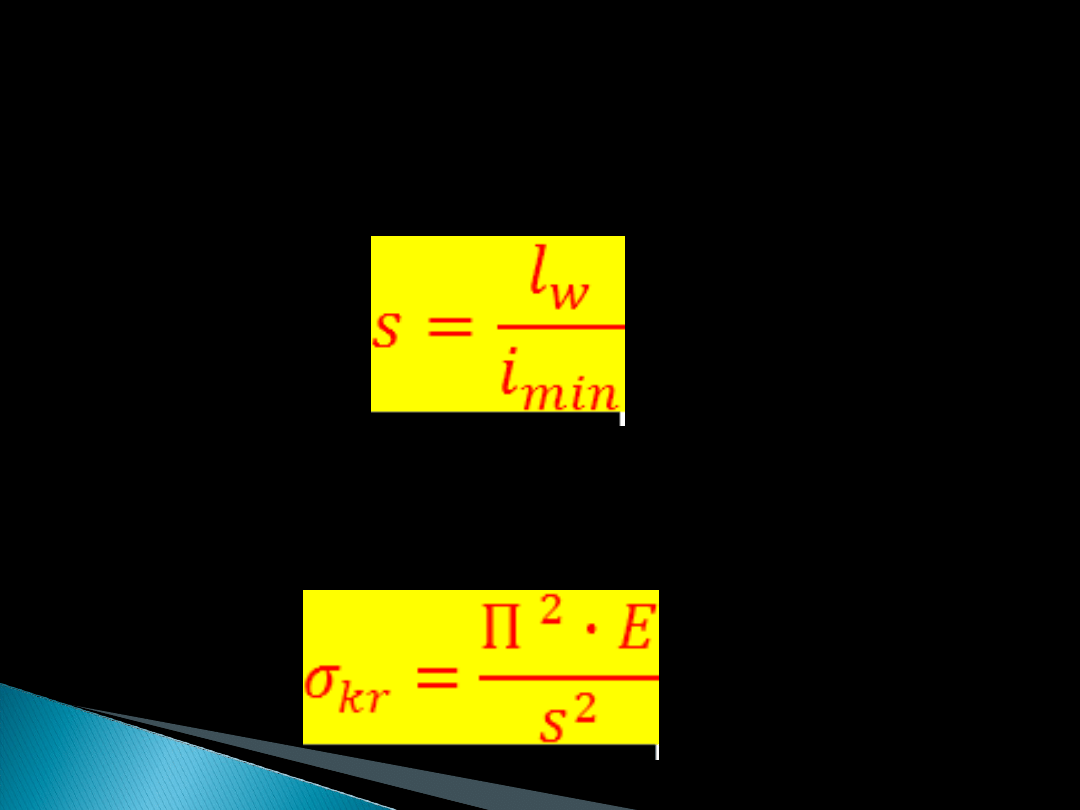
A następnie wielkość charakteryzująca wymiary
pręta:



Nazywana smukłością pręta, w powyższym
przypadku otrzymamy wzór na naprężenie
krytyczne zwane wzorem Eulera:



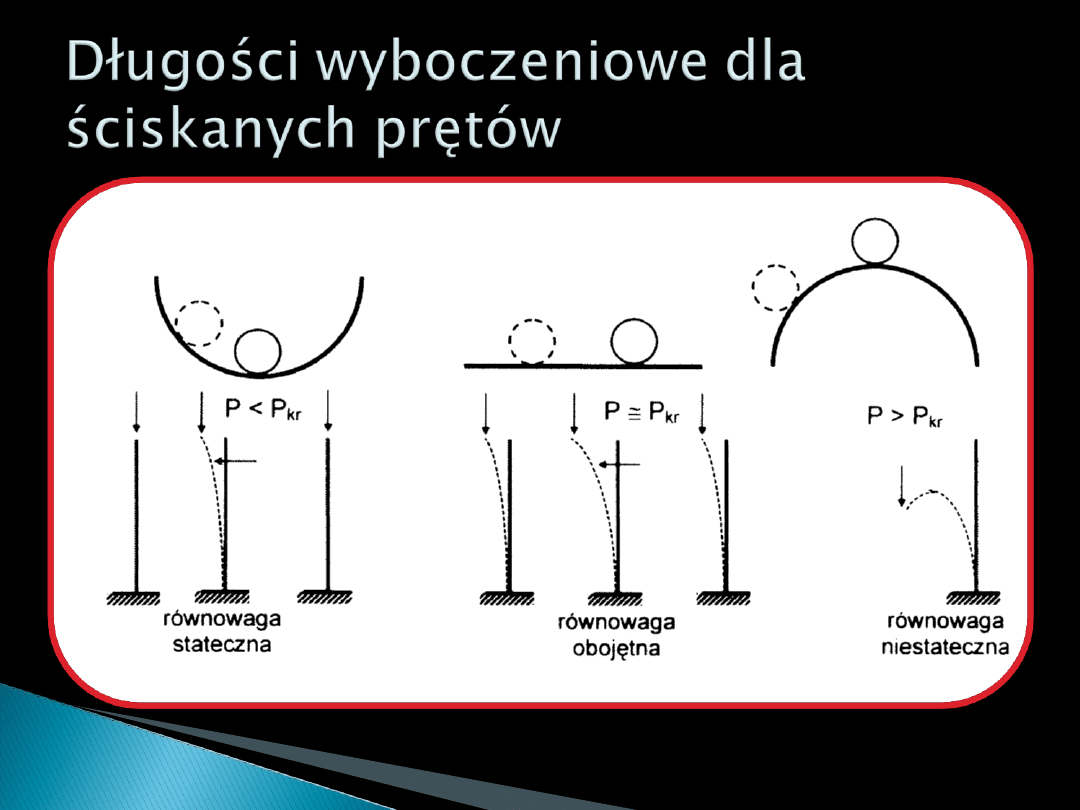
W układach sztywnych wartości występujących sił nie mają wpływu na rodzaj
równowagi.



W układach odkształcalnych do pewnej wartości obciążenia układ jest w równowadze
statecznej. Po przekroczeniu owej wartości zmienia się w stan równowagi
niestatecznej.



Zjawisko to nazywamy wyboczeniem i występuje ono przy:



Ściskaniu



Zginaniu



Skręcaniu

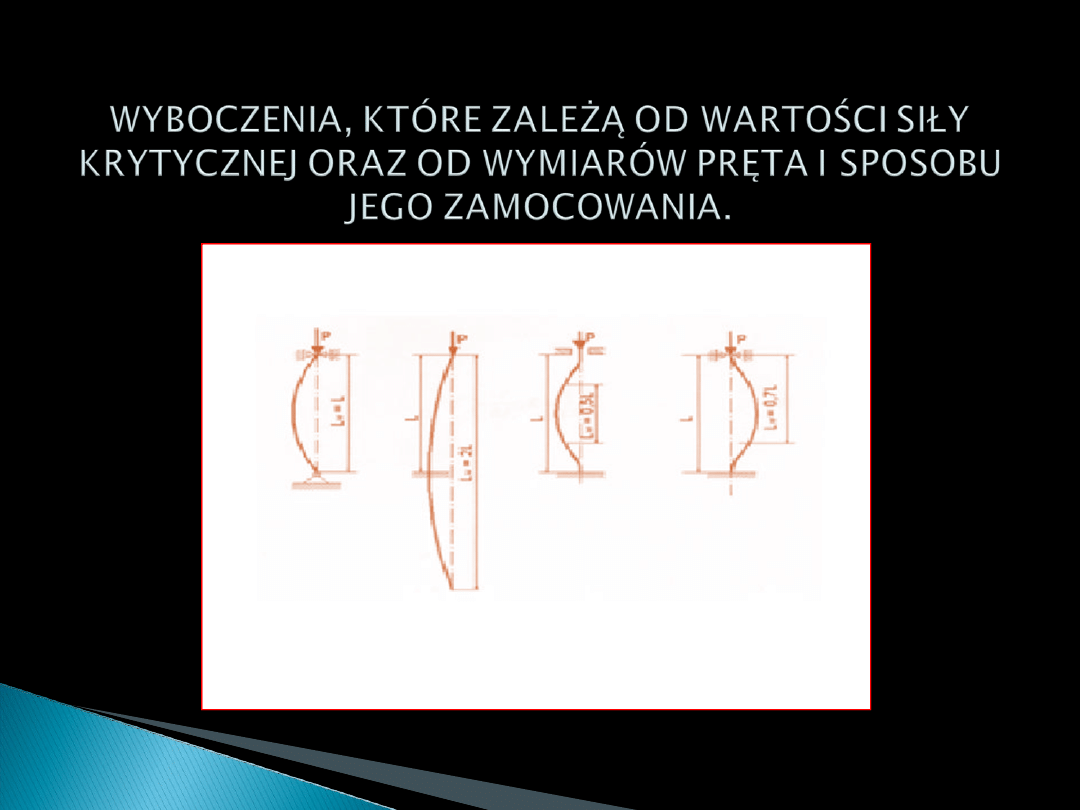
Przypadek najprostszego wyboczenia występuje przy zwykłym osiowym ściskaniu pręta

prostego.

Wyboczeniu takiemu podlegają pręty smukłe, cienkie płyty oraz powłoki.



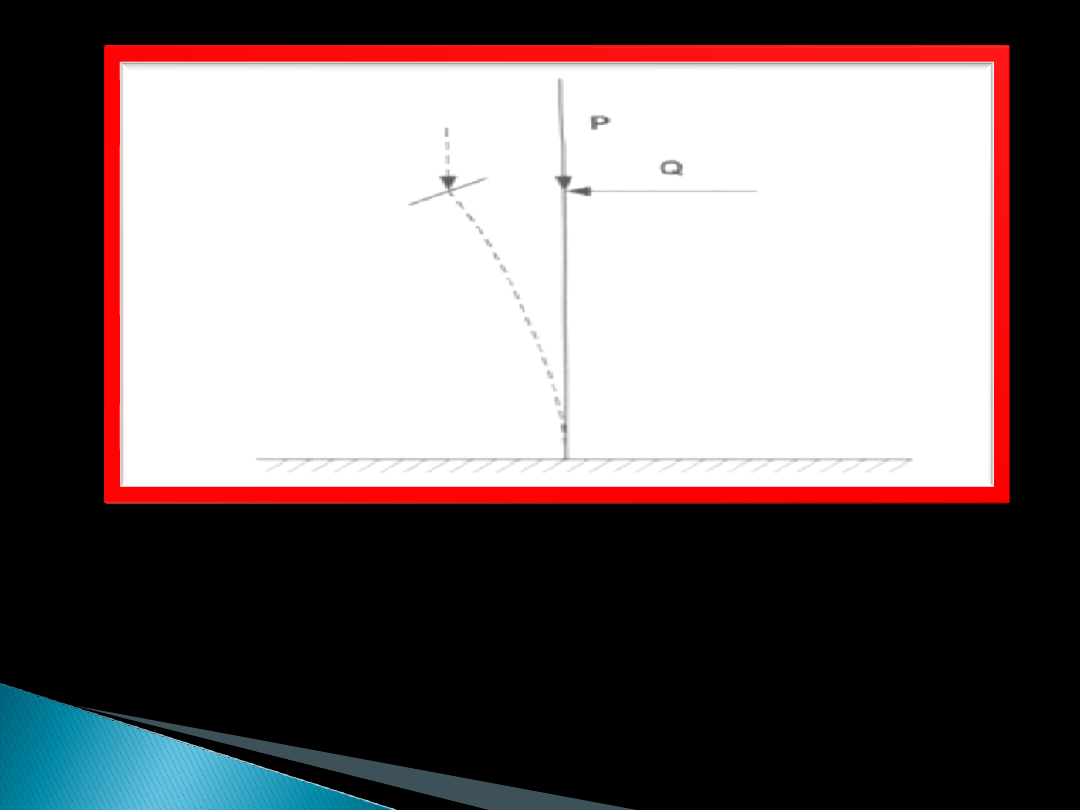
Jeżeli na pręt działa stosunkowo niewielka siła P to po

usunięciu poprzecznej zginającej siły Q = 0 pręt powróci do

postaci prostoliniowej. W przeciwnym wypadku po

przekształceniu wartości siły, zwaną krytyczną P kr. Po

usunięciu siły Q pręt pozostanie w postaci krzywej.



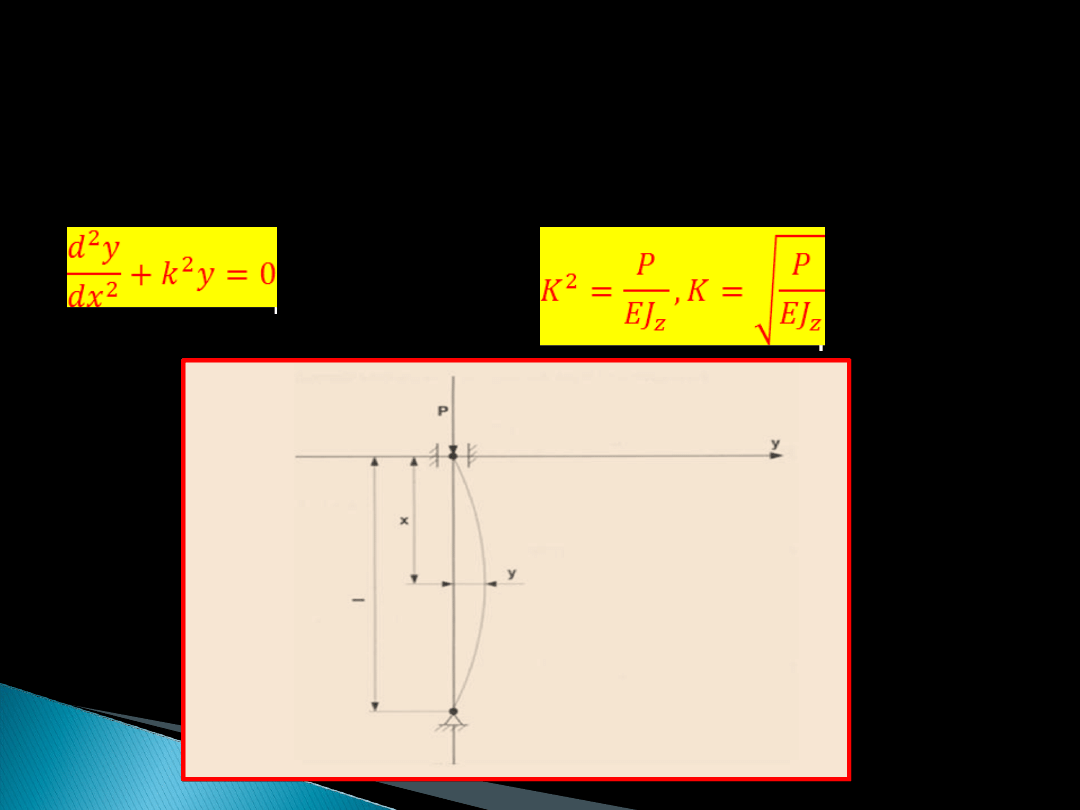
Równanie różniczkowe osi ugiętego pręta

określono wzorem



Moment zginający, który spowodowany jest

przemieszczeniem środkowych przekrojów pręta

wynosi:

Po dokończeniu przekształceń algebraicznych otrzymano:

gdzie

Model fizyczny



Rozważmy

warunki

równowagi

konieczne

dla

zachowania równowagi ściskanego pręta w postaci
wygiętej

(wyboczeniowej).

Doniosły

wpływ

na

stateczność pręta na zginanie tzn. na wyboczenie
wystąpi w płaszczyźnie najmniejszej sztywności na
zaginanie EJ.



Całkę ogólną równania określono następującą zależnością:



Gdzie:



A i B - stale całkowite



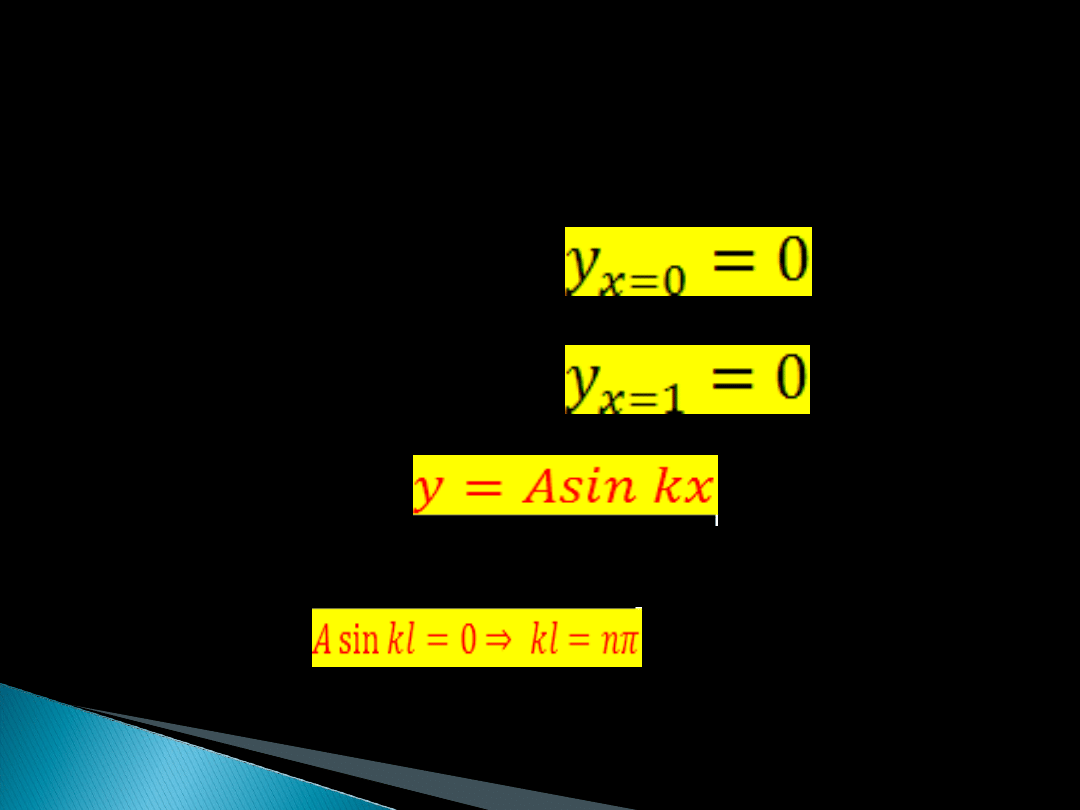
Stałe całkowanie wyznaczono z następujących

warunków brzegowych:



Dla B = 0 mamy:



Po wykorzystaniu otrzymujemy:



Gdzie:



n=0,1,2,3,…



n

w

=…



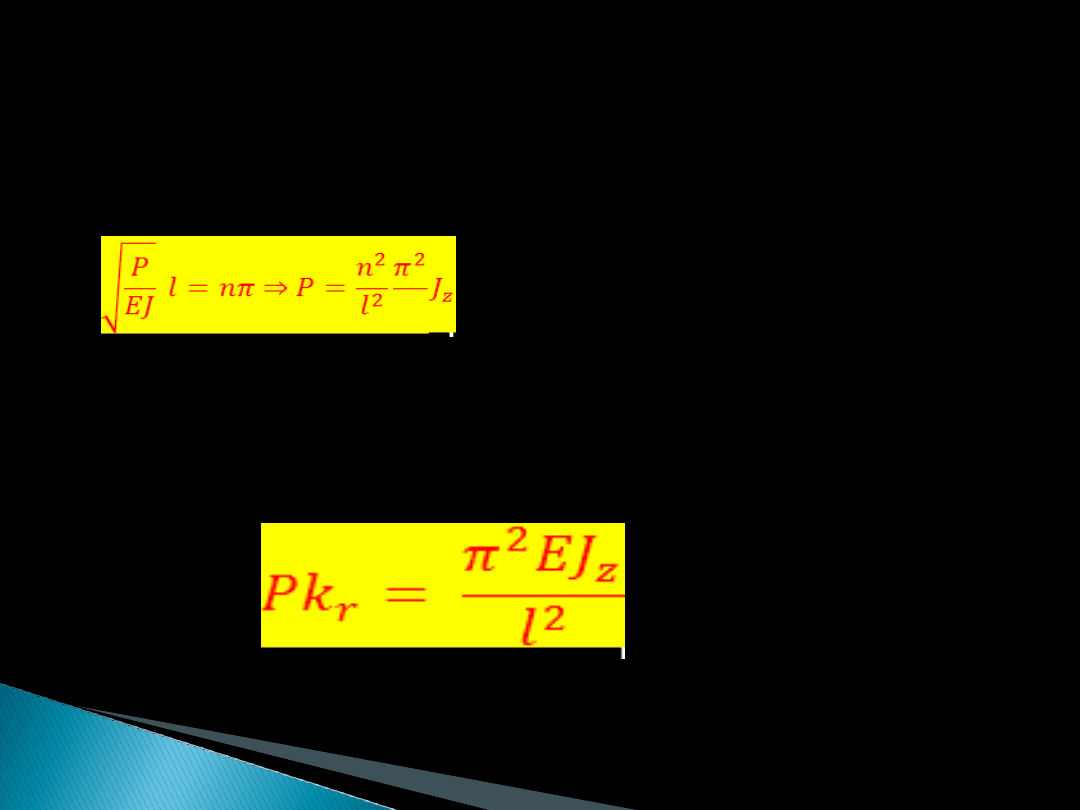
Po uwzględnieniu otrzymujemy



Dla n = 1 przedstawia wzór na siłę krytyczną P kr:



Lub

Gdzie:

P dop – dopuszczalne naprężenie

wybaczające

n w – współczynnik bezpieczeństwa na

wyboczenie



Gdzie:



σ - naprężenie, które są iloczynem siły ściskającej przez pole
przekroju poprzecznego pręta.



n w – współczynnik bezpieczeństwa na wyboczenie



k w – dopuszczalne naprężenie wybaczające



Przykładowe zadania z odkształceń

sprężystych według Eulera i

sprężysto – plastycznych według

Tetmajera



Stalowy pręt wykonany ze stali miękkiej o przekroju kołowym

zamocowano przegubowo na obu końcach ściskany jest on

osiowo działającą siłą P.



Określić granicznie wymiary przekroju poprzecznego pręta przy

danej długości „ 1”



Dla których można jeszcze stosować wzór Eulera. Znaleźć

wartość siły ściskającej pręt:



Dane:



Długość pręta: l = 1,2 m = 120 cm



E = 2,1 x 10 7 N / cm 2



RM = 19000 N / cm 2



N w = [ 1,5 : 9 ]



Przyjmuje współczynnik pewności na wyboczenie :nw =2



Smukłość graniczna = 105



Dopuszczalne naprężenia wybaczające kw



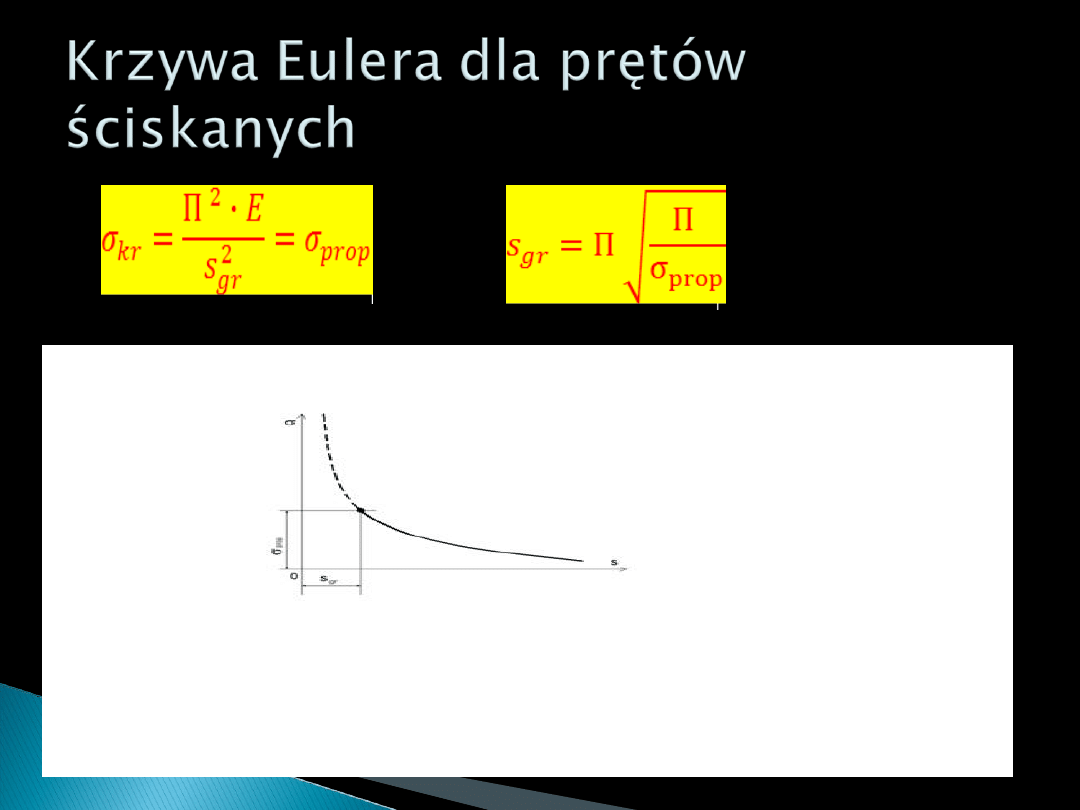
Stosowanie wzoru Eulera do wyznaczania
naprężeń krytycznych ogranicza się
wyłącznie do prętów o smukłości większej
od smukłości granicznej



Wyboczenie prętów o smukłości mniejszej
od granicznej zachodzi przy naprężeniach
określonych wzorem Eulera, co jest
wynikiem przeprowadzonych badań.



Wyboczenie pręta nie musi koniecznie

doprowadzić do jego zniszczenia,

aczkolwiek skutki będą odczuwalne w całej

konstrukcji i będą zależne od rodzaju i

charakteru wyboczenia.



Można powiedzieć, iż pręt wyboczony

wyczerpuje swą sztywność, po nie

znacznym przekroczeniu siły krytycznej w

prętach smukłych gwałtownie wzrastają

przemieszczenia, co wywołuje gwałtowny

wzrost naprężeń.