PROJEKTOWANIE

OPTYMALNE

Już od bardzo dawna wszelkiej działalności

człowieka, zwłaszcza związanej z
projektowaniem i konstruowaniem różnych
obiektów i urządzeń, towarzyszył problem
poszukiwania najlepszego możliwego
rozwiązania.

Ludzkość dążyła i dąży do realizowania

wariantów najlepszych z możliwych, takich,
które przyniosą największe korzyści przy
najmniejszym nakładzie sił i środków.

Optymalizacja

jest to dążenie do znalezienia wariantu ocenianego

według ustalonego kryterium wyboru, jako

najlepszy spośród wariantów uznanych za

dopuszczalne.

Zgodnie z tą definicją, optymalizacja polega

na znalezieniu ekstremum funkcji, w której

zmiennymi są elementy podlegające optymalizacji.

Zadanie to jest stosunkowo proste przy małej ilości

zmiennych oraz warunków, które ograniczają nasze

zmienne. Wówczas proces optymalizacji może się

ograniczyć do porównywania parami różnych

zmiennych według ustalonego kryterium i wybrania

najlepszego rozwiązania.

Problem zaczyna się, gdy tych zmiennych i

kryteriów jest wiele. Wielokryteriowa optymalizacja
nosi nazwę

polioptymalizacji

.

Szczególnie silny rozwój metod

optymalizacji nastąpił w okresie II Wojny
Światowej, wraz z rozwojem analizy
systemowej i badań operacyjnych. Wzrost
złożoności obiektów i systemów, który
nastąpił od tamtej pory, spowodował
konieczność rozwoju metod znajdujących
skuteczne i efektywne sposoby ich
projektowania i realizacji.

Obecnie metody optymalizacji znajdują

zastosowanie również w analizie konstrukcji i
innych dziedzinach, nie zawsze związanych
bezpośrednio z problemami optymalizacji.

Typowym przypadkiem optymalizacji w

projektowaniu jest sytuacja, gdy ma się
gotową koncepcję projektowanego obiektu, a
zadaniem optymalizacji jest wyznaczenie
optymalnych wartości głównych cech
konstrukcyjnych projektowanego urządzenia.

Rozwiązaniem zadania optymalizacji lub

polioptymalizacji nazywa się każdy
uporządkowany zbiór wartości wszystkich
zmiennych decyzyjnych: [x1,…,xp]. Jest to
wektor w przestrzeni zmiennych decyzyjnych
o współrzędnych będących wartościami tych
cech.

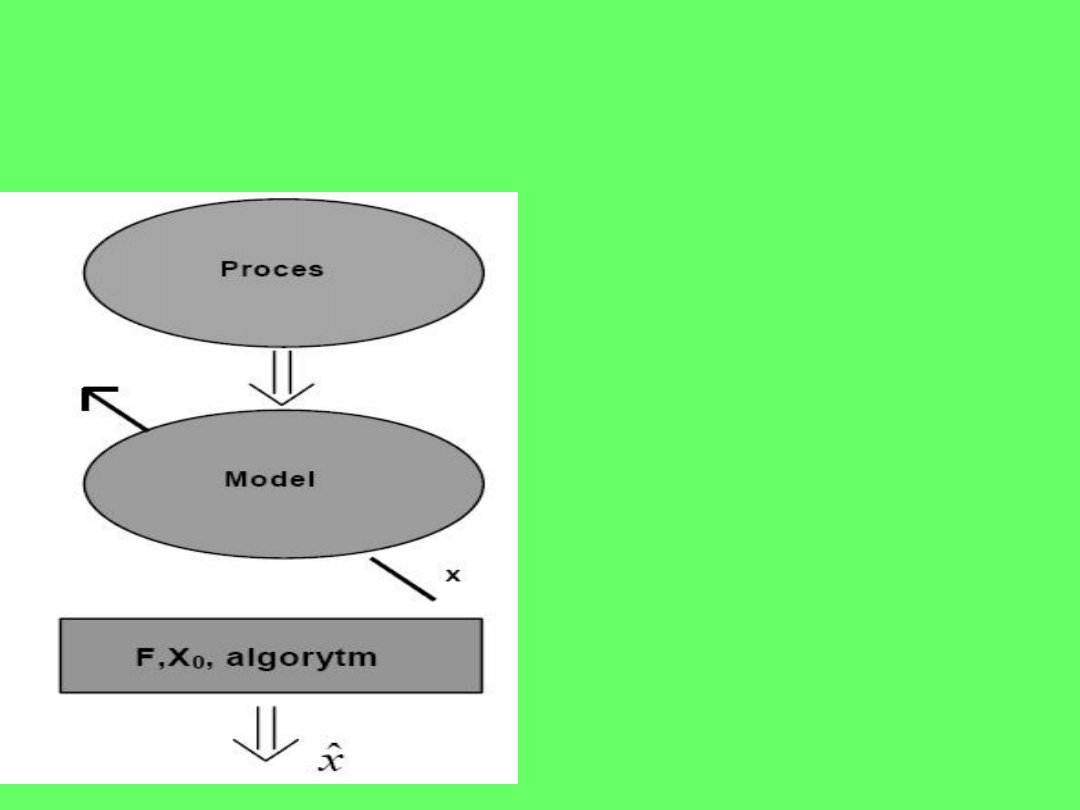
Proces formułowania i rozwiązywania problemu

optymalizacji (które w większości sprowadzają się do

znalezienia minimum funkcji) przebiega w następujący

sposób:

Proces

– zjawisko fizyczne,

proces technologiczny, system
ekonomiczny, planowanie
produkcji, itp.

Model

– opis matematyczny

procesu, sformułowany pod
kątem optymalizacji,

x

– zmienna decyzyjna,

F(x)

– ocena jakości (funkcja

celu, kryterium jakości),

X

0

– zbiór rozwiązań

dopuszczalnych,

- rozwiązanie (optymalna
wartość zmiennej decyzyjnej)

xˆ

xˆ

x

ˆ

Najczęściej, tak sformułowane

zadanie optymalizacyjne rozwiązuje
się przez znalezienie minimum
funkcji celu:

X

X

x

x

F





0

)}

(

min{

Proces optymalizacji zaczyna się od

ustalenia problemów optymalizacji.

Prawidłowe sformułowanie problemu optymalizacji

musi zawierać:

• określenie warunków optymalizacji - będą one miarą
spełnienia założonych celów,
• określenie parametrów optymalizacji - są to

elementy

opisu systemu nie zależne od projektanta,
• określenie zmiennych projektowych - są to elementy
opisu systemu zależne od projektanta,
• określenie ograniczeń – wartości, które będą
ograniczały zakres wartości analizowanych

zmiennych

projektowych.

Kryteria optymalizacji

Nadrzędnym kryterium optymalizacji nazywa

się taką wielkość w stosunku do której żąda się, by

była ona ekstremalna, np. wyraża się życzenie, aby

efektywność jakiegoś urządzenia była maksymalna.

Wybór kryterium nadrzędnego zależy od

rozwiązywanego problemu. Najczęstszym kryterium

optymalizacji jest koszt realizacji produkcji obiektu

optymalizowanego. Jednak, ponieważ zależy on od

bardzo wielu czynników, których wpływ często

bardzo trudno określić, w projektowaniu kryterium

kosztu jest zastępowane przez kryterium wymiarów

i objętości. Odpowiada ono w przybliżony sposób

kryterium cenowemu, gdyż wymiary obiektu

decydują o ilości potrzebnych surowców, a więc w

pośredni sposób określają one koszty. Kryterium to

jest poprawne dla elementów wykonanych z

jednego materiału. Przy konstrukcjach wykonanych

z niejednorodnych materiałów pozwala tylko na

orientacyjne określenie kosztów minimalnych.

Najczęściej problemy optymalizacji nie dają się

ograniczyć do jednego kryterium. Prowadzi to do
problemów optymalizacji wielokryteriowej –
polioptymalizacji. Gdy kryterium nadrzędne nie
jest jednoznacznie sformułowane, wyprowadza się
z niego zbiór kryteriów.

Problem polioptymalizacji rozwiązuje się

najczęściej sprowadzając go do problemu z
jednym kryterium, które nazywane jest zazwyczaj
funkcją celu i określane jako kombinacja liniowa
wszystkich kryteriów z odpowiednimi wagami:







n

i

i

i

F

c

F

1

Zmienne projektowe i parametry

optymalizacji

Zmienne projektowe i parametry optymalizacji

to wartości liczbowe lub funkcje, które określają

obiekt. Te spośród tych zmiennych, które podlegają

pewnym ograniczeniom, czy to technologicznym,

czy też normowych i ich wielkości muszą być z góry

ustalone, nazywa się parametrami

optymalizacji. Projektant nie ma żadnego wpływu

na ich wartości. Pozostałe wartości są natomiast

jak najbardziej od niego zależne i noszą nazwę

zmiennych projektowych. Tworzą one pewien

wektor o składowych {x

1

,…,x

n

} i określają punkt w

przestrzeni n-wymiarowej.
Zbiór zmiennych projektowych nosi też nazwę

zmiennych decyzyjnych, które są podzbiorem

cech konstrukcyjnych, tzn. wielkości potrzebnych

do fizycznego wykonania obiektu. Zmienne

decyzyjne dobiera się tak, aby jednoznacznie

określały projektowany obiekt.

Ograniczenia w optymalizacji

Rozpatrywane zmienne projektowe często nie

mogą być dowolne. Narzucone są na nie pewne

ograniczenia. Szereg ograniczeń wynikających z

wymagań normowych, technologicznych,

eksploatacyjnych i innych stawianych

projektowanej konstrukcji, z matematycznego

punktu widzenia można podzielić na:

• nierównościowe:

• równościowe:

gdzie: oznacza funkcję wektora zmiennych

projektowych. Oznacza to, że argumentami tych

ograniczeń są tylko zmienne decyzyjne.

n

i

x

g

i

,...,

2

,

1

,

0

)

(





n

j

x

g

j

,...,

2

,1

,0

)

(





)

(x

g

i

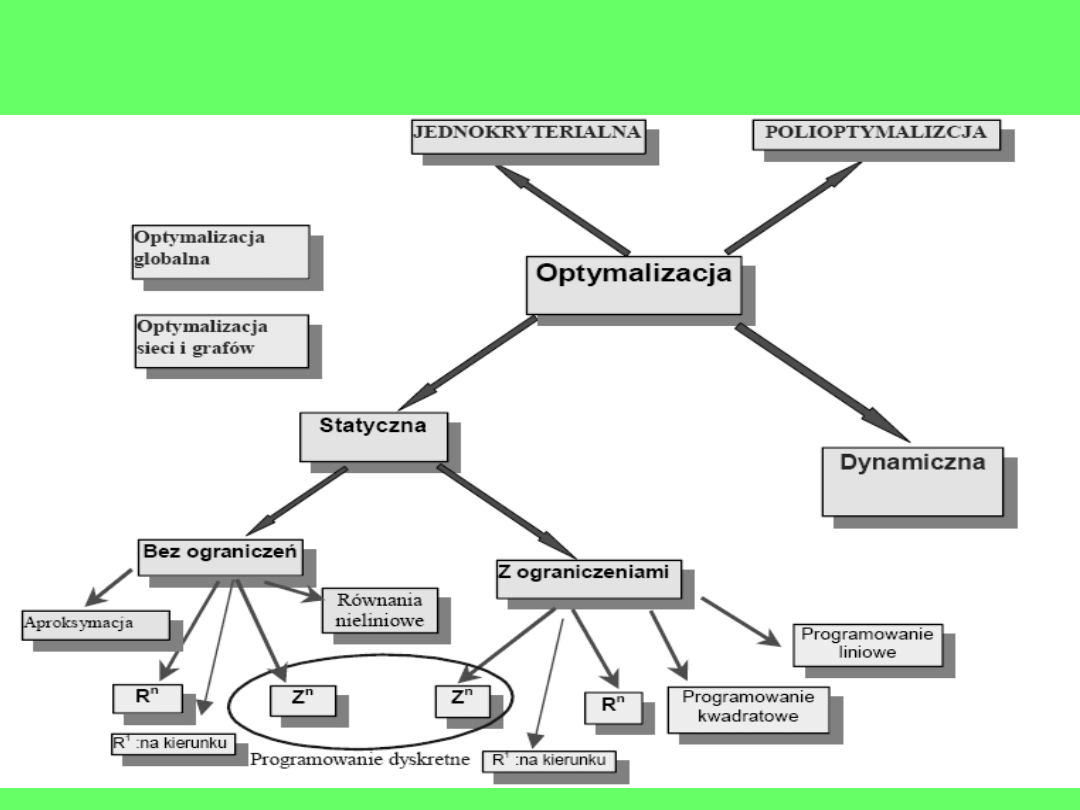
Metody optymalizacji optymalizacji można podzielić na

kilka sposobów, zależnych od postawionego problemu.

Metody optymalizacji

Wybór metody rozwiązywania

problemu optymalizacji, których jest
bardzo dużo, zależy od sposobu
zmiany zmiennych projektowych oraz
od postaci funkcji celu i funkcji
opisujących ograniczenia.