Figury Podobne

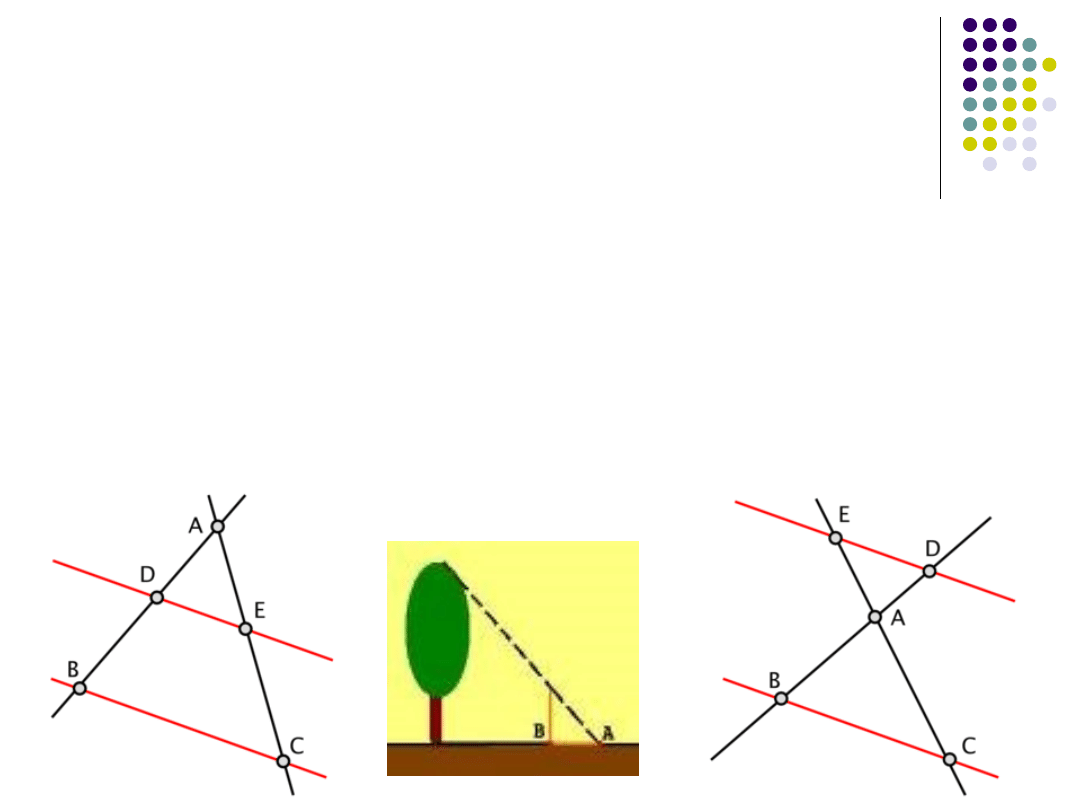
Twierdzenie Talesa



Jeżeli ramiona kąta przetniemy
prostymi równoległymi, to odcinki
wyznaczone na jednym ramieniu kąta
są proporcjonalne do odpowiednich
odcinków wyznaczonych na drugim
ramieniu kąta

.

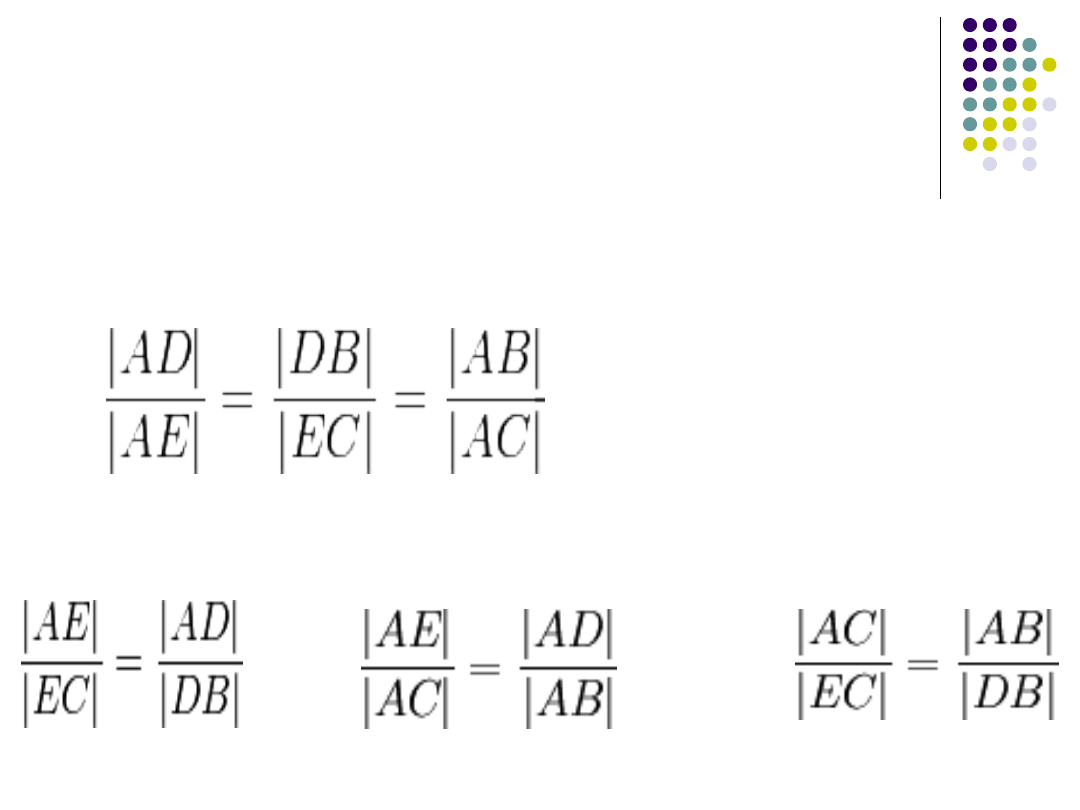
Twierdzenie Talesa



Dla powyższych rysunków zachodzi
własność

lub po przekształceniu:   

               

oraz

 

               

  ,

a także

 

                

Podział Odcinka



Konstrukcja krok po kroku.



1. Rysujemy dowolną półprostą o początku w punkcie A,

nachyloną do odcinka AB pod kątem różnym od 180 °.



2. Na półprostej p, z punktu A, odkładamy odcinek o

dowolnej długości.



3. Na półprostej p odkładamy kolejne odcinki o tej samej

długości. Powtarzamy to tyle razy na ile dzielimy odcinek

.



4. Teraz kreślimy prostą przechodzącą przez punkt B i

punkt, który narysowaliśmy jako ostatni na półprostej p.



5. Kreślimy proste równoległe do narysowanej prostej,

przechodzące przez punkty znajdujące się na półprostej

p. Dzielą one odcinek AB na pięć równych części.

Podobieństwo Figur



Figury, mające ten sam kształt, a różniące
się co najwyżej wielkością, nazywamy
figurami podobnymi.

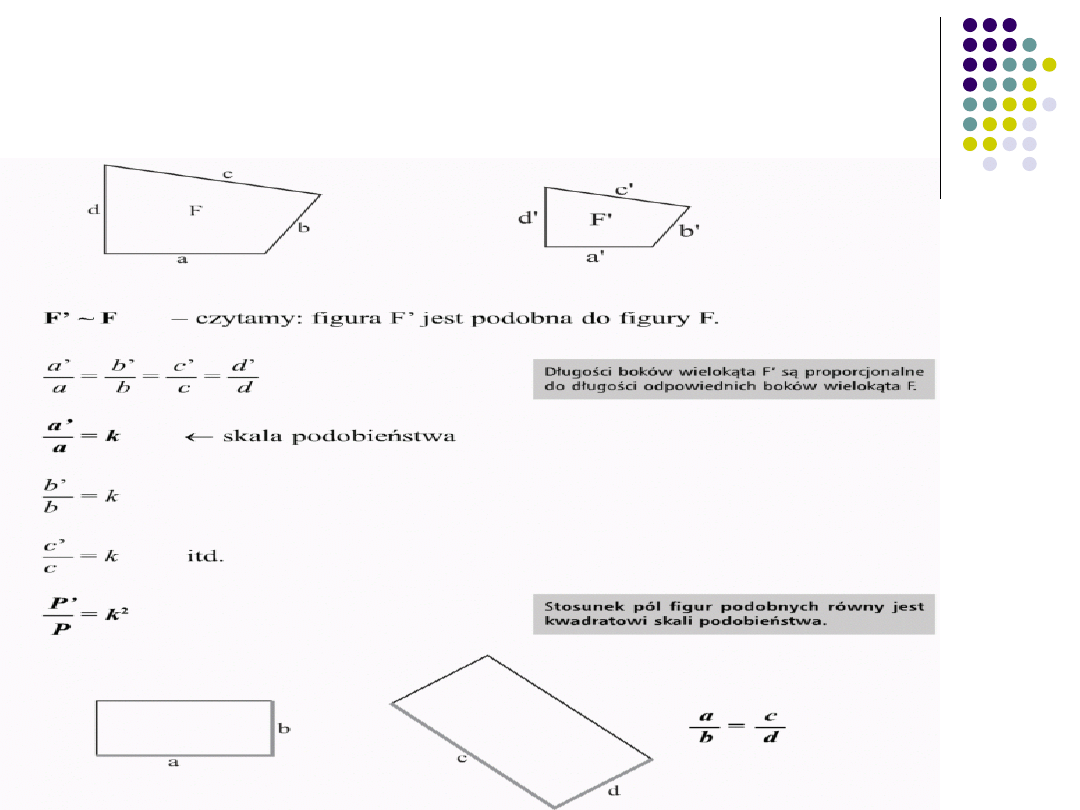
Podobieństwo Figur

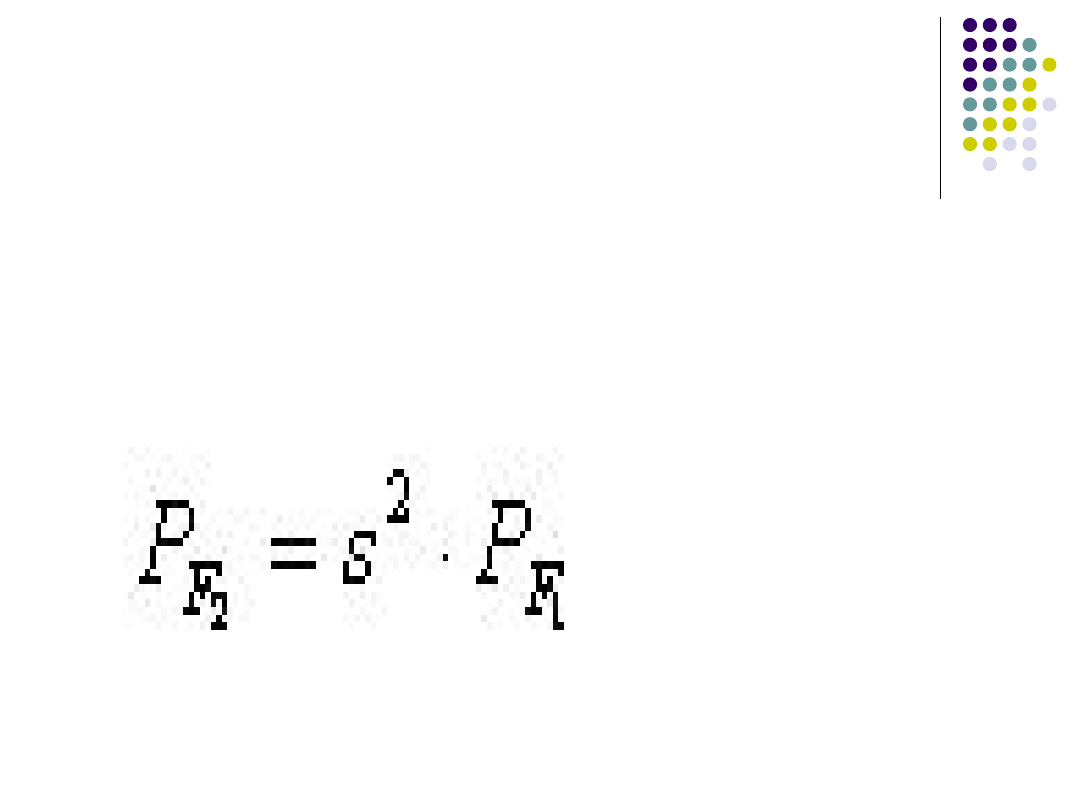
Pola Figur Podobnych



Twierdzenie :



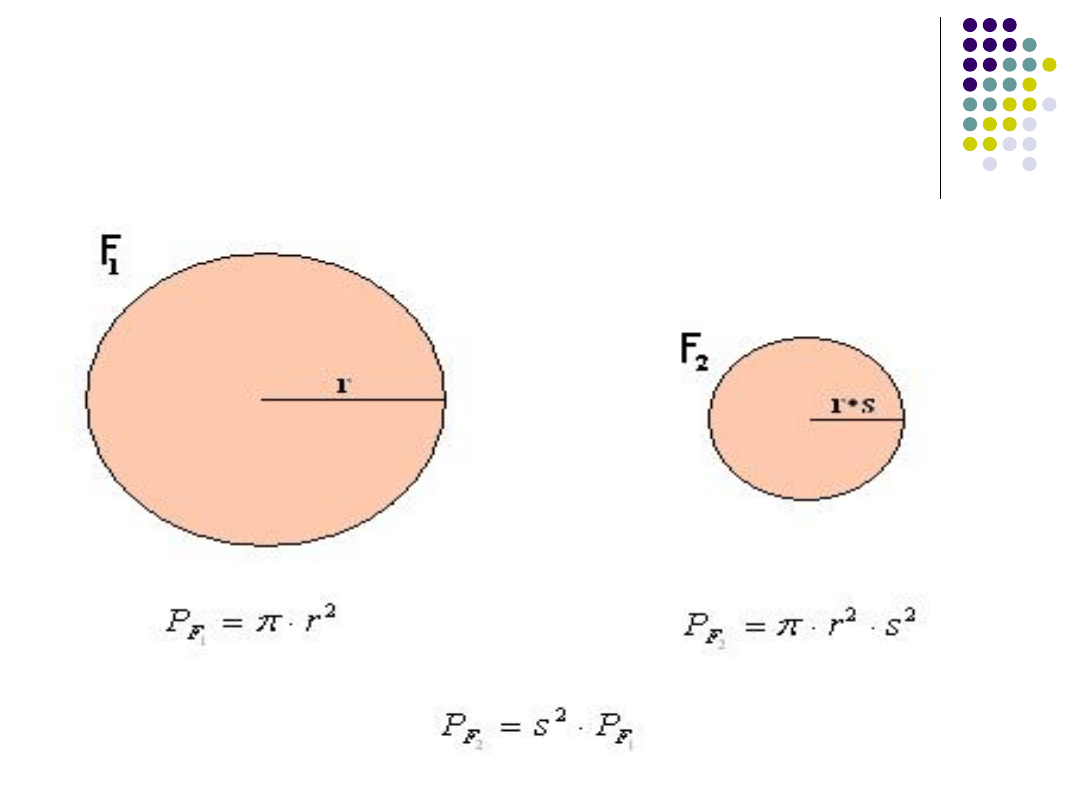
Jeżeli figura F2 jest obrazem figury F1 w

podobieństwie o skali s (s>0), to pole figury

F2 jest iloczynem kwadratu skali

podobieństwa i pola figury F1:

Pola Figur Podobnych



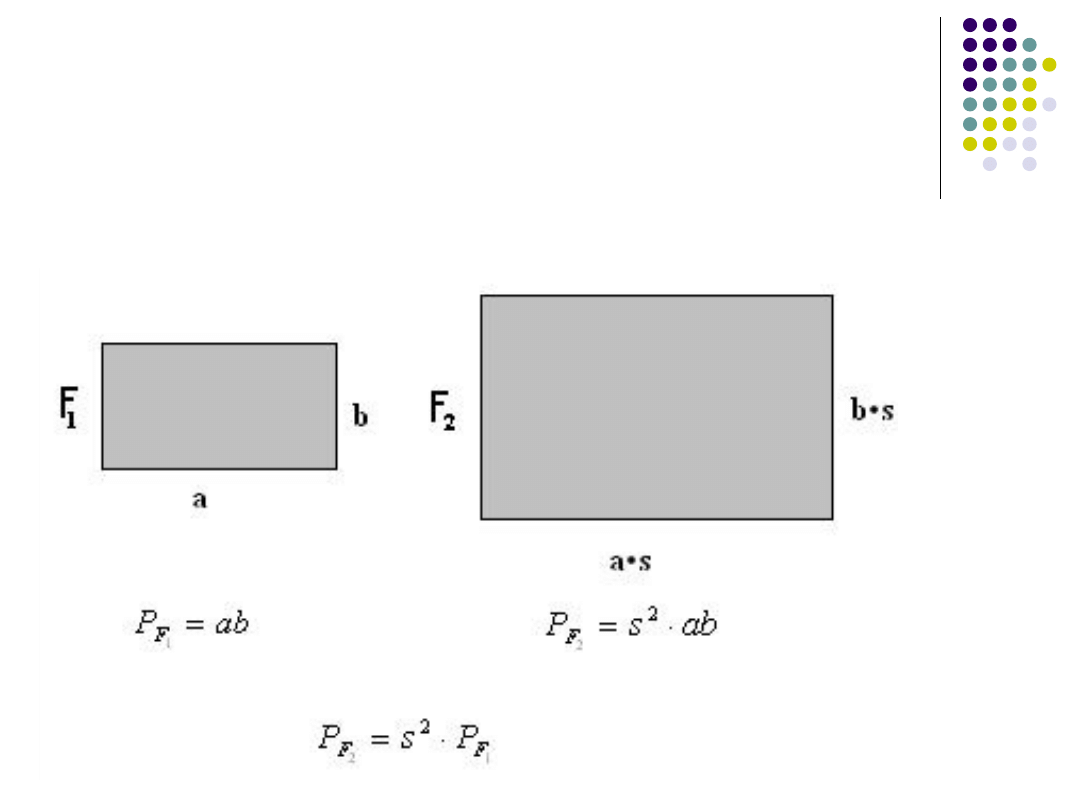
Poniżej rozpatrzono trzy pary figur
podobnych:

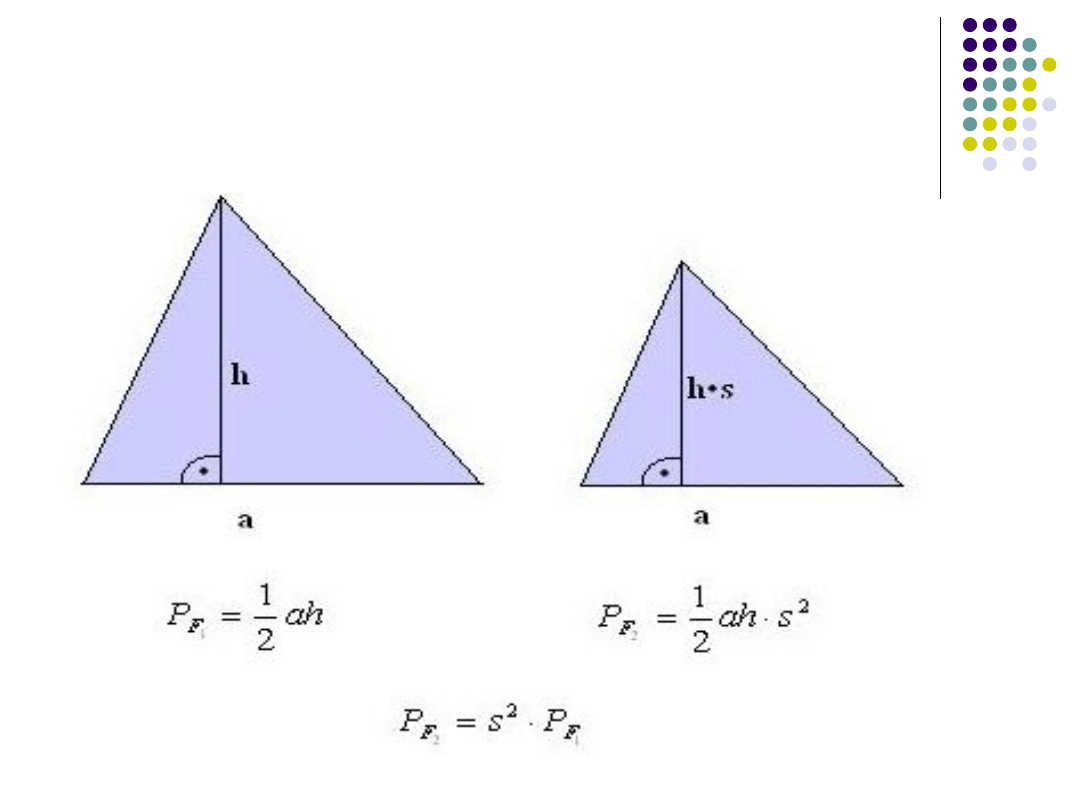
Pola Figur Podobnych

Pola Figur Podobnych

Cechy Podobieństwa
Trójkątów



Cechy podobieństwa trójkątów, to
warunki konieczne i wystarczające na
to, aby dwa trójkąty były podobne.
Podobieństwo trójkątów oznaczamy
symbolem ~.

Cechy Podobieństwa
Trójkątów



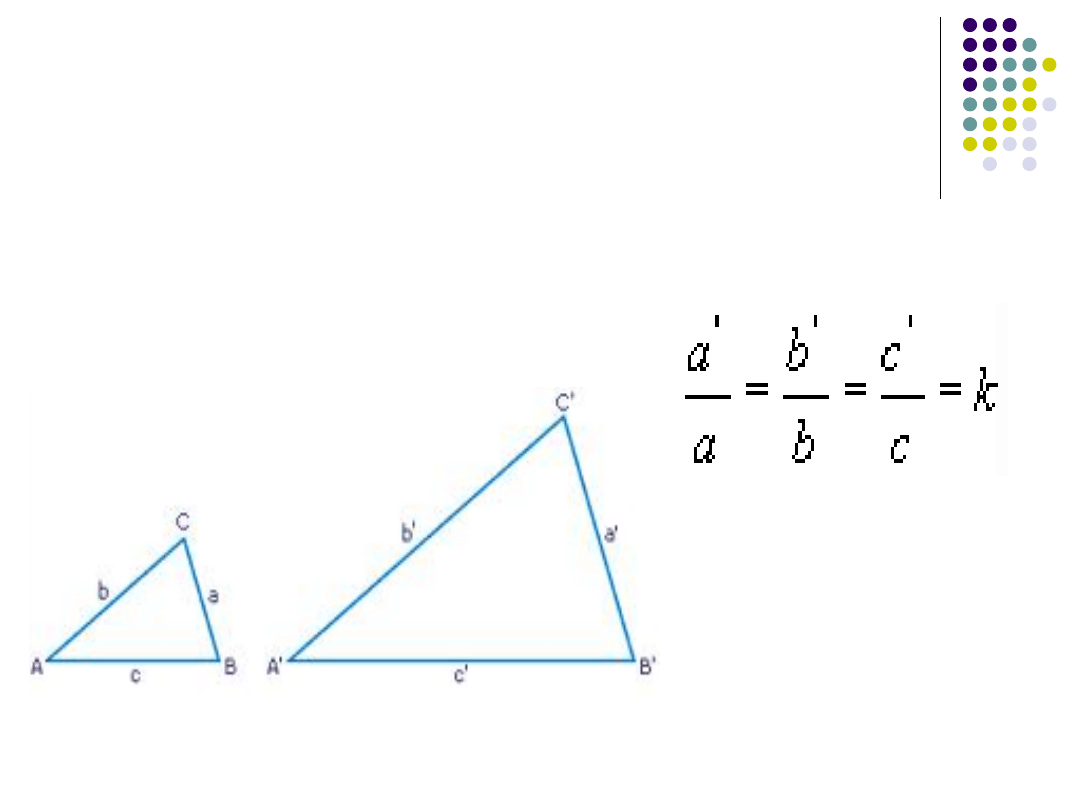
I cecha podobieństwa trójkątów.

(bok-bok-bok)

(k - skala podobieństwa)

ABC ~ A'B'C'

Jeżeli boki jednego trójkąta są

proporcjonalne do odpowiednich boków

drugiego

trójkąta

, to trójkąty są

podobne.

Cechy Podobieństwa
Trójkątów



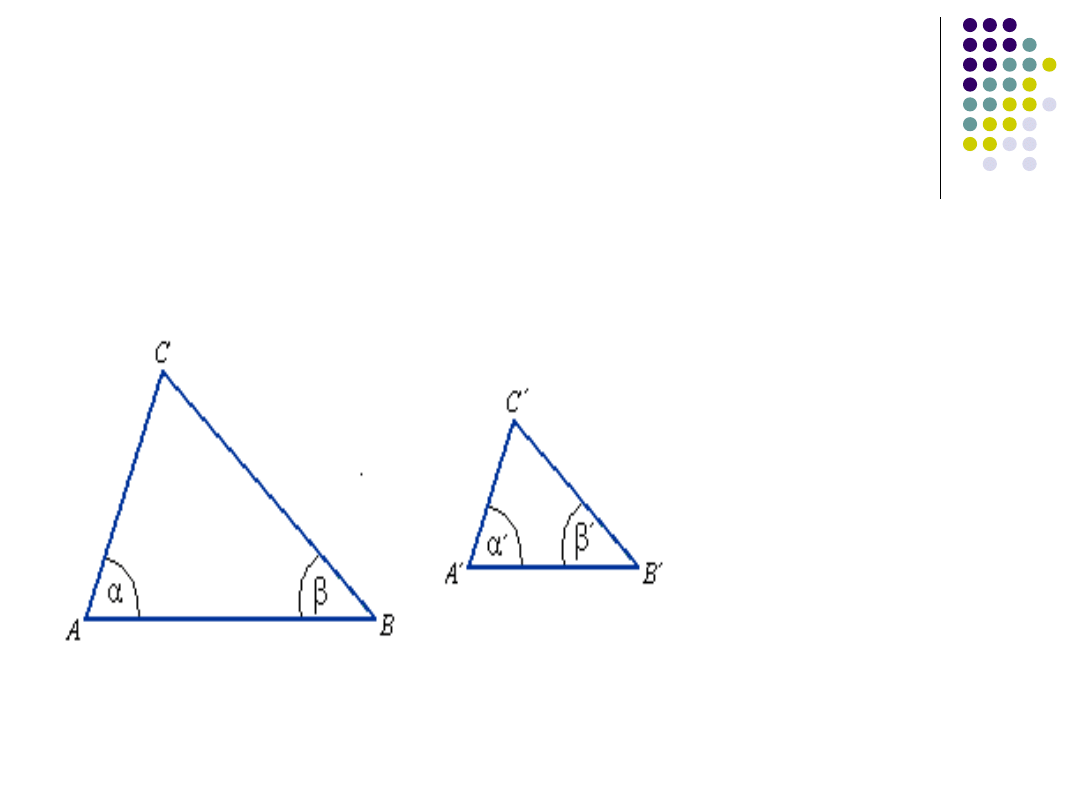
II cecha podobieństwa trójkątów.

(kąt-kąt)

a = a (alfa = alfa’)
b = b (beta = beta’)
ABC ~ A'B'C'

Jeżeli miary dwóch kątów jednego trójkąta są
równe miarom odpowiednich dwóch kątów
drugiego trójkąta, to te trójkąty są podobne
(miary trzecich kątów wtedy też muszą być
równe).

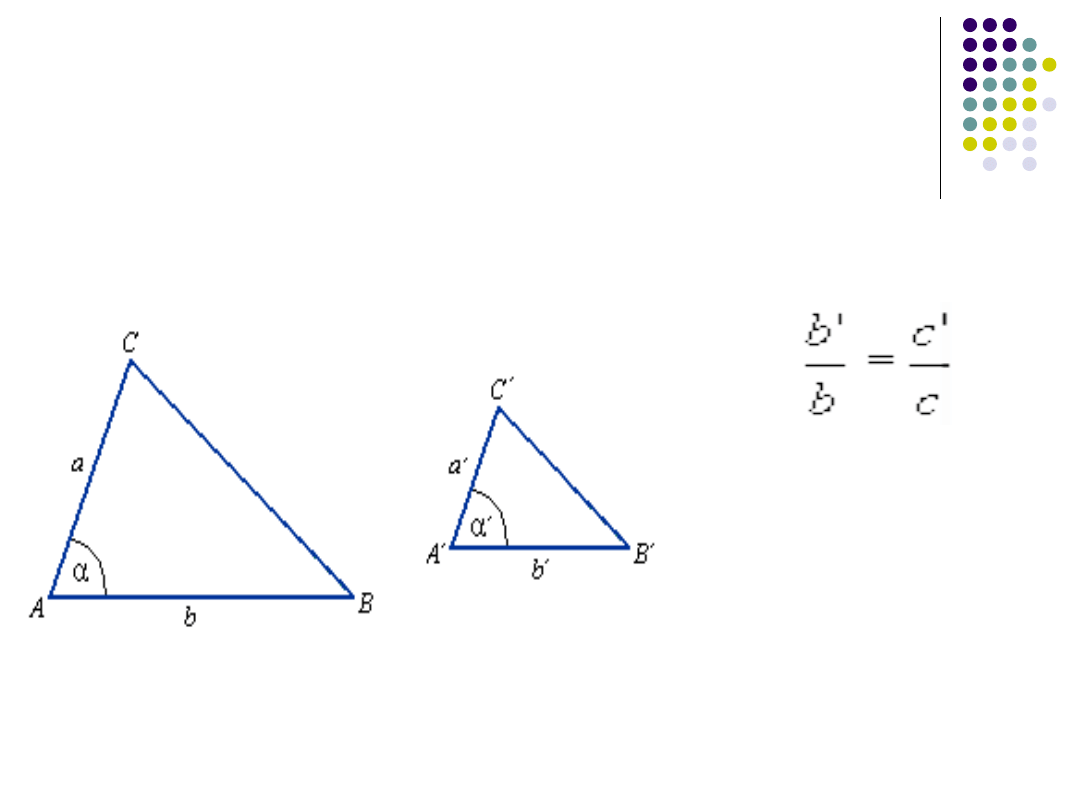
Cechy Podobieństwa
Trójkątów



III cecha podobieństwa trójkątów.

(bok-kąt-bok)

ABC ~
A'B'C'

α = α'

Jeżeli dwa boki jednego trójkąta są proporcjonalne do
dwóch boków drugiego trójkąta, a kąty między nimi
zawarte są przystające, to te trójkąty są podobne.