„Między duchem a materią

pośredniczy matematyka.

”

Hugo Steinhaus

FIGURY PODOBNE.

Podobieństwo w matematyce ma wiele
wspólnego z podobieństwem rozumianym w
sposób potoczny. W życiu codziennym
podobieństwo dwóch rzeczy jest kwestią
subiektywną, w matematyce jest określone
ścisłą definicją. Nie wystarczy stwierdzić „na
oko”, że dwie figury są podobne, trzeba to
sprawdzić.

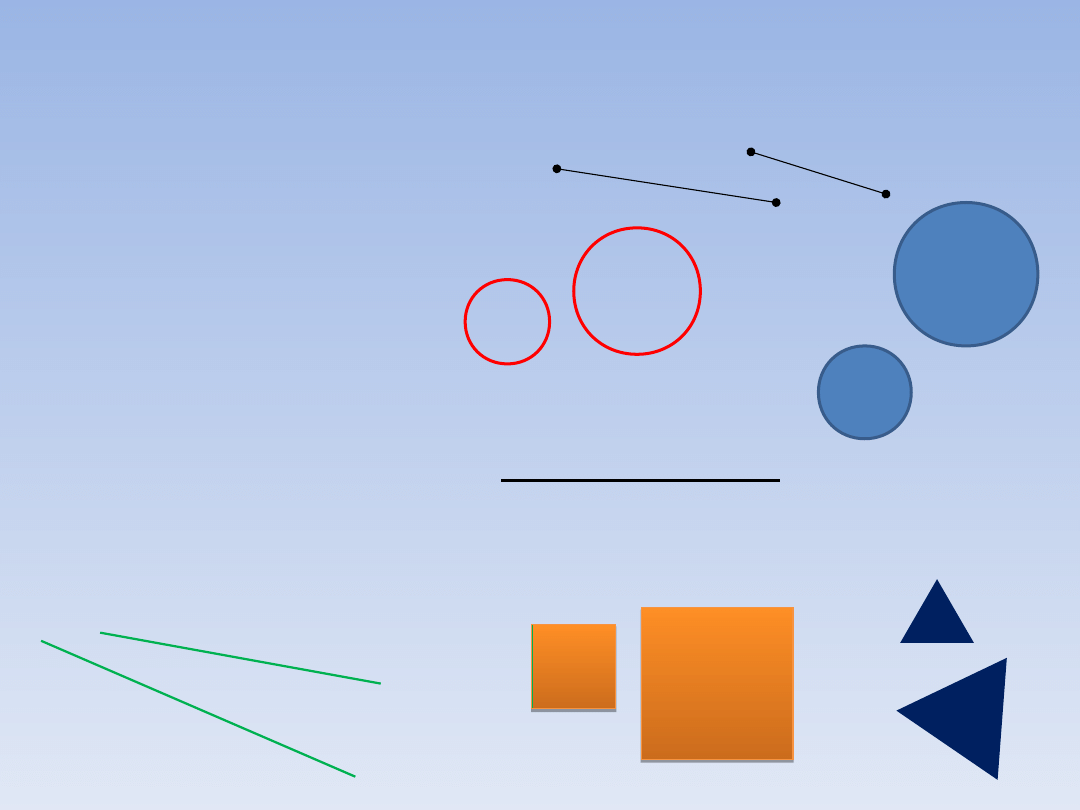
FIGURY PODOBNE.

Figurami podobnymi są:

- każde dwa odcinki

- każde dwa koła

- każde dwa okręgi

- każde dwie proste

- każde dwa kwadraty

- każde dwa trójkąty równoboczne

- każde dwie figury, które mają taki sam
kształt, a różnią się najwyżej wielkością

FIGURY PODOBNE.

Dwa wielokąty o takiej samie liczbie boków

nazywamy wielokątami podobnymi, jeżeli:

• mają odpowiednie kąty wewnętrzne równe

• stosunek odpowiadających sobie boków

jest równy

Liczbę k równą stosunkowi długości

odpowiadających sobie odcinków figur

podobnych nazywamy skalą

podobieństwa.

Podobieństwo oznaczamy: A  B (czytaj:

figura A jest podobna do figury B)

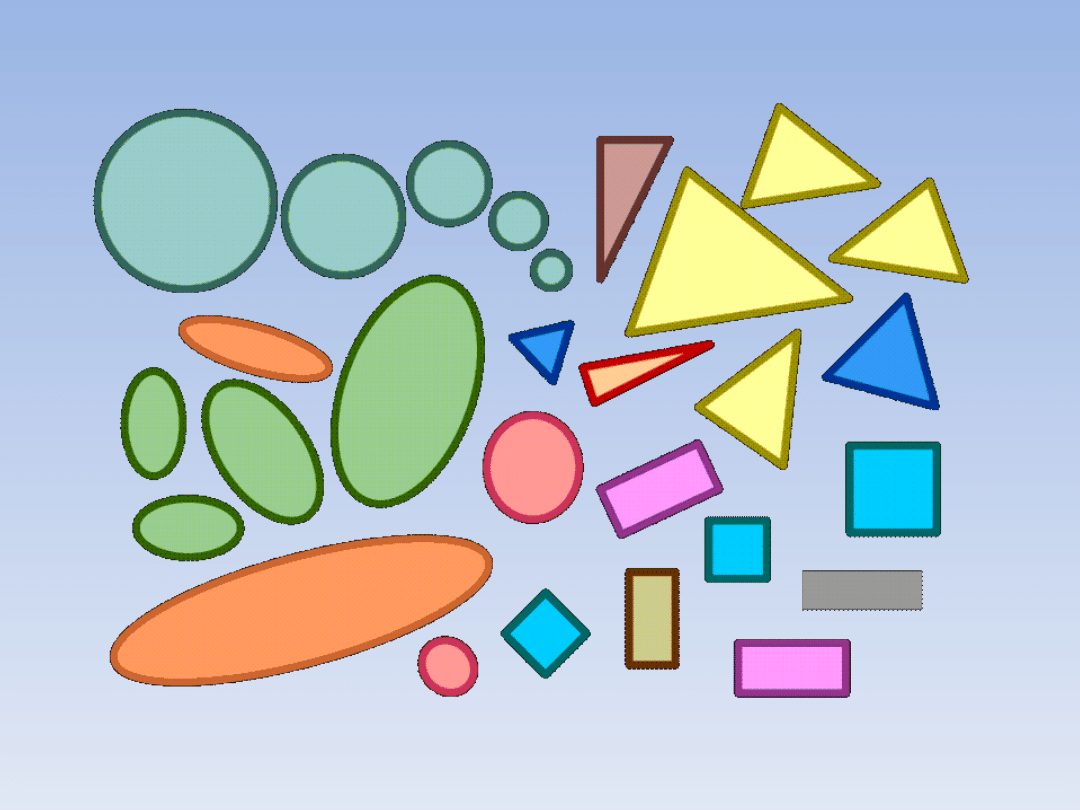
PRZYKŁADY FIGUR

PODOBNYCH.

Figury o tym samym kolorze są podobne.

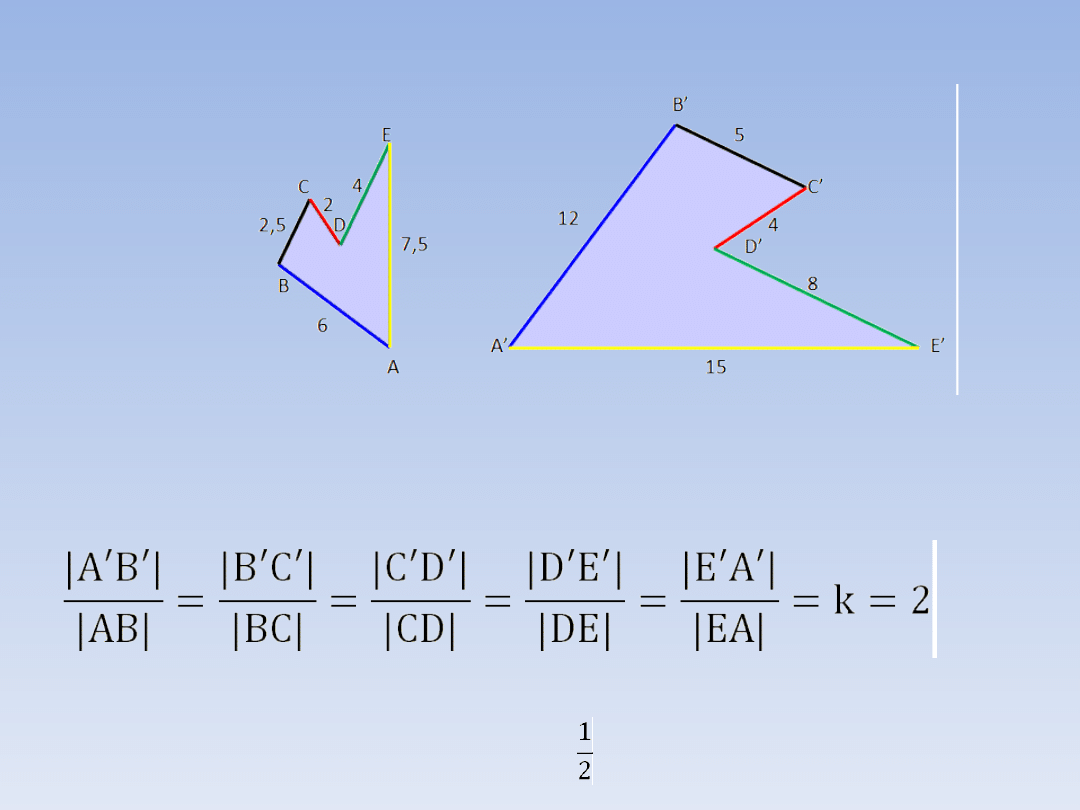
PRZYKŁADY FIGUR

PODOBNYCH.

Wielokąt

A’B’C’D’E’

jest

podobny

do

wielokąta ABCDE ponieważ: ∢A = ∢ A’; ∢ B
= ∢ B’; ∢ C = ∢C’; ∢ D = ∢ D’; ∢ E = ∢ E’,
oraz:

A’B’C’D’E’  ABCDE w skali k = 2
ABCDE  A’B’C’D’E’ w skali k =

SKALA.

Skala mówi nam ile razy figury podobne są
większe lub mniejsze od siebie. Jest to
zawszę liczba dodatnia (k > 0). Jeżeli:
k < 1 – to figura podobna jest mniejsza od
wyjściowej;
k = 1 – to figura podobna jest identyczna jak
figura
wyjściowa;
k > 1 – to figura podobna jest większa od
wyjściowej.
Gdy dana jest długość odcinka figury
wyjściowej – a, oraz skala podobieństwa – k,
w prosty sposób możemy obliczyć długość
tego odcinka w figurze podobnej do danej –
a’.

a‘ = k ∙ a

PRZYKŁADY.

PRZYKŁAD 1.
W jakiej skali kwadrat o boku 9 cm jest
podobny do kwadratu o boku 22,5 cm?
Oznaczmy:
a‘ – długość boku kwadratu podobnego,
a – długość boku kwadratu wyjściowego.
Skalę

podobieństwa

obliczamy

dzieląc

długość boku figury podobnej do danej, przez
długość boku figury wyjściowej:

PRZYKŁADY.

PRZYKŁAD 2.
Prostokąt WILK ma wymiary 5,5 cm x 6,9 cm.
Czy prostokąt SOWA o wymiarach 38,5 cm x
48,3 cm jest podobny do prostokąta WILK?
Sprawdzamy, czy stosunek odpowiednich
boków prostokątów WILK i SOWA jest stały.
Dzielimy krótszy bok przez krótszy, a dłuższy
przez dłuższy:

W obu dzieleniach otrzymaliśmy
tę samą liczbę a więc stosunek
odpowiednich boków jest stały.
Prostokąt SOWA jest podobny do
prostokąta

WILK,

skala

podobieństwa k = 7.

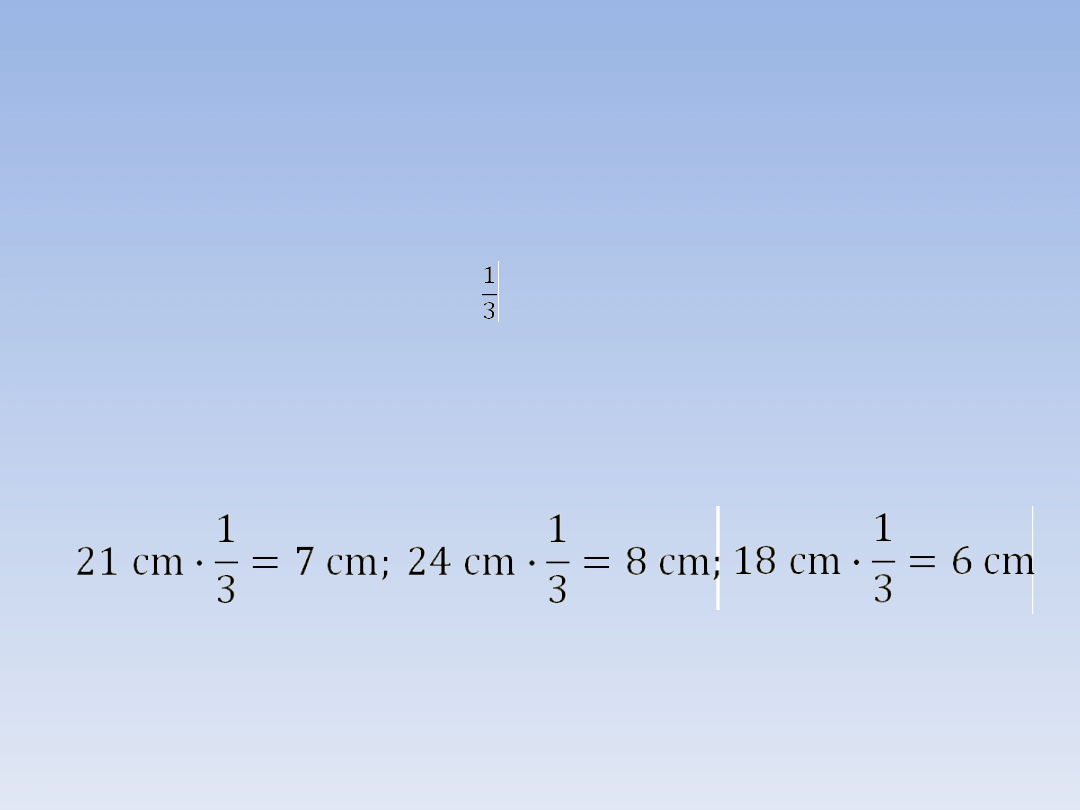
PRZYKŁADY.

PRZYKŁAD 3.
Trójkąt KOT ma boki długości 21 cm, 24 cm i 18 cm.

Jakie długości mają boki trójkąta LEW podobnego
do trójkąta KOT w skali k = ? Ile razy obwód
trójkąta LEW jest mniejszy od obwodu trójkąta
KOT?

Aby obliczyć długości boków trójkąta LEW,

mnożymy długości boków trójkąta KOT przez
skalę podobieństwa:

Obliczamy teraz obwody:
Ob

KOT

= 21 cm + 24 cm + 18 cm = 63 cm

Ob

LEW

= 7 cm + 8 cm + 6 cm = 21 cm

PRZYKŁADY.

PRZYKŁAD 3 – ciąg dalszy.

Obwód trójkąta LEW jest trzy razy mniejszy od

obwodu trójkąta KOT.

Tak naprawdę nie musieliśmy wyliczać

obwodów i dzielić ich przez siebie,
wystarczyło spojrzeć na skalę podobieństwa.
Trójkąt LEW jest podobny do trójkąta KOT w
skali k = , oznacza to, że trójkąt LEW jest
trzy razy mniejszy od trójkąta KOT, a więc
jego obwód także jest trzy razy mniejszy.

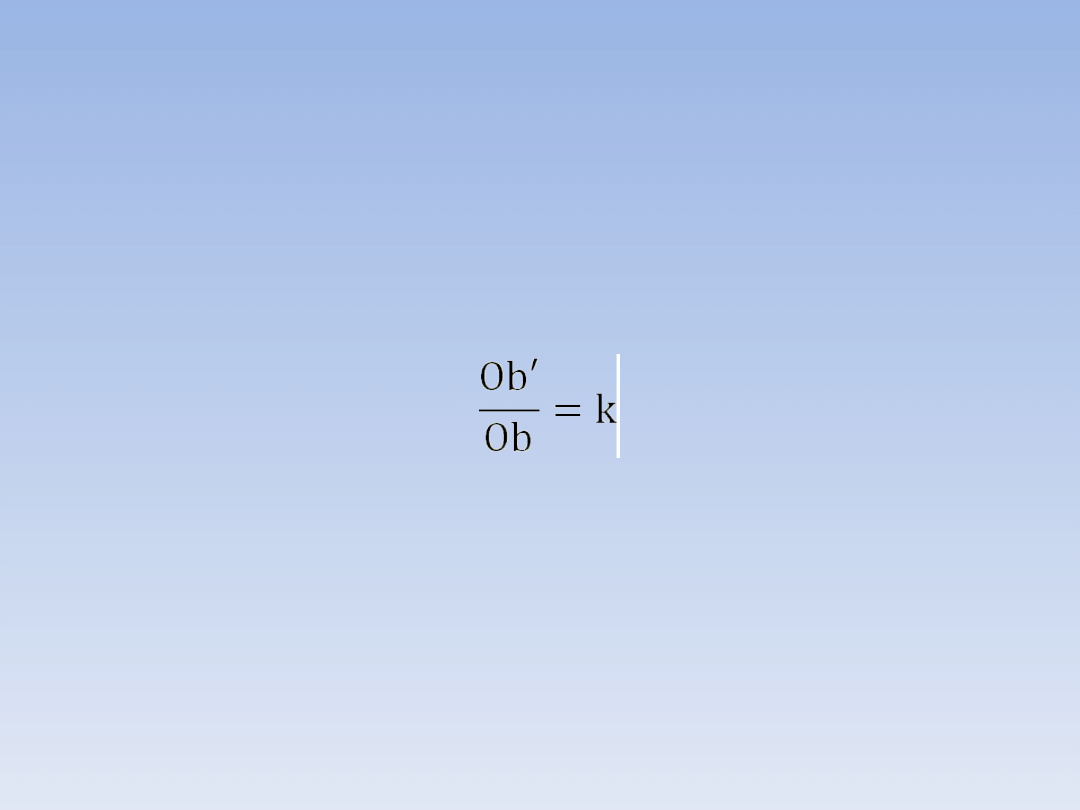
UWAGA.

Stosunek obwodów figur podobnych jest

równy skali podobieństwa.

Ob – obwód figury wyjściowej
Ob’ – obwód figury podobnej do figury
wyjściowej
k – skala podobieństwa

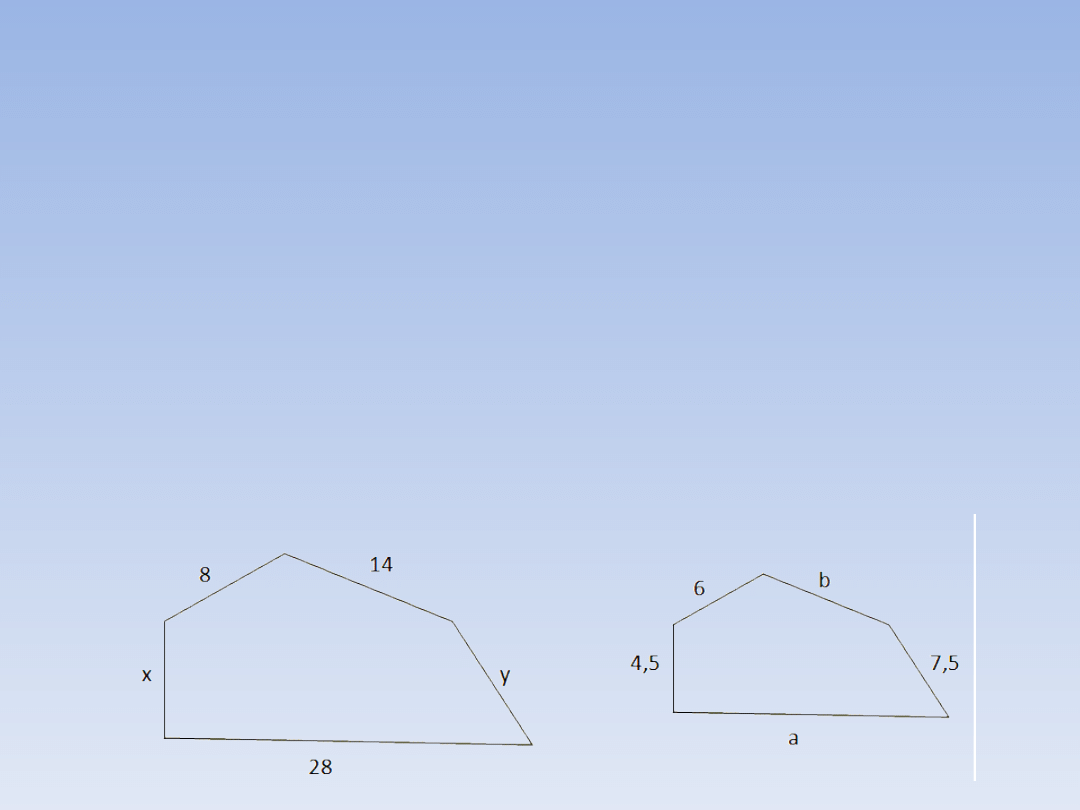
PRZYKŁADOWE ZADANIA.

ZADANIE 1.
Narysowane poniżej wielokąty są podobne.
a)Jaka jest skala podobieństwa większego
wielokąta do mniejszego?
b)Jaka jest skala podobieństwa mniejszego
wielokąta do większego?
c)Oblicz

długości

boków

oznaczonych

literami.

PRZYKŁADOWE ZADANIA.

ZADANIE 1 – ciąg dalszy.
a)Aby

obliczyć

skalę

podobieństwa

większego wielokąta do mniejszego, dzielimy
przez siebie długość jednego z boków
większego

wielokąta

przez

długość

odpowiadającego mu boku z mniejszego
wielokąta:

b) Skala podobieństwa mniejszego wielokąta
do większego jest liczbą odwrotną do skali
obliczonej w podpunkcie a, czyli:

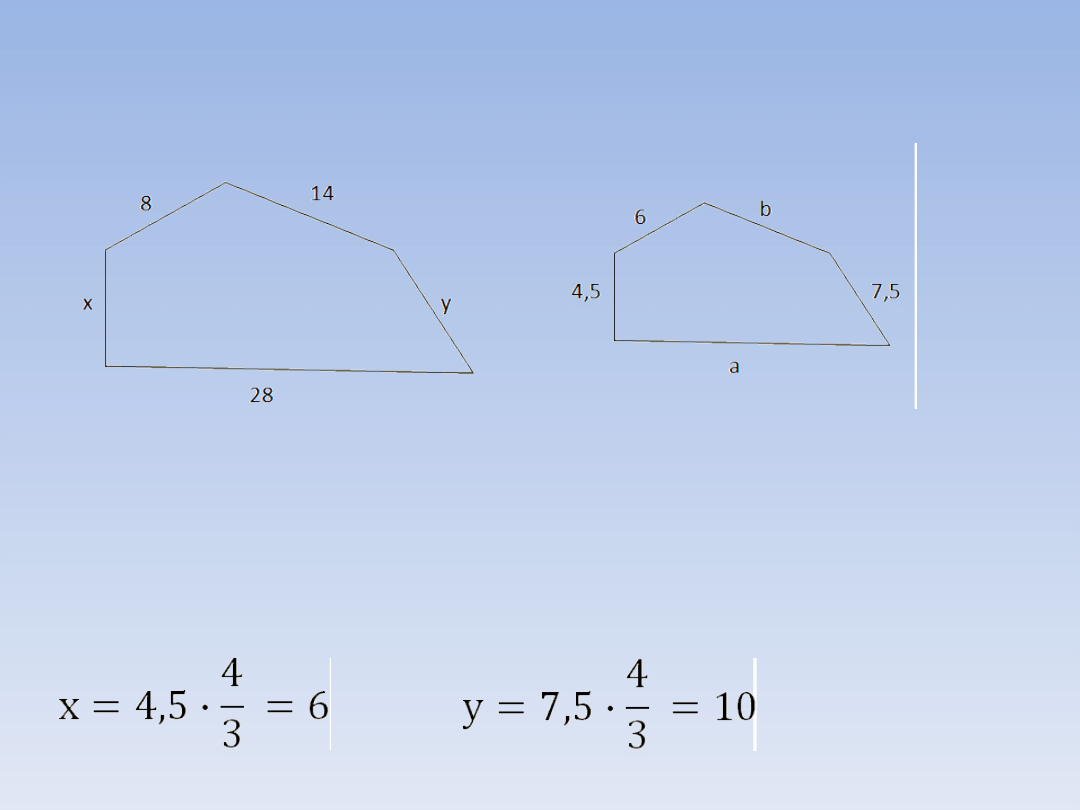
PRZYKŁADOWE ZADANIA.

ZADANIE 1 – ciąg dalszy.

c) Aby obliczyć długość boków x i y mnożymy
długości odpowiadających im boków z
mniejszej figury przez skalę podobieństwa
większego

wielokąta

do

mniejszego

(powiększamy boki):

;

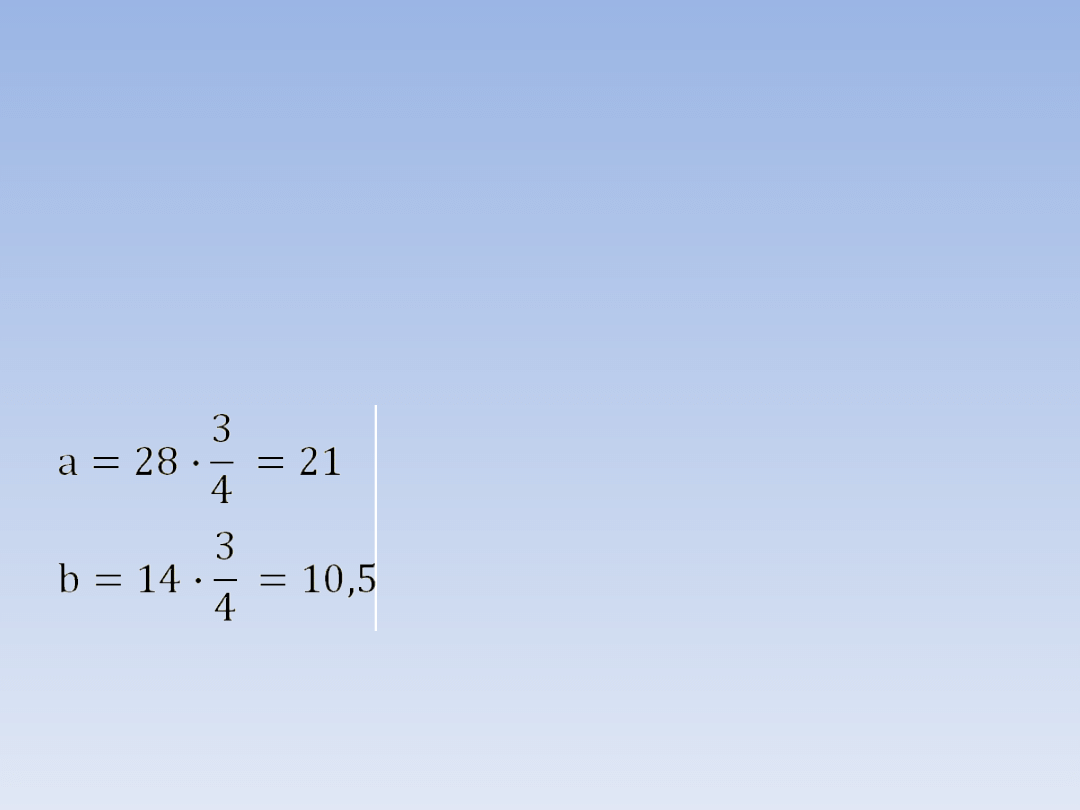
PRZYKŁADOWE ZADANIA.

ZADANIE 1 – ciąg dalszy.
Aby obliczyć długości boków a i b mnożymy
odpowiadające im długości boków większego
wielokąta

przez

skalę

podobieństwa

mniejszego

wielokąta

do

większego

(pomniejszamy boki):

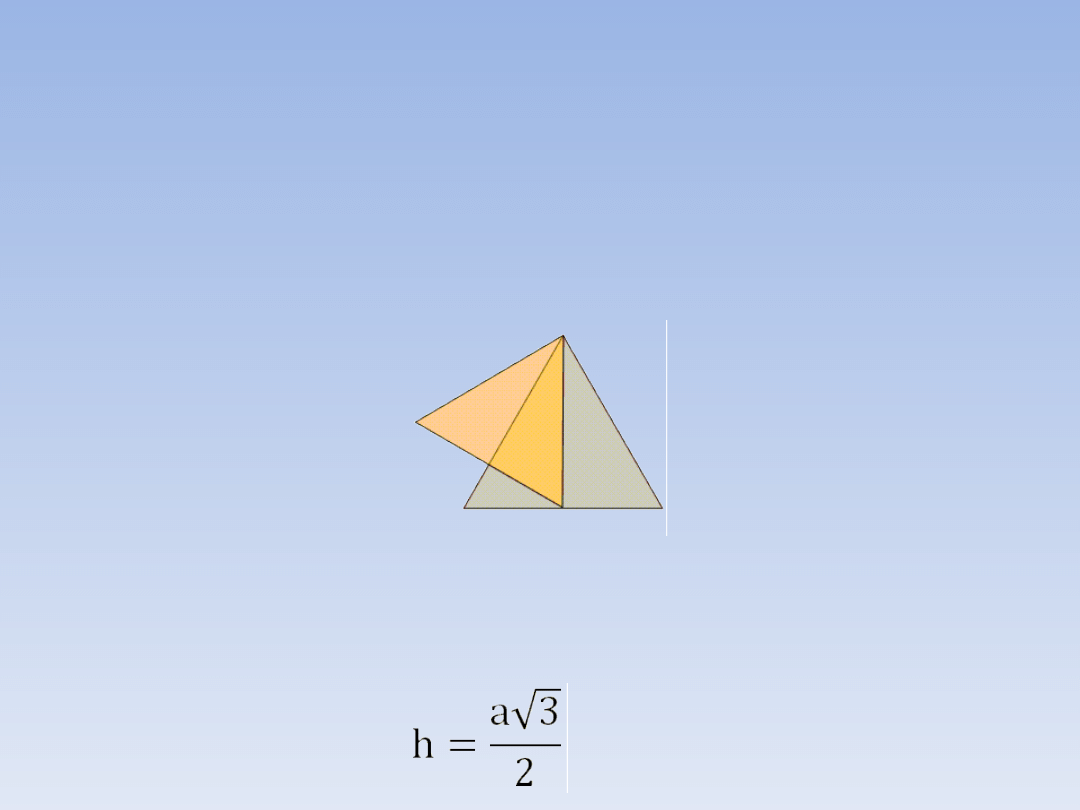
PRZYKŁADOWE ZADANIA.

ZADANIE 2.
Przedstawione na rysunku trójkąty są
równoboczne. Jaka jest skala podobieństwa
mniejszego trójkąta do większego?

Bok mniejszego trójkąta jest jednocześnie
wysokością

większego

trójkąta.

Jeśli

oznaczymy bok większego trójkąta przez a,
jego wysokość można wyliczyć ze wzoru:

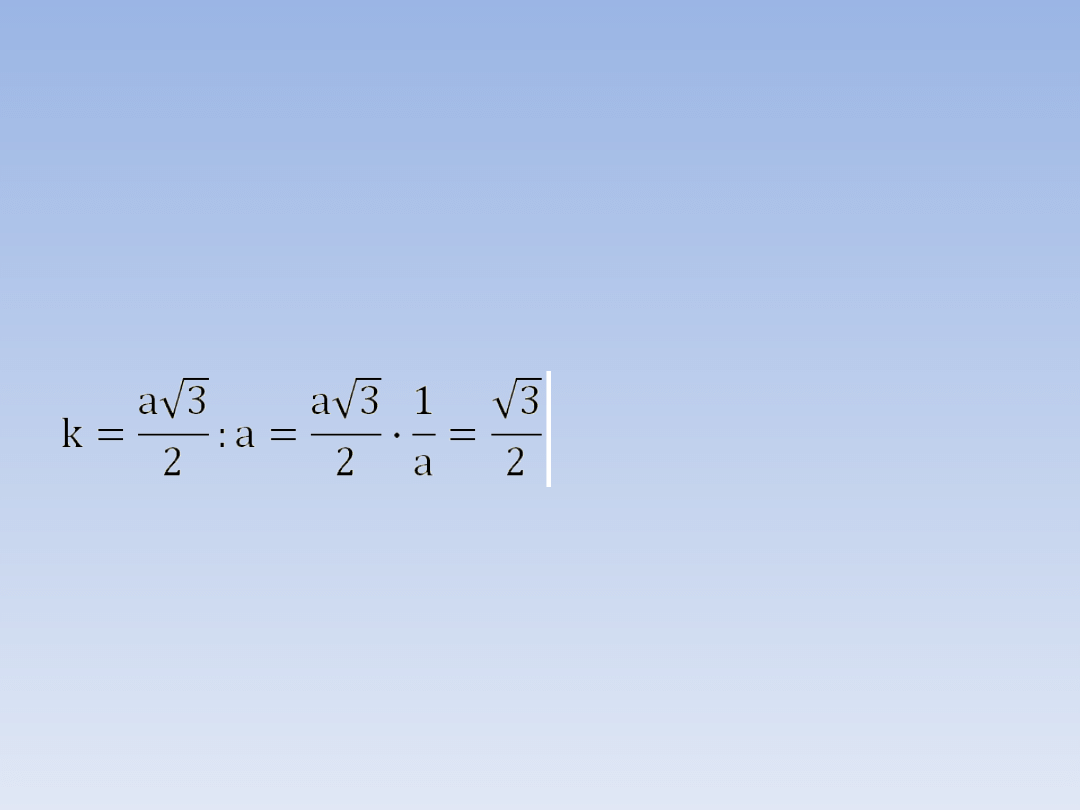
PRZYKŁADOWE ZADANIA.

ZADANIE 2 – ciąg dalszy.
Skalę

podobieństwa

obliczamy

dzieląc

długość boku mniejszego trójkąta – h, przez
długość boku większego trójkąta – a:

FAKT.

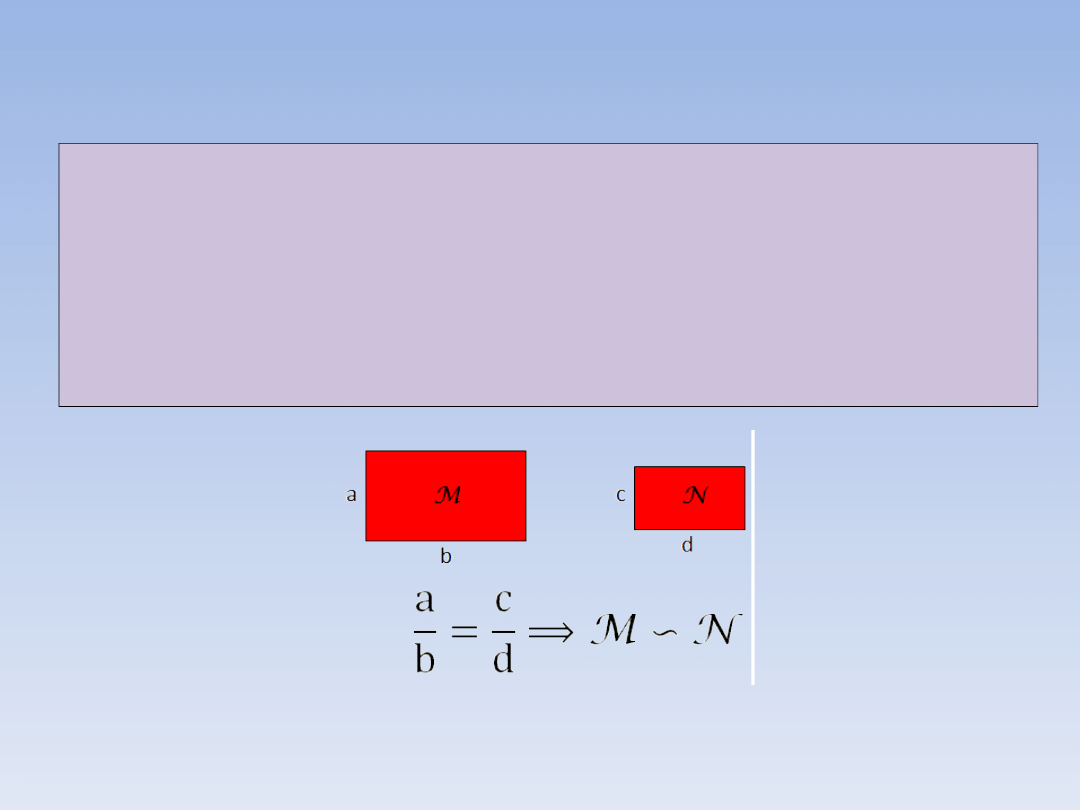
Aby rozstrzygnąć, czy dwa prostokąty są

podobne, wystarczy sprawdzić, czy stosunek

dwóch prostopadłych boków jednego

prostokąta jest równy stosunkowi długości

odpowiednich boków drugiego prostokąta.

FAKT.

Gdy figury F i F’ są podobne, to dla

dowolnych dwóch odcinków figury F

stosunek ich długości jest równy stosunkowi

odpowiadających im odcinków figury F’.

PRZYKŁADOWE ZADANIA.

ZADANIE 3.
Dowiedź, że prostokąty o wymiarach: 9 cm x
12 cm i
32 dm x 24 dm są podobne. Jaka jest skala
podobieństwa większego prostokąta do
mniejszego?
Podobieństwo tych prostokątów wynika z
poprzednich faktów. Jeżeli podzielę przez
siebie krótszy i dłuższy bok w każdym
prostokącie, to otrzymam tę samą liczbę:

Skracamy jednostki i upraszczamy ułamek przez 3.

Skracamy jednostki i upraszczamy ułamek przez 8.

PRZYKŁADOWE ZADANIA.

ZADANIE 3 – ciąg dalszy.

UWAGA.

Powyższa równość świadczy o tym, że dane

prostokąty są podobne, nie określa ona

jednak skali podobieństwa.

Aby obliczyć skalę podobieństwa dzielę
długość np. dłuższego boku większego
prostokąta przez długość dłuższego boku
mniejszego

prostokąta,

sprowadzając

wcześniej długości do wspólnej jednostki:
32 dm = 320 cm

PRZYKŁADOWE ZADANIA.

ZADANIE 4.
W pewnym prostokącie przekątna jest cztery
razy dłuższa niż krótszy bok tego prostokąta.
W prostokącie do niego podobnym krótszy
bok ma 2,75 cm długości. Jaką długość ma
przekątna tego prostokąta?
Skoro drugi prostokąt jest podobny do
pierwszego, zgodnie z podanymi wcześniej
faktami odpowiedni odcinki pozostają w
takim samym stosunku. Jeśli w pierwszym
prostokącie przekątna jest cztery razy
dłuższa niż krótszy bok, to w prostokącie do
niego podobnym jest tak samo, więc:
d = 4 ∙ 2,75 cm = 11 cm.