1

6. Center of mass,

Collisions

6.1. The center of mass

To describe the motion of a system of particles (also for their
continuous distribution – a solid body), one introduces the
concept of the center of mass.

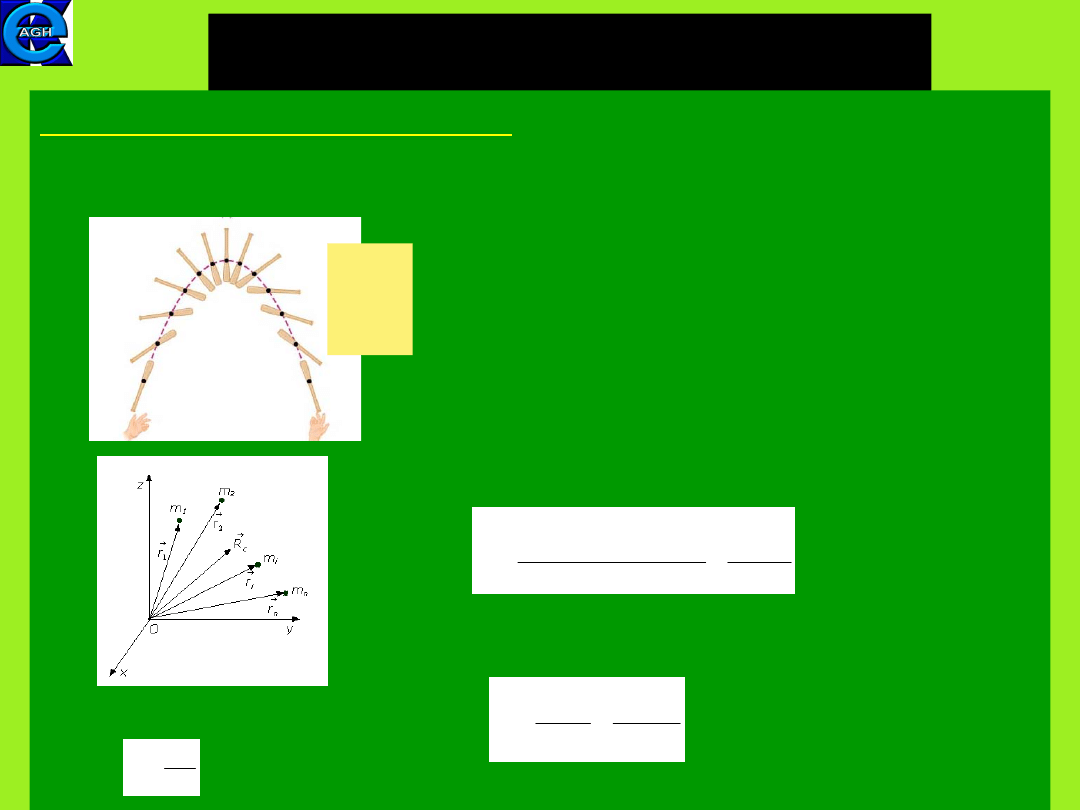
A baseball bat thrown into the air

moves in a

complicated manner but one of its

points, the

center of mass (CM), moves

in a parabolic

path.

CM moves as if all the system’s mass

were

concentrated there and all

external forces were

applied to it (to

be proved).

We define the position of CM by a vector

equation

(6.1)

For a solid body summation in Eq.(6.1)

must be

replaced by integration

(6.2)

where is a mass density.

(figur
e
from
HRW)



















dV

dV

r

dm

dm

r

R

c





dV

dm





M

r

m

m

m

m

r

m

r

m

r

m

R

i

i

i

n

n

n

c





























...

...

2

1

2

2

1

1

2

For a uniform body (ρ=const), position of its CM depends on the

body’s shape only

(6.3)

Examples
1. Two particles of masses m

1

and m

2

separated by distance d.

The position of CM we find placing both particles on an x
axis.

From Eq.(6.1) one obtains

Putting x

1

=0, we have

2. The center of mass of a triangle

.

In this case there is no need to use Eq.(6.3), but dividing
a triangle into segments it can be concluded that CM is
placed at the intersection of triangle medians.

2

1

1

2

1

1

2

1

2

2

1

1

m

m

)

d

x

(

m

x

m

m

m

x

m

x

m

x

C

































dV

dV

r

dV

dV

r

R

c





2

1

2

m

m

d

m

x

C





The center of

mass, cont.

3

For a system of n particles one can write from a CM definition

(6.1)

(6.4)

Differentiating both sides of Eq.(6.4) vs. time gives

(6.5)

By differentiating Eq.(6.5) in respect to time one obtains

(6.6)

Eq.(6.6) can be rewritten as

(6.6a)

The right side of Eq.(6.6a) includes all forces, both the internal

forces between the

particles and the external forces acting from tha outside. From

the Newton’s third

law the sum of all internal forces reduces to zero and the right

side of Eq.(6.6a) is

the vector sum of all external forces, the net force. In this case

one obtains

(6.7)

This proves the statement given at the beginning of this chapter.

6.2. Motion of a system of

particles

















n

n

c

r

m

...

r

m

r

m

MR

2

2

1

1















n

n

C

v

m

...

v

m

v

m

v

M

2

2

1

1

















n

C

F

...

F

F

a

M

2

1

















n

n

C

a

m

...

a

m

a

m

a

M

2

2

1

1



C

net

a

M

F







Neton’s second

law applied to the center of mass

4

Eq.(6.5) can be rewritten as

(6.8)

Thus, the linear momentum of a system of particles (RHS of

above equation)

is equal to the product of the total mass of the system and the

velocity of the center

of mass:

(6.9)

Calculating the time derivative of Eq.(6.9) we have

(6.10)

From above relation and taking into account Eq.(6.7) one

obtains

(6.11)

From (6.11) it follows, that if is zero, then

(6.12)

The linear momentum of the system is changed by the
net external force (Newton’s second law for a system of
particles).















n

C

p

...

p

p

v

M

2

1



P

v

M

C







C

C

a

M

dt

P

d

dt

v

d

M











dt

P

d

F

net







net

F



const

P 



The momentum of a system is not changed if it is isolated
(law of momentum conservation for a system of particles).

6.3. Momentum of a system of

particles

5

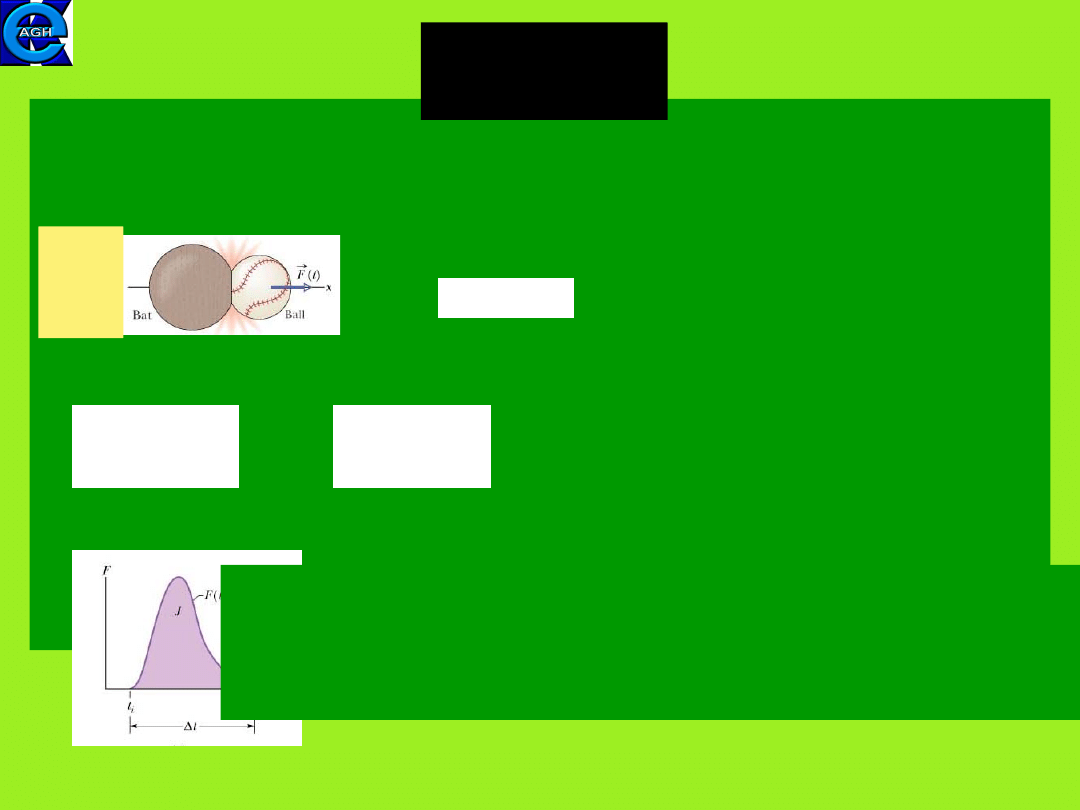
The object’s momentum can be changed by the collision with

other object.

The forces during collision act for a short time and are large. An

example is the

collision of a baseball with a baseball bat.

From the Newton’s second law

(6.13)

The net change in the momentum is obtained after integrating

Eq.(6.13) in time Δt

or

(6.14)

The change in objet’s mometum is equal to the force impuls.

6.4.

Collisions

dt

)

t

(

F

p

d













f

i

f

i

t

t

t

t

dt

)

t

(

F

p

d









f

i

t

t

dt

)

t

(

F

p







(figur
e
from
HRW)

In the figure to the left we see the magnitude of force
varying with time for the collision of a ball with a bat.
The area under the curve is equal to the force impulse in
the collision.

6

In many cases we consider the system isolated in which the

objects mutually

collide. In that case the vector of linear momentum of the system

cannot change.
The total kinetic energy of colliding bodies can be conserved
and in this case

we have an

elastic collision

.

When the kinetic energy of the system is not conserved, a
collision is called

inelastic.

If the colliding bodies stick together, the collision is

called

completely

inelastic.

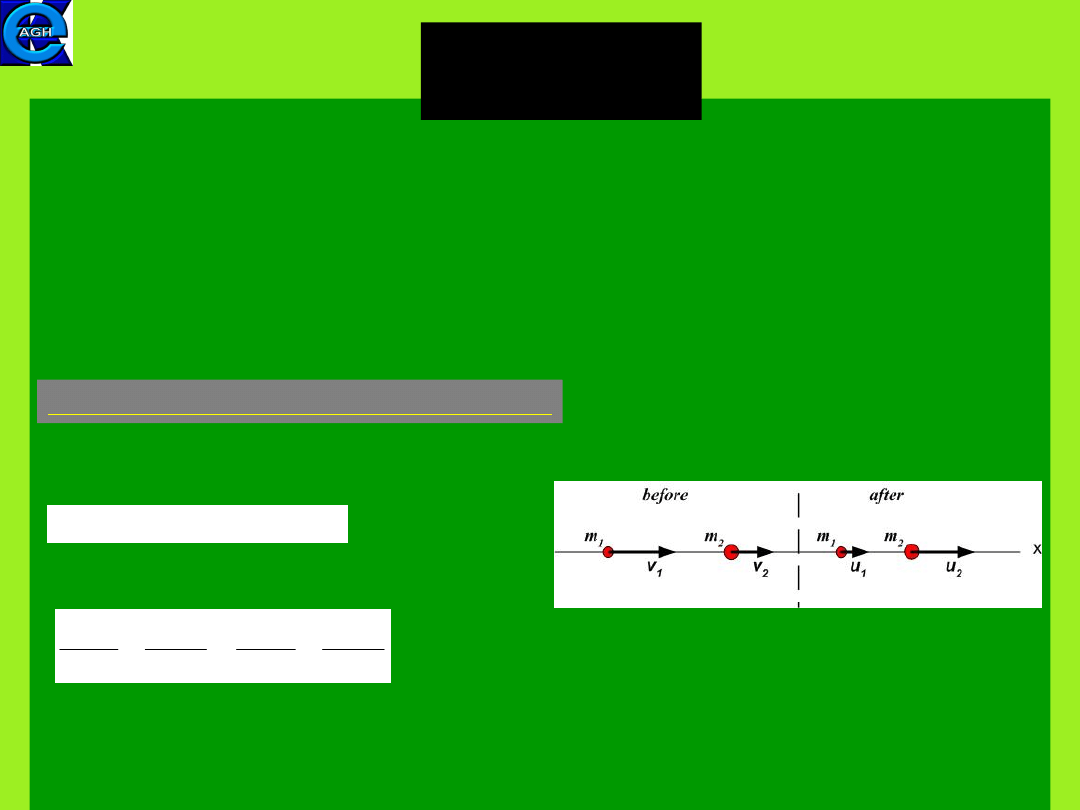
Two bodies collide moving along an x axis. From the

conservation of a linear

momentum

(6.15)

The total kinetic energy is also conserved

(6.16)

Collisions,

cont.

2

2

1

1

2

2

1

1

u

m

u

m

v

m

v

m







2

2

2

2

2

2

2

2

1

1

2

2

2

2

1

1

u

m

u

m

v

m

v

m







Elastic collision in one dimension

7

Solving the simulaneous equations (6.15) and (6.16) for u

1

and

u

2

one obtains

When the particles have the same

masses,

they exchange the velocities after

collision

Collisions,

cont.

2

2

1

2

1

1

2

1

2

2

2

2

1

2

1

2

1

2

1

1

2

2

v

m

m

m

m

v

m

m

m

u

v

m

m

m

v

m

m

m

m

u





















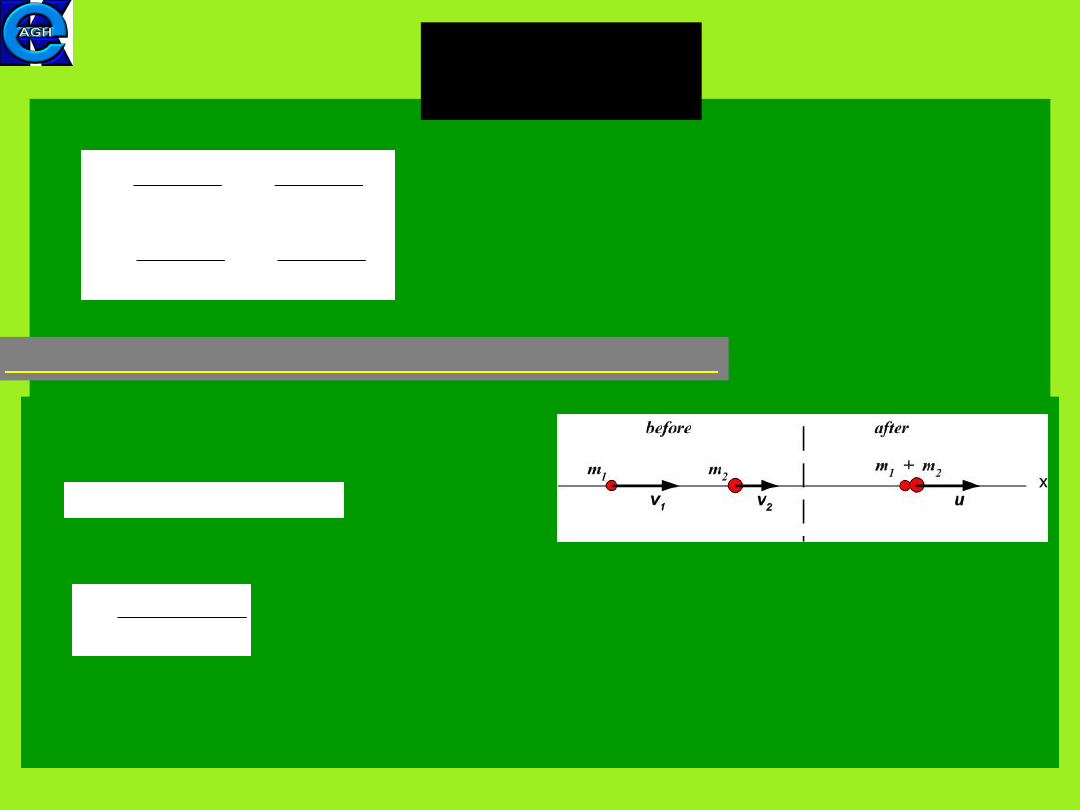
Completely inelastic collision in one dimension

From the conservation of linear momentum
we have

(6.17)

and hence the velocity of sticked together masses is

It is easy to check that the kinetic energy of the body after the
collision is less than the sum of kinetic energies of the bodies
before the collision.

u

)

m

m

(

v

m

v

m

2

1

2

2

1

1







2

1

2

2

1

1

m

m

v

m

v

m

u





