PODEJMOWANIE OPTYMALNYCH

DECYZJI NA PODSTAWIE DECYZJI

MARGINALNEJ

Czym jest analiza

marginalna?

Analiza marginalna umożliwia badanie

zmian zysku wywołanych niewielkimi
zmianami zmiennej decyzyjnej.

Służy ona do określenia optymalnej

wielkości produkcji, w której zysk jest
maksymalny.

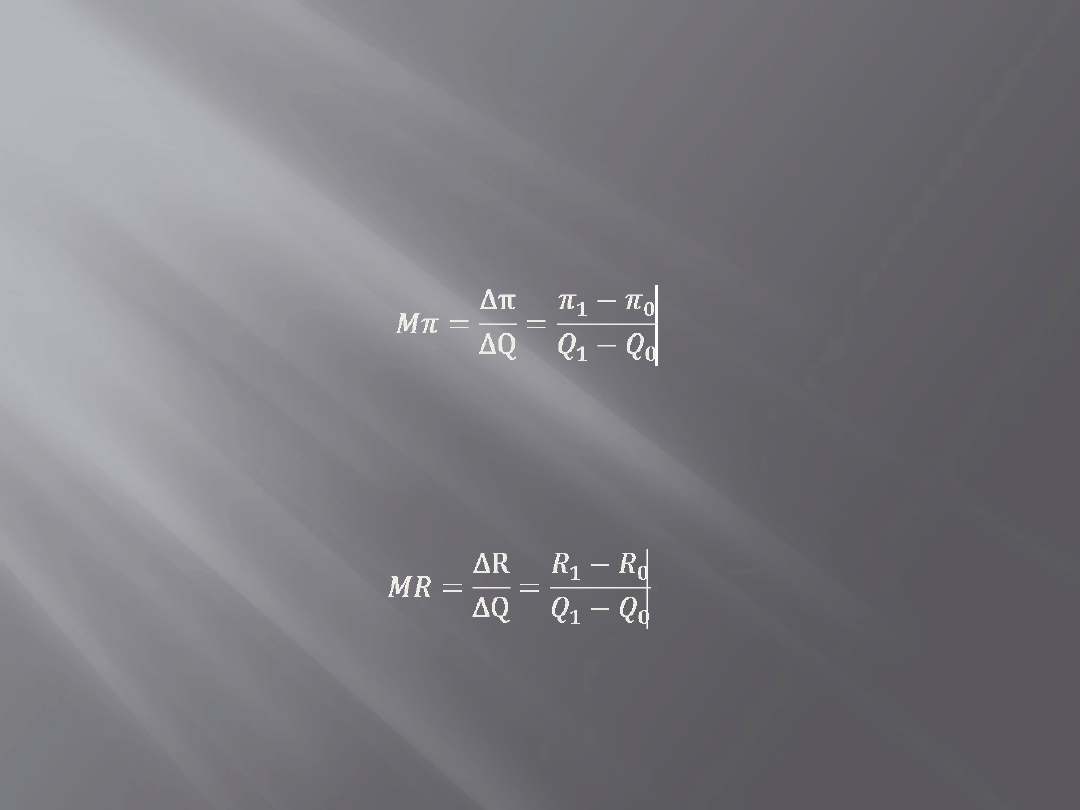
Ważne wzory i pojęcia



Zysk marginalny (krańcowy) - M

Π

– jest to przyrost

zysku całkowitego wynikający z niewielkiego zwiększenia
wartości zmiennej decyzyjnej.



Utarg marginalny (krańcowy) - MR – jest to zmiana
zysku całkowitego ∆R wynikającą ze zmiany wielkości
produkcji o dodatkową jednostkę ∆Q

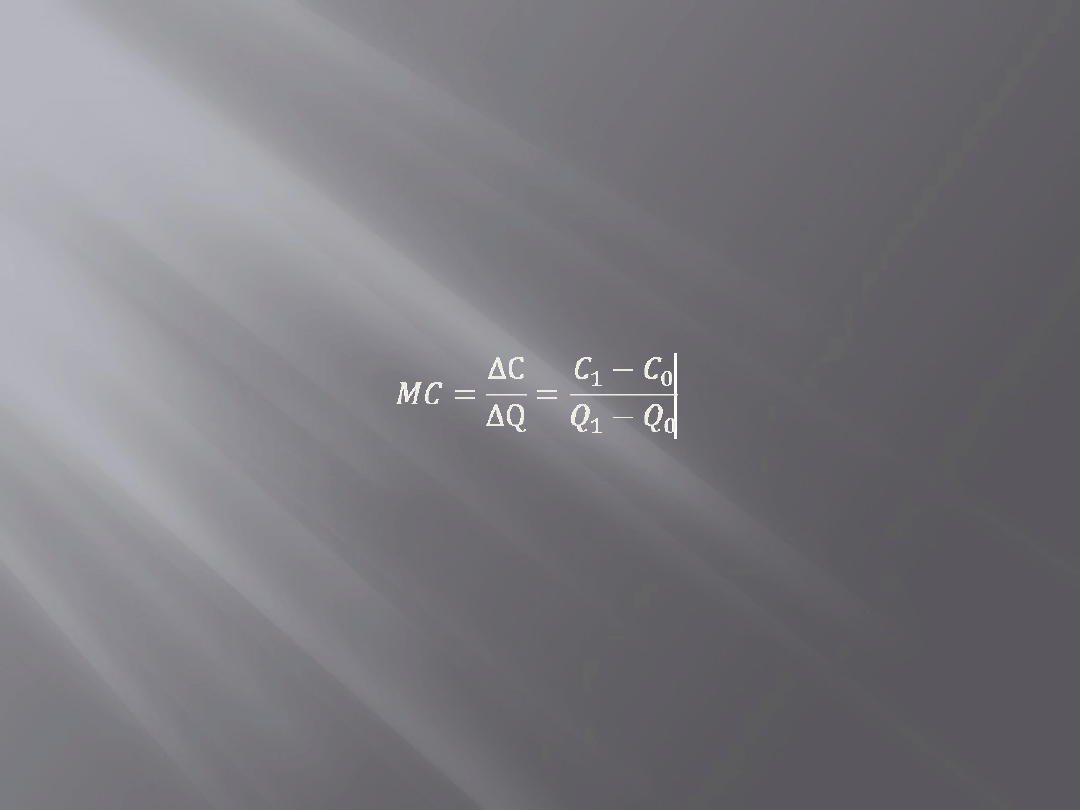
Ważne wzory i pojęcia cd.



Koszt marginalny (krańcowy) - MC – jest to zmiana
kosztu ∆C wynikającą za zmiany wielkości produkcji o
dodatkową jednostkę ∆Q,

Podstawowe zasady

maksymalizacji zysku:

Zysk osiąga maksimum przy takim poziomie

produkcji, przy którym zysk krańcowy jest równy
zero.

M

Π

= 0

Przedsiębiorstwo osiąga maksymalny zysk przy

takiej wielkości produkcji, przy której utarg ze
sprzedaży dodatkowej jednostki produktu staje
się równy kosztowi jej wytworzenia.

MR = MC

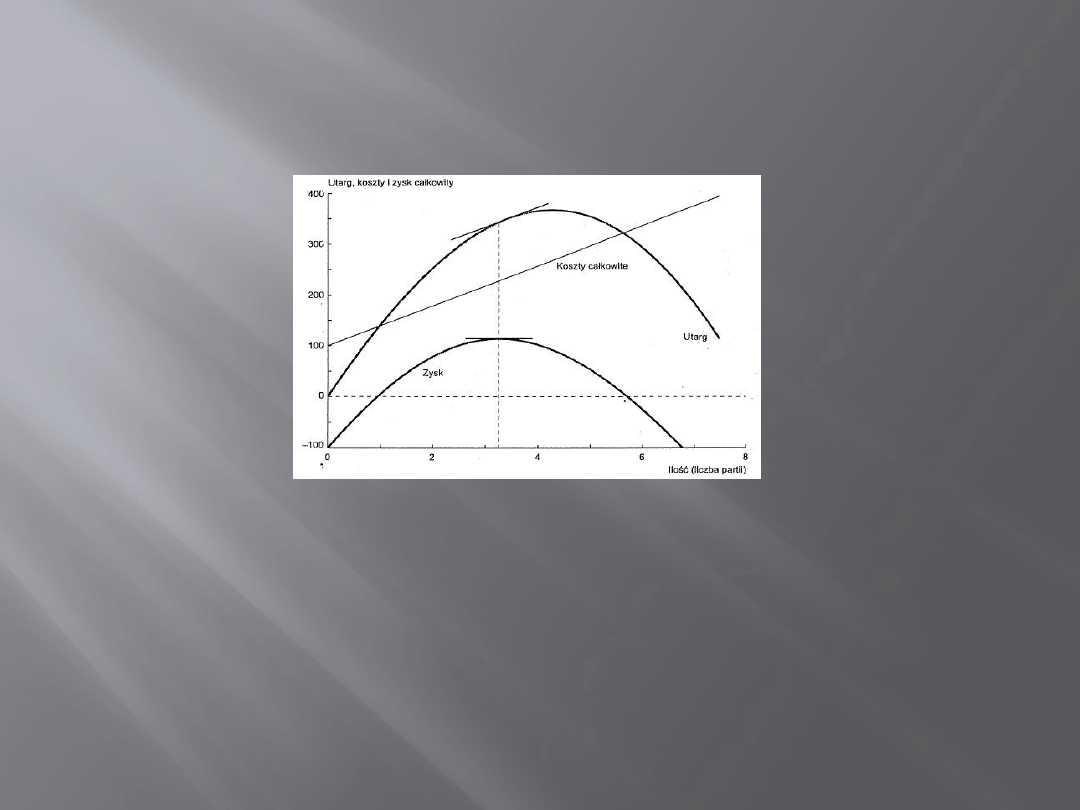
Utarg i zysk krańcowy

Na powyższym rysunku widoczne są dwa punkty zrównania utargu i
kosztów, w tych punktach zysk z produkcji jest równy zeru.

Zysk dodatni z produkcji znajduje się pomiędzy dwoma punktami
przecięcia kosztów i utargu.

rys 1 - Samuelson, Ekonomia menedżerska, wydanie 2 zmienione, Warszawa 2009, str. 70

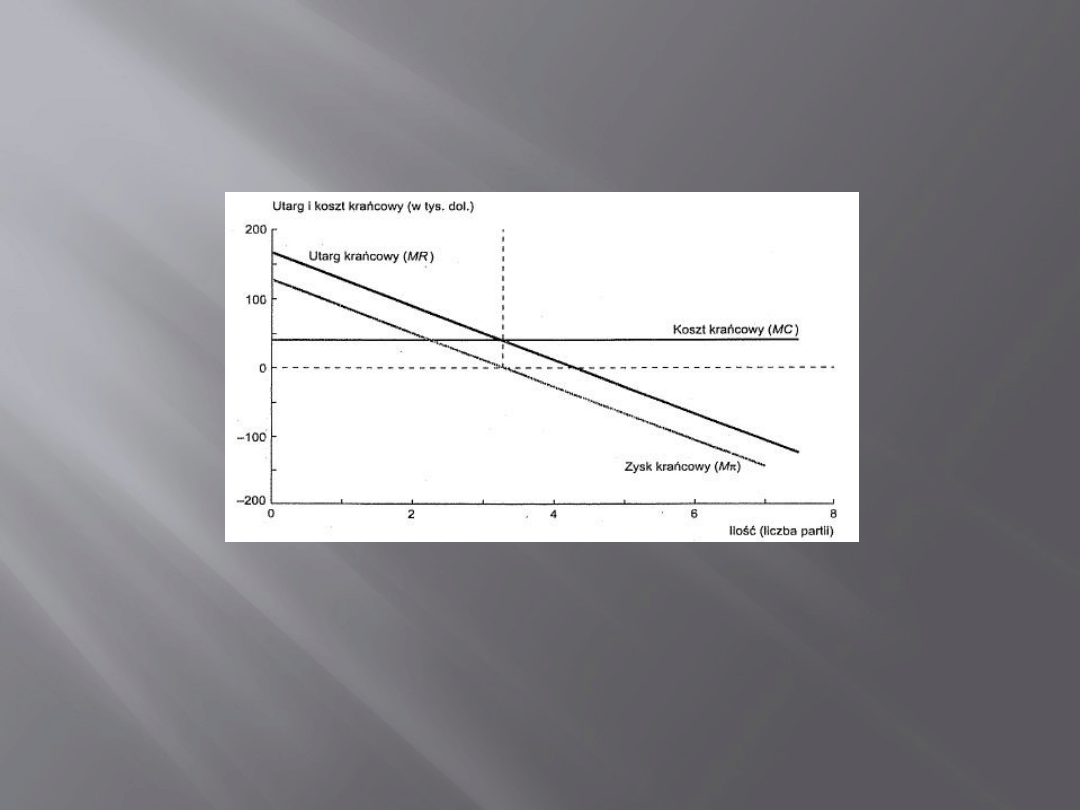
Utarg, koszt i zysk

krańcowy

Warunki MΠ=0 i MR=MC są równoważne co widać na
rysunku powyżej. Obydwa warunki wskazują na tę samą
wielkość produkcji, która maksymalizuje zysk.

rys 2 - Samuelson, Ekonomia menedżerska, wydanie 2 zmienione, Warszawa 2009, str. 70

Analiza wrażliwości

Analiza wrażliwości pozwala decydentowi na

właściwą

modyfikację

postępowania

dotyczącego wielkości produkcji, gdy zmieniają
się warunki panujące na rynku.

„Przy zmianie warunków ekonomicznych należy

określić ich wpływ na utarg i koszt krańcowy
przedsiębiorstwa,

a

następnie

ponownie

odwołać się do zasady MR=MC, aby wyznaczyć
nową optymalną deyzję.”

1

Samuelson, Ekonomia menedżerska, wydanie 2 zmienione, Warszawa 2009, str. 72

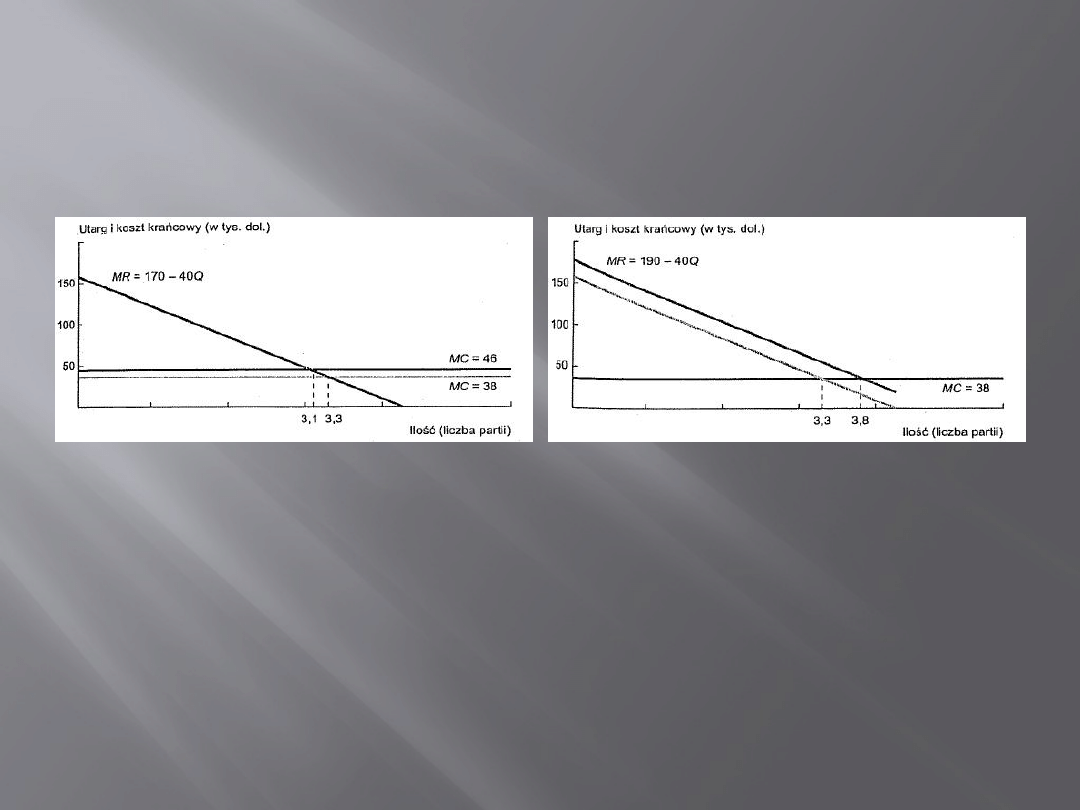
Przykłady podejmowania decyzji

w warunkach zmian na rynku

Wzrost kosztu krańcowego

spowodował zmniejszenie

optymalnej wielkości

produkcji przedsiębiorstwa.

Wzrost utargu krańcowego

(wzrost popytu na produkt),

spowodował wzrost wielkości

produkcji przedsiębiorstwa.

rys 3 i 4 - Samuelson, Ekonomia menedżerska, wydanie 2 zmienione, Warszawa 2009, str. 73

Przykłady podejmowania decyzji w

przypadku zmian warunków

ekonomicznych



Wzrost kosztów stałych – powoduje zmniejszenie
zysku firmy, jednakże wielkość produkcji
pozostaje bez zmian.



Wzrost kosztów surowca (półproduktu) –
spowoduje zmniejszenie ilości produkcji, a także
wzrost kosztów produkcji, który zostanie
przeniesiony na nabywców w postaci podwyżki
ceny za produkt finalny.

Przykłady podejmowania decyzji w

przypadku zmian warunków

ekonomicznych



Wzrost popytu – w tym przypadku prosta MR
zostanie przesunięta równolegle w górę.
Punkt równowagi znajdzie się przy wyższym
poziomie produkcji.
W rezultacie przedsiębiorstwo zwiększy
produkcję, oraz jednocześnie podniesie cenę
na produkt.

przykładowe zadanie

Przedsiębiorstwo dążąc do maksymalizacji stara się

ustalić taką wielkość produkcji mikroprocesorów, przy
której następuje zrównanie utargu marginalnego i
kosztu marginalnego.

dane:



funkcja popytu: Q = 8,5 – 0,05P



odwrócona funkcja popytu:

P = 170 – 20Q



funkcja kosztu: C = 100 + 38Q

 



za jednostkę produkcji przyjmujemy: partię - 100
szt.



cena: podawana w tysiącach zł.

wzory



Π

max

= R − C → MR = MC



R = Q * P

rozwiązanie

R = Q (170 – 20Q) = 170Q – 20Q

2

C = 100 + 38Q

obliczamy pochodne funkcji R i C:
R’ = 170 – 40Q
C’ = 38

MR = MC → 170 – 40Q = 38
170 – 40Q = 38
-40Q = -132
Q = 3,3

R = 170*3,3 – 20*3,3 = 561 – 217,8 = 343,2
C = 100+38*3,3 = 225,4

P = 170 – 20*3,3 = 104
Π

max

= R – C = 343,2 – 225,4 = 117,8

odpowiedź

Wielkość produkcji pozwalająca na

maksymalizację zysku jest równa 3,3
partii (330 sztuk).

Optymalna cena wyprodukowanej ilości

mikroprocesorów wyniesie 104 (tyś. zł.)

Natomiast zysk maksymalny będzie równy

117,8 (tyś. zł.)

DZIĘKUJĘ ZA UWAGĘ

Marcin Morawski