Podejmowanie optymalnych decyzji

na podstawie analizy marginalnej

Ekonomia menedżerska

Przygotowała:
Justyna Nowak, grupa C

AKADEMIA OBRONY NARODOWEJ

AKADEMIA OBRONY NARODOWEJ – WYDZIAŁ ZARZĄDZANIA I DOWODZENIA – 2013

Lokalizacja



Według starego porzekadła trzema najważniejszymi czynnikami
w inwestowaniu nieruchomości są lokalizacja, lokalizacja i jeszcze raz
lokalizacja;



Najdogodniejsza lokalizacja => miejsce położone możliwie najbliżej jak
największej liczby potencjalnych klientów;



Analiza marginalna (jedna z podstawowych metod podejmowania decyzji)
pozwala na wybór optymalnej lokalizacji przy nieznacznym wysiłku
obliczeniowym i z całkowitą dokładnością;



Analiza marginalna polega na tym, że rozpatrujemy niewielkie zmiany
w rozważanej decyzji i badamy ich wpływ na oczekiwany wynik;



Podstawowa zasada analizy marginalnej jest następująca:

Wykonaj niewielki ruch w kierunku najbliższego alternatywnego

wariantu, jeżeli sądzisz, że poprawi on wynik. Kontynuuj ruch

w kierunku poprawy i zatrzymaj się w momencie, gdy dalsza

próba nie poprawia wyniku.



Unikatowość tej metody polega na koncentracji uwagi na zmianach;



Metodę tę i jej myśl przewodnią można zastosować w rozwiązywaniu
prawie każdego problemu optymalizacyjnego, to jest w sytuacji, gdy osoba
podejmująca decyzję chce osiągnąć określony cel (tzn. zmaksymalizować
lub zminimalizować oczekiwany wynik).

AKADEMIA OBRONY NARODOWEJ – WYDZIAŁ ZARZĄDZANIA I DOWODZENIA – 2013

Prosty model przedsiębiorstwa

- utarg



Analiza utargu opiera się na prawie popytu, zgodnie z którym:

Przy innych czynnikach niezmienionych podwyżka ceny

dobra powoduje spadek zapotrzebowania zgłaszanego

przez nabywców

i, w konsekwencji, zmniejszenie wielkości sprzedaży.



Przedsiębiorstwo wykorzystuje krzywą popytu jako podstawę
do przewidywania wpływu różnych wariantów decyzji
produkcyjnych
i cenowych na wielkość osiąganego utargu;



Równanie popytu pozwala przewidzieć, jaka ilość towaru zostanie
sprzedana przy każdej cenie.

Q = a/b - P/b

Q - liczba nabywanych partii towaru P - cena jednej partii



Po odpowiednim przekształceniu algebraicznym możemy
uzyskać inną, równoważną postać równania

P = a - bQ

jest to odwrócone równanie popytu.

AKADEMIA OBRONY NARODOWEJ – WYDZIAŁ ZARZĄDZANIA I DOWODZENIA – 2013

Prosty model przedsiębiorstwa

- utarg c.d.



Równanie popytu odzwierciedla obecną zależność
ilościową między popytem na produkt danego
przedsiębiorstwa a ceną;



Faktyczna wielkość sprzedaży przedsiębiorstwa zależy
również m.in. od: ilości i jakości podobnych wyrobów
dostarczanych na rynek przez konkurentów oraz ich cen, a
także ogólnego stanu koniunktury w danym przemyśle;



Wykorzystując równanie popytu, traktujemy pozostałe
czynniki określające popyt jako dane, tzn. zakładamy ich
niezmienność;



Krzywa popytu ma charakter deterministyczny, co
oznacza, że przy danej cenie można dokładnie przewidzieć
wielkość sprzedaży. I odwrotnie,
dla każdej planowanej wielkości sprzedaży odwrócone
równanie popytu wyznacza ściśle poziom ceny, która
zapewni równowagę rynkową;



Równanie popytu może być zadowalającą podstawą
prognozowania
w przypadku produktu o długiej i stabilnej historii
rynkowej, umożliwiając przewidywanie wielkości sprzedaży
z bardzo niewielkim błędem;

AKADEMIA OBRONY NARODOWEJ – WYDZIAŁ ZARZĄDZANIA I DOWODZENIA – 2013

Prosty model przedsiębiorstwa

- utarg c.d.



Utarg jest definiowany jako:

R = P * Q

R - utarg

P - cena

Q - wielkość sprzedaży



Prawo popytu oznacza, że dwie wielkości określające utarg
(P i Q) pozostają względem siebie w odwrotnej zależności.
Zwiększenie Q wymaga zmniejszenia P, przy czym
pierwszy efekt zwiększa utarg,
a drugi go zmniejsza;



Warianty krańcowe – oferowanie małej ilości towaru
po bardzo wysokiej cenie lub wyprzedaż dużej ilości
towaru po bardzo niskiej cenie – przynoszą niewielki utarg.

AKADEMIA OBRONY NARODOWEJ – WYDZIAŁ ZARZĄDZANIA I DOWODZENIA – 2013

Prosty model przedsiębiorstwa

- koszty



Koszty produkcji określa równanie:

koszty produkcji = koszty stałe + koszt jednej partii towaru * liczba

wytwarzanych partii



Równanie to nazywamy funkcją kosztów,
ponieważ opisuje ono zależność sumy kosztów
od wielkości produkcji.

AKADEMIA OBRONY NARODOWEJ – WYDZIAŁ ZARZĄDZANIA I DOWODZENIA – 2013

Prosty model przedsiębiorstwa

- zysk



Równanie zysku (lub funkcja zysku) ma postać:

Π = R – C

Π - zysk

R - utarg

C - suma kosztów przedsiębiorstwa



Zysk to różnica między całkowitym utargiem i
sumą kosztów przedsiębiorstwa;



Ważną zaletą równania zysku jest to, że dla
dowolnej wielkości produkcji Q dostarcza ono
liczbowej prognozy wielkości zysku.

AKADEMIA OBRONY NARODOWEJ – WYDZIAŁ ZARZĄDZANIA I DOWODZENIA – 2013

Analiza marginalna



Analiza marginalna umożliwia badanie zmian zysku wywołanych
niewielkimi zmianami zmiennej decyzyjnej;



Skalę wzrostu zysku możemy obliczyć, dzieląc przyrost zysku przez
przyrost produkcji;



Zysk krańcowy to przyrost całkowitego zysku wynikający z
niewielkiego zwiększenia wartości zmiennej decyzyjnej;



Algebraiczna formuła zysku krańcowego jest następująca:

Zysk krańcowy =

=

=

AKADEMIA OBRONY NARODOWEJ – WYDZIAŁ ZARZĄDZANIA I DOWODZENIA – 2013

Przyrost
zysku

Przyrost produkcji

∆ ∏
∆ Q

∏

1

- ∏

0

Q

1

- Q

0

∆ - przyrost wartości
odpowiedniej
zmiennej
Q

0

- wyjściowy

poziom produkcji
∏

0

- zysk z produkcji

Q

1

i ∏

1

-

odpowiednie
wartości zmiennych
po zaistniałej
zmianie.

Zasada analizy marginalnej:

Zmieniaj stopniowo wielkość produkcji, jeżeli zwiększa to

sumę zysku. Kontynuuj zmiany – zawsze w kierunku

zapewniającym wyższe zyski

– i zatrzymaj się w momencie, gdy dalsze zmiany nie

poprawiają wyniku.

Zysk krańcowy to dodatkowy zysk, który można osiągnąć,
zwiększając o jednostkę wolumen produkcji i sprzedaży. Dopóki zysk
krańcowy jest ujemny, należy zmniejszać produkcję w celu
zwiększenia sumy zysku.

Analiza marginalna

- rachunek marginalny



Chcąc dokładnie wyznaczyć optymalną wielkość produkcji dla
przedsiębiorstwa (tzn. poziom produkcji, przy którym osiągnie ono
maksymalny zysk), trzeba obliczyć wielkość zysku krańcowego dla
każdego poziomu produkcji.



Maksymalny zysk całkowity występuje przy takiej wielkości produkcji,
przy której zysk krańcowy jest równy zeru, tzn. nachylenie stycznej do
krzywej zysku jest zerowe.



Zysk krańcowy równy zeru to warunek wyznaczający optymalną wielkość
produkcji. Gdyby zysk krańcowy był dodatni lub ujemny, wówczas sumę
zysku można byłoby zwiększyć przez odpowiednie zwiększenie lub
zmniejszenie produkcji. Możliwości zwiększenia zysku zostają wyczerpane
dopiero wówczas, gdy zysk krańcowy przyjmie wartość zerową.



Kiedy nachylenie funkcji zysku staje się zerowe, możemy być pewni, że
znajdujemy się na samym wierzchołku krzywej zysku.



Podstawowa zasada optymalizacji:

Maksymalny zysk jest osiągany przy takiej wielkości produkcji,

przy której zysk krańcowy jest równy zeru (Mπ = 0).

AKADEMIA OBRONY NARODOWEJ – WYDZIAŁ ZARZĄDZANIA I DOWODZENIA – 2013

Utarg krańcowy i koszt krańcowy



Zalety koncepcji zysku krańcowego:



do optymalizacji decyzji można dojść, dokonując
niewielkich zmian w już podjętych decyzjach i
sprawdzając, jak dokonywane korekty wpływają
na wielkość zysku, przy czym zawsze należy
poruszać się w kierunku zapewniającym
zwiększenie zysku;



dostarcza narzędzi do określenia optymalnej dla
przedsiębiorstwa decyzji;



przy rozpoznaniu czynników determinujących
wielkość zysku i jego zmiany jest bardzo
pomocna analiza marginalna.

AKADEMIA OBRONY NARODOWEJ – WYDZIAŁ ZARZĄDZANIA I DOWODZENIA – 2013

Utarg krańcowy i koszt krańcowy

- utarg krańcowy



Utarg krańcowy to dodatkowy utarg wynikający
ze zwiększenia o jednostkę produkcji i
sprzedaży;



Utarg krańcowy (MR – ang. marginal revenue)
związany
ze zwiększeniem sprzedaży z Q

0

do Q

1

opisuje

formuła:

Utarg krańcowy = = =

AKADEMIA OBRONY NARODOWEJ – WYDZIAŁ ZARZĄDZANIA I DOWODZENIA – 2013

Przyrost
utargu

Przyrost
produkcji

∆ R
∆
Q

R

1

– R

0

Q

1

–

Q

0

Utarg krańcowy i koszt krańcowy

- utarg krańcowy a cena



Można zauważyć podobieństwo między
równaniem utargu krańcowego, a równaniem
ceny.
Dla każdej liniowej funkcji popytu wyrażonej w
postaci odwróconego równania: P = a – bQ,
formuła utargu krańcowego ma postać: MR = a –
2bQ.



Równanie dla MR ma ten sam wyraz wolny i
podwojony współczynnik kierunkowy (kąt
nachylenia) w porównaniu
z równaniem ceny.

AKADEMIA OBRONY NARODOWEJ – WYDZIAŁ ZARZĄDZANIA I DOWODZENIA – 2013

Utarg krańcowy i koszt krańcowy

- koszt krańcowy



Koszt krańcowy (MC – ang. marginal cost) to przyrost
kosztów związany z wytworzeniem dodatkowej
jednostki produktu. Definicja algebraiczna jest
następująca:

Koszt krańcowy = = =



Wysokość kosztu krańcowego nie zależy od tego,
o ile zwiększona została produkcja: zarówno przy
małej,
jak i dużej zmianie wielkości produkcji koszt
krańcowy
w przeliczeniu na jednostkę produktu jest taki sam.

AKADEMIA OBRONY NARODOWEJ – WYDZIAŁ ZARZĄDZANIA I DOWODZENIA – 2013

Przyrost
kosztów

Przyrost
produkcji

∆ C
∆
Q

C

1

–

C

0

Q

1

–

Q

0

Utarg krańcowy i koszt krańcowy

- maksymalizacja zysku



Skoro π = R – C, to

Mπ = MR – MC.

Zysk krańcowy równa się różnicy między
utargiem krańcowym i kosztem krańcowym.



Zysk całkowity osiąga maksimum wówczas,
gdy zysk krańcowy równa się zeru. Zważywszy
jednak, że
Mπ = MR – MC, warunek ten można również
zapisać jako MR – MC = 0



Wynika z tego taka reguła:

Przedsiębiorstwo osiąga maksymalny zysk

przy takiej wielkości produkcji, przy której

utarg ze sprzedaży dodatkowej jednostki

produktu staje się równy kosztowi jej

wytworzenia, tzn. gdy MR = MC.

AKADEMIA OBRONY NARODOWEJ – WYDZIAŁ ZARZĄDZANIA I DOWODZENIA – 2013

Utarg krańcowy i koszt krańcowy

- maksymalizacja zysku c.d.



Warunki: Mπ = O i MR = MC są równoważne. Obydwa
warunki wskazują na ten sam poziom produkcji,
zapewniający maksymalizację zysku.



Maksymalny zysk osiągany jest przy takiej wielkości
produkcji, przy której następuje zrównanie utargu
krańcowego
z kosztem krańcowym.



W rzeczywistości zasada MR = MC jest często
najkrótszą drogą do ustalenia optymalnej wielkości
produkcji przedsiębiorstwa. Zamiast wyznaczać funkcję
zysku krańcowego i przyrównywać ją do zera, bierzemy
po prostu funkcje utargu krańcowego oraz kosztu
krańcowego
i przyrównujemy je do siebie.

AKADEMIA OBRONY NARODOWEJ – WYDZIAŁ ZARZĄDZANIA I DOWODZENIA – 2013

Analiza wrażliwości



Analiza wrażliwości pozwala znaleźć odpowiedź na
pytanie, jak powinien zmodyfikować decydent swoje
postępowanie, gdy następują określone zmiany warunków
działania.
Za pomocą analizy marginalnej można udzielić na to
pytanie następującej odpowiedzi:

Przy zmianie warunków ekonomicznych należy

określić ich wpływ na utarg i koszt krańcowy

przedsiębiorstwa, a następnie ponownie odwołać

się do zasady MR = MC, aby wyznaczyć nową

optymalną decyzję.



Do zmian warunków ekonomicznych możemy zaliczyć np.:



wzrost kosztów ogólnych;



wzrost kosztów surowca;



wzrost popytu;



zmiany kursu walutowego.

AKADEMIA OBRONY NARODOWEJ – WYDZIAŁ ZARZĄDZANIA I DOWODZENIA – 2013

Podsumowanie

- reguły decyzyjne



Podstawowym problemem decyzyjnym w
przedsiębiorstwie jest określenie wolumenu produkcji i
ceny sprzedawanego dobra lub usługi;



Zysk przedsiębiorstwa stanowi różnicę między
przewidywanym utargiem i kosztami. Produkcję i
sprzedaż należy zwiększać, jeżeli prowadzi to do
zwiększenia sumy zysku, tzn. dopóki dodatkowy utarg
przewyższa przyrost kosztów. Produkcję i sprzedaż
należy zmniejszać, gdy oszczędności na kosztach są
większe od sumy utraconego utargu;



Zmiany warunków ekonomicznych, w których działa
przedsiębiorstwo, rzutują na układ utargu krańcowego i
kosztów krańcowych, powodując w konsekwencji zmianę
optymalnego wolumenu produkcji i poziomu ceny.

AKADEMIA OBRONY NARODOWEJ – WYDZIAŁ ZARZĄDZANIA I DOWODZENIA – 2013

Podsumowanie - najważniejsze

ustalenia



Podstawowymi czynnikami wyznaczającymi optymalną wielkość
produkcji
i wysokość ceny w przedsiębiorstwie są krzywe popytu i kosztów.
Krzywą popytu można wykorzystać do prognozowania: 1) wielkości
sprzedaży przy danej cenie
lub 2) poziomu ceny zapewniającego określony wolumen
sprzedaży. Mnożąc ceny przez odpowiadające im ilości na krzywej
popytu, otrzymujemy funkcję utargu. Funkcja kosztów z kolei
określa koszt wytworzenia określonej ilości produktu. Zestawiając
funkcję utargu z funkcją kosztów, możemy przewidzieć wielkość
zysku osiąganego przy dowolnym wolumenie produkcji Q.



Następnym krokiem istotnym przy wyznaczaniu optymalnej
decyzji przedsiębiorstwa jest określenie utargu krańcowego,
kosztu krańcowego i zysku krańcowego.

a.

Zyskiem krańcowym nazywamy przyrost zysku osiągnięty dzięki
sprzedaży dodatkowej jednostki produktu.

b.

Utargiem krańcowym nazywamy przyrost utargu uzyskany ze
sprzedaży dodatkowej jednostki produktu.

c.

Kosztem krańcowym nazywamy przyrost kosztów związany z
wytworzeniem dodatkowej jednostki produktu.

d.

Z definicji zysk krańcowy równa się różnicy między utargiem
krańcowym
i kosztem krańcowym; Mπ, MR i MC można wyznaczyć, obliczając
pochodne funkcji zysku, utargu i kosztów.

AKADEMIA OBRONY NARODOWEJ – WYDZIAŁ ZARZĄDZANIA I DOWODZENIA – 2013

Podsumowanie

- najważniejsze ustalenia c.d.



Optymalną wielkość produkcji w
przedsiębiorstwie charakteryzują następujące,
równoważne sobie warunki: (1) Mπ = 0 lub (2)
MR = MC. Po określeniu optymalnej wielkości
produkcji z równania ceny można wyznaczyć
optymalny poziom ceny, a następnie obliczyć
zysk.

AKADEMIA OBRONY NARODOWEJ – WYDZIAŁ ZARZĄDZANIA I DOWODZENIA – 2013

Rachunek optymalizacyjny

(dodatek do rozdziału)



Decyzje podejmowane są po to, aby
zmaksymalizować określone cele.



Podstawowym warunkiem optymalizacji decyzji
jest kwantyfikacja ostatecznych celów, np. jeżeli
celem jest maksymalizacja zysku, musimy
potrafić ocenić i zmierzyć wpływ różnych
wariantów działania.

AKADEMIA OBRONY NARODOWEJ – WYDZIAŁ ZARZĄDZANIA I DOWODZENIA – 2013

Rachunek optymalizacyjny

- maksymalizacja zysku



Funkcja zysku określa zależność między zmienną
decyzyjną,
a przyjętym celem (z tego względu równanie to
jest często nazywane funkcją celu).

AKADEMIA OBRONY NARODOWEJ – WYDZIAŁ ZARZĄDZANIA I DOWODZENIA – 2013

Rachunek optymalizacyjny

- analiza marginalna



Wartością krańcową danej zmiennej nazywamy przyrost
wartości tej zmiennej następujący po zwiększeniu o jednostkę
wartości zmiennej decyzyjnej;



Bezpośrednią miarą wielkości zysku krańcowego jest
nachylenie funkcji zysku przy danym poziomie produkcji;



Analiza marginalna pozwala menadżerowi podjąć optymalną
decyzję, tzn. umożliwia określenie, co należy zrobić, aby
zmaksymalizować postawiony cel;



Analiza marginalna pozwala dokładnie wskazać optymalna
wielkość produkcji w sposób bezpośredni, uwalniając nas
od żmudnych poszukiwań metodą prób i błędów. Zasada jest
następująca:

Cel, do którego dąży menadżer, zostanie

zmaksymalizowany, gdy pochodna funkcji celu

względem zmiennej decyzyjnej przyjmie wartość

zerową (przechodząc od wartości dodatnich

do ujemnych)

AKADEMIA OBRONY NARODOWEJ – WYDZIAŁ ZARZĄDZANIA I DOWODZENIA – 2013

Rachunek optymalizacyjny

- rachunek różniczkowy



Wyznaczenie nachylenia stycznej to inaczej obliczanie pochodnej
(czyli zróżniczkowanie) funkcji.



y - zmienna zależna; x - zmienna niezależna;
y = f(x), gdzie f(x) oznacza nieokreśloną bliżej zależność
funkcyjną między tymi zmiennymi;
dy/dx oznacza pochodną funkcji, czyli tempo jej zmian albo
nachylenie przy określonej wartości x;
d – przyrost wartości zmian odnośnej zmiennej.

Podstawowe reguły różniczkowania funkcji:
1. Pochodna wielkości stałej równa jest zeru. Jeżeli np. y=7, to

dy/dx=0

2. Pochodna iloczynu wielkości stałej oraz zmiennej jest równa

wielkości stałej stojącej przed zmienną. Jeżeli y = bx, to dy/dx = b

3. Funkcja potęgowa ma postać y=ax, gdzie a i n to wielkości stałe.

Pochodną funkcji potęgowej obliczamy według wzoru:

= n * ax

AKADEMIA OBRONY NARODOWEJ – WYDZIAŁ ZARZĄDZANIA I DOWODZENIA – 2013

n

dy

d
x

n -
1

Rachunek optymalizacyjny

- rachunek różniczkowy c.d.



Podstawowe reguły różniczkowania funkcji c.d.:

4. Pochodna sumy funkcji jest równa sumie pochodnych

tych funkcji, tzn. jeżeli y = f(x) + g(x), to dy/dx = df/dx +
dg/dx. Oznacza to, że możemy obliczać po kolei
pochodną każdej funkcji z osobna.

5. Przyjmijmy, że y jest iloczynem dwóch funkcji: y = f(x)

g(x).

Mamy wówczas:

=

( )

g +

( )

f

6. Przyjmijmy, że y jest ilorazem dwóch funkcji: y =

f(x)/g(x). Mamy wówczas:

=

AKADEMIA OBRONY NARODOWEJ – WYDZIAŁ ZARZĄDZANIA I DOWODZENIA – 2013

d
y

d
x

d
fd

x

d
g

d
x

d
y

d
x

(df/dx)g –
(dg/dx)fg ²

Rachunek optymalizacyjny

- druga pochodna



Zawsze trzeba się upewnić, czy obliczone
ekstremum to maksimum, a nie minimum;



W odróżnieniu tych dwóch ekstrem pozwoli nam
druga pochodna. Obliczamy ją jako pochodną
zysku krańcowego, tzn. pochodną od dπ/dQ. Jeśli
druga pochodna jest ujemna (tzn. jeżeli nachylenie
funkcji zysku maleje), to mamy do czynienia z
lokalnym maksimum funkcji. Jeśli natomiast druga
pochodna jest dodatnia, oznacza to, że dany punkt
zwrotny stanowi lokalne minimum;
Obliczając pochodną od dπ/dQ, znajdujemy drugą
pochodną funkcji zysku:

=

=

AKADEMIA OBRONY NARODOWEJ – WYDZIAŁ ZARZĄDZANIA I DOWODZENIA – 2013

d
²π

dQ²

d(dπ/d
Q)dQ

d
Mπ

dQ

Rachunek optymalizacyjny

- utarg krańcowy i koszt

krańcowy



dπ/dQ = 0 ten sam warunek można wyrazić w
innej formie, wyodrębniając dwa czynniki
określające zysk.
Zysk stanowi różnicę między utargiem i kosztami.
Stąd funkcję zysku możemy zapisać jako:

π(Q) = R(Q) - C(Q)

Z kolei warunek, zgodnie z którym zysk krańcowy

równa się zeru, zapiszemy:

= - = MR – MC = 0

Zysk jest maksymalny wówczas, gdy utarg
krańcowy zrówna się z kosztem krańcowym.

AKADEMIA OBRONY NARODOWEJ – WYDZIAŁ ZARZĄDZANIA I DOWODZENIA – 2013

dπ
dQ

dR
dQ

dC
dQ

Rachunek optymalizacyjny

- maksima funkcji kilku

zmiennych



Niejednokrotnie menedżer musi określić
jednocześnie optymalne wartości różnych
zmiennych. Na przykład, może to być cena
produktu oraz wysokość podatków na reklamę.

AKADEMIA OBRONY NARODOWEJ – WYDZIAŁ ZARZĄDZANIA I DOWODZENIA – 2013

Rachunek optymalizacyjny

- optymalizacja przy istnieniu

ograniczeń



zobowiązania umowne;



zysk łączny z różnych rynków;



metoda mnożników Lagrange’a.

AKADEMIA OBRONY NARODOWEJ – WYDZIAŁ ZARZĄDZANIA I DOWODZENIA – 2013

Studio przypadku



Równanie popytu:

Q = 8,5 – 0,05P przy cenie P=50 => Q=6.



Odwrócone równanie popytu:

P = 170 – 20Q gdy Q=3,5 => P=100



Funkcja utargu:

R= P * Q = (170 – 20Q)Q = 170Q – 20Q²
przy Q=2 => P=130 000 dol. a zatem utarg R=260 000 dol.



Funkcja kosztów:

C=100+38Q przy Q=2, całkowite koszty produkcji wyniosą

C=176 000 dol.

koszty stałe (w tys.)

koszt wytworzenia jednej partii towaru (w tys.)



Funkcja zysku:

Π = R – C = (170Q-20Q²)-(100+38Q) = -100 + 132Q – 20Q²

dla Q=2, zysk wyniesie π=84 tys. dol.

AKADEMIA OBRONY NARODOWEJ – WYDZIAŁ ZARZĄDZANIA I DOWODZENIA – 2013

Studio przypadku c.d.



Zysk krańcowy:

Mπ = ∆π/∆Q = (π1-π0)/(Q1-Q0)
np. dla Q0=2,9 i Q1=3,0 (∆Q=0,1); π1=116 000 i π0=114 600 =>

Mπ = (116 000 – 114 600)/0,1= 14 000 dol.

Zysk krańcowy można obliczyć jako pochodną tego równania:

Π= -100 + 132Q - 20Q²

względem Q:

Mπ = ∆π/∆Q = 132 – 40Q

Za pomocą tej formuły możemy znaleźć wartość zysku krańcowego
przy dowolnym poziomie produkcji, podstawiając do równania
odpowiednią wielkość produkcji.
Np. przy Q=3,0 zysk krańcowy wyniesie 12 000 dol. za 1 partię.
Nietrudno wskazać wolumen produkcji, który zapewnia maksymalny
zysk. Wykorzystują równanie zysku krańcowego, wystarczy mianowicie
wstawić Mπ = 0 i rozwiązać równanie:

Mπ = 132 – 40Q = 0

skąd wyliczamy Q=132/40=3,3 partii

Jaka cena zapewnia sprzedaż 3,3 partii?
przy Q=3,3 => P = 170 – 20 * 3,3= 104 tys. dol.

AKADEMIA OBRONY NARODOWEJ – WYDZIAŁ ZARZĄDZANIA I DOWODZENIA – 2013

Studio przypadku c.d.



Utarg krańcowy:

MR = ∆R/∆Q = (R

1

- R

0

)/(Q

1

-Q

0

)

Np. utarg krańcowy uzyskany dzięki zwiększeniu sprzedaży z 2,0 do

2,1 partii produktu wyniesie:

(268,8 – 260,0)/(2,1 - 2,0)= 88 tys. dol. za partię

268,8 oznacza tu utarg ze sprzedaży 2,1 partii;

260,0 – utarg ze sprzedaży 2,0 partii

Aby obliczyć utarg krańcowy przy danej wielkości produkcji i
sprzedaży, wychodzimy od równania utargu: R=170Q – 20Q² i
obliczamy pochodną względem ilości:

MR = ∆R/∆Q = 170 – 40Q

Np. przy Q=3 => utarg krańcowy MR= 170 – 40 * 3 = 50 tys. dol.



Koszt krańcowy:

MC = ∆C/∆Q = (C

1

-C

0

)/(Q

1

-Q

0

)

Z równania kosztów: C = 100 + 38Q wynika, że wytworzenie
dodatkowej partii towaru (tzn. zwiększenie Q o jednostkę)
powiększa sumę kosztów o 38 000 dol. MC = 38 000 dol. za 1 partię

AKADEMIA OBRONY NARODOWEJ – WYDZIAŁ ZARZĄDZANIA I DOWODZENIA – 2013

Studio przypadku c.d

.



Utarg krańcowy i koszt krańcowy:

MR = MC

=>MR=170 – 40Q i MC=38

oznacza to, że 170 - 40Q=38, rozwiązanie: Q=3,3

Jest to taki sam wynik, jaki otrzymaliśmy, przyrównując zysk krańcowy do zera.



Analiza wrażliwości:

MR = 170 – 40Qprzy Q = 0, MR = 170

wychodząc od zerowej wielkości sprzedaży, przedsiębiorstwo uzyskuje
początkowo bardzo wysoki utarg krańcowy ze sprzedaży dodatkowych
jednostek produktu. W miarę zwiększania sprzedaży przyrost utargu
wynikający ze sprzedaży dodatkowych jednostek produktu maleje.



Wzrost kosztów ogólnych:

Załóżmy, że koszty stałe wynosiły 100 000 dol. Tygodniowo, a obecnie wynoszą

112 000 dol. Jak wpłynie to na decyzje operacyjne przedsiębiorstwa?
Wzrost kosztów stałych nie wpłynie na podjęte decyzje. Przedsiębiorstwo
powinno produkować tyle samo, co poprzednio, i sprzedawać po
dotychczasowej cenie.

- zysk przedsiębiorstwa zmniejsza się o 12 000 dol. bez względu na wielkość

produkcji. Wolumen produkcji, który zapewniał maksymalny zysk przed
zmianą, musi zapewnić maksymalny zysk również obecnie.

AKADEMIA OBRONY NARODOWEJ – WYDZIAŁ ZARZĄDZANIA I DOWODZENIA – 2013

Studio przypadku c.d.



Wzrost kosztów surowca:



podwyżka ceny krzemu powoduje wzrost kosztów produkcji układów
scalonych z 38 000 dol. do 46 000 dol. za jedną partię. Jak powinien
zareagować producent? W tym przypadku koszt krańcowy mikroprocesora
uległ zmianie. Ponieważ wytwarzanie dodatkowej produkcji stało się bardziej
kosztowne, właściwą reakcją przedsiębiorstwa będzie zmniejszenie produkcji.



Jaka wielkość produkcji jest obecnie optymalna?
MR = MC => 170-40Q=46, czyli Q=3,1 partii
Cena równowagi obliczona z równania: P=170-20Q wyniesie 108 000 dol.
Wzrost kosztów zostanie częściowo przerzucony na nabywców poprzez
podwyżkę ceny.



Wzrost popytu:



rośnie popyt na układy scalone wytwarzane przez nasze przedsiębiorstwo;
przy zwiększonym popycie mogłoby ono podnieść cenę 1 partii o 20 000 dol.
(o 200 dol. na sztuce) i sprzedawać tę samą ilość towaru co poprzednio.
Mamy nowe równanie ceny: P=190-20Q. Obecne równanie utargu
krańcowego ma postać: MR=190-40Q.



Jaka wielkość produkcji jest obecnie optymalna?
MR=MC => 190-40Q=38, a więc Q=3,8. Cena równowagi wynosi 114 000
dol.
Przedsiębiorstwo wykorzysta najlepiej wzrost popytu, jeżeli zwiększy
produkcje (do 380 sztuk tygodniowo), a jednocześnie podniesie cenę.

AKADEMIA OBRONY NARODOWEJ – WYDZIAŁ ZARZĄDZANIA I DOWODZENIA – 2013

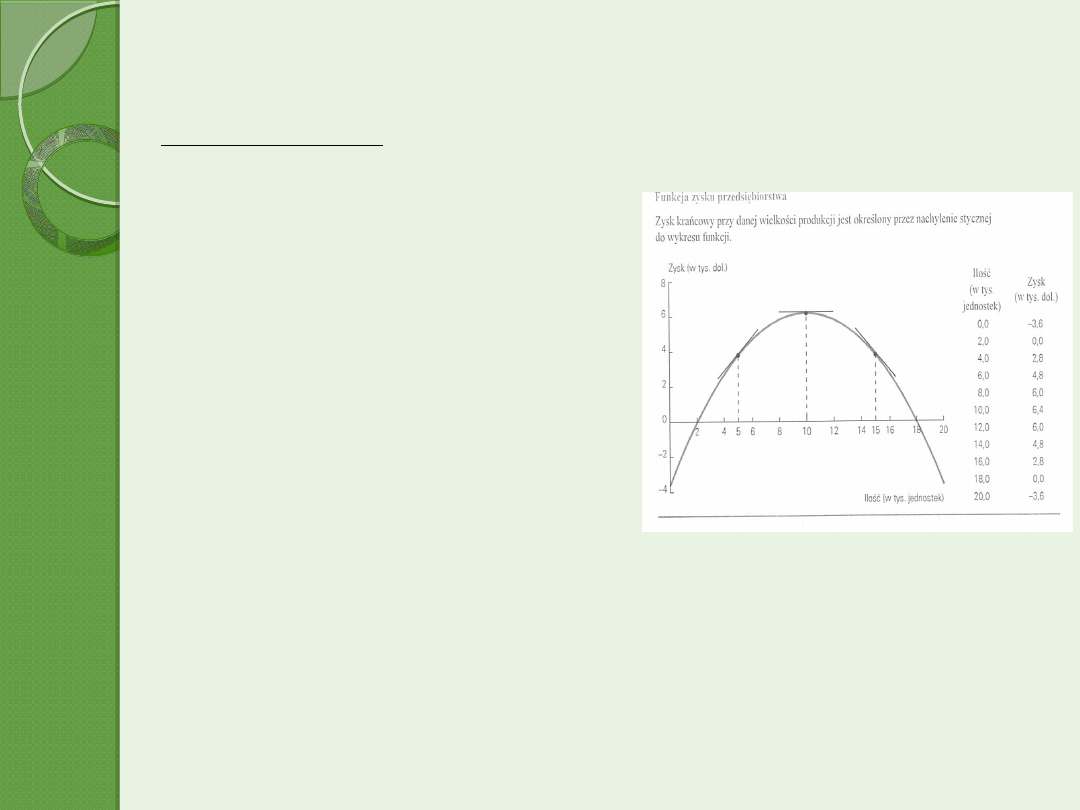
Studio przypadku c.d.



Analiza marginalna:



wybieramy interesujący nas wolumen produkcji, np. Q=5;



wykreślamy styczną do krzywej zysku
przy tym wolumenie produkcji;



mierzymy nachylenie stycznej;



nachylenie stycznej, mierzone jako stosunek
odcinka pionowego do poziomego,
wyznaczonego przez punkt styczności,
jest w tym przypadku równe 1;



zysk krańcowy przy Q=5 mierzymy
stosunkiem 1000 dol. do 1000 jednostek
produktu, czyli 1 dol. na jednostkę produktu.



styczna o nachyleniu dodatnim wskazuje, że
zysk wzrasta w miarę wzrostu produkcji;



wielkość zysku krańcowego zależy od nachylenia tej stycznej, tzn. od tego, jak
szybko wzrasta suma zysku w miarę wzrostu produkcji;



na wykresie zostały zaznaczone również styczne przy wielkościach produkcji
Q=10
i Q=15, przy zwiększaniu produkcji powyżej 10 (Q>10) suma zysku maleje.



maksymalny zysk występuje przy produkcji Q=10 000 jednostek, kiedy styczna
do krzywej zysku przyjmuje położenie poziome, a jej nachylenie jest równe zeru.

AKADEMIA OBRONY NARODOWEJ – WYDZIAŁ ZARZĄDZANIA I DOWODZENIA – 2013

Studio przypadku c.d.

AKADEMIA OBRONY NARODOWEJ – WYDZIAŁ ZARZĄDZANIA I DOWODZENIA – 2013



Rachunek różniczkowy:



wyprowadzamy za pomocą reguł funkcję zysku krańcowego z
naszej funkcji zysku całkowitego: π = 2Q - 0,1Q² - 3,6;



zgodnie z regułą 4 możemy obliczać pochodną dla każdego
wyrazu
z osobna. Wg 2 reguły pochodna pierwszego wyrazu wynosi 2,
wg 3 pochodna drugiego wyrazu wynosi -0,2Q, wg reguły 1
pochodna trzeciego wyrazu równa się 0. A zatem: Mπ=∆ π/∆Q=
2-0,2Q;



podstawiając konkretne wartości Q, możemy wyznaczyć wielkość
zysku krańcowego przy dowolnym poziomie produkcji, np. przy
Q=5 => Mπ=1;



aby ustalić optymalna wielkość produkcji przedsiębiorstwa,
podstawiamy Mπ=0. Stąd mamy: 2 - 0,2Q = 0; rozwiązując
względem Q znajdujemy Q=10. Potwierdza to, że wielkość
produkcji zapewniająca maksymalny zysk wynosi 10 000
jednostek.

LITERATURA

AKADEMIA OBRONY NARODOWEJ – WYDZIAŁ ZARZĄDZANIA I DOWODZENIA – 2013



William F. Samuelson, Stephen G. Marks,
Ekonomia menedżerska, Polskie
Wydawnictwo Ekonomiczne, Warszawa 2009.