Projekt budynku (magazynu) 3-kondygnacyjnego w układzie płytowo-słupowym Projekt budynku (magazynu) 3-kondygnacyjnego w układzie płytowo-słupowym POLITECHNIKA GDAŃSKA

WYDZIAŁ INŻYNIERII LĄDOWEJ I ŚRODOWISKA

KATEDRA KONSTRUKCJI BETONOWYCH

Projekt budynku (magazynu) 3-kondygnacyjnego w

układzie płytowo-słupowym

TEMAT

Ćwiczenie projektowe z przedmiotu:

Podstawy Inżynierskich Konstrukcji Betonowych

PROJEKTANT:

Bartłomiej Górski 127250

grupa KB1

semestr 7 inż. (zimowy)

r.ak. 2013/2014

SPRAWDZAJĄCY: mgr inż. Marek Kin; mgr inż. Paweł Kowalczyk DATA ODDANIA: 6.12.2013 r.

OCENA:

Gdańsk, 2013 r.

1

2

Projekt budynku (magazynu) 3-kondygnacyjnego w układzie płytowo-słupowym Projekt budynku (magazynu) 3-kondygnacyjnego w układzie płytowo-słupowym O B L I C Z E N I A S T A T Y C Z N E

Spis treści

i W Y M I A R O W A N I E

0. DANE MATERIAŁOWE I GEOMETRYCZNE

Strona tytułowa

1

Karta tematu

2

Beton - C25/30

Spis treści

3

•

wytrzymałość charakterystyczna na ściskanie – fck = 25 MPa = 2,5 kN/cm2

1.0 Zebranie obciążeń

4

•

wytrzymałość obliczeniowa na ściskanie – fcd : 1.1. Płyta

5

α ⋅

1.1.1. Sprawdzenie pracy płyty

5

f

f

= cc ck

γ

= 1,0⋅25 =17,86 MPa=1,79 kN / cm 2

1.1.2. Dobór grubo

cd

ści płyty - h

c

1,4

f

6

1.2. Żebro

6

1.2.1. Dobranie wysokości żebra – h

gdzie: αcc = 1,0 oraz γc = 1,4

ż

6

1.2.2. Dobranie szerokości żebra – bż

6

1.3. Słup

6

•

średnia wytrzymałość betonu na rozciąganie – fctm = 2,5 MPa = 0,26 kN/cm2

1.3.1. Określenie geometrii słupa

6

•

charakterystyczna wytrzymałość na rozciąganie – fctk = 1,8 MPa = 0,18 kN/cm2

1.4. Stopa fundamentowa

7

1.4.1. Stopa zewnętrzna

7

•

obliczeniowa wytrzymałość na rozciąganie (αcc = 1,0 i γc = 1,4 ) – fctd = 1,29 MPa = 0,13 kN/cm2

1.4.2. Stopa wewnętrzna

7

•

średnia wytrzymałość betonu na rozciąganie w chwili zarysowania – f 1.5. Ława fundamentowa

7

ct,eff = fctm (założono

1.5.1. Określenie geometrii ławy

7

zarysowanie po 28 dniach) = 2,6 Mpa = 0,26 kN/cm2

Wizualizacja 1/1

8

•

sieczny moduł sprężystości – Ecm = 31 GPa = 3200 kN/cm2

Część rysunkowa:

•

obliczeniowa wartość siecznego modułu sprężystości – Ecd: Rys.1 – Rzut fundamentów 1:100

Rys. 2 – Rzut parteru 1:100

E

E = cm =3100 =2583 kN / cm 2

Rys. 3 – Rzut piętra 1:100

cd

γ cE

1,2

Rys. 4 – Przekrój pionowy A-A 1:50

gdzie: γcE = 1,2

Rys. 5 - Wizualizacja 1/1 (str. 8 w tekście)

•

zasięg granicznej względnej strefy ściskanej - ξeff.lim:

|ε

|

ξ

=0,8⋅

cu3

=0,8⋅

3,5⋅10 3

=0,493 [-]

eff.lim

|ε

|+|ε |

cu3

sy

3,5⋅10 3+ 2,174⋅10 3

gdzie: εcu3 – odszktałcenia w betonie ściskanym = 3,5 ‰ = 3,5 . 10-3

εsy – odszktałcenia zbrojenia w punkcie uplastycznienia stali równe: f

ε = yd = 43,478 =0,0021739=2,174⋅10 3[-]

sy

E

20000

s

•

klasa ekspozycji – XC1

•

klasa konstrukfcji – S4

Stal – klasa C (A-IIIN) (B500SP)

•

charakterystyczna granica plastyczności - fyk = 500 MPa= 50 kN/cm2

•

obliczeniowa granica plastyczności – fyd = fywd: f

f

= f

= yk = 500 =434,78 MPa=43,48 kN / cm 2

yd

ywd

γ s

1,15

gdzie: γs = 1,15

•

moduł sprężystości – Es = 200 GPa = 20000 kN/cm²

3

4

Projekt budynku (magazynu) 3-kondygnacyjnego w układzie płytowo-słupowym Projekt budynku (magazynu) 3-kondygnacyjnego w układzie płytowo-słupowym Otulina

Poz.1.0 Płyta stropowa

•

otulina nominalna – cnom:

1. Statyka

c

= c +∆ c =15+5=20 mm=2,0 cm nom

min

dev

1.0. Zebranie obciążeń

gdzie: cmin – minimalna wartość otuliny wg wyrażenia:

≥

Grubość

Ciężar

Wart. char.

γ

Wart. obl.

ϕ

Lp.

Rodzaj obciążenia

f

[m]

[kN/m3]

[kN/m2]

[-]

[kN/m2]

c

= max {

cmin,b

}= max{14}=15 mm

min

c

+∆ c

∆ c

∆ c

15

min ,dur

dur , γ

dur , st

dur , add

Obciążenia stałe

10 mm

10

1

lastryko

0,02

24

0,48

1,35

0,65

2

beton dociskowy

0,03

24

0,72

1,35

0,97

Przyjęto :

3

styropian

0,05

0,5

0,03

1,35

0,03

cmin,b – minimalna otulina ze względu na przyczepność = ϕ – zakładana maksymalna średnica 4

1x folia PE

-

-

-

-

-

pręta – 14 mm i maksymalny wymiar kruszywa <= 32 mm 5

płyta żelbetowa

0,25

25,0

6,25

1,35

8,44

cmin,dur – 15 mm (klasa S4; środowisko XC1) 6

tynk cem-wap

0,02

24,0

0,36

1,35

0,49

∆cdur,γ – poprawka ze względu na bezpieczeństwo – 0 mm Razem na 1m2

gk = 7,84 kN/m2

go = 10,58 kN/m2

∆cdur,st – poprawka ze względu na stosowanie stali nierdzewnej – 0 mm Obciążenia zmienne

∆cdur,add – poprawka ze względu dodatkowych – 0 mm 1

powierzchnia magazynu

7,5

1,5

11,25

∆cdev – poprawka ze względu na wykonawstwo wg zakresu: Razem na 1m2

pkf = 7,5 kN/m2

pof = 11,25 kN/m2

(0

dla el. prefabrykowanych) (0)5 mm≤∆ c

≤10 mm→ przyjęto∆ c =5 mm dev

dev

1.1. Schemat statyczny

Przyjęte wymiary elementów:

Strop płaski został obliczony metodą ram wydzielonych , zebranie obc. z pasma na kierunku X = 6,1 m

•

wysokość płyty – h

Y = 5,2

f

h =30 cm [ w uproszczeniu dla magazynu]

f

RYSUNKI

•

wysokość (c1) i szerokość (c2) słupa

Obliczenie wartości obciążeń charaktersytycznych działających na dane pasmo: c = c =45 cm[ w uproszczeniu dla magazynu]

1

2

· kierunek x

· kierunek y

g k= g k⋅ l =7,84⋅6,1=47,82 kN / m g k= gk⋅ l =7,84⋅5,2=40,77 kN / m x

x

y

y

pk= pk⋅ l =7,5⋅6,1=45,75 kN / m pk = pk⋅ l =7,5⋅5,2=39,0 kN / m x

x

y

y

1.2. Wyznaczenie sił wewnętrznych

1.2.1. Przypadki obliczeniowe

•

ULS (SGN) – stan granicznej nośności

◦ Mnożnik obc. stałego – 1,35

◦ Mnożnik obc. zmiennego – 1,5

◦ Współczynnik redukcyjny obc. zmiennego – ψ ; przyjęto 1,0 (zal. 1,0 dla magazynu - kat.E)

•

SLS (SGU) – stan granicznego użytkowania (kombinacja quasi-stała) 5

6

Projekt budynku (magazynu) 3-kondygnacyjnego w układzie płytowo-słupowym Projekt budynku (magazynu) 3-kondygnacyjnego w układzie płytowo-słupowym

◦ Mnożnik obc. stałego – 1,0

1.2.3. Wyniki obliczeń statycznych

◦ Mnożnik obc. zmiennego – 1,0

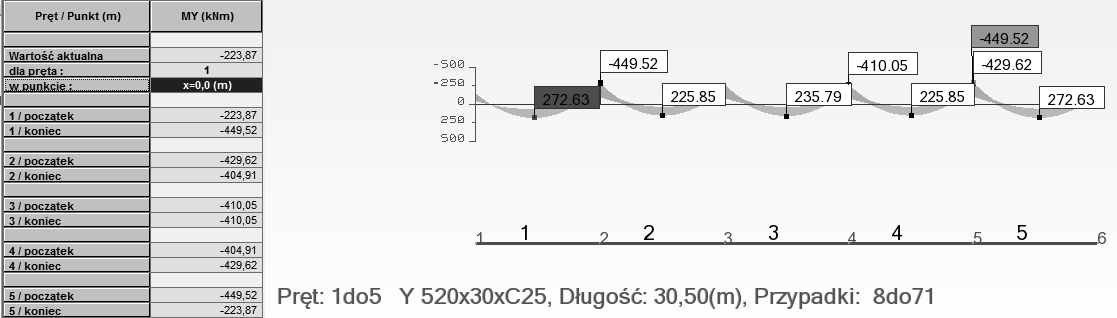
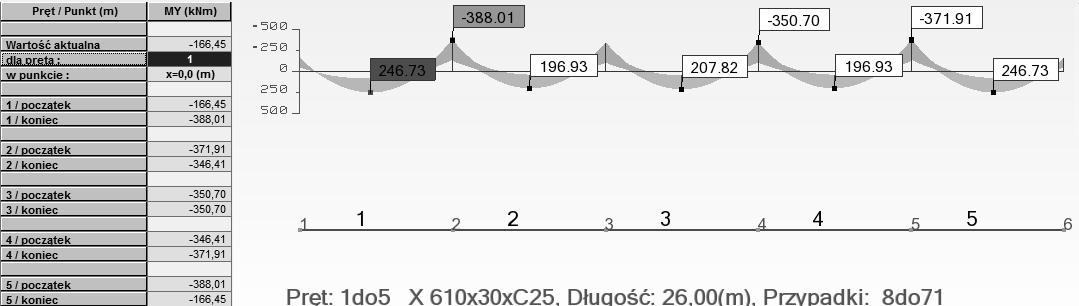
Wykres sił wewnętrznych – SGN – Kierunek X

◦ Współczynnik redukcyjny obc. zmiennego – ψ ; przyjęto 0,8 (zal. 0,8 dla magazynu - kat.E) 1.2.2. Kombinacje obciążeń

Utworzono kominacje obciążeń automatycznie w programie robot wg poniższych relacji:

•

Grupa G1 i G2 – obciążenie stałe słupa (G1) i płyty (G2)

•

Grupa E1 lub E2 lub E3 lub E4 lub E5 – obciążenie zmienne rozłożone na osobnym przęśle ramy G1 i G2 + E1 lub E2 lub E3 lub E4

Wykres sił wewnętrznych – SGN – Kierunek Y

Efekt końcowy: uzyskano wszystkie możliwe kombinacje rozłożenia obciążenia zmiennego na przęsłach.

7

8