Probabilistyka i statystyka – ćwiczenia (28.10.2010) Wybrane rozkłady dyskretne
1) Rozkład Poissona
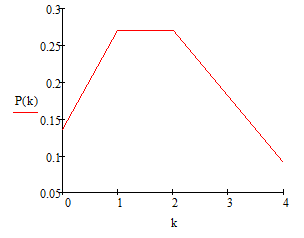
= 2000, = 0,001, = 0,1,2,3,4
= ∗ !
= ∗
= 2000 ∗ 0,001 = 2
2
1
= ∗ 0! = = 0,135
1 2
2
= ∗ 1! = = 0,27
1 2
2
= ∗ 2! = = 0,27
1 2
4
= ∗ 3! = 3 == 0,18
1 2
2
= ∗ 4! = 3 = 0,09
2) Rozkład geometryczny
W schemacie Bernouliego prawdopodobieństwo sukces zdarzenia = 0,1
Oblicz prawdpodobieństwo zdarzenia : na początku seria 5 porażek, sukces przy 6 próbie
= 0,1
1
!" = 0,9# ∗ 0,1 = 0,81 ∗ 0,81 ∗ 0,9 ∗ 0,1 = 0,729 ∗ 0,81 ∗ 0,1 = 0,059049
!" = !1 − " ∗ = ∗
3) Rozkład hipergeometryczny
W urnie znajduje się 6 kul białych, 5 czarnych. Losujemy bez zwracania 7 kul. Oblicz prawdopodobieństwo, że wylosujemy 4 kule białe i 3 czarne 11
11!
8 ∗ 9 ∗ 10 ∗ 11
Ω% = & 7 ' = 7! ∗ 4! =
24
= 330
6
5
6!
5!
A% = &4' ∗ &3' = 4!2! ∗ 3!2! = 15 ∗ 10 = 150
150 15
5
!" = 330 = 33 = 11 = 0,45
Dany jest rozkład
)*
1
3
5
*
1
1
1
2
3
6
Oblicz wartość oczekiwaną +,, -./!,", 0
Rozproszenie zmiennej losowej
1 = +|, − +,|
Współczynnik zmiennej
0
3 = +,,+, ≠ 0
Współczynnik nierównomierności
1
ℎ =
+, , +, ≠ 0
1
1
1 1
5 3 + 6 + 5 14 7
+, = Σ*7)* ∗ * = 1 ∗ 2 + 3 ∗ 3 + 5 ∗ 6 = 2 + 1 + 6 = 6 = 6 = 3
-./!)" = +!," − !+,"
1
1
1 1
25 3 + 18 + 25 46 23
+!," = Σ
*7)* ∗ * = 1 ∗ 2 + 9 ∗ 3 + 25 ∗ 6 = 2 + 3 + 6 =
6
= 6 = 3
23 49 69 − 49 20
-./!)" = 3 − 9 = 9 = 9
2
3
14 1
14 1
14 1 8 1 4 1 16 1
1 = +|, − +,| = ;1 − 6 ;∗ 2 + ;3 − 6 ; ∗ 3 + ;5− 6 ; ∗ 6 = 6 ∗ 2 + 6 ∗ 3 + 6 ∗ 6 =
8
4
16 12 + 4 + 8 24 4
= 12 + 18 +36 = 18 = 18 = 3
√20
0
3 =
3
+, = 7 = √20
7
3
4 3 4
ℎ = 3 ∗ 7 = 7
Autor: shenlon (http://shenlon.eu)
3