1. Wstęp teoretyczny
Systemy fotowoltaiczne przetwarzają promieniowanie słoneczne bezpośrednio
w energię elektryczną.
Podstawą tej technologii są materiały półprzewodnikowe takie jak krzem. Typowe ogniwo
słoneczne składa się z dwóch różnie domieszkowanych półprzewodników. Domieszkowanie
jest to kontrolowane wprowadzanie zanieczyszczeń do materiału bazowego. W przypadku
czystego kryształu półprzewodnika (np. krzemu) zastępuje się niektóre atomy w siatce
krystalicznej pierwiastkami mającymi o jeden elektron walencyjny więcej lub o jeden
elektron walencyjny mniej niż materiał podstawowy (elektrony walencyjne określają
zachowanie chemiczne materiału, są one umiejscowione na zewnętrznej powłoce
elektronowej atomu). Pierwiastki półprzewodzące mają cztery elektrony walencyjne z których
wszystkie są wykorzystane w wiązaniach w siatce krystalicznej.
Jeśli materiał domieszki ma pięć elektronów walencyjnych, jeden z nich będzie
dodatkowym, słabo związanym z atomem domieszkującym. „Wolne„ elektrony mogą
poruszać się łatwo w siatce i są odpowiedzialne za zwiększenie przewodności. Ponieważ mają
one ładunek ujemny, materiał domieszkowany w ten sposób jest nazywany półprzewodnikiem
typu „n”.
Jeśli z kolei materiał domieszkujący ma tylko trzy elektrony walencyjne, siatka
krystaliczna będzie miała niedomiar elektronów to znaczy będzie miała jedna „dziurę”
(ładunek dodatni) na atom domieszki. Podobnie do powyższych wolnych elektronów dziury mogą się łatwo przemieszczać w siatce zwiększając ponownie przewodność. Ponieważ w tym
przypadku wolne ładunki są dodatnie, ten rodzaj półprzewodnika jest nazywany
półprzewodnikiem typu „p”.
Jeśli półprzewodnik typu n zostanie połączony z półprzewodnikiem typu p, powstaje
złącze p-n. Różnice koncentracji dziur i wolnych elektronów pomiędzy rejonami n i p, powodują powstanie prądu dyfuzyjnego: elektrony przepływają z obszaru n do obszaru p i wypełniają dziury. To tworzy region który jest prawie pozbawiony wolnych nośników
ładunku i dlatego jest nazywany warstwa zubożoną.
W warstwie zubożonej po stronie n jest dodatni ładunek netto, a po stronie p ujemny co
powoduje powstanie pola elektrycznego zapobiegającego dalszemu przepływowi elektronów.
Im więcej elektronów przepłynie ze strony n na stronę p tym silniejsze jest to pole. Prowadzi
to do ustalenia się stanu równowagi w którym przepływ elektronów ustaje. Różnica
1
potencjałów w polu równowagowym jest nazywana napięciem dyfuzji. To napięcie nie może
być wykorzystane w zewnętrznym obwodzie. Jednakże gdy światło pada na ogniwo
słoneczne, równowaga zostaje zaburzona i tak zwany wewnętrzny efekt fotowoltaiczny
powoduje powstanie dodatkowych nośników ładunku mogących poruszać się w polu
elektrycznym warstwy zubożonej.
Dziury poruszają się w kierunku regionu p a elektrony w kierunku n, powodując
powstanie zewnętrznego napięcia (biegu jałowego) ogniwa. Napięcie biegu jałowego ogniwa
słonecznego zależy od materiału a nie od jego powierzchni. Fotoogniwa krzemowe mają
napięcie biegu jałowego około 0,5 V. Większe napięcia można uzyskać łącząc ogniwa
szeregowo.
Rys.1.1 Budowa ogniwa słonecznego
Prąd dostarczany przez fotoogniwo zależy od natężenia światła padającego na nie.
Równoległe łączenie ogniw pozwala na uzyskanie większego prądu. Moc ogniwa zależy nie
tylko od samego ogniwa ale również od przyłączonego obciążenia elektrycznego. Punkt mocy
maksymalnej można określić z charakterystyki napięciowo-prądowej ogniwa.
2. Sprawność ogniwa słonecznego
Sprawność ogniwa słonecznego jest stosunkiem maksymalnej mocy elektrycznej Pel, wydzielonej na obciążeniu, do padającej mocy promieniowania Prad:
P
P
out
el
η =
=
P
P
in
rad
Z powyższego równania wynika, że dla uzyskania maksymalnej sprawności
zasadnicze znaczenie ma osiągnięcie maksymalnej mocy elektrycznej w danych warunkach
oświetleniowych, co wymaga rozwiązania szeregu problemów. Na rysunku 2.1 przedstawiono
2
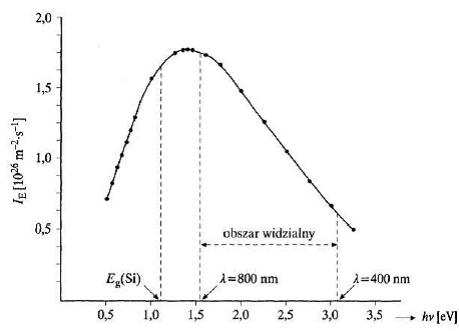
rozkład widmowy promieniowania Słońca ( T = 5800 K). Jak łatwo się przekonać, górnej granicy przerwy energetycznej w krzemie Eg = 1 , 12 eV odpowiada długość fali λg = 1100
nm. Zatem wszystkie fotony widma słonecznego o energii E < Eg mają zbyt małą energię aby wykreować w złączu parę elektron-dziura. Oznacza to, że ok. 23% energii fotonów widma nie
ma wpływu na sprawność η. Należy podkreślić, że w przypadku materiałów o szerszej przerwie energetycznej Eg sytuacja jest jeszcze mniej korzystna. Jak już wspomniano, jedynie fotony o energii E > Eg produkują pary elektron - dziura o energii E. Nadwyżka energii E −
Eg tracona jest w półprzewodniku na ciepło co oznacza, ze jedynie energia Eg zamieniana jest na energię elektryczną. Obydwa efekty prowadzą do wykorzystania jedynie 44% energii
fotonów widma, co jest górną, „teoretyczną” granicą sprawności.
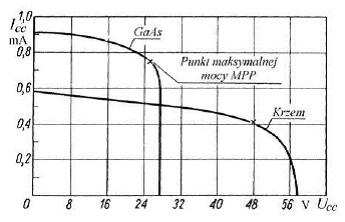
Na rysunku 2.2 porównano charakterystyki prądowo - napięciowe ogniw, wykonanych
z arsenku galu GaAs ( Eg = 1 , 41 eV) oraz krzemu, badanych w tych samych warunkach. Jak wynika z rysunku, materiał o szerszej przerwie energetycznej wytwarza niższe napięcie w obwodzie otwartym Uoc (większy jest prąd zwarcia Is). Materiał o mniejszej Eg (absorbujący większą część padającego widma — por. rys. 2.12) wytwarza wyższe Uoc (mniejszy prąd Is).
Rysunek 2.1 Widmo emisyjne Słońca (przybliżone krzywą promieniowania ciała
doskonale czarnego) w funkcji energii fotonow z zaznaczoną wartością przerwy
energetycznej Si
3
Rysunek 2.2 Porównanie charakterystyk ogniw słonecznych wykonanych z arsenku
galu GaAs i krzemu Si
Ponieważ droga dyfuzji nośników w krzemie jest większa niż w arsenku galu, w
krzemie zbiera się więcej generowanych światłem nośników. Analizując położenie MPP
można wykazać, że bardziej „prostokątny” przebieg charakterystyki oznacza większą
sprawność ogniwa. Widmo słoneczne ogranicza zatem grupę materiałów możliwych do
zastosowania w ogniwach. Przy projektowaniu ogniw słonecznych konieczna jest
optymalizacja czułości widmowej materiału. Z kolei, aby wychwycić nośniki generowane na
oświetlonej powierzchni przez fotony nie wnikające w głąb materiału ( hν >> Eg), warstwa wierzchnia ogniwa musi być — jak wspomniano na wstępie — bardzo cienka. Im cieńsza jest
warstwa, przez którą dyfundują nośniki, tym większy jest opór wewnętrzny ogniwa.
Konieczny jest więc rozważny kompromis pomiędzy wysoką sprawnością wychwytywania a
małym oporem wewnętrznym. Straty promieniowania wskutek odbić są zazwyczaj
ograniczone poprzez zastosowanie powłok antyodbiciowych. Z powyższych względów
przykładowe, realne sprawności ogniw słonecznych osiągają następujące wartości:
— krzem monokrystaliczny: ok. 14 - 16%;
— krzem polikrystaliczny: ok. 13 - 15%;
— krzem amorficzny: ok. 5 - 7%;
— monokrystaliczny arsenek galu: ok. 11%.[2]
3. Wyznaczenie sprawności i punktu mocy maksymalnej MPP
Aby wyznaczyć sprawność modułu słonecznego musimy znać wartość mocy
promieniowania słonecznego padającego na moduł Pin i jego moc elektryczną.
Należy dokonać pomiaru mocy promieniowania świetlnego padającego na
jednostkę powierzchni modułu E[W/m2]. Tę wartość należy pomnożyć przez
efektywną powierzchnię modułu S[m2] aby wyznaczyć moc Prad.
4
Sprawność można wyznaczyć ze wzoru
P
P
P
out
el
el
η =
=
=
P
P
E ⋅ S
in
rad
W przypadku braku możliwości zmierzenia natężenia promieniowania świetlnego
można posłużyć się faktem, że prąd zwarciowy modułu jest proporcjonalny do
ilości fotonów padających na ogniwo, a więc i do mocy promieniowania
świetlnego. Napięcie biegu jałowego zależy od materiału fotoogniwa, a nie od jego
oświetlenia, więc nie może być wykorzystane w tym pomiarze. Aby wyznaczyć
moc promieniowania należy pomnożyć wartość prądu zwarcia ogniwa przez
współczynnik F i powierzchnię modułu. Ten współczynnik jest zależny od
wartości maksymalnej prądu zwarcia ogniwa. Wartość maksymalną prądu zwarcia
fotoogniwa podaje wytwórca dla mocy promieniowania 1000 W/m2.
Przykład:
Producent podał wartość maksymalną prądu zwarcia fotoogniwa dla mocy
promieniowania 1000 W/m2; Iscmax = 350 mA. Wymiary ogniwa: 25mm x 50mm, zmierzona
moc elektryczna Pel = 0,311W
W
1000
2
W
m
F =
= 8
,
2 6
2
350 mA
mAm
Dla wyznaczenia mocy promieniowania padającego na moduł, należy pomnożyć
zmierzony prąd zwarcia Isc przez współczynnik F i powierzchnię modułu S.
np. zmierzony prąd zwarcia Isc = 180mA:
W
P = P
= F ⋅ I ⋅ S = 8
,
2 6
⋅180 mA ⋅5 ⋅10−3 m 2 = 5
,
2
W
7
in
rad
sc
mAm 2
P
3
,
0 11
η = el =
= 1,
0 2 = 1 %
2
P
5
,
2 7
rad
Wyznaczanie MPP
Punktem maksymalnej mocy (MPP) jest maximum krzywej mocy P = f(U) rys3.1. MPP
może być również wyznaczony z charakterystyki prądowo-napięciowej jako prostokąt
o maksymalnym polu powierzchni oparty na osiach współrzędnych i wierzchołku należącym
do krzywej rys.3.2. Rezystancję optymalną Ropt w punkcie MPP określa wzór
U
MPP
R
=
opt
I MPP
5
Rys.3.1 Krzywa mocy ogniwa
Rys.3.2 Charakterystyka prądowo-napięciowa modułu słonecznego
Dla charakterystyki I = f(U) definiowany jest współczynnik wypełnienia FF –
P
U
⋅ I
współczynnik wypełnienia (ang. Fill Factor), który ma postać
MPP
MPP
FF =
max
=
i
U
⋅ I
U
⋅ I
OC
SC
OC
SC
osiąga jedność gdy krzywa I = f(U) zbliża się kształtem do prostokąta o bokach Uoc i Isc.
6
4. Schemat układu pomiarowego
Rys.4.1 Schemat układu pomiarowego
5. Przebieg ćwiczenia
Przed przystąpieniem do pomiarów należy zapisać dane znamionowe badanego ogniwa
5.1 Wyznaczanie charakterystyki prądowo napięciowej
Tabela pomiarów
U[V]
0
I[mA] 0
5.2 Wyznaczanie krzywej mocy ogniwa
Tabela obliczeń
U[V]
0
P[W] 0
0
5.3 Wyznaczanie rezystancji optymalnej
Tabela obliczeń
P[W] 0
0
R[Ω] ∞
0
7
6. Wyznaczenie mocy ogniwa w funkcji kąta padania
Tabela pomiarów i obliczeń
α[˚]
U[V]
I[A]
P[W]
7. Wzory
Sprawność badanego modułu
P
FF
max
⋅ U ⋅ I
U
P
OC
SC
η =
=
= FF ⋅ J
OC
⋅
=
max
E ⋅ S
E ⋅ S
SC
E
F ⋅ I
⋅ S
SC
Pmax = PMPP – maksymalna moc ogniwa [W] ( ang. MPP – Maximum Power Point)
E – natężenie promieniowania słonecznego [W/m2]
S- powierzchnia badanego modułu [m2]
FF – współczynnik wypełnienia (ang. Fill Factor)
UOC – napięcie ogniwa otwartego, nieobciążonego (ang. Open-Circuit Voltage) [V]
ISC – prąd zwarciowy (ang. Short-Circuit Current) [A]
JSC –gęstość prądu zwarcia [A/m2]
F – współczynnik zależny od wartości maksymalnej prądu zwarcia ogniwa
1000
W
F =
[
] I
2
SCmax – maksymalny prąd zwarcia podany przez producenta
I
m ⋅ A
SC max
Współczynnik wypełnienia FF
P
U
⋅ I
MPP
MPP
FF =
max
=
U
⋅ I
U
⋅ I
OC
SC
OC
SC
Ropt
2
U
R
MPP
=
opt
P max
8. Sprawozdanie
Sprawozdanie powinno zawierać:
Charakterystykę prądowo-napięciową badanego modułu I = f(U) z zaznaczonym
punktem MPP
Krzywą mocy, z zaznaczonym punktem mocy maksymalnej P = f(U)
Wykres P = f(R), z zaznaczonym Ropt
Wyznaczony współczynnik FF, oraz sprawność maksymalną modułu
Wykres η = f(P)
8
1. Sarniak M. – Podstawy fotowoltaiki – Oficyna Wydawnicza Politechniki
Warszawskiej 2008
2. Piotr Grygiel i Henryk Sodolski - Laboratorium Konwersji Energii - Wydział Fizyki
Technicznej i Matematyki Stosowanej, Politechnika Gdańska 2006
3. Ewa Klugmann-Radziemska – Fotowoltaika w teorii i praktyce - Wydawnictwo BTC
Legionowo 2010
9