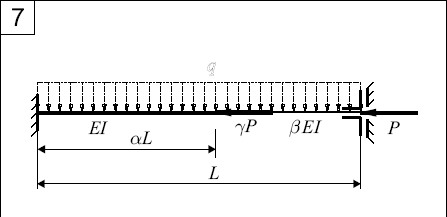
ZADANIE 6

Dla pręta pokazanego na rysunku wyznaczyć krytyczną wartość siły P oraz współczynnik wyboczeniowy µ. Wykorzystać kryterium energetyczne Timoshenki przyjmując jako postulowaną postać wyboczenia linię ugięcia belki wyznaczoną dla zadanego obciążenia rozłożonego q.

x − −− >

< − − − y

x = α

x =

3

,

0 2

y = 1− α = 8

,

0 2

α = 3

,

0 2

β = ,

0 6

γ =

1

,

1 28

2

2

M = M − qL kNm A

B

2

L = ,

5 22 m

2

EI = 1128 kNm 1 Postać wyboczenia

1.1 Równanie różniczkowe osi odkształconej I przedział

II przedział

0 ≤ x ≤ α L

0 ≤ y ≤ L − α L

2

q ⋅ y

M

=

+

⋅ − ⋅

M

= −

+

y ( y )

M

y ( x )

2

x

M

V

x

q

A

A

2

2

B

x

2

3

q ⋅ y

EI "

w ( x)

2

= q ⋅

− V ⋅ x − M

⋅ EI "

w ( y) =

− M

2

A

A

5

2

B

x

x

3

3

q ⋅ y

EI '

w ( x)

3

2

= q ⋅

− V ⋅

− M ⋅ x + C

⋅ EI '

w ( y) =

− M ⋅ y + C

A

A

1

6

2

B

2

5

6

4

2

3

q ⋅ y

y

EI (

w x)

4

3

2

x

x

M x

= q ⋅

− V

A

⋅

−

+ C ⋅ x + D

⋅ EI (

w y) =

− M ⋅

+ C ⋅ y + D

A

1

1

24

6

2

B

2

2

5

24

2

14

C = 0

1

w 0 = 0

I ( )

C = 0

2

'

D

w 0 =

I ( )

0

= 0

⇒

1

4

'

D

w 0 = 0

II ( )

= 0

,

0 3125 ⋅ qL

2

'

'

V = 1⋅ qL

w α

= −

− α

I (

L)

wII ( L

L)

A

2

'

M = − 3

,

0 613 ⋅ qL

w α

=

− α

I (

L) wII ( L

L)

A

2

M = 1

,

0 378 ⋅ qL

B

Kontrola w’(αL):

2

1

1

1

1

qx 3 − V x 2 − M x + C =

qx 3 −

x 2

1

− − 3

,

0 613

+ 0 = 0

,

0 6988

A

A

1

(

)

qL

x

6

2

6

2

EJ

2 Obciążenie krytyczne

2.1 Kryterium energetyczne Timoshenki

∫ EI ⋅( w"( x) 2 dx +∫ N ⋅( w'( x) 2 dx = 0

L

L

I przedział

1

2





w"( x) x

=

q ⋅

−1⋅ qL ⋅ x − (− 3

,

0 61 )

3 qL 2





EI 

2



1

3

2





w'( x)

x

x

=

q ⋅

−1⋅ qL



⋅

− (− 3

,

0 61 )

3 x ⋅ qL 2 + 0

EI 

6

2



N ( x) = ( 1

− − γ ) P = −1− ,128

I

(

) P

II przedział

1



3



w '

=

⋅

− 1

,

0 387 ⋅ + 0

II ( x )

y

q

y





6

.

0 EI 

6



1



2



w "

=

⋅

− 1

,

0 387

II

( x)

y

q





6

.

0 EI 

2



N ( x) = − P

II

2.2 Wartość krytyczna siły P

α ⋅ L

L −α ⋅ L

α ⋅ L

L −α ⋅ L

∫ EI ⋅ "2

w dx

β

γ

I

+ ∫ ⋅ EI ⋅ "2

w dy

II

− P ∫(1+ )⋅ '2

w dx

I

− P ∫ '2

w dy

II

= 0

0

0

0

0

0,32⋅ L

L −0,32⋅ L

0,32⋅ L

L −0,32⋅ L

∫ EI ⋅ "2

w dx

I

+ ∫ 6,

0 ⋅ EI ⋅ "2

w dy

II

− P ∫ ,228⋅ '2

w dx

I

− P ∫ '2

w dy

II

= 0

0

0

0

0

15

2

α L

2

 1  qx 2

0,32 L



1  qx 2



q 2 L 5

I =

EI

∫ 

− V ⋅ x ⋅ q ⋅ L − M xL



 dx = ∫

− xqL + 3

,

0 613 xL

dx





= ,

0 01719

1

EI

A

A

 2



EI





 2



EI

0

0

2

L−α L

2

−

 1  qy 2

L 0,32 L



6

,

1 6666667  qy 2



− q 2

3

L 5

I = ∫ β EI 

− M



 dy =

∫

− 1

,

0 387 dy





= 6

,

9 901⋅10

2

β

EI

B

 2



EI





 2



EI

0

0

2

2

α L

 1  qx

1

L



,

2 28  qx

1



− q L

I = ∫ 1+ γ 

− V ⋅ x ⋅ q ⋅ L − M xL + C



 dx = ∫

− x qL + 3

,

0 613 xL dx





= 5

,

1 9332 ⋅10

3

(

)

3

0,32

3

2

7

2

2

3

A

A

1

2

2

EI  6

2



EI





 6

2



EI

0

0

2

L−α L

3

L 0

− ,32

2

L

3

2

7

 1  qy



7

,

2 777779  qy



− q L

3

I = ∫ 

− M y + C



 dy =

∫

− 1

,

0 387 y dy





= 6

,

2 0749⋅10

4

B

2

2

2

β EI  6



EI





 6



EI

0

0

q 2 L 5

− q 2

3

L 5

(

01719

,

0

+ 6901

,

9

⋅10

I + I

1

2 )

EI

EI

EI

P =

=

= 3989

,

6

=

895

,

264

kr

( I + I

3

4 )

kN

− q 2

3

L 7

− q 2

3

L 7

L 2

59332

,

1

⋅10

+ 60749

,

2

⋅10

EI 2

EI 2

2

2

= π

µ

EI =

π

= ,

1 24193

2

Pkr ⋅ L

3

,

6 989

16