Wykład 1
1)
założenia przyjęte w Wytrzymałości materiałów
Ciągłość materiału. W materiale nie występują mikropęknięcia, pustki. Rozpatrywane materiałymożna uważać za continuum materialne.
Jednorodność materiału. Właściwości mechaniczne materiału nie są funkcjami położenia, czyli są jednakowe w każdym punkcie elementu konstrukcyjnego.
Izotropowość materiału. Właściwości mechaniczne materiału nie zależą od orientacji rozpatrywanej objętości elementarnej ciała.
Liniowa sprężystość materiału. Zakłada się, że do pewnej granicy obciążenia ciało zachowuje ciągłość struktury oraz, że istnieje jednoznaczny, bez naprężeniowy stan ciała, do którego badane ciało powraca, ilekroć zostaną usunięte siły zewnętrzne.
2)
postulaty jakie musi spełniać projektowana konstrukcja :
-Wytrzymałości albo bezpieczeństwa – konstrukcja powinna spełniać swoje zadanie techniczne z zadanym stopniem pewności, ze nie ulegnie zniszczeniu, przenosząc obciążenia do określonej wartości;
-Sztywności – konstrukcja powinna spełniać swoje zadanie techniczne, ulegając co najwyżej z góry zadanym wielkościom odkształceń, zachowując swój kształt;
-Ekonomii – konstrukcja powinna być wykonana i eksploatowana przy minimalnych możliwych kosztach finansowych;
-Estetyki i wartości architektonicznych – konstrukcja powinna być estetyczna i ładna.
3)
siły wewnętrzne generowane przez obciążenie czynne
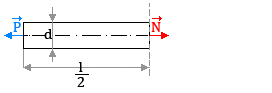
Na rysunku pokazano przykład ciała obciążono zewnętrznymi siłami czynnymi
ప i reakcjami ప.
4)
obliczanie sił wewnętrznych metodą przekrojów
W celu przeprowadzenia analizy równowagi układu czynnych sił obciążających i biernych sił reakcji generowanych w przekrojach elementów konstrukcyjnych w stereodynamice (wytrzymałości materiałów), stosuje się metodę przekrojów.
Po myślowym wykonaniu przekroju i odrzucenia nieinteresującej nas w danej chwili części konstrukcji, do przekroju wprowadzamy wewnętrzne siły reakcji, które zastępują oddziaływanie sił wewnętrznych z części odrzuconej i stanowią układ równoważący obciążenie zewnętrzne tego fragmentu konstrukcji. Jeżeli cały element konstrukcyjny jest w równowadze, to również w równowadze pozostania każda z jego części po dokonaniu przekroju. Parametr opisując gęstość rozdziału sił wewnętrznych na powierzchni przekroju, nazywamy naprężeniem.
5)
definicja naprężenia jako symetrycznego tensora drugiego stopnia
= ఙ
= ௫, ௬, ௭
௫
௫௬ ௫௭
ଵଵ ଵଶ ଵଷ
ఙ =
௬௫
௬
௬௭ ఙ = ଶଵ ଶଶ ଶଷ
௭௫ ௭௬
௭
ଷଵ ଷଶ ଷଷ
gdzie:
௫, ௬, ௭ − Składowe tensora naprężenia w analizowanym przekroju,
௫, ௬, ௭,
ଵ, ଶ, ଷ − Składowe normalne tensora naprężenia na ściankach bocznych czworościanu, ௫௬, ௫௭, ௬௫,
௬௭, ௭௫, ௫௬,
ଵଶ, ଵଷ, ଶଵ,
ଶଷ, ଷଵ, ଷଶ − Składowe styczne tensora naprężenia na ściankach bocznych czworościanu.
6)
odkształcenia bezwzględne i względne
Odkształcenie bezwzględne - różnica końcowego i początkowego wymiaru odkształconego ciała lub jego elementu
∆ = ଵ −
Odkształcenie względne - odkształcenie bezwzględne odniesione do wymiaru początkowego
∆
ଵ =
Wykład 2
1.
prawo Hooke’a
prawo mechaniki określające zależność odkształcenia od naprężenia. Głosi ono, że odkształcenie ciała pod wpływem działającej na nie siły jest wprost proporcjonalne do tej siły. Współczynnik między siłą a odkształceniem jest często nazywany współczynnikiem (modułem) sprężystości.
∆
=
=
Gdzie :
F – siła rozciągająca,
S – pole przekroju,
Δl – wydłużenie pręta,
l – długość początkowa.
2.
granica wytrzymałości
Jest to maksymalne naprężenie uzyskane w próbie wytrzymałościowej.
௫
=
Gdzie:
Pmax – maksymalna siła
F0– powierzchnia przekroju przed obciążeniem
naprężenie dopuszczalne
Naprężenia, które mogą występować w materiale bez obawy naruszenia warunku wytrzymałości i warunku sztywności
=
kr - naprężenie dopuszczalne przy rozciąganiu,
kc - naprężenie dopuszczalne przy ściskaniu,
kg - naprężenie dopuszczalne przy zginaniu,
kt - naprężenie dopuszczalne przy ścinaniu,
ks - naprężenie dopuszczalne przy skręcaniu.
4.
współczynnik bezpieczeństwa
Liczbę n oznaczającą, ile razy naprężenie dopuszczalne jest mniejsze od granicy wytrzymałości (dla materiałów kruchych) lub od granicy plastyczności (dla materiałów plastycznych), nazywa się współczynnikiem bezpieczeństwa.
W przypadku rozciągania materiałów kruchych
ோ
=
Dla materiałów plastycznych
ோ
=
gdzie: Rm - granica wytrzymałości na rozciąganie, otrzymana w wyniku prób wytrzymałościowych, Re -
granica plastyczności.
5.
współczynnik odkształcalności podłużnej (moduł Younga E)
Moduł sprężystości podłużnej (moduł Young’a) E określa proporcjonalność między σ i ε w obszarze 0→ R
H , i definiowany jest jako:
= =
Moduł Young’a charakteryzuje opór, jaki materiał stawia wydłużeniu sprężystemu. Zależność z reguły przedstawiana jest w postaci prawa Hooke'a
࣌
=
ࡱ
6.
współczynnik odkształcalności poprzecznej (Współczynnik Poissona n) Liczba Poisson’a ν określa proporcjonalność wzajemnie do siebie prostopadłych wydłużeń liniowych
௬
௭
= −
= −
௫
௫
ఔఙ
Zależność jest częściej podawana w postaci
ೣ
௬ = ௭ = −௫ = −
ா
1)
ściskanie i rozciąganie
Wytrzymałość próbki na ściskanie bądź rozciąganie :
ೌೣ
ೌೣ
=
=
=
ி
=
బ
ிబ
Natomiast warunek bezpieczeństwa porównuje rzeczywistą wartość naprężenia z wartością dopuszczalną
ࡼࢇ࢞
ࡼࢇ࢞
ࢉ =
≤
≤
ࡲ
ࢉ ࢉ =
࢘
ࡲ
2)
znak składowej tensora naprężenia
prowadzając w kartezjańskim układzie współrzędnych w dowolnym punkcie[1] ciała, w którym występuje stan naprężenia, trzy przekroje prostopadłe do osi współrzędnych dowolnie zorientowanego prostokątnego układu współrzędnych, można wyznaczyć dziewięć składowych stanu naprężenia, są to kolejno: σx, τxy, τxz, σy, τyx, τyz, σz, τzx, τzy.
Jeżeli zwrot wektora naprężenia normalnego skierowany jest od punktu, naprężenie normalne przyjmuje wartość dodatnią i nazywane jest naprężeniem rozciągającym. W przeciwnym razie jest naprężeniem ściskającym.
3)
zagadnienie jednokrotnie statycznie niewyznaczalne (jednokrotnie hiperstatyczne) przy ściskaniu i rozciąganiu
Przez określenie zagadnienia statycznie niewyznaczalne definiujemy zadanie w którym liczba niewiadomych jest większa przynajmniej o jeden od liczby niezależnych równań równowagi statycznej.
Układ izostatyczny – układ w którym liczba niewiadomych jest równa liczbie równań równowagi Układ hiperstatyczny – układ o większej liczbie niewiadomych w stosunku do liczby równań równowagi Stopień statycznej niewyznaczalności – jest równy liczbie będącej różnicą między liczbą niewiadomych i liczbą równań równowagi.
Brakujące równanie, równania będą równaniami fizycznymi porównującymi odpowiednie wielkości odkształceń .
Rozwiązanie zagadnienia statycznie niewyznaczalnego polega na obliczeniu wartości sił lub naprężeń w poszczególnych przekrojach elementu konstrukcyjnego.
4)
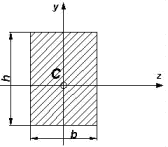
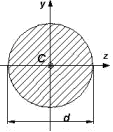
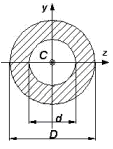
momenty bezwładności przekrojów belek i wałków
࢈ࢎ
=
࢈ࢎ
=
࣊ࢊ
࣊ࢊ
=
=
࣊ࢊ
࣊ࢊ
=
=
࣊(ࡰିࢊ)
࣊(ࡰିࢊ)
=
=
࣊(ࡰିࢊ)
࣊(ࡰିࢊ)
=
ࡰ
=
ࡰ
5)
wskaźnik przekroju
współczynnik wytrzymałości przekroju na zginanie
"
!
௫
௫ =
#௫
Gdzie:
IX- geometryczny moment bezwładności względem osi x pokrywającej się z osią obojętną przekroju emax - maksymalna odległość skrajnych włókien od osi obojętnej współczynnik wytrzymałości przekroju na skręcanie
2"
! =
$
Gdzie:
I –moment bezwładności
D – średnica przekroju
Wyszukiwarka
Podobne podstrony:
wm sciaga, IŚ Tokarzewski 27.06.2016, IV semestr COWiG, Wymiana Masy, WM XYZ, wykład-wm, Wymiana mas
Biotechnologia teoria wykład 1
Wykładz Ceramika budowlana teoria wykład
DRUK, Szkoła, penek, Przedmioty, Nawigacja, Teoria, wykłady II sem o6-07, Wydruk
Teoria?zpieczeństwa wykład 2
Analiza matematyczna egzamin I (lato) calki teoria, Wykłady - Studia matematyczno-informatyczne
teoria i wykłady-Prawo, TiR-materiały na zajęcia i kolosy, Prawo w turystyce
Analiza matematyczna I (lato) teoria, Wykłady - Studia matematyczno-informatyczne
TEORIA?ZPIECZEŃSTWA WYKŁAD 4
Teoria?zpieczeństwa wykład 1 (1)
Egzamin Teoria Wykład 01 (10) 14 (15) v 0 12 63 BETA
Analiza matematyczna 1 teoria wyklady id 60885
Ineichen Hermeneutyka jako teoria wykładni tekstów(1)
Ruciński A Teoria Grafów 1, wyklad6
rozwojowka slajdy, Wyklad 5 Srednia doroslosc teoria czasowa
Ruciński A Teoria Grafów 1, wyklad1
więcej podobnych podstron