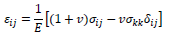1.

D

laczego tylko układy geometrycznie niezmienne mogą być analizowane statycznie?

Analiza statyczna prowadzona jest tylko dla ciał znajdujących się w równowadze a takim układem jest jedynie układ geometrycznie niezmienny. Mechanizmy liczy się dynamicznie za pomocą zasady dynamiki Newtona.

2. K

iedy 2 tarcze są połączone w sposób geometrycznie niezmienny, a kiedy 3 tarcze?

WKW geometrycznie niezmiennego połączenia dwóch tarcz jest połączenie ich trzema prętami, których kierunki nie przecinają się w jednym pkt /także niewłaściwym/

WKW geometrycznego niezmiennego połączenia trzech tarcz jest połączenie ich, kazda z każdą, dwoma prętami, których kierunki nie przecinają się w pkt leżących na jednej osi / pkt niewspółliniowe/. Dwa z nich mogą być niewłaściwe.

3. Cz

y istnieje związek pomiędzy statyczną wyznaczalnością a geometryczną niezmiennością układu? Odpowiedź krótko uzasadnij.

Układy statycznie niewyznaczalne muszą być geometrycznie niezmienne.

4. P

rzedstaw twierdzenie o równoważności układów sił wewnętrznych i zewnętrznych.

(ZI) + (ZII)=0

(ZI) + (WI) = 0

(ZII) + (WII) =0

(WI) + (WII)=0

(WII) = (ZI) → S(WII) = S (ZI) ; Mo(WII) = Mo(ZI)

(WI) = (ZII) → S(WI) = S (ZII) ; Mo(WI) = Mo(ZII)

5. J aki związek istnieje pomiędzy układem sił wewnętrznych a siłami przekrojowymi?

Siły przekrojowe to siły wewnętrzne zredukowane w układzie własnym przekroju

6. P

odaj definicje pręta kratowego. Z jakim układem sił wewnętrznych mamy do czynienia?

Pręt kratowy - pręt prosty połączony przegubowo na obu końcach i obciążony jedynie siłami skupionymi w przegubach; układ sił wewnętrznych – jedna stała siła podłużna, której znak ważniejszy jest od wartości 7. N

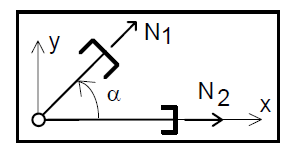
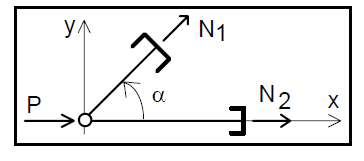
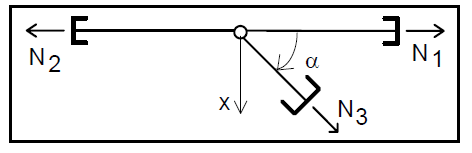
arysuj 3 twierdzenia o prętach zerowych kratownic.

a) N1, N2 = 0

b) N1 = 0

c) N3 = 0

8. J akie właściwości posiada macierz przejścia?

Macierz przejścia:

•

jest ortogonalna

•

jest unormowana

•

ogólnie nie jest symetryczna;

•

jedynie 3 elementy macierzy przejścia są liniowo niezależne

•

wiesze macierzy przejścia to współrzędne wersorów nowego układu wyrażone w układzie starym

•

kolumny macierzy przejścia to współrzędne wersorów starego układu wyrażone w układzie nowym

9. Z

apisz wzór definiujący tensor II rzędu (wystarczy jedna z kilku możliwości).

Tensor II rzędu:

tij ≡ αikαjltkl

αik, αjl – cosinusy kątów między osiami i – k, j- l

10. P

rzedstaw interpretację składowych macierzy naprężenia: na przekątnej głównej i poza nią.

Podaj ich wymiar.

na przekątnej głównej macierzy znajdują się naprężenia normalne, a poza przekątna naprężenia styczne. Indeks przy naprężeniu normalnym pokazuje oś układu, do której to naprężenie jest równoległe. Indeksy przy naprężeniu stycznym pokazują: pierwszy płaszczyznę na której ono występuje, a drugi oś układu do której to naprężenie jest równoległe. Wymiar [Pa]

11. N

a czym polega analiza stanu naprężenia w punkcie?

Analiza stanu naprężeń polega na poszukiwaniu takiego kierunku cięcia względem którego naprężenia są największe. Szukamy trzech szczególnych płaszczyzn przekroju, prostopadłych do osi układu współrzędnych względem, których naprężenia będą największe a odkształcenia tylko liniowe

12. N

arysuj koła Mohra dla przypadku 2D: σ 1 =15, σ2=

5 ( 1,2

– kierunki własne) . Ile wynoszą

ekstremalne naprężenia styczne?

Wartości ekstremalnych naprężeń stycznych wynosi 7,5

13. Z

apisz ogólny wzór dla statycznych warunków brzegowych.

σij ∙ nj = pi

σij – wektor naprężenie tuż pod „brzegiem”

pi - wektor obciążenia

14. J ak wyglądają kierunki główne jeśli wartości własne: a) są różne, b) dwie są sobie równe, wszystkie trzy są równe

a) kierunki są do siebie prostopadłe;

b) istnieje cała płaszczyzna kierunków głównych;

c) istnieje cała przestrzeń kierunków głównych;

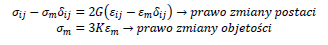
15. P

odaj wzory na wartości własne i kierunki główne dla przypadku 2D.

Wartości własne

σ1,2 = (σx + σy)/2 (+/-) √ ((σx + σy)/2)2 + (τxy)2)

Kierunki główne

tg άi = (σi – σx) / τxy

16. P

odaj interpretację składowych macierzy odkształcenia. Podaj ich wymiar.

ε11 ε12 ε13

Tε =

ε21 ε22 ε23

ε31 ε32 ε33

Na przekątnej głównej leżą odkształcenia normalne /liniowe/ - ε11, ε22, ε33.

Pozostałe to połowa zmiany kąta między osiami x, y / odkształcenia kątowe/

Wielkość jest bezwymiarowa [1].

17. J aka jest różnica pomiędzy jednorodnością a izotropią materiału?

Jednorodność odnosi się do konkretnego punktu natomiast izotropowość do badanego kierunku (większej ilości punktów).

18. Co t

o znaczy że materiał jest sprężysty?

Jeżeli materiał jest sprężysty tzn. że po zdjęciu przyłożonego obciążenia powraca do pierwotnej konfoguracji, kształtu, wymiarów. A więc zmiany, które zasły pod wpływem przyłożonego obciążenia są w pełni odwracalne.

19. Zapisz symbolicznie (macierzowo) trzy postaci równań Hooke’a.

I postać równania Hook’a:

II postać równania Hook’a:

III postać równania Hook’a:

20. U

zasadnij nazwy: prawo zmiany postaci i prawo zmiany objętości.

Nazwy równań wynikają z interpretacji geometrycznej tensora odkształcenia: zmianę postaci opisuje dewiator tensor odkształcenia / punkt nie zmienia objętości, Dewiator naprężeń powoduje odkształcenia kątowe, czyli zmianę postaci/ a zmianę objętości opisuje akcjator tensor odkształcenia./Obciążenia ciała określone aksjatorem (równomierne rozciąganie lub ściskanie) nie powoduje zmiany postaci. Ciało zwiększa natomiast swoją objętość/

21. W

ymień podstawowe stałe materiałowe dla materiału Hooke’a.

Stałe materiałowe:

•

Moduł sprężystości podłużnej Younga: E [Pa]

•

Współczynnik Poissona: v [1]

• Stała Lamego: λ [Pa]

•

Moduł ściśliwości objętościowej Helmholtza: K [Pa]

•

Moduł odkształcenia postaciowego Kirchhoffa G [Pa]

22. O

czym mówi zasada de Saint-Venanta?

Jeżeli na niewielkiej części powierzchni w stosunku do całkowitej powierzchni ciała działa obciążenie i obciążenie to zastąpimy dowolnym innym jednak statycznie mu równoważnym, to istnieje taki przekrój tego ciała dostatecznie odległy od miejsca przyłożenia obciążenia że równice w naprężeniach, odkształceniach i przemieszczeniach pochodzące od obu przypadków obciążenia są dowolnie małe.

23. Co w

ynika z istnienia osi symetrii przekroju?

To że oś symetrii jest osią główną centralną.

24. Co w

ynika z istnienia więcej niż dwóch osi symetrii przekroju?

Każda oś centralna jest główna.

25. Roz

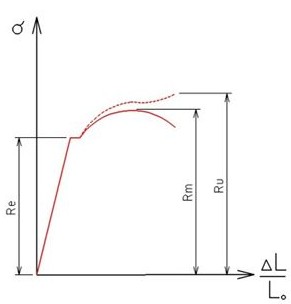
ciąganie – przedstaw interpretację modułu Younga i liczby Poissona ν .

Moduł Younga

Współczynnik Poissona (ν)- Jest stosunkiem odkształcenia poprzecznego do odkształcenia podłużnego przy osiowym stanie naprężenia.

26. O

mów założenie geometrycznej liniowości dla zadań statycznie niewyznaczalnych.

Zakładany, że pręty ulegają wydłużeniu ale kąty nie ulegają zmianie co pozwala na wyznaczenie brakujących równań statycznych.

27. O

d czego zależy krzywizna pręta zginanego?

Krzywizna pręta zginanego zależy od wielkości momentu zginającego i od sztywności zginania.

28. W

ymień dwa podstawowe typy warunków projektowania.

•

Warunek na stan graniczny nośności: np. na wytrzymałość

•

Warunek na stan graniczny użytkowania: np. sztywność

29. Z

ginanie ukośne: jak ma się kierunek osi obojętnej do kierunku wypadkowego momentu zginającego?

oś obojętna odchyla się od kierunku momentu zawsze w stronę tej osi bezwładności względem której moment bezwładności jest mniejszy , przechodzi przez środek ciężkości

30. Zginanie ukośne: jak najprościej określić naprężenia normalne w dowolnym punkcie przekroju?