2008-11-19

1

Mechanika i Wytrzymałość

Materiałów

Imię, nazwisko i tytuł prowadzącego:

Mieczysław Łuźniak, dr inż.

pok. 236B, bud. D – 2,

tel. (071) 320 39 41,

e-mail: mieczyslaw.luzniak@pwr,wroc.pl

Materiały do pobrania na stronie:

http://www.iios.pwr.wroc.pl/tablica_ogl/luzniak_m/ogloszenia/pobierz.php

2008-11-19

2

Zaliczenie kursu

KOLOKWIUM

Data: ??

2008-11-19

3

Literatura

•Mechanika ogólna
– Jerzy Leyko

•Statyka i wytrzymałość materiałów
– Jerzy Rżysko

oraz każda inna książka do statyki
i wytrzymałości materiałów dowolnego
autora

2008-11-19

4

Mechanika jako nauka ścisła powstała w Grecji i Egipcie w IV wieku p.n.e. Jej twórcami byli Arystoteles (384 - 322 p.n.e.) i
Archytas z Tarentu (IV wiek p.n.e.). Prace ich dotyczyły maszyn prostych, stosowanych w technice uzbrojenia i budownictwie.
Punktem zwrotnym w rozwoju mechaniki były prace Archimedesa (287 - 212 p.n.e.). Ustanowił on prawa składania i rozkładania
sił równoległych, teorię dźwigni oraz określił środki ciężkości różnych figur geometrycznych i brył. Od Ptolemeusza - Klaudiusza (II
wiek n.e.) aż do czasów Leonarda da Vinci (1452 - 1519) wystąpił pewien zastój w rozwoju mechaniki. Leonardo da Vinci
zajmował się zagadnieniami dotyczącymi równi pochyłej, tarcia i bloków. Jemu należy przypisywać sformułowanie prawa
równoległoboku i wprowadzenie pojęcia momentu siły.

Nowe problemy układów odniesienia w mechanice postawił polski astronom Mikołaj Kopernik (1473 - 1543), autor słynnego

dzieła "De Revolutionibus Orbitum Coelestium" i twórca zasady równoważności ruchów względnych w układzie heliocentrycznym.
Dalszy postęp w rozwoju mechaniki jest związany z Galileuszem (1564 - 1642), który wprowadził pojęcie przyspieszenia,
opracował prawo bezwładności, prawa ruchu w polu ciężkości, zasady zachowania prac w maszynach prostych, rozwiązał
problem wahadła etc.

Trwałe miejsce w historii mechaniki mają również: Johan Kepler (1571 - 1630), który sformułował trzy prawa ruchu

planetarnego i Kartezjusz (1596 - 1650), który wprowadził prostokątny układ osi współrzędnych, zasadę prac wirtualnych i
rozwiązania rachunkowe zagadnień statycznych. Natomiast zasługą Christiana Huygensa (1629 - 1695) jest określenie pojęcia
reakcji, opracowanie teorii wahadła fizycznego i rewersyjnego, przyspieszenia w ruchu krzywoliniowym oraz uderzenia
sprężystego.

Wielką postacią mechaniki jest Isaac Newton (1642 - 1727), który zebrał i uporządkował naukę mechaniki w epokowym dziele

pt. "Philosophiae naturalis principia mathematica", dając podstawy mechaniki klasycznej, opartej ściśle na faktach
doświadczalnych. Odkrył prawa powszechnego ciążenia i klasycznej dynamiki. Jego rozwiązania dotyczą mechaniki punktu i
układu swobodnego.

Uczonym, który w zasadzie zakończył opracowanie praw statyki, był Pierre Varignon (1654 - 1722). Pojęcie energii kinetycznej

i metody jej zastosowania wprowadził Jan Bernoulli (1667 - 1748). Inni wybitni uczeni to: Michał Łomonosow (1711 - 1765) -
twórca zasady zachowania masy, Leonard Euler (1707 - 1783) - wprowadził analityczne metody rozwiązywania zagadnień ruchu,
mechaniki ciała sztywnego, obrotu ciała sztywnego wokół punktu nieruchomego etc., Jean D'Alembert (1717 - 1783) - odniósł
prawa statyki do dynamiki, Ludwig Lagrange (1737 - 1813) - twórca mechaniki analitycznej, Pierre Laplace (1743 - 1827) -
zajmował się mechaniką ciał niebieskich, Michał Ostrogradski (1801 - 1861) i William Hamilton (1805 - 1865) - twórcy zasad
wariacyjnych.

Uzupełnieniem mechaniki jest mechanika kwantowa, którą zapoczątkowali: Max Planck (1858 - 1947), Erwin Schrödinger

(1887 - 1961) i Paul Dirac (ur. 1902). Twórcą mechaniki relatywistycznej, opartej na teorii względności, jest Albert Einstein
(1879 - 1955).

Spośród polskich uczonych szczególnie zasłużonych w rozwoju mechaniki należy wymienić: Maksymiliana Tytusa Hubera i

Stefana Banacha.

2008-11-19

5

Zakres wykładu 

• zasady statyki, siła, moment, więzy.
• układy sił, redukcja, warunki równowagi.
• siły zewnętrzne i wewnętrzne: kratownice, belki,

ramy, obliczanie cięgien.

• geometria mas, momenty bezwładności

powierzchni płaskich.

• tarcie.
• określanie własności mechanicznych materiałów.
• analiza

jednoosiowego

i

płaskiego

stanu

naprężenia, rozciągania i ściskania.

2008-11-19

6

Zakres wykładu 

• obliczenia wytrzymałościowe prętów prostych,

rozciąganych i ściskanych.

• zginanie proste, ukośne i z uwzględnieniem

naprężeń stycznych.

• wytrzymałość złożona, hipotezy

wytrzymałościowe.

• zbiorniki cienkościenne.
• wyboczenie, ścinanie, skręcanie.
• zmęczenie materiału.

2008-11-19

7

Zakres wykładu 

• energia odkształcania sprężystego

• ruch punktu na płaszczyźnie, ruch obrotowy

i płaski, ruch złożony punktu. .

• doświadczalna analiza naprężeń.

• podstawy dynamiki.

2008-11-19

8

Efekty kształcenia

• rozumienia ogólnych praw ruchu i

równowagi ciał materialnych oraz zjawisk
fizycznych, którym podlegają odkształcane
ciała stałe poddane działaniu obciążeń
zewnętrznych;

• stosowania wiedzy z zakresu mechaniki i

wytrzymałości materiałów w projektowaniu
urządzeń dla potrzeb inżynierii środowiska.

2008-11-19

9

Podstawowe pojęcia i założenia

• Punkt materialny

• Ciało doskonale sztywne

• Siła skupiona

• Siła powierzchniowa

• Siła objętościowa

2008-11-19

10

Podstawowe pojęcia i założenia

Zasady Newtona

• Punkt materialny, na który nie działa żadna siła, pozostaje

w spoczynku lub porusza się ruchem jednostajnym po linii
prostej.

• Przyspieszenie punktu materialnego jest proporcjonalne do

siły działającej na ten punkt i ma kierunek siły.

• Siły wzajemnego oddziaływania dwóch punktów

materialnych są równe co do wartości i są przeciwnie
skierowane wzdłuż prostej łączącej oba punkty.

2008-11-19

11

Jednostki masy i siły

• Od 30.12.1966 w Polsce obowiązuje

międzynarodowy układ jednostek SI

Długość

– [m]

Czas

– [s]

Masa

– [kg]

Siła

– [N]

2

1

1

1

s

m

kg

N





2008-11-19

12

Aksjomaty statyki (1)

• Dwie siły mające jedną linię działania,

jednakowe moduły i przeciwne zwroty
stanowię układ równoważny zeru lub
inaczej układ zerowy

2008-11-19

13

Aksjomaty statyki (2)

• Ruch swobodnego ciała sztywnego nie

ulegnie zmianie, jeśli do działającego
układu sił dodamy lub od niego odejmiemy
układ sił równoważny zeru

2008-11-19

14

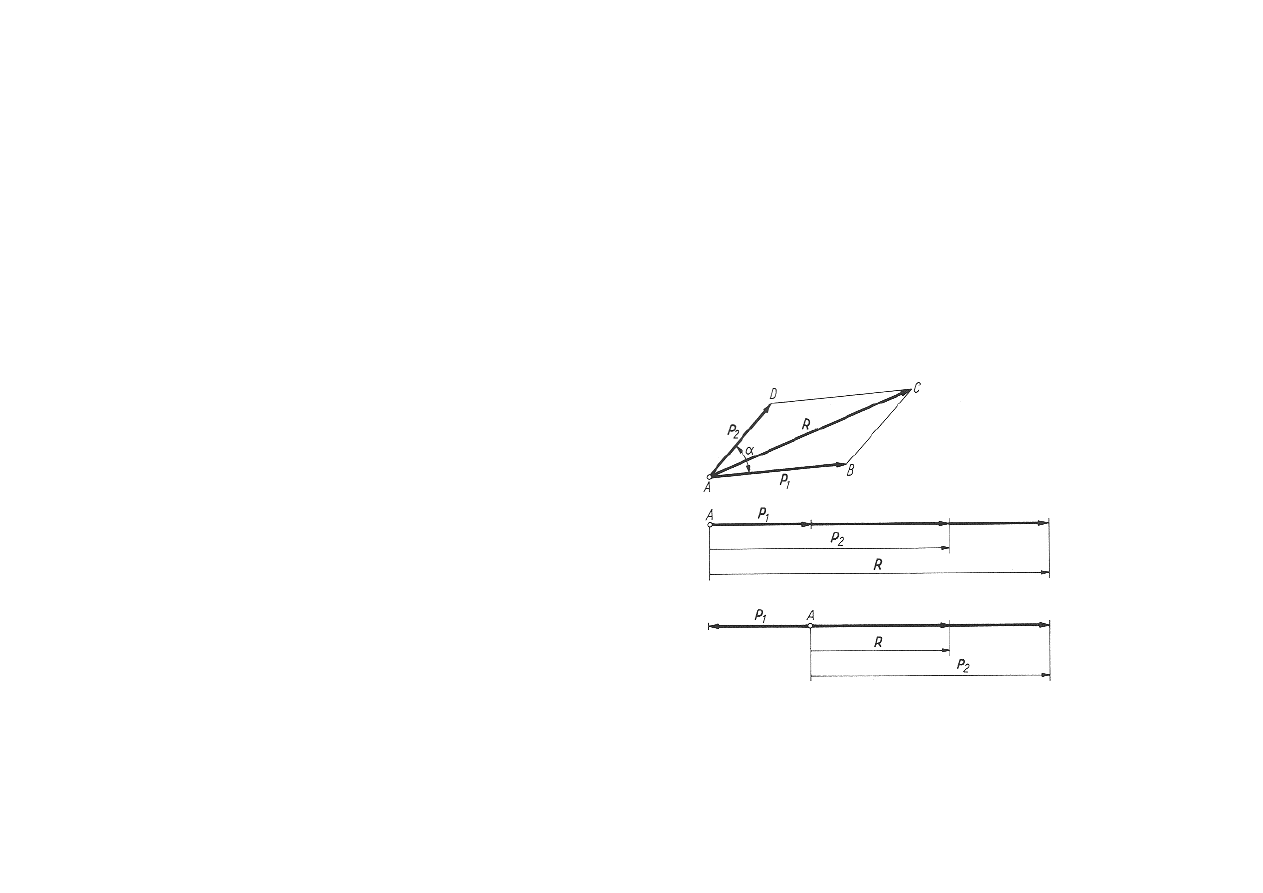
Aksjomaty statyki (3)

• Wypadkowa dwóch sił

działających w jednym
punkcie ciała sztywnego
przyłożona jest w tym
punkcie i jest siłą o
module równym
odpowiedniej przekątnej
równoległoboku i leży
na tej przekątnej

2008-11-19

15

Aksjomaty statyki (4)

• Siły, którymi działają na siebie wzajemnie

dwa ciała, mają równe moduły, są
skierowane wzdłuż jednej prostej i
zwrócone są w przeciwne strony

2008-11-19

16

Aksjomaty statyki (5)

• Jeśli ciało odkształcalne znajduje się w

równowadze pod działaniem pewnego
układu sił, to również zostanie w
równowadze ciało nieodkształcalne
identyczne z poprzednim, pod działaniem
tego samego układu sił

Aksjomat nie działa w drugą stronę

2008-11-19

17

Aksjomaty statyki (6)

• Każde ciało nieswobodne można

rozpatrywać jako ciało swobodne, jeśli
oswobodzimy je myślowo z więzów,
zastępując ich działanie siłami reakcji

2008-11-19

18

Stopnie swobody

• Stopniem swobody nazywa się możliwość

wykonania ruchu ciała niezależnego od innych
ruchów.

• Punkt materialny ma na płaszczyźnie dwa, a w

przestrzeni trzy stopnie swobody.

• Ciało doskonale sztywne ma na płaszczyźnie trzy,

a w przestrzeni sześć stopni swobody.

2008-11-19

19

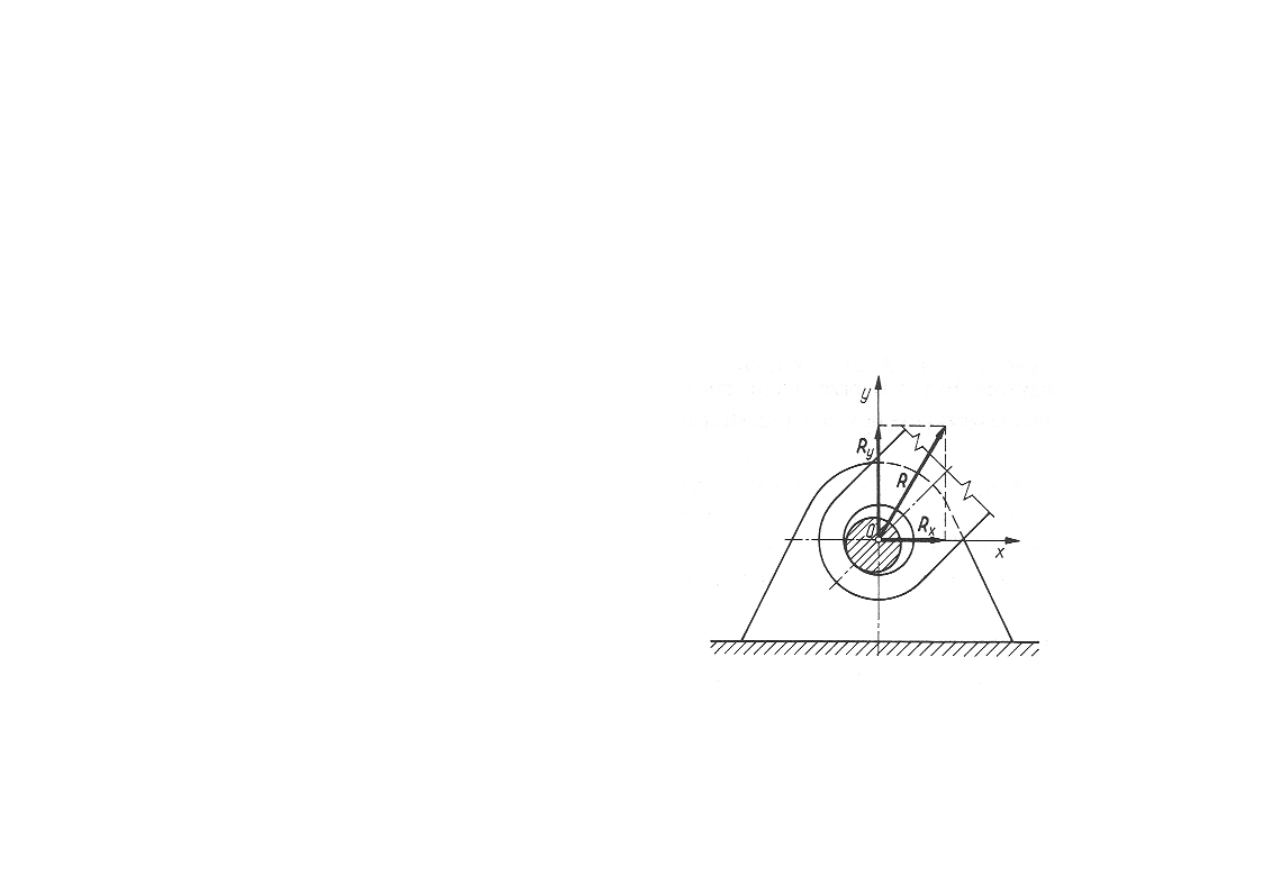
Więzy

Przegub walcowy.

Ciało sztywne jest osadzone na
walcowym sworzniu przechodzącym przez
kołowy otwór wykonany w tym ciele. Po
pominięciu siły tarcia jako małej w
porównaniu z siłą normalną R do
powierzchni styku linia działania tej reakcji
będzie przechodziła przez oś sworznia.
Występujące dwie reakcje R

x

i R

y

stanowią

dwie niewiadome i umożliwiają
wyznaczenie wartości reakcji R i jej
kierunku.

2008-11-19

20

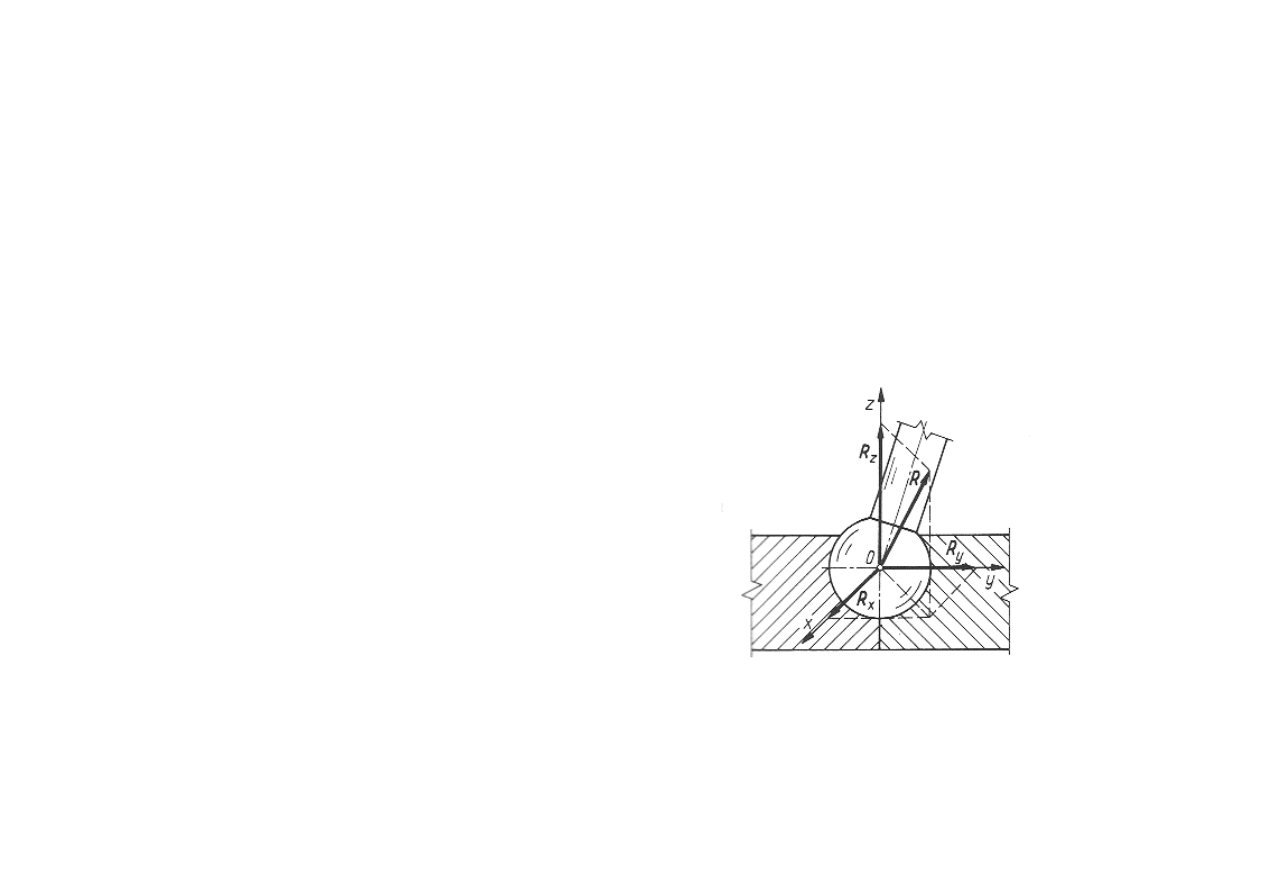
Więzy

Przegub kulisty

W celu unieruchomienia punktu podparcia
w przestrzeni stosuje się przeguby kuliste,
które krępują swobodę przesunięć, ale
umożliwiają obrót wokół dowolnej osi. Ich
zakończenie jest wykonane w kształcie
kuli, która jest osadzona w łożysku
kulistym. W wyniku pominięcia sił tarcia w
przegubie kulistym powstaje reakcja R o
dowolnym kierunku w przestrzeni,
przechodząca przez środek kuli i mająca
trzy niezależne składowe R

x

, R

y

i R

z

.

2008-11-19

21

Więzy

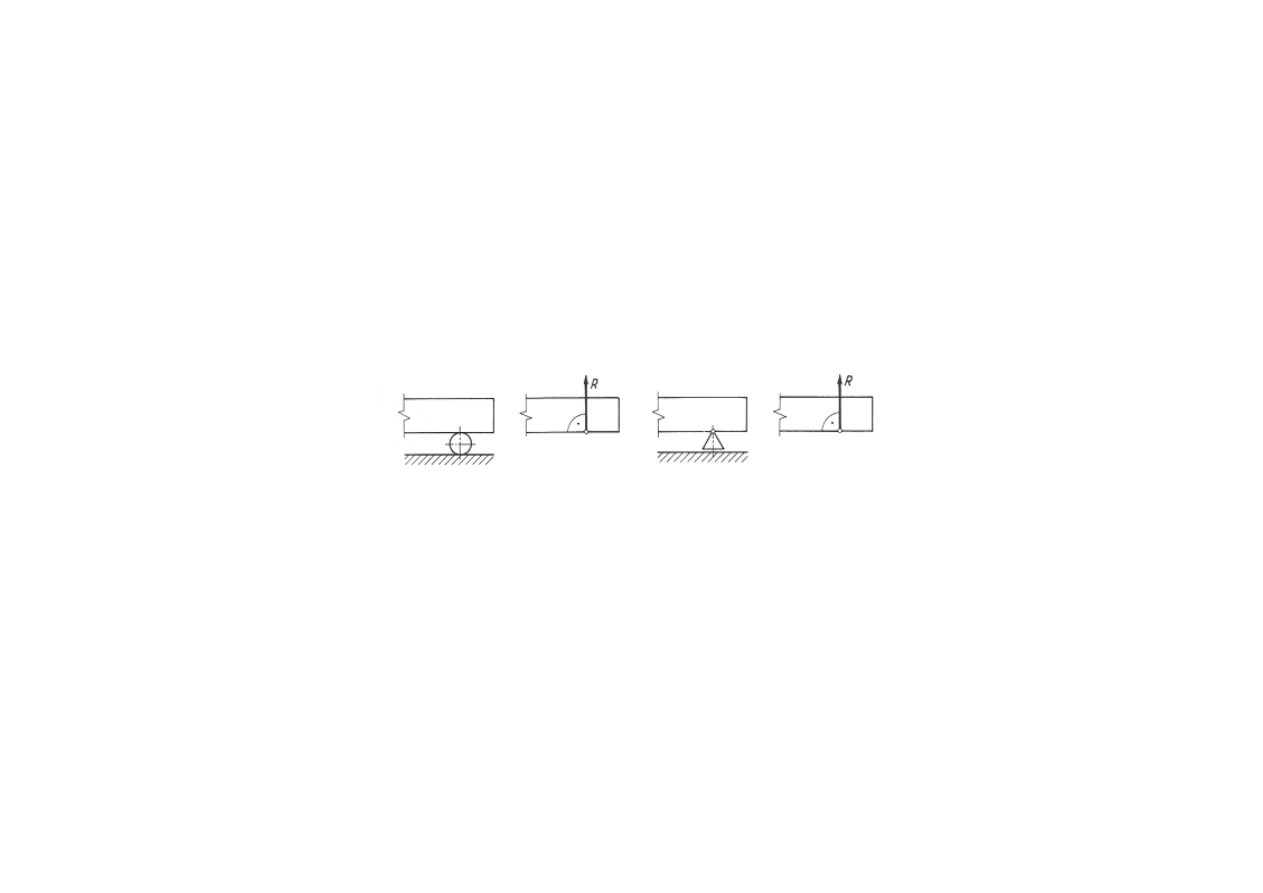
Podpora przegubowa przesuwna (rolkowa).

W przypadku zastosowania podpory przegubowej stałej koniec podparcia
ciała sztywnego może się obracać dookoła osi przegubu, ale nie może
się przemieszczać w dwóch kierunkach. Przy założeniu, że w przegubie
nie ma tarcia, linia działania reakcji R przechodzi przez punkt A. Powstają
dwie niezależne od siebie składowe reakcje R

x

iR

y

. Rozważając podporę

przegubową stałą w przestrzeni należy zauważyć, że koniec podparcia B
nie może się przemieszczać w trzech kierunkach i dlatego występują trzy
niezależne składowe reakcje R

x

, R

y

iR

z

.

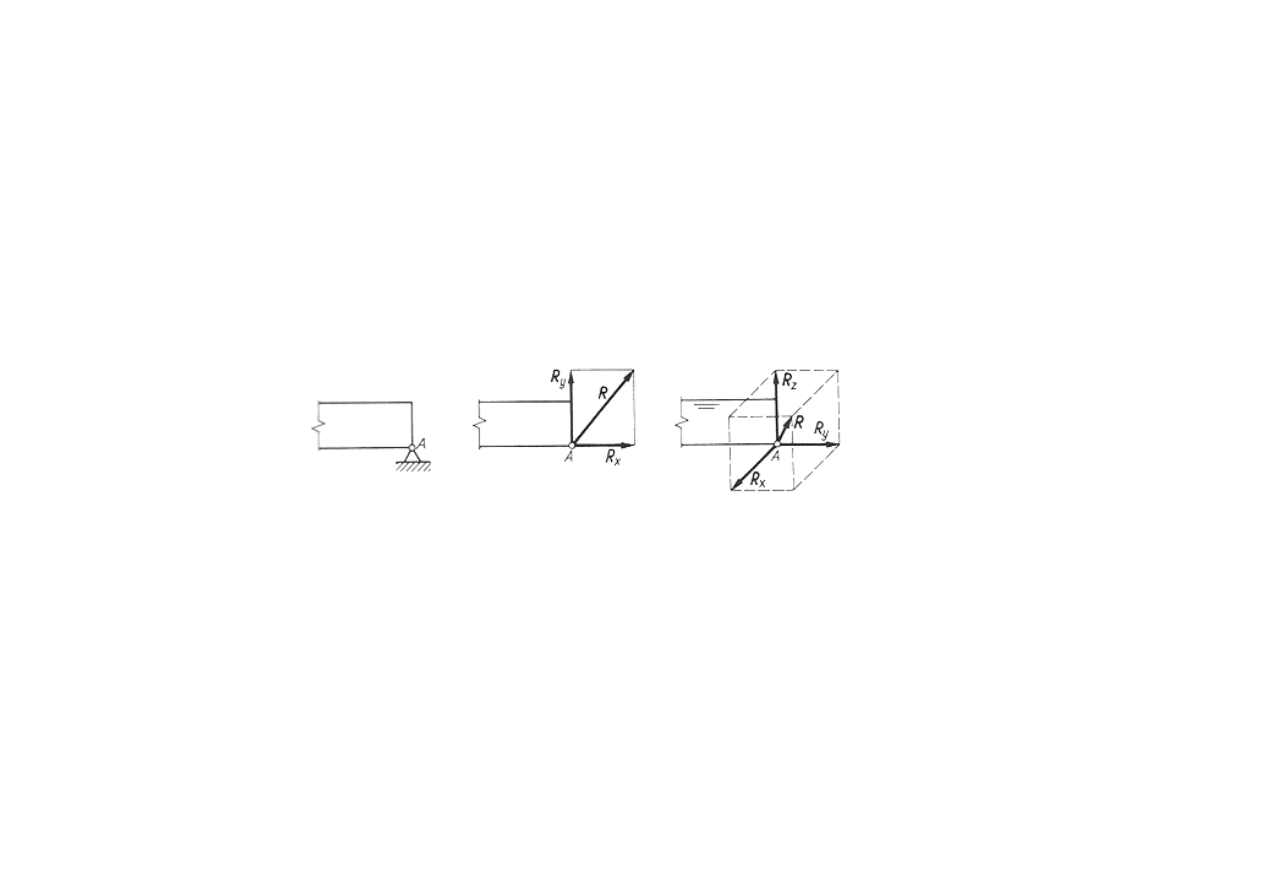
2008-11-19

22

Więzy

Podpora przegubowa stała.

W przypadku zastosowania podpory przegubowej stałej koniec podparcia
ciała sztywnego może się obracać dookoła osi przegubu, ale nie może
się przemieszczać w dwóch kierunkach. Przy założeniu, że w przegubie
nie ma tarcia, linia działania reakcji R przechodzi przez punkt A. Powstają
dwie niezależne od siebie składowe reakcje R

x

i R

y

. Rozważając podporę

przegubową stałą w przestrzeni należy zauważyć, że koniec podparcia B
nie może się przemieszczać w trzech kierunkach i dlatego występują trzy
niezależne składowe reakcje R

x

, R

y

i R

z

.

2008-11-19

23

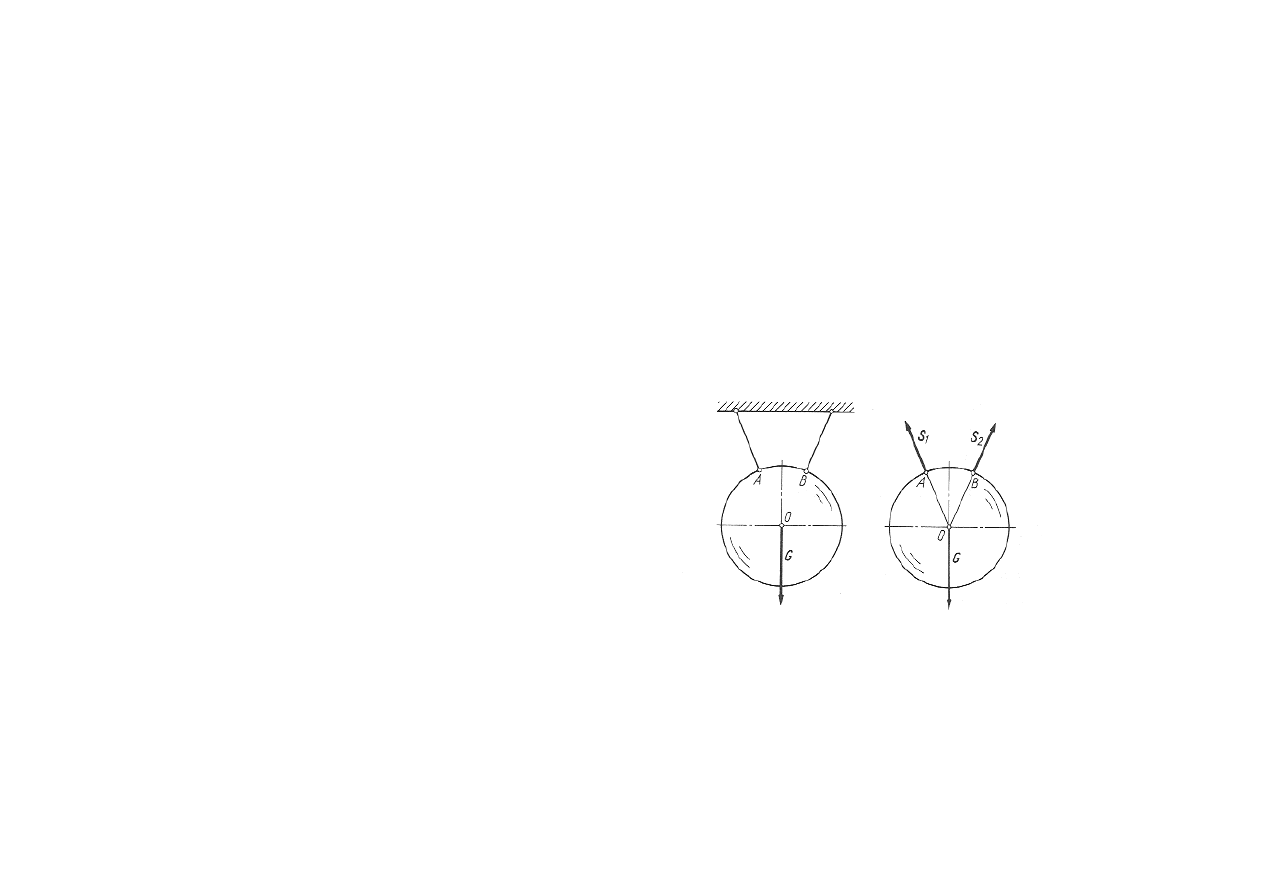
Więzy

Zawieszenie na cięgnach wiotkich.

Podwieszenie ciała za pomocą wiotkich
cięgien stwarza tzw. podpory kierunkowe
jednostronne, bo cięgna mogą być tylko
rozciągane. Reakcje S

1

i S

2

działają na ciało

wzdłuż tych cięgien, zgodnie z rysunkiem.

2008-11-19

24

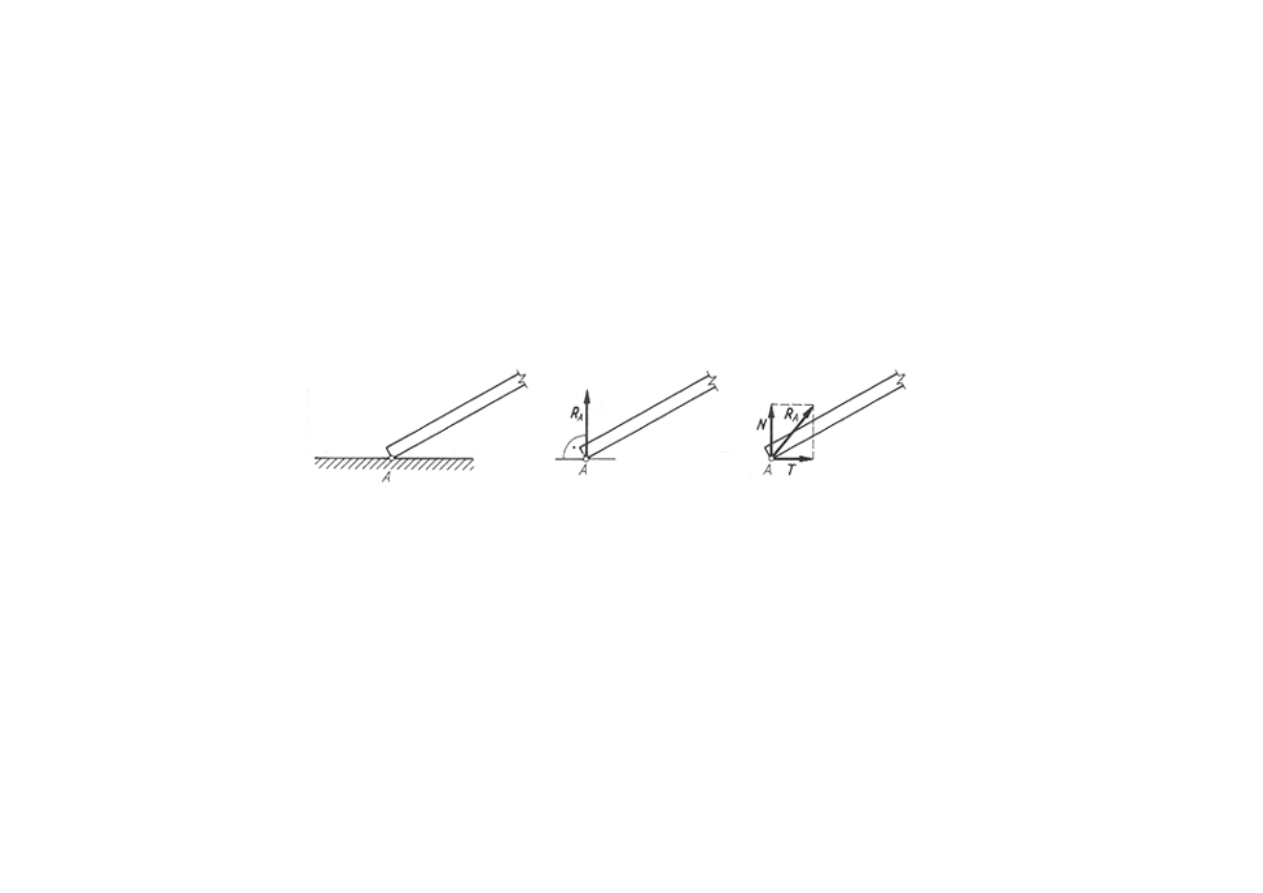
Więzy

Oparcie o gładką i chropowatą powierzchnię.

W przypadku oparcia ciała o gładką powierzchnię (styk punktowy) występuje
jedna reakcja R

A

, prostopadła do powierzchni styku. Jeżeli powierzchnia

będzie chropowata, to wystąpią dwie składowe reakcji R

A

: normalna do

powierzchni N i styczna siła tarcia T.

2008-11-19

25

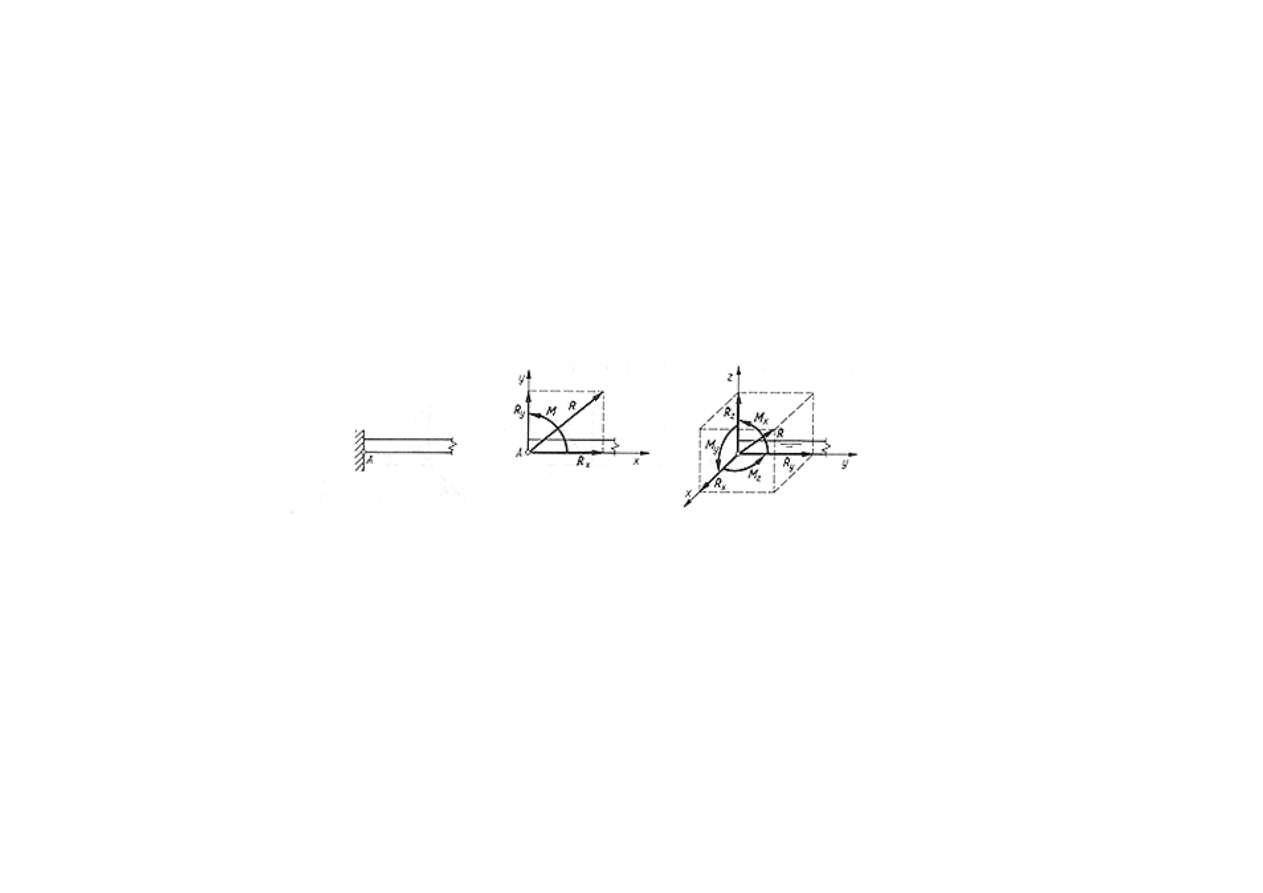
Więzy

Utwierdzenie całkowite.

Gdy chodzi o zupełne unieruchomienie ciała, wtedy stosuje się utwierdzenie
całkowite. Ciało sztywne na płaszczyźnie ma trzy stopnie swobody, a więc
wystąpi reakcja R o dwóch składowych R

x

i R

y

oraz moment utwierdzenia M.

Rozważając całkowite unieruchomienie ciała w przestrzeni, należy zastosować
takie utwierdzenie, które przedstawia sześć więzów. Wystąpi wtedy reakcja R o
trzech składowych R

x

, R

y

i R

z

oraz moment utwierdzenia M o trzech składowych

M

x

, M

y

i M

z

.

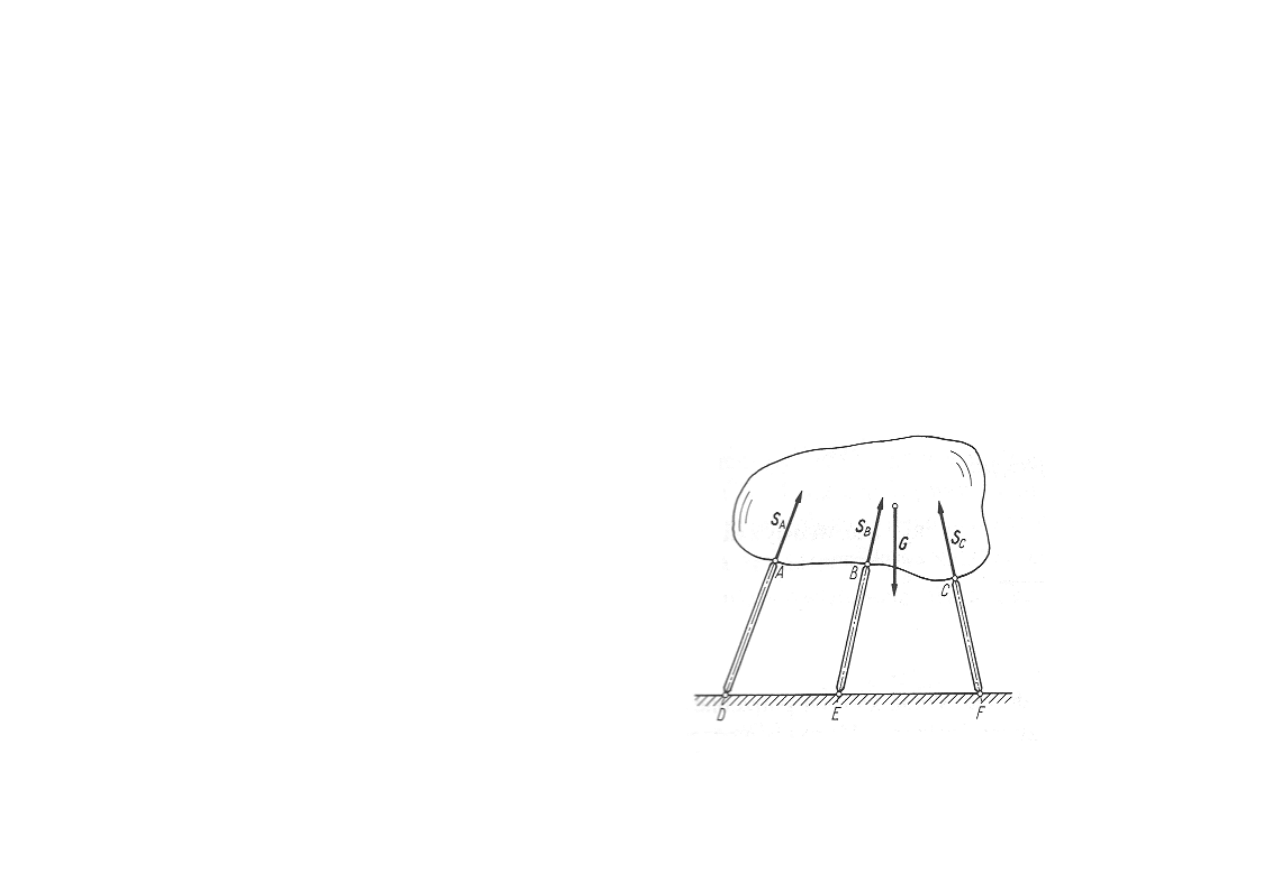
2008-11-19

26

Więzy

Ciało podparte na prętach zamocowanych przegubowo na
obu końcach (prętach przegubowych).

Ciało sztywne można także unieruchomić
przez podparcie na prętach zakończonych
przegubami. Jeżeli pominiemy ciężary
własne prętów i tarcie w przegubach, to
reakcje na ciało będą działać wzdłuż tych
prętów S

A

, S

B

i S

C

, zgodnie z rysunkiem.

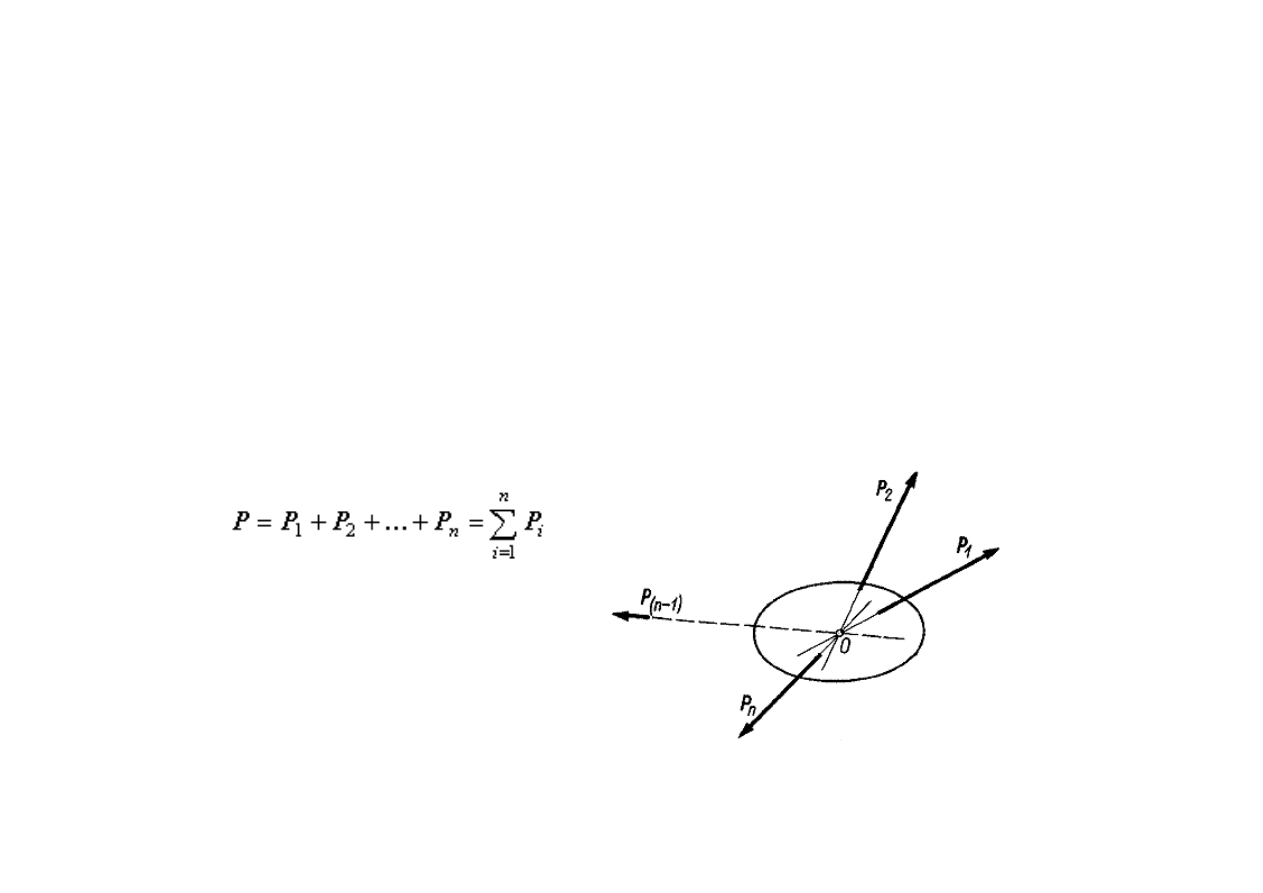
2008-11-19

27

Płaski układ sił zbieżnych

Płaski układ sił zbieżnych P

1

, P

2

,..., P

n

przyłożonych do punktu O można zastąpić
siłą wypadkową P równą sumie
geometrycznej tych sił i przyłożoną również
w punkcie O.

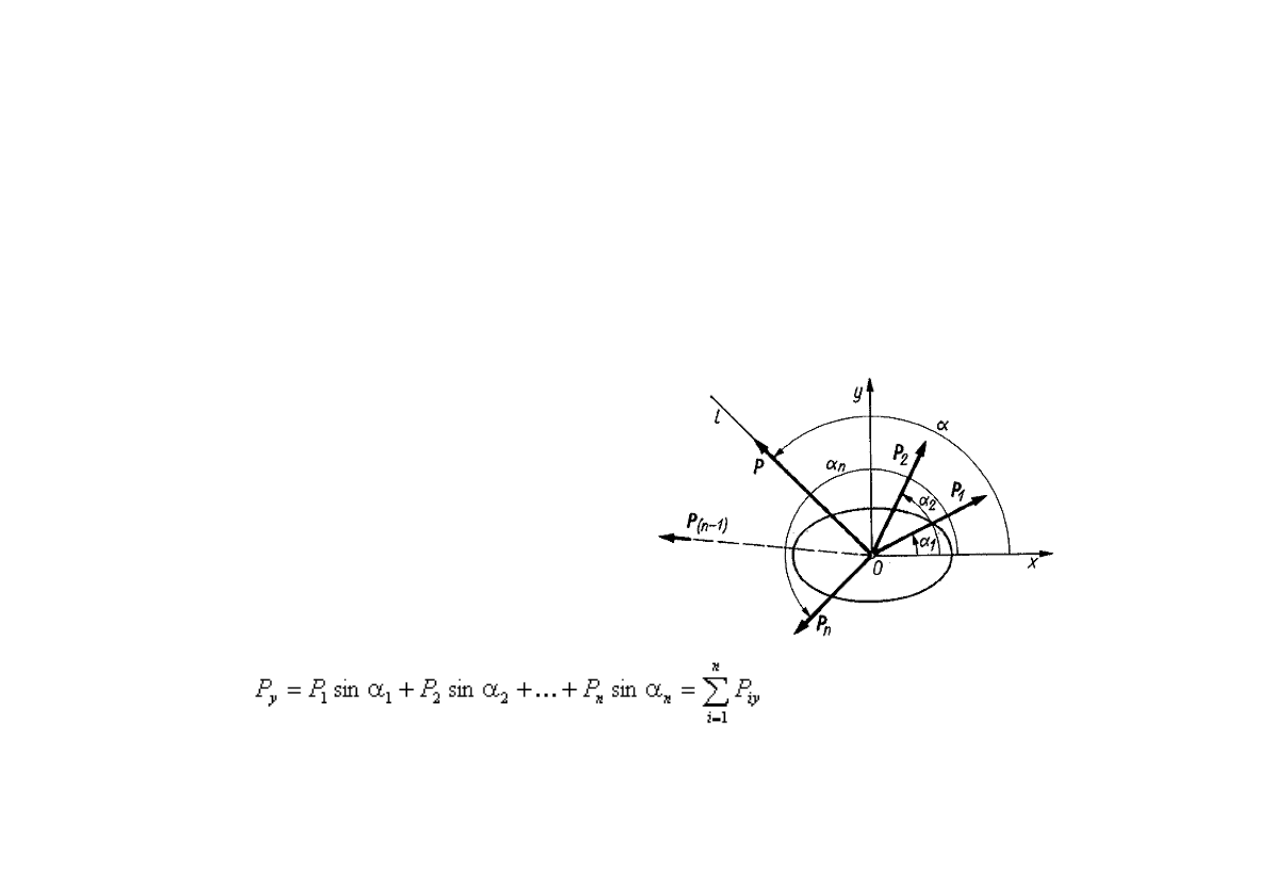
2008-11-19

28

Płaski układ sił zbieżnych

W analitycznym sposobie wyznaczania
wypadkowej korzystamy z twierdzenia o
rzucie sumy wektorów, według którego
rzut sumy geometrycznej wektorów na
dowolną oś jest równy sumie rzutów tych
wektorów na tę samą oś. Przyjmując
układ współrzędnych 0xy, oznaczamy
odpowiednio przez



1

,



2

,...,



n

kąty

nachylenia poszczególnych sił do osi 0x.
Wypadkowa tych sił działa wzdłuż
prostej l przechodzącej przez punkt o i
nachylonej do osi 0x pod kątem



.

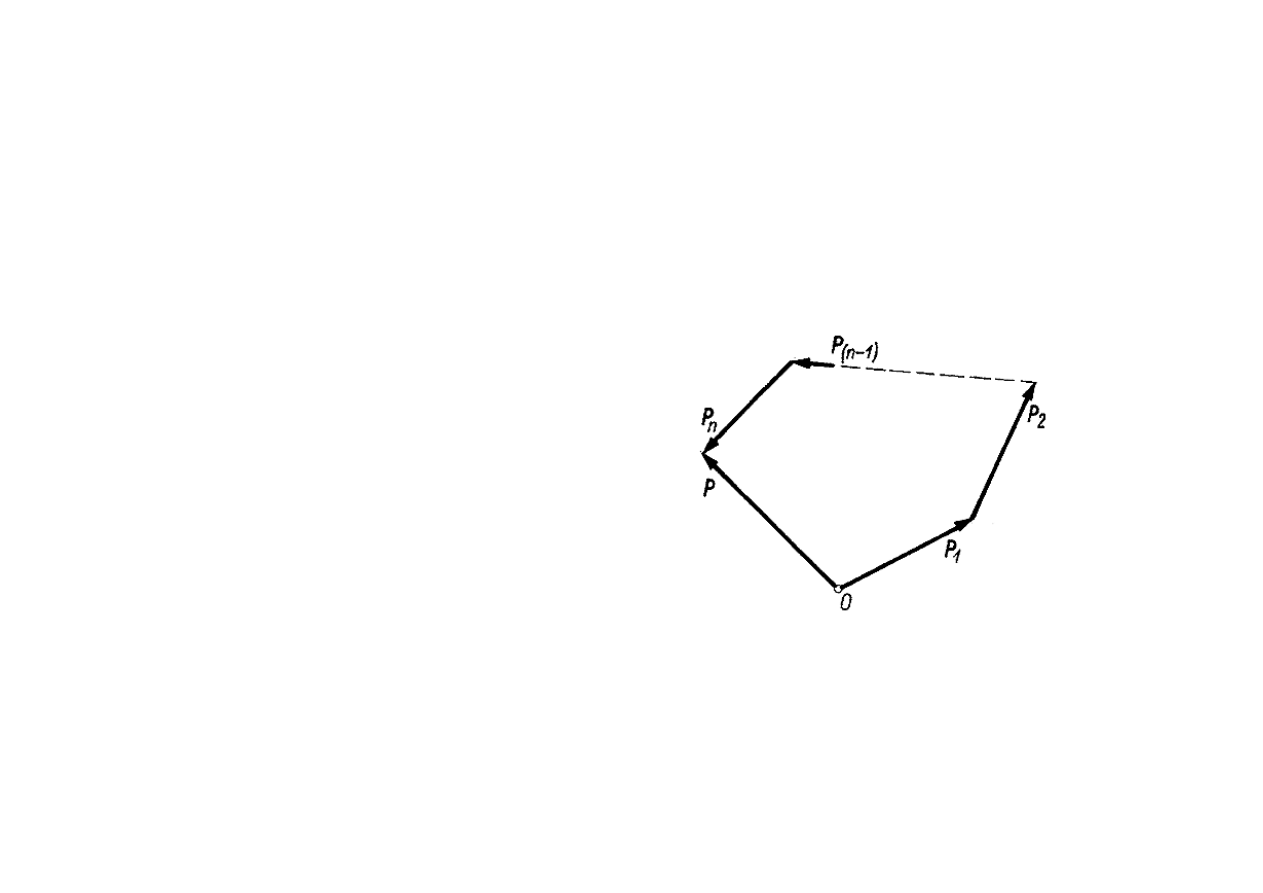
2008-11-19

29

Płaski układ sił zbieżnych

W geometrycznym sposobie
wyznaczania wypadkowej należy
zbudować wielobok sił, w którym wektory
sił odkładamy równolegle do ich linii
działania. Z punktu O odkładamy wektor
P

1

, a z jego końca wektor P

2

i tak kolejne

wektory aż do P

n

.

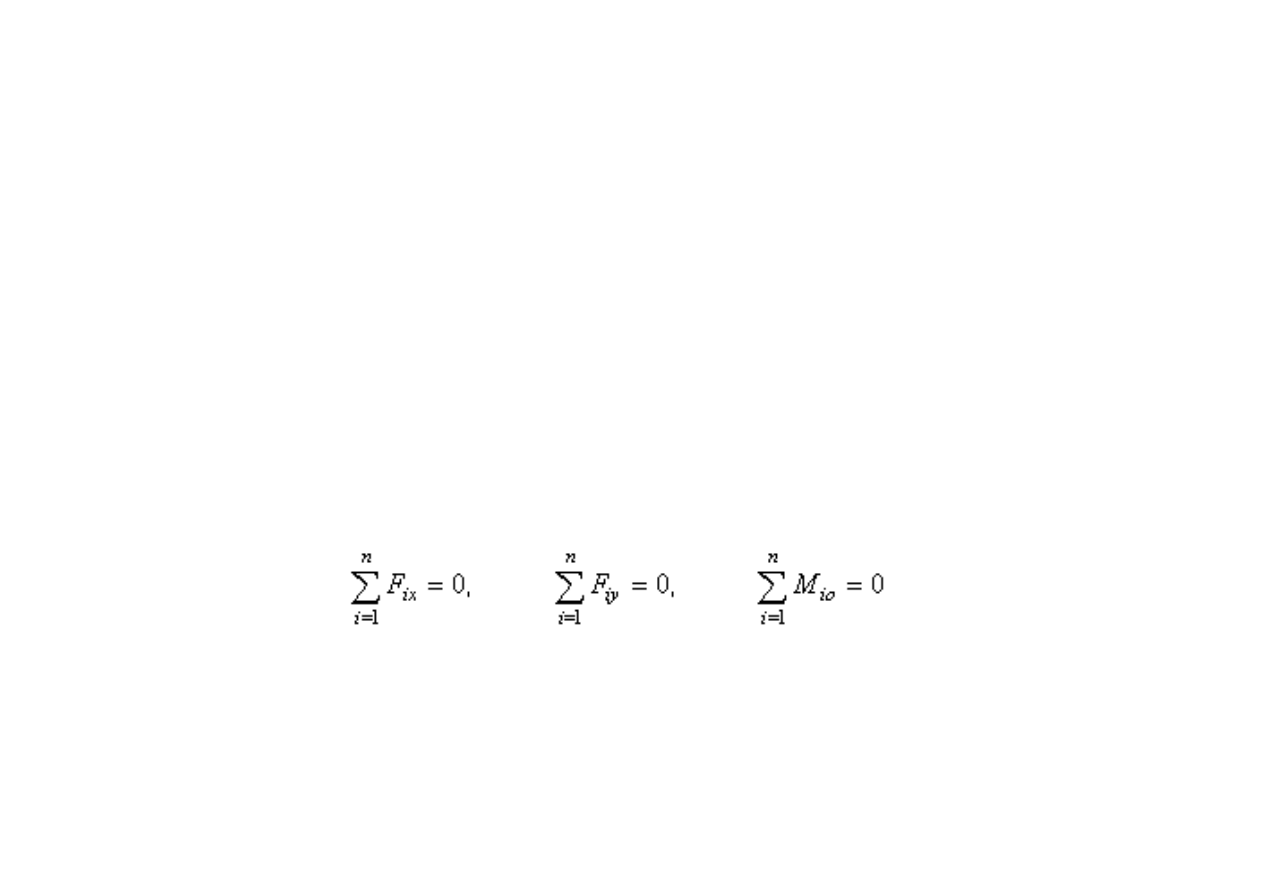
2008-11-19

30

Płaski układ sił zbieżnych

Warunki równowagi

Płaski dowolny układ sił znajduje się w równowadze, jeżeli sumy rzutów
wszystkich sił na osie układu są równe zeru i moment wszystkich sił
względem dowolnego punktu 0 płaszczyzny działania sił jest równy zeru.

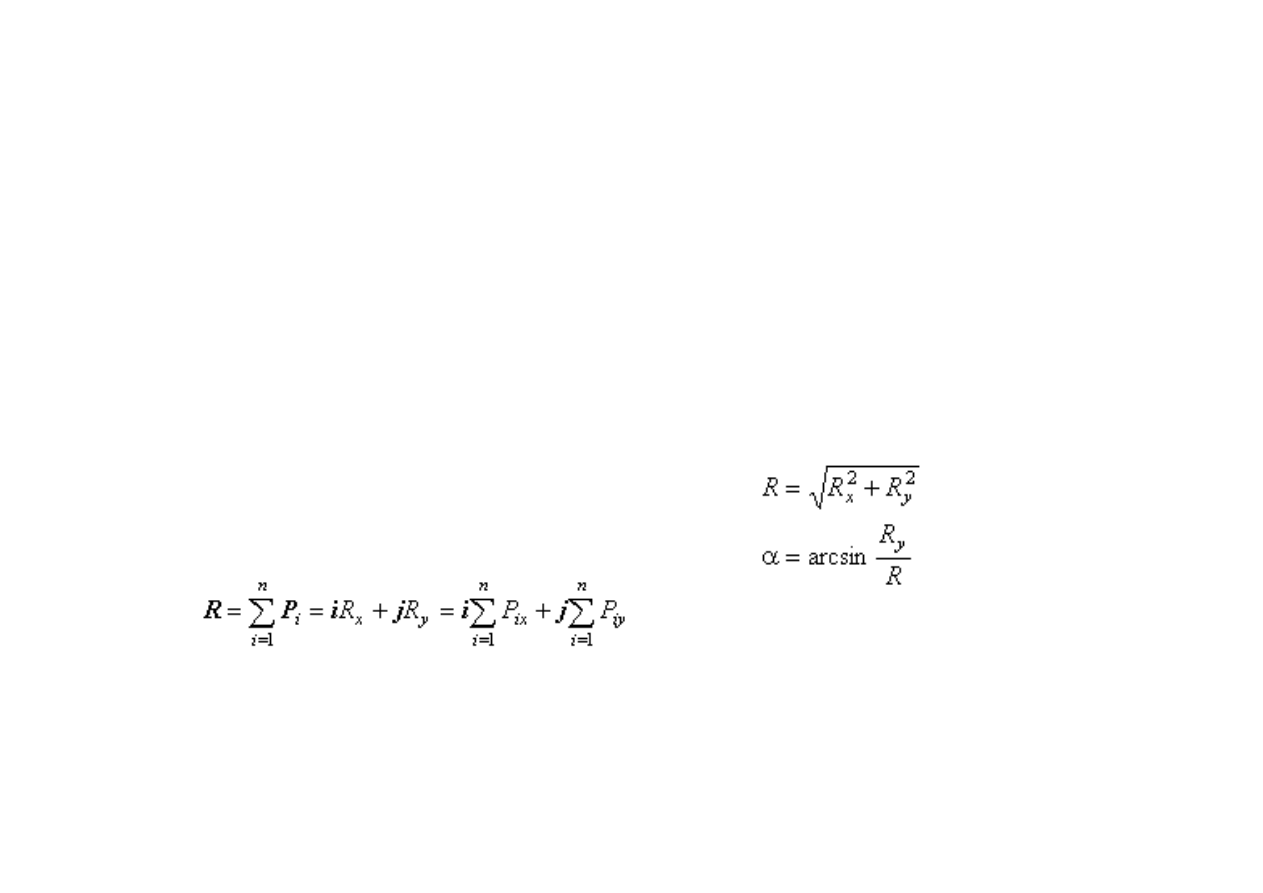
2008-11-19

31

Wektor główny

Dowolny układ sił, działających na
ciało sztywne, o liniach działania
leżących w jednej płaszczyźnie
możemy zastąpić wektorem głównym
R, przyłożonym do dowolnie
wybranego środka redukcji O oraz
momentem głównym M

o

względem

środka redukcji O. Wektor główny R
jest równy sumie geometrycznej
wszystkich sił układu

Wartość wektora głównego oraz

kąt , jaki wektor ten tworzy z osią Ox,
wyznaczamy ze wzorów

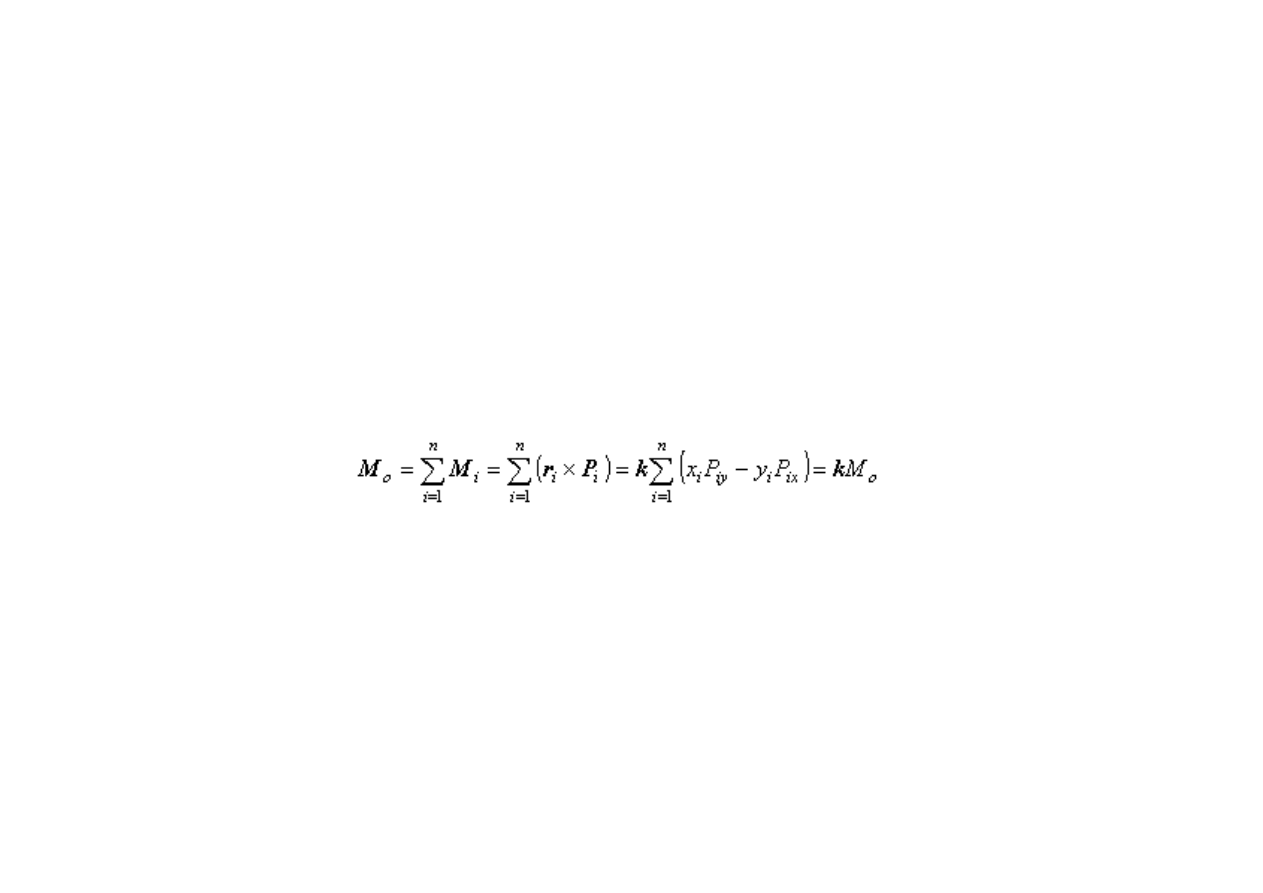
2008-11-19

32

Moment główny

Moment główny M

o

względem środka redukcji 0 jako początku układu

współrzędnych 0xy jest równy sumie momentów danych sił układu
względem punktu 0.

2008-11-19

33

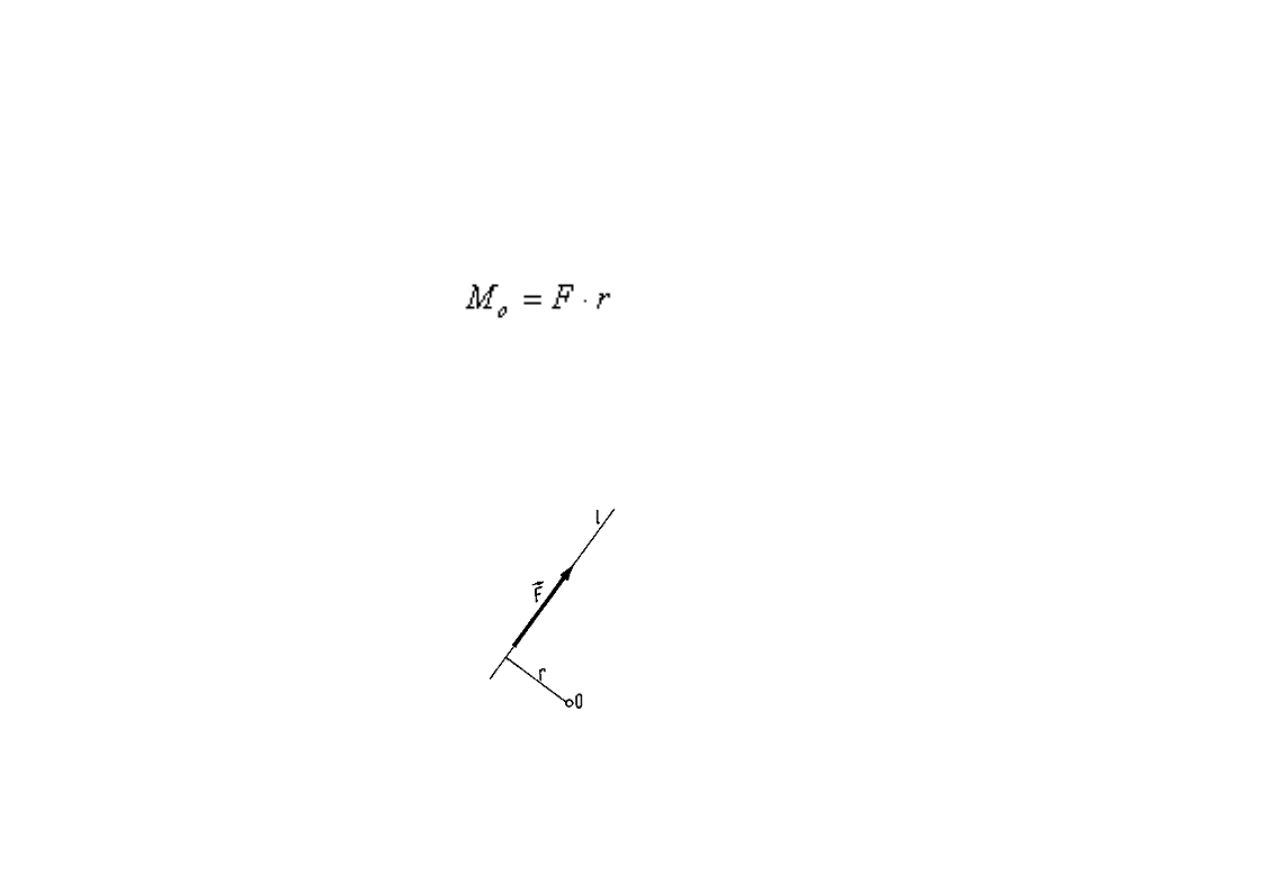
Co to jest moment?

Wyrażenie

gdzie: F jest siłą działającą wzdłuż prostej l, a r jej ramieniem
nazywamy momentem siły względem dowolnego punktu 0.

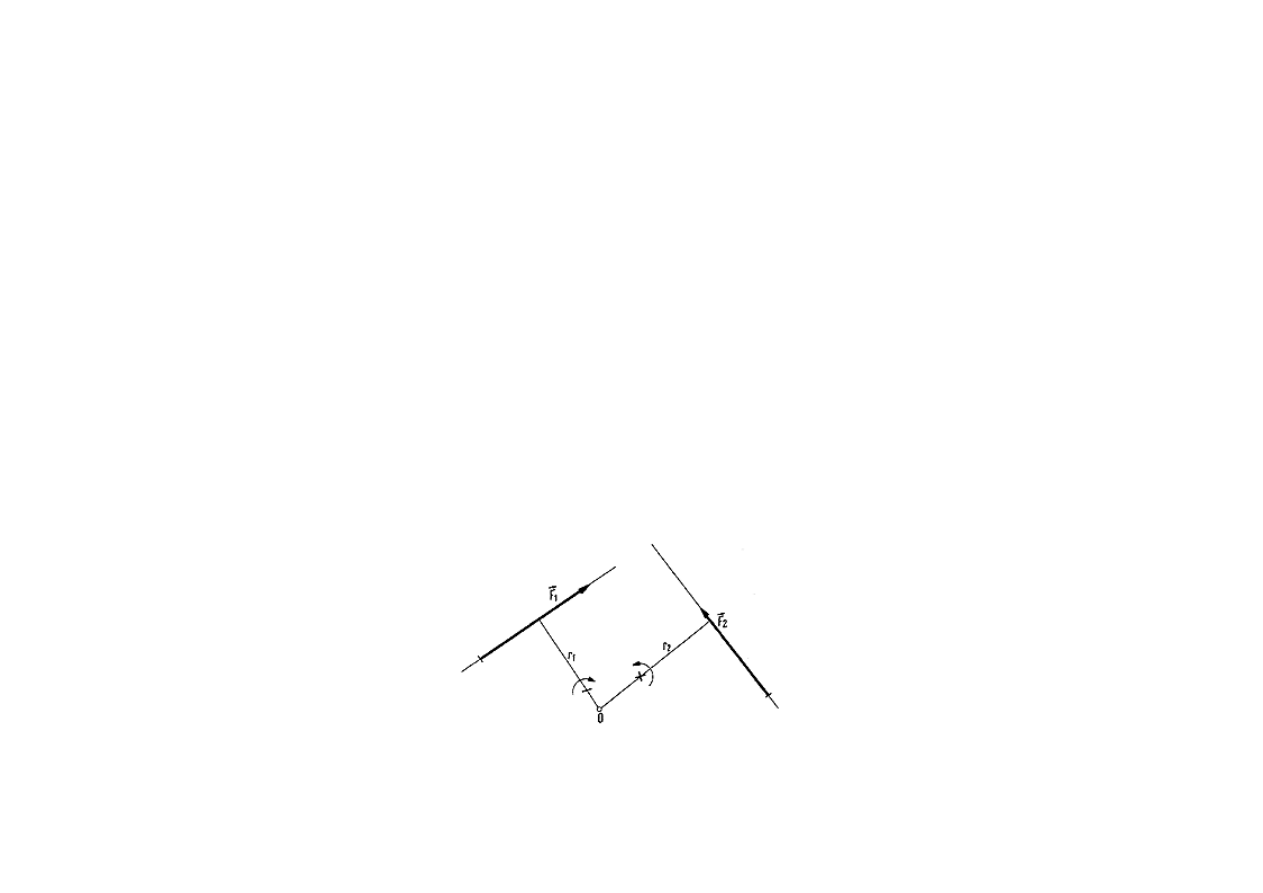
2008-11-19

34

Co to jest moment cd

Jest to wektor mający następujące cechy:

•wartość liczbową równą iloczynowi (F · r) wartości siły F i jej ramienia r

•kierunek prostopadły do płaszczyzny wyznaczonej przez linię działania

siły oraz biegun

•zwrot momentu przyjmujemy zgodnie z regułą śruby prawoskrętnej

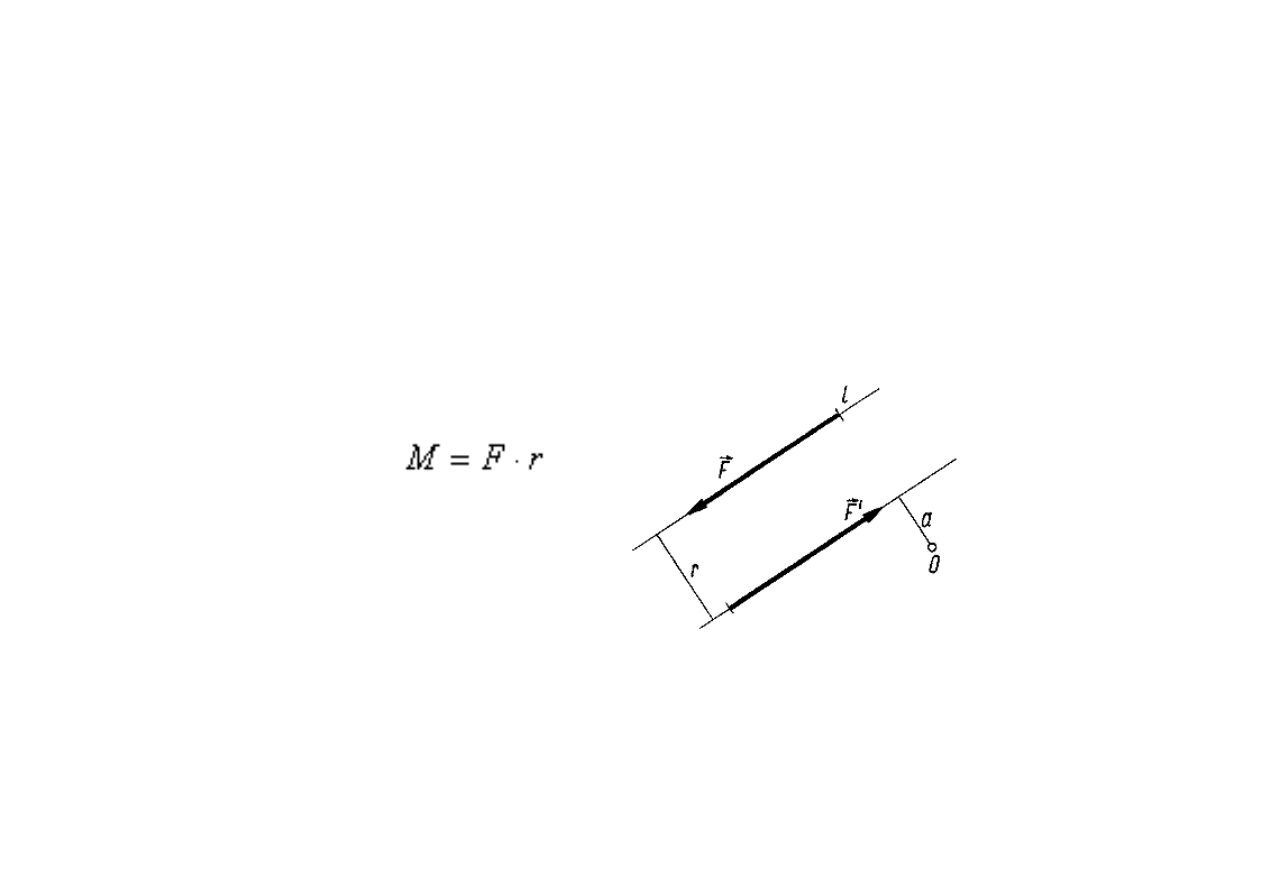
2008-11-19

35

Co to jest moment cd

Parą sił nazywamy układ dwóch sił równej wartości i równoległych
(o jednakowych kierunkach), lecz o przeciwnych zwrotach.
Iloczyn wartości jednej z sił i ramienia pary nazywamy momentem pary sił.

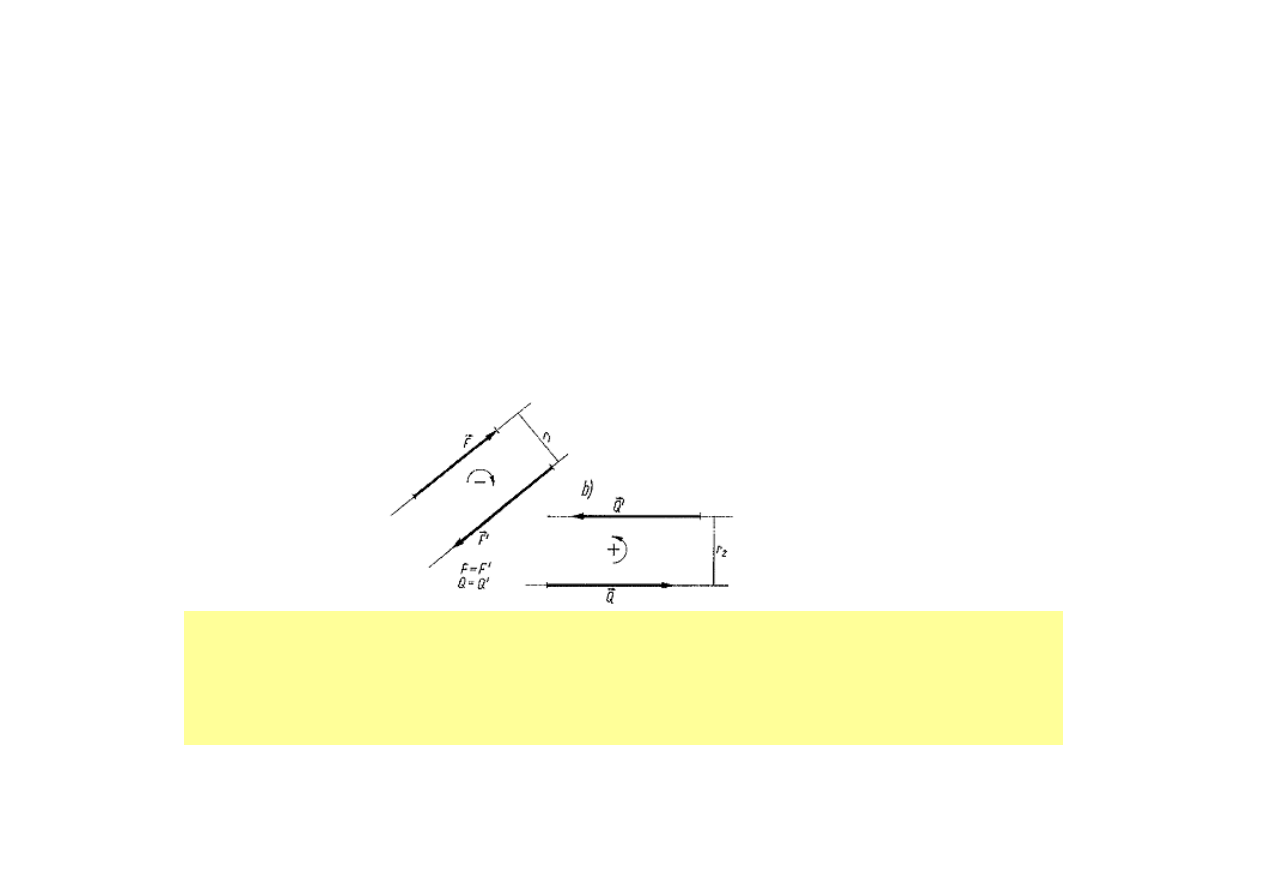
2008-11-19

36

Co to jest moment cd

Każdą parę sił możemy zastąpić wektorem momentu sił i odwrotnie  każdy
wektor momentu sił możemy zastąpić parą sił, jeśli tylko iloczyn wartości siły i
odległości między siłami wynosi M

Moment pary sił uważamy za dodatni, jeżeli para dąży do obrócenia
swego ramienia w stronę przeciwną do ruchu wskazówek zegara. Jeżeli
para dąży do obrócenia swego ramienia w stronę zgodną z ruchem
wskazówek zegara, to jej moment uważamy za ujemny.