2008-12-17

1

Mechanika i Wytrzymałość

Materiałów

Wykład 5

2008-12-17

2

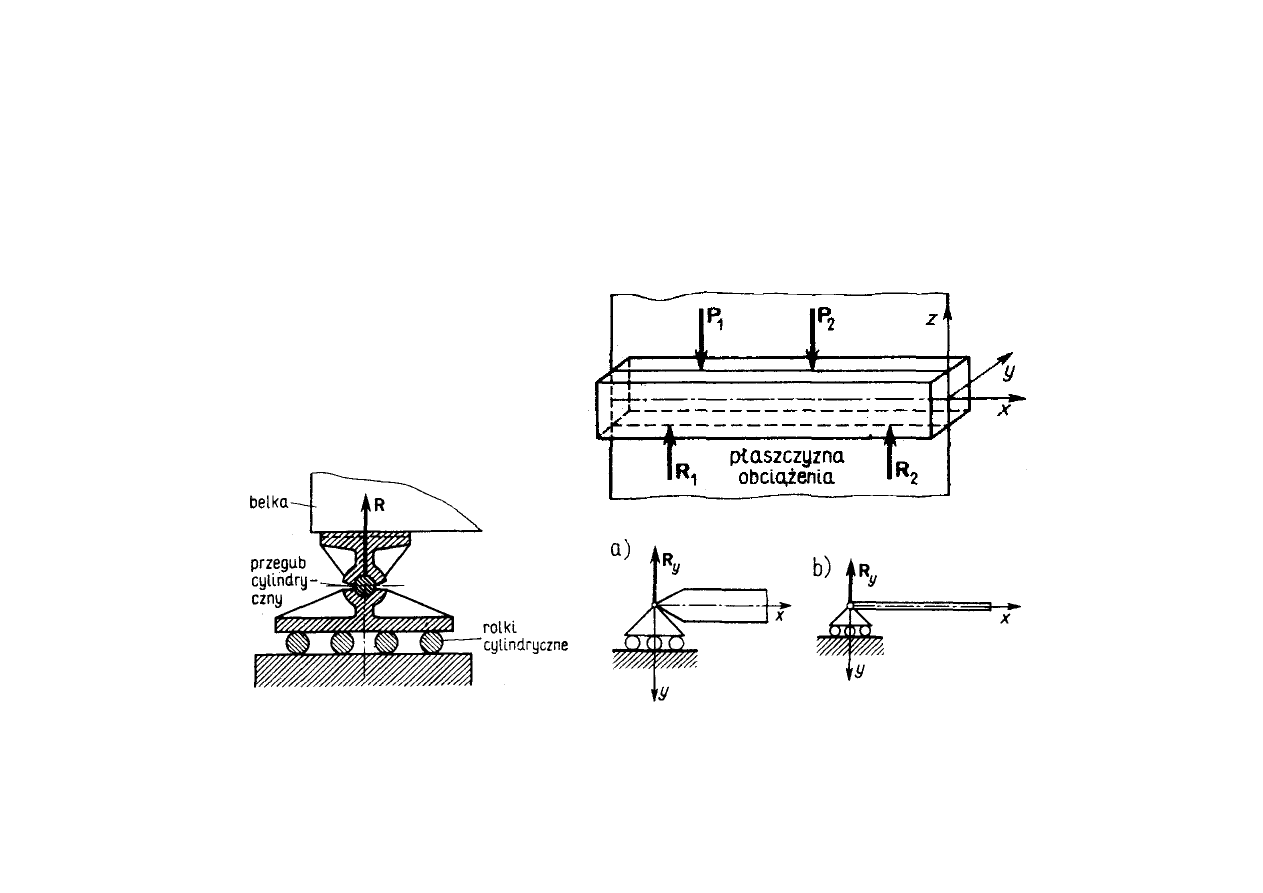
Zginanie prętów prostych

Rodzaje umocowań belek:



podparcie przegubowo
przesuwne (ruchowe)

2008-12-17

3

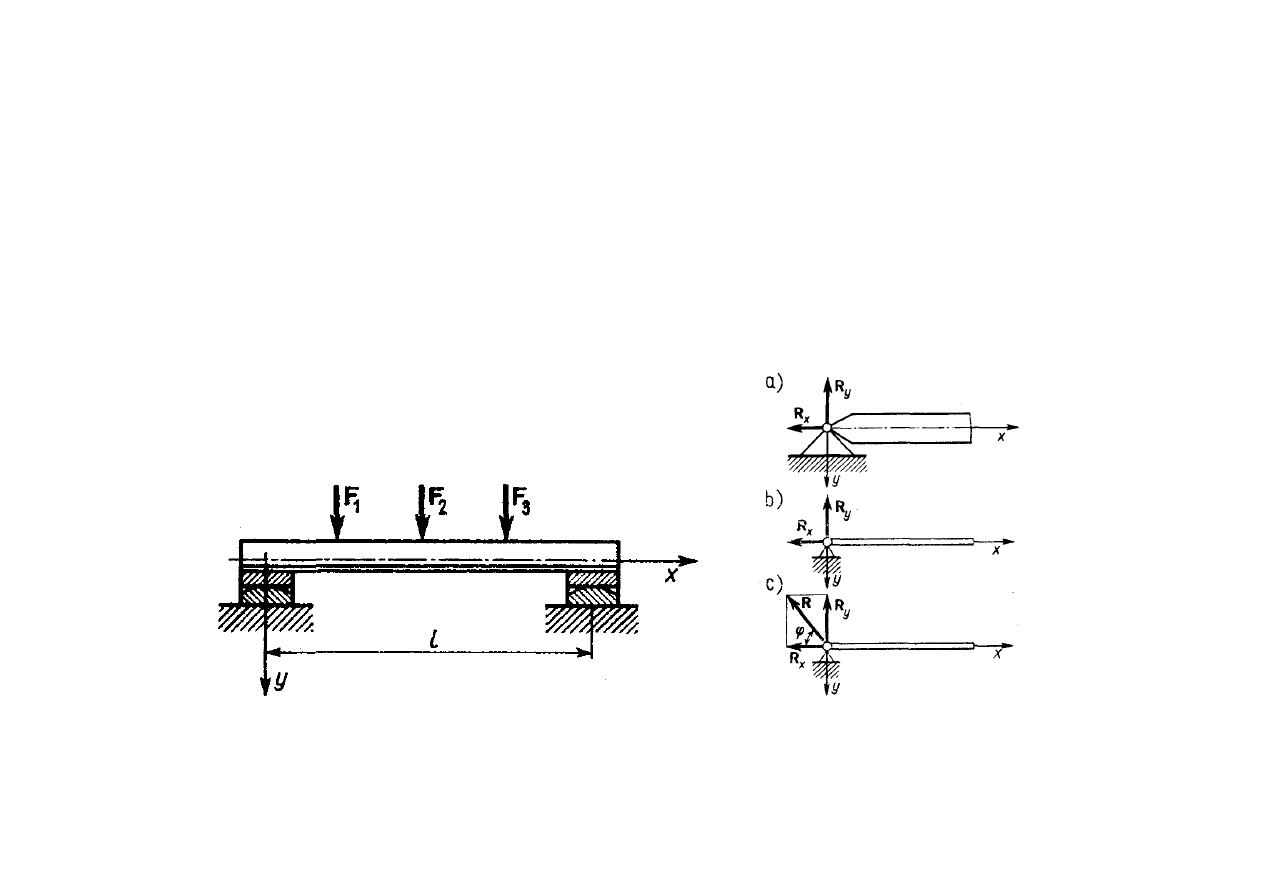
Zginanie prętów prostych

Rodzaje umocowań belek:



podparcie przegubowo
nieprzesuwne (stałe)

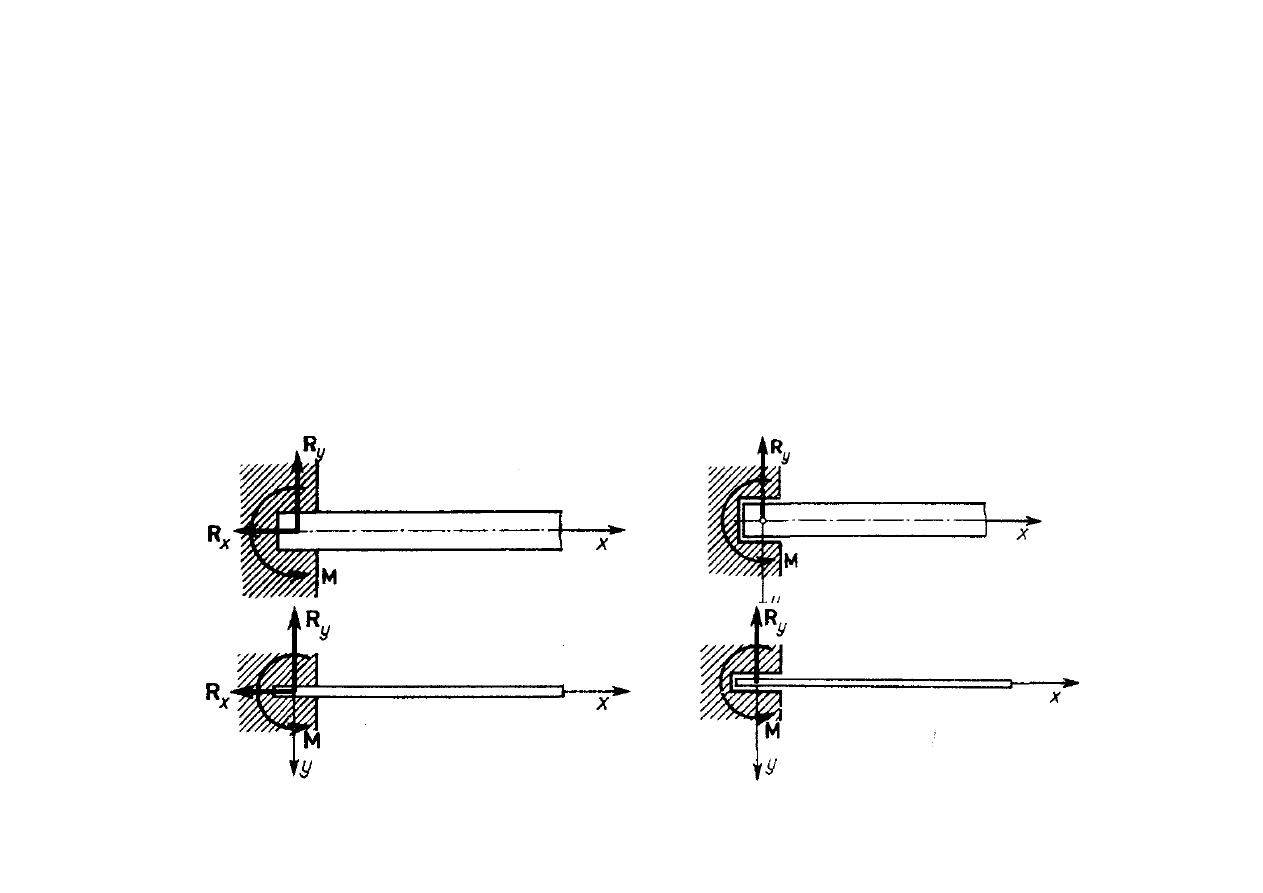
2008-12-17

4

Zginanie prętów prostych

Rodzaje umocowań belek:



podparcie w utwierdzeniu
(utwierdzenie)

2008-12-17

5

Czyste zginanie

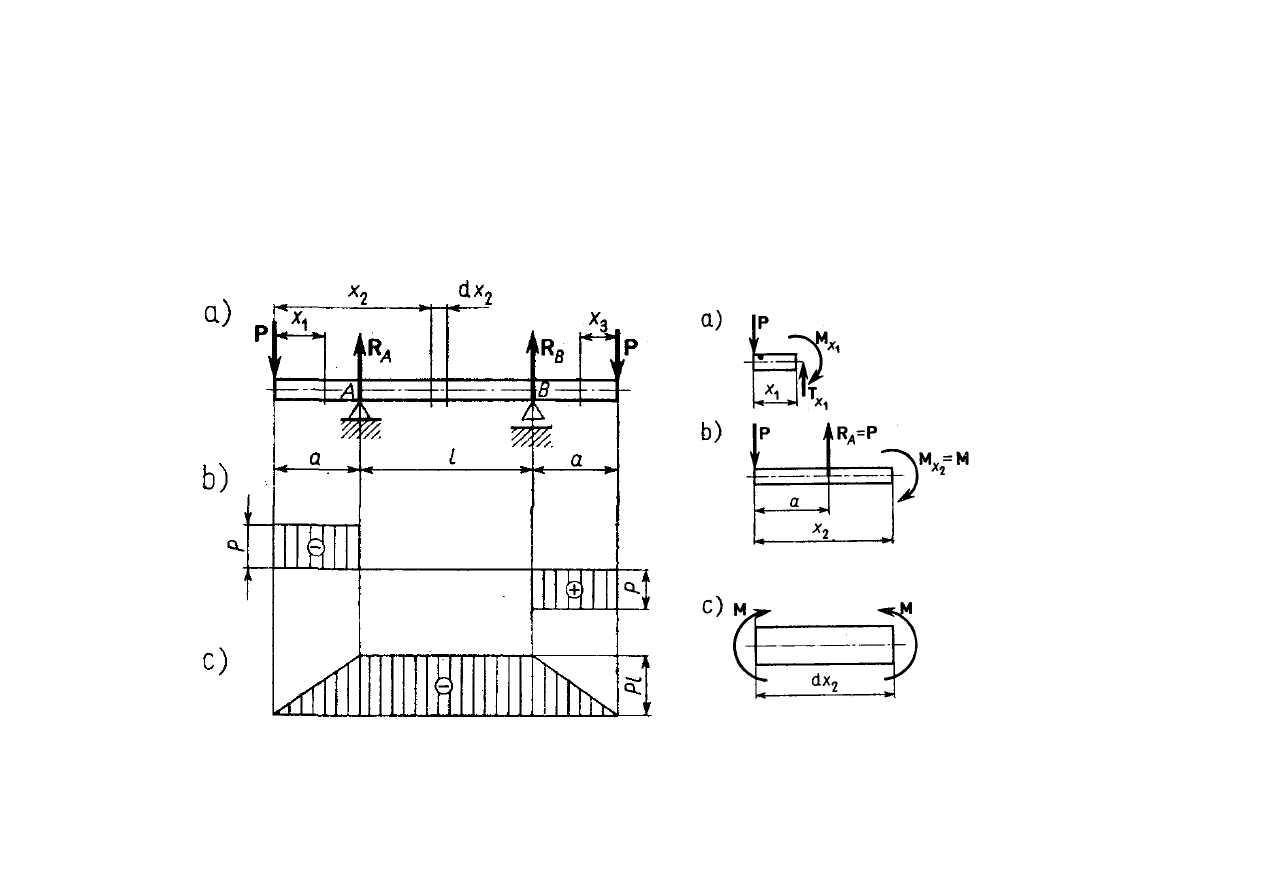
2008-12-17

6

Czyste zginanie

2008-12-17

7

Czyste zginanie

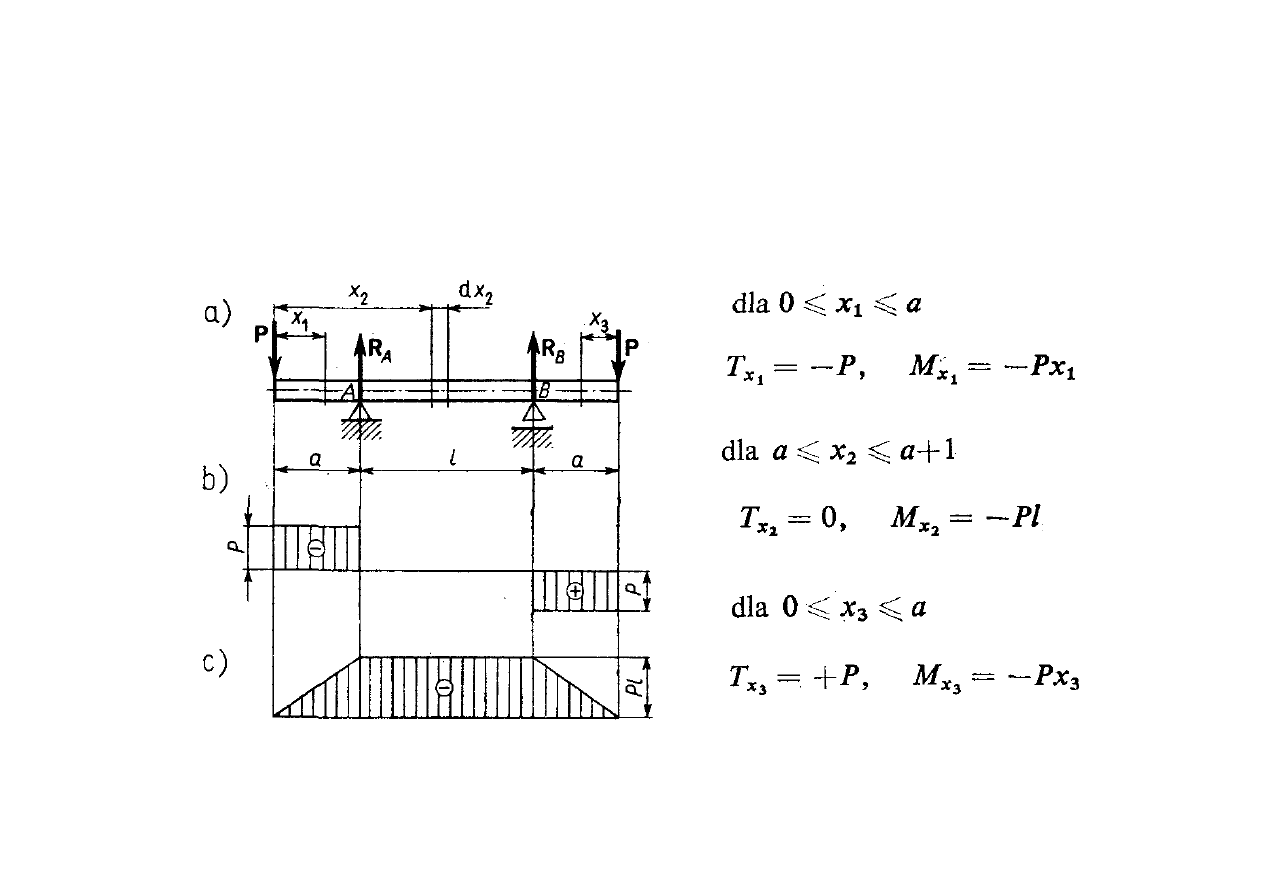
Stan czystego zginania występuje wówczas, gdy w przekroju
poprzecznym belki działa tylko moment zginający, zaś siła
poprzeczna jest równa zeru T

x

.

2008-12-17

8

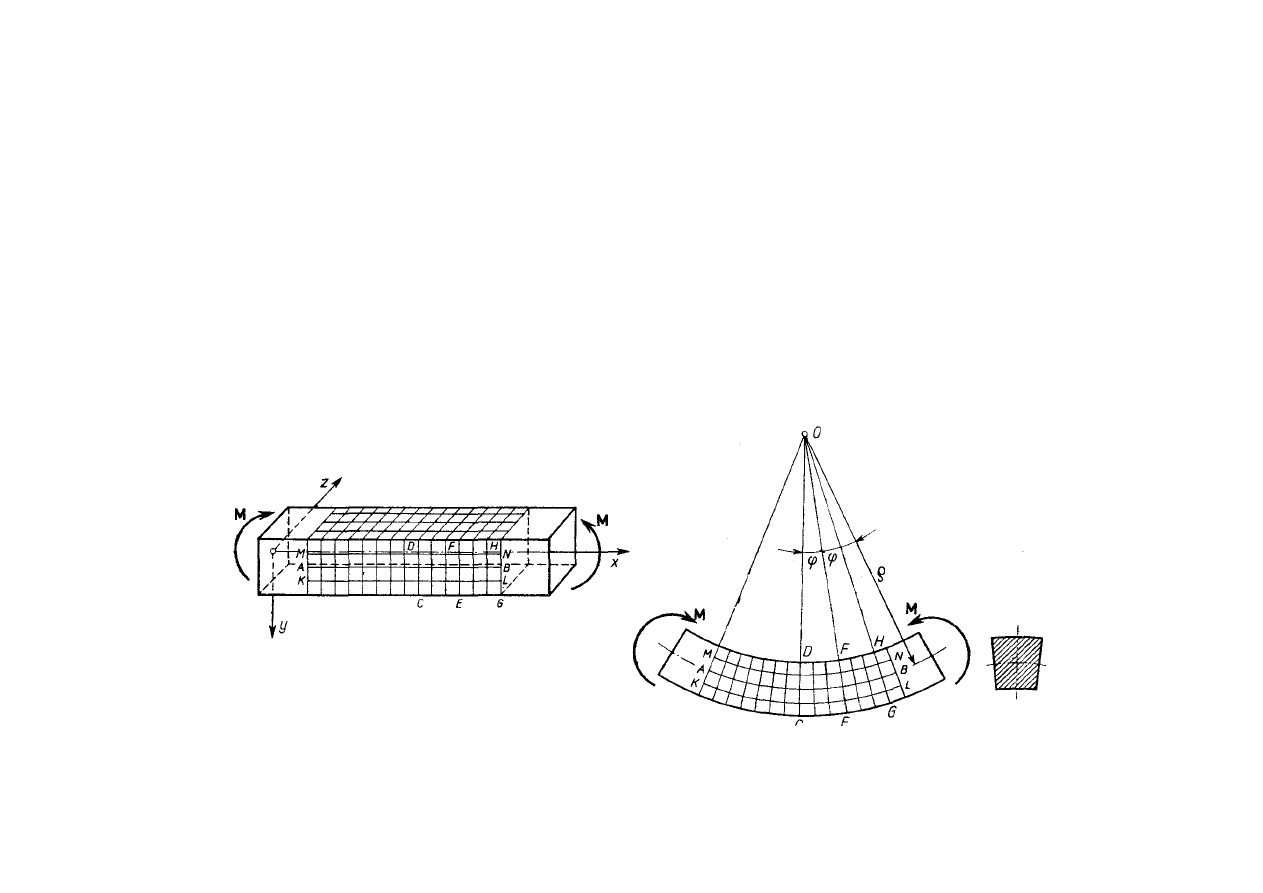
Czyste zginanie

Omówione obserwacje pozwalają na przyjęcie pewnych założeń:

1. Przekroje poprzeczne płaskie przed odkształceniem pozostają

płaskie po odkształceniu (hipoteza płaskich przekrojów),

2. Istnieje warstwa obojętna prostopadła do płaszczyzny

działania pary sił momentu gnącego,

3. Włókna wzdłużne nie wywierają na siebie nacisku – znajdują

się w jednowymiarowym stanie naprężeń,

4. Odkształcenie włókien równoległych do osi pręta i znajdują-

cych się w płaszczyźnie równoległej do warstwy obojętnej nie
zależą od położenia w tej płaszczyźnie.

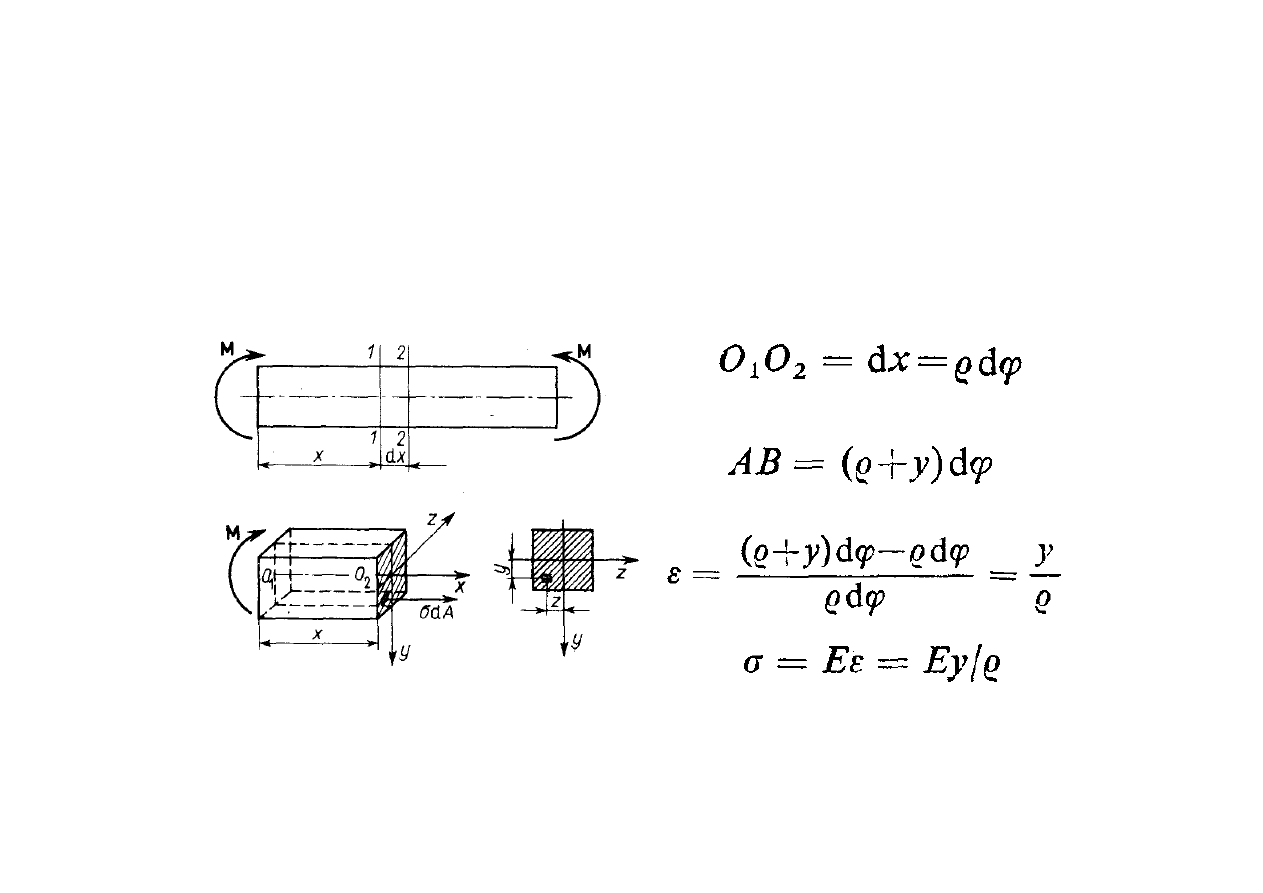
2008-12-17

9

Czyste zginanie

gdzie:  - promień krzywizny

warstwy obojętnej

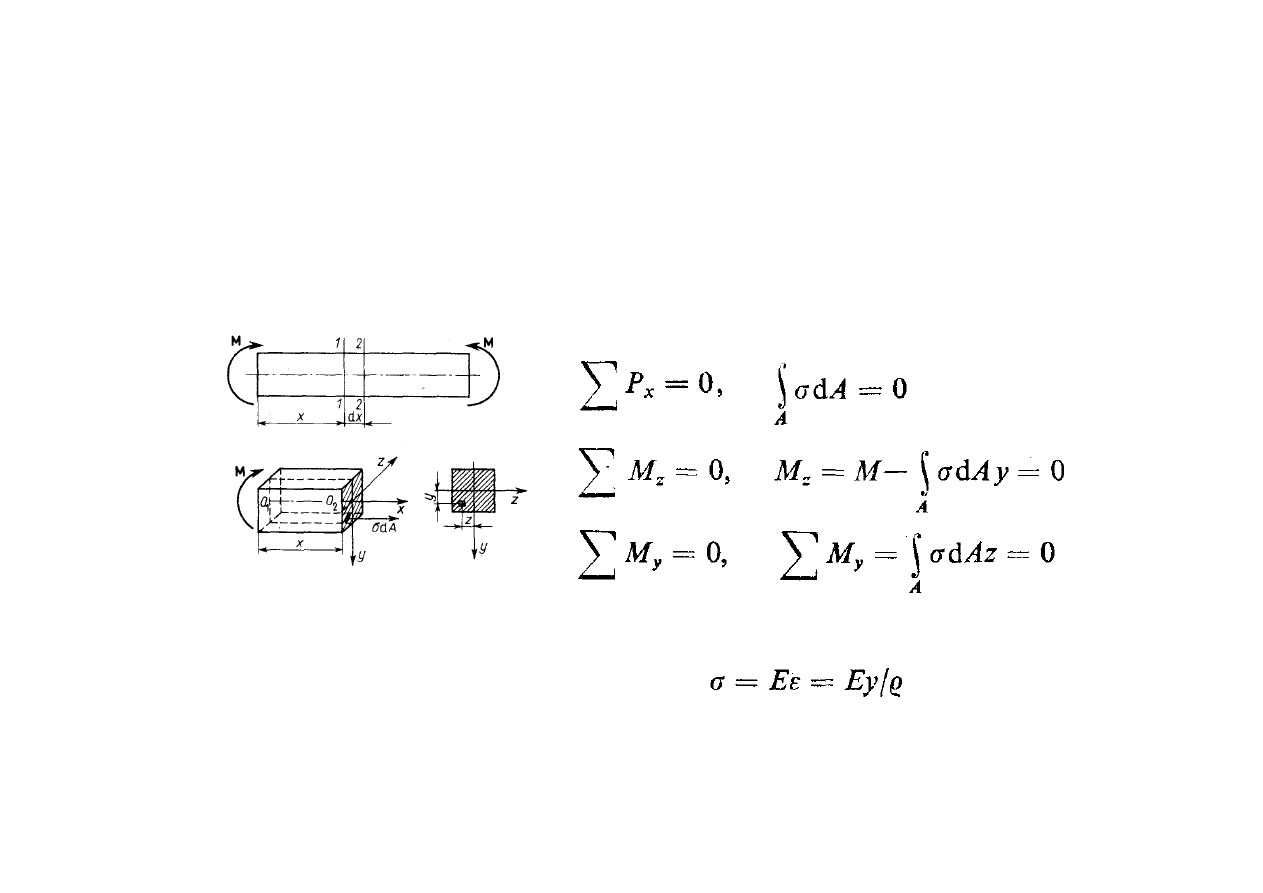
2008-12-17

10

Czyste zginanie

Układając warunki równowagi otrzymamy

wyrażając powyższe równania poprzez

otrzymamy:

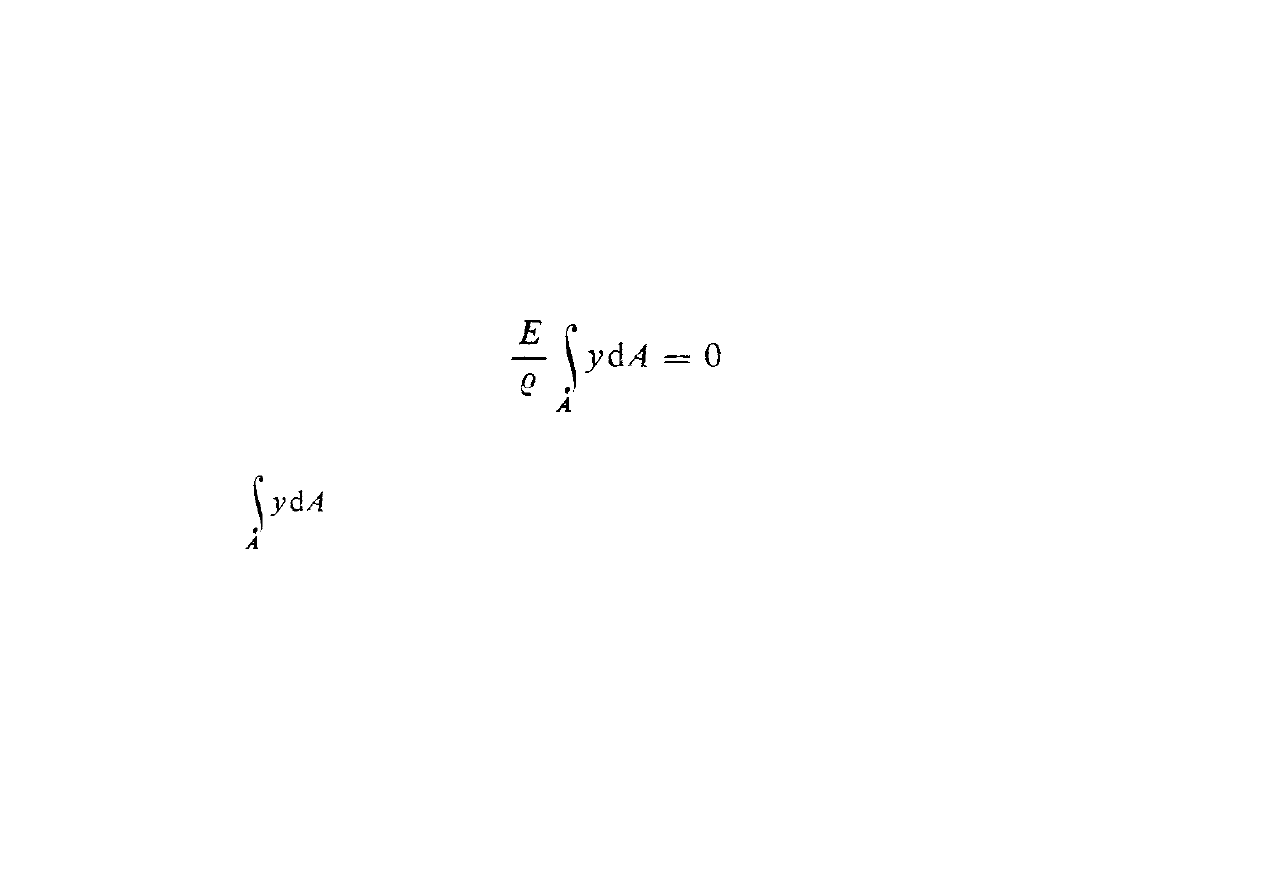
2008-12-17

11

Czyste zginanie

moment statyczny pola przekroju poprzecznego względem osi Z

WNIOSEK: os obojętna przekroju musi przechodzić przez jego
środek ciężkości

gdzie:

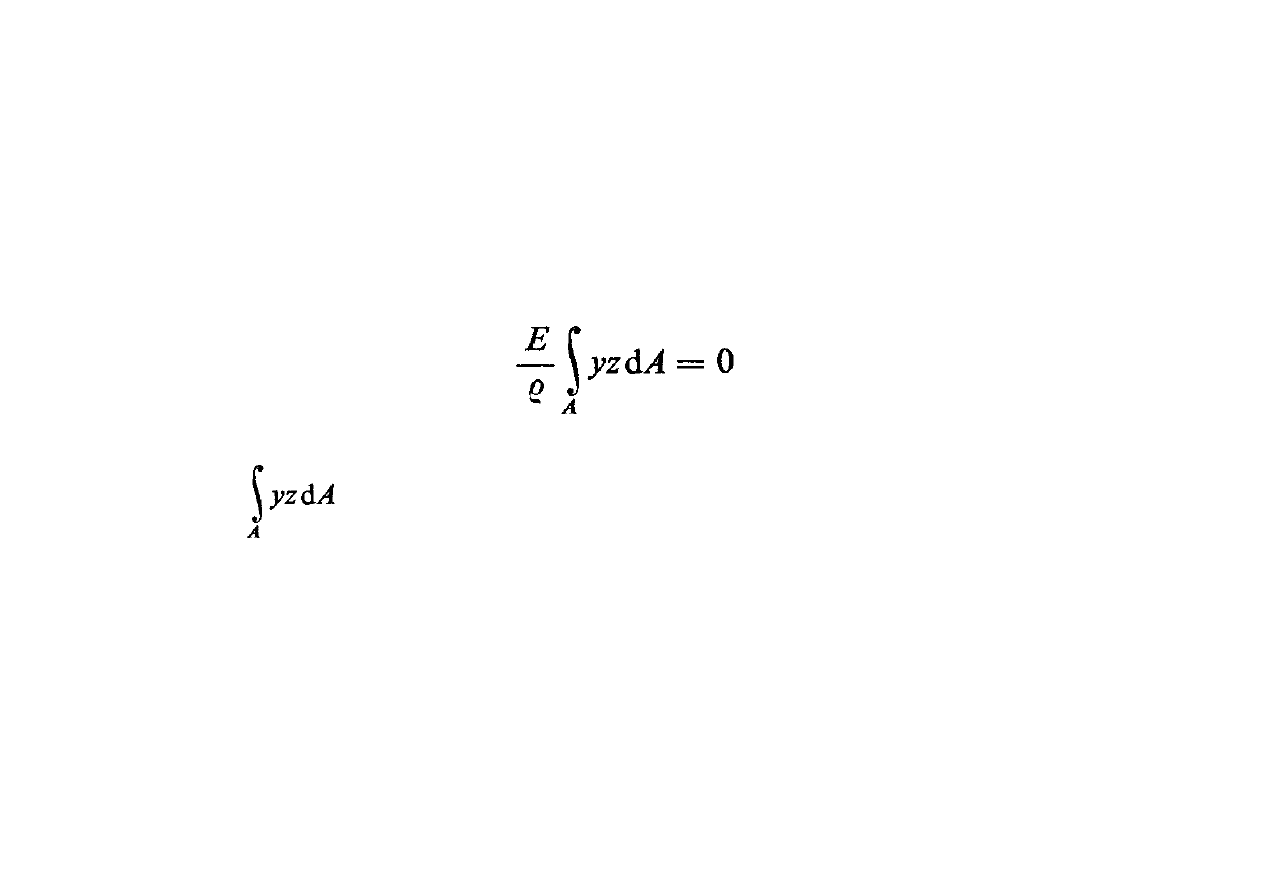
2008-12-17

12

Czyste zginanie

moment dewiacji J

yz

pola przekroju poprzecznego względem

osi Y i Z

WNIOSEK: równanie jest prawdziwe gdy osie Y i Z są
głównymi centralnymi osiami bezwładności pola przekroju.

gdzie:

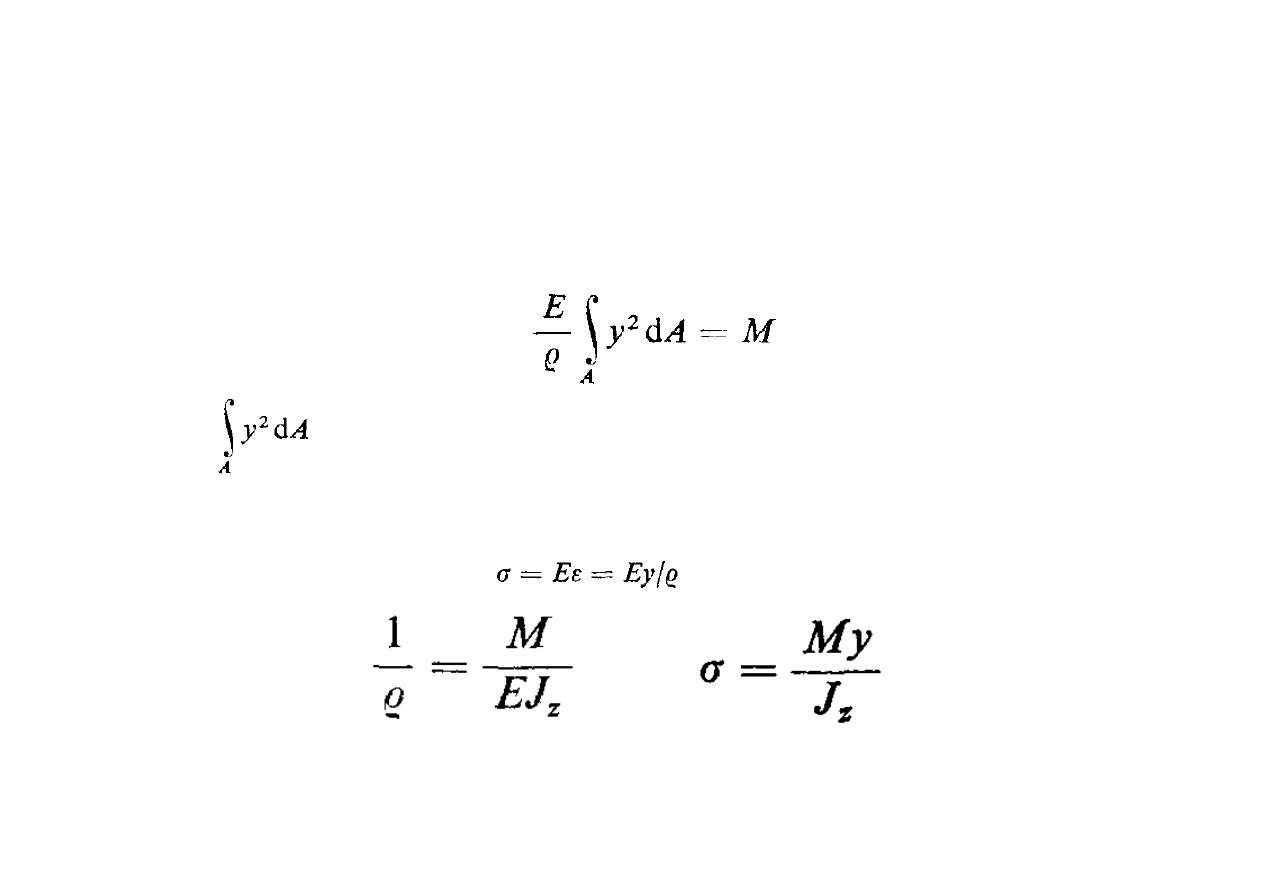
2008-12-17

13

Czyste zginanie

Na podstawie powyższego równania otrzymamy związek
między krzywizną belki i momentem gnącym i naprężeniem:

moment bezwładności J

z

pola przekroju poprzecznego względem osi Z

2008-12-17

14

Czyste zginanie

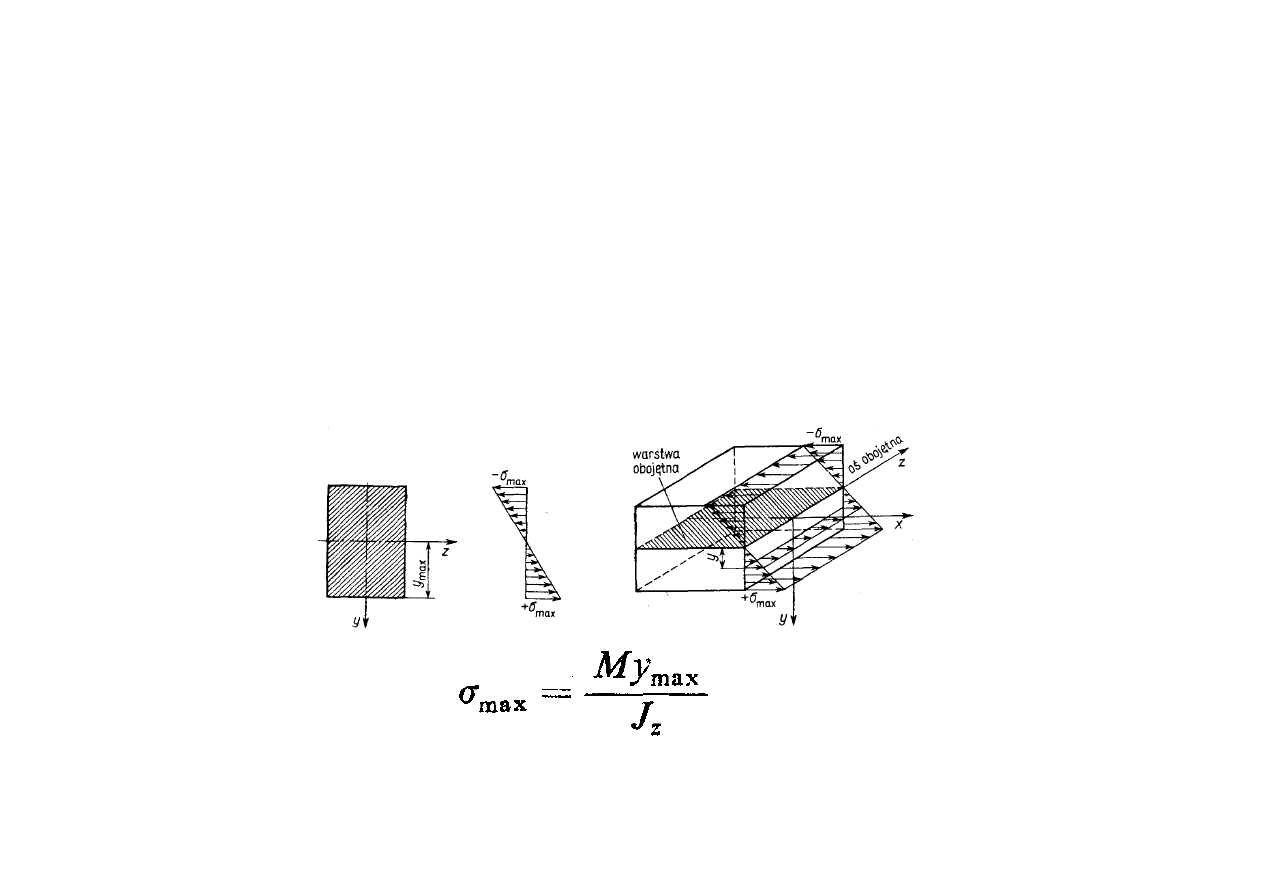
Powyższe zależności pozwalają na wyznaczenie naprężeń
normalnych w punktach przekroju poprzecznego belki
oddalonych o y od osi obojętnej.

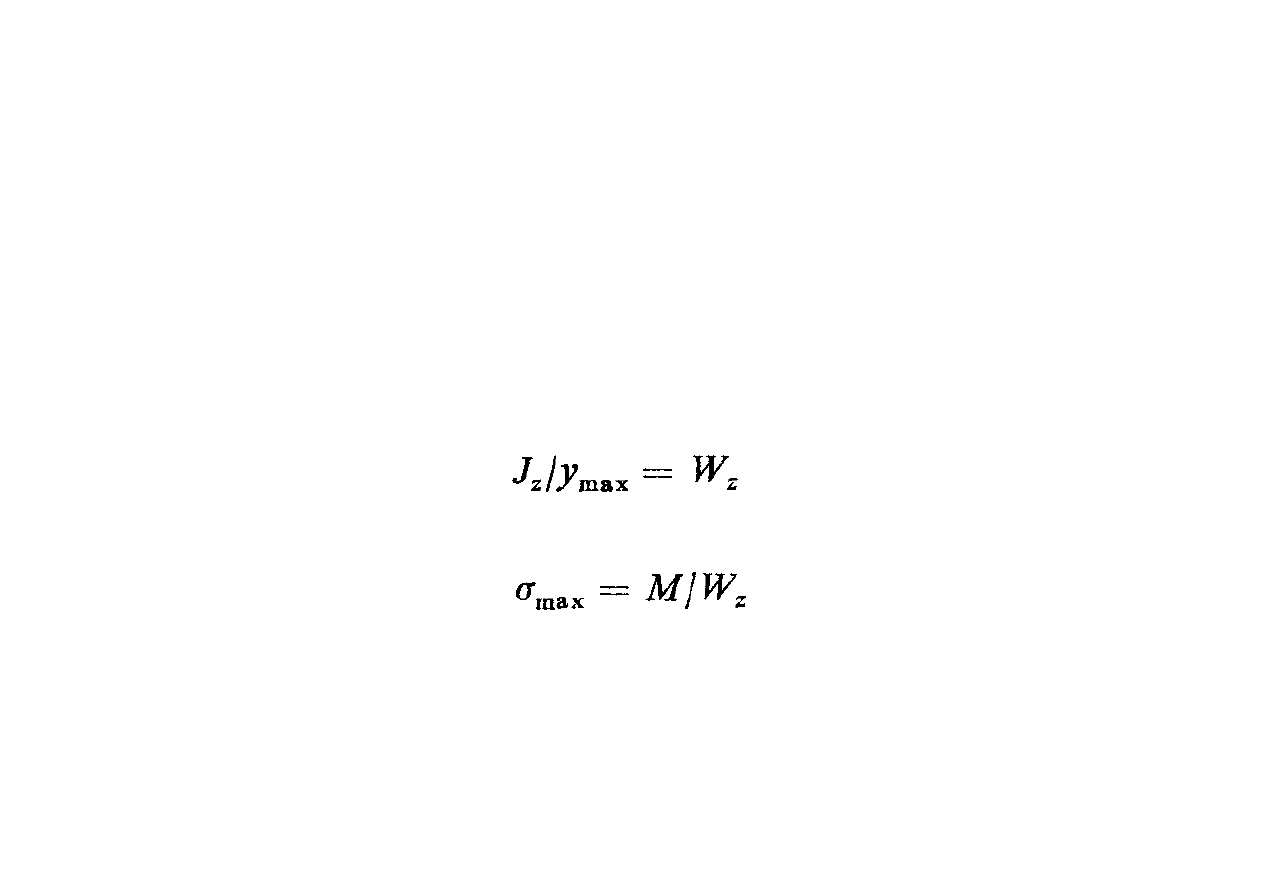
2008-12-17

15

Czyste zginanie

Wprowadźmy iloraz momentu bezwładności pola przekroju
względem osi obojętnej i odległości najdalej oddalonych
punktów przekroju

stąd wartość największych naprężeń normalnych wynosi:

a W

z

określamy jako wskaźnik wytrzymałości przekroju

na zginanie.

2008-12-17

16

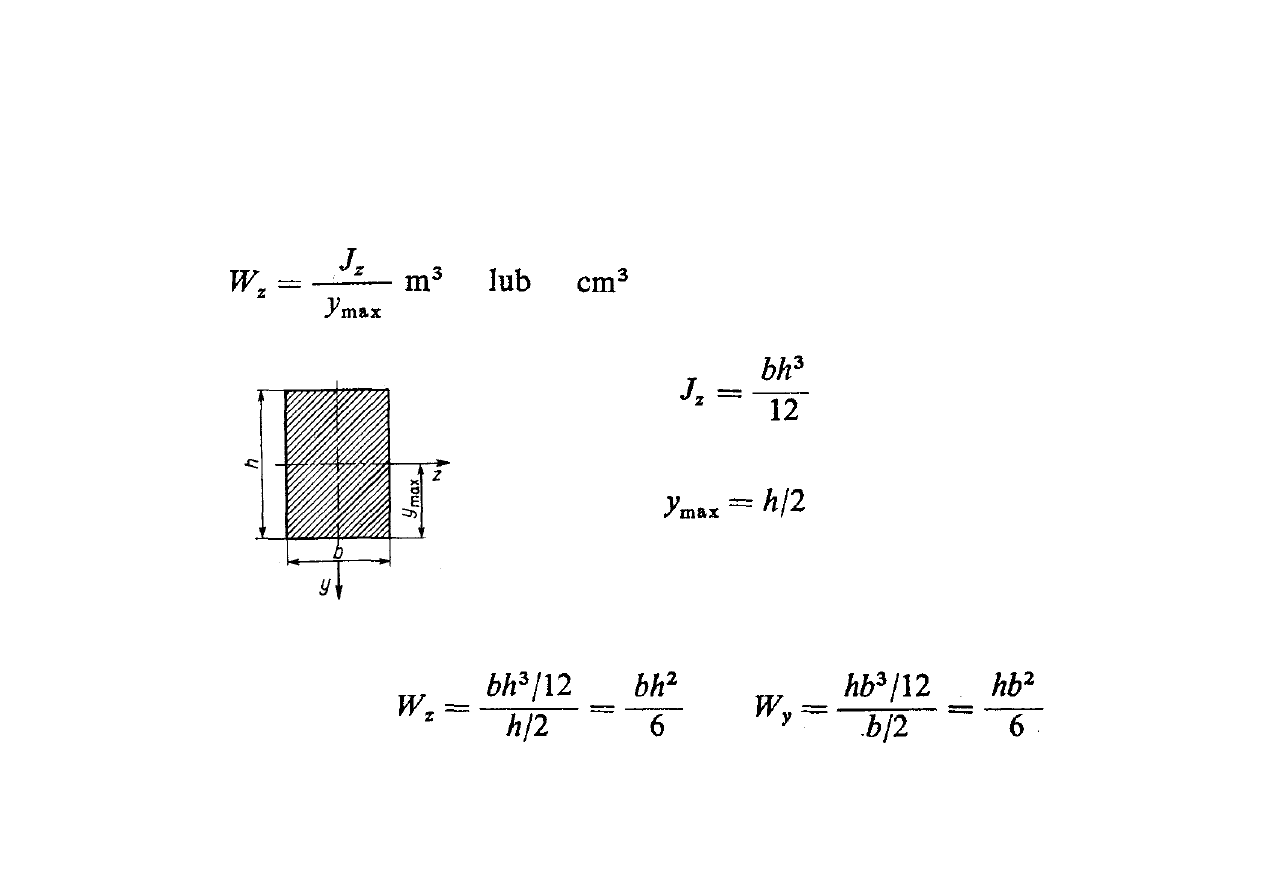
Wskaźnik wytrzymałości przekroju na zginanie

Odległość max oddalonych punktów przekroju

Moment bezwładności pola prostokąta wynosi

Wskaźnik

wytrzymałości

przekroju

prostokątnego dla osi Z i Y wynosi:

2008-12-17

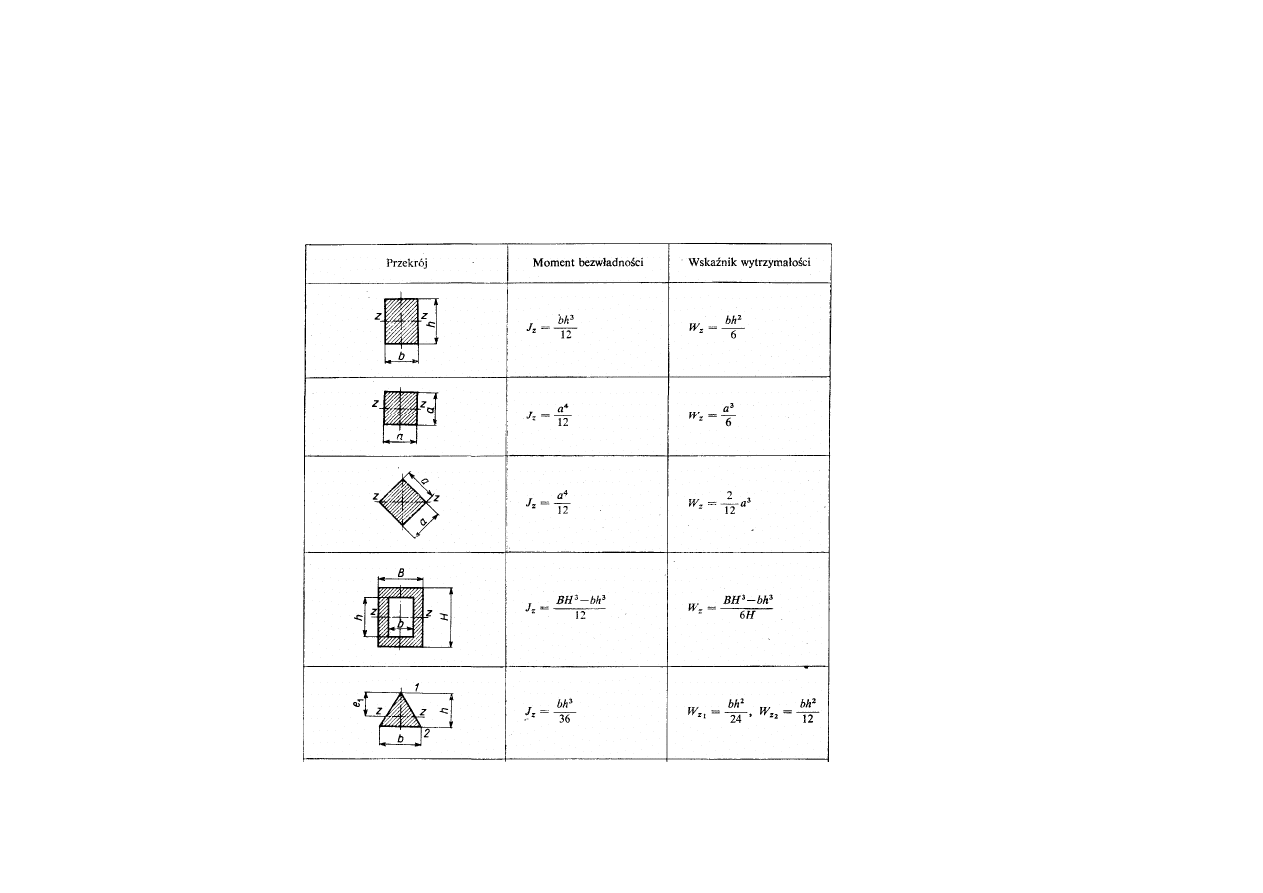
17

Wskaźnik wytrzymałości przekroju na zginanie

2008-12-17

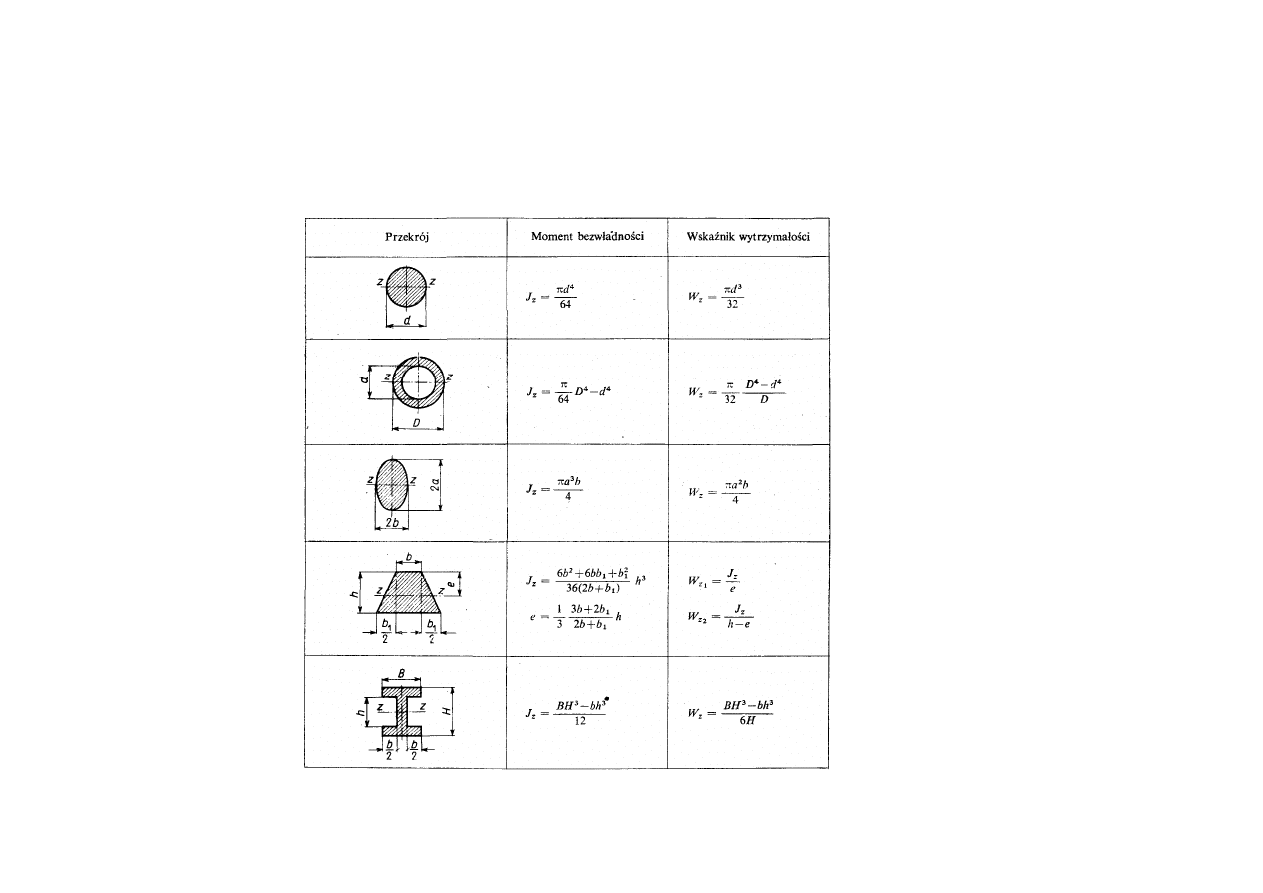
18

Wskaźnik wytrzymałości przekroju na zginanie

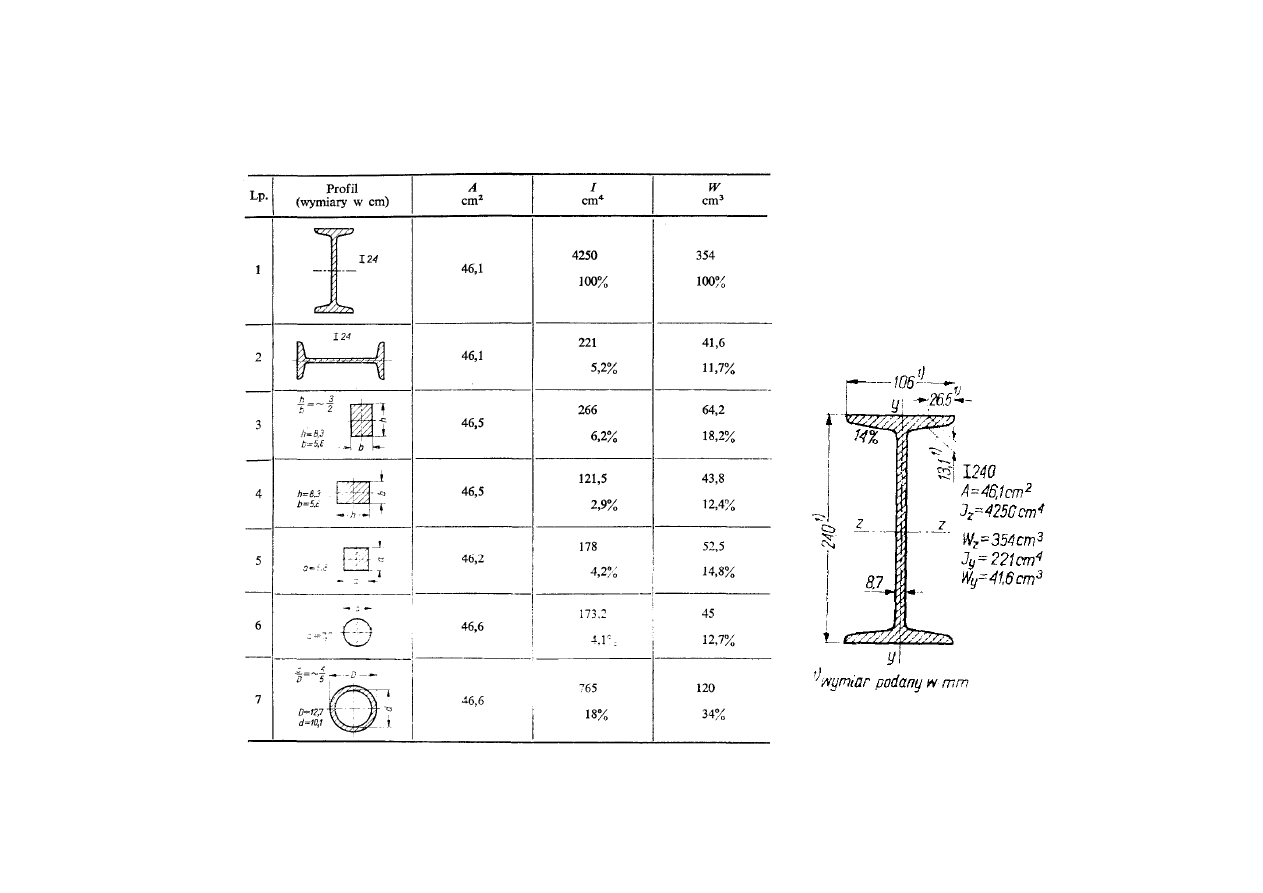
2008-12-17

19

Przydatność

profilu do zginania

przy A=const

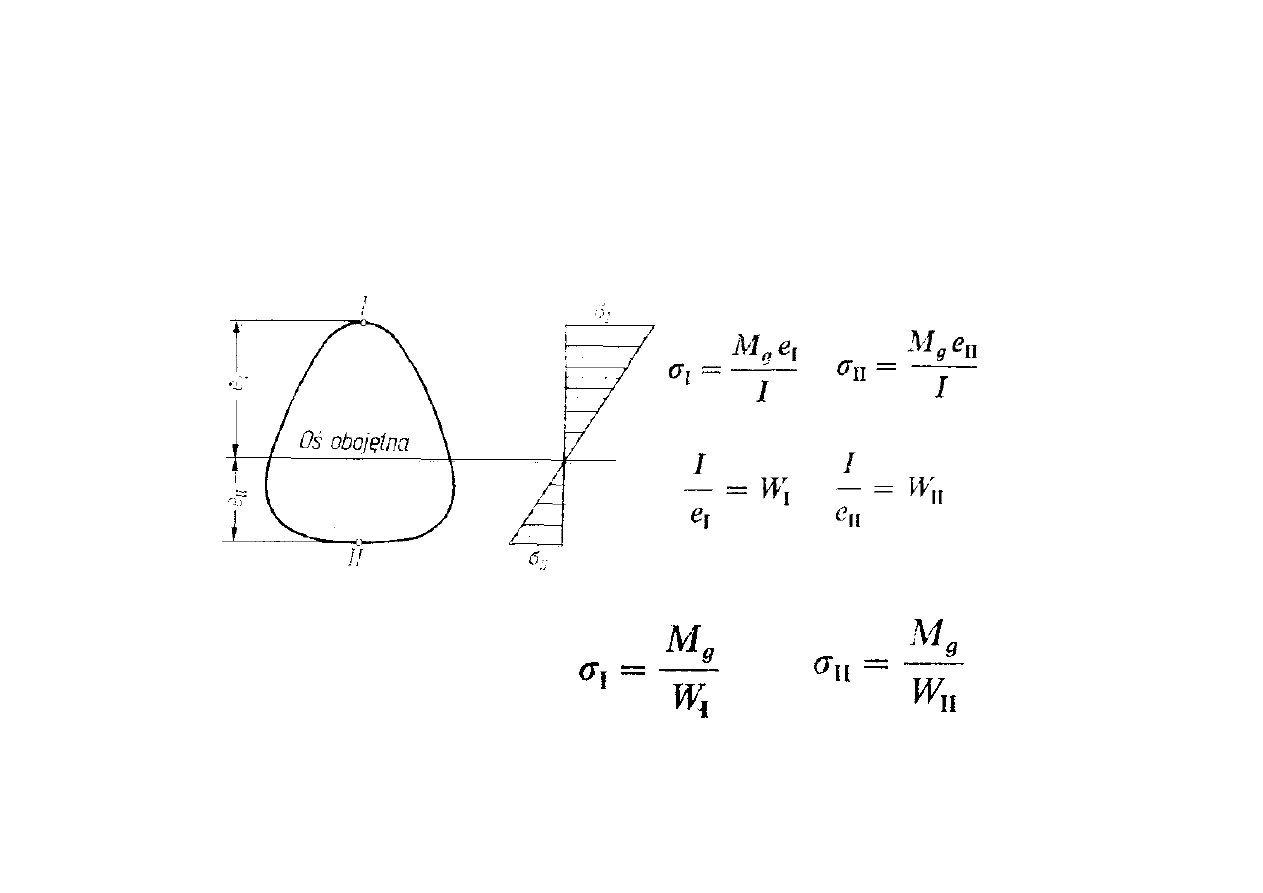
2008-12-17

20

Wytrzymałość na zginanie

otrzymamy:

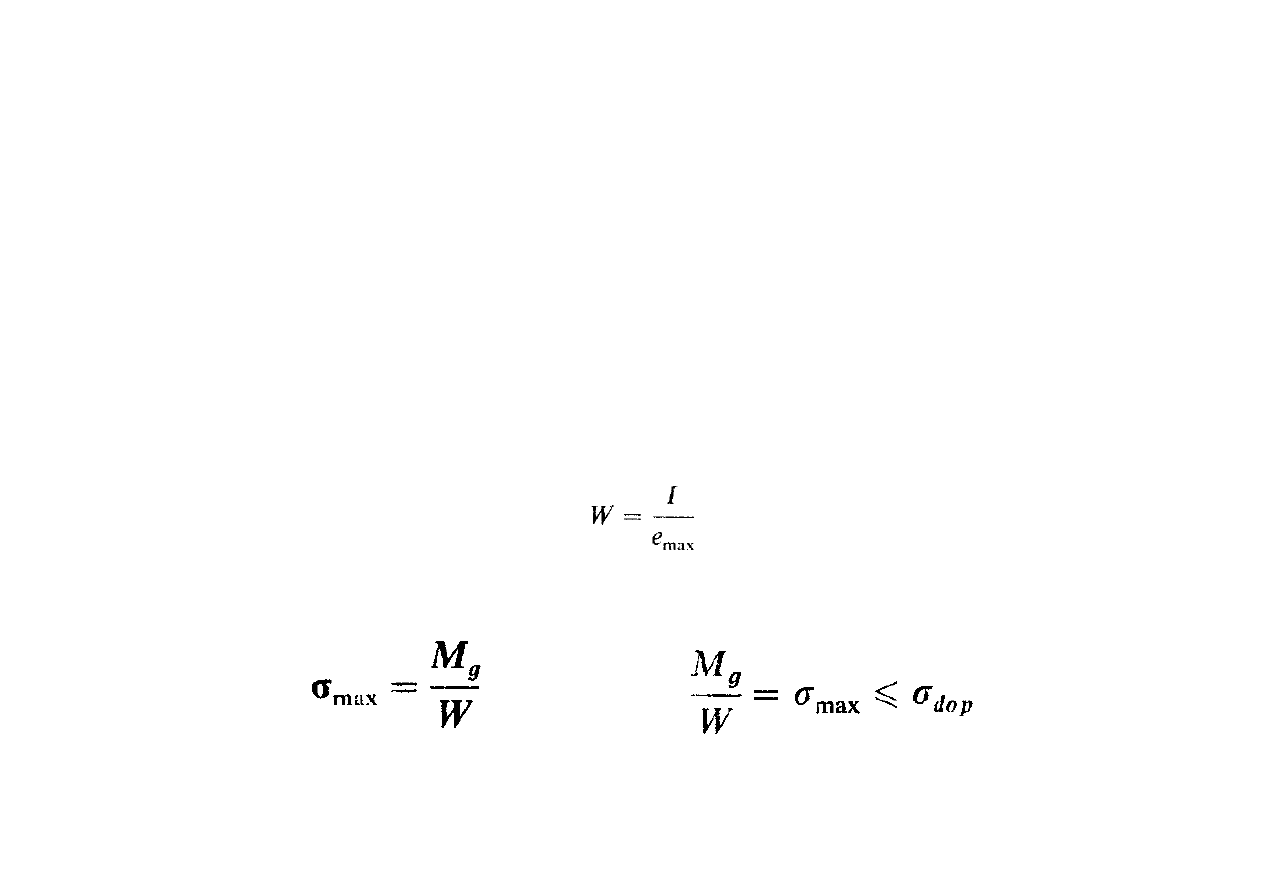
2008-12-17

21

Wytrzymałość na zginanie

UWAGA:

1.

W przypadku gdy odległości są równe (e

I

=e

II

=e) można mówić o jednym

wskaźniku wytrzymałości przekroju na zginanie.

2.

Jeśli materiał ma jednakową wytrzymałość na ściskanie i rozciąganie
podstawą do oceny wytrzymałości pręta zginanego będzie bezwzględnie
największa wartość naprężenia.

Przyjmując jeden wskaźnik

gdzie e

max

jest największą odległością skrajnego włókna od

osi obojętnej otrzymujemy:

2008-12-17

22

Wytrzymałość na zginanie

Przykład

2008-12-17

23

Wytrzymałość na zginanie

2008-12-17

24

Wytrzymałość na zginanie

UWAGA:

1.

W przypadku belek krótkich obliczenia przeprowadza się niezależnie dla
max

naprężeń

zginających

i

max

naprężeń

stycznych

(tnących)

wywołanych siłami poprzecznymi.

Warunki wytrzymałościowe określają nierówności:

Gdzie: T – siła poprzeczna w rozpatrywanym przekroju,

S

(y)

– moment statyczny względem osi obojętnej części pola przekroju

poprzecznego belki,
b

(y)

- szerokość warstwy równoległej do osi obojętnej

Jest to tzw. wzór Żurawskiego

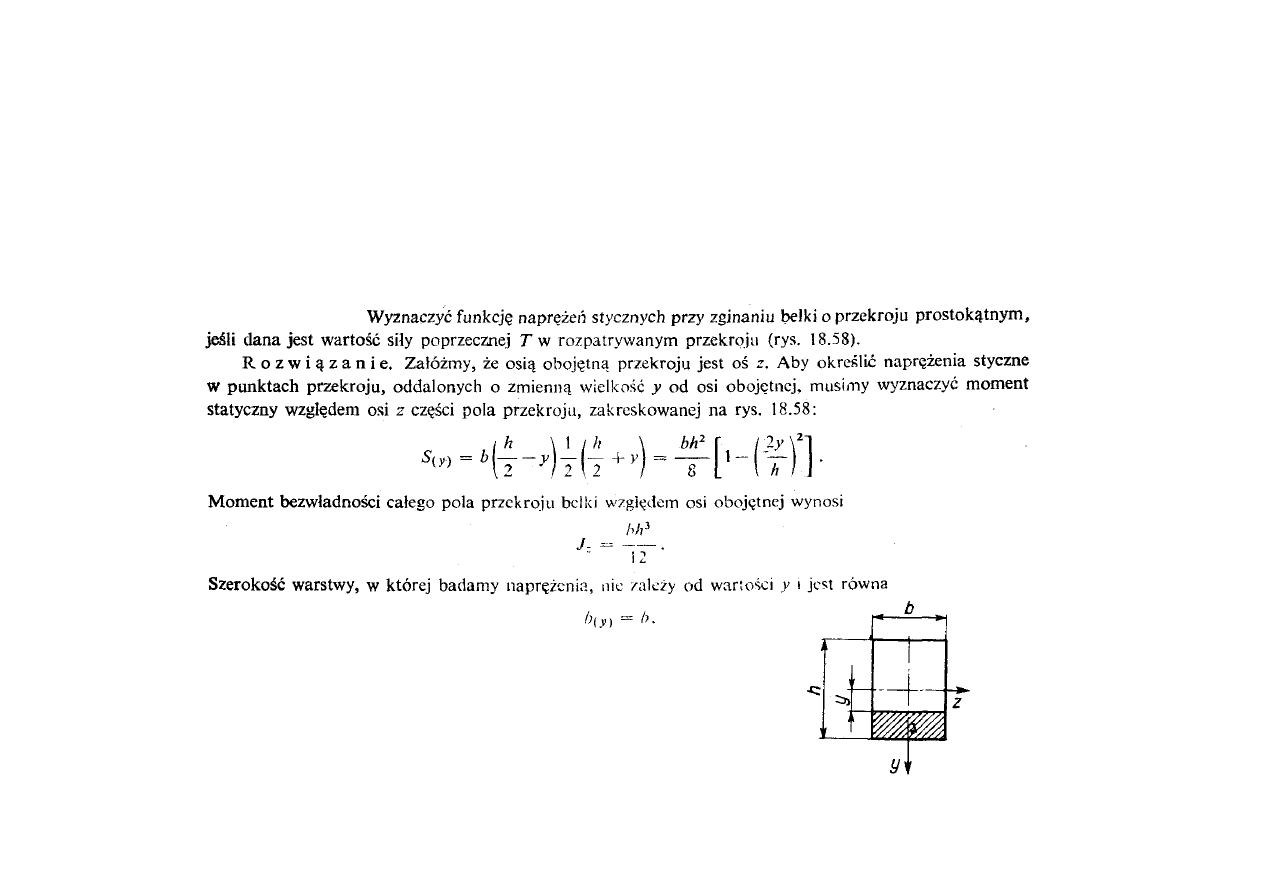
2008-12-17

25

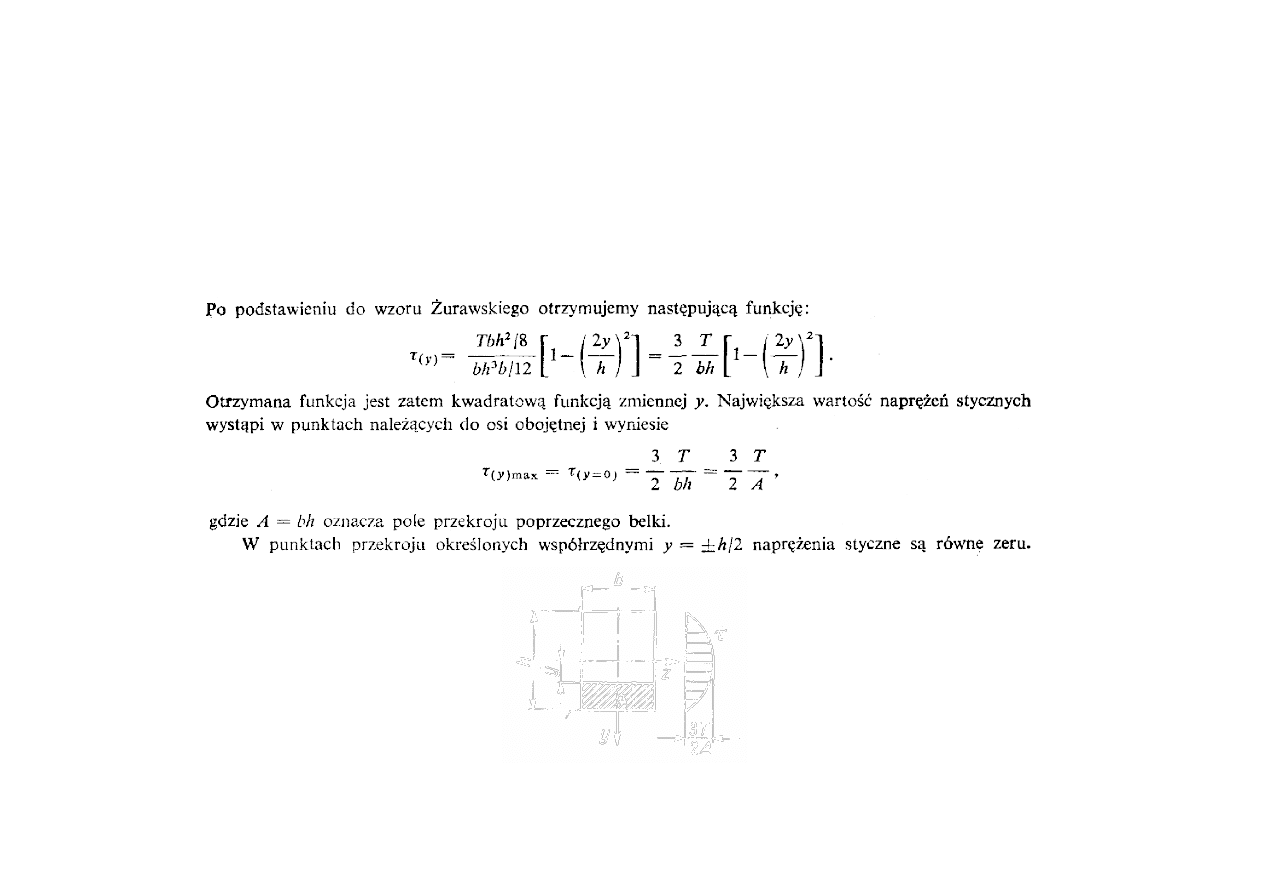
Wytrzymałość na zginanie

Przykład

2008-12-17

26

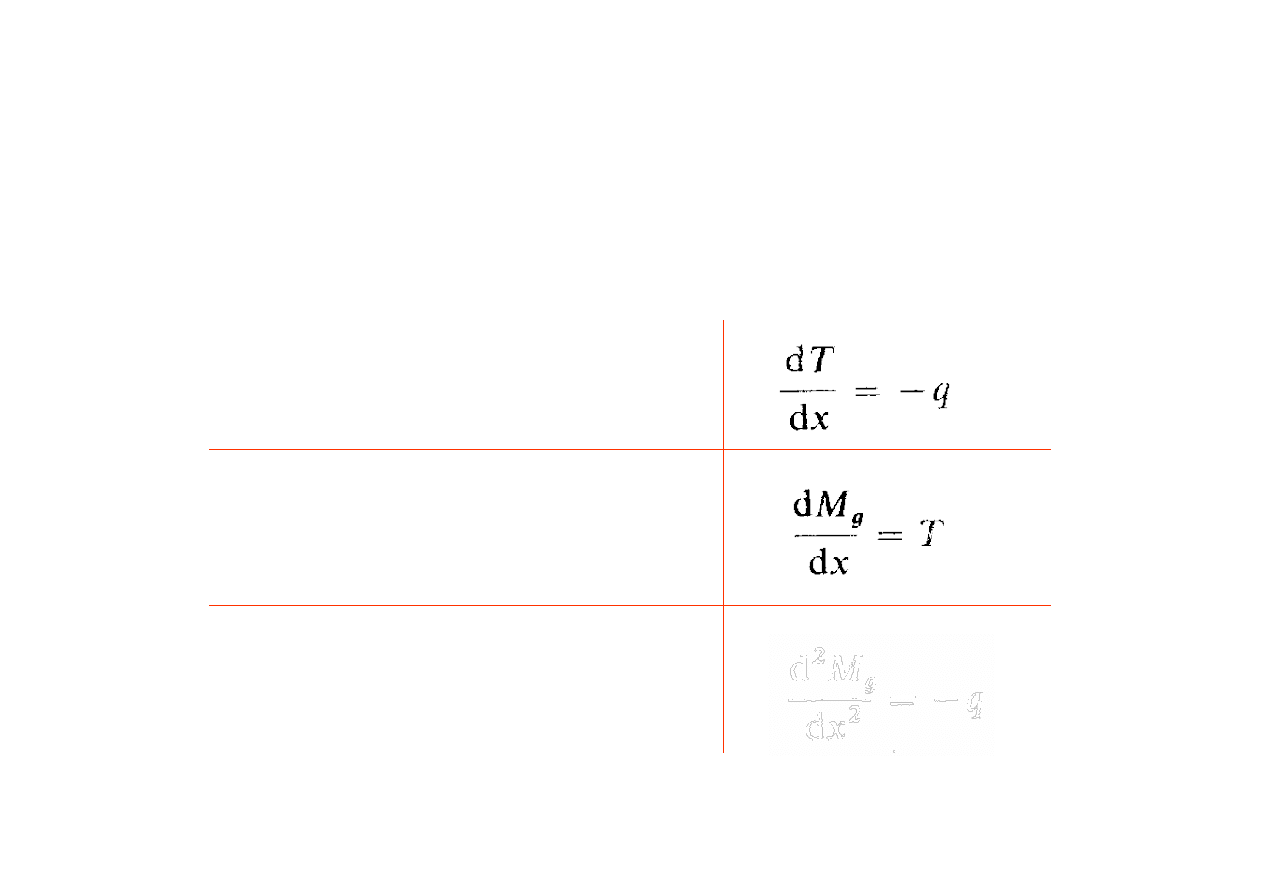
Wytrzymałość na zginanie

2008-12-17

27

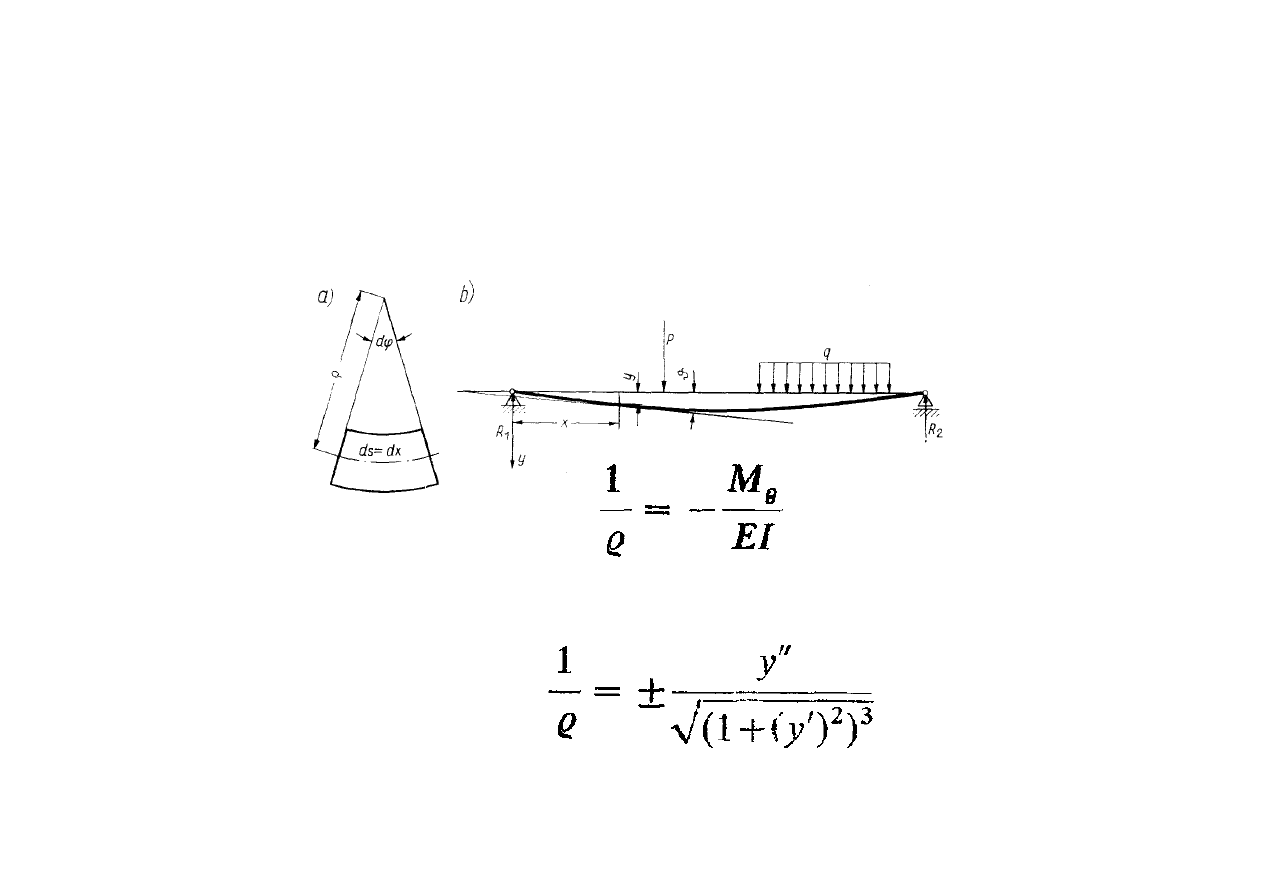
Równanie różniczkowe osi ugiętej

Zależności różniczkowe pomiędzy obciążeniem i siłami wewnętrznymi

Pochodna siły poprzecznej względem
współrzędnej x wzdłuż osi pręta jest
równa natężeniu obciążenia ciągłego.

Pochodna momentu gnącego względem
x jest równa sile poprzecznej.

Druga pochodna momentu gnącego
względem x jest równa natężeniu
obciążenia ciągłego.

2008-12-17

28

Równanie różniczkowe osi ugiętej

Z geometrii różniczkowej krzywiznę dowolnej krzywej płaskiej
przedstawia równanie:

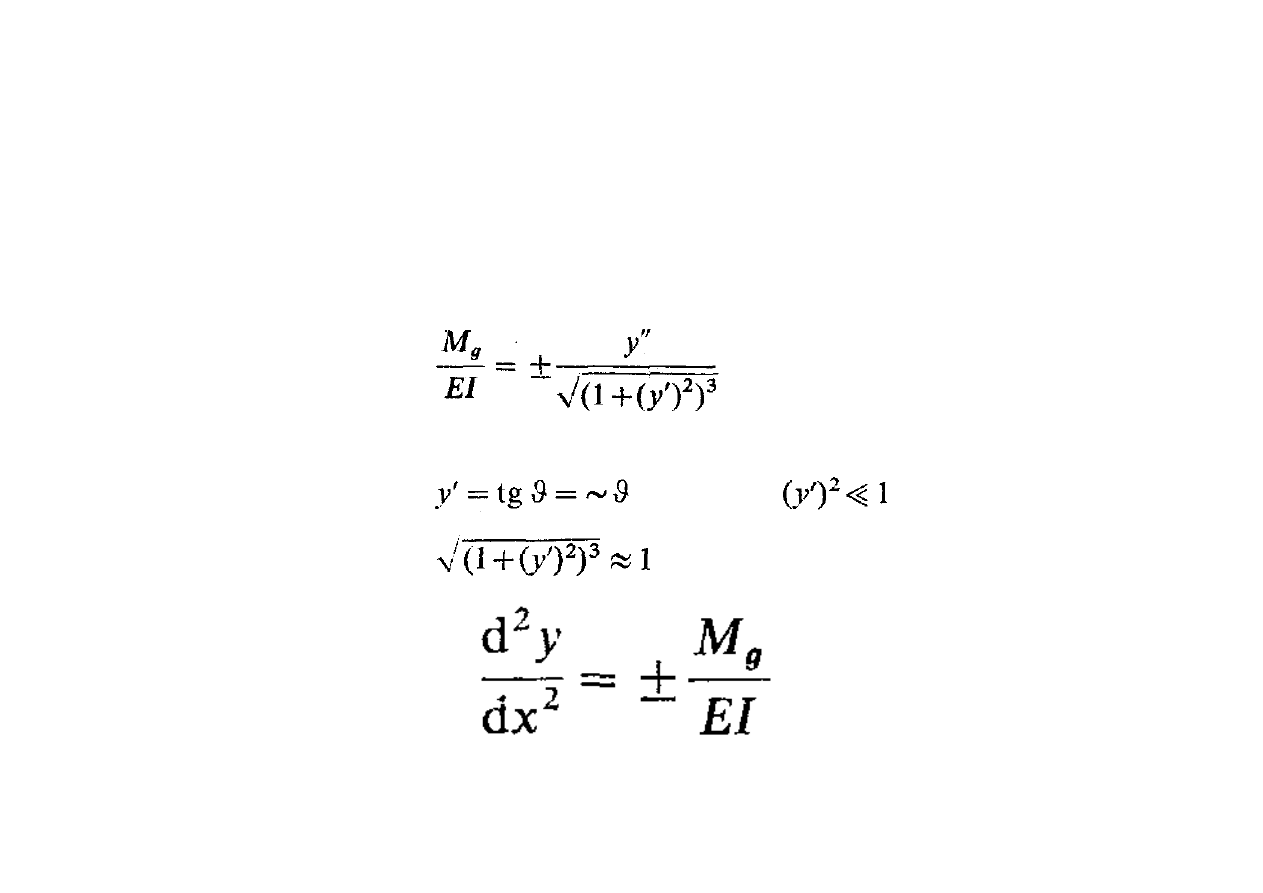
2008-12-17

29

Równanie różniczkowe osi ugiętej

Porównując oba równania otrzymamy:

Równanie te nazywamy równaniem różniczkowym linii ugięcia

Uwzględniając: oraz

otrzymamy:

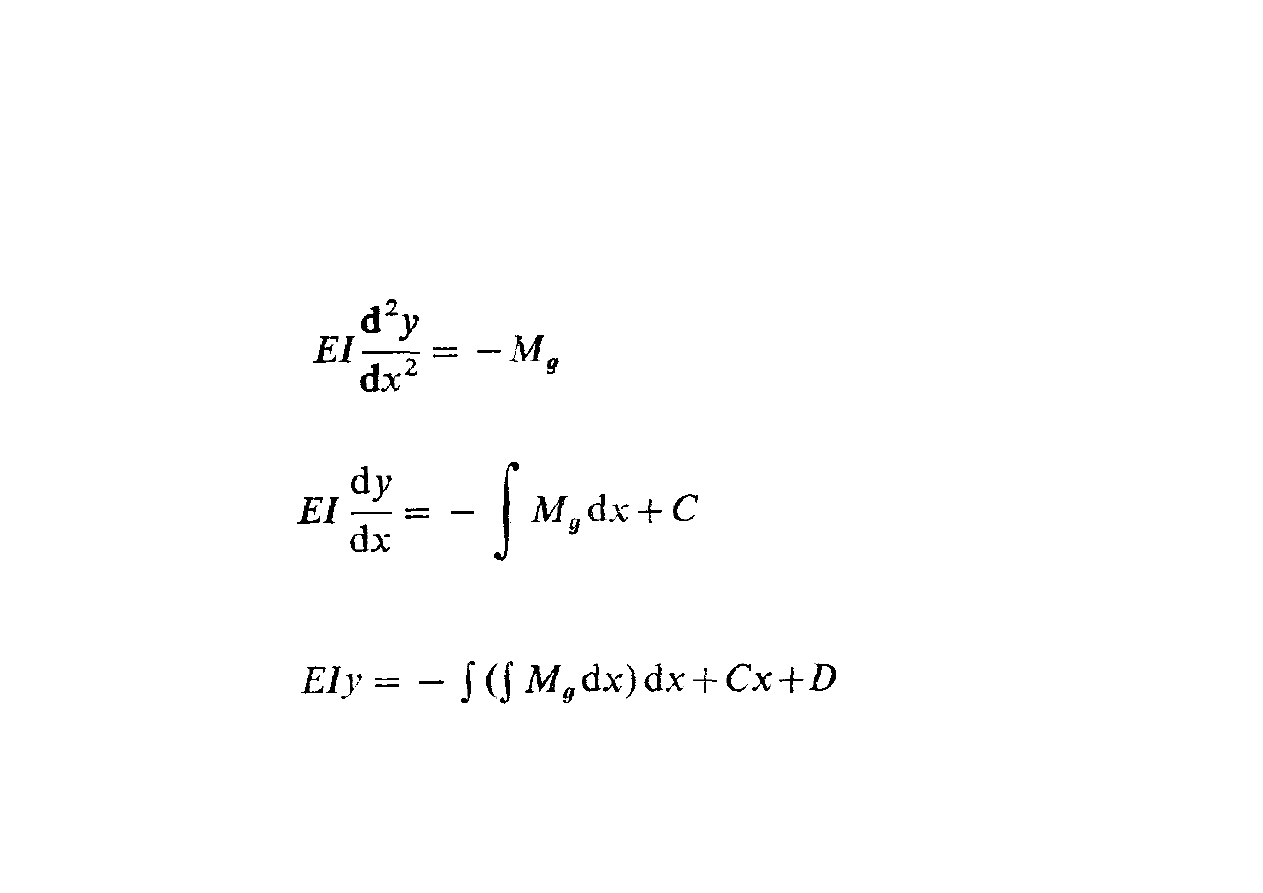
2008-12-17

30

Równanie różniczkowe osi ugiętej

Po jednokrotnym całkowaniu otrzymujemy:

Całkując powtórnie:

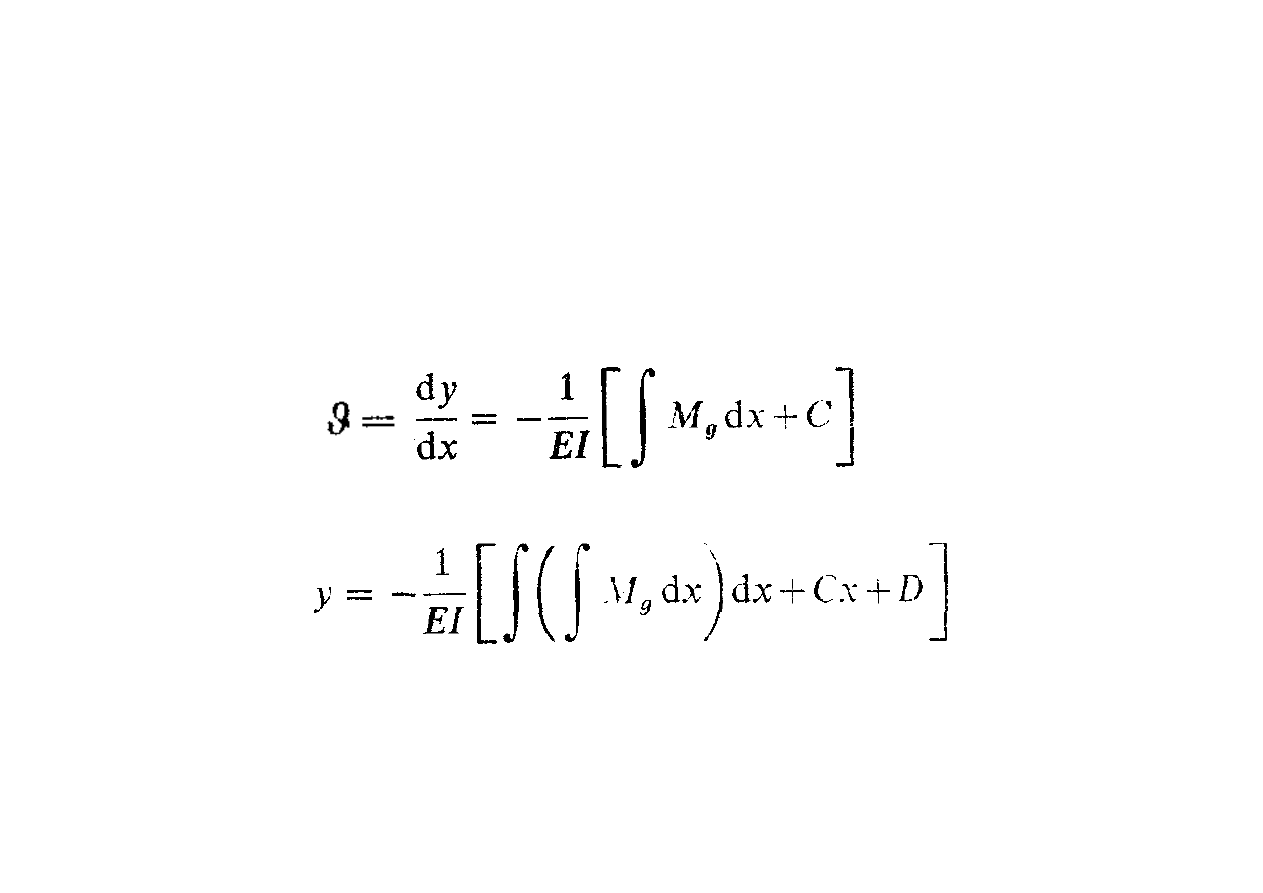
2008-12-17

31

Równanie różniczkowe osi ugiętej

W ten sposób dochodzimy do równań, z których pierwsze określa
równanie kątów obrotu przekrojów

natomiast drugie równanie osi odkształconej belki

2008-12-17

32

Równanie różniczkowe osi ugiętej

Warunki brzegowe do wyznaczania równania osi ugiętej

2008-12-17

33

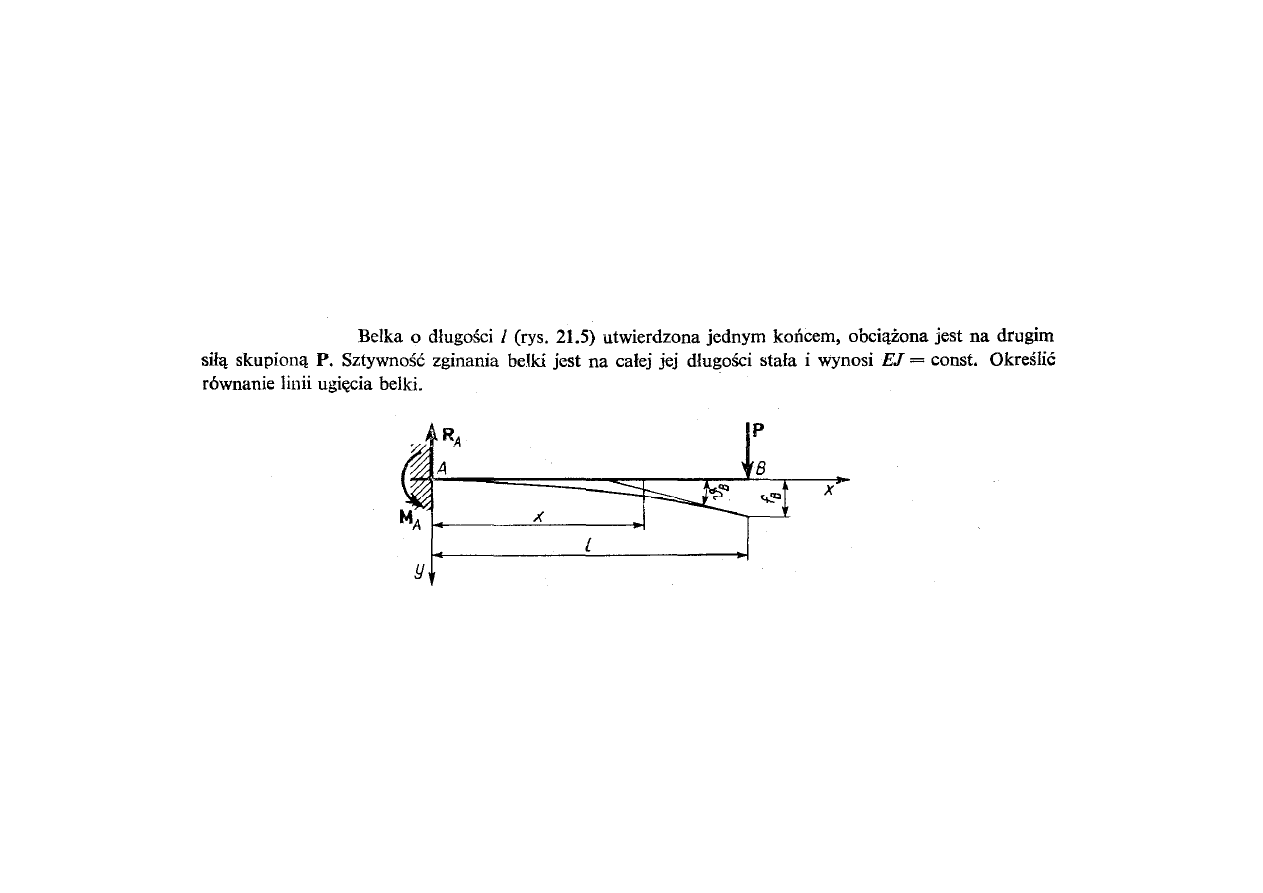
Równanie różniczkowe osi ugiętej

Przykład

2008-12-17

34

Równanie różniczkowe osi ugiętej

2008-12-17

35

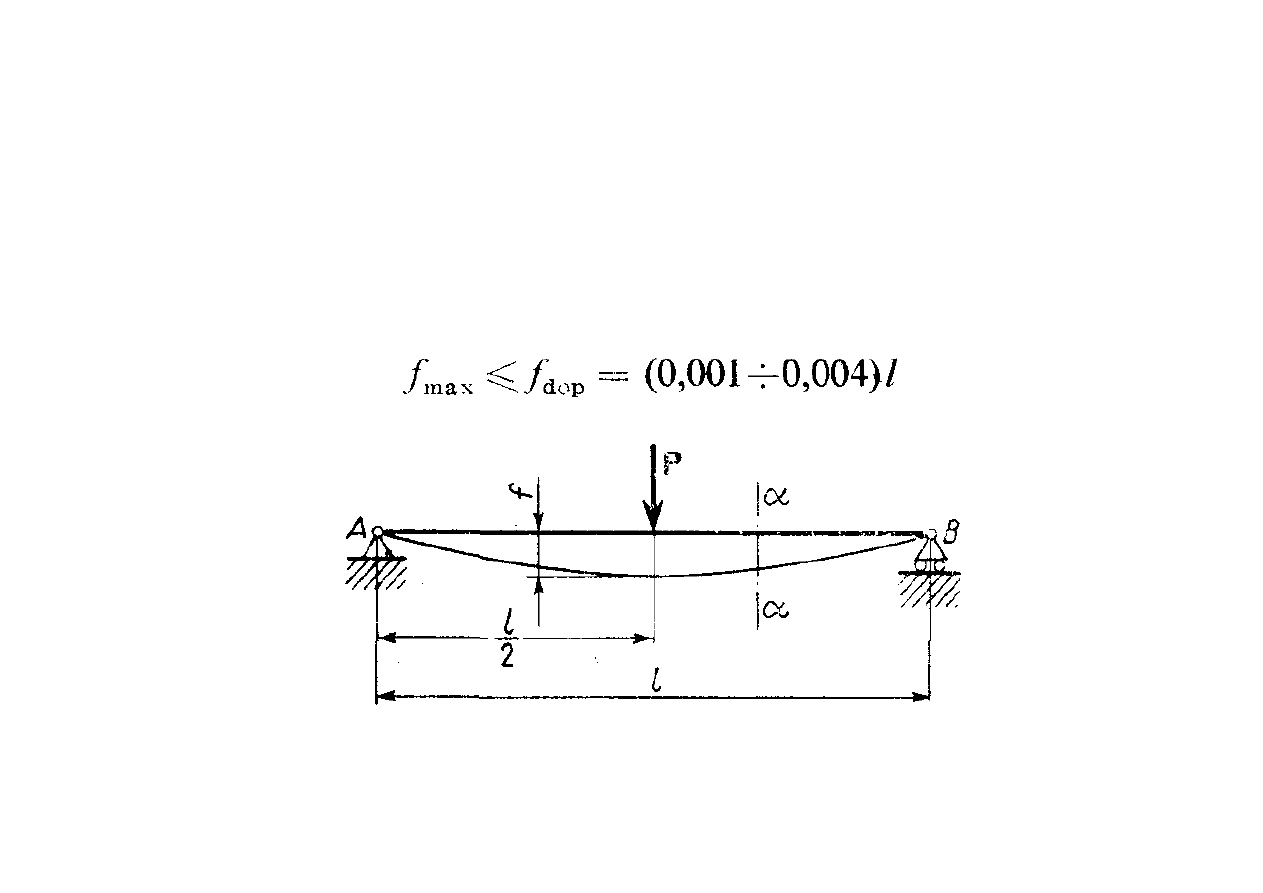
Wyznaczanie odkształceń belek zginanych

Obliczanie wymiarów poprzecznych belki zginanej ze względu na
jej sztywność.

założenie:

2008-12-17

36

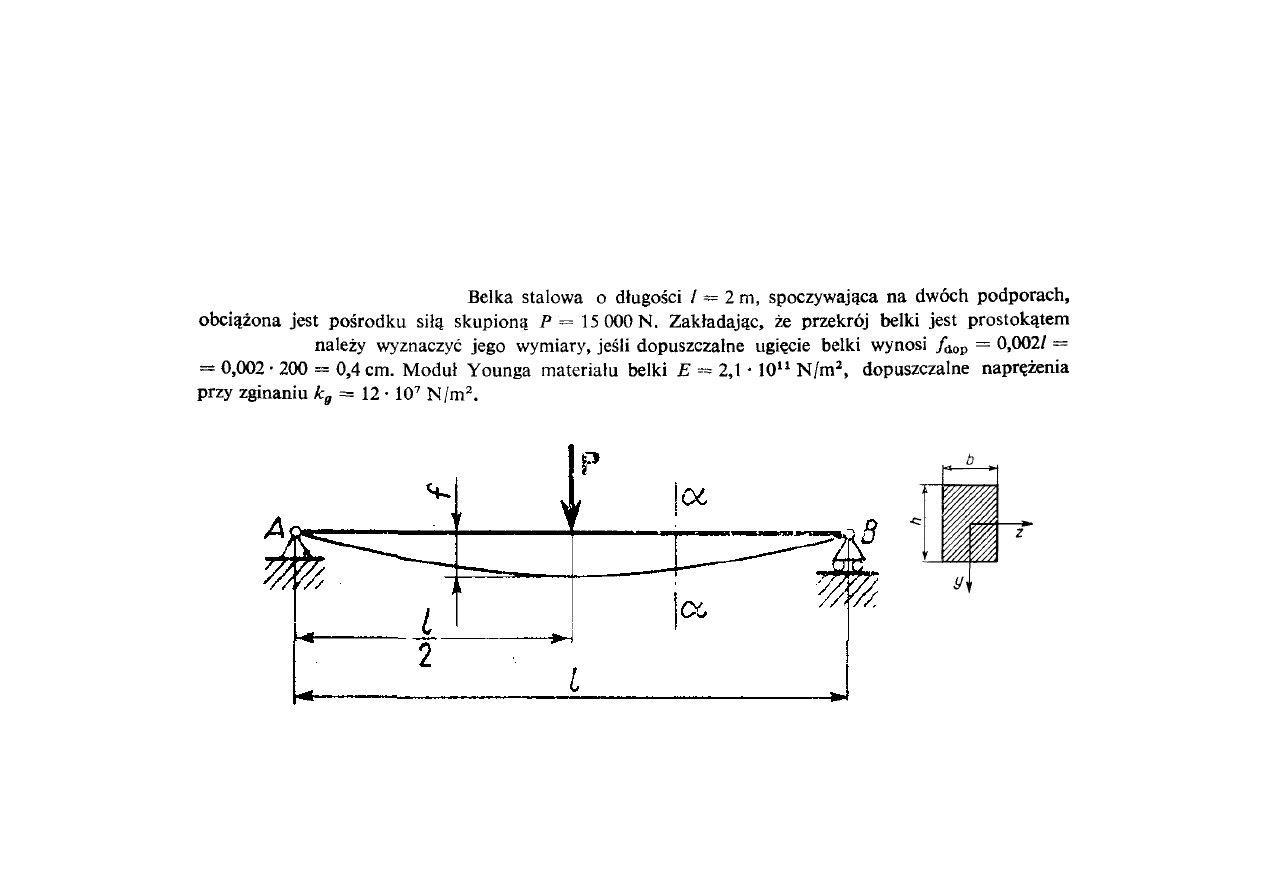
Wyznaczanie odkształceń belek zginanych

Przykład

2008-12-17

37

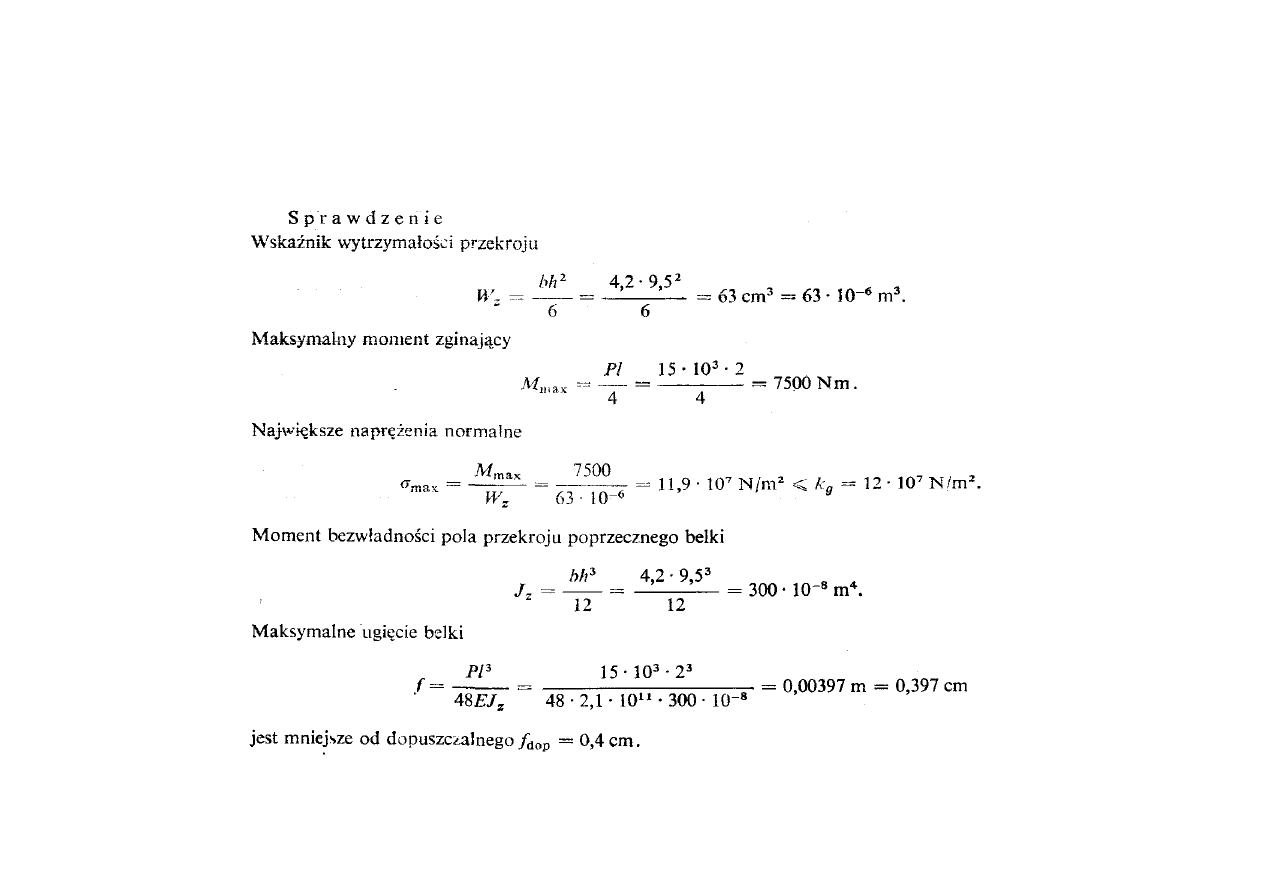
Wyznaczanie odkształceń belek zginanych

2008-12-17

38

Wyznaczanie odkształceń belek zginanych