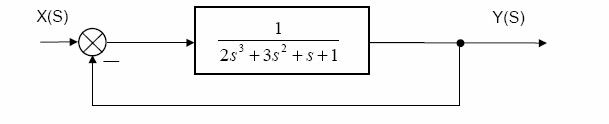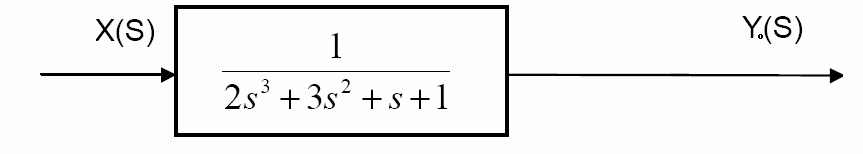PRZYKŁAD 1

Określ dla jakich wartości K oraz T układ zadany poniższą transmitancją jest stabilny w sensie Hurwitza:

3 K ( s + )

3

G( s) =

s 4 + s 3

3

+ 4 s 2 + Ts + K

Rozwią zanie

1. Wyznaczenie równania charakterystycznego: R.CH stanowi zawsze mianownik transmitancji układu: s 4 + 3 s 3 + 4 s 2 + Ts + K

2. Wyznaczenie współczynników potrzebnych do wyznaczenia macierzy Hurwitza: Indeks współczynnika jest zawsze taki sam jak potęga, przy której jest umiejscowiony, więc: a

1

4 =

a

3

3 =

a

4

2 =

a 1 = T

a 0 = K

3. Warunek konieczny stabilności:

1 > ;

0

3 > ;

0

4 > ;

0

T > ;

0

K > ;

0

4. Wyznaczenie macierzy Hurwitza:

 a

a

0 

 3

1



H =  a

a

a

4

2

0 





 0

a

a

3

1 

Stąd:

3 T

0 





H = 1 4 K 





0

3

T 

_________________________________________________

1 _

_______________________________________________

Powered by xtoff®

[e-mail]

5. Konstruowanie wyznaczników kolejnych minorów:

∆ = 3

1

3 T

∆

2 =

=12 − T

1

4

3 T

0

∆ = 1 4 K = [

3 4 T − 3 K ] − T ⋅ 3

3

0

3

T

6. Określenie warunków stabilności

Z ∆ > 0 wynika:

1

T > 0

Z ∆ > 0 wynika:

2

T < 12

Z ∆ > 0 wynika:

3

K < T

Tak więc, aby układ był stabilny:

0<T<12 oraz 0<K<T

PRZYKŁAD 2

Zbadać stabilność poniższego układu za pomocą wybranego kryterium:

Rozwią zanie

Należy zwrócić uwagę, iż bardzo rzadko spotyka się zadanie, w którym jest do wyboru kryterium oceny stabilności. Kiedy można wybrać sposób, należy dobrze przemyśleć, które kryterium wybierzemy. Najczęściej bowiem z pośród całej gamy środków oceny stabilności tylko jeden jest optymalny, a reszta znacznie bardziej uciążliwa w obliczeniach matematycznych i znacznie dłuższa (co nie oznacza, że tymi metodami nie dojdziemy do tych samych wniosków).

Czytelnik może, w ramach samodoskonalenia się, wyznaczyć równanie charakterystyczne CAŁEGO układu i ocenić jego stabilność na podstawie kryterium Hurwitza _________________________________________________

2 _

_______________________________________________

Powered by xtoff®

[e-mail]

W podanym przykładzie należy zauważyć, iż w sprzężeniu zwrotnym nie występuje żadna transmitancja. A więc transmitancja układu OTWARTEGO będzie identyczna jak ta w głównej gałęzi układu zamkniętego. Dzięki czemu można zauważyć, że najbardziej korzystnym kryterium stabilności będzie kryterium Nyquista. Poniżej przedstawiono schemat rozwiązywania takiego układu.

1 Wyznaczenie transmitancji układu OTWARTEGO (czyli takiego, który jest „rozpięty” w węźle sumacyjnym:

Tak więc transmitancja układu otwartego wynosi: 1

G ( s)

o

= 2 3 s + 3 2 s + s +1

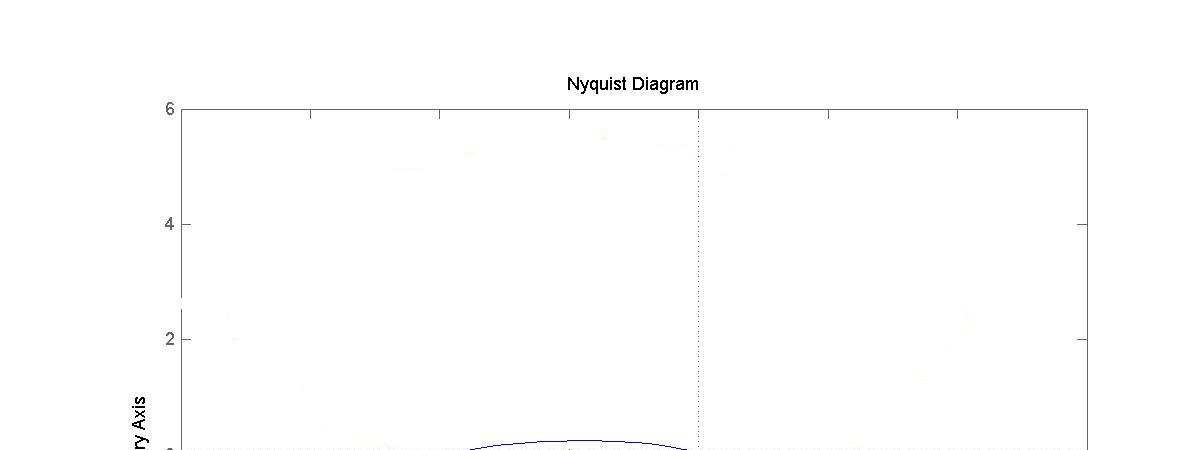
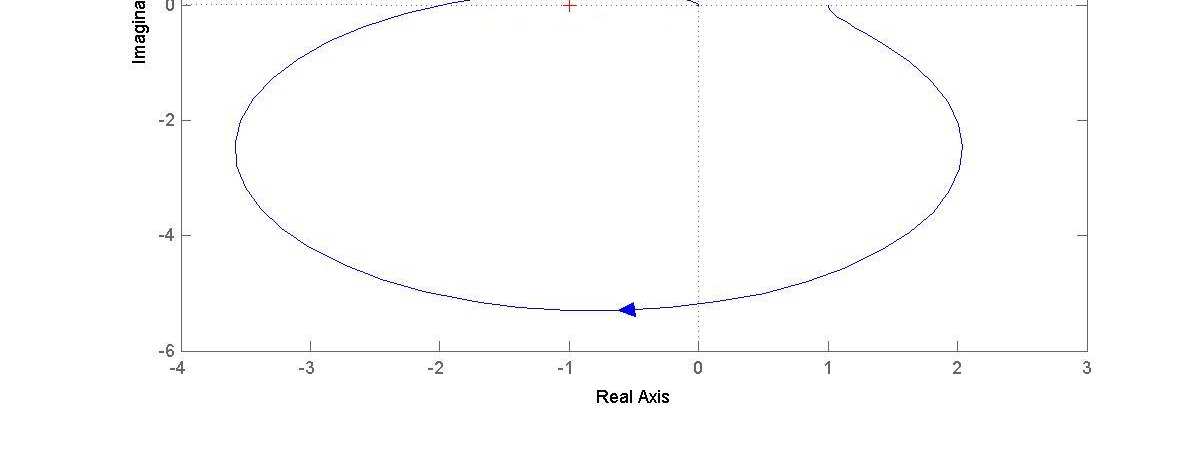
2. Teraz należy narysować charakterystykę amplitudowo-fazową takiego układu (czytelnik, w ramach praktyki zrobi to ręcznie):

3. Określenie stabilności:

Jak widzimy charakterystyka obejmuje punkt [-1,0j] (czerwony krzyżyk obrazuje ten punkt).

Wnioskujemy zatem na podstawie charakterystyk Nyquista układu OTWARTEGO, że układ ZAMKNIĘTY jest niestabilny.

_________________________________________________

3 _

_______________________________________________

Powered by xtoff®

[e-mail]