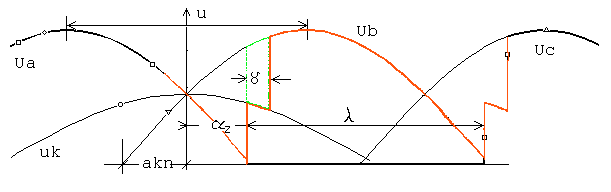
PROSTOWNIK P-PULSOWY (P-IV) Obliczanie warto ci redniej napi cia wyprostowanego prostownika p - pulsowego z uwzgl dnieniem komutacji zaworów na przykładzie układu jednokierunkowego.

Zało enia :

u +

a

u

- u =

sin(ω + π − α ) ,

u =

sin(ω + α ) ,

u

b

=

,

b

U m

t

a

U m

t

kn

kn

k

2

- pr d wyprostowany ma stał warto (brak t tnie ) wskutek b.du ej indukcyjno ci odbiornika; do celów analizy odbiornik mo na zast pi idealnym ródłem pr dowym,

- rezystancja sieci zasilaj cej jest pomini ta a L jest zast pcz indukcyjno ci jednej fazy widzian na wej ciu przekształtnika.

p αz+λ

p αz+γ

U =

ω −

(

−

)dω

d

u bd t

u b u k

t

2π

2π

αz

αz

p αz+λ

p αz+γ

U =

sin(ω + α ) ω −

cosα sin(ω ) ω

d

Um

t

kn d t

Um

kn

t d t

2π

2π

αz

αz

=

p

π

p

π

U

sin cosα

sin

cosα

cos(α

γ)

(*)

m

z − U m

(

z −

z +

)

π

p

2π

p

Uwaga:

• Pierwszy człon wyra enia (*) jest taki sam jak wzór ko cowy uzyskany dla przypadku komutacji

natychmiastowej (P.III).

• Analiza przebiegu pr dów podczas komutacji posłu y do przekształcenia wzoru (*), eliminuj c z niego k t γ.Podstawiaj c zale no uzyskan w wyniku analizy procesu komutacji (P-V), poszukiwany wzór na warto redni napi cia wyprostowanego prostownika p-pulsowego, przyjmie posta : p

π

L

ω ⋅ I

U

d

=

sin cosα −

⋅

d

Um

z

p

π

p

2π

Dla układu 3T podstawiamy p = 3 i Um = Ufm a dla układu 3T-3T odpowiednio p = 6 i Um = Upm.

s_32122 J. Piłaci ski: Podstawy energoelektroniki - materiały do wykładu

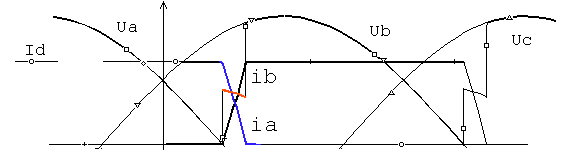
PROSTOWNIK P-PULSOWY (P -V) Komutacja prosta w układzie p - pulsowym prostownika ua

ub

ω di

di

L a

ωL b

I

dωt

dωt

d

ia ib Równanie Kirchoffa dla obwodu zwarcia utworzonego przez komutuj ce fazy ma nast puj c posta : dia

di

u

b

− ω

+ ω

−

= 0

(*)

a

L

L

u

d t

ω

d t

b

ω

Z warunku: i +

= wynika, e pochodne pr dów płyn cych w fazach a i b s równe i maj przeciwne a

ib Id

dia

di

znaki

b

= −

.

Podstawiaj c

w

równaniu

(*)

napi cie

przewodowe

d t

ω

d t

ω

π

u =

−

= −2

sin sin ω i eliminuj c jedn z pochodnych pr du uzyskujemy zale no : ab

ua ub

Um

t

p

U

π

i

m

= −

sin

sin ω ⋅ ω +

a

t d t C

L

ω

p

Stał całkowania wyznacza si podstawiaj c : ia=Id dla ωt = αz, oraz ia = 0 dla ωt = αz + γ.

W wyniku analizy uzyskuje si nast puj c zale no : ωL ⋅ I

cosα

d

−

+

=

.

z

cos(αz γ)

π

Um sin p

Po przekształceniu otrzymamy wzór pozwalaj cy wyznaczy k t komutacji: (sk d wzór pozwalaj cy wyznaczy k t komutacji ma posta :) ωL ⋅

γ =

I

arccos cosα

d

.

z −

π − αz

Um sin p

s_3213b J. Piłaci ski: Podstawy energoelektroniki - materiały do wykładu