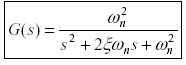Podstawy Automatyki – ćwiczenia w Matlab z przykładami

% wyznaczenie pierwiastkow rownania char

%dane jest rownanie postaci

% a(n)*x^x+a(n-1)*x^(n-1)+....a0*x^0=0

% podaj macierz wspolczynnikow wielomianu

% a=[a(n) a(n-1) a(0)]

% komenda ROOTS(C)

% przyklad

disp(' dla rownania postaci A2*x^2+A1*x-A0=0'); disp(' podaj wspolczynniki');

A(1)=input('A2=');

A(2)=input('A1=');

A(3)=input('A0=');

disp(' macierz A wspolczynnikow rowania'); A

Pierwiastki=Roots(A);

disp(' pierwiastki rowania wynosza');

Pierwiastki(1)

Pierwiastki(2)

disp(' po podstawieniu do rownania uzyskuje sie'); wynik1=A(1)*(Pierwiastki(1)^2)+A(2)*(Pierwiastki(1))+A(3) wynik2=A(1)*(Pierwiastki(2)^2)+A(2)*(Pierwiastki(2))+A(3)

% przeksztalcenie liczb zespolonych

disp(' dla liczby zespolonej postaci a+jb'); disp(' podaj ');

a=input('a=');

b=input('b=');

disp(' podales liczbe');

c=a+b*j

disp(' liczba sprzezona to');

c1=a-b*j

disp(' Modul liczby wynosi');

Modul=sqrt(a^2+b^2)

disp(' kat w radianach wynosi');

if a~=0

fi=atan(b/a)

else fi=pi/2

end

disp(' kat w stopniach wynosi');

alfa=fi*360/(2*pi)

% Operacje na liczbach zespolonych

disp(' dla liczby zespolonej postaci c1=a1+jb1'); disp(' podaj ');

a1=input('a1=');

b1=input('b1=');

disp(' dla liczby zespolonej postaci c2=a2+jb2'); disp(' podaj ');

a2=input('a2=');

b2=input('b2=');

disp(' podales liczby');

c1=a1+b1*j

c2=a2+b2*j

disp(' dodawanie');

c=c1+c2

disp(' mnozenie');

c=c1*c2

disp(' dzielenie');

c=c1/c2

% Operacje na liczbach zespolonych

disp(' dla liczby zespolonej postaci c1=|M1|exp(jfi1)'); disp(' podaj ');

M1=input('|M1|=');

fi1=input('f1=');

disp(' dla liczby zespolonej postaci c2=|M2|exp(jfi2)'); disp(' podaj ');

M2=input('|M2|=');

fi2=input('|fi2|=');

disp(' podales liczby');

c1=M1*exp(j*fi1)

c2=M2*exp(j*fi2)

disp(' dodawanie');

c=c1+c2

disp(' mnozenie');

c=c1*c2

disp(' dzielenie');

c=c1/c2

% transformata laplacea

disp(' dla zaleznosci f(t)=exp(a*t)'); syms a t f %definicja symboli

f=exp(a*t)

disp(' tranfl\formata lapclacea wynosi '); laplace(f)

disp(' dla zaleznosci f(t)=sin(a*t)'); syms a t f %definicja symboli

f=sin(a*t)

disp(' tranfl\formata lapclacea wynosi '); laplace(f)

disp(' dla zaleznosci f(t)=d(sin(a*t))dt'); syms a t f %definicja symboli

% domyslnie liczona jest pochodna po czasie f=diff(sin(a*t))

disp(' tranfl\formata lapclacea wynosi '); laplace(f)

disp(' dla zaleznosci f(t)=exp(-a*t)*sin(w*t)'); syms a t f w %definicja symboli

% domyslnie liczona jest pochodna po czasie f=exp(-a*t)*sin(w*t)

disp(' tranfl\formata lapclacea wynosi '); laplace(f)

% transformata odwrotna laplacea

disp(' dla zaleznosci F(s)=3*s+10/(12+7s+s^2)'); syms s %definicja symboli

%disp(' tranfl\formata lapclacea wynosi '); F=(3*s+10)/(s^2+7*s+12)

ilaplace(F)

disp(' dla zaleznosci F(s)=4/(s*(2*s+1)'); syms s %definicja symboli

%disp(' tranfl\formata lapclacea wynosi '); F=4/(s*(2*s+1))

ilaplace(F)

%wyswietlenie odpowiedzi czasowej przy danej transmitancji disp(' podaj wspolczynniki licznika L1*s+L2'); syms s

L(1)=input('L1=');

L(2)=input('L2=');

disp(' podaj wspolczynniki mianownika (M1*s+M2)*(M3*s+M4)*(M5*s+M6)'); M(1)=input('M1=');

M(2)=input('M2=');

M(3)=input('M3=');

M(4)=input('M4=');

M(5)=input('M5=');

M(6)=input('M6=');

disp(' dana transmitancja');

Fs=((L(1)*s)+L(2))/((M(1)*s+M(2))*(M(3)*s+M(4))*(M(5)*s+M(6))) Licznik=[L(1) L(2)]

Mianownik1=conv([M(1) M(2)], [M(3) M(3)]) Mianownik2=conv(Mianownik1, [M(5) M(6)]) disp(' czas odpowiedzi impulsowej');

t=input('czas=');

g1=tf(Licznik, Mianownik2)

step(g1,t)

%wyswietlenie odpowiedzi czasowej przy danej transmitancji disp(' 20(s-4)/((s+1)(s+2)(s+3))');

disp(' czas odpowiedzi impulsowej');

t=input('czas=');

Licznik=[20 -80]

Mianownik1=conv([1 1], [1 2])

Mianownik2=conv(Mianownik1, [1 3])

g1=tf(Licznik, Mianownik2)

subplot(3,2,1)

step(g1,t)

subplot(3,2,2)

impulse(g1,t)

disp(' 20(s+3)/((s-1)(s^2 +2s+2))');

Licznik=[20 60]

Mianownik1=conv([1 -1], [1 2 2])

g1=tf(Licznik, Mianownik1)

subplot(3,2,3)

step(g1,t)

subplot(3,2,4)

impulse(g1,t)

disp(' 20/((s+2)(s^2 + 2))');

Licznik=[20 40]

Mianownik1=conv([1 2], [1 0 2])

g1=tf(Licznik, Mianownik1)

subplot(3,2,5)

step(g1,t)

subplot(3,2,6)

impulse(g1,t)

Zadania

1

2

s +10 s + 20

Znaleźć odpowiedź skokową oraz impulsową.

Charakterystyki częstotliwościowe

Lista poleceń 1.

>> syms k a b

>>k=10

>>a=1

>>b=2

>> sys=tf(k, [a b])

>> bode(sys)

Lista poleceń 2.

w = logspace(d1,d2,n) – generowanie n punktów czestotliwosci w rozmieszczonych równomiernie w skali logarytmicznej w przedziale 10d1...10d2

w = logspace(d1,d2) – standardowo 50 punktów; np. logspace(-1,1) wygeneruje 50 punktów w przedziale 0.1...10

[Mod, F] = bode(L,M,w)– wyznaczenie modułu Mod i fazy F transmitancji L/M dla czestotliwosci w, gdzie F jest w stopniach (wyjatkowo w Matlabie) subplot(211) – wybór górnej połowy ekranu do umieszczenia wykresu semilogx(w,Mod), grid – wykres modułu w skali logarytmicznej subplot(212) – wybór dolnej połowy ekranu semilogx(w,F), grid – wykres fazy

figure – nowe okno wykresu

Przykład 1.

Zbadać obiekt o transmitacji

G(s) = k

Użyć listy poleceń 1.

Przykład 2.

G(s) = ks

Użyć listy poleceń 1.

Przykład 3.

Dana jest transmitancja członu II rzędu.

Narysować w Matlabie charakterystyki częstotliwościowe?

Wykreślić kilka charakterystyk częstotliwościowych zmieniając współczynnik ksi.

Zaobserwować jak wpływa ksi na przebieg charakterystyki ?

Użyć listy poleceń 2.

Odp.

L=2;

w = logspace(-1,1,10);

ksi=0.1;

M=[1 2*ksi 1];

[Mod, F] = bode(L,M,w);

subplot(211);

semilogx(w,Mod), grid

subplot(212);

semilogx(w,F), grid

Przykład 4.

Zmienić trasmitancję na

1 + s

G(s) =

2

s + 10 s

x - 2

L=[1 1];

w = logspace(-1,1,100);

ksi=0.008;

M=[1 10*ksi -2];

[Mod, F] = bode(L,M,w);

subplot(211);

semilogx(w,Mod), grid;

subplot(212);

semilogx(w,F), grid;

Wykreślić kilka charakterystyk częstotliwościowych zmieniając współczynnik ksi.

Zaobserwować jak wpływa ksi na przebieg charakterystyki?

Użyć listy poleceń 2.

Przykład 5.

Wykreślić charakterystykę częstotliwościową członu całkującego z inercją.