8. Transformacje 3-D
8.1. Transformacje w przestrzeni 3-D
8.1.1. Transformacje elementarne
•
• zmiana skali,
• !
y
x
z
→ [ ]
′ ′ ′ → [′ ′ ′ ]
[
′ ′ ′ ]
= [ ]
"
[
′ ′ ′ ]
= [ ]
[′ ′ ′ ] = [ ]⋅( )
Zmiana skali
[
′ ′ ′ ]
= [ ]
[′ ′ ′ ] = [ ]⋅ (
)
Θ Θ
[
− Θ Θ
′ ′ ′ ]
= [ ]
[′ ′ ′ ] = [ ]⋅ (Θ)
# $
[
Θ Θ
′ ′ ′ ]
= [ ]
− Θ Θ
[′ ′ ′ ] = [ ]⋅ (Θ)
#
Θ
− Θ
[
′ ′ ′ ]
= [ ]
Θ
Θ
[′ ′ ′ ] = [ ]⋅ (Θ)
! "#Θ $
%& ' (
y
Θ
( ) x
( )
z
Dane:
• opis osi obrotu ( ), ( ),
• opis obiektu (np. siatka wieloboków),
• # Θ
%$&'()($ #
#Θ.
Rachunek wektorowy (przypomnienie):
wektor - = [ ]
*+', = + +
Operacje rachunku wektorowego:
= [ ] , = [ ]
1. Suma wektorów
+ = [ + + + ]
2. Iloczyn skalarny
Definicja 1
⋅ = +
+
Definicja 2
⋅ = φ
v2
φ
v1
3. Iloczyn wektorowy
Definicja 1
× =
uy
ux
x
uz
z
Definicja 2
× = ⋅ φ
v1x v2
v2
u
φ
v1
Reprezentacja osi obrotu:
y
Θ
( ) x
u
( )
z
+
punkcie ( ) #-
= [ ]
−
−
−
=
, =
, =
= ( − ) + ( −
) + ( −
)
./& = .
(
1. " )
) !
2. # )
* + , np.z
+-!
, & 0!1,"/
,
3. # +Θ.
4. Transformacja odwrotna do wykonanej w kroku 2.
5. Transformacja odwrotna do wykonanej w kroku 1.
+
y
Θ
u
x
z
'
(− −
−
) =
−
−
−
"+ ( )
do punktu (
)
.
$#
2& 0!1,"
y
′
u
b
x
α
c
z
a
= [ ], #+
′ = [ ], !1,"
= [ ]
- wersor osi z
". /(x-z) jest
. ′ #α .
.'α , lub sinα i cosα ?
Z definicji iloczynu skalarnego
′ ⋅ = ⋅ +
⋅ + ⋅ =
(def.1)
′ ⋅ =
′ ⋅ =
′ ⋅ ⋅
α
(def.2)
′ = + = , =
′ ⋅ =
⋅ α
#
α =
Z definicji iloczynu wektorowego
′ × =
= ⋅
(def.1)
′ × =
′ ⋅ ⋅ α =
⋅
⋅ α
(def.2)
#
α =
!1,"(&' 1#α.
Dokonano obrotu opisanego przez macierz
(α)
=
−
2&
y
β
x
′
′
d
z
a
′ = [ ], &! ( "
0!1," /
′ = [ ], &! ( "
wektor u,
= [ ]
- wersor osi z.
Z definicji iloczynu skalarnego
′ ⋅ =
⋅ + ⋅ + ⋅ =
(def.1)
′ ⋅ =
′ ⋅ =
′ ⋅ ⋅
β
(def.2)
′ = + = + ( + ) = + + =
=
′ ⋅ =
⋅ α
#
β =
Z definicji iloczynu wektorowego
′ × =
= ⋅
(− )
(def.1)
′ × =
′ ⋅ ⋅ β =
⋅
β
(def.2)
#
β = −
#β.
Dokonano obrotu opisanego przez macierz
(β) = −
0 & '*
) + *+
macierze:
Krok 3. # +Θ.
Θ
Θ
− Θ Θ
(Θ ) =
Krok 4. Transformacja odwrotna do wykonanej w kroku 2
−
−
(β) ⋅ (α)
Krok 5. Transformacja odwrotna do wykonanej w kroku 1
−(− −
−
)
* *'* 2
(Θ) = (− −
−
) ⋅ (α) ⋅ (β) ⋅ (Θ) ⋅
⋅ −
−
−
(β) ⋅ (α) ⋅
(− −
−
)
"
Dane:
#) (
" +
( ) =
,
(
) =
.
Obiekt:
Sfera o promieniu =
) (
) =
.
3.24 +Θ
+ )++.
5 , x-y) przed dokonaniem
obrotów pokazuje rysunek.
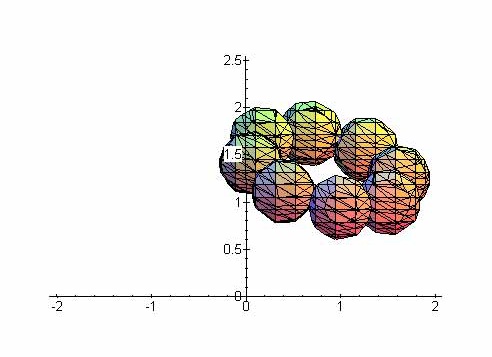
" * 4!
5 ,$6-+
natomiast ich obraz perspektywiczny (bez osi)
*+!