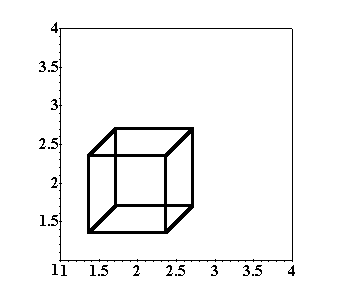
10. Wyznaczanie powierzchni widocznych
!"#
$% !% &
'%(
) * *!"% ! $+%
!,*!
Czy tak uzyskany obraz jednoznacznie pokazuje
-$% - &
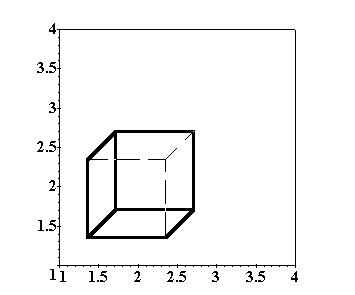
'+% % !
$$
.$$ /!/+%
Wniosek:
) 0$! +% *!
1 0 2" /
niejednoznaczny.
3 /(
1. !#0 0 0 #*!
= { }
2. 4! $
3. /%0*! 0 ! *0$!
00 5 *!
→
4. *#*!1%- -
0!02 % +
rastrowym.
10.1.1.
widocznych
- 0$! !+(
• ' $%0 + # *!"
punktu widzenia obserwatora, uszeregowanie od
0% 0% 0/ 0*!
• 0 + 0!0 *! %- -
!*0 $%
/%$*!/ #
.! #50 !0 % .
• /%- ! + 0/0
/$!$*!+
• 3 5 *! -
00 + 5 *!
! 0*!
/%- / #n *!
.! #50 !0 % ⋅ , przy
czym N 0 !$
Algorytmy mieszane:
!0 ! !5$! +
%/0 %
10.1. - -+%-+ *!
(Depth - sorting method)
Ogólny schemat algorytmu:
Krok 1. + $% *!
Krok 2. ' # + $% !,
*! $%
Krok 3. ' 0!0*!%- $%
uzyskanego w kroku 2.
• /%0*!/$!0%
= { }
! + $ * #+%0z
!,
• 4! S $%0 +%-%
! 0 *!z % *!0+ 0"%
najmniejszej.
'%(
′
′
′
′
′ ′
+ $% %*!′ i ′ %
*!
′
′
′
′
′ ′
+ $% %*!′ i ′ %
dobrego wyniku.
6 ' # + $% !,
*! $%
• ' !-#*!" + $%
" %%0 ++!
• * 0 %0 " 5! +
+
poprzednich miejscach.
7 $ $% %- $!0
% *!
′ ′
′
′
′
′ ′
′
/%*! ′ i ′ %[′ ′ ] i
[′ ′ ] $ $!" 0
pozytywny.
7 6 ' # #+%!,y
/%*! ′ i ′ %[ ′ ′ ] i
[ ′ ′ ] $ $!" 0
pozytywny.
!#0/*!′
′ ′
′
′
kierunek obserwacji
/ 1 $! %/ !0 2 *!
′ / ! ! !$ ! $
*!+′ , to wynik testu jest pozytywny.
:!0#$!" 0 0*%
!,!, #(′ ′ ′ )*!′
0 # *
′ ′′ + ′ ′′ + ′ ′′ + ′ <
gdzie ′ ′ ′ ′ $ #!#
!"#0/*!′ .
!#0/*!′
′ ′
′
′
kierunek obserwacji
/ 1 $! %/ !0 2 *!
′ / ! ! % !$ ! $
*!+′ , to wynik testu jest pozytywny.
:!0" 0 0* %
!, !, # (′ ′ ′ ) *! ′
0 # *
′ ′′ + ′ ′′ + ′ ′′ + ′ <
gdzie ′ ′ ′ ′ $ #!#
!"#0/*!′ .
!+(x-y)
′ ′
′
′
/ *! ′ i ′ !+ (x-y) $
$!" 0
Praktycznie, wykonanie testu polega na sprawdzeniu
! !-# %!# # *!
!0$ + ' % + - $0$!
% % %# #5 !,
%0$!!, $
• * /% +! # %
- + %0
*!
• =% 0 + #
- " $% *! 0
/
0 !% +
* *!
'%(
′
′
4!′ i ′ %%$ + $%
$%&
> / %1!$20%$*!
#!+!0 0% 0+
′ ′
′
′
(Depth - buffer method)
Ogólny schemat algorytmu:
′ ′ ′ ′
prosta rzutowania
Piksel (x,y) * 1
*!2 0 *!" % #0 #+% z punktu
!+! *! $ 0
najmniejsza.
Opis algorytmu:
+ $%+!(
• + 1refresh buffer)
• +-+ *!1depth buffer)
?+!0$ #"0
/%- #+%!,(x,y)
% (
=
=
gdzie
- *+! %
(x,y),
- *+!-+ *!%
piksela (x,y),
- ,
- * #+%0z.
Krok 2. ' #-+ *!
• /%- *!"!
*z(x,y),
• / < % (
=
=
6 % 0!,*! /%
! *!
Podstawowym problemem obliczeniowym algorytmu z- bufora jest obliczanie z(x,y).
Algorytm obliczania z(x,y) %*!
• @ # 1
!, 2*!
• ?! #!A,B,C,D, równania
!"#0/*!
• ?!
= −
−
−
Obliczanie z / *!"
ekranu jest dyskretna
′
−
′
+
′ = − +
− − = − − − −
$%
′ = −
2. Obliczanie ′ (w kolumnie).
′ = − − −
− = − − − +
$%
′ = +
Porównanie algorytmów
1. - -+%-+ *!
•
•
•
2. Algorytm z- bufora
•
•
•
Wyszukiwarka
Podobne podstrony:
grafika komputerowa wykład 8
grafika komputerowa wykład 14
Grafika Inżynierska Wykład 7 10 14
grafika komputerowa wykład 11
grafika komputerowa wykład 13
grafika komputerowa wykład 9
grafika komputerowa wykład 12
grafika komputerowa wykład 7
Elementy grafiki komputerowej 1 i 2 wykład, STUDIA
Grafika komputerowa wykłady
Zastosowanie metod kodowania w programach graficznych, Nauka, Studia, Wykłady, Grafika komputerowa
Wykład Grafika Komputerowa
wyklad 10 MNE
wyklad 10
Wyklady 10 12c PRCz
wyklad 10
więcej podobnych podstron