Ćwiczenia 5

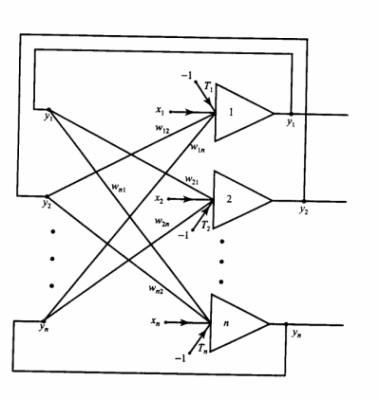
Jednowarstwowa Sieć Neuronowa Hopfielda

1) Stwórz macierz Hadamarda H 8

http://pl.wikipedia.org/wiki/Macierz Hadamarda

wybierz z niej wektory o numerach:

pierwszy wektor: dzień urodzenia (modulo 8) + 1,

drugi wektor: miesiąc urodzenia (modulo 7) + 1,

jeżeli wektory się powtórzą wybierz następny w kolejności wektor, jeżeli wektory bę-

dą identyczne jak w przykładzie poniżej, zmień jeden wektor biorąc kolejny pierwszy z brzegu wektor.

2) Z otrzymanych wektorów macierzy Hadamarda wylicz na kartce macierz wag Hopfielda.

3) W kolejnym kroku uszkodź w wektorze pierwszym bit o numerze rok urodzenia (modulo 5) + 1 i zdekoduj błąd za pomocą macierzy wag.

Przykładowe wykonanie zadania z opisem jednowarstwowej sieci

neuronowej Hopfielda

1. Wybieramy kilka wektorów wzajemnie ortogonalnych np.: z macierzy Hadamarda H 8.

2. Jeżeli wektory są w postaci binarnej konwertujemy je na postać bipolarną (biegunową) (tzn. 0 zamieniamy na − 1, 1 na +1).

2. Ustawiamy wektory uzyskane w punkcie 2 w kolejne kolumny macierzy M .

3. Transponujemy macierz M , powstaje macierz M T .

4. Jednym ze sposobów uczenia sieci Hopfielda jest reguła Hebba, w której wagi wij, połączeń neuronu i z neuronem j, definiujemy jako: 1

K

w

X

ij =

∗

x( k) ∗ x( k)

N

i

j

k=1

gdzie N -ilość neuronów, czyli długość wektora wzorcowego, k - numer wektora wzorcowego,

K - ilość wektorów uczących

x( k) - to i-ty deskryptor wektora o numerze k i

W praktyce, macierz wag W otrzymujemy mnożąc M ∗ M T , gdzie wagi są odro-binę zmodyfikowane,

K

w

X

ij =

x( k) ∗ x( k)

i

j

k=1

mnożenie przez 1 niczego nam nie zmieni, gdy nasz próg aktywacji wynosi 0.

N

5. Zerujemy główną przekątną macierzy wag. Powstała macierz W koduje wzorce (wektory) z punktu 1.

6. W sieci Hopfielda, jeżeli zostanie zaburzony jeden z bitów wejściowych, oraz od-leglosc Hamminga wszystkich wektorow wejsciowych, które wyuczyły macierz wag będzie wystarczajaca, funkcja aktywacji powinna naprawić błąd wejściowy.

7. Wybieramy teraz jeden z wyuczonych wektorów i zaburzamy go na jednej wybra-nej pozycji, ten wektor będzie naszym wektorem do zdekodowania.

8. Ciąg wyjściowy uzyskujemy, mnożąc wektor z punktu 7 (w zwykłej zero-jedynkowej postaci) przez wszystkie kolumny macierzy wag powstalej w punkcie 5.

9. Określamy funkcję aktywacji , f ( x)=0, gdy x < 0 ; 1 , jeśli x ­ 0).

10. Każdy deskryptor ciągu powstałego w punkcie 7 traktujemy jako argument funk-cji f , w ten sposób otrzymujemy odpowiedni wektor wyjściowy: W praktyce, sieć Hopfielda nie zawsze daje dobrą odpowiedź, co może być powodo-wane przez:

• utkwienie w pośrednim minimum lokalnym,

• mieszanie się składowych zapamiętanych wzorców

• możliwa jest zmiana polaryzacji stanów

Metoda Hebba jest metodą najprostszą przez co często tworzy nieskuteczną sieć.

Przykład budowania sieci Hopfielda:

Weźmy losowe wektory ortogonalne z macierzy H8:

A 1 = (1 , 0 , 1 , 0 , 1 , 0 , 1 , 0) A 2 = (1 , 1 , 0 , 0 , 1 , 1 , 0 , 0).

Zapiszmy je w postaci biegunowej

A 1 = (1 , − 1 , 1 , − 1 , 1 , − 1 , 1 , − 1) A 2 = (1 , 1 , − 1 , − 1 , 1 , 1 , − 1 , − 1).

Teraz tworzymy macierz M , M T , i budujemy macierz wag następująco:



1

1 



2

0

0

-2

2

0

0

-2 



-1

1 



0

2

-2

0

0

2

-2

0 











1

-1 



0

-2

2

0

0

-2

2

0 













"

#







-1 -1 

1 -1

1

-1 1 -1

1

-1



-2

0

0

2

-2

0

0

2 

M ∗M T = 

 ∗

= 





1

1 

1

1

-1 -1 1

1

-1 -1



2

0

0

-2

2

0

0

-2 



















-1

1 



0

2

-2

0

0

2

-2

0 











1

-1 



0

-2

2

0

0

-2

2

0 









-1 -1

-2

0

0

2

-2

0

0

2

Po wyzerowaniu głównej przekątnej otrzymujemy macierz wag postaci:



0

0

0

-2

2

0

0

-2 



0

0

-2

0

0

2

-2

0 







0

-2

0

0

0

-2

2

0 











-2

0

0

0

-2

0

0

2 

W = 





2

0

0

-2

0

0

0

-2 











0

2

-2

0

0

0

-2

0 







0

-2

2

0

0

-2

0

0 





-2

0

0

2

-2

0

0

0

Powstała macierz wag zakodowała wzorce:

A 1 = (1 , 0 , 1 , 0 , 1 , 0 , 1 , 0) A 2 = (1 , 1 , 0 , 0 , 1 , 1 , 0 , 0).

Dla zobrazowania przydatności powstałej macierzy wag zaburzamy wektor A 1 na pozycji drugiej, powstaje wektor:

0

A = (1 , 1 , 1 , 0 , 1 , 0 , 1 , 0) Aby uzyskać ciąg wyjściowy, mnożymy nasz zaburzony wektory przez kolejne kolumny macierzy wag:

1 ∗ 0 + 1 ∗ 0 + 1 ∗ 0 + 0 ∗ ( − 2) + 1 ∗ 2 + 0 ∗ 0 + 1 ∗ 0 + 0 ∗ ( − 2) = 2

1 ∗ 0 + 1 ∗ 0 + 1 ∗ ( − 2) + 0 ∗ 0 + 1 ∗ 0 + 0 ∗ 2 + 1 ∗ ( − 2) + 0 ∗ 0 = − 4

1 ∗ 0 + 1 ∗ ( − 2) + 1 ∗ 0 + 0 ∗ 0 + 1 ∗ 0 + 0 ∗ ( − 2) + 1 ∗ 2 + 0 ∗ 0 = 0

1 ∗ ( − 2) + 1 ∗ 0 + 1 ∗ 0 + 0 ∗ 0 + 1 ∗ ( − 2) + 0 ∗ 0 + 1 ∗ 0 + 0 ∗ 2 = − 4

1 ∗ 2 + 1 ∗ 0 + 1 ∗ 0 + 0 ∗ ( − 2) + 1 ∗ 0 + 0 ∗ 0 + 1 ∗ 0 + 0 ∗ ( − 2) = 2

1 ∗ 0 + 1 ∗ 2 + 1 ∗ ( − 2) + 0 ∗ 0 + 1 ∗ 0 + 0 ∗ 0 + 1 ∗ ( − 2) + 1 ∗ 0 = − 2

1 ∗ 0 + 1 ∗ ( − 2) + 1 ∗ 2 + 0 ∗ 0 + 1 ∗ 0 + 0 ∗ ( − 2) + 1 ∗ 0 + 0 ∗ 0 = 0

1 ∗ ( − 2) + 1 ∗ 0 + 1 ∗ 0 + 0 ∗ 2 + 1 ∗ ( − 2) + 0 ∗ 0 + 1 ∗ 0 + 0 ∗ 0 = − 4

Teraz do powstalego wektora (2 , − 4 , 0 , − 4 , 2 , − 2 , 0 , − 4) przykładamy funkcję aktywacji postaci:

f ( x)=0, gdy x < 0 ; 1 , jeśli x ­ 0, otrzymujemy wektor: (1 , 0 , 1 , 0 , 1 , 0 , 1 , 0) = A 1

Dostaliśmy na wyjściu prawidłowy wzorzec, pomimo tego, że na wejściu był uszko-dzony sieć Hopfielda dobrze go rozpoznała.