Wytrzymałość Materiałów 6 35WM

Metoda Maxwella-Mohra obliczania przemieszczeń konstrukcji

Literatura Jan Misiak, Stat. i Wytrz. Mat. strona 254.

Dla belek i ram przemieszczenie konstrukcji wyznaczamy ze wzoru:

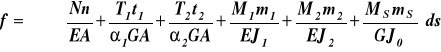
(26)

Dla belek prostych i ram płaskich obciążonych układem sił płaskich T₂ = t₂ = M₂ = m₂ = 0. Wzór (26) ma postać

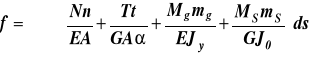
(27)

gdzie siły i momenty oznaczone dużymi literami są siłami i momentami wewnętrznymi wywołanymi obciążeniem zewnętrznym

zaś siły i momenty wewnętrzne wywołane siłami jednostkowymi są

określone literami małymi.

N, n siły normalne

T, t siły tnące

M_g , m_g momenty gnące

M_S , m_S momenty skręcające

A pole przekroju elementu konstrukcji

α współczynnik wynikający z nierównomierności

rozkładu naprężeń tnących w przekroju

Wzór Wereszczagina do całkowania iloczynu dwóch funkcji, z których jedna jest funkcją liniową

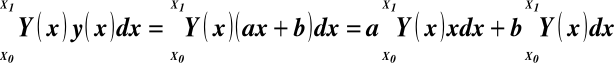
C₁ C₂

Y(x) y(x)

x_ść x_ść

x

y = ax + b

Y(x) C y_c

dA

x₀ dx x x₀ x

x₁ x₁

Rys.29 Sposób obliczania całki

A pole pod krzywą Y(x),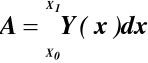

x_ść współrzędna środka ciężkości pola A

C₁ = Aax_ść C₂ = Ab

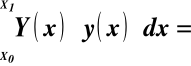
C₁ + C₂ = A(ax_ść + b) = Ay_c (28)

Przykład 12

Określić pionowe przemieszczenie przekroju A pryzmatycznej belki (rys.30) o przekroju kołowym wywołane siłą P. Dana średnica przekroju belki d.

Rozwiązanie.

Pierwszy etap polega na wprowadzeniu w przekroju A

jednostkowej siły pionowej P_c = 1N, jako „czujnika” mierzącego szukane przemieszczenie. W etapie drugim wyznaczamy składowe sił i momentów wewnętrznych w przekroju B jako funkcje x, słuszne w całym przedziale

(0,l).

z P P_c = 1N

x B x B

C A C A

l l

M_g= -P(l-x) m_g = -1(l-x)

C A C A

Pl 1⋅l

T = P t = 1N

T + t

C A C A

Rys.30 Przykład obliczenia ugięć belki

M_g = -P(l-x), T = P, N = 0, m_g = -(l-x)Nm/N, t = 1N/N, n = 0

W etapie trzecim funkcje te podstawiamy do (27) i całkujemy

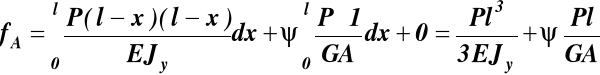
(a) (b)

gdzie: Ψ = 1/α =1.185 i wynika z nierównomierności

rozkładu naprężeń stycznych w przekroju

ν = 0.3,

E/G =2(1+ν) = 2(1+0.3) = 2.6

J_y = πd⁴/64, A = πd²/4

przy czym uwzględniono, że iloczyn wartości ujemnych jest dodatni.

• człon (a) reprezentuje wpływ momentu gnącego na

ugięcie belki

• człon (b) reprezentuje wpływ siły tnącej na ugięcie belki

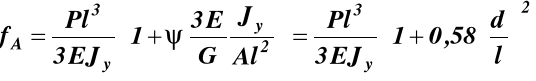
Widać, że wpływ siły tnącej jest rzędu (d/l)²

w stosunku do jedności i gdy l/d > 8, wówczas

wpływ ten nie przekracza 1% wartości ugięcia wywołanego momentem gnącym.

Przykład 13

Obliczyć wypadkowe przemieszczenie węzła B stalowej kratownicy obciążonej siłami P₁ = 50kN i P₂ = 40kN (rys.31).

E = 2*10⁵MPa. Długości i przekroje prętów podano w tabeli a.

Wartości sił od obciążenia zewnętrznego N_i określono na ćwiczeniach w zadaniu 29.

Rozwiązanie

C 3m B C +0.58 B

P₁ P_c = 1N

3 5 7 +0.58 -1.16

4 6 P₂ -0.58

1 2 A A

3m 3m -0.50

C -1.00 B P_c = 1N

-1.00 0

+1.00 0

A

-0.50 0

Rys.31 Obliczenie wartości przemieszczenia węzła B

W kratownicy pręty są tylko rozciągane lub ściskane wobec tego wzór (27) przyjmuje postać

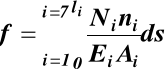
(29)

jeśli Ni, ni, E_i, A_i są stałe dla wszystkich prętów

to wzór (29) przyjmuje postać 39WM

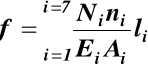
dla E_i = const =E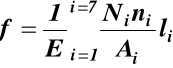
(30)

Całość obliczeń ujmujemy w poniższej tabeli a. Pierwsze trzy kolumny to numeracja i dane geometryczne prętów.

Kolumny 4 i 5 podają siły N_i odpowiadające rzeczywistemu obciążeniu i wywołane tym wydłużenia

*l_i = N_il_i/EA_i. Kolumna 6 to siły n_i^`(N/N) dla „czujnika”,

tj. pionowej siły P_c = 1N przyłożonej w węźle B. Wreszcie w kolumnie 7 mamy iloczyn n_i^`*l_i , których suma to szukane pionowe przemieszczenie węzła B. Dodatnia wartość świadczy, że kierunek przemieszczenia jest zgodny z kierunkiem działania siły P_c.

Tabela a

1	2	3	4	5	6	7	8	9
Pręt nr	li m	Ai cm^2	Ni kN	mm	N/N	*li mm	N/N	ni^''*li mm
1	3.0	10	+1.9	+0.03	-0.50	-0.02	-0.50	-0.02
2	3.0	10	-23.1	-o.35	0	0	0	0
3	3.0	10	+96.2	+1.44	+0.58	+0.83	-1.00	-1.44
4	3.0	20	-96.2	-0.72	-0.58	+0.42	+1.00	-0.72
5	3.0	10	+46.2	+0.69	+0.58	+0.40	-1.00	-0.69
6	3.0	10	-46.2	-0.69	-1.16	+0.80	0	0
7	3.0	10	+46.2	+0.69	0	0	0	0

Obciążając podobnie węzeł B poziomą siłą P_c = 1N obliczamy odpowiednie n_i^'' oraz n_i^''*l_i i w wyniku (suma kolumny 9) mamy poziome przesunięcie węzła B zachodzące na prawo. Wypadkowe przemieszczenie jest geometryczną sumą składowych i wynosi f_B (rys.32)

a) b)

5 B P_c= 1N 5 B

x f_x

f_B

6 7 6

P_c f_y B^'

y 7

Rys.32 a) układ sił P_c tak zwanych „czujników”

b) przemieszczenie węzła B, f_B

Przykład 14

Dla kratownicy z przykładu 2 określ wartości naprężeń *

w prętach oraz wartości współczynników bezpieczeństwa

względem *_e = 350 MPa.

Rozwiązanie

Dzieląc wartość siły N_i działającej w pręcie i przez wartość

jego przekroju A_i (tabela a) określamy wartości naprężeń

*_i =N_i/A_i , współczynnik bezpieczeństwa n_ei = 350/*_i, wyniki

przedstawiono w tabeli b.

Tabela b

Nr.prę.	1	2	3	4	5	6	7
*i(MPa)	1.9	-23.1	96.2	-48.1	46.2	-46.2	46.2
nei	157.8	13.0	3.1	6.2	6.5	6.5	6.5

Wyboczenie prętów prostych J. Misiak st.285

Wyboczenie sprężyste

z

+M

w P x x

x

l

Rys. 33 Pręt zamocowany przegubowo obciążony siła P

M = -Pw podstawiając do wzoru (11) otrzymujemy

(g)

po przeniesieniu -Pw na lewą stronę i po podzieleniu obu stron równania (g) przez P/EJ_y = k² otrzymujemy

(h)

Rozwiązanie ogólne równania (h) jest

(i)

Stałe całkowania C₁, C₂ określamy z warunków brzegowych: x = 0, w = 0 C₂ = 0

x = l, w = 0 C₁sinkl = 0 (j)

ostatecznie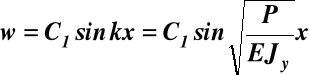
(k)

Gdyby C₁ = 0 to pręt nie mógłby istnieć w stanie wygiętym,

patrz (k) stąd wiosek że C₁≠ 0, tak więc aby spełnić warunki (j) sinkl musi równać się zero czyli

sinkl = 0 stąd kl = πn, gdzie n = 1,2,....

pamiętając że k² =P/EJ_y to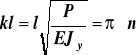
(l ) wartość siły P przy której spełniona jest równość (l ) nazywana jest siłą krytyczną i oznaczana jako P_kr czyli

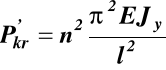
najmniejszą wartość P otrzymamy

dla n=1, siłę tę nazywamy siłą Eulerowską

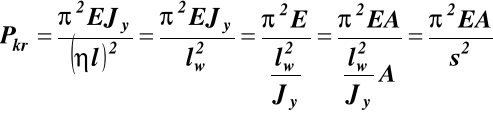
(32)

gdzie A przekrój pręta

długość wyboczeniowa pręta =ηl

s smukłość pręta =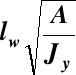

• 
  współczynnik zależny od podparcia pręta

dla pręta z rysunku 33 η = 1

Dzieląc siłę krytyczną P_kr (32) przez przekrój pręta A otrzymujemy wzór na naprężenia krytyczne

(33)

Wzór (33) jest słuszny w zakresie naprężeń w którym

obowiązuje prawo Hooke^'a, czyli w zakresie sprężystym

materiału (rys.34).

*_kr

*_pl Parabola Johsona-Ostenfelda

Prosta Tetmajera-Jasińskiego

*_sp

Hiperbola-Eulera

s_gr s Rys.34

Przykład 15 43WM

Określić kształt przekroju dla ściskanego pręta 4 z przykładu 14 z warunku, że współczynnik na wyboczenie n_kr = 4, *_sp = 300MPa. Proporcje przekroju podaje rys.35.

Rozwiązanie

Pręt 4 jest ściskany *₄ = - 48.1 MPa (tabela b).

Przekrój pręta A₄ = 20cm², długość pręta l = 3m (tabela a).

Przyjmuje się, że pręt jest na końcach podparty przegubowo a więc η = 1 stąd l_w = l = 3m, E = 2*10⁵ MPa.

Z wzoru (33) mamy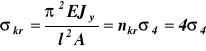

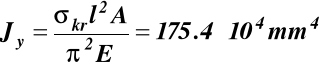
(a1)

y

δ x b

δ Rys.35

b

A = 3bδ = 2000mm² δ = 2000/3b (a2)

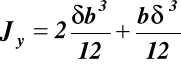
(a3)

Po podstawieniu (a1) i (a2) do (a3) otrzymujemy

b= 125.6mm, podstawiając to do (a2) mamy δ = 5.3mm.

Sprawdzenie czy J_x nie jest mniejsze od J_y

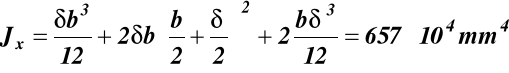
J_x >> J_y

36WM

37WM

38WM

40WM

41WM

42WM

---