Nr ćwicz. 200	Data:		Wydział Elektryczny	Semestr IV	Grupa T3 nr lab. 5
prowadzący					Przygotowanie:	Wykonanie:	Ocena ostat. :

Temat: Wyznaczanie bariery potencjału na złączu p-n .

Wstęp teoretyczny

Dioda p-n jest jednym z najpowszechniej stosowanych elementów elektronicznych . Ze względu na asymetryczną charakterystykę prądowo - napięciową najczęściej stosuje się ją jako diodę prostowniczą . Diodę stanowią dwa zetknięte ze sobą półprzwodniki , z których jeden jest typu p a drugi typu n . W wyniku ścisłego kontaktu półprzewodników następuje przepływ elektronów do części p oraz dziur do części n .Ta wymiana nośników ustaje po zrównaniu się poziomów Fermiego pomiędzy obu częściami diody i po wytworzeniu się różnicy potencjałów j . Schemat energetyczny diody przedstawia poniższy rysunek :

Np , Nn - koncentracje elektro-nów w częściach p i n ,

Pp , Pn - koncentracje dziur w częściach p i n ,

j - bariera potencjału .

Is - prąd nasycenia ,

Id - prąd dyfuzji ,

EF - energia Fermiego .

Przyłożenie do diody zewnętrznego napięcia powoduje zmianę bariery potencjału . Wynosi ona wtedy :
.

W diodzie p-n występują dwie przyczyny ukierunkowanego ruchu nośników :

1) Dążenie do znalezienia się w obszarze o najniższej energii potencjalnej ,

Ten mechanizm powoduje ruch elektronów z obszaru p do obszaru n oraz ruch dziur z obszaru n do obszaru p .Suma strumieni tych nośników tworzy prąd nasycenia Is , który zależy jedynie od koncentracji Np i Pn , nie zalezy natomiast od przyłożonego napięcia . Ponieważ koncentracja nośników określona jest wzorem :
,

a natężenie prądu nasycenia jest proporcjonalne do koncentracji nośników , zatem :

,

C jest stałą .

2) Dążenie do wyrównania koncentracji , czyli dyfuzja nośników .

Prąd dyfuzyjny elektronów jest proporcjonalny do różnicy koncentracji elektronów i do prawdopodobieństwa pokonania bariery potencjału . Wyraża się on wzorem :

.

Wypadkowy prąd jest różnicą tych dwóch prądów i wynosi :

(*).

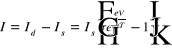
Zasada pomiaru

Wykorzystując charaktertystykę diody w kierunku przewodzenia , przy założeniu :

eV>5kT można zaniedbać jedynkę we wzorze (*) , kóry po zlogarytmowaniu przymie postać :

.

Ponieważ wartość EW - EF jest rzędu 10-2eV i jest o co najmniej rząd wielkości mniejsza niż wysokość bariery ej , wię można ją zaniedbać . Wysokość bariery można wyznaczyć ze wzoru :

.

Jeżeli nie znamy stałej C , to musimy wykonać kilka charakterystyk prądowo - napięciowych

w różnych temperaturach , dla każdej z nich znaleźć prąd nasycenia Is i następnie wykonać wykres : ln Is= f(1/T) . Wykresm jest linia prosta , której współczynnik nachylenia wynosi :

. Obliczamy ten współczynnik metodą regresji liniowej i znajdujemy barierę potencjału z zależności :
.

Układ pomiarowy

Pomiary

Lp	T [K]	I [A]	DI [A]	U [V]	DU [V]
1
2
3
4
5
6
7
8
9
10
11
12
1
2
3
4
5
6
7
8
9
10
11
12
1
2
3
4
5
6
7
8
9
10
11
12

Lp	T [K]	I [A]	DI [A]	U [V]	DU [V]
1
2
3
4
5
6
7
8
9
10
11
12
1
2
3
4
5
6
7
8
9
10
11
12

Wyznaczenie prądu nasycenia

Ponieważ prąd nasycenia jest związany z napięciem i prądem następującą zależnością :

.

Jeśli wykreślimy to równanie we współrzędnych x=V i y=lnI otrzymamy linię prostą przcinającą oś y w punkcie , który ma wartość : lnIs . Punkt ten można zatem znaleźć za pomocą regresji liniowej . Postępując tak dla wszystkich temperatur otrzymujemy :

	T=285.15 K	T=291.15 K	T=295.15 K	T=306.15 K	T=314.15 K
b=lnIs	-19.0681	-18.5136	-18.3591	-17.569	-17.2202
b	0.13565	0.139116	0.150349	0.143321	0.140623
Is[A]	5.234E-09	9.113E-09	1.064E-08	2.344E-08	3.322E-08
Is[A]	0.71E-09	1.268E-09	0.164E-08	0.336E-08	0.467E-08

Prąd nasycenia jest równy :

Błędy pomiaru prądu nasycenia :

.

Wyznaczenie bariery potencjału

Bariera potencjału została wyznaczona także przy pomocy regresji liniowej . Wyznaczamy współczynnik nachylenia prostej o równaniu :

,

gdzie y=1/T ,

x=lnIs .

Współczynnik nachylenia prostej wyznaczony metodą regresji wynosi :

a= -5694.62 ,

Błąd wyznaczenia tego współczynnika :

a=306.4059 .

Korzystając z równania :

,

wyznaczymy barierę potencjału :

= -0.47029 [V] .

Błąd wyznaczenia bariery potencjału :

.

Wynik

= -(47026) [mV]

Wnioski

Z uzyskanych w doświadczeniu wyników można wywnioskować , że badana była dioda germanowa . Ma ona barierę potencjału najbliższą wynikowi .

Wynik końcowy obarczony jest stosunkowo niewielkim błędem . Należy jednak zwrócić uwagę na to , że odchylenie standardowe po zastosowaniu regresji liniowej . Dużym błędem obarczone są natomiast bezpośrednie wyniki pomiaru .

---