Sprawozdanie z ćwiczenia B1

Podstawy fizyczne

Najpopularniejszą metodą wyznaczania mikroskopowych parametrów półprzewodników (znak nośników, ich koncentracja i ruchliwość) jest pomiar oparty na zjawisku Halla. Do próbki wykonanej z metalu lub półprzewodnika, przez który płynie prąd elektryczny o natężeniu I wywołany zewnętrznym polem elektrycznym E, przyłączamy pole magnetyczne o indukcji B prostopadłe do kierunku prądu. Zaobserwujemy między ściankami próbki różnicę potencjałów równą napięciu Halla:
przy czym d jest to grubość płytki a RH - stała proporcjonalności (stała Halla). Jeżeli próbkę zawierającą nośniki tylko jednego znaku umieścimy w polu magnetycznym to działa na nie siła
siła ta powoduje zbaczenie nośników z ich toru, w skutek czego z jednej strony próbki pojawia się nadmiar elektronów, których ładunek nie jest skompensowany obecnością jonów dodatnich. Nieskompensowany ładunek elektryczny staje się żródłem pola elektrycznego EH. EH przeciwdziała dalszemu gromadzeniu się elektronów, w rezultacie składowa siły Lorentza (działająca na poszczególne elektrony) równoważona jest przez siłe pochodzącą od wewnętrznego pola elektrycznego.

, wektory V i B są prostopadłe. Pozwala to obliczyć wielkość różnicy potencjałów między brzegami próbki:
, gdzie VD - można wyrazić wzorem:
, gdzie j - gęstość prądu,

n - koncentracja ładunków

Więc:
porównując to ze wzorem empirycznym widzimy że stała Halla
jest odwrotnie proporcjonalna do koncentracji nośników prądu.

Natomiast jeżeli w półprzewodniku występują nośniki obu znaków to wzór na stałą Halla wygląda następująco:

gdzie p - koncentracja dziur, e - ruchliwość elektronów, d - ruchliwość dziur. Można zauważyć, że jednocześnie występowanie dziur i elektronów powoduje częściowe, a wszczególnym przypadku, gdy liczba dziur jest równa liczbie elektronów, całkowite zniesienie zjawiska Halla.

Pomiar efektu Halla stanowi źródło bardzo ważnych informacji o półprzewodnikach.

Ze znaku napięcia Halla wnioskujemy o znaku dominujących nośników prądu. Wyznaczając stałą Halla możemy obliczyć koncetrację i ruchliwość nośników prądu.

Wykonanie ćwiczenia

Celem ćwiczenia było:

- wyznaczenie charakterystyk napięcia Halla w funkcji indukcji magnetycznej dala dwóch różnych wartości natężenia prądu płynącego przez próbkę oraz napięcia Halla w funkcji prądu płynącego przez próbkę dla dwóch wartości indukcji magnetycznej.

- obliczenie stałej Halla dla wszystkich przypadków

- obliczenie koncentracji ładunków oraz wyznaczenie znaku ładunków dominujących w próbce.

UWAGA . Wartości napięcia Halla podane w tabelkach są to średnie arytmetyczne obliczone z czterech wyników zmierzonych dla tego samego punktu pomiarowego przy czterech różnych kombinacjach kierunku płynącego przez próbkę prądu i wektora indukcji magnetycznej (przy różnych pozycjach przełączników).

1. Charakterystyka napięcia Halla w funkcji prądu sterującego.

Tabela pomiarowa

B=0.197 T	15 mA	12.5 mA	10 mA	7.5 mA	5 mA
U [V]	0.2051	0.1709	0.1364	0.1037	0.0717
B=0.18 T	15mA	12.5mA	10mA	7.5mA	5mA
U [V]	0.1676	0.1522	0.1139	0.0849	0.0592

grubość hallotronu d = (1001)m, szerokość b = (2.60.1)mm, długość l = (100.1)mm

Obydwie linie na wykresie przedstawiają zależność
i wyznaczone zostały metodą najmniejszych kwadratów. Ze współczynników kierunkowych tych prostych będziemy wyznaczać stałą Halla

1.Dla B1 = 0.197 T

a=13.36 Sa=0.12

b=0.0039 Sb=0.0013

Ze współczynnika a wyznaczyliśmy stałą Halla:
=6.78· 10-3

Błąd stałej Halla oszacowaliśmy metodą różniczki zupełnej:

d = (1000.1) m d = 0.1· 10-6 , a = (5.580.03), a = 0.03 , B = (0.820.01), B = 0.01

=0.41· 10-3

Ostatecznie więc RH = (6.78 0.41)· 10-3 [m3/C]

2.Dla B2 = 0.18 T

a=11.36 Sa=0.72

b=1.92· 10-3 Sb=0.0076

Po identycznych obliczeniach jak wyżej (dla a = 11.36 i a = 0.42) otrzymujemy stałą Halla równą

RH = (6.31 0.44)· 10-3 [m3/C]

2. Charakterystyka napięcia Halla w funkcji indukcji magnetycznej.

Tabela pomiarowa

	Indukcja magnetyczna [T]
I=15 mA	0.197	0.18	0.154	0.12	0.082
U	0.2035	0.1693	0.1350	0.1023	0.0677
B=15 mA	0.197	0.18	0.154	0.12	0.082
U	0.1369	0.1152	0.0925	0.0700	0.0460

Obydwie linnie na wykresie przedstawiają zależność
i wyznaczone zostały metodą najmniejszych kwadratów. Ze współczynników kierunkowych tych prostych będziemy wyznaczać stałą Halla

1. dla Is = 15 [mA]

a=1.142 Sa=0.098

b=-3.192 · 10-2 Sb=1.505· 10-2

Podczas obliczania stałej Halla postępujemy tak jak poprzednio z tym że zamiast indukcji we wzorze będziemy mieli prąd

Błąd stałej Halla w tym przypadku także liczyliśmy metodą różniczki zupełnej
d = (1000.1) m, d = 0.1· 10-6, a = (0.07670.0047), a = 0.0047 , Is = (10.00.1)· 10-3, Is = 0.1·10-3

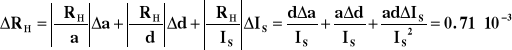
Ostatecznie RH = (7.61 0.71)· 10-3 [m3/C]

- dla Is = 15 [mA]

Wartosci a i b wynoszą odpowiednio:

a=0.768 Sa=0.058

b=-2.047· 10-2 Sb=0.883· 10-2

Korzystamy ze wzoru jak wyzej i w tym wypadku stała Halla wynosi:

RH=7.68· 10-3

Błąd stałej Halla w tym przypadku wynosi:

d = (1000.1) m, d = 0.1· 10-6 , a = (0.11210.0072), a = 0.0072 , Is = (150.1)· 10-3,

Is = 0.1·10-3

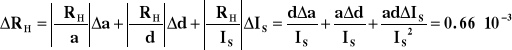
w tym przypadku stała Halla (po obliczeniach dokonanych identycznie jak w poprzednim punkcie) wynosi RH = ( 7.68 0.66 )· 10-3 [m3/C]

3.Obliczenia koncetracji nośników prądu:

Korzystamy ze wzoru:
, a błąd liczyliśmy metodą różniczki zupełnej
, gdzie r - rozproszenie na drganiach sieci równe r = 3· /8.

Wyniki naszych obliczeń zamieściliśmy w tabeli:

Przypadki	RH· 10-3 m3/C	RH·10-3	n· 1021 1/m3	n· 1021
B1 = const = 0.82 T	6.78	0.41	1.086	0.066
B2 = const = 1.54 T	6.31	0.44	1.167	0.081
I1 = const = 10 mA	7.68	0.66	0.958	0.082
I2 = const = 15 mA	7.61	0.71	0.967	0.090

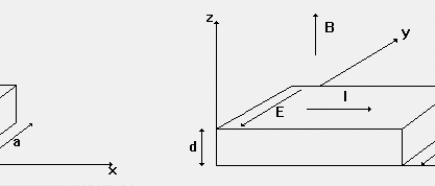
Znając kierunki prądu, indukcji magnetycznej oraz znak napięcia Halla możemy określić rodzaj nośników prądu. W naszym przypadku (wszystkie kierunki przedstawia rysunek) są to dziury.

Wnioski

Wyznaczone stałe Halla mieszczą się w granicach błędu w pobliżu tej samej wartości. Minimalnie różnią się tylko wartości uzyskane w pomiarze w funkcji prądu sterującego przy stałej indukcji.

Najprawdopodobniej ta minimalna rozbieżność spowodowanabyła błędnym odczytaniem indukcji magnetycznej B2 = 0.197 T. Widać także że koncentracja obliczona dla tego pomiaru odbiega nieznacznie od wartości koncentracji obliczonych dla innych przypadków chociarz mieści się w granicach błędu w przedziale wartości koncentracji obliczonych dla pomiarów napięcia Halla w funkcji indukcji magnetycznej przy stałym prądzie sterowania. Można stąd wysnuć wniosek, że wartości stałej Halla i koncentracji nośników dla wyliczone z wyników otrzymanych dla trzech pozostałych pomiarów są bliższe prawdy niż pomiar dla B2 .

Innym problemem z którym spotkaliśmy się podczas opracowania tego ćwiczenia jest wartość b otrzymana w wyniku wyliczania metodą najmniejszych kwadratów współczynników prostych opisujących charakterystyki. Teoretycznie współczynnik b powinien być równy zeru, ale postanowiliśmy nie przyrównywać go do zera ponieważ w ten sposób wypaczylibyśmy otrzymane wyniki dodając do nich punkt (0,0), którego doświadczalnie nie sprawdziliśmy.

Na różną od zera wartość współczynnika b mają z całą pewnością wpływ błędy pomiarowe, a także fakt że przy zerowej wartości, raz pola magnetycznego, raz prądu, działała już wartość stała, przy której mogło powstawać minimalne napięcie Halla. Z teorii wiadomo, że przy stałym prądzie płynącym przez próbkę i wyłączonej indukcji magnetycznej powstaje poprzeczne napięcie w próbce zwane napięciem asymetrii.

---