Politechnika Warszawska

Wydział Inżynierii Lądowej

Instytut Konstrukcji Budowlanych

Konstrukcje Betonowe Specjalne

Projekt Zbiornika
na wodę

Anna Pszczółkowska

Politechnika Warszawska

Wydział Inżynierii Lądowej

Grupa KBI-1

Semestr 8 R.A. 2005/06

Maj 2006

OPIS TECHNICZNY

Przedmiotem projektu jest żelbetowy zbiornik na wodę o pojemności 864 m3

Obiekt znajduje się w I strefie śniegowej.

Fundamenty

Zbiornik jest posadowiony na ławach fundamentowych o wymiarach 0,7x1,4 m. Zbrojony górą
9#16, dołem 9#16.

Powłoka cylindryczna

Ściany walcowe cienkie, grubości 20 cm. Połączone monolitycznie fundamentem, przekazują za jego pośrednictwem na grunt obciążenie własne i kopułowego przekrycia. Walcowe cienkościenne ściany sięgają do wysokości 11,0 m od poziomu płyty dennej.. Zbrojenie równoleżnikowe prętami #12 i #16. Zbrojenie pionowe standardowe 4#12 obustronnie, po wewnętrznej stronie prętów obwodowych.

Powłoka stożkowa

Zbiornik jest przykryty stożkiem o grubości 8 cm i wysokości 3,0 m. Zbrojenie południkowe górne i dolne stożka φ6 co 20 cm. Zbrojenie równoleżnikowe konstrukcyjne #6 co 20 cm.

Wieniec górny

Połączenie powłoki cylindryczne i powłoki stożkowej stanowi żelbetowy wieniec monolityczny o wymiarach 0,24x0,6 m. Zbrojony 5#12 rozmieszczone na obwodzie rdzenia przekroju wieńca w odległościach nie większych niż 25 cm.

Płyta denne

Płyta denna grubości 30 cm zbrojona ortogonalną siatka z prętów o średnicy 12x12 mm co 25.

Izolacje

Ściany są ocieplone wełną mineralną grubości 10 cm. Powłoka stożkowa - wełna mineralna o grubości
8 cm. Wełnę mineralną na powłoce stożkowej folia budowlana oraz dociskowa warstwa gładzi cementowej.

Pokrycie

Pokrycie powłoki stożkowej stanowi papa bitumiczna klejona na gorąco. Pokrycie powłoki cylindrycznej - blacha fałdowa na listwach.

Materiały konstrukcyjne

- beton B37

- stal konstrukcyjna ściany walcowej, wieńca górnego oraz ławy kołowej zbiornika - stal A-II (18G2)

- stal konstrukcyjna kopuły oraz strzemiona w ławie i wieńcu górnym - stal A-I (St3S)

Wykorzystane programy

Do obliczeń wykorzystano program Excel

Rysunki zostały sporządzone programem AutoCAD.

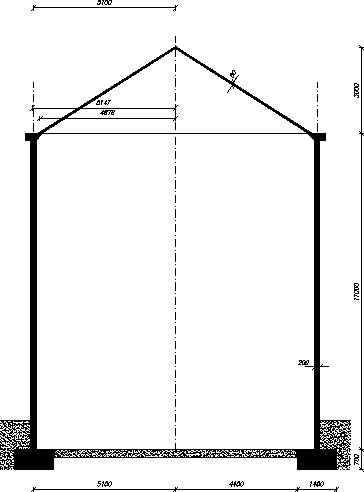
1. Założenia konstrukcyjne i obliczeniowe

1.1. Materiały konstrukcyjne

- Beton konstrukcyjny B37:

- Zbrojenie ściany walcowej, wieńca górnego oraz ławy kołowej zbiornika - stal A-II (18G2)

- Zbrojenie kopuły; strzemiona w ławie i wieńcu górnym - stal A-I (St3S)

- Otulina zbrojenie głównego

kopuła (klasa środowiskowa XC3): - c_min = 20 mm c_nom = c_min + Δc = 20+5=25 mm,

kopuła walcowa (klasa środowiskowa XC4): - c_min = 25 mm c_nom = c_min + Δc = 25+5=30 mm,
ława fundamentowa - c_min = 50 mm c_nom = c_min + Δc = 50+10=60 mm,

wieniec górny - c_min = 20 mm c_nom = c_min + Δc = 20+5=25 mm.

1.2. Wymaganie konstrukcyjne

Graniczna szerokość rozwarcia rys: w_lim = 0,1 mm.

2. ZESTAWIENIE OBCIĄŻEŃ

2.1. Obciążenia powłoki przekecia

Zestawienie obciążeń stałych na 1m² powłoki stożkowej:

lp.	Zestawienie obciążeń kN/m^2 powierzchni powłoki,	qSk	γf	qSd
1.	papa bitumiczna klejona na gorąco,	0,20	1,200	0,24
2.	gładź cementowa zbrojona 5 cm, 0,05x24,0=	1,20	1,300	1,56
3.	folia budowlana	0,05	1,200	0,06
4.	wełna mineralna 8 cm, 0,08x0,50=	0,04	1,200	0,05
5.	kopuła żelbetowa 8 cm, 0,08x25,0=	2,00	1,100	2,20
	razem obciążenia stałe gs=	3,49	1,177	4,11

Papę bitumiczno przyjęto jako produkowaną w zakładzie pracy.

Obciążeni śniegiem I strefa:

2.1. Obciążenia ŚCIANY walcowej

Zestawienie obciążeń pionowych na 1 m² ściany:

lp.	Zestawienie obciążeń kN/m^2 powierzchni powłoki,	qSk	γf	qSd
1.	blacha fałdowa na listwach,	0,20	1,200	0,24
2.	wełna mineralna 10cm, 0,10x5,0=	0,05	1,200	0,06
3.	ściana żelbetowa 20cm, 0,20x25,0=	5,00	1,100	5,50
	razem obciążenia stałe	5,25	1,105	5,80

Ciężar wody:

3. Obliczenia statyczne zbiornika

3.1. Dane geometryczne i parametry sztywnościowe elementów zbiornika

Powłoka przekrycia (stożkowa)

- grubość kopuły stożkowej:

- promień oparcia powierzchni środkowej:

- kąt oparcia powłoki:

- długość powierzchni środkowej:
,

- parametry obliczeniowe:

,

,

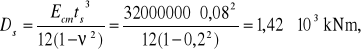
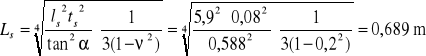
Kopuła spełnia warunki obliczeniowe dla powłok długich

Powłoka cylindryczna:

- grubość kopuły cylindrycznej:

- wysokość powłoki

- promień powierzchni środkowej:

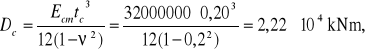
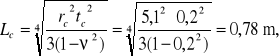
Powłoka cylindryczna spełnia warunki obliczeniowe dla powłok długich.

Ława fundamentowa:

- moduł podatności podłoża:

- wymiary geometryczne

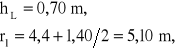
- pole przekroju ławy

- sztywność ławy

Wieniec górny:

- wymiary geometryczne

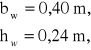
- pole przekroju ławy

- sztywność ławy

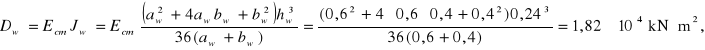
3.2. Równania równowagi węzła górnego

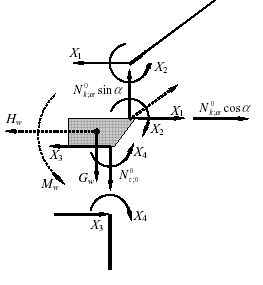
Odległość od środka ciężkości wieńca do jego górnej krawędzi:

Odległość od środka ciężkości wieńca do jego dolnej krawędzi:

Jednostkowe przemieszczenia krawędziowe kopuły , powłoki walcowej i wieńca:

Ostatecznie macierz układu równań przybiera postać:

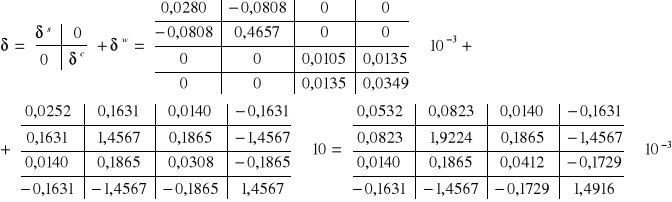
Wielkości krawędziowe przemieszczeń w powłoce stożkowej (brzeg hs=Hs=3,00m; a=30,4655°):

Wielkości krawędziowe przemieszczeń w powłoce cylindrycznej (hc=0,0m):

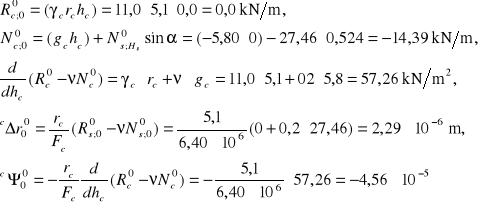
Siły i momenty obciążeń zewnętrznych działające na wieniec:

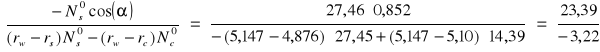
Prawe strony układu równań:

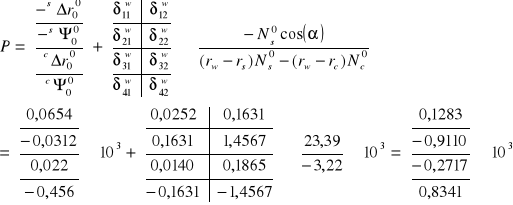
Ostateczny układ równań:

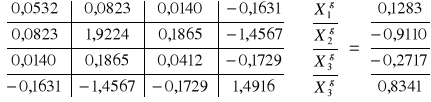
Rozwiązaniem układu są wielkości niewiadomych:

3.3. Równania równowagi węzła dolnego

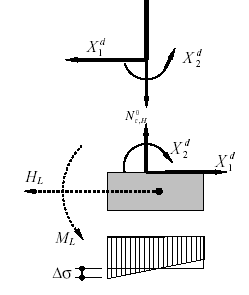
Wymiary przekroju ławy b_Lxh_L=1,40x0,70 m. Moduł podatności podłoża C=20000 kN/m⁴. Na podstawie punktu 3.1 dane geometryczne i parametry sztywnościowe ławy wynoszą:

Macierz sztywności wieńca:

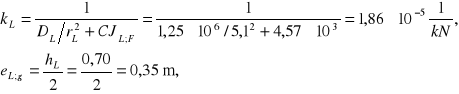
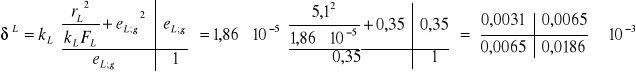
Macierz sztywności powłoki cylindrycznej na podstawie punktu 3.2 wynosi:

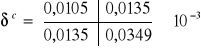
Ostatecznie wyrazy macierzy głównej dla węzła dolnego przybiorą wartości:

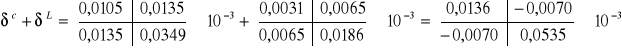
Wielkości krawędziowe przemieszczeń w powłoce cylindrycznej:

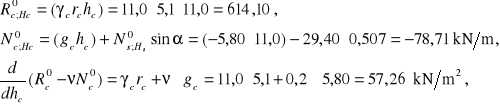
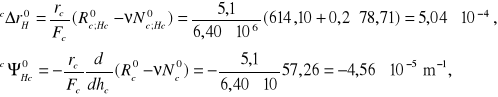
Wektor prawych stron od obciążeń powłoki cylindrycznej:

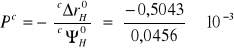
Wektor prawych stron od obciążeń pionowych działających na ławę będzie wektorem zerowym:

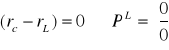
Ostateczny układ równań:

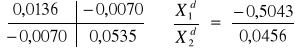
Rozwiązaniem układu są wielkości niewiadomych:

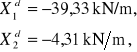
3.4. Siły wewnętrzne w zbiorniku

3.4.1. Powłoka stożkowa

Siły zewnętrzne w stanie błonowym (bezmomentowym).
Obciążenie ciężarem własnym g_s kN/m² i obciążenie powierzchniowe p_s kN/m² rzutu:

,

Siły wewnętrzne

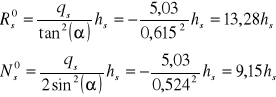
Siły wewnętrzne w stanie zgięciowym.

Wielkości zaburzeń brzegowych (dolnych):

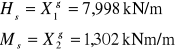
Obliczenie sił wewnętrznych w powłoce stożkowej wykonano za pomocą programu Excel. Wyniki obliczeń przedstawiono w tablicy 3.4.1 oraz na wykresie 3.4.1.

Tablica 3.4.1. Siły wewnętrzne w powłoce stożkowej.

lp.	s	η	Rs^0	Ns^0	Rs,ϕ	Ns,ϕ	Ms,ϕ	Ms,u
0	6,000	8,086	0,0	0,0	0,0	0,0	0,00	0,00
1	5,800	7,817	-1,4	-1,0	-1,4	-1,0	0,00	0,00
2	5,600	7,547	-2,8	-1,9	-2,7	-1,9	0,00	0,00
3	5,400	7,278	-4,2	-2,9	-4,1	-2,9	0,00	0,00
4	5,200	7,008	-5,6	-3,8	-5,5	-3,8	0,00	0,00
5	5,000	6,739	-7,0	-4,8	-6,9	-4,8	0,00	0,00
6	4,800	6,469	-8,4	-5,8	-8,2	-5,7	0,00	0,00
7	4,600	6,199	-9,7	-6,7	-9,6	-6,7	0,00	0,00
8	4,400	5,930	-11,1	-7,7	-11,0	-7,7	0,00	0,00
9	4,200	5,660	-12,5	-8,6	-12,5	-8,6	-0,01	0,00
10	4,000	5,391	-13,9	-9,6	-13,9	-9,6	-0,01	0,00
11	3,800	5,121	-15,3	-10,6	-15,5	-10,5	-0,01	0,00
12	3,600	4,852	-16,7	-11,5	-17,1	-11,5	-0,01	0,00
13	3,400	4,582	-18,1	-12,5	-18,8	-12,5	-0,01	0,00
14	3,200	4,313	-19,5	-13,4	-20,5	-13,5	-0,01	0,00
15	3,000	4,043	-20,9	-14,4	-22,4	-14,5	-0,01	0,00
16	2,800	3,774	-22,3	-15,4	-24,3	-15,5	0,00	0,00
17	2,600	3,504	-23,7	-16,3	-26,1	-16,5	0,02	0,00
18	2,400	3,235	-25,1	-17,3	-27,8	-17,5	0,05	0,01
19	2,200	2,965	-26,4	-18,2	-29,2	-18,6	0,08	0,02
20	2,000	2,695	-27,8	-19,2	-30,1	-19,6	0,12	0,03
21	1,800	2,426	-29,2	-20,1	-30,2	-20,6	0,17	0,04
22	1,600	2,156	-30,6	-21,1	-29,2	-21,6	0,23	0,06
23	1,400	1,887	-32,0	-22,1	-26,8	-22,4	0,27	0,08
24	1,200	1,617	-33,4	-23,0	-22,6	-23,2	0,30	0,09
25	1,000	1,348	-34,8	-24,0	-16,4	-23,7	0,30	0,10
26	0,800	1,078	-36,2	-24,9	-8,3	-24,0	0,23	0,09
27	0,600	0,809	-37,6	-25,9	1,2	-23,9	0,07	0,07
28	0,400	0,539	-39,0	-26,9	11,1	-23,6	-0,21	0,01
29	0,200	0,270	-40,4	-27,8	19,5	-22,9	-0,66	-0,09
30	0,000	0,000	-41,8	-28,8	23,6	-22,0	-1,30	-0,25

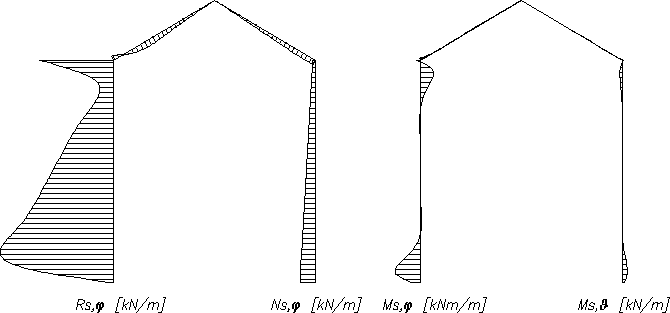
W tablicy sił wewnętrznych dodatnie znaki sił odnoszą się do rozciąganie, ujemne do ściskania. Z kolei dodatnie znaki momentów oznaczają rozciąganie włókien wewnętrznych; ujemne - rozciąganie włókien zewnętrznych.

Wykres 3.4.1 - kombinacja 1 - obciążenie całkowite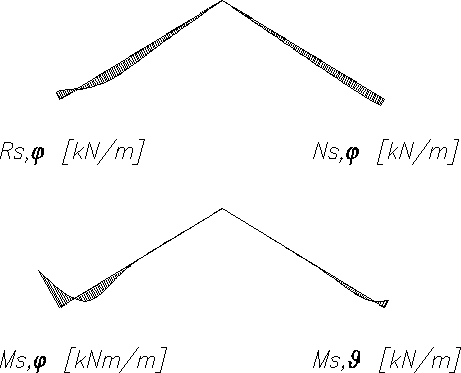

3.4.2. Powłoka cylindryczna

Siły wewnętrzne w stanie błonowym (bezmomentowym).

obciążenia ciężarem własnym g_c kN/m² powierzchni:

obciążenie parciem cieczy γ_c kN/m³

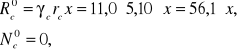
Siły wewnętrzne w stanie zgięciowym.
Wielkości zaburzeń brzegowych (górnych i dolnych):

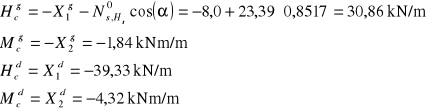
Obliczenie sił wewnętrznych w powłoce cylindrycznej wykonano za pomocą programu Excel. Wyniki obliczeń przedstawiono w tablicy 3.4.2 oraz na wykresie 3.4.2.

Tablica 3.4.2. Siły wewnętrzne w powłoce cylindrycznej.

lp.	x	η	η'	Rc^0	Nc^0	Rc;x	Nc;x	Mc;x	Mc;u
0	0,00	0,000	14,189	0,0	-14,4	374,9	-14,4	-1,84	-0,37
1	0,20	0,258	13,931	11,2	-15,6	297,4	-15,6	2,98	0,60
2	0,40	0,516	13,673	22,4	-16,7	226,3	-16,7	5,55	1,11
3	0,60	0,774	13,415	33,7	-17,9	167,4	-17,9	6,51	1,30
4	0,80	1,032	13,157	44,9	-19,0	123,0	-19,0	6,42	1,28
5	1,00	1,290	12,899	56,1	-20,2	93,0	-20,2	5,70	1,14
6	1,20	1,548	12,641	67,3	-21,4	75,8	-21,4	4,69	0,94
7	1,40	1,806	12,383	78,5	-22,5	69,2	-22,5	3,60	0,72
8	1,60	2,064	12,125	89,8	-23,7	70,7	-23,7	2,58	0,52
9	1,80	2,322	11,867	101,0	-24,8	78,1	-24,8	1,71	0,34
10	2,00	2,580	11,609	112,2	-26,0	89,4	-26,0	1,01	0,20
11	2,20	2,838	11,351	123,4	-27,2	103,0	-27,2	0,49	0,10
12	2,40	3,096	11,093	134,6	-28,3	117,8	-28,3	0,13	0,03
13	2,60	3,354	10,835	145,9	-29,5	132,8	-29,5	-0,10	-0,02
14	2,80	3,612	10,577	157,1	-30,6	147,7	-30,6	-0,23	-0,05
15	3,00	3,870	10,319	168,3	-31,8	162,0	-31,8	-0,28	-0,06
16	3,20	4,128	10,061	179,5	-33,0	175,8	-33,0	-0,28	-0,06
17	3,40	4,386	9,803	190,7	-34,1	188,9	-34,1	-0,25	-0,05
18	3,60	4,644	9,545	202,0	-35,3	201,5	-35,3	-0,21	-0,04
19	3,80	4,902	9,287	213,2	-36,4	213,5	-36,4	-0,16	-0,03
20	4,00	5,160	9,029	224,4	-37,6	225,2	-37,6	-0,12	-0,02
21	4,20	5,417	8,771	235,6	-38,8	236,7	-38,8	-0,08	-0,02
22	4,40	5,675	8,513	246,8	-39,9	247,9	-39,9	-0,05	-0,01
23	4,60	5,933	8,255	258,1	-41,1	259,0	-41,1	-0,03	-0,01
24	4,80	6,191	7,997	269,3	-42,2	270,1	-42,2	-0,02	0,00
25	5,00	6,449	7,739	280,5	-43,4	281,1	-43,4	-0,01	0,00
26	5,20	6,707	7,481	291,7	-44,6	292,1	-44,6	-0,01	0,00
27	5,40	6,965	7,223	302,9	-45,7	303,0	-45,7	-0,01	0,00
28	5,60	7,223	6,965	314,2	-46,9	314,0	-46,9	-0,01	0,00
29	5,80	7,481	6,707	325,4	-48,0	324,9	-48,0	-0,01	0,00
30	6,00	7,739	6,449	336,6	-49,2	335,7	-49,2	-0,01	0,00
31	6,20	7,997	6,191	347,8	-50,4	346,6	-50,4	0,01	0,00
32	6,40	8,255	5,933	359,0	-51,5	357,5	-51,5	0,03	0,01
33	6,60	8,513	5,675	370,3	-52,7	368,4	-52,7	0,06	0,01
34	6,80	8,771	5,417	381,5	-53,8	379,5	-53,8	0,11	0,02
35	7,00	9,029	5,160	392,7	-55,0	390,8	-55,0	0,17	0,03
36	7,20	9,287	4,902	403,9	-56,2	402,5	-56,2	0,25	0,05
37	7,40	9,545	4,644	415,1	-57,3	414,8	-57,3	0,34	0,07
38	7,60	9,803	4,386	426,4	-58,5	427,8	-58,5	0,43	0,09
39	7,80	10,061	4,128	437,6	-59,6	441,8	-59,6	0,51	0,10
40	8,00	10,319	3,870	448,8	-60,8	457,0	-60,8	0,55	0,11
41	8,20	10,577	3,612	460,0	-62,0	473,3	-62,0	0,53	0,11
42	8,40	10,835	3,354	471,2	-63,1	490,9	-63,1	0,40	0,08
43	8,60	11,093	3,096	482,5	-64,3	509,3	-64,3	0,12	0,02
44	8,80	11,351	2,838	493,7	-65,4	528,0	-65,4	-0,37	-0,07
45	9,00	11,609	2,580	504,9	-66,6	545,7	-66,6	-1,13	-0,23
46	9,20	11,867	2,322	516,1	-67,8	560,9	-67,8	-2,21	-0,44
47	9,40	12,125	2,064	527,3	-68,9	571,0	-68,9	-3,63	-0,73
48	9,60	12,383	1,806	538,6	-70,1	572,8	-70,1	-5,40	-1,08
49	9,80	12,641	1,548	549,8	-71,2	562,4	-71,2	-7,42	-1,48
50	10,00	12,899	1,290	561,0	-72,4	535,3	-72,4	-9,53	-1,91
51	10,20	13,157	1,032	572,2	-73,6	486,6	-73,6	-11,43	-2,29
52	10,40	13,415	0,774	583,4	-74,7	412,2	-74,7	-12,64	-2,53
53	10,60	13,673	0,516	594,7	-75,9	309,6	-75,9	-12,48	-2,50
54	10,80	13,931	0,258	605,9	-77,0	179,2	-77,0	-10,08	-2,02
55	11,00	14,189	0,000	617,1	-78,2	26,6	-78,2	-4,31	-0,86

Wykres 3.4.2 - kombinacja 1 - obciążenie całkowite

4. Wymiarowanie konstrukcji

4.1. Kopuła stożkowa pokrycia

4.1.1. Zbrojenie południkowe powłoki stożkowej

zbrojenie południkowe powłoki stożkowej w połączeniu powłok (mimośrodowe ściskanie):

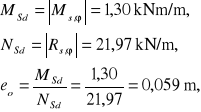
duży mimośród:

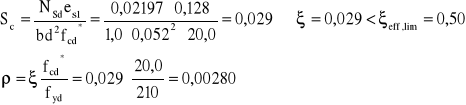
Przyjęto zbrojenie południkowe górne i dolne stożka φ6 co 200 mm o przekroju A_s=1,42cm².

4.1.2. Zbrojenie równoleżnikowe powłoki stożkowej

Zbrojenie w strefie rozciągań brzegowych (mimośrodowe z rozciąganie):

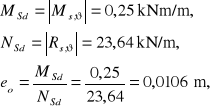
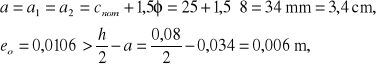
duży mimośród.

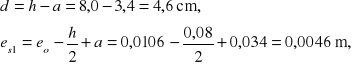
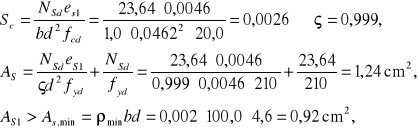
Przyjęto w całym stożku zbrojenie konstrukcyjne #6/200 mm o A_s=1,42 cm²

Zarysowanie przekroju podporowego:

Obwodowy przekrój podporowy powłoki stożkowej nie jest zarysowany.

4.2. Powłoka cylindryczna

4.2.1. Zbrojenie równoleżnikowe powłoki cylindrycznej

Zbrojenie minimalne ściany zbiornika (po każdej stronie ściany):

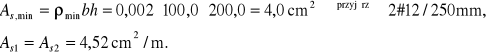
Osiowa siła rysująca ścianę zbiornika:

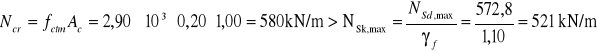
Na całej wysokości ściany siły rzeczywiste są mniejsze od siły rysującej.

STREFA I (górna- przy połączeniu z powłoką stożkową; x=0,0÷2,8 m):

Zbrojenie ze względu na nośność:

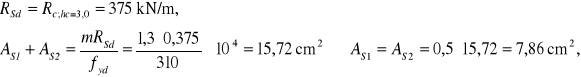
Przyjęto zbrojenie obustronne (minimalne) #12#16/200 mm o przekroju
.

STREFA II (x=2,8÷5,6 m):

Zbrojenie ze względu na nośność:

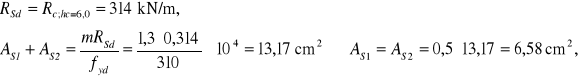
Przyjęto zbrojenie obustronne 2#12/150 mm o przekroju

STREFA III (dolna- przy połączeniu z ławą fundamentową; x=5,6÷8,4 m):

Zbrojenie ze względu na nośność:

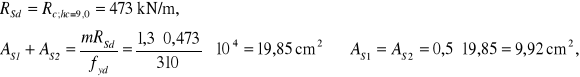
Przyjęto zbrojenie obustronne (minimalne) 2#16/200 mm o przekroju

STREFA IV (dolna- przy połączeniu z ławą fundamentową; x=8,4÷11,0 m):

Zbrojenie ze względu na nośność:

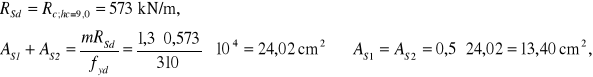
Przyjęto zbrojenie obustronne (minimalne) 2/#16/150 mm o przekroju

4.2.2. Zbrojenie pionowe powłoki cylindrycznej

Miarodajna do obliczeń zbrojenia pionowego jest strefa połączenia powłoki cylindrycznej z ławą fundamentową. Do wymiarowania przyjęto maksymalna wielkość mimośrodu w strefie i największą wielkość siły pionowej (węzłową).

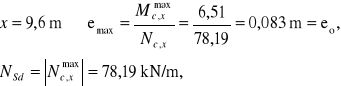
Zbrojenie ze względu na nośność (mimośrodowe ściskanie):

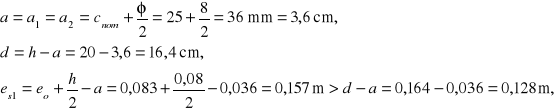
Duży mimośród

Przyjęto zbrojenie standardowe 4#12 obustronnie, po wewnętrznej stronie prętów obwodowych.

Zarysowanie przekroju:

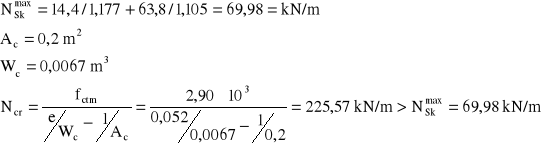
Przekroje równoleżnikowe ściany nie są zarysowane.

4.3. wieniec łączący powłokę stożkową z powłoką walcową

Siły wewnętrzne działające na wieniec:

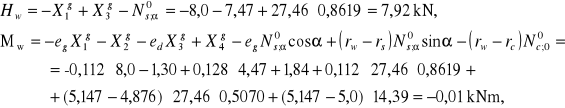
Siła rozciągająca wieniec i moment zginający:

Zbrojenie wieńca obliczono jak dla osiowo rozciąganego elementu zbiornika (
)

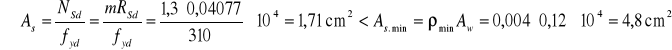
Przyjęto zbrojenie 5#12 o
rozmieszczone na obwodzie rdzenia przekroju wieńca w odległościach nie większych niż 25 cm.

Zarysowanie przekroju (współczynnik obciążenia
jak dla obciążenia stożka)

Przekrój wieńca nie jest zarysowany

4.4. Ława fundamentowa

Kąt obrotu ławy i odpór podłoża pod ławą (od obrotu ławy):

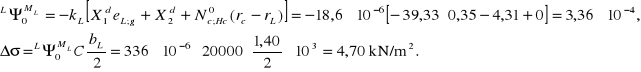
Siły zewnętrzne działające na ławę:

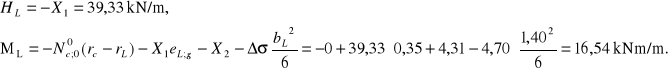
Siła rozciągająca wieniec i moment zginający:

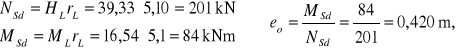
Przekrój mimośrodowo rozciągany- silniej rozciągana jest strefa górna ławy.

Duży mimośród.

Przyjęto zbrojenie górą 9#16/~160 mm o
; dołem (ze względu m= na minimalny stopień zbrojenia) przyjęto również 9#16/~160 o
. Dodatkowo przy powierzchniach bocznych ławy przyjęto po 2#16 (pomiędzy prętami w narożach ławy).

Zarysowanie przekroju:

Przekrój ławy nie jest zarysowany.

Zbiornik na wodę

____________________________________________________________________________________________

- 16 -

____________________________________________________________________________________

Zbiornik na wodę

____________________________________________________________________________________________

---