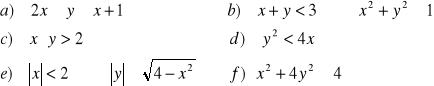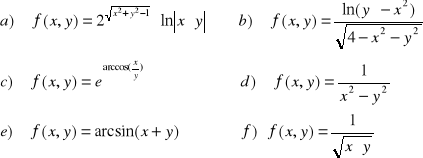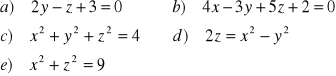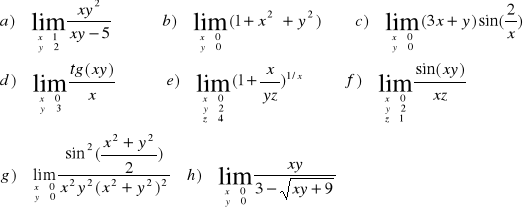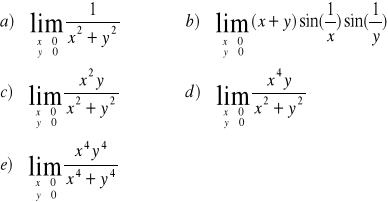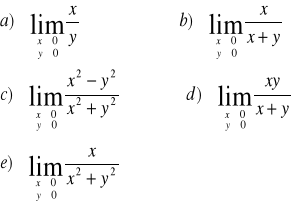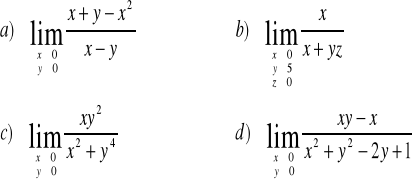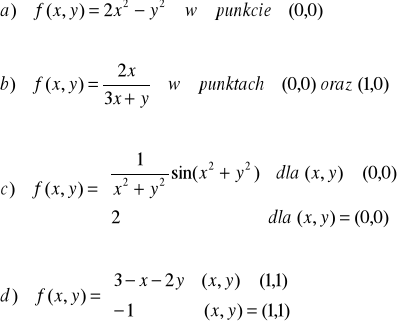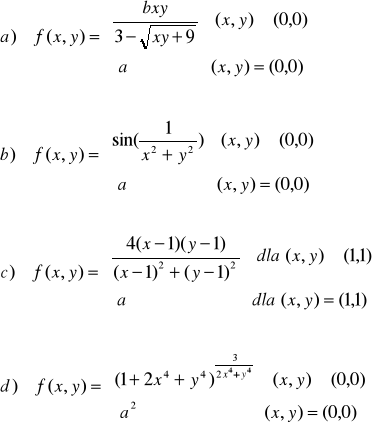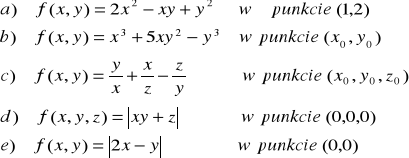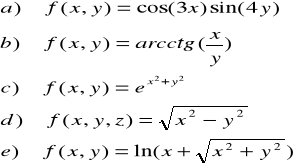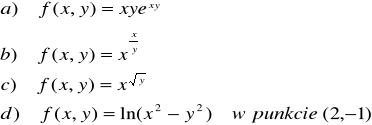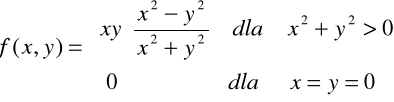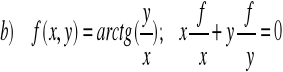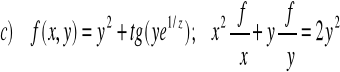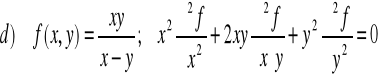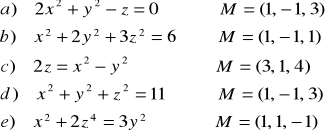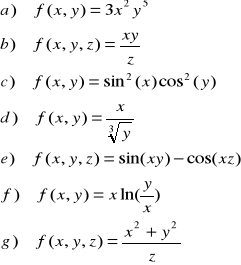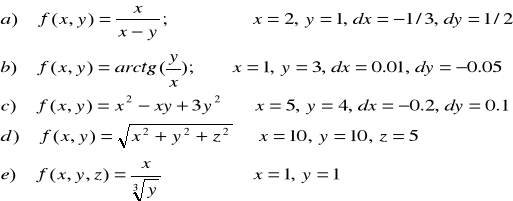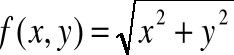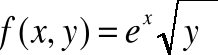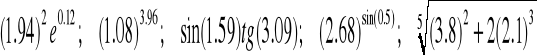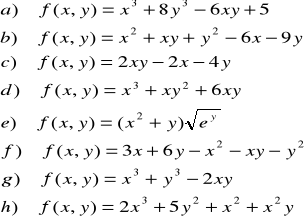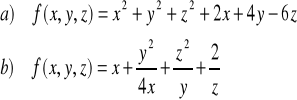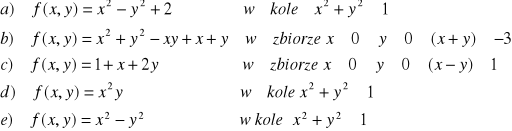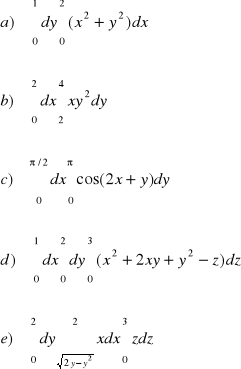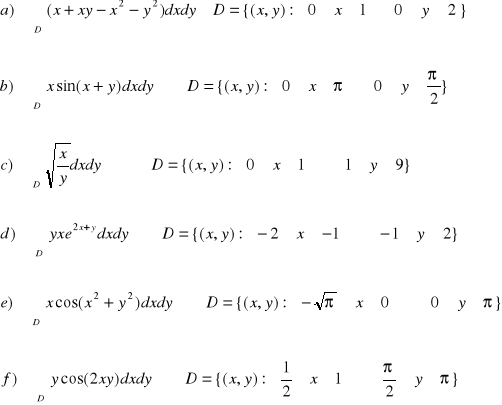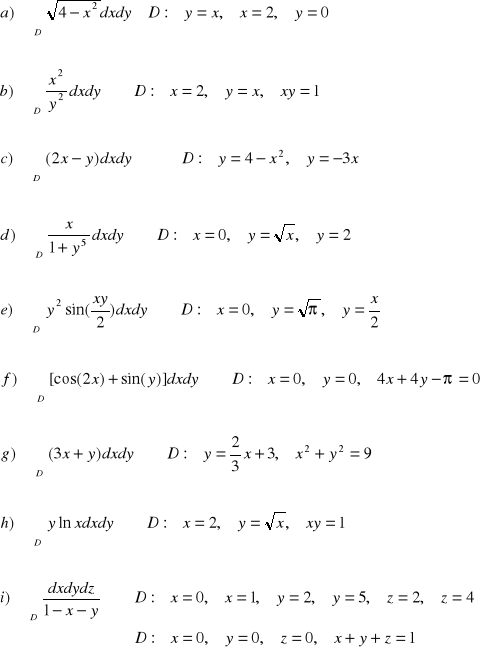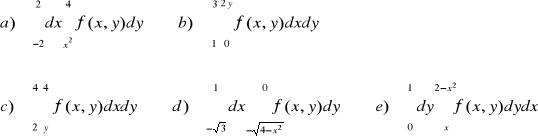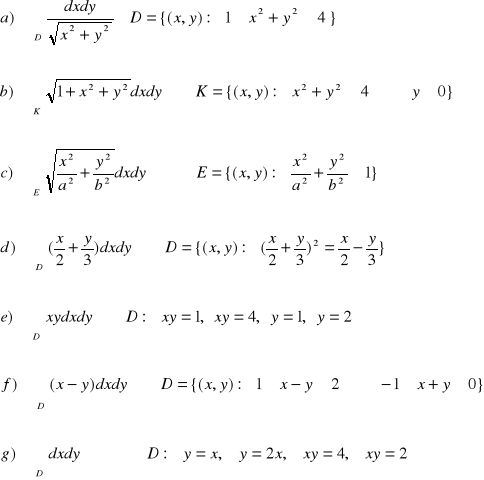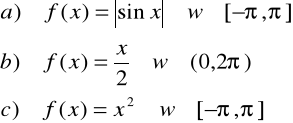ZADANIA DOMOWE Z ANALIZY MATEMATYCZNEJ AM2

ZADANIE-1: Naszkicować zbiór wszystkich punktów płaszczyzny, których współrzędne spełniają warunek:

ZADANIE-2: Wyznaczyć analitycznie i naszkicować na płaszczyźnie dziedzinę naturalną funkcji:

ZADANIE-3: Naszkicować w przestrzeni 3-wymiarowej powierzchnie opisane równaniami:

ZADANIE-4: Wyznaczyć granice funkcji 2 zmiennych f(x,y) lub 3 zmiennych f(x,y,z):

ZADANIE-5: Wyznaczyć granice funkcji 2 zmiennych f(x,y) w punkcie (0,0):

ZADANIE-6: Wykazać że nie istnieją nastepujące granice:

ZADANIE-7: Wykazać że nie istnieją nastepujące granice:

ZADANIE-8: Zbadać ciągłość funkcji:

ZADANIE-9: Czy dane funkcje mogą być określone w punkcie (0,0) tak aby były ciągłe w tym punkcie?

ZADANIE-10: Dla jakich wartości parametrów a i b funkcja jest ciągła w R² ?:

ZADANIE-11: Korzystając z definicji wyznaczyć wszystkie pochodne cząstkowe I rzędu funkcji :

ZADANIE-12: Wyznaczyć wszystkie pochodne cząstkowe do rzędu 3-ciego włącznie :

ZADANIE-13: Wyznaczyć wszystkie pochodne cząstkowe rzędu 2 :

ZADANIE-13a: Dana jest funkcja określona wzorem: Pokazać że:

ZADANIE-14: Sprawdzić czy funkcja f(x,y) jest rozwiązaniem równania :

ZADANIE-15: Wyznaczyć równanie płaszczyzny stycznej i równanie prostej normalnej do powierzchni o podanym równaniu w podanym punkcie M:

ZADANIE-16: Wyznaczyć różniczki zupełne I-rzędu dla funkcji:

ZADANIE-17: Wyznaczyć wartość różniczki zupełnej I-rzędu dla funkcji:

ZADANIE-18: Oblicz przybliżoną wartość różniczki zupełnej funkcji przy przesunięciu punktu (x, y) z położenia M = (3, 4) do położenia M=(4, 5) Oblicz przybliżoną wartość :

ZADANIE-18a: Oblicz przybliżoną wartość funkcji w punkcie P(0.05, 0.98).

ZADANIE-19: Oblicz przybliżone wartości:

ZADANIE-20: Znaleźć ekstrema funkcji 2 zmiennych :

ZADANIE-21: Znaleźć ekstrema funkcji 3 zmiennych :

ZADANIE-22: Znaleźć najmniejszą i największą wartość funkcji w zbiorze domkniętym :

ZADANIE-23: Na płaszczyżnie 2x + y + 2z = 16 znaleźć punkt najbliższy poczatkowi układu współrzędnych .

ZADANIE-24: Na paraboli y² = 6x znaleźć punkty których odległość od punktu (3, 12) jest największa (najmniejsza)

ZADANIE-25: Z kawałka drutu o długości d zrobić prostopadłościan o największej objętości.

ZADANIE-26: Obliczyć całki iterowane :

ZADANIE-27: Obliczyć całki podwójne. Naszkicować obszar D.

ZADANIE-28: Obliczyć całki podwójne.Naszkicować obszar D ograniczony podanymi krzywymi.

ZADANIE-29: Zmienić kolejność całkowania w całkach iterowanych :

ZADANIE-30: Dokonując zamiany zmiennych obliczyć całki :

ZADANIE-31: Obliczyć pole obszaru ograniczonego krzywymi : a) x = 2, y = x, y = 1/x b) x + y = 1, x + 3y = 1, x = y, x = 2y c) y = lnx, x = 2, y = 0 d) y = 2x - x², y = x² e) ρ = cosφ, ρ = 2cosφ

ZADANIE-32: Obliczyć objętość bryły ograniczonej powierzchniami: a) z = 4 - x - y, z = 0, y = x², y = 1 b) x² + y² = 1, z = 0, z = y, x ≥ 0 c) x = 0, y = x, y = 2, z = y² - x² d) x² + y² = 4, x + y + z = 4, z = 0 y = x², z = x² + y², y = 1, z = 0 f) z = 1 + x + y, x = 0, y = 0 z = 0, x + y = 1

ZADANIE-33: Obliczyć pole powierzchni wyciętej przez prostopadłościan o podstawie leżącej w płaszczyźnie Oxy i wierzchołkach (0, 0), (1, 0), (0, 1), (1, 1)

ZADANIE-34: Wyznaczyć pole powierzchni półsfery wycietej przez wycinek walca x²+y²≤1 leżący w I ćwiartce układu.

ZADANIE-35: Obliczyć pole powierzchni leżącej nad trójkątem o wierzchołkach (0, 0), (2, 1), (2, 2)

ZADANIE-36: Obliczyć pole paraboloidy 2z = x² + y² zawartej w walcu x² + y² ≤ 1

ZADANIE-37: Obliczyć pole powierzchni z = 2xy ograniczonej płaszczyznami x + y = 1, x = 0, y = 0

ZADANIE-38:Obliczyć powierzchnię części sfery x² + y ²+ z² = 4 wyciętej przez powierzchnię x² + y² = 2y

ZADANIE-39: Rozwinąć w szereg Fouriera funkcje:

10